Умножение и деление степеней с разными основаниями и показателями: Свойства степеней, действия со степенями

что при этом происходит, формулы, примеры с разными основаниями

Что представляют собой степенные выражения

Определение 1

Степенью n для числа а является произведение множителей, которые по величине равны а, взятое n раз.

an,

здесь а представляет собой основание степени, n определяет ее показатель.

Таким образом, можно составить формулу:

an=a×a×a…×a

Запись можно прочитать, как «a в степени n».

Определение 2

Степенное выражение представляет собой такое выражение, в состав которого входит степень.

Перед тем, как рассмотреть действия со степенными выражениями, полезно вспомнить свойства степени:

1. Произведение степеней. Если степени, которые требуется умножить, имеют одинаковые основания, то основание оставляют неизменным, а показатели степеней суммируют. То есть, an×am=am+n, где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел.
2. Частное степеней. При делении степеней, имеющих одинаковые основания, следует оставить основание прежним, а показатель степени делимого уменьшить на показатель степени делителя. Например, aman=am-n, где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел, m>n.
3. Возведение степени в квадрат. При возведении степени в степень основание степени сохраняют прежним, а показатели перемножают. К примеру, (an)m=an×m, где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел.
4. Степень произведения. Для того чтобы возвести в степень произведение, требуется каждый из множителей возвести в эту степень. Результаты, которые получились в итоге, необходимо перемножить. То есть: (a×b)n=an×bn, где а и b являются основаниями степени, n — это показатель степени в виде какого-либо натурального числа.
5. Степень частного. Для возведения в степень частного нужно возвести в данную степень по отдельности делимое и делитель. Затем первый получившийся результат следует разделить на второй. К примеру, (a÷b)n=an÷bn, где а и b являются основаниями степени, не равными нулю, n — это показатель степени в виде какого-либо натурального числа.

Правила умножения, что происходит

Правило 1

Если степени имеют одинаковые показатели, то в процессе их перемножения следует умножить между собой основания, а показатель записать без изменений:

an× bn=(a÷b)n,

где а и b являются основаниями степени, n — это показатель степени в виде какого-либо натурального числа.

В качестве примера решим несколько простых уравнений:

a5× b5=(a×a×a×a×a)×(b×b×b×b×b)=(a×b)n=(ab)×(ab)×(ab)×(ab)×(ab)=(ab)5

35× 45=(3×4)5=125=248832

16a2=42×a2=(4a)2

Правило 2

Когда требуется найти произведение степеней, которые обладают одинаковыми основаниями, следует сложить показатели степеней:

an×am=am+n, где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел.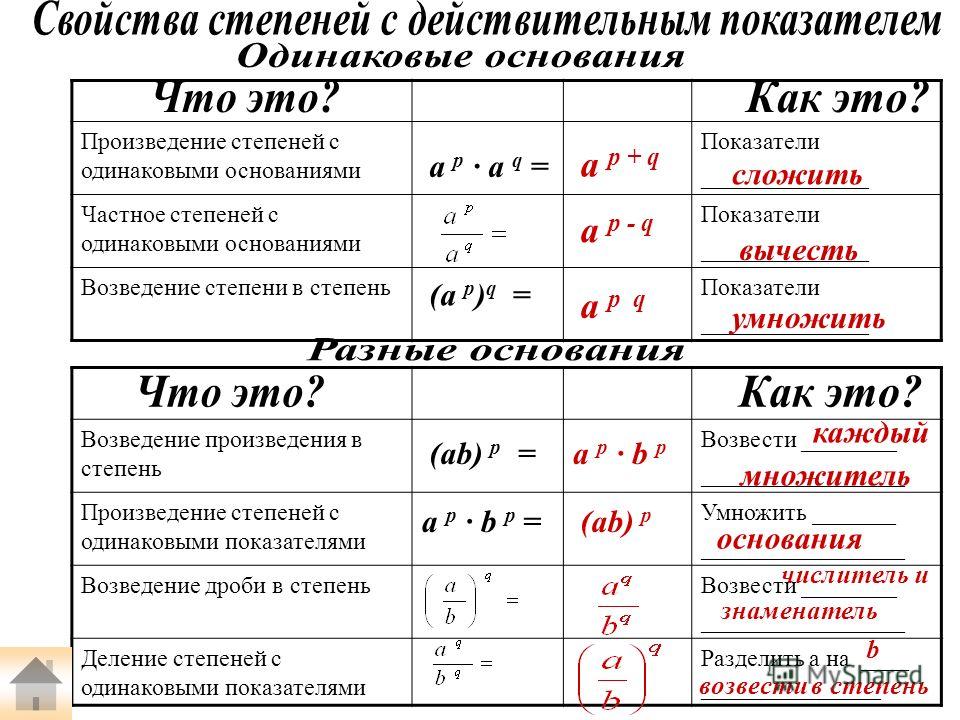

В качестве примеров рассмотрим несколько вычислений:

35× 32=35+3=38=6561

28× 81=28·23=211=2048

При умножении чисел, которые имеют разные степени, но схожи по основаниям, необходимо руководствоваться правилом, рассмотренным в предыдущем примере. То есть:

an×bn=(a×b)n,

где а и b являются основаниями степени, n — это показатель степени в виде какого-либо натурального числа.

Бывают ситуации, когда числа отличаются по степеням и по основаниям, а также какое-то из оснований невозможно преобразовать в число с аналогичной степенью, как у второго числа. В этом случае нужно возвести в степень каждое число, а на втором шаге выполнить умножение.

К примеру:

33×52=27×25=675

Правила деления

Правило 3

Когда требуется выполнить деление степеней, которые имеют разные основания, но схожи по показателям, нужно найти разность показателей и оставить основание без изменений:

aman=am-n,

где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел, m>n.

В качестве примеров рассмотрим несколько выражений:

113×4411×42=113-1×44-2=112×42=(11×4)2=1936

2a42a3=2a4-3=2a

Правило 4

Деление степеней, которые имеют одинаковые показатели, подразумевает возведение результата частного данных чисел в степень:

an÷bn=(a÷b)n,

где а и b являются основаниями степени в виде любых рациональных чисел, не равных нулю, n — это показатель степени в виде какого-либо натурального числа.

Например:

512÷312=(5÷3)12=(123)12

Предположим, что требуется выполнить деление чисел со степенями. При этом степени не одинаковые, а основания идентичные. Тогда следует руководствоваться правилом, рассмотренным в предыдущем примере:

aman=am-n

В том случае, когда отличаются не только степени, но и основания, необходимо возвести в степень каждое из чисел, а затем выполнить умножение. Например:

3352=2725=1,08

Примеры решения заданий для 7 класса

Задача 1

Вычислить:

23×22

Решение

Воспользуемся правилом умножения степеней, имеющих одинаковое основание:

23×22=25=32

Ответ: 32

Задача 2

Решить выражение:

27

Решение

Воспользуемся правилом умножения степеней, имеющих одинаковое основание, чтобы избавиться от необходимости возводить число в большую степень:

27=23×24=8×16=128

Ответ: 128

Задача 3

Вычислить:

32×22

Решение

Воспользуемся правилом умножения степеней, имеющих разные основания, но одинаковые показатели:

32×22=(3×2)2=62=36

Ответ: 36

Задача 4

Вычислить:

3332

Решение

Здесь можно применить правило деления степеней с одинаковым основанием и разными показателями:

3332=33-2=31=3

Ответ: 3

Задача 5

Решить пример:

2222

Решение

Здесь можно применить правило деления степеней с одинаковым основанием и разными показателями:

2222=22-2=30=1

Ответ: 1

Задача 6

Решить пример:

4323

Решение

Воспользуемся свойством деления степеней, когда основания отличаются, а показатели совпадают:

4323=(42)3=23=8

Ответ: 8 

Блок 2.

4 — Закон экспонент I

блок 2.4 — Закон экспонент:
Произведение степеней (Умножение)
Частное степеней (Деление)

Что нам нужно знать и экспоненты (определения)
Powers с базой 10
ЭКСПОНЕРЫ 0 и 1
Повторное умножение

Примечания класса

9_UNIT_2.4.PDF

9_UNIT_4.0033

Загрузить файл

---

подробнее

Помните, что произведение — это произведение. Первый закон показателей говорит, что для умножения степеней с одинаковыми основаниями необходимо сложить показатели степени:

Второй закон показателей, частное степеней, позволяет нам делить степени равных оснований. Помните, что «частное» означает деление.

Этот закон можно резюмировать следующим образом:

При делении степеней с одинаковым основанием необходимо вычесть показатели степени. Это противоположность умножению, и если подумать, то становится понятно: умножать означает увеличивать число (сложение), а делить означает разбивать (вычитание).

Вот несколько примеров:

Взгляните на следующий пример, чтобы понять, почему при делении степени вычитаются. Помните, что число, которое умножается в числителе дроби, «отменяет» то же число, которое также должно умножаться, в знаменателе той же дроби:

Подводя итог:

видео, которые могут вам помочь Умножение со степенями

Умножение и деление с показателями

STUDY.com

дополнительные рабочие листы

document_6_.pdf Скачать файл

document_7_. pdf Скачать файл

document_8_.pdf Скачать файл

2.4exponentlaws1.pdf Скачать файл

exponentsandmultiplication.pdf Скачать файл

power_of_products_and_quotients.pdf Скачать файл

оценка-выражение-easy1.pdf Скачать файл

properties_of_exponents.pdf Скачать файл

Обзор — Рабочая книга

Рабочая книга _ -_ UNIT_2. 4.PDF

Загрузить файл

---

Можно ли разделить эксплуататоры с разными базовыми?? – Gzipwtf.com

Лайфхаки

Диана Монтгомери 2020-12-29

Можно ли делить степени с разными основаниями?

Деление экспоненциальных выражений с разными основаниями разрешено, но создает уникальные проблемы, когда дело доходит до упрощения, которое можно сделать лишь иногда.

Можно ли умножать основания с разными показателями степени?

Можно умножать степени с разными основаниями, но есть одна важная загвоздка: степени должны быть одинаковыми. Во-первых, умножьте основания вместе. Затем добавьте показатель степени. Вместо того, чтобы складывать два показателя вместе, оставьте их одинаковыми.

Как складывать показатели степени с разными основаниями?

Помните, что для сложения или вычитания чисел с показателями степени вы должны сначала убедиться, что основание и показатель степени двух членов, которые вы пытаетесь сложить или вычесть, совпадают. Если они одинаковы, то все, что вам нужно сделать, это сложить их коэффициенты и сохранить одинаковые основание и показатель степени.

Как сложить степени с разными степенями?

Чтобы добавить показатели степени, и показатели степени, и переменные должны быть одинаковыми. Вы добавляете коэффициенты переменных, оставляя показатели без изменений. Добавляются только термины с одинаковыми переменными и степенями. Это правило также согласуется с умножением и делением показателей.

Как умножать показатели степени с разными основаниями и разными показателями степени?

Умножение показателей степени с разными основаниями Сначала перемножьте основания. Затем добавьте показатель степени. Вместо того, чтобы складывать два показателя вместе, оставьте их одинаковыми. Это происходит из-за правила четвертой степени: распределять мощность по каждому основанию при возведении нескольких переменных в степень.

При умножении или делении различных оснований с одним и тем же показателем степени объединяйте основания и сохраняйте показатель степени одинаковым.

No related posts.