Формула периметра и площади квадрата и прямоугольника: , , . — 136 -7708 . 8

Периметр и площадь прямоугольника. Периметр и площадь прямоугольника По какой формуле можно найти периметр

Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.

Основные понятия

Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника, например, поверхность стола, тетрадь и прочее.

Рассмотрим пример: по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.

Рис. 1. Земельный участок формой прямоугольника.

Земельный участок имеет стороны длиной 2 м., 4 м., 2 м., 4 м. потому чтобы общую узнать длину забора необходимо сложить длины всех сторон:

2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.

Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют букву P.

Для вычисления периметра прямоугольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.

Периметр прямоугольника измеряется в мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одинаковую систему измерения.

Периметр прямоугольника измеряется в различных единицах: мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одну систему измерения.

Формула периметра фигуры

Если принять к вниманию тот факт, что противоположные стороны прямоугольника равны, то можно вывести формула периметра прямоугольника:

$P = (a+b) * 2$, где а, b – стороны фигуры.

Рис. 2. Прямоугольник, с обозначенными противоположными сторонами.

Существует и другой способ найти периметр. Если в задание дано лишь одну сторону и площадь фигуры, можно использовать выразить другую сторону через площадь.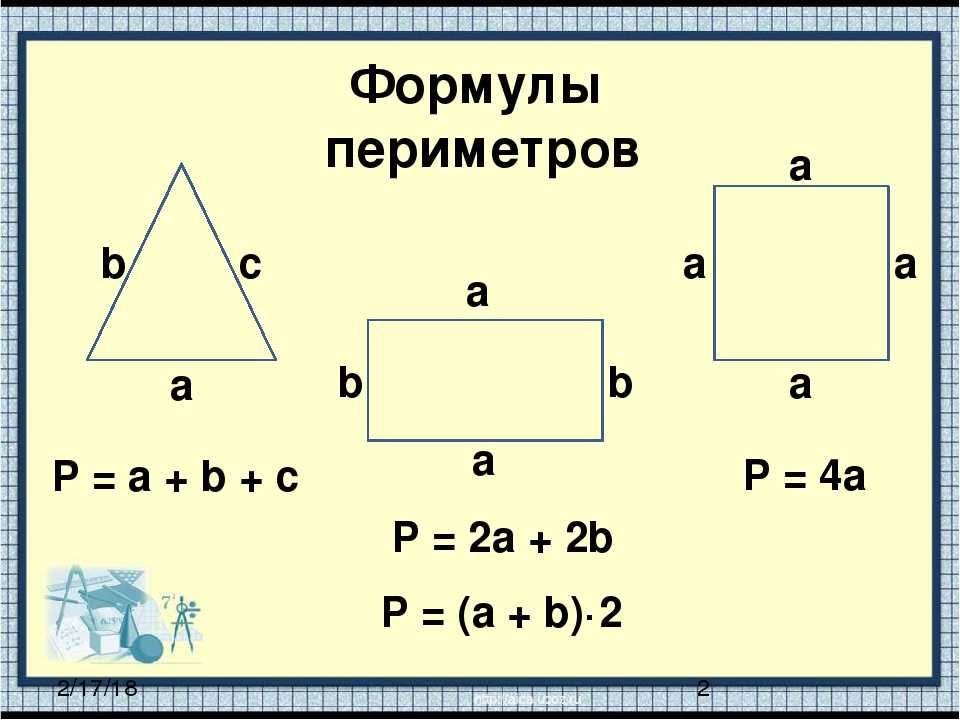 Тогда формула будет выглядеть следующим образом:

$P = {{2S + 2a2}\over{a}}$, где S – площадь прямоугольника.

Рис. 3. Прямоугольник с сторонами a, b .

Задание : Вычислить периметр прямоугольника, если его стороны равны 4 см. и 6 см.

Решение:

Используем формулу $P = (a+b)*2$

$P = (4+6)*2=20 см$

Таким образом, периметр фигуры $P = 20 см$.

Так как периметр – это сумма все сторон фигуры, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.

Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.

Что мы узнали?

Мы узнали, как найти периметр прямоугольника. А также ознакомились с формулой его вычисления. С этой темой можно столкнуться не только при решении математических задач, но и в реальной жизни.

Тест по теме

Оценка статьи

Средняя оценка: 4.5 . Всего получено оценок: 363.

На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.

На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.

Рассмотрим следующую геометрическую фигуру (рис. 1):

Рис. 1. Прямоугольник

Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.

Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.

Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.

Рассмотрим следующую задачу:

Задача 1 (рис. 2)

Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?

Рис. 2. Иллюстрация к задаче 1

Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.

Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.

Ответ: 30 метров.

Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром .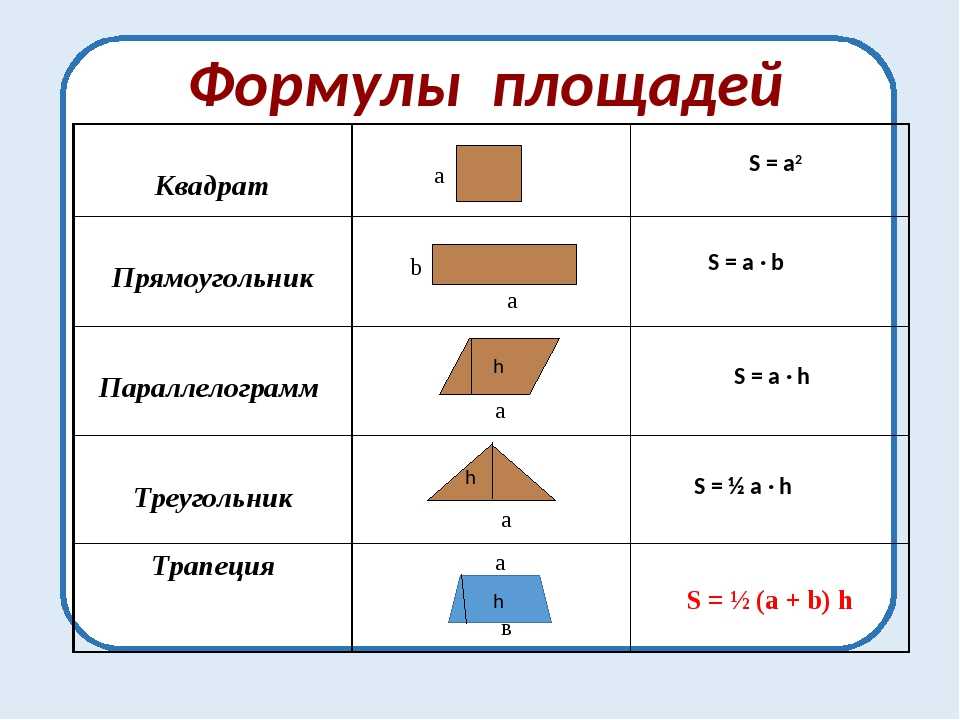

Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.

Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).

Периметр любой фигуры измеряется в линейных единицах.

На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.

Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.

Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).

Список литературы

1. Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
2. Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
3. Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.

1. Festival.1september.ru ().
2. Nsportal.ru ().
3. Math-prosto.ru ().

Домашнее задание

1. Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
2. Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
3. Найти периметр прямоугольника, если его полупериметр — 21 дм.

Ниже в статье вы узнаете что такое и как найти периметр прямоугольника если известны его стороны. А также как найти стороны прямоугольника, если известен его периметр. И ещё одна интересная строительная прикладная задача.

Немного теории:

Периметр — это длина геометрической фигуры по её внешней границе.

Периметр прямоугольника — это сумма длин его сторон.

Формулы для вычисления периметра прямоугольника: P = 2*(a+b) или P = a + a + b + b.

Резюмируем! Для того чтобы вычислить периметр прямоугольника необходимо сложить все его стороны.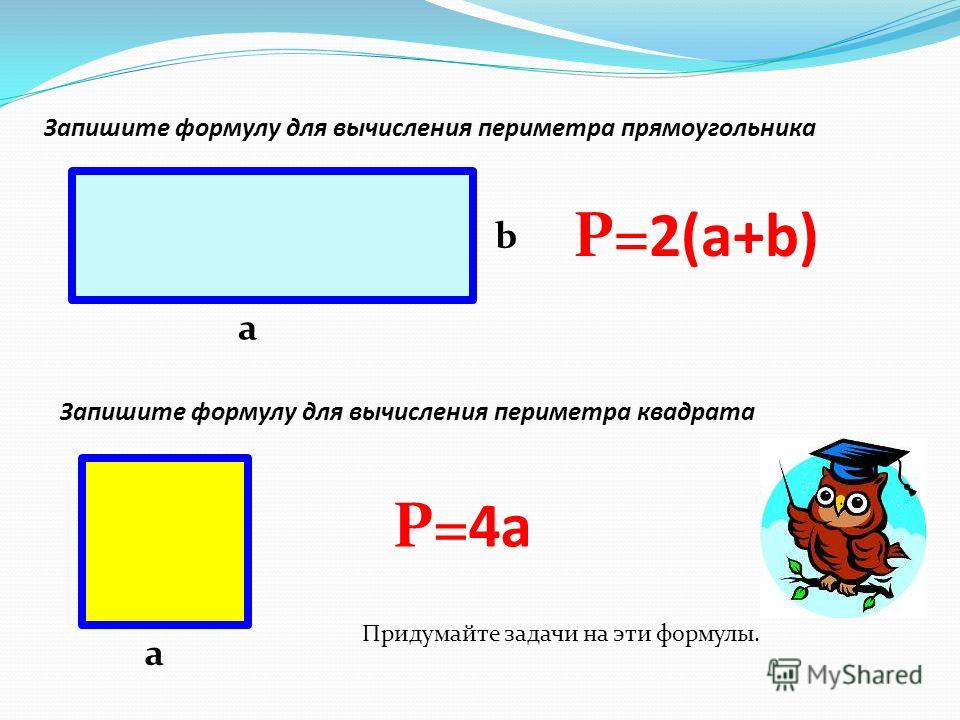

Типовые математические и практические задачи:

Задача №1:

Исходные данные: Определить периметр прямоугольника с длинами сторон 5 см и 10 см.

Решение:

Согласно формуле периметр прямоугольника равен = 2 * (5 + 10) = 30 см.

Ответ: 30 см.

Задача №2:

Исходные данные: Определить стороны прямоугольника выраженные целыми числами, если периметр прямоугольника равен 10.

Решение:

По формуле определяем сумму длин сторон (a + b) = P / 2 = 10 / 2 = 5
Целыми значениями сторон могут быть только значения 1 + 4 = 5 и 2 + 3 = 5

Ответ: Длины сторон могут быть только 2 и 3 или 1 и 4.

Задача №3 (практическая):

Исходные данные: Определить число плинтусов в достаточном количестве для ремонта пола в комнате длиной 5 метров и шириной 3 метра, если длина одного плинтуса равна 3 метра.

Решение:

Периметр комнаты = 2 * (5 + 3) = 16 метров
Количество плинтусов = 16 / 3 = 5,33 штук
Обычно в строительных магазинах плинтусы продаются не погонными метрами, а поштучно. Поэтому принимаем следующее целое число. Это шесть.

Ответ: Количество плинтусов 6 штук.

В заключение:

Решение задачи вычисления периметра является достаточно простой математической задачей, но имеющей очень важное практическое значение например в строительстве или генеральном планировании территории.

На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника. С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина.

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые.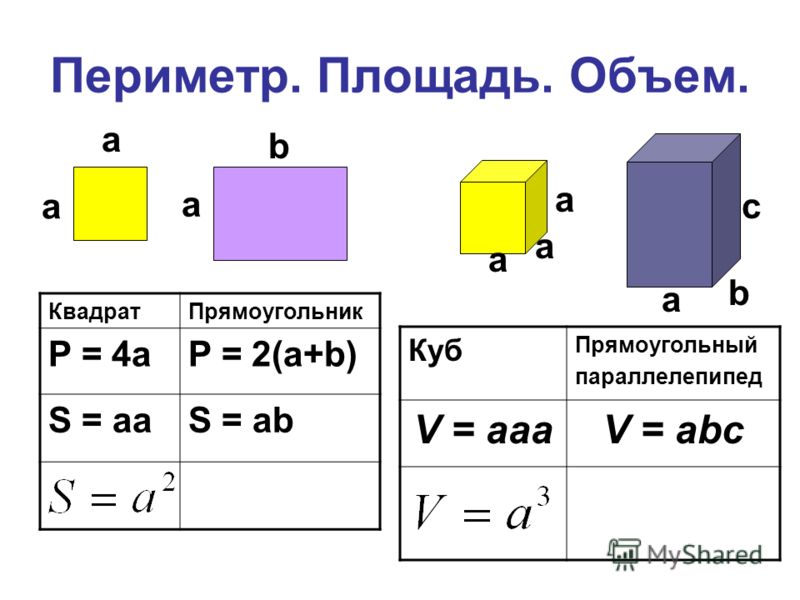 Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры.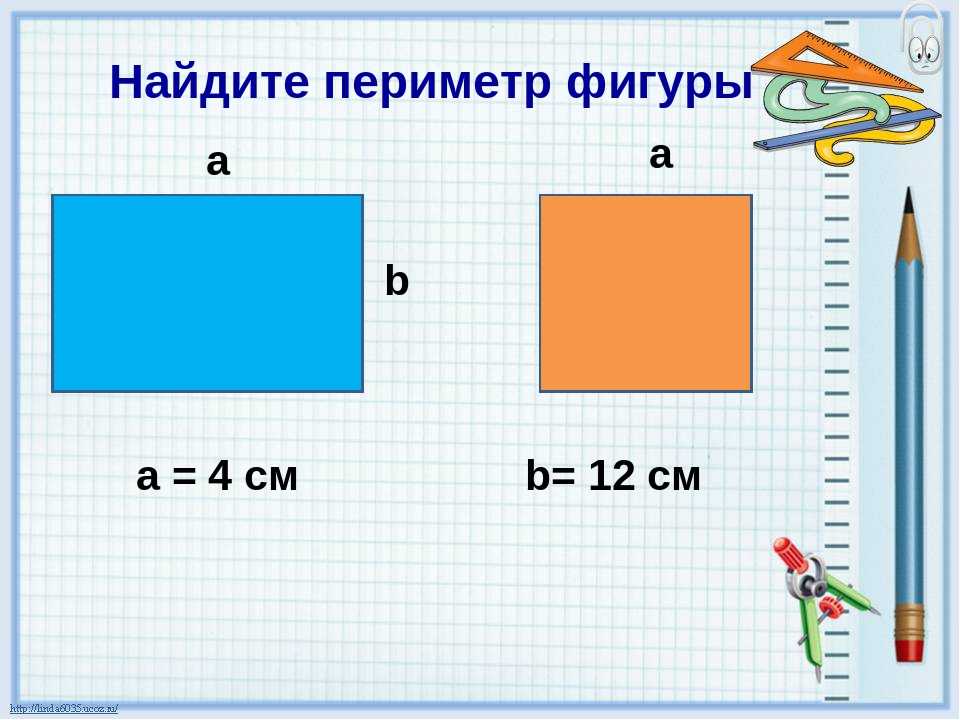 Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Периметр — это сумма длин всех сторон многоугольника.

• Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
• Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

• Прямоугольник – это четырехугольник.
• Все параллельные стороны равны
• Все углы = 90º.
• Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

• 1 способ. Складываем все стороны. P = a + а + b + b
• 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.

• Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
• Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

• : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

1. Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
   • Прямоугольник — это четырехугольник со всеми прямыми углами.
   • Квадрат — прямоугольник, у которого все стороны равны.
2. Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)

5.4: Периметр квадратов и прямоугольников

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2150

Используйте основные формулы четырехугольника, чтобы найти полные меры ребер прямолинейных четырехугольников.

Найдите периметр и площадь квадратов и прямоугольников с помощью формул

Рисунок \(\PageIndex{1}\)

У Раджа есть небольшой участок земли, который он хочет превратить в огород. Однако он хочет построить вокруг него небольшой забор, прежде чем что-либо посадить. Он знает, что площадь земли составляет 240 квадратных футов и что длина одной стороны равна 15 футам. Чтобы построить забор, ему нужно знать и ширину участка. Как Радж может написать и решить уравнение, чтобы определить ширину своего будущего сада?

В этой концепции вы научитесь находить периметр и площадь квадратов и прямоугольников, используя формулы.

Периметр и площадь квадратов и прямоугольников

Формула — это метод, который доказал свою эффективность при решении определенных типов задач.

Давайте изучим некоторые из этих знакомых формул, взглянув на прямоугольники, квадраты, площадь и периметр.

периметр фигуры — это расстояние вокруг фигуры.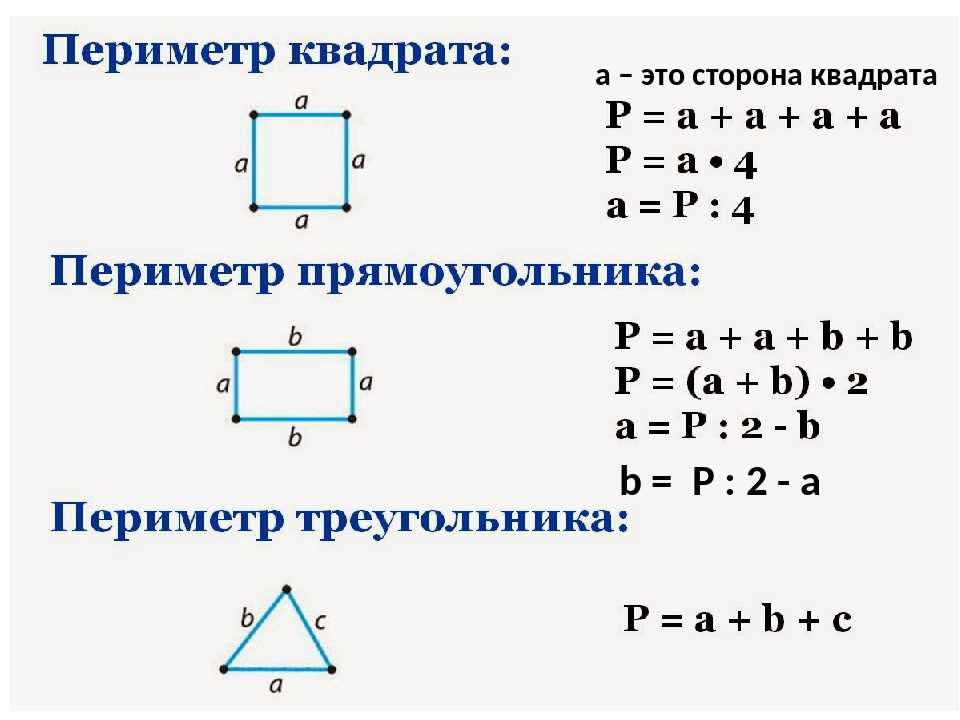 Периметр – это сумма всех сторон квадрата или прямоугольника. Поскольку прямоугольник имеет два набора параллельных сторон, формула для определения периметра (\(P\)) прямоугольника:

\(P=2L+2W\)

\(L=длина\: и\: W=ширина\)

Давайте рассмотрим пример.

Рисунок \(\PageIndex{2}\)

Прямоугольник выше показывает его размеры. Найдите периметр.

Сначала подставьте значения ширины (\(W\)) и длины (\(L\)) в формулу периметра.

\(P=2(12)+2(9)\)

Затем выполните умножение и сложение, чтобы найти периметр.

\(\begin{выровнено} P&=2(12)+2(9) \\ P&=24+18 \\ P&=42\end{выровнено}\)

Ответ: 42.

Периметр прямоугольника равен 42 дюймам.

Площадь — количество квадратных единиц внутри фигуры. Площадь находится путем умножения длины на ширину. Формула для нахождения площади прямоугольника:

\(A=L\×W\)

Вы можете использовать размеры прямоугольника выше, чтобы найти площадь этого прямоугольника.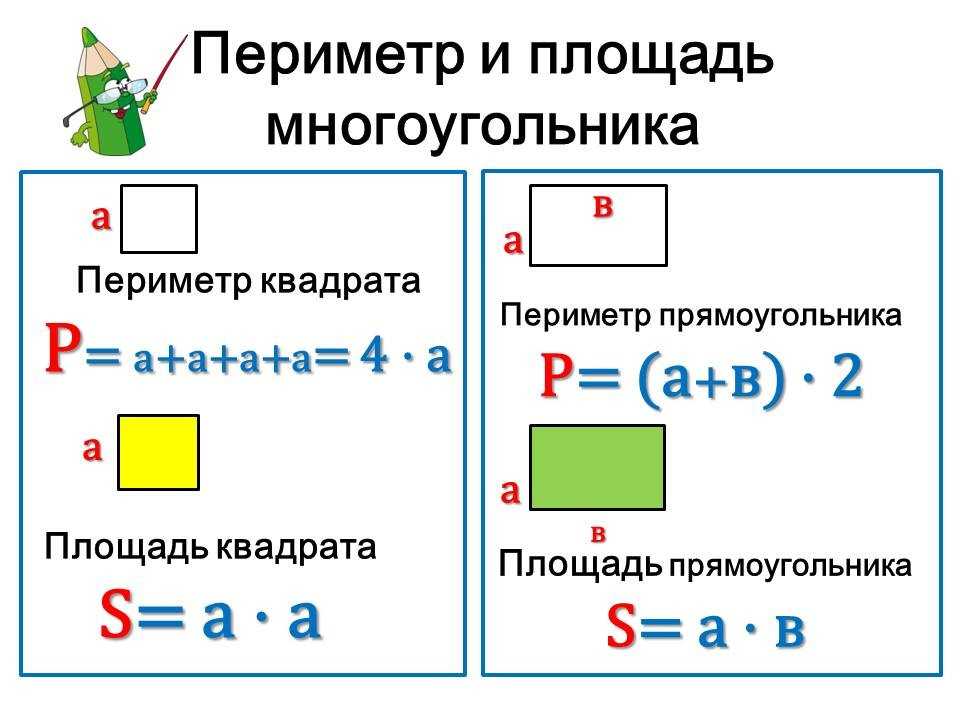

Сначала введите значения \(L\) и \(W\) в формулу площади.

\(\begin{align} A&=L\times W \\ A&=12\times 92\). Площадь всегда указывается в квадратных единицах.

Вы также можете найти периметр и площадь квадрата. Помните, что квадрат имеет четыре равные стороны, если задан символ s. Вы можете использовать следующую формулу для нахождения периметра квадрата:

\(P=4s\)

Давайте рассмотрим пример.

Прямоугольник имеет длину 12 футов и периметр 72 фута. Напишите и решите уравнение, чтобы определить ширину прямоугольника.

Сначала подставьте значения периметра (\(P\)) и длины (\(L\)) в формулу периметра.

\(72=2(12)+2W\)

Затем завершите умножение.

\(72=24+2W\)

Затем вычтите 24 из обеих сторон, чтобы получить одну переменную с правой стороны.

\(\begin{aligned} 72−24&=24−24+2W \\ 48 &=2W \end{aligned}\)

Затем умножьте обе части на обратную величину 2, чтобы изолировать вашу переменную.

\(\begin{align} \dfrac{1}{2}\times \dfrac{48}{1} &=\dfrac{1}{2}\times \dfrac{2W}{1} \\ \ dfrac{48}{2}&=W \\ W&=24\end{выровнено}\)

Ответ: 24.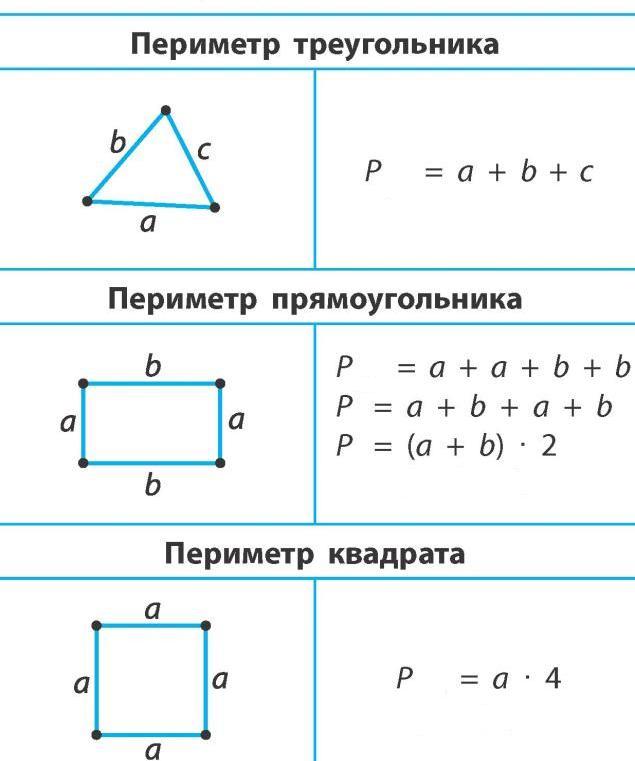 2 &=15\text{ft} \times W\end{aligned}\)

Затем умножьте обе стороны на величину, обратную 15, чтобы выделить переменную W.

\(\begin{aligned} \dfrac{1}{15}\times \dfrac{240}{1}&=\ dfrac{1}{15}\times \dfrac{15}{1} \times W \\ W&=16 \end{aligned}\)

Ответ: 16.

Ширина сада Раджа составляет 16 футов. Таким образом, размеры сада составляют 16 на 15 футов.

Пример \(\PageIndex{2}\)

Периметр квадрата 196 дюймов. Определить длину одной стороны квадрата.

Решение

Сначала подставьте значение периметра (\(P\)) в формулу периметра.

\(196=4s\)

Затем умножьте обе части на обратную величину 4, чтобы изолировать вашу переменную.

\(\begin{align} \dfrac{1}{4}\times \dfrac{196}{1}&=\dfrac{1}{4}\times \dfrac{4s}{1} \\ \ dfrac{196}{4}&=s \\ s&=49 \end{aligned}\)

Ответ: 49.

Пример \(\PageIndex{3}\)

Найдите периметр следующего квадрата если длина стороны равна \(4,5\: дюймы\).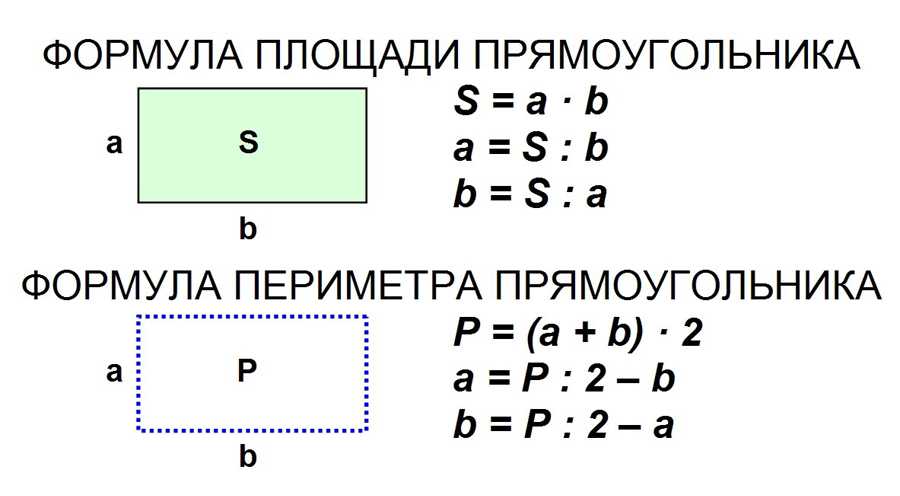

Решение

Сначала подставьте значение длины стороны в формулу периметра.

\(\begin{align} P&=4s \\ P&=4(4.5) \end{aligned}\)

Затем умножьте на 4, чтобы найти периметр.

\(\begin{aligned} P&=4(4.5) \\ P&=18 \end{aligned}\)

Ответ: 18.

Пример \(\PageIndex{4}\)

Можете ли вы найти площадь квадрата в примере 1?

Раствор 92 \\ s&=\sqrt{144} \\ s&=12 \end{aligned}\)

Ответ: 12.

Обзор

Найдите площадь и периметр каждого квадрата или прямоугольника, используя формулы и заданные размеры . Каждая задача будет иметь два ответа.

1. Квадрат со стороной 5 дюймов.
2. Прямоугольник длиной 5 дюймов и шириной 3 дюйма.
3. Прямоугольник длиной 8 см и шириной 6 см.
4. Квадрат со стороной 11 футов.
5. Прямоугольник длиной 9 дюймов и шириной 4,5 дюйма.
6. Квадрат со стороной 7 футов.
7. Прямоугольник длиной 12 метров и шириной 11 метров.
8. Квадрат со стороной 13 метров.
9. Прямоугольник длиной 15 футов и шириной 8 футов.
10. Квадрат со стороной 12,5 футов.

Найдите недостающую длину стороны, зная площадь каждого квадрата. 92\)

Обзор (ответы)

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 1.13.

Словарь

Срок	Определение
Площадь	Площадь — это пространство внутри периметра двумерной фигуры.
Формула	Формула — это тип уравнения, показывающий взаимосвязь между различными переменными.
Периметр	Периметр — это расстояние вокруг двухмерной фигуры.
Квадратный блок	Квадратная единица — это квадрат с четырьмя сторонами, каждая из которых имеет размер 1 единица.

Дополнительные ресурсы

Интерактивный элемент

Видео: определение площади прямоугольника с использованием целых чисел

Практика: периметр квадратов и прямоугольников

Реальный мир: стежок во времени

---

Эта страница под названием 5.4: Периметр квадратов и прямоугольников распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

ПОД ЛИЦЕНЗИЕЙ

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   СК12

   Лицензия

   СК-12

   Программа OER или Publisher

   СК-12

   Показать оглавление

   нет

2. Теги

   1. источник@https://www. ck12.org/c/geometry

Как вычислить квадратные футы по периметру

••• FERKHOVA/iStock/GettyImages

Обновлено 16 ноября 2020 г. можно использовать на протяжении всей жизни. Это пригодится каждый раз, когда вы что-то строите, что-то устраиваете или просто пытаетесь выяснить, поместится ли один объект внутри или рядом с другим. Зачастую гораздо проще измерить периметр, чем площадь реальных объектов. Как только вы узнаете пару простых формул, вы сможете легко преобразовать этот периметр в площадь, используя базовые вычисления.

TL;DR (слишком длинный; не читал)

Формула площади квадрата: (​ P ​/4) ² , где ​ P ​ — периметр.

Формула площади круга: ​ C ​ ² /4π, где ​ C ​ — длина окружности (специальное слово для периметра круглых или яйцевидных объектов).

Вычисление площади квадрата

Квадрат является самой простой формой для вычисления площади на основе периметра, между каждой из сторон которого находится 1/4 длины периметра. Если вы хотите, чтобы ваш ответ был выражен в квадратных футах, убедитесь, что ваши измерения либо в футах, либо переведены в футы, прежде чем начинать расчеты. 92

Вычисление площади круга

Вы также можете вычислить площадь круга на основе его периметра. Как всегда, если вы хотите, чтобы ваш результат был в квадратных футах, вы должны сначала убедиться, что все ваши измерения указаны в футах.

• Периметром круга обычно называют его окружность. Два разных слова означают одно и то же — расстояние по всей внешней стороне фигуры, — но окружность относится только к круглым или овальным объектам, а периметр может относиться к любой двумерной форме. 92

  • Символ π представляет постоянное число, которое математики все еще вычисляют. На данный момент они нашли более квадриллиона цифр справа от запятой. Очевидно, что все эти цифры не поместятся на вашей странице или экране, поэтому большинство учителей позволят вам сократить число π до значения 3,14.

    No related posts.