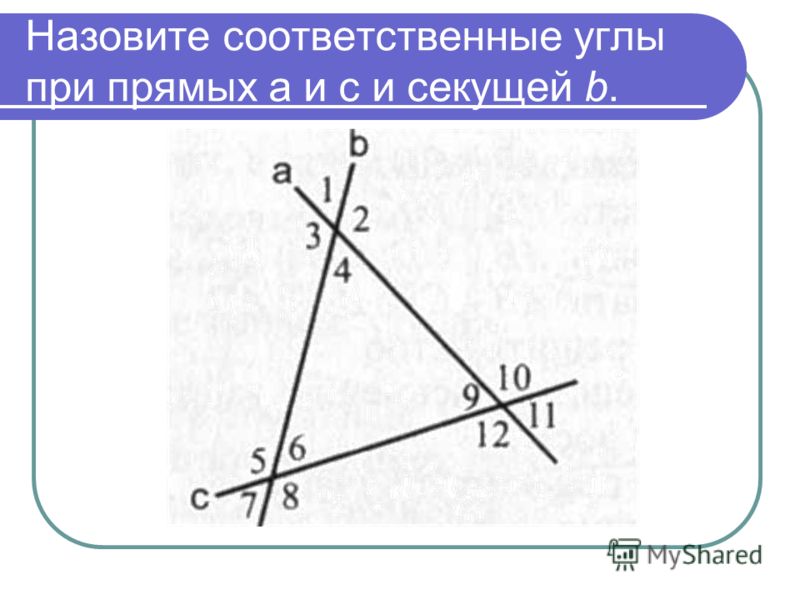
Углы, образованные параллельными прямыми. Презентация по геометрии на тему:»Теоремы об углах, образованных двумя параллельными прямыми и секущей»
Теоремы об углах, образованных
Геометрия, Глава III, 7 класс
К учебнику Л.С.Атанасяна
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
Теорема, обратная данной
Теорема: В равнобедренном треугольнике углы при основании равны .
Теорема: Если треугольник – равнобедрен-ный, то в нём углы при основании равны .
Условие теоремы (Дано): треугольник — равнобедренный
Заключение теоремы (Доказать): углы при основании равны
Условие теоремы : углы при основании равны
Заключение теоремы : треугольник — равнобедренный
НОВОЕ УТВЕРЖДЕНИЕ
Обратная
теорема
Если в треугольнике два угла
равны, то он — равнобедренный .
Теорема, обратная данной
Всегда ли обратное утверждение верно?
Теорема
Обратная теорема
Если сумма двух углов равна 180 0 , то углы — смежные
Сумма смежных углов
равна 180 0 .
Если углы равны,
то они — вертикальные
Вертикальные углы равны
Если в треугольнике биссектриса, проведенная к одной из его сторон, является и медианой, проведенной к этой стороне, то этот треугольник -равнобедренный
В равнобедренном треугольнике, биссектриса, проведенная к основанию, является медианой и высотой
Если в треугольнике биссектриса, проведенная к одной из его сторон, является и высотой, проведенной к этой стороне, то этот треугольник -равнобедренный
Е сли треугольник — равнобедренный, то биссектриса, проведенная к основанию , является и медианой и высотой
Углы, образованные двумя параллельными прямыми и секущей
Всегда ли обратное утверждение верно?
Теорема
Обратная теорема
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
накрест лежащие углы равны то прямые параллельны .
Но это противоречит
МЕТОД ОТ
ПРОТИВНОГО
Выдвигаем предположение, противоположное тому, что надо доказать
Путем рассуждений приходим к противоречию с известной аксиомой или теоремой
Делаем вывод о неверности нашего предположения и верности утверждения теоремы
Но это противоречит аксиоме параллельных
Следовательно, наше допущение неверно
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой
Углы, образованные
двумя параллельными прямыми и секущей
Теорема
Обратная теорема
Если при пересечении двух прямых секущей соответственные углы равны , то прямые параллельны .
Если две параллельные прямые пересечены секущей, то соответственные углы равны
Углы, образованные
двумя параллельными прямыми и секущей
Теорема
Обратная теорема
Если при пересечении двух прямых секущей 0 , то прямые параллельны .
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0
Прямые а и b параллельны.
Найдите угол 2.
Прямые а и b параллельны.
Найдите неизвестные углы
Прямые а и b параллельны.
Найдите неизвестные углы
Найдите неизвестные углы
Найдите неизвестные углы
Найдите неизвестные углы
Прямые а и b параллельны.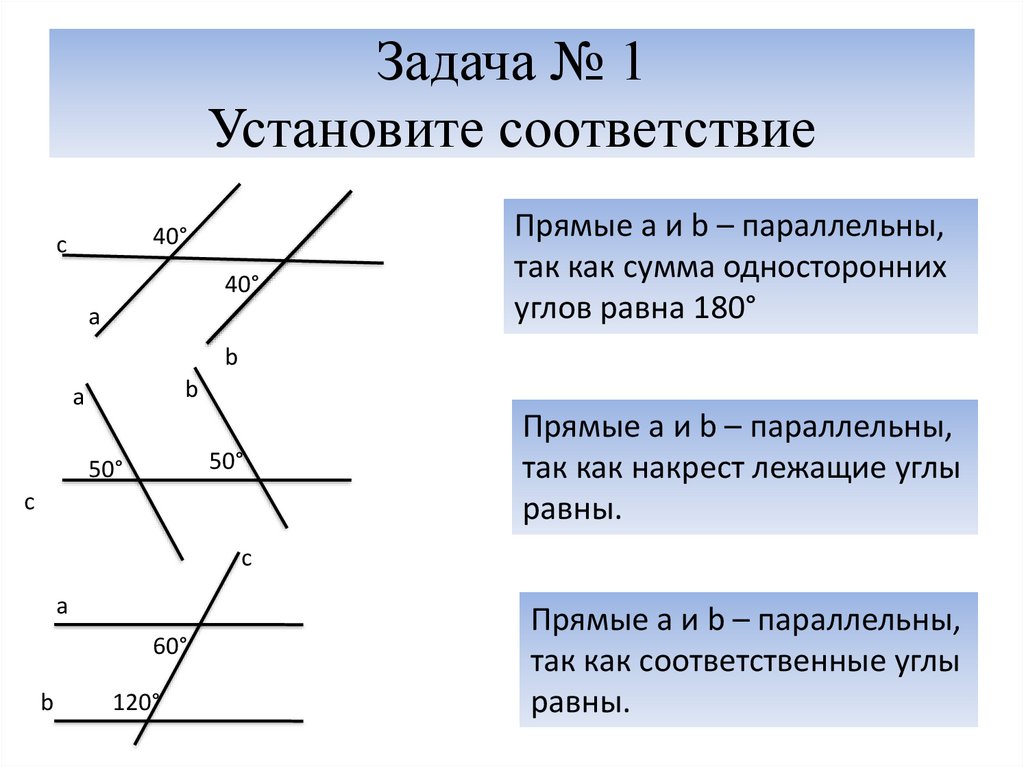
Найдите неизвестные углы, если сумма двух накрест лежащих углов равна 100 0 .
Прямые а и b параллельны. Найдите неизвестные углы, если сумма двух соответст-венных углов равна 260 0 .
Прямые а и b параллельны. Найдите неизвестные углы, если разность двух одно-сторонних углов равна 50 0 .
Теорема: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. а в А В 1 2 1 = 2 c
Доказательство: A B C DM N 1 2 K O Пусть прямые АВ и СD параллельны, МN — их секущая. Докажем, что накрест лежащие углы 1 и 2 равны между собой. Допустим, что 1 и 2 не равны. Проведем через точку О прямую К F. Тогда при точке О можно построить KON , накрест лежащий и равный 2. Но если KON = 2, то прямая К F будет параллельна СD. Получили, что через точку О проведены две прямые АВ и К F, параллельные прямой СD. Но этого не может быть. Мы пришли к противоречию, потому что допустили, что 1 и 2 не равны.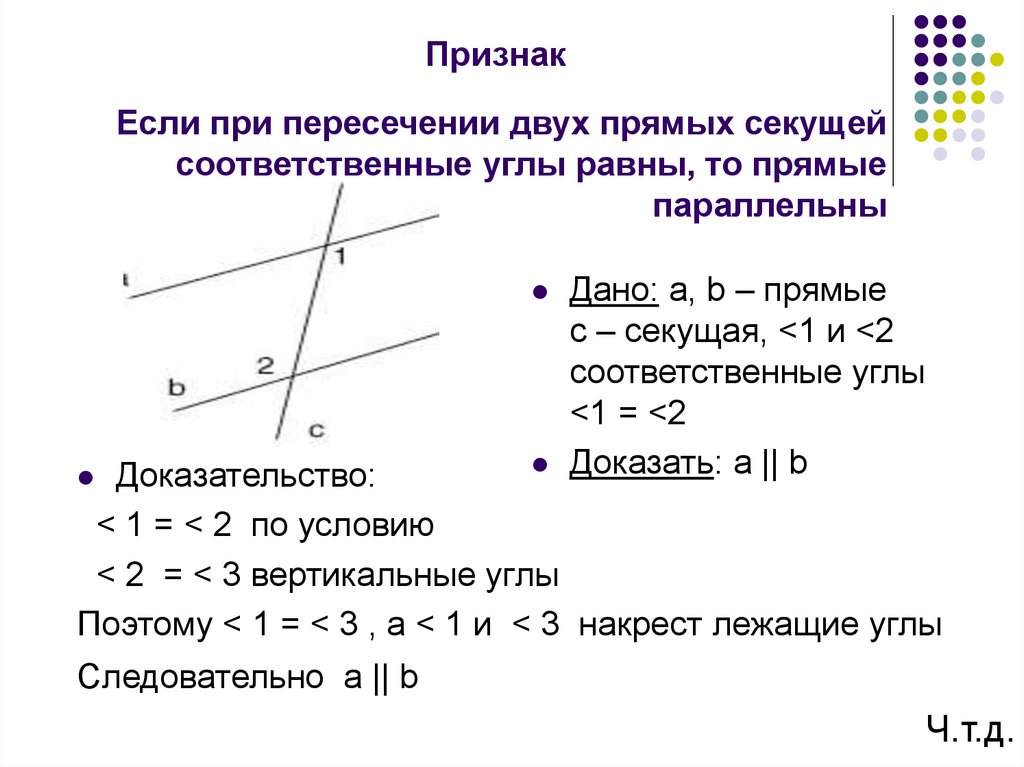
Следовательно, наше допущение является неправильным и 1 должен быть равен 2, т. е. накрест лежащие углы равны.
Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равн ы. а в А В 1 2 1 =
Доказательство: 2 а в А В 3 1 Пусть параллельные прямые а и b пересечены секущей АВ, то накрест лежащие 1 и 3 будут равны. 2 и 3 равны как вертикальные. Из равенств 1 = 3 и 2 = 3 следует, что 1 = 2. Теорема доказана
Теорема: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°. а в А В 3 1 1 + 3 = 180°
Доказательство: Пусть параллельные прямые а и b пересечены секущей АВ, то соответственные 1 и 2 будут равны, 2 и 3 – смежные, поэтому 2 + 3 = 180 °. Из равенств 1 = 2 и 2 + 3 = 180 ° следует, что 1 + 3 = 180 °. Теорема доказана. 2 а в А В
Решение: 1. Пусть Х – это 2, тогда 1 = (Х+70°), т. к. сумма углов 1 и 2 = 180°, в силу того, что они смежные. Составим уравнение: Х+ (Х+70°) = 180° 2 Х = 110 ° Х = 55° (Угол 2) 2.
Найдем 1. 55° + 70° = 125° 3. 1 = 3, т. к. они вертикальные. 3 = 5, т. к. они накрест лежащие. 125° 5 = 7, т. к. они вертикальные. 2 = 4, т. к. они вертикальные. 4 = 6, т. к. они накрест лежащие. 55° 6 = 8, т. к. они вертикальные. Задача № 1: A B 4 3 5 8 7 21 6 Условие: найдите все углы, образованные при пересечении двух параллельных A и B секущей C, если один из углов на 70° больше другого.
Решение: 1. Т. к. 4 = 45°, то 2 = 45°, потому что 2 = 4(как соответственные) 2. 3 смежен с 4, поэтому 3+ 4=180°, и из этого следует, что 3= 180° — 45°= 135°. 3. 1 = 3, т. к. они накрест лежащие. 1 = 135°. Ответ: 1=135°; 2=45°; 3=135°. Задача № 2: A B 1 Условие: на рисунке прямые А II B и C II D, 4=45°. Найти углы 1, 2, 3.
Решение: 1. 1= 2, т. к. они вертикальные, значит 2= 45°. 2. 3 смежен с 2, поэтому 3+ 2=180°, и из этого следует, что 3= 180° — 45°= 135°. 3. 4 + 3=180°, т. к. они односторонние. 4 = 45°. Ответ: 4=45°; 3=135°. Задача № 3: A B 2 Условие: две параллельные прямые А и B пересечены секущей С.
Найти, чему будут равны 4 и 3, если 1=45°.
Рыбалко Павел
В данной презентации содержатся: 3 теоремы с доказательствами и 3 задачи на закрепление изученного материала с подробным решением. Презентация может быть полезна учителю на уроке, т. к. сэкономит много времени. Также её можно использовать в качестве обобщающего повторения в конце учебного года.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Теоремы об углах, образованных двумя параллельными прямыми и секущей. Исполнитель: ученик 7 «А» кл асса Рыбалко Павел г. Мытищи, 2012 год
Теорема: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. а в А В 1 2 1 = 2 c
Доказательство: A B C D M N 1 2 A B C D M N 1 2 K O Пусть прямые АВ и СD параллельны, МN — их секущая. Докажем, что накрест лежащие углы 1 и 2 равны между собой.
Допустим, что 1 и 2 не равны. Проведем через точку О прямую К F. Тогда при точке О можно построить KON , накрест лежащий и равный 2. Но если KON = 2, то прямая К F будет параллельна СD. Получили, что через точку О проведены две прямые АВ и К F, параллельные прямой СD. Но этого не может быть. Мы пришли к противоречию, потому что допустили, что 1 и 2 не равны. Следовательно, наше допущение является неправильным и 1 должен быть равен 2, т. е. накрест лежащие углы равны. F
Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равн ы. а в А В 1 2 1 = 2
Доказательство: 2 а в А В 3 1 Пусть параллельные прямые а и b пересечены секущей АВ, то накрест лежащие 1 и 3 будут равны. 2 и 3 равны как вертикальные. Из равенств 1 = 3 и 2 = 3 следует, что 1 = 2. Теорема доказана
Теорема: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°. а в А В 3 1 1 + 3 = 180°
Доказательство: Пусть параллельные прямые а и b пересечены секущей АВ, то соответственные 1 и 2 будут равны, 2 и 3 – смежные, поэтому 2 + 3 = 180 °.
Решение: 1. Пусть Х – это 2, тогда 1 = (Х+70°), т.к. сумма углов 1 и 2 = 180°, в силу того, что они смежные. Составим уравнение: Х+ (Х+70°) = 180° 2Х = 110 ° Х = 55° (Угол 2) 2. Найдем 1. 55° + 70° = 125° 3. 1 = 3, т.к. они вертикальные. 3 = 5, т.к. они накрест лежащие. 125° 5 = 7, т.к. они вертикальные. 2 = 4, т.к. они вертикальные. 4 = 6, т.к. они накрест лежащие. 55° 6 = 8, т.к. они вертикальные. Задача №1: A B 4 3 5 8 7 2 1 6 Условие: найдите все углы, образованные при пересечении двух параллельных A и B секущей C, если один из углов на 70° больше другого.
Решение: 1. Т.к. 4 = 45°, то 2 = 45°, потому что 2 = 4(как соответственные) 2. 3 смежен с 4, поэтому 3+ 4=180°, и из этого следует, что 3= 180° — 45°= 135°. 3. 1 = 3, т.к. они накрест лежащие. 1 = 135°. Ответ: 1=135°; 2=45°; 3=135°. Задача №2: A B 1 Условие: на рисунке прямые А II B и C II D, 4=45°.
Найти углы 1, 2, 3. 3 2 4
Решение: 1. 1= 2, т.к. они вертикальные, значит 2= 45°. 2. 3 смежен с 2, поэтому 3+ 2=180°, и из этого следует, что 3= 180° — 45°= 135°. 3. 4 + 3=180°, т.к. они односторонние. 4 = 45°. Ответ: 4=45°; 3=135°. Задача №3: A B 2 Условие: две параллельные прямые А и B пересечены секущей С. Найти, чему будут равны 4 и 3, если 1=45°. 3 4 1
Видеоурок о теоремах об углах между двумя параллельными прямыми и их секущей содержит материал, представляющий особенности строения теоремы, примеры формирования и доказательства обратных теорем, следствий из них. Задача данного видеоурока — углубить понятие теоремы, разложив ее на составляющие, рассмотрев понятие обратной теоремы, формировать умение строить теорему, обратную данной, следствий из теоремы, формировать умение доказывать утверждения.
Форма видеоурока позволяет удачно расставить акценты при демонстрации материала, облегчая понимание и запоминание материала. Тема данного видеоурока сложная и важная, поэтому использование наглядного пособия не только целесообразно, но и желательно.
Он дает возможность повысить качество обучения. Анимированные эффекты улучшают представление учебного материала, приближают процесс обучения к традиционному, а использование видео освобождает учителя для углубления индивидуальной работы.
Видеоурок начинается с объявления его темы. В начале урока рассматривается разложение теоремы на составляющие для лучшего понимания ее строения и возможностей для дальнейшего исследования. На экране демонстрируется схема, демонстрирующая, что теорема состоит их условия и заключения. Понятие условия и заключения описывается на примере признака параллельности прямых, отметив, что часть утверждения является условием теоремы, а вывод — заключением.
Углубляя полученные знания о строении теоремы, ученикам дается понятие теоремы, обратной данной. Она образуется в результате замены — условие становится заключением, заключение — условием. Чтобы сформировать умение учеников строить теоремы, обратные данным, умение доказывать их, рассматриваются теоремы, обратные тем, которые рассмотрены в уроке 25 о признаках параллельности прямых.
На экране отображается теорема, обратная первой теореме, описывающей признак параллельный прямых. Поменяв местами условие и заключение, получаем утверждение, что если пересечены секущей какие-либо параллельные прямые, то образованные при этом накрест лежащие углы будут равными. Доказательство демонстрируется на рисунке, где изображены прямые а, b, а также секущая, проходящая через эти прямые в их точках M и N. На изображении отмечаются накрест лежащие углы ∠1 и ∠2. Необходимо доказать их равенство. Сначала в ходе доказательства делается предположение, что данные углы не являются равными. Для этого через точку М проводится некоторая прямая Р. Строится угол `∠PMN, являющийся накрест лежащим с углом ∠2 по отношению к MN. Углы `∠PMN и ∠2 по построению равны, следовательно МР║b. Вывод — через точку проведены две прямые, параллельные b. Однако это невозможно, потому что не соответствует аксиоме параллельных прямых. Сделанное предположение оказывается ошибочным, доказывая справедливость изначального утверждения.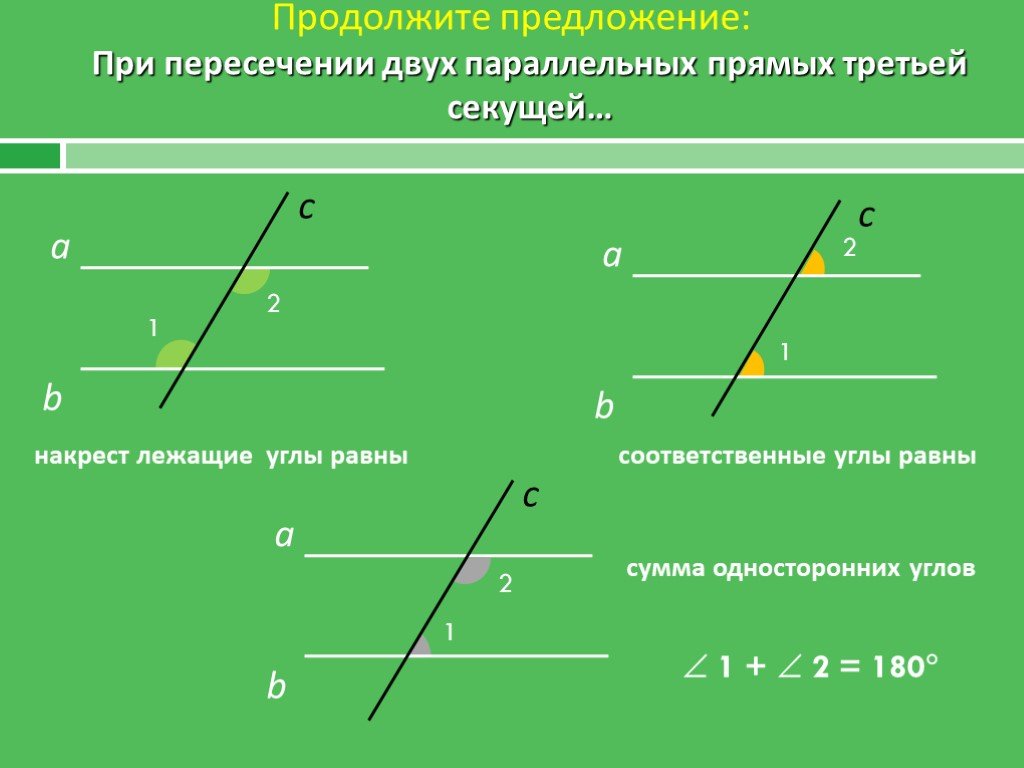
Теорема доказана.
Далее обращается внимание учеников на способ доказательства, который был использован в ходе рассуждений. Доказательство, в котором предполагается ошибочность доказываемого утверждения, называется в геометрии доказательством от противного. Данный способ часто используется для доказательства различных геометрических утверждений. В данном случае, предположив, неравенство накрест лежащих углов, в ходе рассуждений выявилось противоречие, что отрицает справедливость такого противоречия.
Ученикам напоминается, что подобный способ уже был использован ранее в доказательствах. Примером этому служит доказательство теоремы в уроке 12 о том, что две прямые, которые перпендикулярны третьей, не пересекаются, а также доказательства следствий в уроке 28 из аксиомы параллельности прямых.
Еще одно доказываемое следствие утверждает, что прямая перпендикулярна к обеим параллельным прямым, если она перпендикулярна к одной из них. На рисунке изображаются прямые а и b и перпендикулярная им прямая с.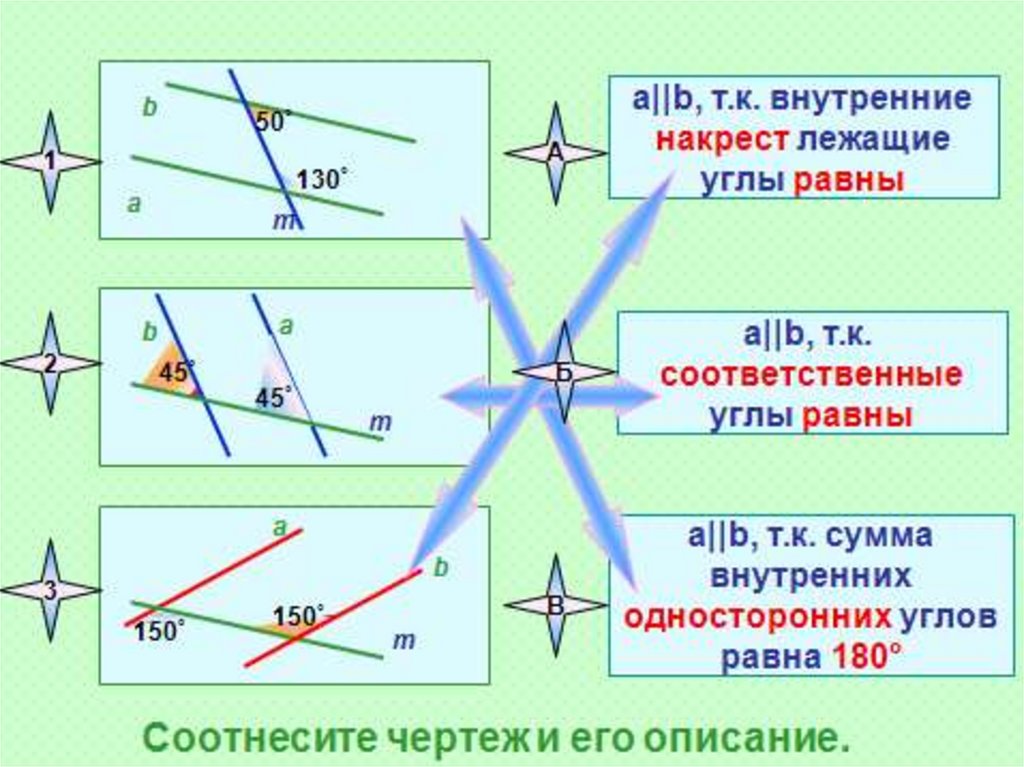
Перпендикулярность прямой c к а означает, что образуемый с ней угол равен 90°. Параллельность а и b, пересечение их прямой с означает, что прямая с пересекает b. Угол ∠2, образованный с прямой b, является накрест лежащим к углу ∠1. А так как по условию прямые параллельны, то данные углы равны. Соответственно, величина угла ∠2 также будет равна 90°. Это означает, прямая с оказалась перпендикулярной прямой b. Рассматриваемая теорема доказана.
Следующей доказывается теорема, обратная ко второму признаку параллельных прямых. Обратная теорема утверждает, при условии параллельности двух прямых образованные соответственные углы будут равными. Доказательство начинается с построения секущей с, параллельных между собой прямых а и b. Созданные при этом углы отмечаются на рисунке. Имеется пара соответственных углов, названные ∠1 и ∠2, также отмечен угол ∠3, который накрест лежащий углу ∠1. Параллельность а и b означает равенство ∠3=∠1 как накрест лежащих. Учитывая, что ∠3, ∠2 — вертикальные, они также равны.
Следствием таких равенств является утверждение, что ∠1=∠2. Рассматриваемая теорема доказана.
Последняя доказываемая на данном уроке теорема — обратная последнему признаку параллельных прямых. Ее текст гласит, что в случае прохождения через параллельные прямые некоторой секущей, сумма образованных при этом односторонних углов равна величине в 180°. Ход доказательства демонстрируется на рисунке, где изображены прямые а и b, пересекающиеся с секущей с. Необходимо доказать, что величина суммы односторонних углов будет равняться 180°, то есть ∠4+∠1 = 180°. Из параллельности прямых а и b следует равенство соответственных углов ∠1 и ∠2. Смежность углов ∠4, ∠2 означает, что в сумме они составляют 180°. При этом углы ∠1= ∠2 — значит, ∠1 в сумме с углом ∠4 будет составлять 180°. Теорема доказана.
Для более глубокого понимания, как формируются и доказываются обратные теоремы, отдельно отмечается, что если теорема доказана и верна, то это не значит, что также верна будет обратная теорема.
Чтобы это понять, приводится простой пример. Есть теорема о том, что все вертикальные углы равны. Обратная теорема звучит так, что все равные углы вертикальны, что не соответствует действительности. Ведь можно построить два равных угла, которые не будут вертикальны. Это можно увидеть на продемонстрированном рисунке.
Видеоурок «Теоремы об углах, образованных двумя параллельными прямыми и секущей» является наглядным пособием, которое может быть использовано учителем на уроке геометрии, а также успешно сформировать представление об обратных теоремах и следствиях, а также их доказательстве при самостоятельном изучении материала, быть полезным в дистанционном обучении.
§ 1 Обратная теорема
В этом уроке выясним, какие теоремы называются обратными, приведем примеры обратных теорем, сформулируем теоремы об углах, образованных двумя параллельными прямыми и секущей, и познакомимся с методом доказательства от противного.
При изучении различных геометрических фигур обычно формулируются определения, доказываются теоремы, рассматриваются следствия из теорем.
Во всякой теореме различают две части: условие и заключение.
Условие теоремы — это то, что дано, а заключение — это то, что требуется доказать. Очень часто условие теоремы начинается со слова «если», а заключение начинается со слова «то». Например, теорему о свойствах равнобедренного треугольника можно сформулировать так: «Если треугольник равнобедренный, то углы при его основании равны». Первая часть теоремы «Если треугольник равнобедренный» — это условие теоремы, вторая часть теоремы «то углы при его основании равны» — это заключение теоремы.
Теорема, где меняются местами условие с заключением, называется обратной теоремой. Обратная теорема к теореме о свойствах равнобедренного треугольника будет звучать так: «Если в треугольнике два угла равны, то такой треугольник равнобедренный».
Запишем коротко каждую из них:
Мы видим, что условие и заключение поменялись местами.
Каждое из этих утверждений справедливо.
Возникает вопрос: всегда ли является верным утверждение, где условие меняется с заключением местами?
Рассмотрим пример.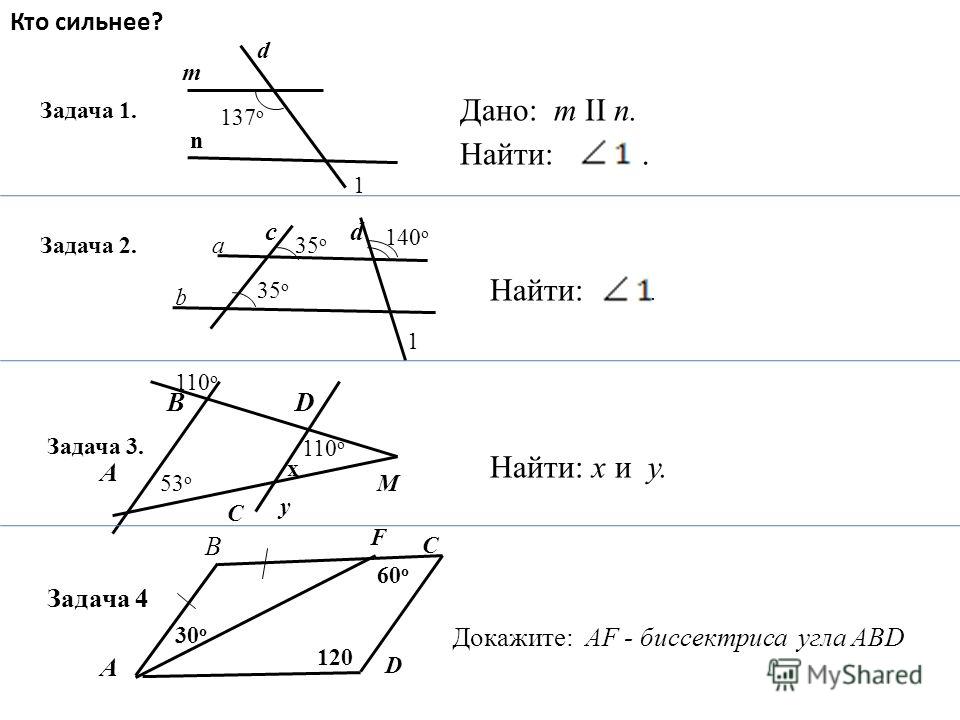
Если углы вертикальные, то они равны. Это верное утверждение, у него есть доказательство. Сформулируем обратное утверждение: если углы равны, то они вертикальные. Данное утверждение неверное, в этом легко убедиться, приведя опровергающий пример: возьмем два прямых угла (см. рисунок), они равны, но при этом не являются вертикальными.
Таким образом, обратные утверждения (теоремы) по отношению к уже доказанным утверждениям (теоремам) всегда требуют доказательства.
§ 2 Теоремы об углах, образованных двумя параллельными прямыми и секущей
Давайте теперь вспомним доказанные утверждения — теоремы, выражающие признаки параллельности двух прямых, сформулируем обратные им теоремы и убедимся в их справедливости, приведя доказательства.
Первый признак параллельности прямых.
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Обратная теорема:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Докажем это утверждение.
Дано: параллельные прямые а и b пересечены секущей АВ.
Доказать: накрест лежащие углы 1 и 2 равны. (см. рис.)
Доказательство:
Допустим, что углы 1 и 2 не равны.
Отложим от луча АВ угол САВ, равный углу 2, так, чтобы угол САВ и угол 2 были накрест лежащими углами при пересечении прямых СА и b секущей АВ.
По построению эти накрест лежащие углы равны, значит, прямая СА параллельна прямой b.
Мы получили, что через точку А проходят две прямые а и СА, параллельные прямой b. Это противоречит аксиоме параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Значит, наше допущение неверно, углы 1 и 2 равны.
Теорема доказана.
§ 3 Метод доказательства от противного
При доказательстве этой теоремы мы использовали способ рассуждений, который называется методом доказательства от противного. Начиная доказательство, мы предположили противоположное тому, что требовалось доказать.
Считая это предположение верным, путем рассуждений пришли к противоречию с аксиомой параллельных прямых. Из этого сделали вывод, что наше предположение не верно, а верно утверждение теоремы. Такой способ доказательства часто используется в математике.
Рассмотрим следствие доказанной теоремы.
Следствие:
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
Пусть прямая а параллельна прямой b, прямая с перпендикулярна прямой а, т.е. угол 1 = 90º.
Прямая с пересекает прямую а, значит, прямая с пересекает также прямую b.
При пересечении параллельных прямых секущей, накрест лежащие углы равны, значит, угол 1 = углу 2.
Так как угол 1 = 90º, то и угол 2 = 90º, значит, прямая с перпендикулярна прямой b.
Следствие доказано.
Обратная теорема для второго признака параллельности прямых:
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Обратная теорема для третьего признака параллельности прямых:
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180º.
Итак, в этом уроке мы выяснили, какие теоремы называются обратными, сформулировали и рассмотрели теоремы об углах, образованных двумя параллельными прямыми и секущей, а также познакомились с методом доказательства от противного.
Список использованной литературы:
- Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. – 383 с.: ил.
- Гаврилова Н.Ф. Поурочные разработки по геометрии 7 класс. — М.: «ВАКО», 2004, 288с. – (В помощь школьному учителю).
- Белицкая О.В. Геометрия. 7 класс. Ч.1. Тесты. – Саратов: Лицей, 2014. – 64 с.
Как доказать параллельность прямых. Н.Никитин Геометрия Правила параллельных прямых
AB и С D пересечены третьей прямой MN , то образовавшиеся при этом углы получают попарно такие названия:
соответственные углы : 1 и 5, 4 и 8, 2 и 6, 3 и 7;
внутренние накрест лежащие углы : 3 и 5, 4 и 6;
внешние накрест лежащие углы : 1 и 7, 2 и 8;
внутренние односторонние углы : 3 и 6, 4 и 5;
внешние односторонние углы : 1 и 8, 2 и 7.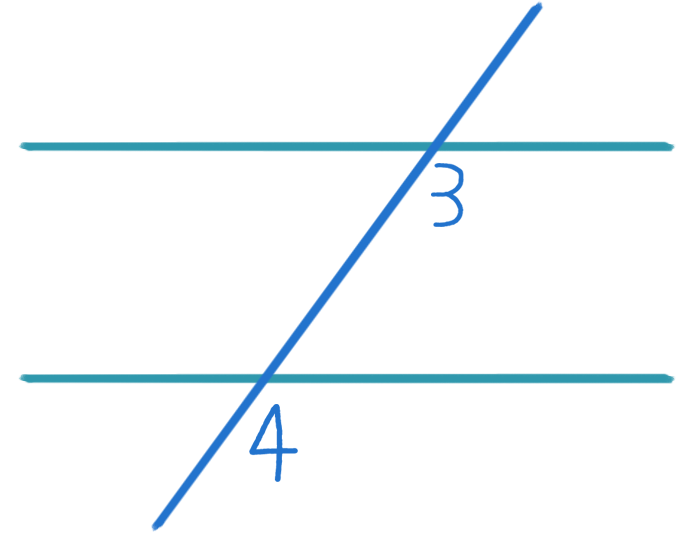
Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.
Следовательно, ∠ 2 =∠ 8.
3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.
4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d.
5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам , как углы вертикальные .
Из выше доказанного обоснования получаем обратные теоремы.
Когда при пересечении двух прямых произвольной третьей прямой получим, что:
1. Внутренние накрест лежащие углы одинаковы;
или 2. Внешние накрест лежащие углы одинаковые;
или 3. Соответственные углы одинаковые;
или 4.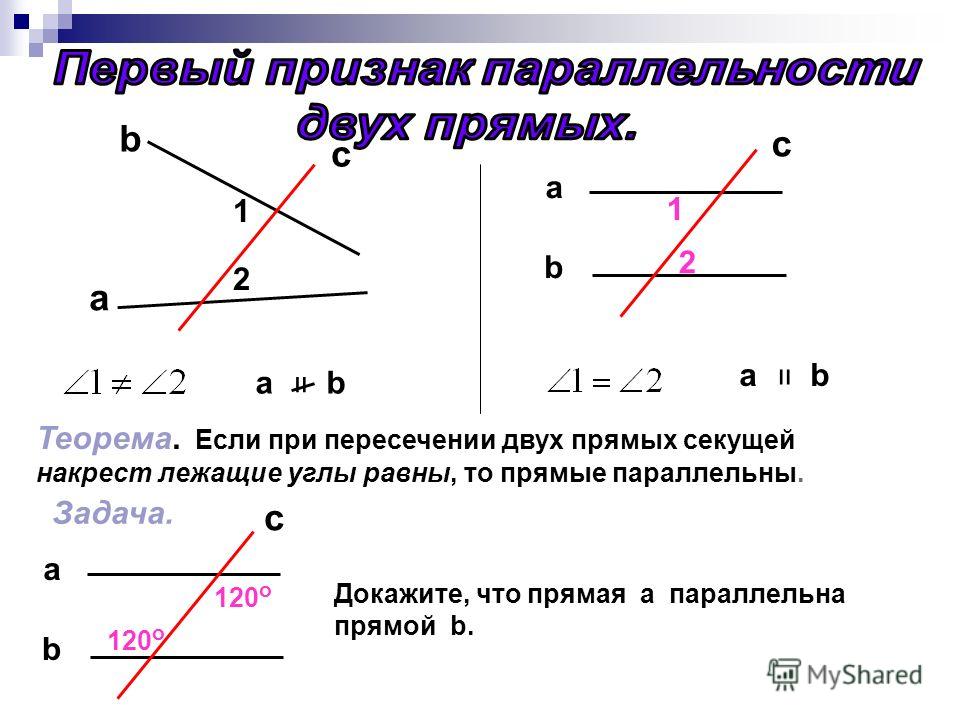
С D , что возможно. Прямая CE параллельна AB .
Для доказательства допустим противное, т.е., что CE пересекается с AB в некоторой точке M . Тогда из точки M к прямой С D мы имели бы два различных перпендикуляра M D и MС , что невозможно. Значит, CE не может пересечься с AB , т.е. С E параллельна AB .
Следствие.
Два перпендикуляра (С E и DB ) к одной прямой (С D ) параллельны.
Аксиома параллельных линий.
Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой.
Так, если прямая С D , проведенная через точку С параллельна прямой AB , то всякая другая прямая С E , проведенная через ту же точку С , не может быть параллельна AB , т.е. она при продолжении пересечется с AB .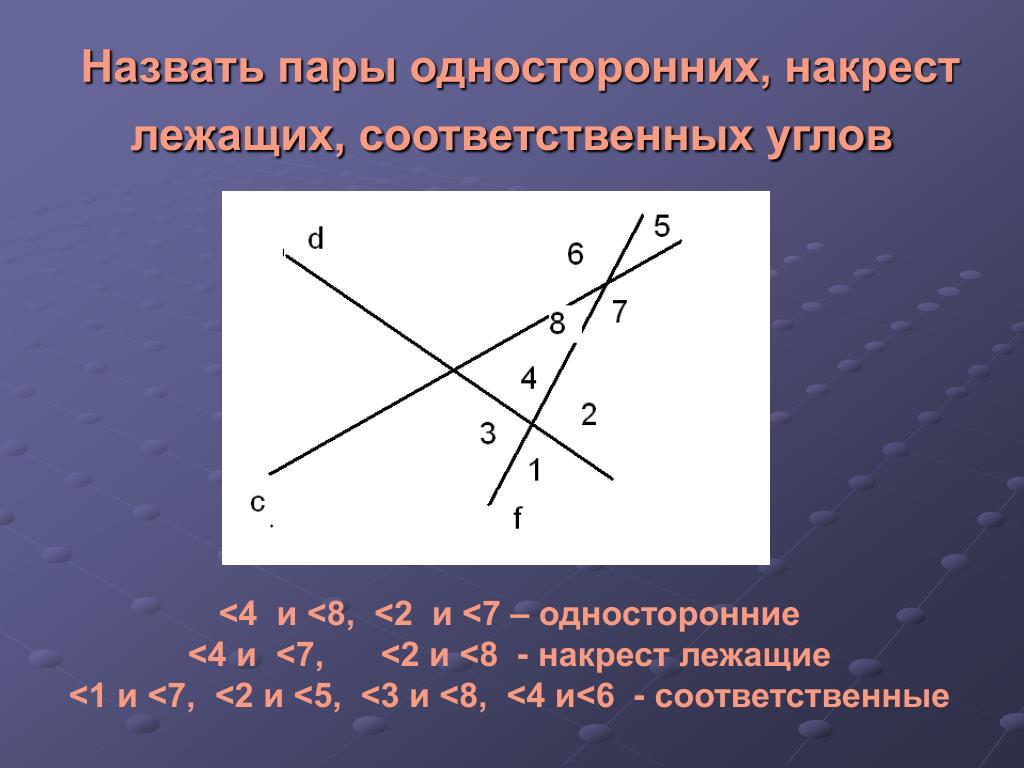
Доказательство этой не вполне очевидной истины оказывается невозможным. Ее принимают без доказательства, как необходимое допущение (postulatum).
Следствия.
1. Если прямая (С E ) пересекается с одной из параллельных (СВ ), то она пересекается и с другой (AB ), потому что в противном случае через одну и ту же точку С проходили бы две различные прямые, параллельные AB , что невозможно.
2. Если каждая из двух прямых (A и B ) параллельны одной и той же третьей прямой (С ) , то они параллельны между собой.
Действительно, если предположить, что A и B пересекаются в некоторой точке M , то тогда через эту точку проходили бы две различные прямые, параллельные С , что невозможно.
Теорема .
Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой параллельной .
С D .
Перпендикуляр E F , пересекаясь с AB , непременно пересечет и С D . Пусть точка пересечения будет H .
Предположим теперь, что С D не перпендикулярна к EH . Тогда какая-нибудь другая прямая, например HK , будет перпендикулярна к EH и, следовательно через одну и ту же точку H будут проходить две прямые параллельные AB : одна С D , по условию, а другая HK по доказанному раньше. Так как это невозможно, то нельзя допустить, что СВ была не перпендикулярна к EH .
Класс: 2
Цель урока:
- сформировать понятие о параллельности 2-х прямых, рассмотреть первый признак параллельности прямых;
- выработать умение применять признак при решении задач.
Задачи:
- Образовательные: повторение и закрепление изученного материала,
формирование понятия о параллельности 2-х прямых, доказательство 1-го
признака параллельности 2-х прямых.
- Воспитательные: воспитывать умение аккуратно вести записи в тетради и соблюдать правила построения чертежей.
- Развивающие задачи: развитие логического мышления, памяти, внимания.
Оборудование урока:
- мультимедийный проектор;
- экран, презентации;
- чертёжные инструменты.
Ход урока
I. Организационный момент.
Приветствие, проверка готовности к уроку.
II. Подготовка к активной УПД.
Этап 1.
На первом уроке геометрии мы рассматривали взаимное расположение 2-х прямых на плоскости.
Вопрос. Сколько общих точек могут иметь две прямые?
Ответ. Две прямые могут иметь либо одну общую точку, либо не имеют не
одной общей точки.
Вопрос. Как будут расположены относительно друг друга 2-е прямые, если
они имеют одну общую точку?
Ответ. Если прямые имеют одну общую точку, то они пересекаются
Вопрос. Как расположены 2-е прямые относительно друг друга, если они
не имеют общих точек?
Ответ.
То в этом случае данные прямые не пересекаются.
Этап 2.
На прошлом уроке Вы получили задание сделать презентацию, где мы встречаемся с непересекающимися прямыми в нашей жизни и в природе. Сейчас мы посмотрим эти презентации и выберем из них лучшие. (В жюри вошли учащиеся, которым в силу низкого интеллекта сложно создать свои презентации.)
Просмотр презентаций, выполненных учащимися: «Параллельность прямых в природе и жизни», и выбор из них лучших.
III. Активная УПД (объяснение нового материала).
Этап 1.
Рисунок 1
Определение. Две прямые на плоскости, которые не пересекаются, называются параллельными.
На данной таблице изображены различные случаи расположения 2-х параллельных прямых на плоскости.
Рассмотрим, какие отрезки будут параллельными.
Рисунок 2
1) Если прямая a параллельна b, то и отрезки AB и CD параллельны.
2) Отрезок может быть параллелен прямой. Так отрезок MN параллелен прямой a.
Рисунок 3
3) Отрезок AB параллелен лучу h. Луч h параллелен лучу k.
4) Если прямая a перпендикулярна прямой c, и прямая b перпендикулярна прямой c, то прямые a и b параллельны.
Этап 2.
Углы, образованные двумя параллельными прямыми и секущей.
Рисунок 4
Две параллельные прямые пересекаются третьей прямой в двух точках. При этом образуются восемь углов, обозначенных на рисунке числами.
Некоторые пары этих углов имеют специальные названия (см. рисунок 4).
Существует три признака, параллельности двух прямых , связанных с этими углами. На этом уроке мы рассмотрим первый признак .
Этап 3.
Повторим материал, необходимый для доказательства этого признака.
Рисунок 5
Вопрос. Как называются углы, изображённые на рисунке 5?
Ответ. Углы AOC и COB называются смежными.
Вопрос. Какие углы называются смежными? Дайте определение.
Ответ.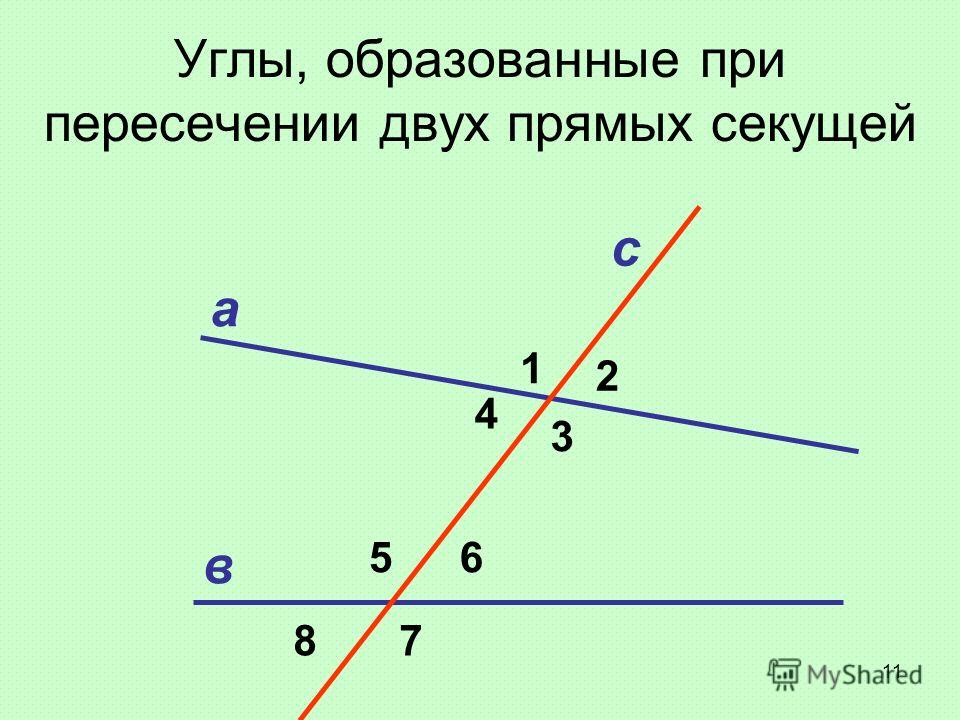
Два угла называются смежными, если у них одна сторона является
общей, а две другие являются продолжениями друг друга.
Вопрос. Каким свойством обладают смежные углы?
Ответ. Смежные углы в сумме дают 180 градусов.
AOC + COB
= 180°
Вопрос. Как называются углы 1 и 2?
Ответ. Углы 1 и 2 называются вертикальными.
Вопрос. Какими свойствами обладают вертикальные углы?
Ответ. Вертикальные углы равны между собой.
Этап 4.
Доказательство первого признака параллельности.
Теорема. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Рисунок 6
Дано: а и b – прямые
AB – секущая
1 =
2
Доказать: a//b.
1-ый случай.
Рисунок 7
Если 1 и 2 прямые, то a перпендикулярен AB, и b перпендикулярен AB, то а//b.
2-ой случай.
Рисунок 8
Рассмотрим случай, когда
1 и
2 не
прямые Разделим отрезок AB пополам точкой O.
Вопрос. Какими будут отрезки AO и OB по длине?
Ответ. Отрезки AO и OB равны по длине.
1) Из точки O проведём перпендикуляр к прямой а, ОН перпендикулярен a.
Вопрос. Каким будет угол 3?
Ответ. Угол 3 будет прямым.
2) От точки А на прямой b отложим циркулем отрезок АН 1 = ВН.
3) Проведём отрезок ОН 1 .
Вопрос. Какие треугольники образовались в результате доказательства?
Ответ. Треугольник ОНВ и треугольник ОН 1 А.
Докажем, что они равны.
Вопрос. Какие углы равны по условию теоремы?
Ответ. Угол 1 равен углу 2.
Вопрос. Какие стороны равны по построению.
Ответ. АО = ОВ и АН 1 = ВН
Вопрос. По какому признаку равны треугольники?
Ответ. Треугольники равны по двум сторонам и углу между ними (первый признак
равенства треугольников).
Вопрос. Каким свойством обладают равные треугольники?
Ответ. В равных треугольниках против равных сторон лежат равные углы.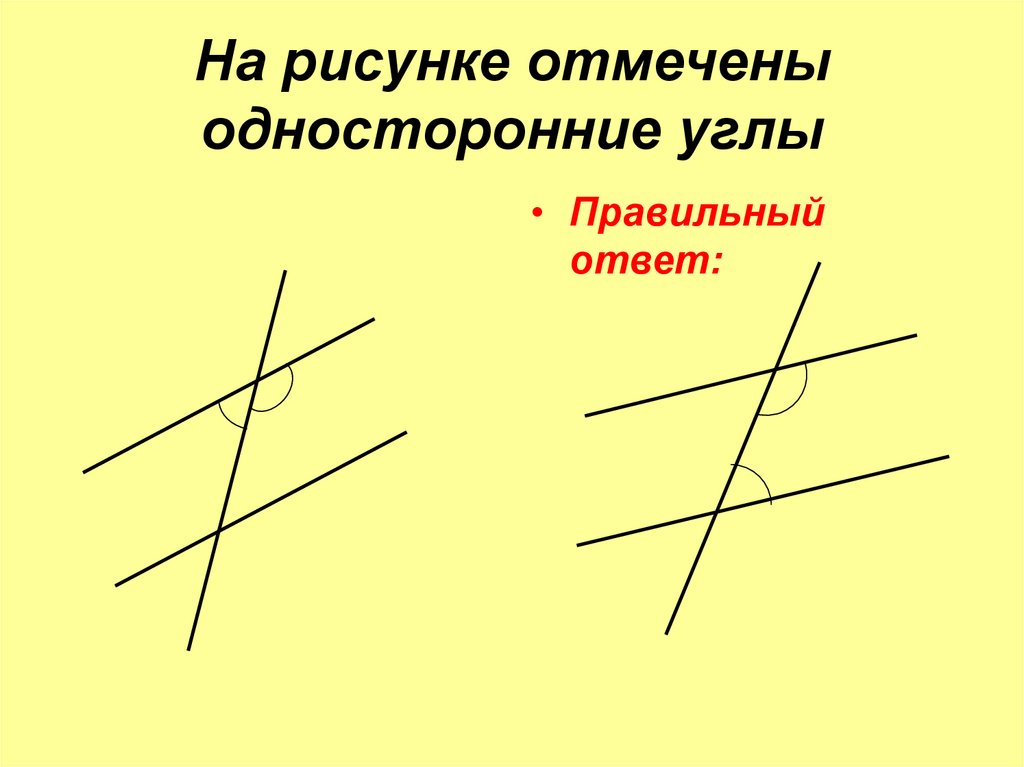
Вопрос. Какие углы будут равны?
Ответ. 5 =
6,
3 =
4.
Вопрос. Как называются
5 и
6?
Ответ. Эти углы называются вертикальными.
Из этого следует, что точки: Н 1 , О, Н лежат на одной прямой.
Т.к.
3 – прямой, а
3 =
4, то
4 – прямой.
Вопрос. Как расположены прямые а и b по отношению к прямой НН 1 ,
если углы 3 и 4 прямые?
Ответ. Прямые а и b перпендикулярны HH 1 .
Вопрос. Что мы можем сказать о двух перпендикулярах к одной прямой?
Ответ. Два перпендикуляра одной прямой параллельны.
Итак, а//b. Теорема доказана.
Сейчас я повторю все доказательство сначала, а Вы внимательно меня послушаете постараетесь все понять запомнить.
IV. Закрепление нового материала.
Работа по группам с разным уровнем развития интеллекта, с последующей проверкой на экране и на доске. У доски работают 3 ученика (по одному из каждой группы).
№1 (для учащихся со сниженным уровнем интеллектуального развития).
Дано: а и b прямые
с – секущая
1 = 37°
7 = 143°
Доказать: а//b.
Решение.
7 =
6
(вертикальные)
6 = 143°
1 +
4 = 180° (смежные)
4 =180°
– 37° = 143°
4 =
6 = 143°,
а они накрест лежащие
а//b 5 = 48°,
3 и
5 –
накрест лежащие углы, они равны
a//b.
Рисунок 11
V. Итог урока.
Итог урока проводится с использованием рисунков 1-8.
Производится оценка деятельности учащихся на уроке (каждый ученик получает соответствующий смайлик).
Домашнее задание: учить – стр. 52-53; решить №186 (б, в).
Эта глава посвящена изучению параллельных прямых. Так называются две прямые на плоскости, которые не пересекаются. Отрезки параллельных прямых мы видим в окружающей обстановке — это два края прямоугольного стола, два края обложки книги, две штанги троллейбуса и т. д. Параллельные прямые играют в геометрии очень важную роль. В этой главе вы узнаете о том, что такое аксиомы геометрии и в чём состоит аксиома параллельных прямых — одна из самых известных аксиом геометрии.
В п. 1 мы отмечали, что две прямые либо имеют одну общую точку, т. е. пересекаются, либо не имеют ни одной общей точки, т. е. не пересекаются.
Определение
Параллельность прямых а и b обозначают так: а || b.
На рисунке 98 изображены прямые а и b, перпендикулярные к прямой с. В п. 12 мы установили, что такие прямые а и b не пересекаются, т. е. они параллельны.
Рис. 98
Наряду с параллельными прямыми часто рассматривают параллельные отрезки. Два отрезка называются параллельными , если они лежат на параллельных прямых. На рисунке 99, а отрезки АВ и CD параллельны (АВ || CD), а отрезки MN и CD не параллельны. Аналогично определяется параллельность отрезка и прямой (рис. 99, б), луча и прямой, отрезка и луча, двух лучей (рис. 99, в).
Рис. 99 Признаки параллельности двух прямых
Прямая с называется секущей по отношению к прямым а и b, если она пересекает их в двух точках (рис. 100). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 100 обозначены цифрами.
Некоторые пары этих углов имеют специальные названия:
накрест лежащие углы : 3 и 5, 4 и 6;
односторонние углы : 4 и 5, 3 и 6;
соответственные углы : 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Рис. 100
Рассмотрим три признака параллельности двух прямых, связанные с этими парами углов.
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны: ∠1 = ∠2 (рис. 101, а).
Докажем, что а || b. Если углы 1 и 2 прямые (рис. 101, б), то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны.
Рис. 101
Рассмотрим случай, когда углы 1 и 2 не прямые.
Из середины О отрезка АВ проведём перпендикуляр ОН к прямой а (рис. 101, в). На прямой b от точки В отложим отрезок ВН 1 , равный отрезку АН, как показано на рисунке 101, в, и проведём отрезок ОН 1 . Треугольники ОНА и ОН 1 В равны по двум сторонам и углу между ними (АО = ВО, АН = ВН 1 , ∠1 = ∠2), поэтому ∠3 = ∠4 и ∠5 = ∠6.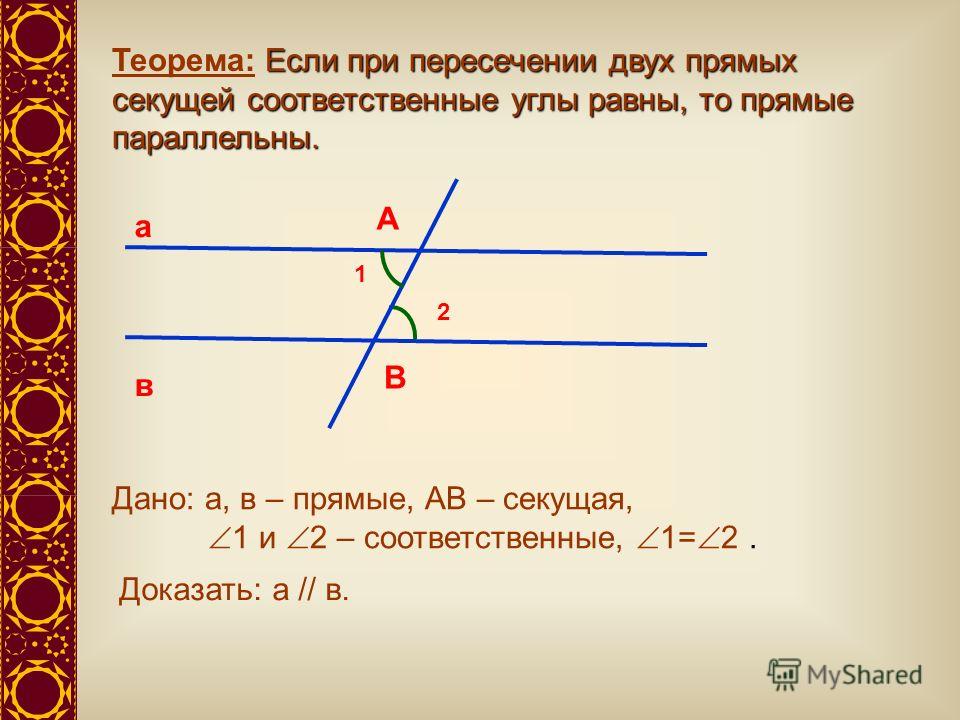
Из равенства ∠3 = ∠4 следует, что точка Н 1 лежит на продолжении луча ОН, т. е. точки Н, О и Н 1 лежат на одной прямой, а из равенства ∠5 = ∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Итак, прямые а и b перпендикулярны к прямой HH 1 поэтому они параллельны. Теорема доказана.
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей с соответственные углы равны, например ∠1 =∠2 (рис. 102).
Рис. 102
Так как углы 2 и 3 — вертикальные, то ∠2 = ∠3. Из этих двух равенств следует, что ∠1 = ∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые а и b параллельны. Теорема доказана.
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей с сумма односторонних углов равна 180°, например ∠1 + ∠4 = 180° (см. рис. 102).
Так как углы 3 и 4 — смежные, то ∠3 + ∠4 = 180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые а и b параллельны.
Теорема доказана.
Практические способы построения параллельных прямых
Признаки параллельности прямых лежат в основе способов построения параллельных прямых с помощью различных инструментов, используемых на практике. Рассмотрим, например, способ построения параллельных прямых с помощью чертёжного угольника и линейки. Чтобы построить прямую, проходящую через точку М и параллельную данной прямой а, приложим чертёжный угольник к прямой а, а к нему линейку так, как показано на рисунке 103. Затем, передвигая угольник вдоль линейки, добьёмся того, чтобы точка М оказалась на стороне угольника, и проведём прямую b. Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами α и β, равны.
Рис. 103 На рисунке 104 показан способ построения параллельных прямых при помощи рейсшины. Этим способом пользуются в чертёжной практике.
Рис. 104 Аналогичный способ применяется при выполнении столярных работ, где для разметки параллельных прямых используется малка (две деревянные планки, скреплённые шарниром, рис.
105).
Рис. 105
Задачи
186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что а || b, если:
а) ∠1 = 37°, ∠7 = 143°;
б) ∠1 = ∠6;
в) ∠l = 45°, а угол 7 в три раза больше угла 3.
Рис. 106
187. По данным рисунка 107 докажите, что АВ || DE.
Рис. 107
188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АС и BD параллельны.
189. Используя данные рисунка 108, докажите, что ВС || AD.
Рис. 108
190. На рисунке 109 АВ = ВС, AD = DE, ∠C = 70°, ∠EAC = 35°. Докажите, что DE || АС.
Рис. 109
191. Отрезок ВК — биссектриса треугольника АВС. Через точку К проведена прямая, пересекающая сторону ВС в точке М так, что ВМ = МК. Докажите, что прямые КМ и АВ параллельны.
192. В треугольнике АВС угол А равен 40°, а угол ВСЕ, смежный с углом АСВ, равен 80°. Докажите, что биссектриса угла ВСЕ параллельна прямой АВ.
193. В треугольнике ABC ∠A = 40°, ∠B = 70°. Через вершину В проведена прямая BD так, что луч ВС — биссектриса угла ABD. Докажите, что прямые АС и BD параллельны.
194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертёжного угольника и линейки проведите прямую, параллельную противоположной стороне.
195. Начертите треугольник АВС и отметьте точку D на стороне АС. Через точку D с помощью чертёжного угольника и линейки проведите прямые, параллельные двум другим сторонам треугольника.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.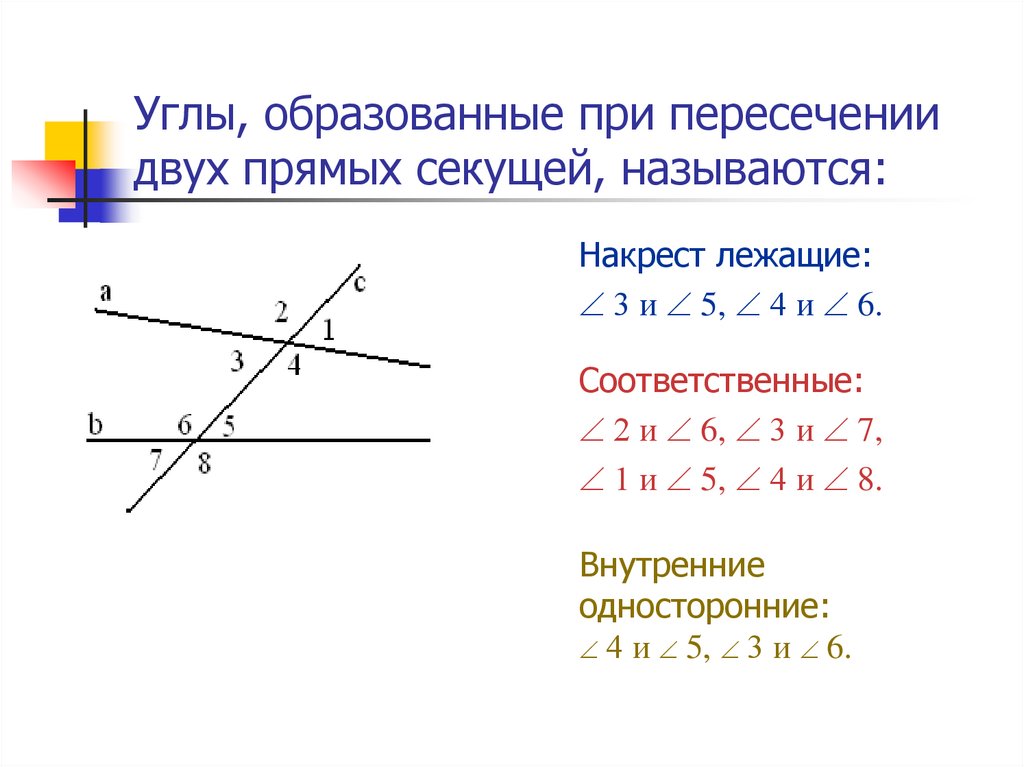
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Соответствующие углы — ChiliMath
ПоискСоответствующие углы — это два угла, которые лежат в сходных относительных положениях на одной и той же стороне секущей или на каждом пересечении. Обычно они образуются при пересечении двух параллельных или непараллельных прямых секущей.
Помните, что секущая — это линия, пересекающая две или более прямых.
На приведенном выше рисунке параллельные прямые a и b пересекаются секущей, в результате чего образуются 4 соответствующих угла. Например, \угол 2 и \угол 6 являются соответствующими углами. Почему? Потому что оба угла расположены в совпадающих углах или соответствующих позициях с правой стороны поперечной.
Другими словами, каждый угол расположен на выше линии и правее поперечной.
Вот наши соответствующие углы (должны быть парами) из диаграммы и их расположение.
- \angle \textbf{1} и \angle \textbf{5} – над линией, слева от поперечной
- \angle \textbf{3} и \angle \textbf{7} – под линией, слева поперечной
- \angle \textbf{2} и \angle \textbf{6} – над линией, справа от поперечной
- \angle \textbf{4} и \angle \textbf{8} – под линией , справа от поперечной
При работе с соответствующими углами следует помнить несколько вещей.
Соответствующие углы Постулат
Когда две параллельные прямые пересекаются секущей, то пары соответствующих углов конгруэнтны или имеют одинаковую меру .
Возьмем, к примеру, нашу диаграмму выше, так как угол 1 и угол 5 являются соответствующими углами, они конгруэнтны.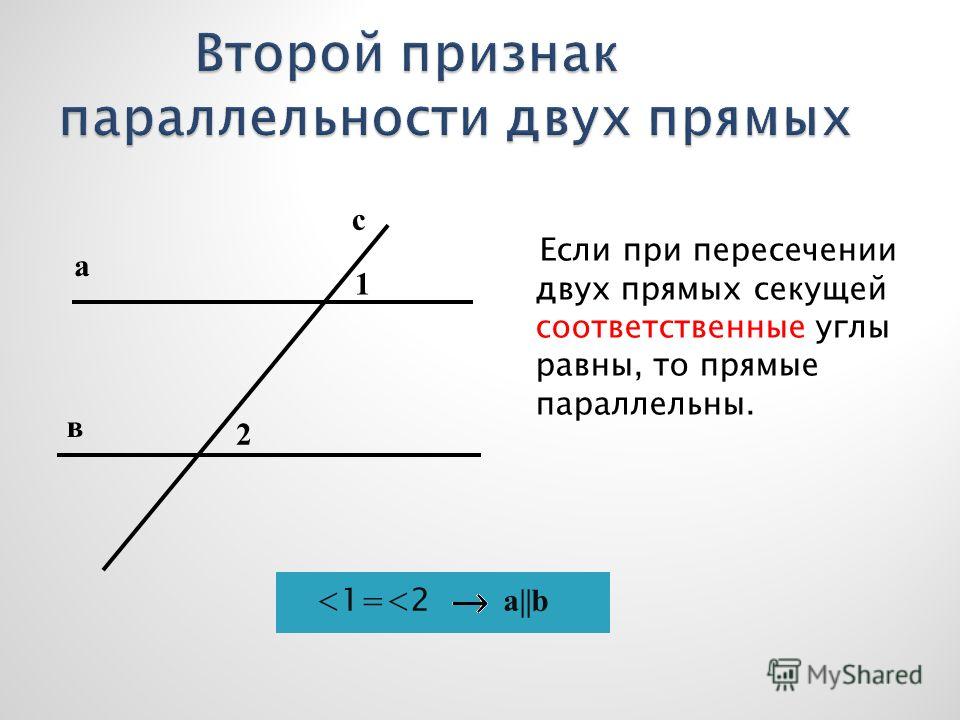
\circ. Следовательно, \угол 1 \конг \угол 5.
С другой стороны, если секущая пересекается с двумя непараллельными прямыми , образующиеся соответствующие углы не конгруэнтны и не имеют определенного отношения друг к другу.
Следовательно, \угол a и \угол e являются соответствующими углами, но НЕ конгруэнтными.
Примеры задач с соответствующими углами
Пример 1: Определите соответствующие углы.
Здесь мы имеем две параллельные прямые, прямые k и g, которые пересекаются секущей t. Напомним, что соответствующие углы — это углы, находящиеся в одинаковых положениях по одну и ту же сторону от секущей.
Таким образом, соответствующие углы равны:
- \угол 2 и \угол 1
- \угол 4 и \угол 3
- \угол 6 и \угол 5
- \угол 8 и \угол 7 9003 9
- Автор WonderHowTo
8 Пример 2: Назовите пары соответствующих углов и их расположение.
Как видите, секущая пересекает две непараллельные прямые, образуя 4 соответствующих угла.
\окр.
Вас также могут заинтересовать:
Альтернативные внешние углы
Альтернативные внутренние углы
Дополнительные углы
Дополнительные вертикальные углы
0
Как понять правило соответствующих углов « Математика :: WonderHowTo
В этом видео рассказывается о правиле соответствующих углов. При измерении угла между параллельными линиями (т.е.) Line1 и Line2 поперек прямой линии.
Угол А и угол В равны. Угол С и угол D равны. Угол E и угол F равны. В итоге угол G равен углу F. Значит, углы между параллельными прямыми во всех углах равны. Следовательно, это правило соответствующих углов. Это видео очень полезно для базовых курсов геометрии средней школы. Соответственные углы также состоят из острого угла, тупого угла, прямого угла. Угол А и угол В являются соответственными углами. Угол C и угол D являются соответственными углами. Угол E и угол F являются соответственными углами. Угол G и угол H являются соответственными углами. С помощью линейки измерьте углы между линией 1 и линией 2. То есть параллельные линии. Очевидно, углы между пересечением параллельных прямых составляют соответствующие углы. На листе бумаги нарисуйте горизонтальную линию. Теперь нарисуйте диагональную линию, которая делит эту линию пополам. Теперь вы создали четыре угла. Над линией обозначьте углы А и В слева направо. Под линией отметьте углы C и D, на этот раз справа налево. Углы A и C являются соответствующими углами, так как они имеют одинаковую градусную меру, а углы B и D являются соответствующими углами по той же причине.
Обозначьте пару несмежных углов, один внутренний и один внешний, на одной стороне обхода эти парные углы равны, если линии, пересекаемые обходом, параллельны. Когда обход пересекает две параллельные прямые, соответствующие углы равны. Соответствующие углы — это два равных угла, лежащих по одну сторону от пересечения и лежащих одинаково на двух разных параллельных прямых. Вы узнали два факта о параллельных прямых. Во-первых, параллельные прямые не пересекаются. Во-вторых, непараллельные прямые пересекаются. Теперь мы узнаем об углах параллельных прямых.
Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Начните свою карьеру с нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам базовых и продвинутых инструкций по функциям, формулам, инструментам и многому другому.