Сколько единиц в числах от 1 до 35: Сколько единиц в числах от 1 до 35

Числа от 1 до 100. Состав числа. Круглые числа / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Числа от 1 до 100. Состав числа. Круглые числа

Числа от 1 до 100

Предыдущее и последующее число

Предыдущее число — то число, которое при счете следует перед данным числом.

56, 57

Последующее число — то число, которое при счете называют сразу после данного числа.

56, 57

---

Однозначные и двузначные числа

Вспомни, что каждая цифра в записи занимает определенное место.

Единицы стоят на первом месте справа.

Десятки стоят на втором месте справа.

Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.

Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.

Самое маленькое однозначное число — 0.

Самое большое однозначное число — 9.

Самое маленькое двузначное число — 10.

Самое большое двузначное число — 99.

---

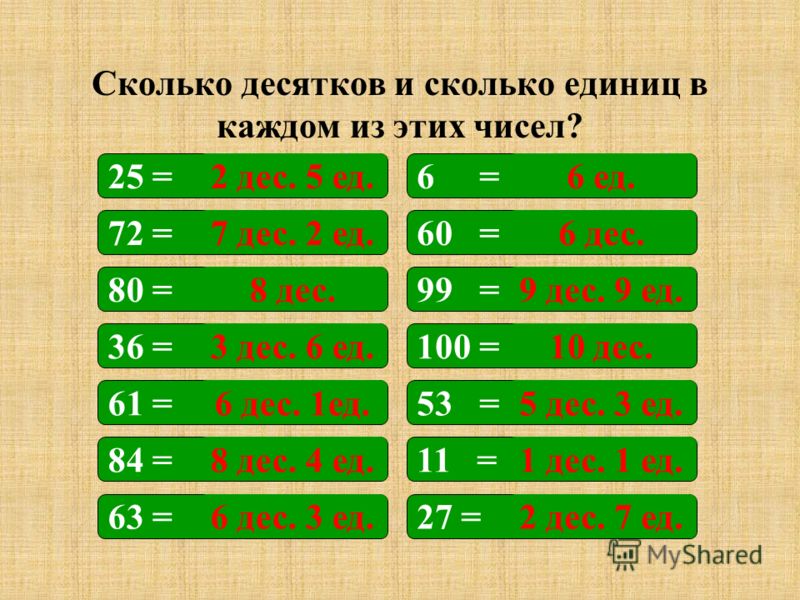
Состав двузначного числа

Всего на рисунке 35 палочкек.

35 = 3 дес. 5 ед.

35 = 30 + 5

Состав числа 35 — 3 дес. 5 ед.

---

Красных палочек 12.

12 = 1 дес. 2 ед.

12 = 10 + 2

Состав числа 12 — 1 дес. 2 ед.

---

Синих палочек всего 23.

23 = 2 дес. 3 ед.

23 = 20 + 3

Состав числа 23 — 2 дес. 3 ед.

---

---

---

Теперь научимся представлять числа в виде суммы разрядных слагаемых.

Какие разряды выделяют в двузначных числах?

В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:

десятки + единицы

В числе 35 три десятка и 9 единиц:

35 = 30 + 5

---

Сравнение двузначных чисел

Числа 42 и 24 похожи тем, что в их записи использованы одинаковые цифры: цифра 4 и цифра 2. Но цифра 4 для числа 42 означает десятки, а для 24 — единицы, цифра 2 для числа 42 означает единицы, а для 24 — десятки.

Число	42	24
Количество десятков	4	2
Количество единиц	2	4

42 > 24

1. Сравнение двузначных чисел всегда начинается с десятков.

2. Если количество десятков одинаково, тогда переходят к сравнению единиц.

---

Круглые числа

Числа, которые оканчиваются на 0, называются круглыми. — 60, 30, 20.

или

В разряде единиц у круглого числа — число 0. — 70, 90, 40.

10, 20, 30, 40, 50, 60, 70, 80, 90, 100.

10 + 40 = ?

1 дес. + 4 дес. = 5 дес.

5 дес. = 50, значит,

10 + 40 = 50

---

Счёт десятками

Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.

Десятками можно считать:

— это 2 десятка — записываю так: 2 дес.

---

Действия с десятками и единицами

— это 31

Как решить пример 34 + 25?

34 — это 3 дес. и 4 ед.

25 — это 2 дес. и 5 ед.

3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.

5 дес. — 50

50 + 9 = 59

Можно записать короче:

Рассуждаю так:

Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:

Сначала складываю единицы:

4 + 5 = 9

Теперь складываю десятки:

30 + 20 = 50

Запись решения выглядит так:

34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59

34 + 25 = 59

Десятки складываются с десятками.

Единицы складываются с единицами.

---

Как решить пример 38 — 16?

Число 38 — можно представить как 3 дес. и 8 ед.

Число 16 — это 1 дес. 6 ед.

3 дес. 8 ед. — 1 дес. 6 ед. = 2 дес. 2 ед.

38 — 16 = (30 — 10) + (8 — 6) = 20 + 2 = 22

38 — 16 = 22

Можно рассуждать так:

Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.

38 — 16 = 22

Вывод:

Десятки вычитаются из десятков.

Единицы вычитаются из единиц.

Мы рассмотрели случаи устных вычислений с двузначными числами.

Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.

1 класс

Страница 48. Урок 25, Петерсон, Учебник, часть 3

Страница 49. Урок 25, Петерсон, Учебник, часть 3

Страница 50. Урок 26, Петерсон, Учебник, часть 3

Страница 53. Урок 27, Петерсон, Учебник, часть 3

Страница 55. Урок 28, Петерсон, Учебник, часть 3

Страница 62. Урок 32, Петерсон, Учебник, часть 3

Страница 63. Урок 32, Петерсон, Учебник, часть 3

Страница 68. Урок 35, Петерсон, Учебник, часть 3

Страница 70. Урок 36, Петерсон, Учебник, часть 3

Страница 87. Урок 44, Петерсон, Учебник, часть 3

2 класс

Страница 12, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 8, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 20, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 37, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 13. Тест 1. Вариант 2, Моро, Волкова, Проверочные работы

Страница 31, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 16, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 45, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 37. Урок 14, Петерсон, Учебник, часть 2

3 класс

Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 61, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 90, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 44, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 49, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 60, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 70, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 5.

ПР 1. Вариант 2, Моро, Волкова, Проверочные работы

Страница 6. ПР 2. Вариант 1, Моро, Волкова, Проверочные работы

4 класс

Страница 7, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 86, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 87, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 88, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

---

Дискретная математика, комбинаторика, теория чисел

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Whitaker	Сколько нужно цифр для записи всех чисел от 1 до 999999 24. 06.2011, 19:35
12/01/11 1320 Москва	Сколько и каких цифр понадобится, чтобы написать все числа от 1 до 999 999 включительно? Я решил эту задачку и ответ у меня получился. Если кто-нибудь решит её напишите пожалуйста только ответ так как мне бы хотелось проверить свой ответ Заранее благодарю!

Vince Diesel	Re: Комбинаторная задачка. 24.06.2011, 20:00
Заслуженный участник 25/02/11 1775	Напишите свой.

JMH	Re: Комбинаторная задачка. 24.06.2011, 20:35
25/02/10 687	Чесла записывать нужно только целые? В какой системе счисления? P. S. Строго говоря, достаточно двух цифр: 0 и 1.

Zealint	Re: Комбинаторная задачка. 24.06.2011, 21:16
26/01/10 959

PAV	Re: Комбинаторная задачка. 24.06.2011, 23:21
Супермодератор 29/07/05 8248 Москва	Цифр с 1 по 9 нужно по 600000, а нулей — 488889.

Whitaker	Re: Комбинаторная задачка. 25.06.2011, 12:32
12/01/11 1320 Москва	PAV в сообщении #461984 писал(а): Цифр с 1 по 9 нужно по 600000, а нулей — 488889. Да да большое спасибо Вам PAV у меня точно также получилось.

Whitaker	Re: Комбинаторная задачка. 25.06.2011, 21:05
12/01/11 1320 Москва	Я решил эту задачу, но мое решение довольно таки трудное и громоздкое в отличие от решения, приведённое в книге. В книге дано следующее решение. Дополним все числа впереди нулями до 6-значных и еще включим число 000 000. Чисел всего будет ровно , для их записи потребуется цифр, а поскольку все 10 цифр равноправны и должны входить одинаковое число раз, каждая будет употреблена раз. Но нулей будет 488 889. Может ли кто-нибудь объяснить что почему все цифры должны входить одинаковое число раз? Честно говоря, я не понял почему это так. P.S. Тут написано, что число нулей в k-значном числе будет Почему это так?

ИСН	Re: Комбинаторная задачка. 25.06.2011, 22:00
Заслуженный участник 18/05/06 13406 с Территории	Всех цифр поровну, потому что если поменять местами любую цифру и любую другую, получится тоже число из нашей кучи. Есть такое слово — биекция. А последнюю Вашу фразу я игнорирую как недостоверную, потому что, например, 123456 — это очевидным образом k-значное число, в котором нулей не столько.

Whitaker	Re: Комбинаторная задачка. 25.06.2011, 22:17
12/01/11 1320 Москва	ИСН в сообщении #462200 писал(а): А последнюю Вашу фразу я игнорирую как недостоверную, потому что, например, 123456 — это очевидным образом k-значное число, в котором нулей не столько. Тут имеется в виду, что нулей среди всех k-значных ровно . ИСН в сообщении #462200 писал(а): Всех цифр поровну, потому что если поменять местами любую цифру и любую другую, получится тоже число из нашей кучи.. И что? Я Вас не понял.

ИСН	Re: Комбинаторная задачка. 25.06.2011, 22:38
Заслуженный участник 18/05/06 13406 с Территории	Ёлки, ну заменили мы все двойки — на единицы, а единицы — на двойки. Получилась какая-то другая куча чисел. Если в нашей куче было (ну, допустим) единиц больше, чем двоек, то здесь — наоборот, двоек больше. Но постойте, числа-то те же самые. Это же наша куча! Так кого в ней больше?

Whitaker	Re: Комбинаторная задачка. 26.06.2011, 12:13
12/01/11 1320 Москва	Я понял то, что всех цифр поровну. Но я не понял почему нулей среди всех k-значных ровно . Может кто-нибудь это объяснить?

PAV	Re: Комбинаторная задачка. 26.06.2011, 19:31
Супермодератор 29/07/05 8248 Москва	Ну смотрите: есть позиций, на старшей должен стоять не-ноль — отсюда , далее берем одну из оставшихся позиций, ставим на нее ноль, а оставшиеся позиции заполняем любыми цифрами. И так делаем для каждой из позиции. Хотя я считал немного иначе (но может быть это окажется то же самое). То, что любой ненулевой цифры нужно по — это очевидно. Для нуля же рассуждаем отдельно для каждой позиции. Последняя: перед ней можно поставить любую комбинацию цифр, кроме нулевой, это вариантов. Предпоследняя: после нее можно поставить любую цифру, а перед ней — любую комбинацию четырех цифр, кроме опять всех нулей, это дает вариантов. И так далее, в итоге получается общий результат: А можно подсчитать количество всех цифр во всех числах, это несложно, и вычесть число всех не-нулей Я использовал это для дополнительной проверки того, что не ошибся.

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 12 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Место Значение

fshyCNqHIbw

Мы записываем числа, используя только десять символов (называемых цифрами).
Важно, где мы их размещаем.

Десять цифр

Цифры, которые мы используем сегодня, называются «индийско-арабскими цифрами»:

.

0 1   2   3   4   5   6   7   8   9

Мы можем использовать их сами по себе, чтобы считать до 9:

0
1
2
3
4
5
6
7
8
9
??

Но что будет после 9?

Десять и более …

Когда у нас есть более 9 элементов, мы начинаем другой столбец — столбец «десятки» — и записываем сколько у нас «десятков», а затем сколько «единиц» (также называемых «единицами»).

Итак, мы пишем:

 

Пример: так мы записываем

двенадцать :

Десятки	Единицы
1	2

Число «12»

Здесь сказано, что у нас есть 1 Десять и 2 Единицы , что составляет 12.

Это также можно записать как 1 × 10 + 9 2 ×0003

Пример: «35» означает 3 десятка и 5 единиц, что также равно 3 × 10 + 5 × 1

Десятки	Единицы
3	5

Номер «35»

Ноль

Что, если у нас есть 1 Десятка, но нет Единиц? Мы показываем «Нет» по , ставя ноль там:

Десятки	Единицы
1	0

Цифра «10»

Мы должны поставить ноль вместо единиц, иначе «10» выглядит как «1».

Сотня или больше…

Когда у нас есть более 99 элементов, мы начинаем другой столбец — столбец «сотни». Теперь нам нужно чтобы показать, сколько сотен, десятков и единиц:

Сотни	Десятки	Единицы
1	4	3

Номер 143

Это показывает, что у нас есть 1 сотня, 4 десятка и 3 единицы:

Это также может быть записано как 1 × 100 + 4 × 10 + 3 × 1.

Пример: «369» означает 3 сотни, 6 десятков и 9 единиц

Что также равно 3 × 100 + 6 × 10 + 9 × 1

Мы также используем ноль, когда нет десятков:

Пример: «104» означает 1 сотню,

ноль десятки и 4 единицы.

Сотни	Десятки	Единицы
1	0	4

Номер 104

И так далее.

..

Каждый раз, когда мы хотим показать большее число, мы просто добавляем один столбец слева от , и мы знаем, что это всегда В 10 раз больше , чем столбец справа.

каждый новый столбец слева в десять раз больше

Итак, важно, где мы РАЗМЕЩАЕМ цифру!

имен для каждого столбца

Это имена каждого столбца:

Миллионы

Сотни тысяч

Десять тысяч

Тысячи

Сотни

Десятки

Единицы

(для больших сумм см. метрические номера)

Пример: число одиннадцать тысяч триста двадцать семь в таблице разрядов:

Десять тысяч	Тысячи	Сотни	Десятки	Единицы
1	1	3	2	7

Номер 11 327

 

1686, 1687, 1688, 1689, 1690, 1691, 5875, 5876, 5877, 5878

Сколько раз цифра 1 встречается в числах от 1 до 1000?

Системы счисления — это значение, используемое для счета и измерения объектов, а также для выполнения арифметических вычислений. Это метод записи для выражения чисел. Он обеспечивает уникальное представление каждого числа и представляет арифметическую и алгебраическую форму числа. Это позволяет нам выполнять арифметические операции, такие как сложение, вычитание, умножение и деление.

Уравнение — это объявление, которое связывает два алгебраических выражения с одинаковыми значениями с помощью знака «=». Например: в уравнении 8x + 4 = 7, 8x + 4 — это выражение в левой части, а 7 — это выражение в правой части, связанное знаком «=».

Что такое число?

Слово или символ, обозначающий сумму, называется числом. Числа 4, 6, 8 и т. д. — четные числа, а 3, 5, 7 и т. д. — нечетные числа. Число – это значение, образованное комбинацией цифр. Эти числа используются для выражения алгебраических величин. Целое число — это указание из набора из 10 символов в диапазоне от 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Любое объединение целых чисел представляет собой число. Размер числа зависит от количества цифр, которые используются для его построения. Например: 126, 128, 0,356, -12, 78, 94 и т. д.

Целые числа

Целые числа такие же, как натуральные числа, но они также включают «ноль». Мы можем подарить целые числа символом W. Целые числа включают в себя все натуральные числа и 0 (ноль).

Мы знаем, что числа 1, 2, 3, 4, 5 — натуральные числа. А числа 0, 1, 2, 3, 4, 5, 6 и т. д. — это целые числа, так как они включают в себя и 0. Целые числа представлены как W, а натуральные числа представлены как N. Поэтому правильно сказать,

                                                                       W= {N} + 0

В числовой строке все, что находится справа от 0 (включая .

Сколько раз цифра 1 встречается в числах от 1 до 1000?

Решение:

Подсказка: Самый простой способ — написать числа в диапазоне от 10 до 100, а затем подсчитать количество единиц в них

Шаги, чтобы найти решение:

Сначала возьмем числа в диапазоне 10:

В диапазоне чисел от 0 до 10 цифра 1 появляется 2 раза.

Теперь складываем числа в диапазоне 100

В диапазоне чисел от 0 до 99 цифра 1 появляется 20 раз.

(Они: 1, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 21, 31, 41, 51, 61, 71, 81, 91)

Обратите внимание, что в числе 11, 1 появляется два раза.

Теперь от 100 до 199 цифра 1 появляется 120 раз.

В этом случае цифра на разряде сотен равна 1. Следовательно, имеется 120 единиц от 100 до 199.

Объяснение- мы должны найти единицы из разряда 100, 101, 102……….. 199. На разряде сотен из этих 3 цифра 1 появится 100 раз. На месте десятков 1 появится 10 раз

То есть в случаях 110, 111, 112, 113, 114…… 119. На месте единиц 1 появится 10 раз (101, 111, 121, 131……. 191) 

Итак, добавьте это:

100 + 10 + 10 = 120, поэтому 1 встречается 120 раз.

Теперь с 200 до 299 имеем 201, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 221, 231, 241, 251, 261, 271, 281, 291 цифра 1 встречается 20 раз.

Аналогично,

От 300 до 399 имеем 301,…311,…. 391. Опять 20 раз

От 400 до 499 имеем 401,…411,…491. Опять 20 раз

От 500 до 599 имеем 501,…511,…591. Опять 20 раз.

От 600 до 699 имеем 601,…611,…691. Опять 20 раз

От 700 до 799 имеем 701,…711,…791. Опять 20 раз

От 800 до 899 имеем 801,…811,…891. Снова 20 раз

От 900 до 999 имеем 901,…911,…991. Снова 20 раз

и тогда у нас есть 1000, в котором цифра 1 появляется 1 раз

Складывая все вышеперечисленное, мы получаем:

Общее количество раз = (20).(9) + 120 + 1

= 180 + 120 + 1

= 301

Следовательно, когда мы перечисляем числа от 1 до 1000, цифра 1 пишется 301 раз.

Примечание: Не забывайте подсчитывать цифру 1 дважды в числах типа 11, а также не забывайте подсчитывать цифру 1 в сотом месте в числах от 100 до 199, а также в тысячном разряде, например 1000.

Аналогичные вопросы

Вопрос 1: При перечислении чисел от 1 до 1000 сколько раз встречается цифра 5.

Ответ:

Этапы поиска решения:

Сначала возьмем числа в диапазоне 10:

Из диапазона чисел от 0 до 10 цифра 5 появляется 1 раз.

Теперь складываем числа в диапазоне 100

В диапазоне чисел от 0 до 99 цифра 5 появляется 20 раз.

(Они: 5, 15, 25, 35, 45, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 65, 75, 85, 95)

Обратите внимание, что в числе 55, 5 появляется два раза.

Теперь от 100 до 199 имеем: 105, 115, 125, 135, 145, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 165, 175, 185, 195. Цифра 5 появляется 20 раз.

Аналогично,

От 200 до 299 имеем 205,215…….245, 250,…255,…..,295. Опять 20 раз.

От 300 до 399 имеем 305,…355,…,395. Опять 20 раз

От 400 до 499 имеем 405,…455,…,495. Опять 20 раз

От 600 до 699 имеем 605,…655,…,695. Опять 20 раз

От 700 до 799 имеем 705,…755,…,795. Снова 20 раз

От 800 до 899 имеем 805,…855,…,895. Снова 20 раз

От 900 до 999 имеем 905,…955,…,995. Снова 20 раз

Теперь оставшийся диапазон от 500 до 599:

Теперь от 500 до 599 цифра 5 появляется 120 раз.

В этом случае цифра сотен равна 5. Следовательно, имеется 120 пятерок от 500 до 599.

Объяснение: Нам нужно найти пятерки из 500, 501, 502……….. 599. В сотнях место этих трехзначных чисел, 5 придет 100 раз. На месте десятков 5 будет 10 раз

То есть в случаях 550, 551, 552, 553, 554…… 559. На месте единиц 5 будет 10 раз (505, 555, 525, 535……. 595)

Итак, добавьте это:

100 + 10 + 10 = 120, так что 5 появится 120 раз.

Складывая все вышеперечисленное, мы получаем:

Общее количество раз = (20).(9) + 120 

= 180 + 120

= 300

Следовательно, когда мы перечисляем числа от 1 до 1000, цифра 5 написано 300 раз.

Примечание: Не забудьте дважды подсчитать цифру 5 в числах типа 55, а также не забудьте подсчитать цифру 5 в сотых долях в числах от 500 до 599.

Вопрос 2: Как сколько раз цифра 2 встречается в числах от 1 до 100?

Ответ:

Полное пошаговое решение:

Нужно найти, сколько раз цифра 2 встречается в числах от 1 до 100.

От 1 до 10 цифра 2 появляется только один раз для 2.

От 11 до 20 цифра 2 появляется два раза для чисел от 12 до 20.

От 21 до 30 цифра 2 появляется в числах 21, 22, 23, 24, 25, 26, 27, 28 , 29 и 22

встречается дважды. Итак, оно появляется десять раз.

От 31 до 40 цифра 2 появляется только один раз для 32.

От 41 до 50 цифра 2 появляется только один раз для 42.

От 51 до 60 цифра 2 появляется только один раз для 52.

От 61 до 70 цифра 2 появляется только один раз для 62.

От 71 до 80 цифра 2 появляется только один раз для 72.

От 81 до 90 цифра 2 появляется только один раз для 82.

От 91 до 100 цифра 2 появляется только один раз для 92.

No related posts.