Cos2X sin pi 2 x: Решите уравнение: cos 2x = sin (x + π/2). Найдите все корни… — Задание 13 ЕГЭ по математике (Уравнения)

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28
Найти точное значение		sin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )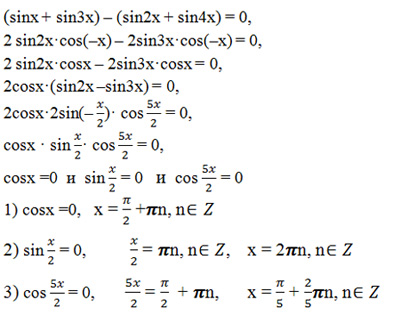
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Решить уравнение sin(3Pi/2-2x)=sinx

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2013-03-24

  Здравствуйте, Дорогие друзья! В данной статье мы с вами рассмотрим решение тригонометрического уравнения, и найдём корни принадлежащие определённому (заданному) отрезку. Подобный пример мы уже рассмотрели в предыдущей статье данной рубрики. Но в этом примере мы разберём другой способ определения  корней на отрезке.

Дано уравнение

а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие отрезку

Решение:

а) Используем формулу приведения для синуса и формулу косинуса двойного угла:

Привели уравнение к квадратному. Производим замену переменной, обозначим sin x = t.

Решая квадратное уравнение  2t2 – t – 1 = 0, получим:

Это простейшие тригонометрические уравнения.

Решая  sin x = 1,  получим:

Решая sin x = –½,  получим:

Итак, мы получили корни:

б) С помощью единичной окружности отберём корни на отрезке

Без расчётов, визуально сходу определить корни принадлежащие отрезку может далеко не каждый. Для этого необходима большая практика и отличное «понимание» тригонометрической окружности. Рассмотрим способ, при использовании которого, вы безошибочно определите корни на заданном интервале. Переведём  радианы в  градусы. Так  как Пи  радиан  это 180 градусов, то отрезок

в (градусах) будет выглядеть следующим образом: [2700;4500]. Отберём  корни.

Суть подхода такова: мы берём произвольные коэффициенты k, подставляем в каждый из корней и вычисляем. Получаем корни (углы) и смотрим – попадают ли они в интервал. Те, которые попадают мы отмечаем как верный ответ.

При k = 1:

При k = 2:

При k = 3  и  далее можно не проверять, так как уже видно, что при этом значении k углы будут находиться вне пределов интервала.

Таким образом, отрезку [2700;4500] принадлежат корни  4500  и  3300 в радианах это

Возникает вопрос: какие «произвольные»  коэффициенты k брать?

Ответ прост: в пределах от –3 до 3, так как границы заданного интервала в подобных заданиях обычно лежат «недалеко» от нуля. Для начала берите k = 0, затем по полученным значениям корней поймете какие коэффициенты брать, положительные или отрицательные.

Конечно, данный способ совершенным не назовёшь, кому-то наиболее понятен подход изложенный в уже указанной выше статье. Но он, безусловно, позволяет находить верное решение. Да и в градусной мере оценивать принадлежность угла указанному интервалу многим удобнее.

Кстати, если сравнивать объём вычислений представленного способа и описанного в уже указанной статье (см. ссылку выше), то он практически одинаков.

На этой странице вы можете посмотреть примеры уравнений.

На этом всё. Успехов Вам!


Категория: №12 Урав-ия и системы | ЕГЭ-№12Уравнения

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.


Исчисление

— Решение $\cos(2x)\cos\left(x — \frac{\pi}{6}\right) = \sin(2x)\sin\left(\frac{\pi}{6} — x\right)$ для $x\in(0,\pi/2)$

спросил

Изменено 2 года, 7 месяцев назад

Просмотрено 365 раз

$\begingroup$

Решите это уравнение относительно $x\in (0 , \frac{\pi}{2})$

$$\cos(2x)\cos\left(x — \frac{\pi}{6}\right) = \sin(2x)\sin\left(\frac{\pi}{6} — x\ справа)$$

Я попробовал использовать формулы $\cos(a-b)$ и $\sin(a-b)$, но проблема кажется немного сложнее.

Есть ли другое элегантное решение для этого?

  • исчисление
  • тригонометрия

$\endgroup$

$\begingroup$

Это несложно, уравнение принимает вид

$$\cos(2x)\cos(x-\frac{\pi}{6})+\sin(2x)\sin(x-\frac{\pi {6})=0$$

, что эквивалентно

$$\cos(x+\frac{\pi}{6})=0$$ Таким образом, решение

$x+\frac{\pi}{6}=\frac{\pi}{2}+k\pi$

$x=\frac{\pi}{3}+k\pi

$

Это самое элегантное решение для меня.

$\endgroup$

1

$\begingroup$

$$\cos(2x)\cos(\pi/6-x)-\sin(2x)\sin(\pi/6-x)=0$$ $$\Rightarrow \cos(2x+\pi/6-x)=0$$ (используя $\cos(a+b)=\cos a \cos b -\sin a \sin b$) $$\стрелка вправо x+\pi/6=\pi/2$$ $$\Rightarrow \boxed{x=\pi/3}$$

$\endgroup$

$\begingroup$

Уравнение $\cos (2x) \cos (x-\frac {\pi} 6)+\sin (2x)\sin (x-\frac {\pi} 6)=0$. Это то же самое, что $\cos (2x-(x-\frac {\pi} 6))=0$ или $\cos (x+\frac {\pi} 6)=0$. Итак, $x+\frac {\pi} 6=\frac {(2n+1)\pi} 2$ для некоторого целого числа $n$. Для $x \in (0,\frac {\pi} 2)$ мы должны иметь $n=0$, поэтому $x =\frac {\pi} 3$.

$\endgroup$

$\begingroup$

В качестве альтернативы, поскольку $x=k\frac \pi 4$ и $x = \frac{\pi}{6}+k\frac \pi 2$ не являются решениями, мы имеем

$$\ cos(2x)\cos\left(x — \frac{\pi}{6}\right) = \sin(2x)\sin\left(\frac{\pi}{6} — x\right) \iff \ frac {\ sin (2x)} {\ cos (2x)} = \ frac {\ cos \ left (\ frac {\ pi} {6} — x \ right)} {\ sin \ left (\ frac {\ pi}{6} — x\right)}$$

$$\iff \tan (2x)=\cot\left(\frac{\pi}{6} — x\right)$$

и так как

$$\tan A=\cot B \iff A=\frac \pi 2-(B+k\pi)$$

получаем

$$2x=\frac \pi 2-\ frac{\pi}{6} + x+k\pi \iff x=\frac \pi 3 +k\pi $$

$\endgroup$

Решите cos 2x=|sin x|, x in (-pi/2, pi).

  • Курс
    • NCERT
      • Класс 12
      • Класс 11
      • Класс 10
      • Класс 9
      • Класс 8
      • 2 Класс 4 0024
    • ИИТ СО
  • Экзамен
    • JEE MAINS
    • JEE ADVANCED
    • X BOARDS
    • XII BOARDS
    • Neet Year

    • Физика Предыдущий год
    • Химия Предыдущий год
    • Биология Предыдущий год
    • Нет Все образцы работ
    • Образцы работ по биологии
    • Образцы работ по физике
    • Образцы работ по химии
  • Загрузить PDF-файлы
    • Класс 12
    • Класс 11
    • Класс 10
    • Класс 9
    • Класс 8
    • Класс 7
    • Класс 6 9024 7
      • 9000 022
    • Экзаменационный уголок
    • Онлайн-класс
    • Викторина
    • Ask Doubt в WhatsApp
    • Поиск Doubtnut
    • Английский словарь
    • Toppers Talk
  • 0024
  • О нас
  • Карьера
  • Скачать
  • Получить приложение

Обновления

04/on:

4 021

CENGAGE АНГЛИЙСКИЙ-ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ-ИЛЛЮСТРАЦИЯ

20 видео

РЕКЛАМА

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

Видео по теме

Решить sin−1(x2−2x+1)+cos−1(x2−x)=π2

35613888

01:24

Решите уравнение 2(cosx+cos2x)+sin2x(1+2cosx)=2sinx для x∈[−π,π].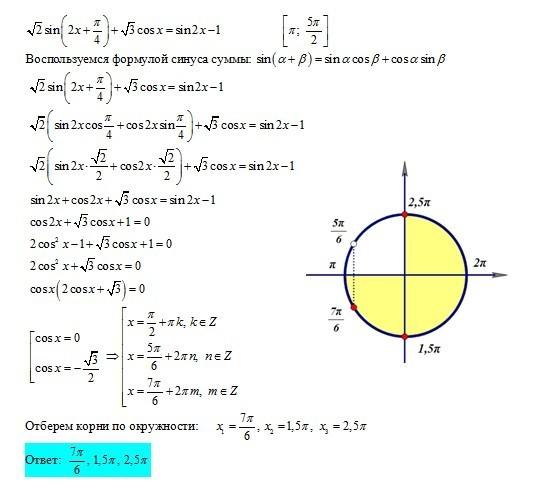

68806759

04:27

Решите cos2x=|sinx|,x∈(−π2,π).

68806820

02:18

Докажите, что: cos(π+x)cos(−x)sin(π−x)cos(π2+x)=cot2x

571219511

9003 уравнение 2(cosx+cos2x)+sin2x(1+2cosx)=2sinx для x∈[−π,π].

642549641

03:41

Решить cos2x=|sinx|,x∈(−π2,π).

642549683

02:24

Докажите, что: cos(π+x)cos(−x)sin(π−x)cos(π2+x)=cot2x

642563461

900:19 Решить: 19 потому что 2x gt | грех х | х в [-пи,пи] .

642718318

02:19

Докажите: что cos(π+x)cos(−x)sin(π−x)cos(π2+x)=cot2x

643293466

03:02

:- cos(π+x)cos (−x)sin(π−x)cos(π2+x)=cot2x

643579617

02:40

Решите следующие уравнения: sin-1(x2-2x+3)+cos-1(x2-x)=π2 sinx+cosx)1+sin2x=2 , когда −π≤x≤π .

644749429

01:57

Решите cos 2x=|sin x|, x in (-pi/2, pi) .

645288465

05:05

Решите cos 2x=|sin x|, x in (-pi/2, pi) .

645288470

02:52

РЕКЛАМА

  • CENGAGE ENGLISH-ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ-ИЛЛЮСТРАЦИЯ

  • Найдите наименьшее положительное значение xa n dy x-y=pi/4a n dc…

    08:11

  • Для какого значения k уравнение sinx+cos(k+x)+cos(k-x)=2 имеет действительное решение…

    04:56

  • Число решений уравнения cos(pisqrt(x-4)cos(pi sqrtx)=…

    02:47

  • Если х, у в [0,2pi] , затем найдите общее количество упорядоченных пар (x ,… 92x…

    05:52

  • Найти число решений уравнения Sin x = x/10

    02:05

  • Найти число корней уравнения xsinx=1

    0 90: 45

  • Докажите, что наименьшее положительное значение x , удовлетворяющий tanx=x+1,l i e s…

    04:06

  • Если m и n(n > m) являются целыми положительными числами, затем найдите число решений…

    06:01

  • Решите sin x gt -1/2 9(2) lt «sin» pi/2 x.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *