Сколько трёхзначных чисел можно составить из цифр 0 1 2 3 4 5?
Сколько трёхзначных чисел можно составить из цифр 0 1 2 3 4 5?
Сколько трехзначных чисел можно составить из цифр 0,1,3,5, если цифры в записи числа не повторяются? Решение. Всего 18 чисел. 2.
Сколько чисел можно составить из цифр 0 1 2 3 4 5 6 7 8 9?
а) Первую цифру можно выбрать девятью различными способами (0 не может быть первым), вторую — тоже девятью (0 может быть вторым, а вот цифра, которая была первой, уже отлетает), третью — восемью (отлетают первая и вторая цифры). Итого: 9*9*8=648.
Сколько различных четырехзначных чисел можно записать?
Ответ: 18 различных чисел.
Сколько шестизначных чисел можно составить из цифр 1 2 3 5 7 9 без повторений?
Сколько шестизначных чисел можно составить из цифр 1 2 3 5 7 9? Люблю смотреть российские сериалы, играть в шахматы и путешествовать. Ответ:720.
Ответ:720.
Сколько чётных четырехзначных чисел все цифры которых различны можно записать с помощью цифр 2 3 4 7 и 9?
Ответ: 48 чисел.
Сколько двузначных чисел можно составить из цифр 1 2 3 4?
Ответ: 44,45. laminiaduo7 и 12 других пользователей посчитали ответ полезным!৮ ফেব, ২০২১
Сколько всего двузначных чисел можно составить из цифр 1 2 3?
Ответ, проверенный экспертом Шесть двузначных чисел можно составить: ৩০ অক্টোবর, ২০১২
Сколько двузначных чисел можно составить из цифр 1 2 3 4 Если цифры в записи числа повторяются?
Составим все возможные числа из представленных: 1, 2, 3, 4 и 0. Получим следующие двузначные числа: 11, 12, 13, 14, 10, 21, 22, 23, 24, 20, 31, 32, 33, 34, 30, 41, 42, 43, 44, 40. Ответ: из заданных чисел можно составить 20 чисел.
Сколько можно составить двузначных чисел 3 6 8?
Ответ:6 двузначных чисел можно составить.
Сколько можно составить чисел из 3 6 8?
Во-первых, из 4 цифр можно взять по 3 — четырьмя способами: 356, 368, 358, 568. Из каждой тройки можно составить по 6 чисел. Из чисел 3, 5 и 6 получим числа: 356, 365, 536, 563, 635, 653. Из чисел 3,6 и 8 получим числа: 368, 386, 638, 683, 836, 863.
Из каждой тройки можно составить по 6 чисел. Из чисел 3, 5 и 6 получим числа: 356, 365, 536, 563, 635, 653. Из чисел 3,6 и 8 получим числа: 368, 386, 638, 683, 836, 863.
Сколько двузначных чисел можно составить из 3 цифр?
Ответ, проверенный экспертом На 1-м месте нашего двузначного числа может стоять любая из 3-х цифр (то есть — всего 3), на 2-м — оставшиеся две, то есть всего возможно 3 · 2 = 6 двузначных чисел!২ অক্টোবর, ২০১৪
Сколько двузначных чисел можно составить из цифр 6 9 0 Если цифры повторяются?
Ответ, проверенный экспертом Ответ:9 двухзачных цифр. Ответ: 6 двухзначных цифр. e3radg8 и 104 других пользователей посчитали ответ полезным!২৭ এপ্রিল, ২০১৬
Сколько двузначных чисел можно составить из цифр 6 7 8?
На первом месте двузначного числа может стоять любая из 4-х цифр, а на втором месте — 3 цифры (так как нельзя, чтобы были повторения цифр). По правилу комбинаторного произведения всего существует 4 × 3 = 12 таких двузначных чисел, составленных из не повторяющихся цифр 6, 7, 8, 9.
По правилу комбинаторного произведения всего существует 4 × 3 = 12 таких двузначных чисел, составленных из не повторяющихся цифр 6, 7, 8, 9.
Сколько двузначных чисел можно составить из цифр 3 4 5 6?
1) Сколько двузначных чисел можно составить из цифр 3, 4, 5, 6 при условии, что цифры в числе не повторяются? Ответ: 24.
Сколько двузначных чисел можно составить из цифр 1 3 5 7 9?
Ответ: 95,97; всего 20 чисел,если еще с повторяющими цифрами, то 25.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре. Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа… Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Интересное: Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 2 Решение: Так как натуральное число не может начинаться с цифры 0, исключаем те числа, которые начинаются с цифры 0. Р4 = 1·2·3·4= 24 Р5 – Р4 = 1·2·3·4·5-1·2·3·4 = 120-24=96 Ответ: 96 чисел.
На собрание пришли 3 девочки и 4 мальчика. Сколькими способами можно их рассадить, если девочки хотят сидеть рядом? Решение: Если рассмотреть девочек как одну, всего перестановок будет Р5. В каждой из полученных комбинаций можно выполнить Р3 перестановок девочек. Искомое число перестановок: Р5·Р3 = 5!·3!=1·2·3·4·5·1·2·3=720 Ответ: 720 способов. Размещения
Задача: Даны четыре различных шара: белый, зеленый, красный и синий. Их нужно поместить в 3 пустые ячейки. Сколько всего будет способов размещения шаров? Решение: Сначала выпишем все варианты, которые начинаются с белого шара, затем – с зеленого и т. д. бзк, бкз, бзс, бсз, бкс, бск. збк, зкб, зсб, збс, зкс, зск. кбз, кзб, ксб, кбс, кзс, ксз. сбз, сзб, скб, сбк, скз, сзк. Всего способов 24. В первую ячейку можно выбрать четырьмя способами.
Определение: Размещением из n элементов по к (к≤n) называется любое множество, состоящее из любых к элементов, взятых в определенном порядке из данных n элементов. Каждое множество при размещении отличается порядком элементов или их составом. к Число размещений из n элементов по к обозначают Аn. Первый элемент можно выбрать n способами, второй n-1 и последний к-й элемент n-(к-1) способами. к Аn = n(n-1)(n-2)… (n-(k-1))
Задачи: 1. Учащиеся одного класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предметов. Решение: Расписание на один день отличаются либо порядком следования предметов, либо самими предметами. Значит, здесь речь идет о размещении из 8 элементов по 4. А8= 8·7·6·5=1680 Ответ: 1680 способов.
2. Сколькими способами тренер может распределить 10 спортсменов, на эстафете 4·100 на первом, во втором, третьем и четвертом этапах? Решение: А10 = 10·9·8·7·=5040 Ответ: 50400 способов.
3. Сколько существует пятизначных телефонных номеров, в каждом из которых все цифры различны и первая цифра различна отнуля? 5 Решение:Число размещений из десяти элементов по пять – А10. Число размещений начинающихся с цифры ноль – А9. Число телефонных номеров равно: 5 4 А10 – А9 =10·9·8·7·6 – 9·8·7·6 = 27216 Ответ: 27216 номеров. Сочетания
Задача: На столе лежат 5 разноцветных карандашей. Сколько способов для выбора 3 из них? Решение: Обозначим карандаши буквами а, в, с, d, е. Можно составить такие сочетания: авс, авd, abe, acd, ace, ade, bcd, bce, bed, cde. Всего: 10 способов.
Определение: Сочетанием из n элементов по к называется любое множество, составленное из к элементов, выбранных из данных n элементов. к Число сочетаний из n элементов по к обозначается Сn. В сочетаниях не имеет значения порядок элементов, сочетания отличаются составом элементов. Допустим, имеется множество, содержащее n элементов, и из его элементов составлены всевозможные сочетания по к элементов. Число таких сочетаний равно Сn. В каждом сочетании можно выполнить Рк перестановок. В результате мы получим все размещения, к которые можно составить из n элементов по к. Их число равно Аn. К к к к Значит, Аn = Cn·Pк. Отсюда Сn = Аn кРк Сn = n(n-1)(n-2)…(n-(k-1)) 1·2·3·…·k Умножим числитель и знаменатель, на (n-к)!
к Сn= (n-1)(n-2)…(n-(k-1)(n-k)! = n 1·2·3·…·k·(n-k)! k!(n-k)! Задачи: Из 12 учеников нужно выбрать 3 ученика на улусный новогодний бал. Сколькими способами можно сделать этот выбор? Решение: Каждый выбор отличается от другого хотя бы одним учеником. С12 = 1·2·3·…·9·10·11·12 = 220 Ответ: 220 способов 1·2·3·1·2·3·…·9
2. В классе 10 девочек и 8 мальчиков. Нужно выбрать троих дежурных. Сколькими способами можно сделать этот выбор, если: а) среди них должен быть 1 мальчик; б) это могуть быть любые 3 ученика? Решение: а) выбрать одного мальчика можно С8 способами:
С8 = 1·2…·8 = 8 1!·1·2·..·7
Выбрать из 10 девочек 2 дежурных можно С10 способами: С10 = 1·2·…·8·9·10 = 45 1·2·1·2·…·8 Способов из 3 дежурных, среди которых 1 мальчик, всего: 1 2 С8 ·С10 = 8·45=360 Ответ: 360 способов. б) любых 3 учеников из 18 учащихся можно выбрать С18 = 1·2·3…15·16·17·18 = 816 Ответ: 816 способов. 1·2·3·1·2·3·…·15
В корзине имеются 15 груш и 7 яблок. Нужно выбрать 5 груш и 3 яблока. Сколькими способами это можно сделать? Решение: Способов выбора 5 груш: С15 = 1·2·…·10·11·12·13·14·15 = 360360 = 3003 1·2·3·4·5·1·2·3·4·…·10 120 Способов выбора 3 яблок: С7 = 1·2·3·4·5·6·7 = 35 1·2·3·1·2·3·4 5 3 Всего указанный выбор можно сделать С15 ·С7 способами: 5 3 С15·С7 = 3003·35=105105 Ответ: 105105 способов. ЗАДАЧИ
1. Сколькими способами можно расставить в ряд на одной полке 7 книг? 2. Сколькими способами можно выбрать трех человек на 3 различные должности из восьми кандидатов? 3. Из 11 футболистов нужно делегировать 3 человека. Сколькими способами это можно сделать? 4. Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет? 5. На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда? 6. Сколькими способами можно изготовить трехцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов? 7. На соревнованиях по легкой атлетике приехала команда из 12 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4 по 100 м на первом, втором, третьем и четвертом этапах? 8. Сколькими способами могут быть распределены первая, вторая и третья премии между 15 участниками конкурса? 9. 10. Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр: а) 1, 3, 5, 7, 9; б) 0, 2, 4, 6, 8. 11. Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отличная от нуля? 12. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде? 13. Учащимся дали список из 10 книг, которые рекомендуются прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг? 14. Из лаборатории в которой работают заведующий и 10 сотрудников, надо отправить 5 человек в командировку. Сколькими способами это можно сделать, если: а) заведующий лабораторией должен ехать в командировку; б) заведующий лабораторией должен остаться? 15. В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить 4 мальчиков и трех девочек. 16. В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами он может выбрать из них 3 книги и 2 журнала? 17. Для ремонта школы прибыла бригада, состоящая из 12 человек. Трех из них надо отправить на четвертый этаж, а четырех — на пятый этаж. Сколькими способами это можно сделать? 18. В отделе работают 5 ведущих и 8 старших научных сотрудников. В командировку надо послать двух ведущих и трех старших научных сотрудников. Сколькими способами может быть сделан выбор сотрудников, которых надо послать в командировку? 19. Встретились 11 футболистов и 6 хоккеистов, и каждый стал по одному разу играть с каждым в шашки. а) сколько встреч было между футболистами? б) сколько встреч было между хоккеистами? в) сколько встреч было между футболистами и хоккеистами? г) сколько встреч было всего? 20. Встретились несколько человек и стали здороваться друг с другом. Известно, что рукопожатий было от 60 до 70. а) каждый здоровался с каждым; б) только один человек не здоровался ни с кем; в) только двое не поздоровались между собой. 21. В классе 15 девочек и 13 мальчиков. Нужно выбрать двух дежурных по классу. Сколькими способами это можно сделать: а) при условии, что пару обязательно должны составить мальчик и девочка? б) без указанного условия? 22. В оперном театре 10 певцов и 8 певиц, а в опере по замыслу композитора 5 мужских и 3 женских партии. Сколько существует различных певческих составов для спектакля, если известно, что: а) все певицы и певцы прекрасно ладят между собой; б) певцы А и Б ни за что не будут петь вместе; в) 6 певцов накануне сорвал голос на футболе, и одной певице придется петь мужскую партию. 23. В шахматном кружке занимаются 16 человек. Сколькими способами тренер может выбрать из них для предстоящего турнира: а) команду из 4 человек; б) команду из четырех человек, указав при этом, кто из членов команды будет играть на первой, второй, третьей и четвертой досках? 24. а) двух дежурных; б) старосту и помощника старосты.
25. Из 20 вопросов к экзамену Вова 12 вопросов выучил, 5 совсем не смотрел, а в остальных что– то знает, а что- то нет. На экзамене в билете будет три вопроса. а) сколько существует вариантов билетов? б) сколько из них тех, в которых Вова знает все вопросы? в) сколько из них тех в которых есть вопросы всех трех типов?
Литература
1. Вишенкин Н. Я., Ивашев – Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса. – М.: Просвещение, 1993. 2. Гусев В. А., Орлов А. И., Розенталь А. П. Внеклассная работа по математике в 6 – 8 классах. – М.: Просвещение, 1997. 3. Дмитриев И. Г., Попов М. В., Федоров М. П. Решение олимпиадных задач по математике. – Якутск: ДНСПО МО РС(Я), 2000. 4. Когаловский С.Р. Роль комбинаторных задач в обучении математики. 5. Макарычев Ю. Н., Миндюк Н. Г. Алгебра: элементы статистики и теории вероятностей. – М.: Просвещение, 2003. 6. Семеновых А. Комбинаторика. // Математика. – 2004, №15, № 16.
⇐ Предыдущая12 Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
Глава 3a.jnt
%PDF-1.6
%
73 0 объект
>
эндообъект
70 0 объект
>поток
Версия PScript5. dll 5.2.22010-09-20T14:01:07-04:002010-09-20T13:59:57-04:002010-09-20T14:01:07-04:00application/pdf
dll 5.2.22010-09-20T14:01:07-04:002010-09-20T13:59:57-04:002010-09-20T14:01:07-04:00application/pdf
комбинаторика — Количество четырехзначных чисел, оканчивающихся на четные целые числа, цифры которых не повторяются
спросил
Изменено 1 год, 4 месяца назад
Просмотрено 135 раз
$\begingroup$
Сколько существует четырехзначных четных положительных целых чисел без повторения цифр?
Моя попытка :
Во-первых, мы разделим такие необходимые договоренности на две группы:
$1$. Те, которые содержат $0$ в качестве конечной цифры
Те, которые содержат $0$ в качестве конечной цифры
Чтобы вычислить это, мы видим, что существует $9$ способов заполнить первое место, $8$ способов заполнить второе (мы не можем использовать $0$ и цифру на первом месте ), $7$, чтобы занять третье место. Таким образом, имеется $8\times 9\times 7$ для создания требуемых размещений вида $1$.
$2$. Те, которые не содержат $0$ в качестве конечной цифры.
Предположим, что мы выбрали $i$ как четное число с $i\in {2,4,6,8}$. Затем у нас есть варианты по 8 долларов для заполнения первого и второго места и варианты по 7 долларов для заполнения третьего. Это дает нам $8\times8\times 7$ способов за $2$. Для каждой из $4$ четных конечных цифр мы получаем всего $4\times8\times8\times 7$ способов сделать это.
Теперь, если мы сложим окончательные результаты $1$ и $2$, мы получим $ 4\times8\times8\times 7+8\times 9\times 7=2296$ способов получить заданные схемы. Но ответ моей книги — 4500 долларов. Что не так с моим расчетом? Пожалуйста, дай мне знать.
- комбинаторика
- решение-верификация
$\endgroup$
3
$\begingroup$
Ваша работа верна, если не допускается повторение цифр. $4500$ — это количество $4$-значных четных чисел с разрешенным повторением. Мы знаем, что между $1000$ и $9999$ есть числа $9000$. Половина из них ровные.
Альтернативная работа, если повторение цифр не допускается —
Если мы позволим тысячному разряду быть нулем, у нас всего $10 \cdot 9 \cdot 8 \cdot 7 = 5040$ чисел и половина из них ($2520$) будут четными числами.
Теперь мы вычтем количество четных чисел с $0$ в тысячном разряде, поскольку они не являются действительно четырехзначными числами — есть $4$ вариантов для места, чтобы оно было четным числом ($2, 4, 6, 8$), а затем что дает $8 \cdot 7 = 56$ вариантов для десятков и сотен.
Это приводит к $2520 — 4 \cdot 56 = 2296$ четных чисел.

 ..
..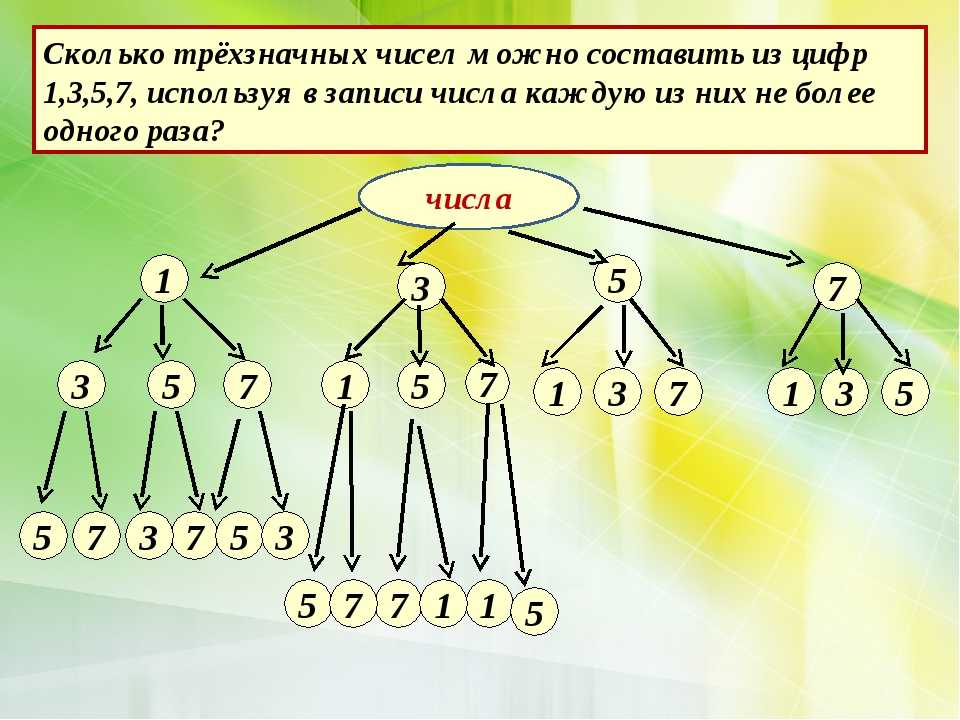 Количество таких чисел
Количество таких чисел Во вторую – тремя, в третью – двумя. Всего способов 4·3·2=24. Каждую упорядоченную тройку, которую можно составить из четырех элементов, называют размещением из четырех элементов по три.
Во вторую – тремя, в третью – двумя. Всего способов 4·3·2=24. Каждую упорядоченную тройку, которую можно составить из четырех элементов, называют размещением из четырех элементов по три.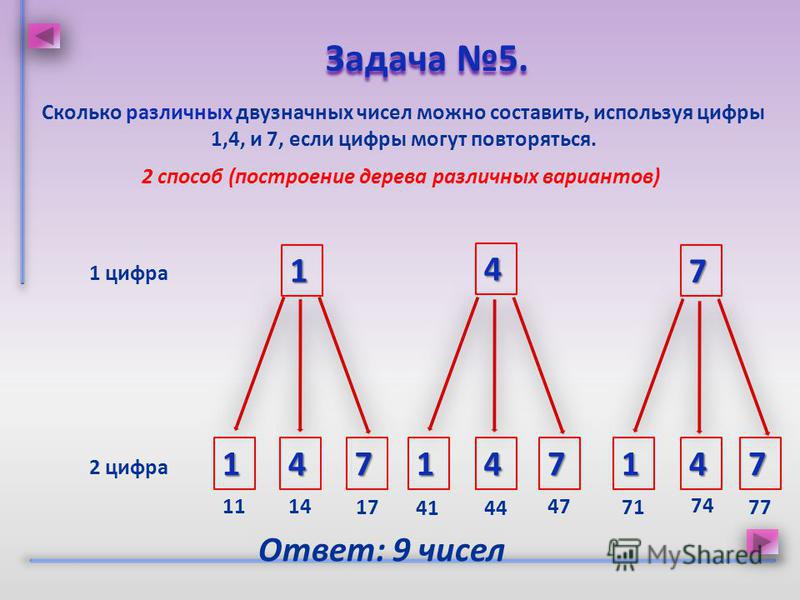

 Значит, здесь речь идет о сочетаниях из 12 элементов по 3:
Значит, здесь речь идет о сочетаниях из 12 элементов по 3:


 Сколько человек встретились, если известно, что:
Сколько человек встретились, если известно, что: Сколькими способами из класса, где учатся 24 учащихся, можно выбрать:
Сколькими способами из класса, где учатся 24 учащихся, можно выбрать: // Математика в школе. – 2004. — №4.
// Математика в школе. – 2004. — №4.