Сколько вариантов 3 из 5: Сколько вариантов комбинаций из 5 цифр? Формула решения.

5 = 100,000. Логически подумайте — каждая из комбинаций от 000,001 до 100,000 повышают общее число комбинаций на одну, итого кол-во комбинаций равно собственно числу.

• Возник вопрос: сколько комбинаций из 5 цифр от 1 до 5?
• Первое заблуждение, что это 5 в степени 10, но на самом деле это 10 в степени 5, что даёт 100 000 комбинаций.
• Общая формула для нахождения числа сочетаний из n объектов по k имеет вид Ckn=n!(n−k)!⋅k!.
• Если нужны комбинации из 5 цифр с повторениями, то это 5 в степени 10, что даёт 9 765 625 вариантов.
• В случае комбинаций из цифр 12345, количество всевозможных комбинаций равно 120, но нужно учитывать и такие варианты, как 11234, 11123, 11112, 12234, 12333, 12222, 12344 и др.
• Если нужны комбинации из 4 цифр от 1 до 5, то это всего 10 000 вариантов.
• Если нужны комбинации из 6 цифр от 0 до 9, то это 720 вариантов.
• Если нужно посчитать количество комбинаций из 10 цифр по 4, то это 10 000 вариантов.
• Чтобы посчитать количество вариантов комбинаций без повторений, можно использовать альтернативную формулу ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4).
• Если нужно узнать количество вариантов для 6-значного кода, то это 1 миллион комбинаций.

1. Как посчитать количество комбинаций цифр
2. Сколько комбинаций из 5 цифр с повторениями
3. Сколько комбинаций из цифр 12345
4. Сколько комбинаций из 4 цифр от 1 до 5
5. Сколько комбинаций из 6 цифр от 0 до 9
6. Сколько комбинаций из 10 цифр по 4
7. Как посчитать количество вариантов комбинаций без повторений
8. Сколько вариантов у 6 значного кода
9. Сколько комбинаций из 6 вариантов
10. Сколько вариантов комбинаций из 24 цифр
11. Сколько получится комбинаций из 3 цифр
12. Сколько нужно комбинаций из 3 цифр
13. Сколько комбинаций может быть из 999 цифр

Как посчитать количество комбинаций цифр

Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n!(n−k)!⋅k!. 10 = 9,765,625 (это будет кол-во комбинаций для строки из 10 символов с пятью вариациями).

Сколько комбинаций из цифр 12345

Комбинаторика. Сколько всего возможных комбинаций из пяти чисел 12345, да 120, надо лишь эти числа между собой перемножить 12345=120, но есть одно «но» нужно подсчитать еще и такие варианты как например 11234, 11123, 11112, 12234, 12333, 12222, 12344 и т.

Сколько комбинаций из 4 цифр от 1 до 5

Ответ: 10 000 комбинаций.

Сколько комбинаций из 6 цифр от 0 до 9

То есть N=6, и число возможных комбинации N!, 6!= 720 вариантов.

Сколько комбинаций из 10 цифр по 4

Очевидно, что количество всех возможных комбинаций из 10 цифр по 4 равно 10.000. Число всех возможных комбинаций из 30 букв по две равно.

Как посчитать количество вариантов комбинаций без повторений

Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4). Очевидно, что k меньше или равно n, т. к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются).

Сколько вариантов у 6 значного кода

6 цифр — это 1 миллион комбинаций.

Сколько комбинаций из 6 вариантов

= 1 * 2 * 3 * 4 * 5 * 6 =720. При условии, что числа могут повторяться, на каждом месте могут быть все 6 чисел и количество таких комбинаций равно: 6 * 6 * 6 * 6 * 6 * 6 = 66 = 46 656.

Сколько вариантов комбинаций из 24 цифр

Вы немного ошиблись, комбинаций не 12, а из 24 чисел по 12 есть почти 3 млн. комбинаций, точнее 2 704 156 комбинаций.

Сколько получится комбинаций из 3 цифр

3 = 60 способов расстановки цифр, т. е. искомое количество трехзначных чисел есть 60. (Вот некоторые из этих чисел: 243, 541, 514, 132, )

Сколько нужно комбинаций из 3 цифр

При условии, что цифры в одной комбинации не должны повторяться, из трех цифр можно составить трехзначных комбинаций всего: 3! = 1 * 2 * 3 = 6. Ответ: из трех цифр можно составить всего 6 трехзначных чисел.

Сколько комбинаций может быть из 999 цифр

Комбинаций цифр 999. 12*999)12*12 = 1 726 272 вариантов номеров.

• Сколько комбинаций из 4 цифр от 1 до 5
• Сколько комбинаций можно составить из 5 цифр

строки — Подсчитать количество комбинаций

Вопрос задан 5 лет 5 месяцев назад

Изменён 5 лет 5 месяцев назад

Просмотрен 53k раза

Как посчитать количество комбинаций строки состоящей из 10 символов, где используются только латинские буквы в нижнем регистре и цифры.

Очень бы хотелось узнать формулу.

• строки
• математика
• комбинаторика

2

Всего символов — 36.

Если повторы могут быть — на первое место сколькими способами можно выбрать символ? 36.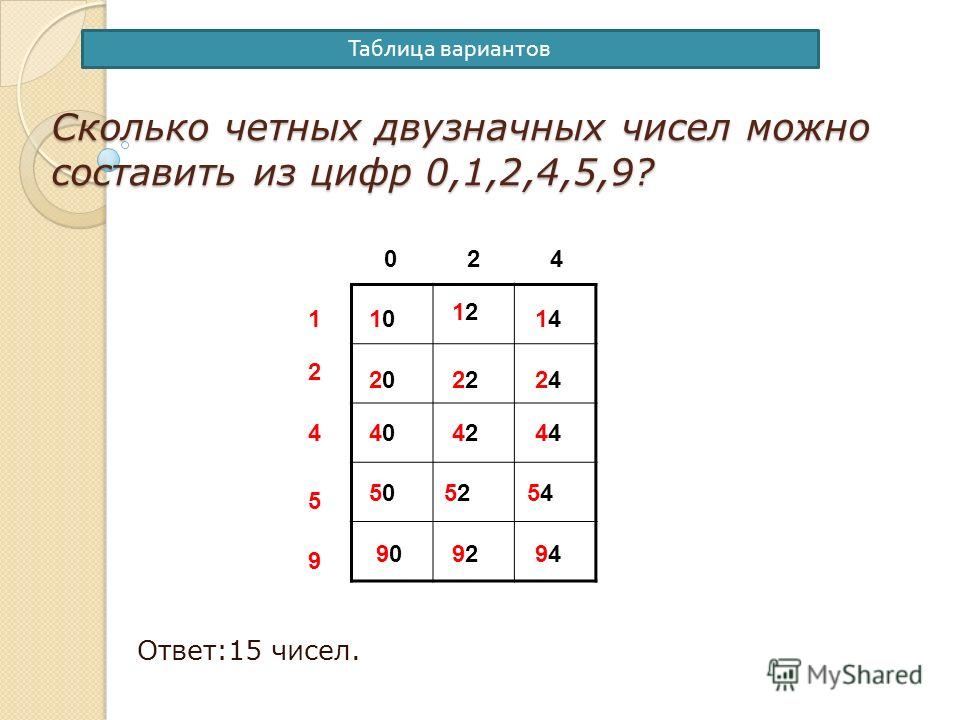 Для каждого первого сколькими можно выбрать второй? 36. Итого — 36*36. Для каждых первых двух… — ну, и так далее.

Всего — 36¹⁰.

Для алфавита из N символов и длины строки m —

Если повторов быть не может — то на второе место — уже только 35 (один уже выбран), на третье — 34 (выбраны уже два)… И так далее. Итого — 36*35*34*33*32*31*30*29*28*27 = 36!/26!.

Для алфавита из N символов и длины строки m — число размещений

2

Могут быть использованы две формулы.

Если символы могут повторяться, то любой из 10-ти символов может принимать одно 36 значений (26 латинских букв плюс 10 цифр). Можно сказать, что это 10-тизначное число в 36-ричной системе счисления. Количество комбинаций будет равно 36

10 или 3,6561584×10¹⁵.

Если символы не могут повторяться, то мы имеем дело с размещениями. Есть ещё сочетания, но в данном случае они не подходят, потому что размещения 123abc и abc123 будут разными, а вот сочетание это будет одно и то же.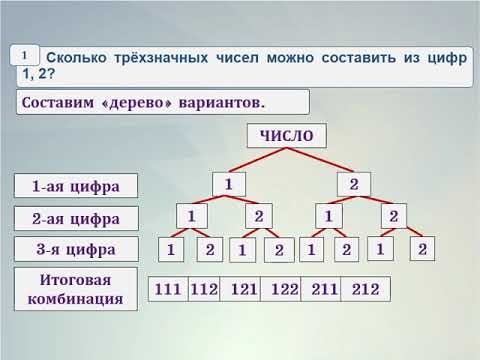

Количество размещений из n по k считается по формуле A^k_n = n!/(n — k)!, то есть в вашем случае это будет 36!/26! или 9,2239326×10¹⁴

0

Используемый алфавит содержит 36 символов: 26 букв и 10 цифр.

Число размещений без повторов = n!/(n-k)! = 36!/26!
Число размещений с повторами = n^k = 36¹⁰

0

кол-во комбинаций = С!

Т.е. в вашем случае 10! комбинаций…

2

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Комбинаторный калькулятор, калькулятор комбинаций, вариаций, перестановок

Узнайте, сколькими способами можно выбрать k предметов из n предметов набора. С/без повторения, с/без порядка.

Расчет:

Ck​(n)=(kn​)=k!(n−k)!n!​  n=10 k=4 C4​(10)=(410​)=4!(10 −4)!10!​=4⋅3⋅2⋅110⋅9⋅8⋅7​=210

Количество комбинаций: 210

Вариантов

Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, образованная из множества n элементов. Элементы не повторяются и зависят от порядка элементов группы (поэтому расположены).

Количество вариаций можно легко подсчитать, используя комбинаторное правило произведения. Например, если у нас есть набор n = 5 чисел 1,2,3,4,5, и мы должны сделать вариации третьего класса, их V ₃ (5) = 5 * 4 * 3 = 60.

Vk​(n)=n(n−1)(n−2)…(n−k+1)=(n−k)!n!​

н! мы называем факториалом числа n, которое является произведением первых n натуральных чисел. Обозначение с факториалом только более ясное и эквивалентное. Для вычислений вполне достаточно использовать процедуру, вытекающую из комбинаторного правила произведения.

Перестановки

Перестановка является синонимом вариации n-го класса n-элементов. Таким образом, это любая упорядоченная группа из n элементов, состоящая из n элементов. Элементы не повторяются и зависят от порядка элементов в группе.

P(n)=n(n−1)(n−2)…1=n!

Типичный пример: у нас есть 4 книги, сколькими способами мы можем расположить их рядом на полке?

Вариации с повторением

Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, состоящая из множества n элементов, причем элементы могут повторяться и зависят от их порядка. Типичным примером является образование чисел из чисел 2,3,4,5 и нахождение их числа. Рассчитываем их количество по комбинаторному правилу произведения:

Vk′​(n)=n⋅n⋅n⋅n…n=nk

Перестановки с повторением

Повторяющаяся перестановка представляет собой упорядоченную группу k-элементов из n-элементов, при этом некоторые элементы повторяются в группе.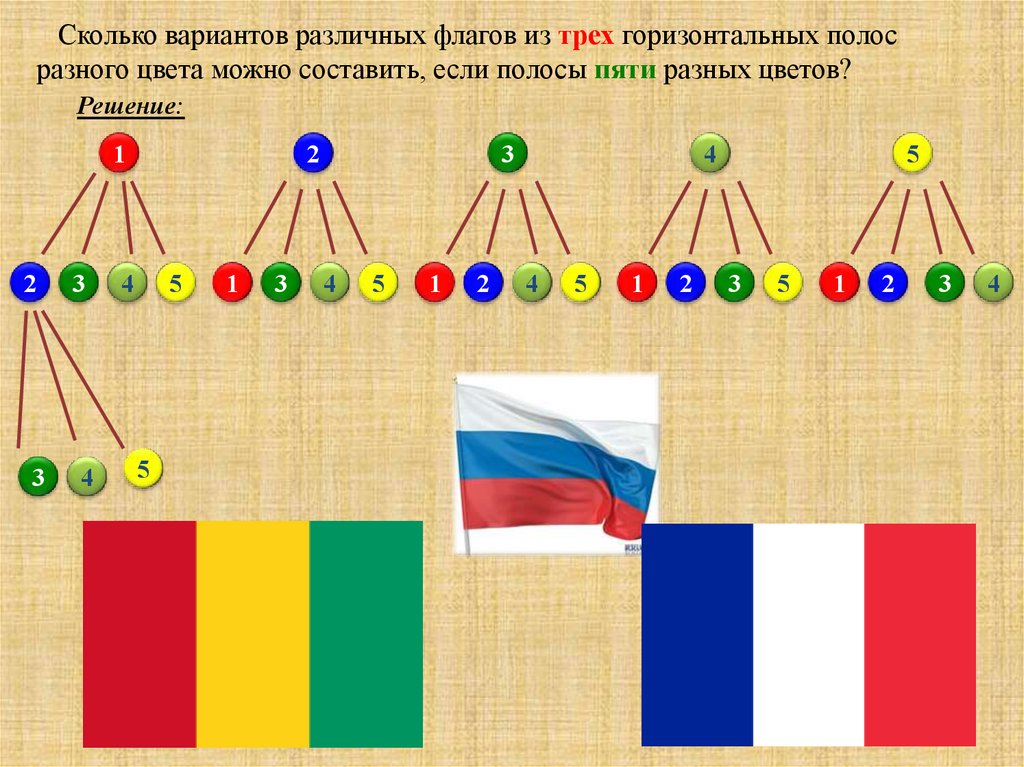 Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок.

Pk1​k2​k3​…km​′​(n)=k1​!k2​!k3​!…km​!n!​

Типичный пример — выяснить, сколько семизначных чисел образовано из чисел 2,2,2, 6,6,6,6.

Комбинации

Комбинация k-го класса из n элементов представляет собой неупорядоченную группу k-элементов, образованную из множества n элементов. Элементы не повторяются, и порядок элементов группы не имеет значения. В математике неупорядоченные группы называются множествами и подмножествами. Их количество является комбинационным числом и рассчитывается следующим образом:

Ck​(n)=(kn​)=k!(n−k)!n!​

Типичный пример комбинаций: у нас 15 учеников, и мы должны выбрать троих. Сколько их будет?

Комбинации с повтором

Здесь мы выбираем k групп элементов из n элементов, независимо от порядка, и элементы могут повторяться.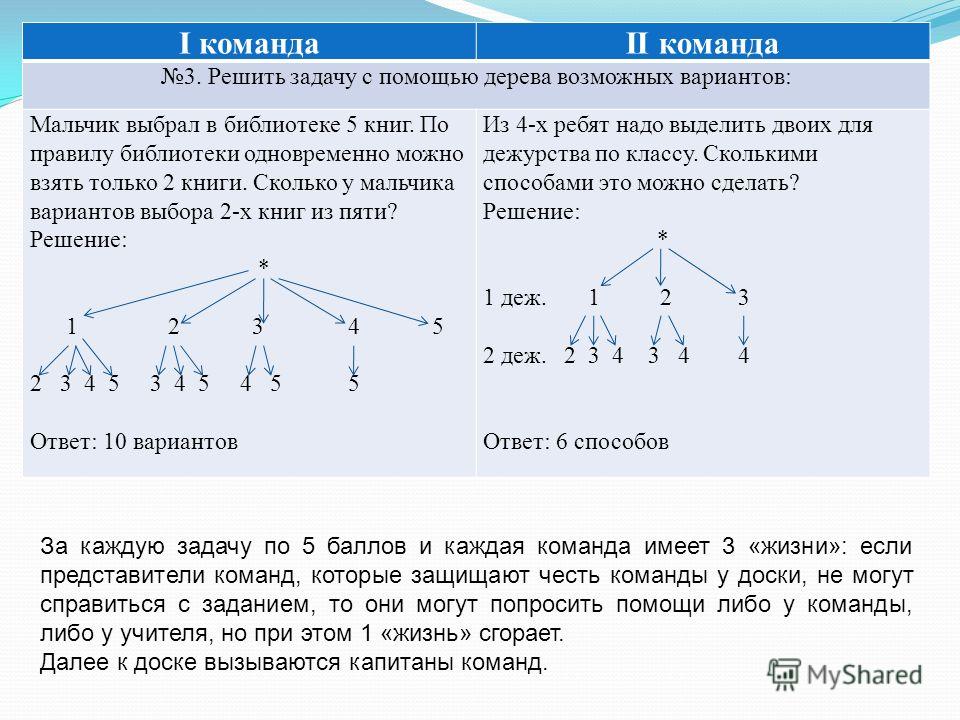 k логически больше n (иначе мы получили бы обычные комбинации). Их счет:

Ck′​(n)=(kn+k−1​)=k!(n−1)!(n+k−1)!​

Пояснение к формуле — количество комбинаций с повторением равно количеству мест расположения n − 1 разделителей на n-1 + k местах. Типичный пример: мы идем в магазин, чтобы купить 6 шоколадок. Предлагают всего 3 вида. Сколько вариантов у нас есть? к = 6, п = 3.

Фонд комбинаторики в текстовых задачах

• Представитель 81580
  В шахматном клубе 5 членов, в том числе две девушки. Лидер кружка хочет определить по жребию, кто из участников будет представлять кружок на представительном турнире. Какова вероятность того, что будет нарисована девочка?
• Одновременно 80530
  Товар имеет 10% вероятность дефекта внешнего вида, 6% вероятность функционального дефекта и 3% вероятность обоих дефектов одновременно. Являются ли случайными события А — товар имеет дефект внешнего вида и В — товар имеет функциональные свойства?
• Вероятность 2
  Вероятность того, что у взрослого есть кредитная карта, равна 0,71. Исследователь случайным образом выбирает двух взрослых. Вероятность (округленная до трех знаков после запятой) того, что у первого взрослого есть кредитная карта, а у второго взрослого нет кредитной карты, равна
• Вероятность 1775
  На данный момент компания произвела 500 000 автомобилей, из которых 5 000 были бракованными. Какова вероятность того, что не более чем один автомобиль из ежедневно выпускаемых 50 автомобилей будет бракованным?
• Меню
  В меню 12 видов блюд. Сколькими способами мы можем выбрать четыре разных блюда для ежедневного меню?
• Медали
  Сколькими способами можно разделить золотые, серебряные и бронзовые медали между 21 участником?
• Вероятность 3080
  В словацком языке существует восемь стилей выпускных тем. Министр образования рисует 4 из них. Какова вероятность того, что он выберет хотя бы одну из пар?
• Первый мужчина
  Какова вероятность случайного события, когда пять мужчин и семь женщин первыми оставят мужчину?
• Жетоны
  В непрозрачных мешочках находятся красные, белые, желтые и синие жетоны.

  No related posts.