Операции с векторами, сложение векторов, умножение вектора на действительное число.
Рассмотрим вектор v с начальной точкой в начале координат в любой координатной системе x-y и с конечной точкой в (a,b). Мы говорим, что вектор находится в стандартном положении и ссылаемся на него как на радиус-вектор. Обратите внимание, что пара точек определяет этот вектор. Таким образом, мы можем использовать это для обозначения вектора. Чтобы подчеркнуть, что мы имеем в виду вектор, и, чтобы избежать путаницы, как правило, пишут:
v = .
Координата a есть скаляром горизонтальной компоненты вектора, и координата b есть скаляром вертикальной компоненты вектора. Под скаляром мы подразумеваем численное количество, а не векторную величину. Таким образом, это рассматривается как компонентная форма v. Обратите внимание, что a и b НЕ вектора и их не надо путать с определением компонента вектора.
Теперь рассмотрим с A = (x1, y1) и C = (x2
 Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C. Таким образом, P = (x2 — x1, y2 — y1) и радиус вектор есть .
Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C. Таким образом, P = (x2 — x1, y2 — y1) и радиус вектор есть .Можно показать, что и имеют одну и ту же величину и направление, и поэтому эквивалентны. Таким образом, = = 2 — x1, y2 — y1 >.
Компонентная форма с A = (x1, y1) и C = (x2, y2) есть
= 2 — x1, y2 — y1 >.
Пример 1 Найдите компонентную форму если C = (- 4, — 3) и F = (1, 5).
Решение Мы имеем
= = .
Обратите внимание, что вектор есть равным радиус-вектору , как показано на рисунке вверху.
Теперь, когда мы знаем, как записать вектор в компонентной форме, давайте изложим некоторые определения.
Длину вектора v легко определить, когда известны компоненты вектора. Для v = 1, v2 >, мы имеем
|v|2 = v21 + v22 Используя теорему Пифагора
|v| = √v21 + v22.
Длина, или величина ветктора v = 1, v2 > находится как |v| = √v21 + v22.
Два вектора равны или эквивалентны, если они имеют одну и ту же величину и одно и то же направление.
Пусть u = 1, u2 > и v = 1, v2 >. Tогда
1, u2 > = 1, v2 > только если u1 = v1
Операции с векторами
Чтобы умножить вектор V на положительное число, мы умножаем его длину на это число. Его направление остается прежним. Когда вектор V умножается на 2, например, его длина увеличивается в два раза, но его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное.
Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.
Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное.
Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.
Для действительного числа k и вектора v = 1, v 2 >, скалярное произведение k и v есть
kv = k.1, v2 > = 1, kv2 >.
Вектор kv есть скалярным кратным вектора v.
Пример 2 Пусть u = и w = . Найдите — 7w, 3u и — 1w.
Решение
— 7w = — 7. = ,
3u = 3. = ,
— 1w = — 1. = .
Теперь мы можем сложить два вектора, используя компоненты. Чтобы сложить два вектора в компонентной форме, мы складываем соответствующие компоненты. Пусть u = 1, u2 > и v = 1, v2 >. Тогда
Чтобы сложить два вектора в компонентной форме, мы складываем соответствующие компоненты. Пусть u = 1, u2 > и v = 1, v2 >. Тогда
u + v = 1 + v1, u2 + v2 >
Например, если v = и w = , тогда
v + w = =
Если u = 1, u2 > и v = 1, v2 >, тогда
u + v = 1 + v1, u2 + v2 >.
Перед тем, как мы определим вычитание векторов нам нужно дать определение — v. Противоположный вектору v = 1, v
— v = (- 1).v = (- 1)1, v2 > = 1, — v2 >
Вычитание векторов, такое как u — v вовлекает вычитание соответствующих компонент. Мы покажем это представлением u — v как u + (- v). Если u = 1, u2 > и v = 1, v2 >, тогда
u — v = u + (- v) = 1, u2 > + 1, — v2 > = 1 + (- v1), u2 + (- v2) > = 1 — v1, u2 — v2 >
Мы можем проиллюстрировать вычитание векторов с помощью параллелограмма , как мы это делали для сложения векторов.
Вычитание векторов
Если u = 1, u2 > и v = 1, v2 >, тогда
u — v = 1 — v1, u2 — v2 >.
Интересно сравнить суммы двух векторов с разницей тех же двух векторов в одном параллелограмме. Векторы u + v и u — v есть диагоналями параллелограмма.
Пример 3 Сделайте следующие вычисления, где u = и v = .
a) u + v
b) u — 6v
c)3u + 4v
d)|5v — 2u|
Решение
a) u + v = + = = ;
b)u — 6v = — 6. = — = ;
c) 3u + 4v = 3. + 4. = + = ;
d) |5v — 2u| = |5. — 2.| = | — | = || = √(- 29)2 + 212 = √1282 ≈ 35,8
Прежде чем сформулировать свойства векторного сложения и умножения, мы должны дать определение еще одному специальному вектору — нулевому вектору. Вектор, чья начальная точка совпадает с конечной точкой, называется нулевым вектором, обозначается O, или . Его величина равна 0. В сложении векторов:
v + O = v. 1, v2 > + = 1, v2 >
1, v2 > + = 1, v2 >
Операции над векторами обладают те же самыми свойствами, что и операции над вещественными числами.
Для всех векторов u, v, и w, и для всех скаляров b и c:
1. u + v = v + u.
2. u + (v + w) = (u + v) + w.
3. v + O = v.
4 1.v = v; 0.v = O.
5. v + (- v) = O.
6. b(cv) = (bc)v.
7. (b + c)v = bv + cv.
8. b(u + v) = bu + bv.
Орты
Вектор величиной, или длиной 1 называется орт. Вектор v = есть орт, потому что
|v| = || = √(- 3/5)2 + (4/5)2 = √9/25 + 16/25 = √25/25 = √1 = 1.
Пример 4 Найдите орт, который имеет то же самое направление, что и вектор w = .
Решение Найдем сначала длину w:
|w| = √(- 3)2 + 52 = √34. Таким образом, мы ищем вектор, с длиной 1/√34 от w и с таким же самым направлением, что и вектор w. Этот вектор есть
u = w/√34 = /√34 = 34, 5/√34 >.
Вектор u есть орт, потому что
|u| = |w/√34| = = √34/34 = √1 = 1.
Если v есть вектор и v ≠ O, тогда
(1/|v|)• v, or v/|v|,
есть орт в направлении v.
Хотя орты могут иметь любое направление, орты, параллельные осям x и y особенно полезны. Они определяются как
i = and j = .
Любой вектор может быть выражен как линейная комбинация орта i и j. Например, пусть v = 1, v2 >. Tогда
v = 1, v2 > = 1, 0 > + 2 > = v1 + v2 = v1i + v2j.
Пример 5 Выразите вектор r = как линейную комбинацию i и j.
Решение
r = = 2i + (- 6)j = 2i — 6j.
Пример 6 Запишите вектор q = — i + 7j в компонентной форме.
Решениеq = — i + 7j = -1i + 7j =
Векторные операции могут быть также выполнены, когда векторы записаны как линейные i и j.
Пример 7 Если a = 5i — 2j и b = -i + 8j, найдите 3a — b.
Решение
3a — b = 3(5i — 2j) — (- i + 8j) = 15i — 6j + i — 8j = 16i — 14j.
Углы обзора
Конечная точка P орты в стандартной позиции есть точкой на единичной окружности, определенной (cosθ, sinθ). Таким образом, орт может быть выражен в компонентной форме,
u = ,
или как линейная комбинация орт i и j,
u = (cosθ)i + (sinθ)j,
где компоненты u есть функциями угла обзора θ измеряемого против часовой стрелки от оси x к этому вектору. Так как θ изменяется от 0 до 2π, точка P отслеживает круг x2 + y2 = 1. Это охватывает все возможные направления ортов и тогда уравнение u = (cosθ)i + (sinθ)j описывает каждый возможный орт на плоскости.
Пример 8 Вычислите и сделайте эскиз орта u = (cosθ)i + (sinθ)j для θ = 2π/3. Изобразите единичную окружность на эскизе.
Решение
u = (cos(2π/3))i + (sin(2π/3))j = (- 1/2)i + (√3/2)j
Пример 9 Определите угол обзора θ вектора w = — 4i — 3j.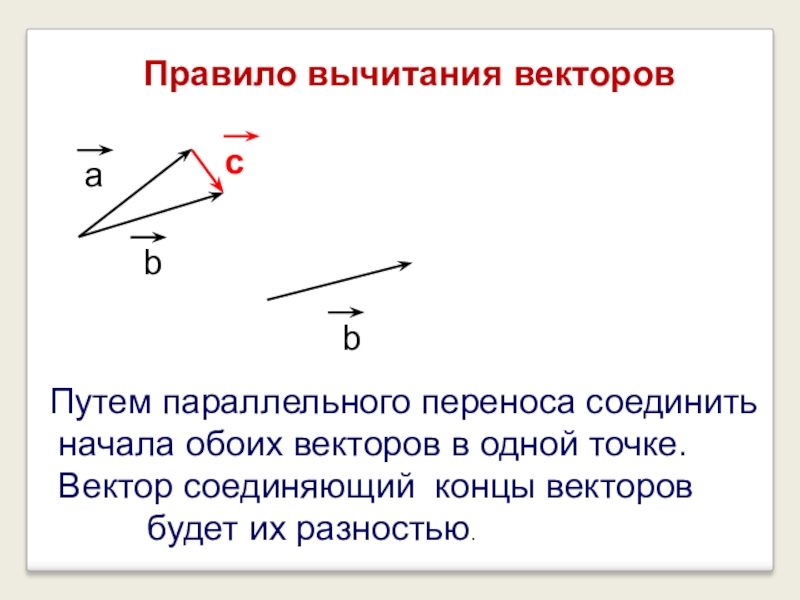
Решение Мы знаем, что
w = — 4i — 3j = .
Таким образом, имеем
tanθ = (- 3)/(- 4) = 3/4 и θ = tan— 1(3/4).
Так как w находится в третьем квадранте, мы знаем, что θ есть углом третьего квадранта. Соответствующий угол есть
tan— 1(3/4) ≈ 37°, и θ ≈ 180° + 37°, или 217°.
Это удобно для работы с прикладными задачами, а в последующих курсах, чтобы иметь способ выразить вектор так, чтобы его величина и направление могли быть легко определены или прочитаны. Пусть v это вектор. Тогда v/|v| есть орт в том же самом направлении, что и v. Таким образом, мы имеем
v/|v| = (cosθ)i + (sinθ)j
v = |v|[(cosθ)i + (sinθ)j]
v = |v|(cosθ)i + |v|(sinθ)j.
Углы между векторами
Когда вектор умножается на скаляр, результатом есть вектор. Когда складываются два вектора, результатом также есть вектор. Таким образом, мы могли бы ожидать, что произведение двух векторов есть вектор, но это не так. Скалярное произведение двух векторов есть действительное число или скаляр. Этот результат полезен в нахождении угла между двумя векторами и в определении, являются ли два вектора перпендикулярными.
Скалярное произведение двух векторов есть действительное число или скаляр. Этот результат полезен в нахождении угла между двумя векторами и в определении, являются ли два вектора перпендикулярными.
Скалярное произведение двух векторов u = 1, u2 > и v = 1, v2 > is
u • v = u1.v1 + u2.v2
(Обратите внимание, что u1v1 + u2v2 есть скаляром, а не вектором.)
Пример 10Найдите скалярное произведение, когда
u = , v = и w = .
a)u • w
b)w • v
Решение
a) u • w = 2(- 3) + (- 5)1 = — 6 — 5 = — 11;
b) w • v = (- 3)0 + 1(4) = 0 + 4 = 4.
Скалярное произведение может быть использовано для нахождения угла между двумя векторами. Угол между двумя векторами это самый маленький положительный угол, образованный двумя направленными отрезками. Таким образом, θ между u и v это тот же самый угол, что и между v и u, и 0 ≤ θ ≤ π.
Если θ есть углом между двумя ненулевыми векторами u и v, тогда
cosθ = (u • v)/|u||v|.
Пример 11Найдите угол между u = и v = .
Решение Начнем с нахождения u • v, |u|, и |v|:
u • v = 3(- 4) + 7(2) = 2,
|u| = √32 + 72 = √58, and
|v| = √(- 4)2 + 22 = √20.
Tогда
cosα = (u • v)/|u||v| = 2/√58.√20
α = cos— 1(2/√58.√20)
α ≈ 86,6°.
Равновесие сил
Когда несколько сил действуют на одну и ту же точку на объекте, их векторная сумма должна быть равна нуля, для того, чтобы был баланс. Когда есть баланс сил, то объект является стационарным или движется по прямой линии, без ускорения. Тот факт, что векторная сумма должна быть равна нулю вывода для получения баланса, и наоборот, позволяет решать нам многие прикладные задачи с участием сил.
Пример 12 Подвесной блок 350- фунтовый блок подвешен с помощью двух кабелей. осталось. В точке А есть три силы, действующие так: W блок тянет вниз, а R и S (два кабеля) тянут вверх и наружу. Найдите нагрузку каждого кабеля.
Найдите нагрузку каждого кабеля.
Решение Нарисуем диаграмму с начальными точками каждого вектора в начале кооординат. Для баланса, сумма векторов должна быть равна О:
R + S + W = О.
Мы можем выразить каждый вектор через его величину и угол обзора :
R = |R|[(cos125°)i + (sin125°)j],
S = |S|[(cos37°)i + (sin37°)j], и
W = |W|[(cos270°)i + (sin270°)j]
= 350(cos270°)i + 350(sin270°)j
= -350j cos270° = 0; sin270° = — 1.
Заменяя R, S, и W in R + S + W + O, мы имеем
[|R|(cos125°) + |S|(cos37°)]i + [|R|(sin125°) + |S|(sin37°) — 350]j = 0i + 0j.
Это дает нам систему уравнений:
|R|(cos125°) + |S|(cos37°) = 0,
|R|(sin125°) + |S|(sin37°) — 350 = 0.
Решая эту систему, мы получаем
|R| ≈ 280 и |S| ≈ 201.
Таким образом, нагрузка на кабели 280 фунтов и 201 фунт.
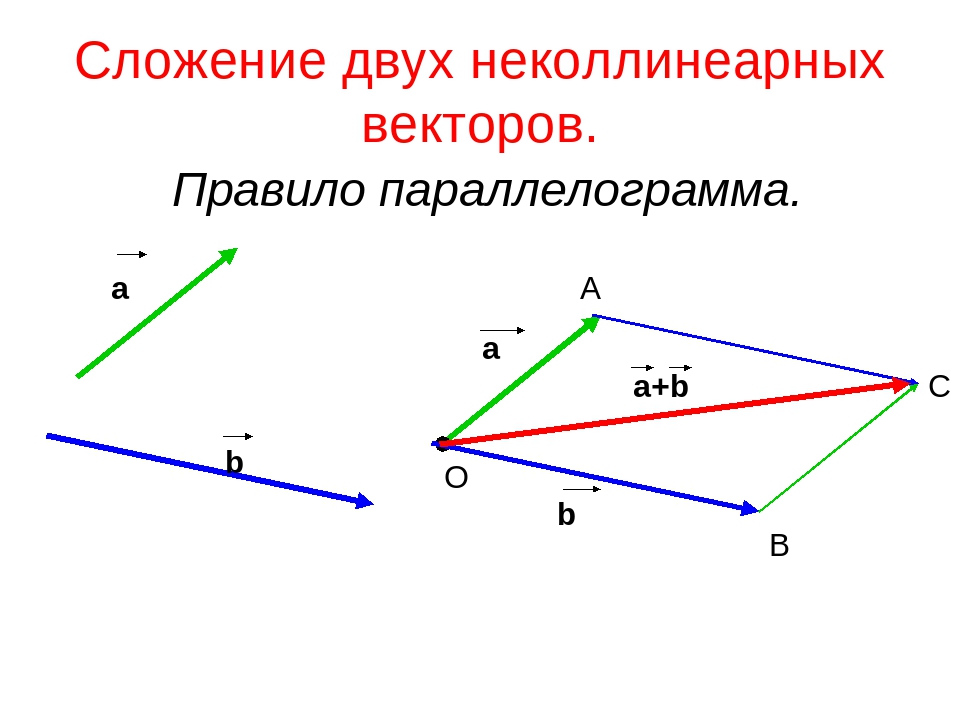
Сложение и вычитание векторов [wiki.eduVdom.com]
Пусть $\overrightarrow{a}$ и $\overrightarrow{b}$ — два вектора (рис.1, а).
Сложение двух векторов
Рис. 1
1
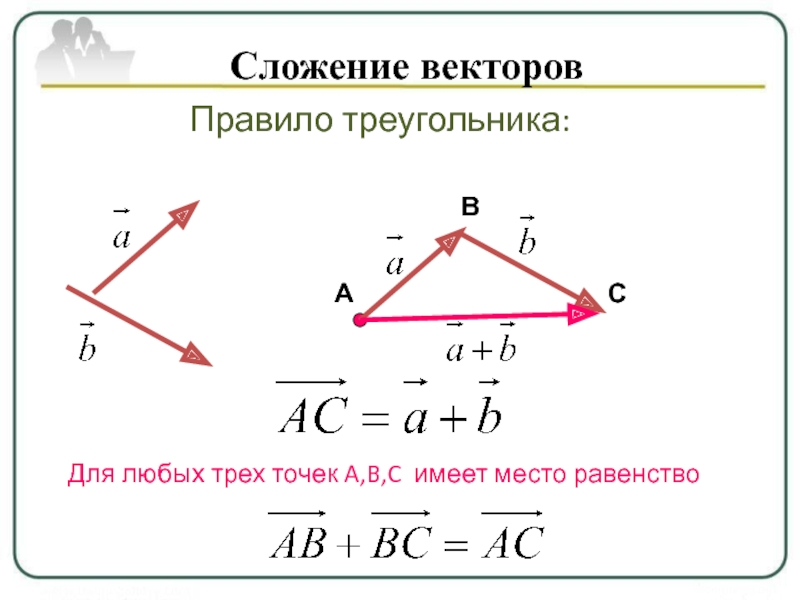
Возьмем произвольную точку О и построим вектор $\overrightarrow{ОА} = \overrightarrow{a}$ . Затем от точки А отложим вектор $\overrightarrow{AB} = \overrightarrow{b}$. Вектор $\overrightarrow{OB}$, соединяющий начало первого слагаемого вектора с концом второго (рис.1, б), называется суммой этих векторов и обозначается $\overrightarrow{a} + \overrightarrow{b}$$ (правило треугольника).
Ту же самую сумму векторов можно получить иным способом. Отложим от точки О векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{ОС} = \overrightarrow{b} $ (рис.1, в). Построим на этих векторах как на сторонах параллелограмм ОABC. Вектор $\overrightarrow{ОВ}$, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов $\overrightarrow{a} + \overrightarrow{b}$ {правило параллелограмма). Из рисунка 1, в непосредственно следует, что сумма двух векторов обладает переместительным свойством: $\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$
Действительно, каждый из векторов $\overrightarrow{a} + \overrightarrow{b} \,и\, = \overrightarrow{b} + \overrightarrow{a}$ равен одному и тому же вектору $\overrightarrow{OB}$ . 2} = \sqrt{9 + 16} = 5
\\ т.е.\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = 5.
$$
2} = \sqrt{9 + 16} = 5
\\ т.е.\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = 5.
$$
Понятие суммы векторов можно обобщить на случай любого конечного числа слагаемых векторов.
Пусть, например, даны три вектора $\overrightarrow{a}, \overrightarrow{b} \,и\, \overrightarrow{c}$ (рис.2).
Сложение трех векторов
Рис.2
Построив сначала сумму векторов $\overrightarrow{a} + \overrightarrow{b}$ , а затем прибавив к этой сумме вектор $\overrightarrow{c}$, получим вектор $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}$ . На рисунке 2
$$ \overrightarrow{ОА} = \overrightarrow{a}\,; \overrightarrow{АВ} = b\,; \overrightarrow{ОВ} = \overrightarrow{a} + \overrightarrow{b}\,; \overrightarrow{BC} = \overrightarrow{c}
\\ и
\\ \overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС} = (\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}
$$
Из рисунка 2 видно, что тот же вектор $\overrightarrow{ОС}$ мы получим, если к вектору $\overrightarrow{ОА} = \overrightarrow{a}$ прибавим вектор
$\overrightarrow{АВ} = \overrightarrow{b} + \overrightarrow{c}$ . Таким образом, $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством.
Поэтому сумму трех векторов $\overrightarrow{a}\,,\,\overrightarrow{b}\,,\,\overrightarrow{c}$ записывают просто $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$ .
Таким образом, $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством.
Поэтому сумму трех векторов $\overrightarrow{a}\,,\,\overrightarrow{b}\,,\,\overrightarrow{c}$ записывают просто $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$ .
Разностью двух векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ называется третий вектор $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ , сумма которого с вычитаемым вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$. Таким образом, если $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}\,,\, то\, \overrightarrow{c} + \overrightarrow{b} = \overrightarrow{a}$ .
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис.3).
Вычитание векторов
Рис.3
Откладываем векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{OB} = \overrightarrow{b}$ из общей точки О. Вектор $\overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $\overrightarrow{a}$ и вычитаемого вектора $\overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ . Действительно, по правилу
сложения векторов $\overrightarrow{ОВ} + \overrightarrow{ВА} = \overrightarrow{ОА} \text{ , или } \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{a}$ .
Вектор $\overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $\overrightarrow{a}$ и вычитаемого вектора $\overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ . Действительно, по правилу
сложения векторов $\overrightarrow{ОВ} + \overrightarrow{ВА} = \overrightarrow{ОА} \text{ , или } \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{a}$ .
Пример 2. Сторона равностороннего треугольника ABC равна а. Найти: $а) |\overrightarrow{ВА} — \overrightarrow{ВС}|\,;\,\ б)\,\,\ |\overrightarrow{АВ} — \overrightarrow{АС}|$ .
Решение а) Так как $\overrightarrow{ВА} — \overrightarrow{ВС} = \overrightarrow{СА}\text{ , а }|\overrightarrow{СА}| = а\text{ , то }|\overrightarrow{ВА} — \overrightarrow{ВС}| = а$ .
б) Так как $\overrightarrow{АВ} — \overrightarrow{АС} = \overrightarrow{СВ}\text{ , а }|\overrightarrow{СВ}| = а\text{ , то }|\overrightarrow{АВ} — \overrightarrow{АС}| = а$ .
Произведением вектора $\overrightarrow{a}$(обозначается $=\lambda\overrightarrow{a}$ или $\overrightarrow{a}\lambda$) на действительное число $\lambda$ называется вектор $\overrightarrow{b}$, коллинеарный вектору $\overrightarrow{a}$, имеющий длину, равную $|\lambda||\overrightarrow{a}|$, и то же направление, что и вектор $\overrightarrow{a}$, если $\lambda > 0$ , и направление, противоположное направлению вектора $\overrightarrow{a}$, если $\lambda < 0$ . Так, например, $2\overrightarrow{a}$ есть вектор, имеющий то же направление, что и вектор $\overrightarrow{a}$ , а длину, вдвое большую, чем вектор $\overrightarrow{a}$ (рис.4).
Умножение вектора на число
Рис.4
В случае, когда $\lambda = 0$ или $\overrightarrow{a} = 0$ , произведение $\lambda\overrightarrow{a}$ представляет
собой нулевой вектор. Противоположный вектор $-\overrightarrow{a}$ можно рассматривать как результат умножения вектора $\overrightarrow{a}$ на $\lambda = -1$ (см. рис.4):
$$ -\overrightarrow{a} = \ (-1)\overrightarrow{a} $$
Очевидно, что $\overrightarrow{a} + (-\overrightarrow{a}) = \overrightarrow{0}$ .
рис.4):
$$ -\overrightarrow{a} = \ (-1)\overrightarrow{a} $$
Очевидно, что $\overrightarrow{a} + (-\overrightarrow{a}) = \overrightarrow{0}$ .
Пример 3. Доказать, что если О, А, В и С — произвольные точки, то $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{ВС} + \overrightarrow{СО} = 0$ .
Решение. Сумма векторов $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{СВ} = \overrightarrow{ОС}$ , вектор $\overrightarrow{CO}$ — противоположный вектору $\overrightarrow{ОС}$ . Поэтому $\overrightarrow{ОС} + \overrightarrow{СО} = \overrightarrow{0}$ .
Пусть дан вектор $\overrightarrow{a}$. Рассмотрим единичный вектор $\overrightarrow{a_0}$ , коллинеарный вектору $\overrightarrow{a}$ и одинаково с ним направленный. Из определения умножения вектора на число следует, что
$$ \overrightarrow{a} = |\overrightarrow{a}|\,\ \overrightarrow{a_0} $$
, т.е. каждый вектор равен произведению его модуля на единичный вектор того же направления. Далее из того же определения следует, что если $\overrightarrow{b} = \lambda\overrightarrow{a}$ , где $\overrightarrow{a}$ — ненулевой вектор, то векторы $\overrightarrow{a} \,и\, \overrightarrow{b}$ коллинеарны. Очевидно, что и обратно, из коллинеарности векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ следует, что $\overrightarrow{b} = \lambda\overrightarrow{a}$.
Далее из того же определения следует, что если $\overrightarrow{b} = \lambda\overrightarrow{a}$ , где $\overrightarrow{a}$ — ненулевой вектор, то векторы $\overrightarrow{a} \,и\, \overrightarrow{b}$ коллинеарны. Очевидно, что и обратно, из коллинеарности векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ следует, что $\overrightarrow{b} = \lambda\overrightarrow{a}$.
Таким образом, получаем следующую теорему.
Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5. Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.
Видео-решение.
Сложение и вычитание векторов.
Определение.
Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:сi = ai + bi
Определение.
сi = ai — bi
Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
В случае плоской задачи сумму и разность векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующими формулами:
a + b = {ax + bx; ay + by}
a — b = {ax — bx; ay — by}
Формулы сложения и вычитания векторов для пространчтвенных задач
В случае пространственной задачи сумму и разность векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующими формулами:
a + b = {ax + bx; ay + by; az + bz}
a — b = {ax — bx; ay — by; az — bz}
Формулы сложения и вычитания n -мерных векторов
В случае n -мерного пространства сумму и разность векторов a = {a1 ; a2 ; . .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующими формулами:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующими формулами:
a + b = {a1 + b1; a2 + b2; … ; an + bn}
a — b = {a1 — b1; a2 — b2; … ; an — bn}
Самостоятельная работа по геометрии «Сложение и вычитание векторов. Умножение вектора на число»
Самостоятельная работа
«Сложение и вычитание векторов. Умножение вектора на число»
Вариант 1
1. Начертите 4 попарно неколлинеарных вектора . Постройте вектор .
2. Упростите выражение:
3. Найдите вектор из условия:
а)
б)
4. Начертите 2 неколлинеарных вектора Постройте вектор
Самостоятельная работа
«Сложение и вычитание векторов. Умножение вектора на число»
Умножение вектора на число»
Вариант 2
1. Начертите 5 попарно неколлинеарных вектора . Постройте вектор .
2. Упростите выражение:
3. Найдите вектор из условия:
а)
б)
4. Начертите 2 неколлинеарных вектора Постройте вектор
Самостоятельная работа
«Сложение и вычитание векторов. Умножение вектора на число»
Вариант 1
1. Начертите 4 попарно неколлинеарных вектора . Постройте вектор .
2. Упростите выражение:
3. Найдите вектор из условия:
а)
б)
4. Начертите 2 неколлинеарных вектора Постройте вектор
Самостоятельная работа
«Сложение и вычитание векторов. Умножение вектора на число»
Вариант 2
1. Начертите 5 попарно неколлинеарных вектора . Постройте вектор .
Постройте вектор .
2. Упростите выражение:
3. Найдите вектор из условия:
а)
б)
4. Начертите 2 неколлинеарных вектора Постройте вектор
Самостоятельная работа
«Сложение и вычитание векторов. Умножение вектора на число»
Вариант 1
1. Начертите 4 попарно неколлинеарных вектора . Постройте вектор .
2. Упростите выражение:
3. Найдите вектор из условия:
а)
б)
4. Начертите 2 неколлинеарных вектора Постройте вектор
Самостоятельная работа
«Сложение и вычитание векторов. Умножение вектора на число»
Вариант 2
1. Начертите 5 попарно неколлинеарных вектора . Постройте вектор .
2. Упростите выражение:
3. Найдите вектор из условия:
а)
б)
4. Начертите 2 неколлинеарных вектора Постройте вектор
Начертите 2 неколлинеарных вектора Постройте вектор
Тест на тему: «Векторы в пространстве. Сложение и вычитание векторов. Умножение векторов на число»
Восточный техническо-гуманитарный колледж
Составитель: преподаватель математики
Серикпаева А.Д.
Предмет: Алгебра и начала анализа
Для студентов 1 курса
Тест на тему: «Векторы в пространстве. Сложение и вычитание векторов.
Умножение векторов на число».
Бланк ответов:
№ п/п вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | В1 |
1 | 2 | 1 | 3 | 3 | 3 | 3 | 2 | 2 | 3 | |
2 | 1 | 2 | 1 | 1 | 3 | 1 | 2 | 1 | 2 | |
тест по теме: «Векторы в пространстве. Сложение и вычитание векторов.
Сложение и вычитание векторов.
Умножение вектора на число»
Вариант №1
Уровень А
1. Какое утверждение неверное?
1) Любые два противоположно направленных вектора коллинеарны.
2) Любые два коллинеарных вектора сонаправлены.
3) Любые два равных вектора коллинеарны.
2. Даны точки А, В, С, D, K. Известно, что
Тогда неверно, что…
1) все точки лежат в одной плоскости;
2) прямые ВС и DK параллельны;
3) точки А, С и D не лежат на одной прямой.
3. Какое утверждение неверное?
1) Длины противоположных векторов не могут быть неравны.
2) Если длины векторов неравны, то и векторы неравны.
3) Если длины векторов равны, то и векторы равны.
4. причём точки А, В и С не лежат на одной прямой. Прямые АС и BD не могут быть…
1) параллельными;
2) пересекающимися;
3) скрещивающимися.
5. ABCA1B1C1 – правильная призма. A1F = FB1, B1K = KC1.
Какое утверждение неверное?
1)
2)
3 )
6. ABCA1B1C1 – правильная призма. CE = EC1, BF = FB1, FM = MB1, AD : DC = 3 : 1.
Какое утверждение верное?
1)
2)
3 )
7. ABCDA1B1C1D1 – параллелепипед. …
1)
2)
3)
8. Векторы и являются…
1 ) равными;
2) противоположными;
3) сонаправленными.
9. DABC – тетраэдр.
Тогда …
1)
2)
3)
Уровень В
1. ABCDA1B1C1D1 – параллелепипед.
Тогда …
тест по теме: «Векторы в пространстве. Сложение и вычитание векторов.
Сложение и вычитание векторов.
Умножение вектора на число»
Вариант №2
Уровень А
1. Какое утверждение верное?
1) Любые два сонаправленных вектора коллинеарны.
2) Любые два коллинеарных вектора противоположно направлены.
3) Любые два коллинеарных вектора равны.
2. Какое утверждение верное?
1) Если то
2) Если то
3) Существуют векторы и такие, что и не коллинеарны, и не коллинеарны, а и коллинеарны.
3. Какое утверждение неверное?
1) Если длины векторов равны, то и векторы равны.
2) Если векторы равны, то их длины равны.
3) Длины противоположных векторов равны.
4 . причём точки А, В и С не лежат на одной прямой. Прямые АС и BD являются параллельными, если…
Прямые АС и BD являются параллельными, если…
1) k = 1;
2) k = –1;
3) k = 3.
5. ABCA1B1C1 – правильная призма. A1F = FB1, B1E = EC1. Какое утверждение неверное?
1)
2)
3 )
6. FABCD – правильная пирамида. FE = EC, EN = NC, OP = PD. Какое утверждение верное?
1)
2)
3 )
7. ABCA1B1C1 – призма. …
1)
2)
3)
8. Векторы – и являются…
Векторы – и являются…
1 ) противоположными;
2) равными;
3) сонаправленными.
9. DABC – тетраэдр.
…
1)
2)
3)
Уровень В
1. ABCDA1B1C1D1 – параллелепипед.
Тогда
План-конспект урока геометрии в 11 классе «Сложение и вычитание векторов» | План-конспект урока по геометрии (11 класс):
Дата________ Геометрия 11
Урок 2
Тема: Сложение и вычитание векторов.
Цель: ввести правила сложения и вычитания векторов, умножения вектора на число.
Ход урока
I. Устная работа.
Найдите векторы, начало и конец которых являются вершинами параллелепипеда: а) сонаправленные вектору ; б) противоположнонаправленные вектору ; в) равные вектору . |
II. Объяснение нового материала (п. 36 – 38).
I. Сумма векторов.
Правило треугольника Суммой векторов, конец одного из которых является началом другого, называется вектор, начало которого – начало первого вектора, а конец – конец второго. | Правило параллелограмма Суммой двух векторов, начала которых совпадают, называется вектор, содержащий диагональ параллелограмма, построенного на данных векторах, и исходящий из общей точки векторов. |
Правило многоугольника
III. Решение задач: №№ 327, 328, 333 (а), 335 (а).
II. Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены.
IV. Решение задач: № 329.
Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору , то есть , .
.
V. Решение задач: №№ 330, 331, 333 (б), 337 (б, в).
III. Умножение вектора на число.
Произведением ненулевого вектора на число k называется такой вектор , длина которого равна , причем векторы и сонаправлены при k ≥ 0 и противоположно направлены при k
1. k > 0 2. k
Векторы и kколлинеарны для любого и числа k, и наоборот, если векторы и коллинеарны и ≠ , то существует такое число k, что = k.
VI. Решение задач: №№ 343, 344, 347 (а).
Домашнее задание: теория (п. 40–42). №№ 334, 335 (б, в, г), 336, 347 (б).
Сложение и вычитание векторов. Умножение вектора на число
1. Сложение векторов. Векторы складываются геометрически по правилу параллелограмма или многоугольника.
Векторы складываются геометрически по правилу параллелограмма или многоугольника.
Правило параллелограмма. Суммой двух векторов и называют такой третий вектор , выходящий из их общего начала, который служит диагональю параллелограмма, сторонами которого являются сами векторы (рис.1) и обозначают так: .
Рис.1
Правило многоугольника. Чтобы построить сумму любого конечного числа векторов, нужно в конце первого слагаемого вектора построить второй, в конце второго построить третий и т. д. Вектор, замыкающий полученную ломаную линию, представляет собой искомую сумму. Начало его совпадает с началом первого слагаемого вектора, а конец — с концом последнего.
Рис.2
Например, сумма векторов , , и d получается так (рис.2). Строим векторы
Тогда вектор суммы
Два вектора и , имеющие равные длины, но противоположные направления, называются противоположными векторами (рис.3).
Рис.3
Если вектор , противоположен вектору , то можно записать:

Сумма противоположных векторов равна нуль-вектору:
Сумма векторов удостоверяет:
а) закону переместительности:
б) закону сочетательности:
2. Вычитание векторов. Вычитание двух векторов определяется как действие, обратное сложению.
Разностью двух векторов и называется такой третий вектор , который нужно сложить с вектором , чтобы получить вектор , т. е. , если .
Чтобы из вектора вычесть вектор , нужно отнести их к общему началу и провести вектор из конечной точки вектора-вычитаемого конечную точку вектора-уменьшаемого (рис.4).
Рис.4
То же действие вычитания двух векторов можно произвести иначе.
Чтобы вычесть из вектора вектор , надо прибавить к вектору равный и противоположно направленный вектору вектор (- ).
Построим вектор , длина которого равна длине вектора , а направление его противоположно направлению вектора .
Кроме того, дополним треугольник ABC до параллелограмма АСВВ₁.

Очевидно равно . Следовательно, (рис.4).
Искомая разность
Мы получим следующее равенство:
3. Умножение вектора на скаляр. При умножении вектора на скаляр n получим вектор , коллинеарный с вектором и имеющий длину в n раз больше, чем . Этот новый вектор
имеет одинаковое направление с вектором , если n>0, и противоположное с ним направление, если n
Рис.5
Если обозначить одноименной буквой с нуликом вверху вектор длины, равной 1, и того же направления, что и вектор , то из определения умножения вектора на скаляр следует
Единичный вектор направления вектора называется его ортом.
Сложение и вычитание векторов
Чтобы сложить или вычесть два вектора, сложите или вычтите соответствующие компоненты.
Позволять
ты
→
знак равно
〈
ты
1
,
ты
2
〉
а также
v
→
знак равно
〈
v
1
,
v
2
〉
быть двумя векторами.
Тогда сумма ты → а также v → это вектор
ты → + v → знак равно 〈 ты 1 + v 1 , ты 2 + v 2 〉
Разница ты → а также v → является
ты → — v → знак равно ты → + ( — v → ) знак равно 〈 ты 1 — v 1 , ты 2 — v 2 〉
Сумма двух или более векторов называется результирующей. Результат двух векторов можно найти, используя либо метод параллелограмма или метод треугольника .
Результат двух векторов можно найти, используя либо метод параллелограмма или метод треугольника .
Метод параллелограмма:
Нарисуйте векторы так, чтобы их начальные точки совпадали. Затем нарисуйте линии, чтобы сформировать полный параллелограмм. Диагональ от начальной точки до противоположной вершины параллелограмма является результирующей.
Добавление вектора:
- Поместите оба вектора ты → а также v → в той же начальной точке.
- Завершите параллелограмм. Результирующий вектор ты → + v → — диагональ параллелограмма.
Вычитание вектора:
- Завершите параллелограмм.

- От начальной точки начертите диагонали параллелограмма.
Метод треугольника:
Нарисуйте векторы один за другим, помещая начальную точку каждого последующего вектора в конечную точку предыдущего вектора.Затем проведите результат от начальной точки первого вектора к конечной точке последнего вектора. Этот метод также называют метод «голова к хвосту» .
Добавление вектора:
Вычитание вектора:
Пример:
Найти)
ты
→
+
v
→
и (б)
ты
→
—
v
→
если
ты
→
знак равно
〈
3
,
4
〉
а также
v
→
знак равно
〈
5
,
—
1
〉
.
Подставьте указанные значения ты 1 , ты 2 , v 1 а также v 2 в определение сложения векторов.
ты → + v → знак равно 〈 ты 1 + v 1 , ты 2 + v 2 〉 знак равно 〈 3 + 5 , 4 + ( — 1 ) 〉 знак равно 〈 8 , 3 〉
Перепиши разницу
ты
→
—
v
→
как сумма
ты
→
+
(
—
v
→
)
. Нам нужно будет определить компоненты
—
v
→
.
Нам нужно будет определить компоненты
—
v
→
.
Напомним, что — v → является скалярным кратным — 1 раз v . Из определения скалярного умножения имеем:
— v → знак равно — 1 〈 v 1 , v 2 〉 знак равно — 1 〈 5 , — 1 〉 знак равно 〈 — 5 , 1 〉
Теперь добавьте компоненты
ты
→
а также
—
v
→
.
ты → + ( — v → ) знак равно 〈 3 + ( — 5 ) , 4 + 1 〉 знак равно 〈 — 2 , 5 〉
векторов в математике: сложение, вычитание, деление и умножение — видео и стенограмма урока
Добавление векторов
Перво-наперво, расслабьтесь! Да, у вас будут векторы, идущие под разными углами друг к другу, но это не значит, что вам придется изучать какую-либо продвинутую тригонометрию. Фактически, для добавления векторов вам вообще не понадобится никакой тригонометрии. Просто начните с хвоста одного из векторов и проведите линию до конца другого. Поскольку векторы показывают свою величину в течение заданного времени, эта новая линия представляет, как рассматриваемый объект будет фактически перемещаться в течение этого заданного времени.
Фактически, для добавления векторов вам вообще не понадобится никакой тригонометрии. Просто начните с хвоста одного из векторов и проведите линию до конца другого. Поскольку векторы показывают свою величину в течение заданного времени, эта новая линия представляет, как рассматриваемый объект будет фактически перемещаться в течение этого заданного времени.
Допустим, у вас есть вектор величиной десять, идущий на северо-восток, и вектор величиной четыре, идущий на север. Перво-наперво нарисуйте первый вектор. Неважно, что вы выберете.Теперь на кончике этого вектора нарисуйте хвост второго. Нарисуйте вектор, как в любом другом месте. Теперь просто проведите линию от хвоста первого вектора до конца второго вектора. Это результат сложения этих двух векторов! Как ни странно, результирующий вектор называется результирующим .
Вычитание векторов
Чтобы вычесть векторы, вы делаете в основном то же самое, но с одной незначительной корректировкой. Вместо того, чтобы рисовать второй вектор как есть, переверните его на 180 градусов, чтобы он полностью изменил направление. Фактически, вы добавляете отрицательную величину к первому вектору, поэтому он будет идти в направлении, противоположном указанному в списке. Оттуда просто выполните сложение векторов, как раньше.
Фактически, вы добавляете отрицательную величину к первому вектору, поэтому он будет идти в направлении, противоположном указанному в списке. Оттуда просто выполните сложение векторов, как раньше.
Умножение векторов
Сложение и вычитание векторов довольно просто, но ни то, ни другое не так просто, как умножение вектора на скаляр. Позже по математике вы узнаете, как умножить два вектора вместе, но сейчас нам просто нужно знать, как использовать скаляр. Кстати, что такое скаляр? Скаляр — это просто число, на которое мы умножаем вектор.Например, если бы у нас был вектор, показывающий, что мы движемся на северо-запад со скоростью 30 миль в час, можно было бы использовать скаляр для изменения величины этого вектора. Если бы мы хотели удвоить нашу скорость, мы бы использовали скаляр, равный двум. Просто умножьте скаляр на величину, чтобы получить новую величину величины.
Деление векторов
Но подождите, если вы можете складывать и вычитать векторы, то разве вы не сможете делить их, если можете их умножать? Фактически, вы можете. Однако так же, как вычитание вектора связано с переключением направления, так что это больше похоже на добавление отрицательного числа, деление на вектор на самом деле означает просто умножение на скаляр, который является обратным к числу, на которое нужно разделить.Например, если у вас есть вектор движущегося корабля и вы хотите снизить его скорость вдвое, вы должны разделить его на скаляр два, что равносильно умножению на скаляр половины.
Однако так же, как вычитание вектора связано с переключением направления, так что это больше похоже на добавление отрицательного числа, деление на вектор на самом деле означает просто умножение на скаляр, который является обратным к числу, на которое нужно разделить.Например, если у вас есть вектор движущегося корабля и вы хотите снизить его скорость вдвое, вы должны разделить его на скаляр два, что равносильно умножению на скаляр половины.
Резюме урока
В этом уроке мы узнали, как складывать, вычитать, умножать и делить векторов . Помните, что вектор должен иметь величину и направление . Чтобы сложить или вычесть векторы, просто соедините векторы вместе, не забудьте перевернуть второй вектор, если это проблема вычитания.Затем проведите линию от хвоста первого вектора до конца второго. Для умножения мы научились умножать величину на скаляров . Кроме того, для деления мы научились умножать на обратную величину скаляра, чтобы получить тот же эффект.
векторов | Безграничная физика
Компоненты вектора
Векторы — это геометрические представления величины и направления, которые могут быть выражены в виде стрелок в двух или трех измерениях.
Цели обучения
Контрастность двумерных и трехмерных векторов
Основные выводы
Ключевые моменты
- Векторы можно разбить на две составляющие: величину и направление.
- Взяв вектор, который нужно проанализировать, как гипотенузу, можно найти горизонтальную и вертикальную составляющие, заполнив прямоугольный треугольник. Нижний край треугольника — это горизонтальная составляющая, а сторона, противоположная углу, — вертикальная составляющая.
- Угол, который вектор образует с горизонталью, можно использовать для вычисления длины двух компонентов.
Ключевые термины
- координаты : числа, указывающие положение относительно некоторой оси. Пример: [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] координаты указывают положение относительно [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] топоры.

- ось : воображаемая линия, вокруг которой объект вращается или симметрично расположен.
- величина : Число, присвоенное вектору, указывающее его длину.
Обзор
Векторы — это геометрические представления величины и направления, которые часто представлены прямыми стрелками, начинающимися в одной точке на оси координат и заканчивающимися в другой точке. Все векторы имеют длину, называемую величиной, которая представляет некоторое интересное качество, так что вектор можно сравнивать с другим вектором. Векторы, будучи стрелками, тоже имеют направление.Это отличает их от скаляров, которые представляют собой простые числа без направления.
Вектор определяется его величиной и ориентацией относительно набора координат. При анализе векторов часто бывает полезно разбить их на составные части. Для двумерных векторов эти компоненты бывают горизонтальными и вертикальными. Для трехмерных векторов компонент величины такой же, но компонент направления выражается в терминах [латекс] \ text {x} [/ latex], [latex] \ text {y} [/ latex] и [latex] \ text {z} [/ латекс].
Разложение вектора
Чтобы визуализировать процесс разложения вектора на его компоненты, начните с рисования вектора из начала набора координат. Затем нарисуйте прямую линию от начала координат по оси x до тех пор, пока линия не сравняется с концом исходного вектора. Это горизонтальная составляющая вектора. Чтобы найти вертикальный компонент, нарисуйте линию прямо вверх от конца горизонтального вектора, пока не дойдете до конца исходного вектора. Вы должны обнаружить, что у вас есть прямоугольный треугольник, в котором исходный вектор является гипотенузой.
Разложение вектора на горизонтальные и вертикальные компоненты — очень полезный метод для понимания физических задач. Всякий раз, когда вы видите движение под углом, вы должны думать о нем как о движении одновременно по горизонтали и вертикали. Такое упрощение векторов может ускорить вычисления и помочь отслеживать движение объектов.
Скаляры и векторы : Г-н Андерсен объясняет различия между скалярными и векторными величинами. Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
Компоненты вектора : исходный вектор, определенный относительно набора осей. Горизонтальный компонент простирается от начала вектора до его самой дальней координаты x. Вертикальный компонент простирается от оси x до самой вертикальной точки вектора. Вместе два компонента и вектор образуют прямоугольный треугольник.
Скаляры против векторов
Скаляры — это физические величины, представленные одним числом, а векторы представлены как числом, так и направлением.
Цели обучения
Определите разницу между скалярами величин и векторами, которые представляют
Основные выводы
Ключевые моменты
- Скаляры — это физические величины, представленные одним числом без направления.
- Векторы — это физические величины, требующие как величины, так и направления.
- Примеры скаляров: высота, масса, площадь и объем.
 Примеры векторов включают смещение, скорость и ускорение.
Примеры векторов включают смещение, скорость и ускорение.
Ключевые термины
- Оси координат : набор перпендикулярных линий, определяющих координаты относительно начала координат. Пример: оси координат x и y определяют горизонтальное и вертикальное положение.
Физические величины обычно можно разделить на две категории: векторы и скаляры. Эти две категории типичны в зависимости от того, какая информация им требуется. Векторы требуют двух частей информации: величины и направления. Напротив, скаляры требуют только величины.Скаляры можно рассматривать как числа, тогда как векторы следует рассматривать как стрелки, указывающие в определенном направлении.
Вектор : пример вектора. Векторы обычно представлены стрелками, длина которых представляет величину, а направление — направлением, указанным стрелкой.
Векторы требуют как величины, так и направления. Величина вектора — это число для сравнения одного вектора с другим.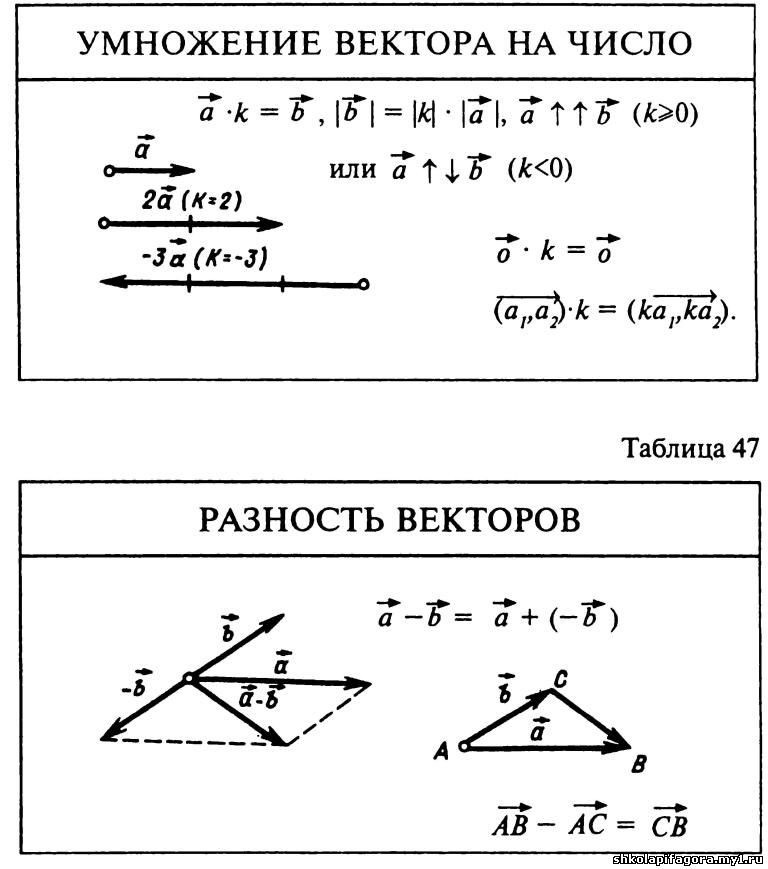 В геометрической интерпретации вектора вектор представлен стрелкой.Стрелка состоит из двух частей, определяющих ее. Две части — это его длина, которая представляет величину и направление относительно некоторого набора осей координат. Чем больше величина, тем длиннее стрелка. Физические понятия, такие как смещение, скорость и ускорение, являются примерами величин, которые могут быть представлены векторами. Каждая из этих величин имеет как величину (как далеко или как быстро), так и направление. Чтобы указать направление, должно быть что-то, относительно чего это направление.Обычно эта контрольная точка представляет собой набор осей координат, таких как плоскость x-y.
В геометрической интерпретации вектора вектор представлен стрелкой.Стрелка состоит из двух частей, определяющих ее. Две части — это его длина, которая представляет величину и направление относительно некоторого набора осей координат. Чем больше величина, тем длиннее стрелка. Физические понятия, такие как смещение, скорость и ускорение, являются примерами величин, которые могут быть представлены векторами. Каждая из этих величин имеет как величину (как далеко или как быстро), так и направление. Чтобы указать направление, должно быть что-то, относительно чего это направление.Обычно эта контрольная точка представляет собой набор осей координат, таких как плоскость x-y.
Скаляры отличаются от векторов тем, что у них нет направления. Скаляры используются в основном для представления физических величин, для которых направление не имеет смысла. Вот некоторые из них: масса, высота, длина, объем и площадь. Говорить о направлении этих величин не имеет смысла, и поэтому они не могут быть выражены в виде векторов.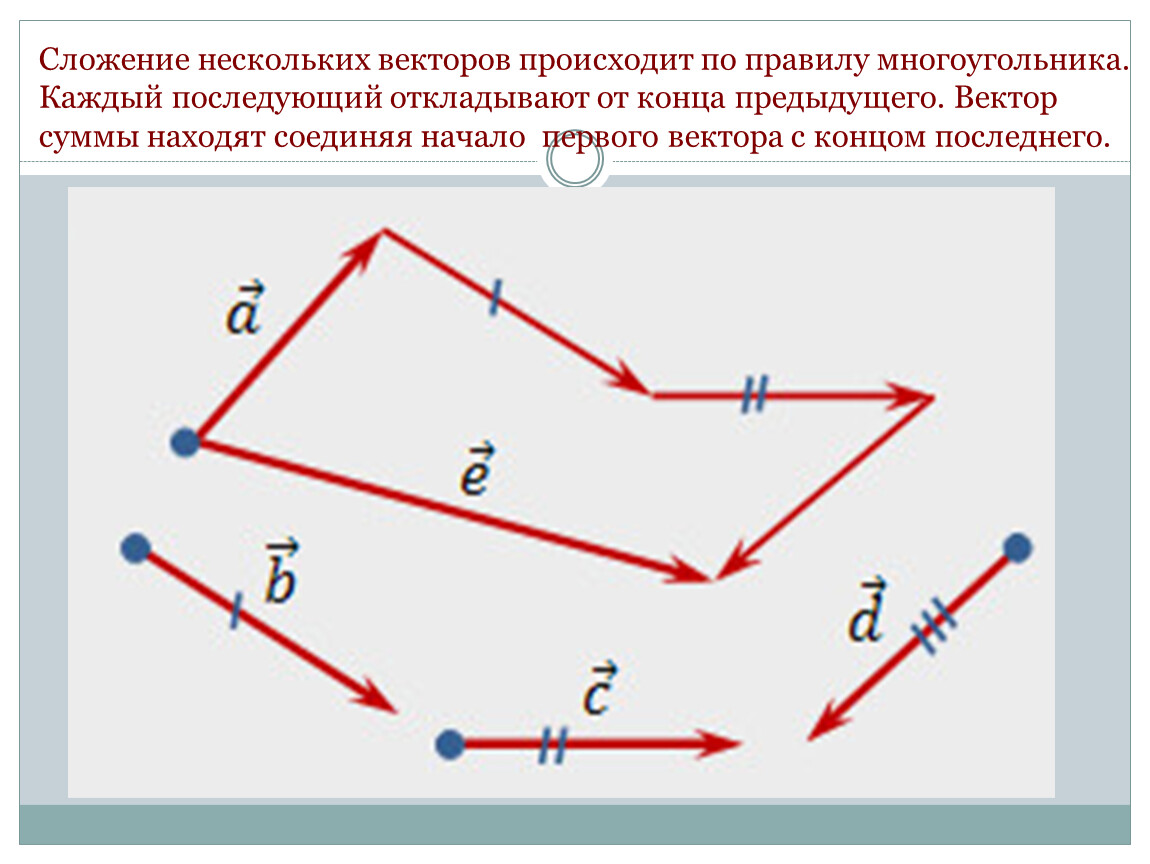
Разница между векторами и скалярами, Введение и основы : В этом видео представлена разница между скалярами и векторами.Представлены идеи о величине и направлении, а также приведены примеры векторов и скаляров.
Сложение и вычитание векторов графически
Векторов можно добавлять или вычитать графически, накладывая их встык по набору осей.
Цели обучения
Смоделируйте графический метод сложения и вычитания векторов
Основные выводы
Ключевые моменты
- Чтобы добавить векторы, положите первую на наборе осей хвостом в начале координат.Поместите следующий вектор хвостом в голову предыдущего вектора. Когда векторов больше нет, проведите прямую линию от начала до конца последнего вектора.
 Эта линия представляет собой сумму векторов.
Эта линия представляет собой сумму векторов. - Чтобы вычесть векторы, действуйте так, как если бы складывались два вектора, но переверните вектор для вычитания по осям, а затем соедините его хвостом к голове, как если бы складывались.
- Сложение или вычитание любого количества векторов дает результирующий вектор.
Ключевые термины
- начало координат : центр координатной оси, определенный как координата 0 по всем осям.
- Оси координат : набор перпендикулярных линий, определяющих координаты относительно начала координат. Пример: оси координат x и y определяют горизонтальное и вертикальное положение.
Сложение и вычитание векторов
Одним из способов, которым представление физических величин в виде векторов упрощает анализ, является легкость, с которой векторы могут быть добавлены друг к другу. Поскольку векторы представляют собой графические визуализации, сложение и вычитание векторов можно выполнять графически.
Графический метод сложения векторов также известен как метод «голова к хвосту». Для начала нарисуйте набор осей координат. Затем нарисуйте первый вектор с его хвостом (основанием) в начале координатных осей. Для сложения векторов не имеет значения, какой вектор вы рисуете первым, поскольку сложение коммутативно, но для вычитания убедитесь, что вектор, который вы рисуете первым, это тот, который вы вычитаете из . Следующий шаг — взять следующий вектор и нарисовать его так, чтобы его хвост начинался с головы предыдущего вектора (сторона стрелки).Продолжайте помещать каждый вектор в начало предыдущего, пока все векторы, которые вы хотите добавить, не соединятся вместе. Наконец, проведите прямую линию от начала координат до головы последнего вектора в цепочке. Эта новая линия является векторным результатом сложения этих векторов вместе.
Графическое сложение векторов : Метод сложения векторов «голова к хвосту» требует, чтобы вы расположили первый вектор вдоль набора осей координат. Затем поместите хвост следующего вектора на голову первого.Нарисуйте новый вектор от начала до конца последнего вектора. Этот новый вектор представляет собой сумму двух исходных.
Затем поместите хвост следующего вектора на голову первого.Нарисуйте новый вектор от начала до конца последнего вектора. Этот новый вектор представляет собой сумму двух исходных.
Сложение векторов Урок 1 из 2: Метод сложения «голова к хвосту» : Это видео знакомит зрителей с добавлением и вычитанием векторов. В первом уроке показано графическое сложение, а во втором видео используется более математический подход и показано сложение векторов по компонентам.
Метод вычитания векторов аналогичен.Убедитесь, что первый вектор, который вы рисуете, — это тот, из которого нужно вычесть. Затем, чтобы вычесть вектор, действуйте так, как если бы добавляли напротив этого вектора. Другими словами, переверните вектор, который нужно вычесть, по осям, а затем соедините его хвостом к голове, как будто складывая.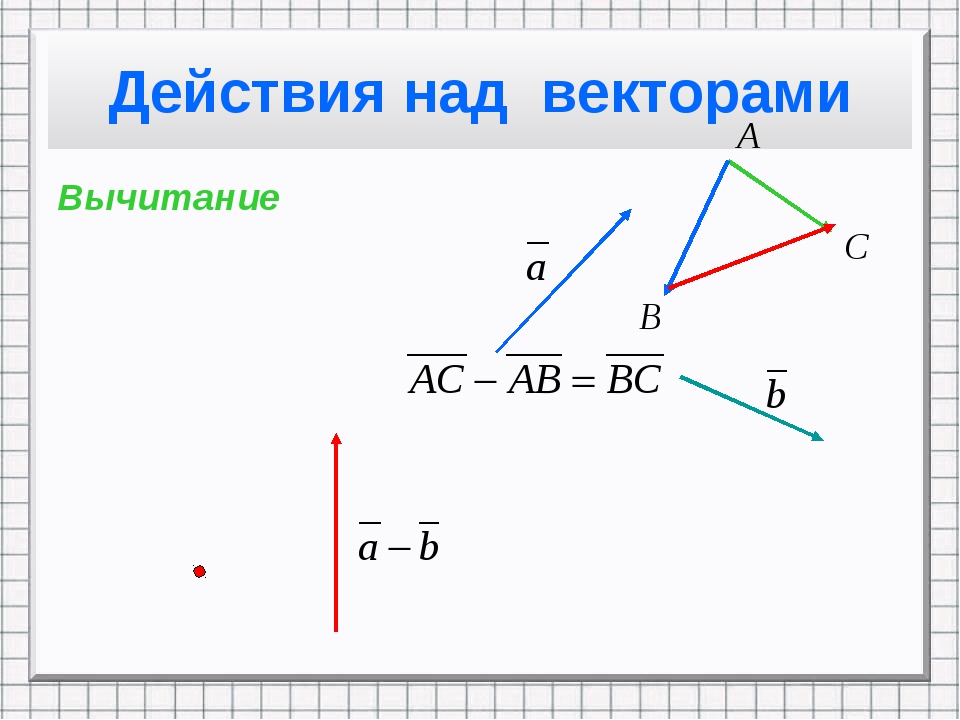 Чтобы перевернуть вектор, просто поместите его голову на место хвоста и хвост на место головы.
Чтобы перевернуть вектор, просто поместите его голову на место хвоста и хвост на место головы.
Сложение и вычитание векторов с использованием компонентов
Часто проще складывать или вычитать векторы, используя их компоненты.
Цели обучения
Продемонстрируйте, как складывать и вычитать векторы по компонентам
Основные выводы
Ключевые моменты
- Векторы можно разложить на горизонтальные и вертикальные компоненты.
- После того, как векторы разложены на компоненты, можно добавлять компоненты.
- Сложение соответствующих компонентов двух векторов дает вектор, который является суммой двух векторов.
Ключевые термины
- Компонент : часть вектора.Например, горизонтальная и вертикальная составляющие.
Использование компонентов для сложения и вычитания векторов
Другой способ добавления векторов — это добавление компонентов. Ранее мы видели, что векторы можно выразить через их горизонтальные и вертикальные компоненты. Чтобы добавить векторы, просто выразите их оба в терминах их горизонтальных и вертикальных компонентов, а затем сложите компоненты вместе.
Ранее мы видели, что векторы можно выразить через их горизонтальные и вертикальные компоненты. Чтобы добавить векторы, просто выразите их оба в терминах их горизонтальных и вертикальных компонентов, а затем сложите компоненты вместе.
Вектор с горизонтальными и вертикальными компонентами : вектор на этом изображении имеет величину 10.3 единицы и направление на 29,1 градуса выше оси абсцисс. Его можно разделить на горизонтальную и вертикальную части, как показано на рисунке.
Например, вектор длиной 5 под углом 36,9 градусов к горизонтальной оси будет иметь горизонтальную составляющую 4 единицы и вертикальную составляющую 3 единицы. Если бы мы добавили это к другому вектору той же величины и направления, мы бы получили бы вектор вдвое большей длины под тем же углом. Это можно увидеть, сложив горизонтальные компоненты двух векторов ([latex] 4 + 4 [/ latex]) и двух вертикальных компонентов ([latex] 3 + 3 [/ latex]).Эти добавления дают новый вектор с горизонтальной составляющей 8 ([latex] 4 + 4 [/ latex]) и вертикальной составляющей 6 ([latex] 3 + 3 [/ latex]). Чтобы найти результирующий вектор, просто поместите хвост вертикального компонента в головку (сторона стрелки) горизонтального компонента, а затем проведите линию от начала до вершины вертикального компонента. Эта новая строка является результирующим вектором. Он должен быть вдвое длиннее оригинала, так как оба его компонента в два раза больше, чем были ранее.
Чтобы найти результирующий вектор, просто поместите хвост вертикального компонента в головку (сторона стрелки) горизонтального компонента, а затем проведите линию от начала до вершины вертикального компонента. Эта новая строка является результирующим вектором. Он должен быть вдвое длиннее оригинала, так как оба его компонента в два раза больше, чем были ранее.
Чтобы вычесть векторы по компонентам, просто вычтите два горизонтальных компонента друг из друга и сделайте то же самое для вертикальных компонентов. Затем нарисуйте получившийся вектор, как вы делали в предыдущей части.
Добавление векторов Урок 2 из 2: Как добавлять векторы по компонентам : Это видео знакомит зрителей с добавлением векторов с использованием математического подхода и демонстрирует сложение векторов по компонентам.
Умножение векторов на скаляр
Умножение вектора на скаляр изменяет величину вектора, но не направление.
Цели обучения
Обобщить взаимодействие между векторами и скалярами
Основные выводы
Ключевые моменты
- Вектор — это величина, имеющая как величину, так и направление.
- Скаляр — это величина, имеющая только величину.
- Умножение вектора на скаляр эквивалентно умножению величины вектора на скаляр. Вектор удлиняется или сжимается, но не меняет направления.
Ключевые термины
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
- величина : Число, присвоенное вектору, указывающее его длину.
- скаляр : величина, имеющая величину, но не направление; сравнить вектор.
Обзор
Хотя векторы и скаляры представляют различные типы физических величин, иногда необходимо, чтобы они взаимодействовали. Хотя добавление скаляра к вектору невозможно из-за их различных пространственных размеров, вектор можно умножить на скаляр.Однако скаляр нельзя умножить на вектор.
Хотя добавление скаляра к вектору невозможно из-за их различных пространственных размеров, вектор можно умножить на скаляр.Однако скаляр нельзя умножить на вектор.
Чтобы умножить вектор на скаляр, просто умножьте аналогичные компоненты, то есть величину вектора, на величину скаляра. Это приведет к новому вектору с тем же направлением, но произведению двух величин.
Пример
Например, если у вас есть вектор A с определенной величиной и направлением, умножение его на скаляр a с величиной 0,5 даст новый вектор с величиной, равной половине исходной.Точно так же, если вы возьмете число 3, которое является чистым скаляром без единиц измерения, и умножите его на вектор, вы получите версию исходного вектора, которая в 3 раза длиннее. В качестве более физического примера возьмем гравитационную силу, действующую на объект. Сила — это вектор, величина которого зависит от скаляра, известного как масса, и его направления вниз. Если масса объекта удваивается, сила тяжести также удваивается.
Умножение векторов на скаляры очень полезно в физике. Большинство единиц, используемых в векторных величинах, по своей сути являются скалярами, умноженными на вектор.Например, единица измерения скорости в метрах в секунду, которая является вектором, состоит из двух скаляров, которые являются величинами: скаляр длины в метрах и скаляр времени в секундах. Чтобы преобразовать величины в скорость, нужно умножить единичный вектор в определенном направлении на эти скаляры.
Скалярное умножение : (i) Умножение вектора [latex] \ text {A} [/ latex] на скаляр [latex] \ text {a} = 0,5 [/ latex] дает вектор [latex] \ text { B} [/ latex] который вдвое короче.(ii) Умножение вектора [латекс] \ text {A} [/ latex] на 3 увеличивает его длину в три раза. (iii) Удвоение массы (скаляр) удваивает силу (вектор) гравитации.
Единичные векторы и умножение на скаляр
Умножение вектора на скаляр — это то же самое, что умножение его величины на число.
Цели обучения
Предсказать влияние умножения вектора на скаляр
Основные выводы
Ключевые моменты
- Единичный вектор — это вектор величины (длины) 1.
- Скаляр — это физическая величина, которая может быть представлена одним числом. В отличие от векторов, скаляры не имеют направления.
- Умножение вектора на скаляр — это то же самое, что умножение величины вектора на число, представленное скаляром.
Ключевые термины
- скаляр : Величина, которая может быть описана одним числом, в отличие от вектора, который требует направления и числа.
- единичный вектор : вектор величины 1.
Помимо сложения векторов, векторы также можно умножать на константы, известные как скаляры. Скаляры отличаются от векторов тем, что они представлены величиной, но не направлением. Примеры скаляров включают массу, высоту или объем объекта.
Скалярное умножение : (i) Умножение вектора A на 0,5 уменьшает его длину вдвое. (ii) Умножение вектора A на 3 увеличивает его длину втрое. (iii) Увеличение массы (скаляр) увеличивает силу (вектор).
(ii) Умножение вектора A на 3 увеличивает его длину втрое. (iii) Увеличение массы (скаляр) увеличивает силу (вектор).
При умножении вектора на скаляр направление вектора не изменяется, а величина умножается на величину скаляра. Это приводит к тому, что новая векторная стрелка указывает в том же направлении, что и старая, но с большей или меньшей длиной. Вы также можете выполнить скалярное умножение с помощью компонентов вектора. Когда у вас есть компоненты вектора, умножьте каждый из компонентов на скаляр, чтобы получить новые компоненты и, следовательно, новый вектор.
Полезной концепцией при изучении векторов и геометрии является концепция единичного вектора. Единичный вектор — это вектор с длиной или величиной, равной единице. Единичные векторы различны для разных координат. В декартовых координатах направлениями являются x и y, обычно обозначаемые [latex] \ hat {\ text {x}} [/ latex] и [latex] \ hat {\ text {y}} [/ latex]. С треугольником над буквами называется «шляпа». Единичные векторы в декартовых координатах описывают круг, известный как «единичный круг» с радиусом один.Это можно увидеть, взяв все возможные векторы длины один под всеми возможными углами в этой системе координат и поместив их в координаты. Если бы вы провели линию, соединяющую все головы всех векторов вместе, вы бы получили круг радиуса один.
Единичные векторы в декартовых координатах описывают круг, известный как «единичный круг» с радиусом один.Это можно увидеть, взяв все возможные векторы длины один под всеми возможными углами в этой системе координат и поместив их в координаты. Если бы вы провели линию, соединяющую все головы всех векторов вместе, вы бы получили круг радиуса один.
Положение, смещение, скорость и ускорение как векторы
Положение, смещение, скорость и ускорение могут быть показаны векторами, поскольку они определены в терминах величины и направления.
Цели обучения
Изучить применение векторов в анализе физических величин
Основные выводы
Ключевые моменты
- Векторы — это стрелки, состоящие из величины и направления. Они используются в физике для представления физических величин, которые также имеют как величину, так и направление.
- Смещение — это физический термин, означающий расстояние объекта от контрольной точки.
 Поскольку смещение содержит две части информации: расстояние от опорной точки и направление от точки, оно хорошо представлено вектором.
Поскольку смещение содержит две части информации: расстояние от опорной точки и направление от точки, оно хорошо представлено вектором. - Скорость определяется как скорость изменения смещения во времени. Чтобы узнать скорость объекта, нужно знать, как быстро изменяется смещение, и в каком направлении. Следовательно, он также хорошо представлен вектором.
- Ускорение, являющееся скоростью изменения скорости, также требует как величины, так и направления относительно некоторых координат.
- При рисовании векторов часто не хватает места, чтобы нарисовать их в масштабе, который они представляют, поэтому важно где-нибудь указать, в каком масштабе они нарисованы.
Ключевые термины
- скорость : Скорость изменения смещения относительно изменения во времени.
- смещение : длина и направление прямой линии между двумя объектами.
- ускорение : скорость, с которой скорость тела изменяется со временем
Использование векторов
Векторы могут использоваться для представления физических величин. Чаще всего в физике векторы используются для обозначения смещения, скорости и ускорения.Векторы представляют собой комбинацию величины и направления и отображаются в виде стрелок. Длина представляет собой величину, а направление этой величины — это направление, в котором указывает вектор. Поскольку векторы строятся таким образом, полезно анализировать физические величины (как с размером, так и с направлением) как векторами.
Чаще всего в физике векторы используются для обозначения смещения, скорости и ускорения.Векторы представляют собой комбинацию величины и направления и отображаются в виде стрелок. Длина представляет собой величину, а направление этой величины — это направление, в котором указывает вектор. Поскольку векторы строятся таким образом, полезно анализировать физические величины (как с размером, так и с направлением) как векторами.
Приложения
В физике векторы полезны, потому что они могут визуально представлять положение, смещение, скорость и ускорение. При рисовании векторов часто не хватает места, чтобы нарисовать их в масштабе, который они представляют, поэтому важно где-нибудь указать, в каком масштабе они нарисованы.Например, при рисовании вектора, представляющего величину 100, можно нарисовать линию длиной 5 единиц в масштабе [латекс] \ displaystyle \ frac {1} {20} [/ latex]. Когда величина, обратная шкале, умножается на нарисованную величину, она должна равняться действительной величине.
Положение и перемещение
Смещение определяется как расстояние объекта в любом направлении относительно положения другого объекта. Физики используют концепцию вектора положения как графический инструмент для визуализации смещений.Вектор положения выражает положение объекта от начала системы координат. Вектор положения также может использоваться для отображения положения объекта относительно опорной точки, вторичного объекта или исходного положения (при анализе того, насколько далеко объект переместился от своего исходного положения). Вектор положения — это прямая линия, проведенная от произвольной исходной точки к объекту. После рисования вектор имеет длину и направление относительно используемой системы координат.
Скорость
Скорость также определяется величиной и направлением.Чтобы сказать, что что-то набирает или теряет скорость, нужно также сказать, насколько и в каком направлении. Например, самолет, летящий в 200 [latex] \ frac {\ text {km}} {\ text {h}} [/ latex] на северо-восток, может быть представлен вектором, указывающим в северо-восточном направлении, с магнитудой 200 [латекс] \ frac {\ text {km}} {\ text {h}} [/ latex].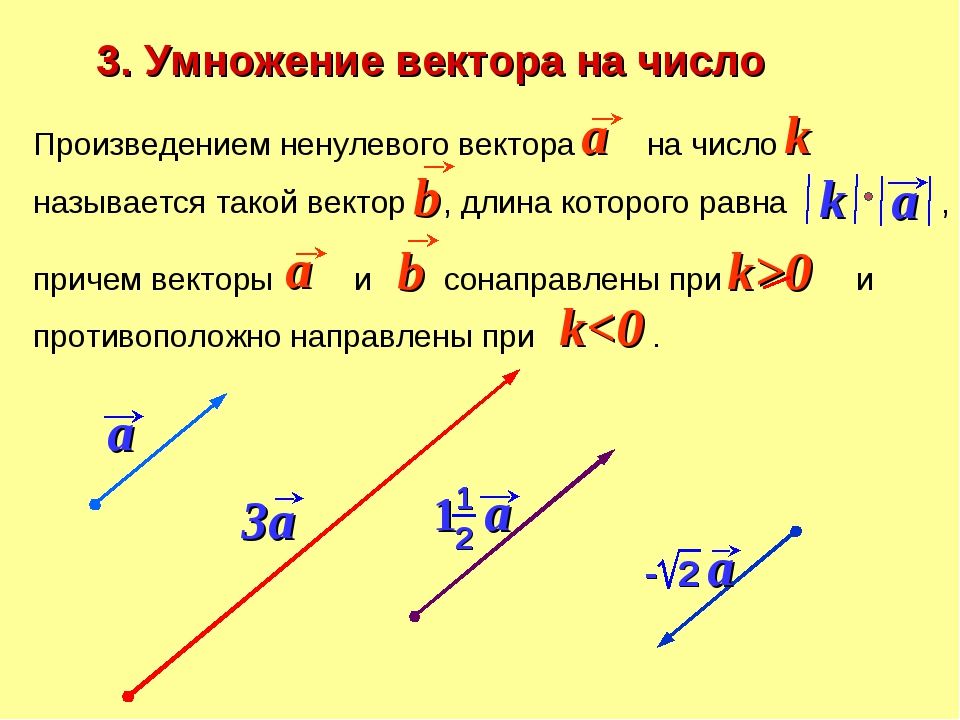 При рисовании вектора величина важна только как способ сравнения двух векторов одинаковых единиц. Итак, если бы другой самолет летел на 100 [latex] \ frac {\ text {km}} {\ text {h}} [/ latex] на юго-запад, векторная стрелка должна быть вдвое короче и указывать в направлении юго-запад.
При рисовании вектора величина важна только как способ сравнения двух векторов одинаковых единиц. Итак, если бы другой самолет летел на 100 [latex] \ frac {\ text {km}} {\ text {h}} [/ latex] на юго-запад, векторная стрелка должна быть вдвое короче и указывать в направлении юго-запад.
Разгон
Ускорение, представляющее собой скорость изменения скорости во времени, состоит из величины и направления и строится по той же концепции, что и вектор скорости. Значение ускорения не помогло бы в физике, если бы величина и направление этого ускорения были неизвестны, поэтому эти векторы важны. На диаграмме свободного тела, например, падающего объекта, было бы полезно использовать вектор ускорения рядом с объектом, чтобы обозначить его ускорение по направлению к земле.2} [/ латекс] .
Векторная диаграмма : Мужчина поднимается на холм. Его направление движения определяется углом тета относительно вертикальной оси и длиной стрелки, идущей вверх по холму. Он также ускоряется вниз под действием силы тяжести.
Он также ускоряется вниз под действием силы тяжести.
Скалярное умножение и сложение векторов
Двумя основными векторными операциями являются скалярное умножение и сложение векторов . Вообще, при работе с векторами числа или константы называются , скалярами, , .Скалярное умножение — это когда вектор умножается на скаляр (число или константу). Если вектор v умножить на скаляр k, результат будет k v . Если k положительно, то k v будет иметь те же направления, что и v . Если k отрицательно, k v будет иметь направление, противоположное v .
СКАЛЯРНОЕ УМНОЖЕНИЕ:
Пусть v = 〈v1, v2〉 и k скаляр.
k v = k 〈v1, v2〉 = 〈kv1, kv2〉
Чтобы сложить два вектора u и v , поместите начальную точку второго вектора (без изменения длины или направления) на конечная точка первого вектора.Затем соедините начальную точку первого вектора с концом второго вектора. Эта линия соединения представляет собой сумму двух векторов.
Эта линия соединения представляет собой сумму двух векторов.
Сумма векторов u и v в компонентной форме равна:
ДОБАВЛЕНИЕ ВЕКТОРОВ:
Пусть u = 〈u1, u2〉 и v = 〈v1, v2〉
u + v = 〈U1 + v1, u2 + v2〉
u − v = u + (- v) = 〈u1 − v1, u2 − v2〉
Скалярное умножение и векторное сложение имеют следующие свойства:
СВОЙСТВА СКАЛЯРНОГО УМНОЖЕНИЯ И ВЕКТОРА ДОПОЛНЕНИЕ:
Пусть u , v и w — векторы, а c и d — скаляры.
1. u + v = v + u 2. ( u + v ) + w = u + ( v + w )
3. u + 0 = u 4. u + (- u ) = 0
5. c (d u ) = (cd) u 6. (c + d) u = c u + d u
7. c ( u + v ) = c u + c v 8.1 · u = u , 0 · u = 0
9. || c v || = | c ||| v ||
|| c v || = | c ||| v ||
Давайте рассмотрим пару примеров.
Пример 1: Если u = 〈- 2,1〉 и v = 〈7, −3〉 найти (а) u + v и (б) u — v.
Шаг 1. Вычислить u + v с помощью сложения векторов. Добавьте x-компонент обоих векторов.Сделайте то же самое для y-компонентов. | и + v = 〈- 2 + 7, 1 + (- 3)〉 и + v = 〈5, −2〉 |
Шаг 2: Вычислить u — v с помощью сложения векторов. Запомните u — v = u + (-v), поэтому вычтите x-компонент v из u .Сделайте то же самое для y-компонентов. | u − v = u + (- v) = 〈- 2−7, 1 — (- 3)〉 u − v = 〈- 9, 4〉 |
Пример 2: Если u = 〈6,15〉 и v = 〈- 5,20〉 находим (а) 2u + v и (б) 5u — 2v.
Шаг 1. Вычислить 2u + v, используя скалярное умножение и сложение векторов. а) Сначала вычислите 2 и , используя скалярное умножение. б) Затем вычислите 2 u + v , используя сложение векторов. | 2u = 2 〈6,15〉 = 〈2 · 6, 2 · 15〉 2u = 〈12, 30〉 2u + v = 〈12 + (- 5), 30 + 20〉 2u + v = 〈7,50〉 |
Шаг 2: Вычислите 5u — 2v, используя скалярное умножение и сложение векторов. a) Сначала вычислите 5 u и 2 v , используя скалярное умножение. б) Затем вычислите 5 u +2 v , используя сложение векторов. | 5u = 5 〈6,15〉 = 〈5 · 6, 5 · 15〉 5u = 〈30, 75〉 2v = 2 〈−5,20〉 = 〈2 · (−5), 2 · 20〉 2u = 〈- 10, 40〉 5u − 2v = 5u + (- 2v) 5u − 2v = 〈30 — (- 10), 75−40〉 5u − 2v = 〈40, 35〉 |
Сложение и вычитание векторов: графические методы
Используйте графическую технику для добавления векторов, чтобы найти полное смещение человека, который идет следующими тремя путями (смещениями) на плоском поле. Сначала она проходит 25,0 м в направлении 49,0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0 ° к югу от востока.
Сначала она проходит 25,0 м в направлении 49,0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0 ° к югу от востока.
Изобразите каждый вектор смещения графически стрелкой, обозначив первый A , второй B и третий C , сделав длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад.Описанный выше метод «голова к хвосту» дает возможность определить величину и направление результирующего смещения, обозначенное как R .
Решение(1) Нарисуйте три вектора смещения.
(2) Поместите векторы голова к хвосту, сохраняя их начальную величину и направление.
(3) Нарисуйте результирующий вектор R .
(4) Используйте линейку, чтобы измерить звездную величину R , и транспортир, чтобы измерить направление R . Хотя направление вектора можно указать разными способами, самый простой способ — измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх дном и измеряем угол между осью, направленной на восток, и вектором.
Хотя направление вектора можно указать разными способами, самый простой способ — измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх дном и измеряем угол между осью, направленной на восток, и вектором.
Рисунок 11
В этом случае видно, что полное смещение R имеет величину 50,0 м и лежит в направлении 7.0º к югу от востока. Используя его величину и направление, этот вектор можно выразить как R, = 50,0 м и θ, = 7,0º к югу от востока.
Обсуждение Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результат не зависит от порядка добавления векторов. Следовательно, мы можем складывать векторы в любом порядке, как показано на рисунке 12, и мы все равно получим то же самое решение.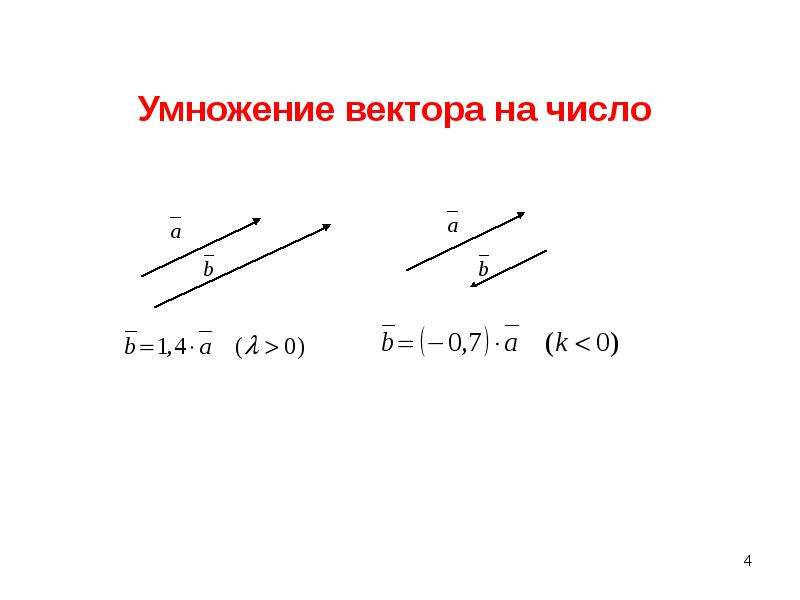
Здесь мы видим, что когда одни и те же векторы добавляются в другом порядке, результат тот же. Эта характеристика верна во всех случаях и является важной характеристикой векторов. Сложение вектора — это коммутативный . Векторы можно добавлять в любом порядке.
А + В = В + А.
(Это также верно и для сложения обычных чисел — вы получите тот же результат, например, прибавляете ли вы 2 + 3 или 3 + 2 ).
операций над векторами, сложение векторов, умножение вектора на действительное число.
Рассмотрим вектор v, начальной точкой которого является начало в системе координат xy, а конечной точкой является. Мы говорим, что вектор находится в стандартной позиции и называем его вектором позиции. Обратите внимание, что упорядоченная пара однозначно определяет вектор. Таким образом, мы можем использовать для обозначения вектора. Чтобы подчеркнуть, что мы думаем о векторе и избежать путаницы с обозначениями упорядоченных пар и интервалов, мы обычно пишем
v =.
Координата a — это скаляр , горизонтальный компонент , вектора, а координата b — это скаляр , вертикальный компонент , вектора. Под скаляром мы подразумеваем числовую величину , а не векторную величину . Таким образом, считается, что это компонент , форма для v. Обратите внимание, что a и b НЕ являются векторами, и их не следует путать с определением компонента вектора.
Теперь рассмотрим с A = (x 1 , y 1 ) и C = (x 2 , y 2 ).Давайте посмотрим, как найти вектор положения, эквивалентный. Как вы можете видеть на рисунке ниже, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся путем вычитания координат A из координат C. Таким образом, P = (x 2 — x 1 , y 2 — y 1 ) и вектор положения равен.
Можно показать, что и имеют одинаковую величину и направление и, следовательно, эквивалентны. Таким образом, = = 2 — x 1 , y 2 — y 1 >.
Таким образом, = = 2 — x 1 , y 2 — y 1 >.
Компонент формирует из с A = (x 1 , y 1 ) и C = (x 2 , y 2 ) составляет
= 2 — x 1 , y 2 — y 1 >.
Пример 1 Найдите форму компонента, если C = (- 4, — 3) и F = (1, 5).
Решение У нас
= =.
Обратите внимание, что вектор эквивалентен вектору положения, как показано на рисунке выше.
Теперь, когда мы знаем, как записывать векторы в компонентной форме, давайте переформулируем некоторые определения.
Длину вектора v легко определить, когда известны компоненты вектора. Для v = 1, v 2 > имеем
| v | 2 = v 2 1 + v 2 2 Использование теоремы Пифагора
| v | = √v 2 1 + v 2 2 .
Длина или величина вектора v = 1, v 2 > задается как | v | = √v 2 1 + v 2 2 .
Два вектора эквивалентны , если они имеют одинаковую величину и одинаковое направление.
Пусть u = 1, u 2 > и v = 1, v 2 >. Тогда
1, u 2 > = 1, v 2 > тогда и только тогда, когда u 1 = v 1 и u 2 = v 2 .
Операции над векторами
Чтобы умножить вектор v на положительное действительное число, мы умножаем его длину на число. Его направление остается прежним.Например, когда вектор v умножается на 2, его длина удваивается и его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а его направление остается прежним. Чтобы умножить вектор v на отрицательное действительное число, мы умножаем его длину на число и меняем его направление на обратное. Когда вектор умножается на 2, его длина удваивается, а его направление меняется на противоположное. Поскольку действительные числа работают как коэффициенты масштабирования при векторном умножении, мы называем их скалярами , а произведения kv называются скалярными кратными v.
Для действительного числа k и вектора v = 1, v 2 >, скалярное произведение k и v равно
kv = k.1, v 2 > = 1, kv 2 >.
Вектор kv представляет собой скалярное кратное вектора v.
Пример 2 Пусть u = и w =. Найти — 7w, 3u и — 1w.
Решение
— 7w = — 7. =,
3u = 3. =,
— 1w = — 1. =.
Теперь мы можем сложить два вектора с помощью компонентов.Чтобы сложить два вектора, представленных в форме компонентов, мы добавляем соответствующие компоненты. Пусть u = 1, u 2 > и v = 1, v 2 >. Тогда
u + v = 1 + v 1 , u 2 + v 2 >
Например, если v = и w =, то
v + w = =
Если u = 1, u 2 > и v = 1, v 2 >, то
u + v = 1 + v 1 , u 2 + v 2 >.
Прежде чем мы определим вычитание векторов, нам нужно определить — v. Противоположность v = 1, v 2 >, показанная ниже, это
Противоположность v = 1, v 2 >, показанная ниже, это
— v = (- 1) .v = (- 1) 1, v 2 > = 1, — v 2 >
Вычитание вектора, такое как u — v, включает вычитание соответствующих компонентов. Покажем это, переписав u — v как u + (- v). Если u = 1, u 2 > и v = 1, v 2 >, то
u — v = u + (- v) = 1, u 2 > + 1, — v 2 > = 1 + (- v 1 ), u 2 + (- v 2 )> = 1 — v 1 , u 2 — v 2 >
Мы можем проиллюстрировать векторное вычитание с помощью параллелограммов, точно так же, как мы делали векторное сложение.
Вычитание вектора
Если u = 1, u 2 > и v = 1, v 2 >, то
u — v = 1 — v 1 , u 2 — v 2 >.
Интересно сравнить сумму двух векторов с разностью тех же двух векторов в одном параллелограмме. Векторы u + v и u — v — диагонали параллелограмма.
Пример 3 Выполните следующие вычисления, где u = и v =.
a) u + v
b) u — 6v
c) 3u + 4v
d) | 5v — 2u |
Решение
а) u + v = + = =;
б) и — 6в = — 6. = — =;
c) 3u + 4v = 3. + 4. = + =;
d) | 5v — 2u | = | 5. — 2. | = | — | = || = √ (- 29) 2 + 21 2 = √1282 ≈ 35,8
Прежде чем мы сформулируем свойства сложения векторов и скалярного умножения, нам нужно определить другой специальный вектор — нулевой вектор. Вектор, у которого обе точки — начальная и конечная, — это нулевой вектор , обозначенный буквой O или.Его величина равна 0. Помимо вектора, нулевой вектор является аддитивным вектором идентичности:
v + O = v. 1, v 2 > + = 1, v 2 >
Операции над векторами имеют много общего. свойства как операции с действительными числами.
Для всех векторов u, v и w и для всех скаляров b и c:
1. u + v = v + u.
u + v = v + u.
2. и + (v + w) = (u + v) + w.
3. v + O = v.
4 1.v = v; 0. v = 0.
5. v + (- v) = 0.
6. b (cv) = (bc) v.
7. (b + c) v = bv + cv.
8. b (u + v) = bu + bv.
Единичные векторы
Вектор величины или длины 1 называется единичным вектором . Вектор v = является единичным вектором, поскольку
| v | = || = √ (- 3/5) 2 + (4/5) 2 = √9 / 25 + 16/25 = √25 / 25 = √1 = 1.
Пример 4 Найдите единичный вектор, который имеет то же направление, что и вектор w =.
Решение Сначала мы находим длину w:
| w | = √ (- 3) 2 + 5 2 = √34. Таким образом, нам нужен вектор, длина которого равна 1 / √34 от w, а направление совпадает с направлением вектора w. Этот вектор равен
u = w / √34 = / √34 = 34, 5 / √34>.
Вектор u является единичным вектором, поскольку
| u | = | w / √34 | = = √34 / 34 = √1 = 1.
Если v — вектор и v ≠ O, то
(1 / | v |) • v или v / | v |,
— это единичный вектор в направлении v.
Хотя единичные векторы могут иметь любое направление, единичные векторы, параллельные осям x и y, особенно полезны. Они определены как
i = и j =.
Любой вектор может быть выражен как линейная комбинация единичных векторов i и j. Например, пусть v = 1, v 2 >. Тогда
v = 1, v 2 > = 1, 0> + 2> = v 1 + v 2 = v 1 i + v 2 j.
Пример 5 Выразите вектор r = как линейную комбинацию i и j.
Решение
r = = 2i + (- 6) j = 2i — 6j.
Пример 6 Запишите вектор q = — i + 7j в компонентной форме.
Решение q = — i + 7j = -1i + 7j =
Операции с векторами также могут выполняться, когда векторы записываются как линейные комбинации i и j.
Пример 7 Если a = 5i — 2j и b = -i + 8j, найдите 3a — b.
Решение
3a — b = 3 (5i — 2j) — (- i + 8j) = 15i — 6j + i — 8j = 16i — 14j.
Углы направления
Конечная точка P единичного вектора в стандартном положении — это точка на единичной окружности, обозначенная (cosθ, sinθ). Таким образом, единичный вектор может быть выражен в форме компонентов,
u =,
или как линейная комбинация единичных векторов i и j,
u = (cosθ) i + (sinθ) j,
, где компоненты u являются функциями угла направления θ, измеренного против часовой стрелки от оси x к вектору. Поскольку θ изменяется от 0 до 2π, точка P следует по окружности x 2 + y 2 = 1.Это принимает все возможные направления для единичных векторов, поэтому уравнение u = (cosθ) i + (sinθ) j описывает все возможные единичные векторы на плоскости.
Пример 8 Вычислите и нарисуйте единичный вектор u = (cosθ) i + (sinθ) j для θ = 2π / 3. Включите единичный круг в свой эскиз.
Решение
u = (cos (2π / 3)) i + (sin (2π / 3)) j = (- 1/2) i + (√3 / 2) j
Пусть v = 1, v 2 > с направленным углом θ. Используя определение касательной функции, мы можем определить угол направления из компонентов v:
Используя определение касательной функции, мы можем определить угол направления из компонентов v:
Пример 9 Определите угол направления θ вектора w = — 4i — 3j.
Решение Мы знаем, что
w = — 4i — 3j =.
Таким образом, имеем
tanθ = (- 3) / (- 4) = 3/4 и θ = tan — 1 (3/4).
Поскольку w находится в третьем квадранте, мы знаем, что θ — угол третьего квадранта. Базовый угол составляет
tan — 1 (3/4) ≈ 37 °, а θ ≈ 180 ° + 37 °, или 217 °.
Для работы с прикладными задачами и для последующих курсов, таких как математика, удобно иметь способ выразить вектор так, чтобы его величину и направление можно было легко определить или прочитать.Пусть v вектор. Тогда v / | v | является единичным вектором в том же направлении, что и v. Таким образом, мы имеем
v / | v | = (cosθ) i + (sinθ) j
v = | v | [(cosθ) i + (sinθ) j] Умножение на | v |
v = | v | (cosθ) i + | v | (sinθ) j.
Пример 10 Скорость и направление самолета.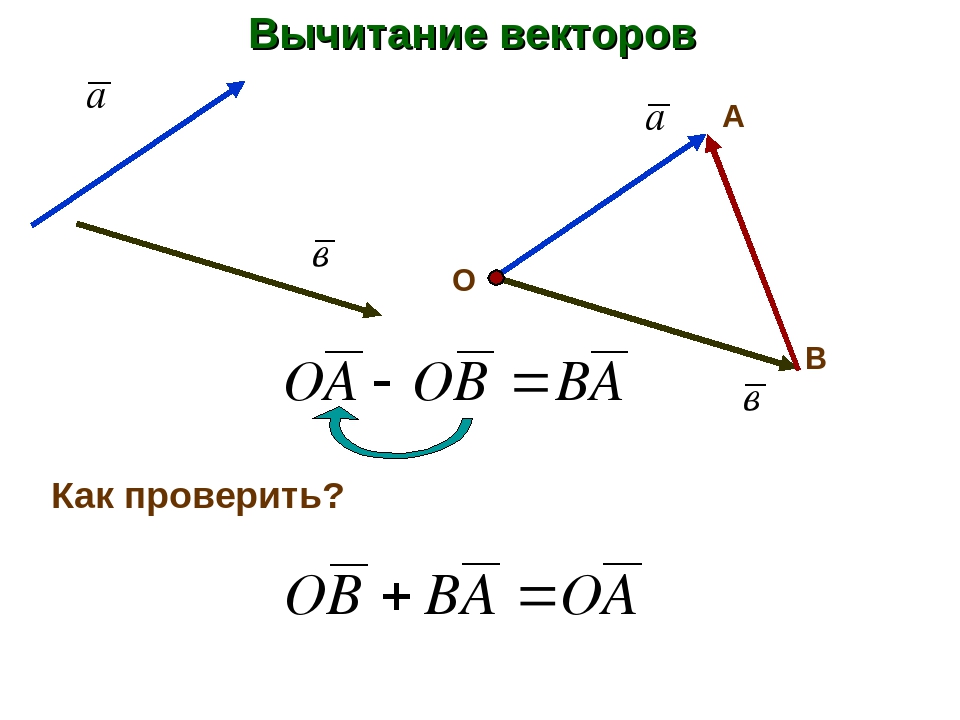 Самолет движется по пеленгу 100 ° со скоростью 190 км / ч, а ветер дует 48 км / ч со скоростью 220 °. Найдите путевую скорость самолета и направление его траектории или курса относительно земли.
Самолет движется по пеленгу 100 ° со скоростью 190 км / ч, а ветер дует 48 км / ч со скоростью 220 °. Найдите путевую скорость самолета и направление его траектории или курса относительно земли.
Раствор Сначала делаем рисунок. Ветер представлен как, а вектор скорости самолета — как. Результирующий вектор скорости равен v, сумме двух векторов:
v = +.
Пеленг (отсчитываемый от севера) вектора воздушной скорости равен 100 °. Угол направления (измеренный против часовой стрелки от положительной оси x) составляет 350 °. Пеленг (отсчитываемый от севера) вектора ветра составляет 220 °. Угол направления (измеренный против часовой стрелки от положительной оси x) составляет 50 °.Величины и равны 190 и 48 соответственно. Имеем
= 190 (cos350 °) i + 190 (sin350 & deg) j и
= 48 (cos50 °) i + 48 (sin50 & deg) j.
Таким образом,
v = +
= [190 (cos350 °) i + 190 (sin350 & deg) j] + [48 (cos50 °) i + 48 (sin50 & deg) j]
= [190 (cos350 °) i + 48 ( cos50 °) i] + [190 (sin350 & deg) j + 48 (sin50 & deg) j]
≈ 217,97i + 3,78j.
Из этой формы мы можем определить путевую скорость и курс:
Путевая скорость ≈ √ (217,97) 2 + (3,78) 2 ≈ 218 км / ч.
Пусть α будет направленным углом v. Тогда
tanα = 3,78 / 217,97
α = tan — 1 3,78 / 217,97 ≈ 1 °.
Таким образом, курс самолета (направление с севера) составляет 90 ° — 1 °, или 89 °.
Угол между векторами
Когда вектор умножается на скаляр, результатом является вектор. Когда два вектора складываются, результат также является вектором. Таким образом, мы могли бы ожидать, что произведение двух векторов также будет вектором, но это не так. Скалярное произведение , , , двух векторов является действительным числом или скаляром.Этот продукт полезен для определения угла между двумя векторами и определения того, являются ли два вектора перпендикулярными.
Точечное произведение двух векторов u = 1, u 2 > и v = 1, v 2 > равно
u • v = u 1 . v 1 + u 2 .v 2
v 1 + u 2 .v 2
(Обратите внимание, что u 1 v 1 + u 2 v 2 — это скаляр , а не вектор.)
Пример 11 Найдите указанное скалярное произведение, когда
u =, v = и w =.
a) u • w
b) w • v
Решение
а) u • w = 2 (- 3) + (- 5) 1 = — 6 — 5 = — 11;
б) w • v = (- 3) 0 + 1 (4) = 0 + 4 = 4.
Скалярное произведение можно использовать, чтобы найти угол между двумя векторами. Угол между двумя векторами является наименьшим положительным углом, образованным двумя направленными отрезками прямой. Таким образом, угол θ между u и v равен углу между v и u, а 0 ≤ θ ≤ π.
Если θ — угол между двумя ненулевыми векторами u и v, то
cosθ = (u • v) / | u || v |.
Пример 12 Найдите угол между u = и v =.
Решение Начнем с нахождения u • v, | u | и | v |:
u • v = 3 (- 4) + 7 (2) = 2,
| u | = √3 2 + 7 2 = √58 и
| v | = √ (- 4) 2 + 2 2 = √20.
Тогда
cosα = (u • v) / | u || v | = 2 / √58.√20
α = cos — 1 (2 / √58.√20)
α ≈ 86,6 °.
Силы в равновесии
Когда несколько сил действуют через одну и ту же точку на объект, их векторная сумма должна быть равна нулю, чтобы произошло равновесие.Когда происходит равновесие, объект либо неподвижен, либо движется по прямой без ускорения. Тот факт, что векторная сумма должна быть равной нулю для баланса, и наоборот, позволяет нам решать многие прикладные задачи, связанные с силами.
Пример 13 Подвесной блок. Блок весом 350 фунтов подвешен на двух тросах, как показано слева. В точке A действуют три силы: W, тянущий вниз блок, и R и S, два троса, тянущие вверх и наружу. Найдите натяжение каждого троса.
Решение Мы рисуем силовую диаграмму с начальными точками каждого вектора в начале координат. Для обеспечения баланса векторная сумма должна быть вектором O:
R + S + W = O.
Мы можем выразить каждый вектор через его величину и угол направления:
R = | R | [( cos125 °) i + (sin125 °) j],
S = | S | [(cos37 °) i + (sin37 °) j] и
W = | W | [(cos270 °) i + (sin270 °) j]
= 350 (cos270 °) i + 350 (sin270 °) j
= -350j cos270 ° = 0; sin270 ° = — 1.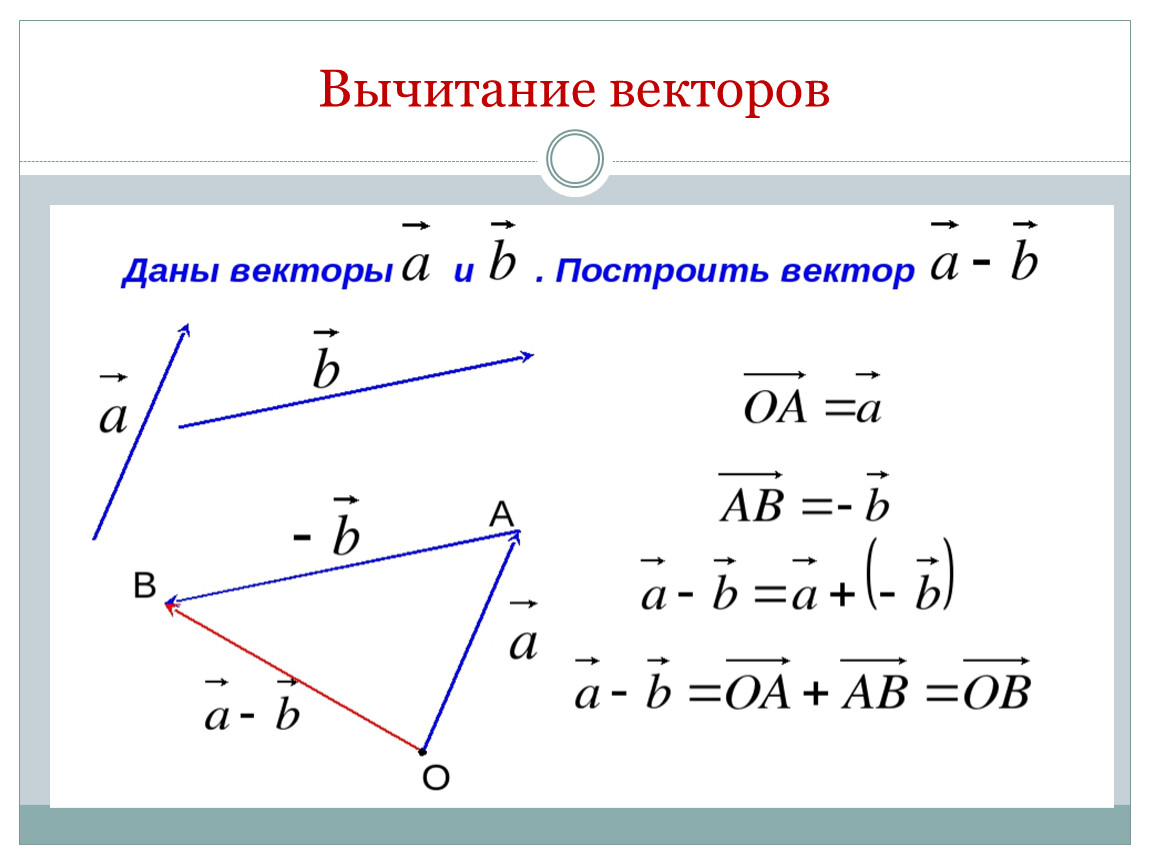
Подставляя R, S и W в R + S + W + O, получаем
[| R | (cos125 °) + | S | (cos37 °)] i + [| R | (sin125 °) + | S | (sin37 °) — 350] j = 0i + 0j.
Это дает нам систему уравнений:
| R | (cos125 °) + | S | (cos37 °) = 0,
| R | (sin125 °) + | S | (sin37 °) — 350 = 0.
Решая эту систему, получаем
| R | ≈ 280 и | S | ≈ 201.
Натяжение тросов составляет 280 фунтов и 201 фунт.
Time — The Physics Hypertextbook
Обсуждение
сколько времени?
Zeit ist das, был человеком an der Uhr наиболее способным .
[Время — это то, что измеряют часы.]
Альберт Эйнштейн (1879–1955)
Nam Tempus, Spatium, Locum & Motum, ut omnibus notiſſima, non Definio .
[Я не определяю время, пространство, место и движение как хорошо известные всем.]
Исаак Ньютон (1642–1727)
τὸ πολυτελέστατον ἀνάλωμα τὸν χρόνον.
[Самое ценное, что может потратить человек, — это время.]
Ἀντιφῶν [Антифон] (480–411 гг. До н.э.)
σπερ οὖν εἰ μὴ ἦν ἕτερον τὸ νῦν ἀλλὰ ταὐτὸ καὶ ἕν, οὐκ ἂν ἦν χρόνος.
[Как, если бы сейчас оставалось прежним, времени не существовало бы.]
ριστοτέλης [Аристотель] (384–322 до н.э.)
quid est ergo tempus? si nemo ex me quaerat, scio; si quaerenti explicare velim, nescio .
[Что же такое время? Если меня никто не спросит, я знаю; если я хочу объяснить тому, кто спрашивает, я не знаю.]
Августин Гиппоненсис [Августин Гиппопотам] (354–430)
οταμός τίς ἐστι τῶν γινομένων καὶ ῥεῦμα βίαιον ὁ αἰών · ἅμα τε γὰρ ὤφθη καστον, καὶ παρεαεαεέ καλαενήνεκτρι
[Время подобно реке, состоящей из происходящих событий, и бурному потоку; ибо как только вещь была увидена, она уносится, а на ее место приходит другая, и эта тоже уносится.
]
Марк Аврелий (121–180)
Мы увидим, что времени не существует.
Джулиан Барбур (1937–0000)
Le temps est ce qui empêche que tout soit donné tout d’un coup .
[Время не дает всему случиться сразу.]
Анри Бергсон (1859–1941)
Le temps est un grand maître, dit-on; le malheur est qu’il soit un maître inhumain qui tue ses élèves .
[Время — великий учитель, но, к сожалению, оно убивает всех своих учеников.]
Гектор Берлиоз (1803–1869)
Комедия — это трагедия плюс время.
Кэрол Бернетт (1933–0000)
Время нас не держит. Время не настало. Как всегда.Как всегда.
Дэвид Бирн (1952–0000)
Время касается всех вещей губительной рукой.
Чарльз Чеснатт (1858–1932)
Время дорого, но правда дороже времени.
Бенджамин Дизраэли (1804–1881)
Вы можете задержаться, но время — нет.
Бенджамин Франклин (1706–1790)
Помните, что время — деньги.
Бенджамин Франклин (1706–1790)
Самая большая разница между временем и пространством состоит в том, что вы не можете повторно использовать время.
Меррик Ферст (1956–0000)
Время — это цирк, он всегда пакуется и уезжает.
Бен Хехт (1894–1964)
ρόνος ἐστὶν ἐν ᾧ καιρός, καὶ καιρὸς ἐν ᾧ χρόνος οὐ πολύς.
[Время — это то, где есть возможность, а возможность — это то, где нет прекрасного времени.]
Ιπποκράτης [Гиппократ] (460–370 гг. До н.э.)
Время, как мы его знаем, — изобретение совсем недавно. Современное чувство времени едва ли старше Соединенных Штатов.Это побочный продукт индустриализма — своего рода психологический аналог синтетических духов и анилиновых красок.
Олдос Хаксли (1894–1963)
Time — универсальный исполнитель. Летит, идет, все раны лечит, выбегает и расскажет.
Франклин П. Джонс (1939–2008)
Życie zabiera ludziom zbyt wiele czasu .
[Люди считают, что жизнь отнимает слишком много времени.]
Станислав Лец (1909–1966)
Самое лучшее в будущем — это то, что оно наступает только один день за раз.
Авраам Линкольн (1809–1865)
Время летит как стрела. Плодовые мушки как банан.
Граучо Маркс (1890–1977)
То, как вы проводите свое время, важнее того, как вы тратите свои деньги. Денежные ошибки можно исправить, но время ушло навсегда.
Дэвид Б. Норрис (1944–0000)
Tempus edax rerum .
[Время пожирает все.]
Овидий (43–18 гг.
До н. Э.)
Время отмечает нас, пока мы топчемся на месте.
Теодор Рётке (1908–1963)
Я потратил время зря, и теперь время теряет меня.
Уильям Шекспир (1564–1616)
Время не вычитает и не делит, а складывает с такой скоростью, что кажется умножением.
Боб Талберт (1936–1999)
Как будто мы можем убить время, не повредив вечности!
Генри Дэвид Торо (1817–1862)
Ясно… любое реальное тело должно иметь четыре направления: оно должно иметь длину, ширину, толщину и продолжительность….На самом деле существует четыре измерения, три из которых мы называем тремя планами пространства, а четвертое — временем. Однако существует тенденция проводить нереальное различие между первыми тремя измерениями и вторым, потому что случается, что наше сознание периодически движется в одном направлении вдоль последнего от начала до конца нашей жизни.
Х. Г. Уэллс (1866–1946)
Везде можно дойти пешком, если у вас есть время.
Стивен Райт (1955–0000)
寸 金 难买 寸 光阴
[За дюйм золота нельзя купить ни дюйма времени.]
неизвестно
Скорость времени — одна секунда в секунду.
неизвестно
Время лечит все раны, кроме смертельных.
неизвестно
Тратить время впустую — важная часть жизни.
неизвестно
Время — это иллюзия, созданная производителями космоса.
неизвестно
Что означает «это» в предложении «Который час?»
неизвестно
Вечность — ужасная мысль.Я имею в виду, где это закончится?
Том Стоппард (1937–0000)
Множество причудливых словечек для того, что можно было бы выразить проще, или можно? Простые концепции зачастую труднее всего объяснить. Часто одно понятие мы носим с собой, а другое, более техническое и конкретное, используется в физике.
Часто одно понятие мы носим с собой, а другое, более техническое и конкретное, используется в физике.
Который час? Довольно простой вопрос, не так ли? Почему это. Ну это в Сьерра-Леоне, но это в Южной Каролине. Это представление о местном времени обычно не то, что мы подразумеваем под временем в физике.
Когда началось время? В год 1 н.э.? Едва. Это просто культурная фиксированная точка. Это не имело бы смысла для людей, которые жили до того, что мы сейчас называем эрой. Как вы думаете, Сократ ходил и думал: «Я не могу поверить, что это уже 535 год до н. Э.. Я не могу перестать писать 536 год до н. Э. На своих чеках»? Когда инопланетные повелители высадятся на горе Шаста, их календари будут подсчитывать количество внеземных единиц времени, начиная с другого первого события — и мы научимся любить это или будем сожжены.
Вы когда-нибудь слышали, чтобы люди говорили: «Летнее время заканчивается, поэтому мы выиграем час в субботу вечером»? Что ж, позвольте мне сказать вам прямо сейчас, что никто никогда не выигрывал час после окончания летнего времени, во всяком случае, не буквально.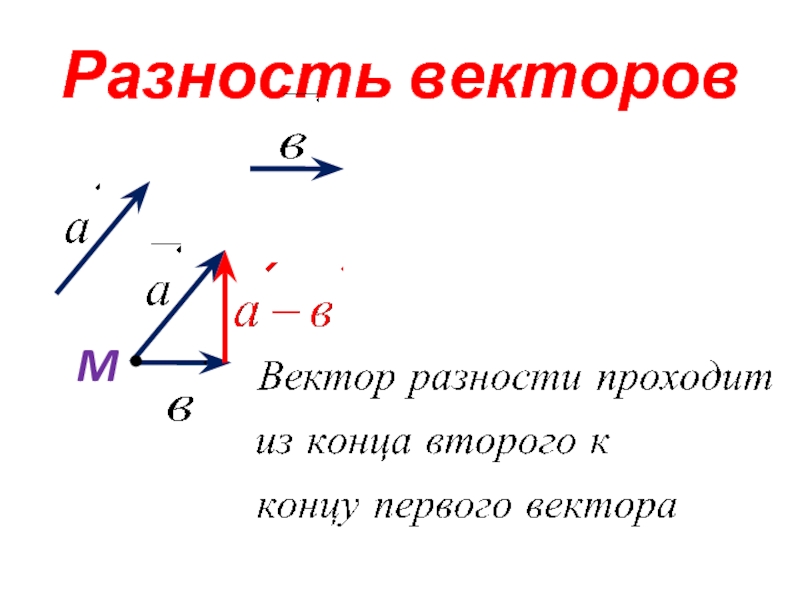 Если бы вы находились в США в больнице и находились на грани смерти в 01:59 в последнюю субботу октября, вы бы не получили ни часа жизни, если бы умерли через две минуты в 1:01. Продолжительность вашей жизни не зависит от часового пояса или календаря, в котором вы живете.
Если бы вы находились в США в больнице и находились на грани смерти в 01:59 в последнюю субботу октября, вы бы не получили ни часа жизни, если бы умерли через две минуты в 1:01. Продолжительность вашей жизни не зависит от часового пояса или календаря, в котором вы живете.
Есть время в смысле «Который час?» А еще есть время в смысле того, сколько времени потребовалось, чтобы что-то произошло. Время в прежнем смысле определяется наручными часами или часами . Время в последнем смысле — , измеренное секундомером или интервальным таймером. В повседневной жизни время является культурной конструкцией, посредством которой событие может быть связано с рядом чисел. В физике времени — это мера интервала между двумя событиями.
натуральных единиц
В Международной системе единиц вторая является фундаментальной единицей времени, но на протяжении большей части человеческого существования (до тех пор, пока существовали вещи, которые выглядели и действовали как люди), естественными единицами времени были день, год. , и месяц.
, и месяц.
день
С точки зрения человека, застрявшего на поверхности Земли, день — это время, когда Солнце видно на небе. День начинается, когда кажется, что Солнце поднимается выше, и заканчивается, когда Солнце, кажется, опускается ниже видимой границы между Землей и небом, называемой горизонтом.Середина одного из этих дней — это момент, когда Солнце находится в самом высоком положении над горизонтом, называемым полднем (от архаичного термина, означающего «девятый час») или полуднем (поскольку это происходит в середине дня, на полпути между восходом солнца. и закат).
Ночь — это время, когда Солнце не видно, потому что оно находится за горизонтом. День также можно рассматривать как переходящий в ночь. Для большинства из нас, живущих в 21 веке, переход от одного дня к другому происходит, когда мы спим (или когда нам, вероятно, следует спать).Когда мы просыпаемся, новый день уже начался. Для людей, которые следуют этому соглашению, конец одного дня и начало следующего наступают, когда Солнце находится в самом низком положении ниже горизонта, называемом полночь (поскольку это происходит посреди ночи, на полпути между закатом одного дня и восход следующего). Эта солнечная полночь отмечает границу того, что называется солнечным днем. Во многих местах установленное законом время, называемое полночь, отмечает границу того, что называется гражданским днем.Солнечная полночь и гражданская полночь в большинстве мест обычно меньше часа.
Эта солнечная полночь отмечает границу того, что называется солнечным днем. Во многих местах установленное законом время, называемое полночь, отмечает границу того, что называется гражданским днем.Солнечная полночь и гражданская полночь в большинстве мест обычно меньше часа.
Мы знаем, что даже когда Солнце не видно, оно все еще там. Это потому, что теперь мы знаем, что Земля вращается. День наступает, когда мы находимся на той стороне Земли, которая обращена к Солнцу. Полдень или полдень наступает, когда сторона Земли, на которой мы находимся, находится ближе всего к Солнцу в этот день. Точно так же ночь наступает, когда мы находимся на той стороне Земли, которая обращена от Солнца, а полночь наступает, когда эта сторона наиболее удалена от Солнца в течение этой ночи.Мы говорим, что Солнце встает днем и опускается ночью, потому что это направления, в которых мы должны были бы двигаться, чтобы достичь его из места на поверхности Земли (или, по крайней мере, слова вверх и вниз дают общее представление о вертикальный компонент этого направления).
год
Продолжительность года зависит от вашего выбора календарей или от того, как вы определяете год.
| тип | в днях | в секундах | банкноты |
|---|---|---|---|
| стандартный | 365 | 31 536 000 | |
| прыжок | 366 | 31 622 400 | |
| юлиан | 365.25 | 31,557,600 | усыновлен Юлием Цезарем в 46 г. до н. Э. |
| грегорианский | 365,2425 | 31,556,952 | принят Папой Григорием XIII в 1582 году н.э. |
| тропический | 365,242189… | 31,556,925,16… | период между весенними равноденствиями |
| сидерический | 365,256363… | 31 558 149,76… | период обращения относительно звезды |
| аномальный | 365. 259635… 259635… | 31,558,432,46… | период между перигелиями |
| затмение | 346,620075… | 29 947 974,48… | период прохождений лунных узлов |
культурных единиц
час минута секунда
неделя
декада века тысячелетие эон
календари
календари
часовых поясов
Среднее время по Гринвичу (GMT)
международное атомное время (тай)
Единица времени в системе СИ — секунд [с].
Сверхтонкий переход лежит в основе Международного атомного времени (TAI). По определению, самый внешний электрон в обычном атоме цезия 133 проходит через этот переход 9 192 631 770 раз за одну секунду.
Международное атомное время (сокращенно TAI от французского T emps A tomique I nternational) началось в полночь по Гринвичу первого дня 1958 года и продолжило движение вперед со скоростью одна секунда каждые 9 192 631 770 периоды сверхтонкого перехода в 133 Cs. TAI поддерживается Международным бюро исследований и измерений (BIPM) в Париже, которое периодически усредняет время, отсчитываемое различными атомными часами по всему миру. Затем BIPM распространяет поправочные коэффициенты, необходимые для синхронизации этих часов с главными часами Парижской обсерватории.
TAI поддерживается Международным бюро исследований и измерений (BIPM) в Париже, которое периодически усредняет время, отсчитываемое различными атомными часами по всему миру. Затем BIPM распространяет поправочные коэффициенты, необходимые для синхронизации этих часов с главными часами Парижской обсерватории.
всемирное координированное время (utc)
Всемирное координированное время (сокращенно UTC ) является основой мирового времени. Все местные гражданские времена отличаются от всемирного координированного времени либо на целое количество часов, либо на нечетное количество получасов, но ни на какую другую величину.Одна секунда всемирного координированного времени такая же, как одна секунда международного атомного времени, но UTC и TAI немного расходятся. TAI движется вперед равномерно, в то время как UTC время от времени корректируется, чтобы синхронизировать его с вращением Земли.
Земля не является эффективным хронометристом. В течение большей части последних двухсот лет средний солнечный день был немного длиннее, чем 86 400 секунд, которые в настоящее время определены Международной системой.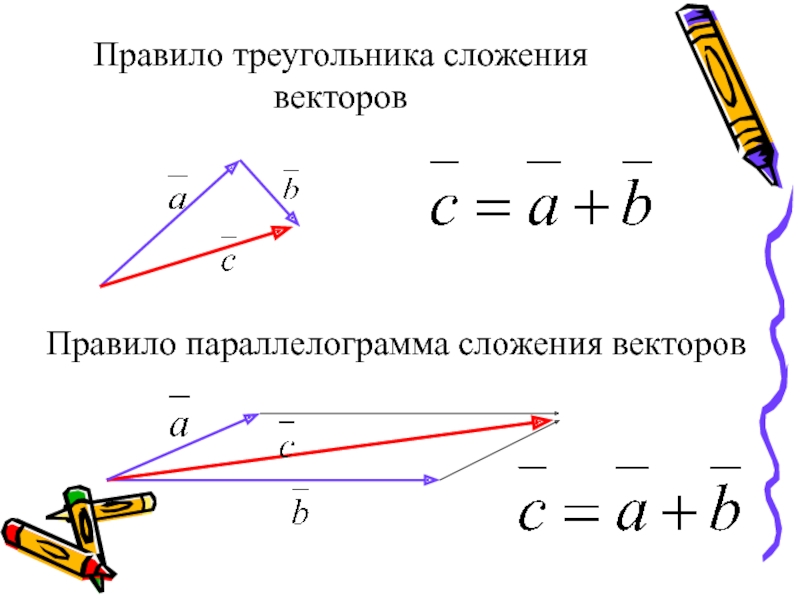 всемирное время ( UT ), или, более конкретно, вариант, известный как UT1 , фактически является средним солнечным временем.Он непрерывен (т.е. нет дополнительных секунд), но имеет переменную скорость из-за неравномерного периода вращения Земли. Это необходимо для вычисления звездного времени, которое является важной частью наведения телескопов в правильном направлении. Величина UT1-UTC, которая обычно изменяется на 1 или 2 мс в год, может быть получена только путем наблюдения, хотя сезонные тенденции известны, и списки IERS могут предсказывать некоторый путь в будущее с достаточной точностью для наведения телескопов.
всемирное время ( UT ), или, более конкретно, вариант, известный как UT1 , фактически является средним солнечным временем.Он непрерывен (т.е. нет дополнительных секунд), но имеет переменную скорость из-за неравномерного периода вращения Земли. Это необходимо для вычисления звездного времени, которое является важной частью наведения телескопов в правильном направлении. Величина UT1-UTC, которая обычно изменяется на 1 или 2 мс в год, может быть получена только путем наблюдения, хотя сезонные тенденции известны, и списки IERS могут предсказывать некоторый путь в будущее с достаточной точностью для наведения телескопов.
Когда UT1 слишком сильно отстает от UTC, в конце дня до 1 января или 1 июля, в зависимости от ситуации, вставляется дополнительная секунда.Когда это происходит, за 23:59:59 следует необычное время 23:59:60 перед переходом на 00:00:00 и началом следующего дня.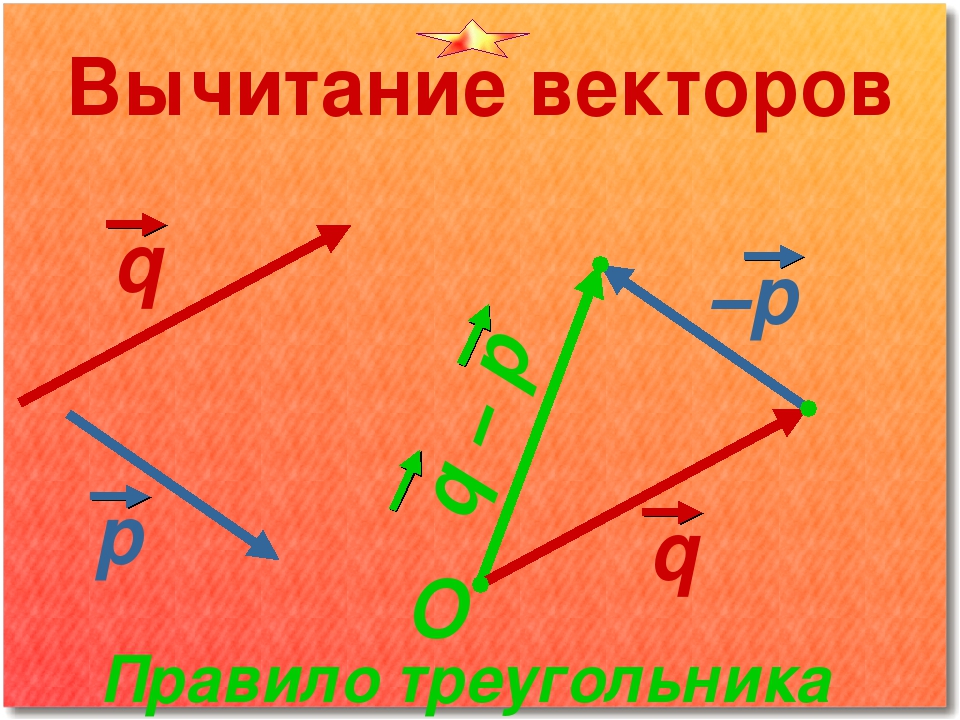 В том маловероятном случае, когда UT1 будет опережать UTC (то есть, если скорость вращения Земли увеличится), существует положение для вставки отрицательной дополнительной секунды. Если бы это произошло, за 23:59:58 одного дня следовало бы 00:00:00 следующего, без 23:59:59. В любом случае абсолютная разница между UTC и UT1 никогда не должна превышать 0,9 с.
В том маловероятном случае, когда UT1 будет опережать UTC (то есть, если скорость вращения Земли увеличится), существует положение для вставки отрицательной дополнительной секунды. Если бы это произошло, за 23:59:58 одного дня следовало бы 00:00:00 следующего, без 23:59:59. В любом случае абсолютная разница между UTC и UT1 никогда не должна превышать 0,9 с.
Решение о том, когда вводить дополнительную секунду, принимается Международной службой вращения Земли (IERS) во Франкфурте на основе наблюдений за ориентацией Земли в космосе.
Добавление дополнительных секунд к всемирному координированному времени (UTC) позволяет согласовывать его с вращением Земли, измеренным по всемирному времени (UT1).
Всемирное координированное время, CUT — Temps universel correonné, TUC
Необходимы ли дополнительные секунды?
- Через семь или восемь веков разница между TAI и UT1 составит около часа.

- К 5000 году день и ночь поменяются местами; то есть 12 часов дня будет посреди ночи, а 12 часов ночи совпадут с полуденным солнцем.
Что в этом плохого? Действительно ли имеет значение, какое число мы присваиваем положению Солнца на небе?
В 1582 году папе Григорию XIII удалось вычленить из календаря десять дней. 4 октября 1582 года католический мир уснул. Когда они проснулись, это было 15 октября 1582 года. К 1752 году протестантская нация Англия и ее американские колонии также приняли изменение.(Им нужно было добавить 11 дней, чтобы наверстать упущенное.) В 1873 году Япония перешла на этот шаг. (Им потребовалось 12 дней.) Затем Россия в 1917 году и Китай в 1949 году (13 дней). Греческая православная церковь, возможно, единственное европейское агентство, которое не приняло это изменение (хотя нация Греции сделала это в 1923 году).
Я думаю, что важнее всего то, что все согласны с , который час (или день) сейчас. Не то чтобы время было каким-то конкретным числом. Помните, время — это социальная конструкция.
Помните, время — это социальная конструкция.
| год | мес | вычет | год | мес | офсет | год | мес | вычет | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1961 | Январь | 0 | 1987 | 23 | 2004 | 32 | ||||
| 1971 | * | 10 | 1988 | Январь | 24 | 2005 | 32 | |||
| 1972 | июль | 11 | 1989 | 24 | 2006 | Январь | 33 | |||
| 1973 | Январь | 12 | 1990 | Январь | 25 | 2007 | 33 | |||
| 1974 | Январь | 13 | 1991 | Январь | 26 | 2008 | 33 | |||
| 1975 | Январь | 14 | 1992 | июль | 27 | 2009 | Январь | 34 | ||
| 1976 | Январь | 15 | 1993 | июль | 28 | 2010 | 34 | |||
| 1977 | Январь | 16 | 1994 | июль | 29 | 2011 | 34 | |||
| 1978 | Январь | 17 | 1995 | 29 | 2012 | июль | 35 | |||
| 1979 | Январь | 18 | 1996 | Январь | 30 | 2013 | 35 | |||
| 1980 | Январь | 19 | 1997 | июль | 31 | 2014 | 35 | |||
| 1981 | июль | 20 | 1998 | 31 | 2015 | июль | 36 | |||
| 1982 | июль | 21 | 1999 | Январь | 32 | 2016 | 36 | |||
| 1983 | июль | 22 | 2000 | 32 | 2017 | Январь | 37 | |||
| 1984 | 22 | 2001 | 32 | 2018 | 37 | |||||
| 1985 | июль | 23 | 2002 | 32 | 2019 | 37 | ||||
| 1986 | 23 | 2003 | 32 | 2020 | 37 |
протокол сетевого времени (ntp)
Протокол сетевого времени (NTP) — это 64-битный двоичный счетчик, который движется синхронно с международным атомным временем (TAI). Первые 32 бита (двоичные цифры) подсчитывают секунды, а вторые 32 бита подсчитывают доли секунды.
Первые 32 бита (двоичные цифры) подсчитывают секунды, а вторые 32 бита подсчитывают доли секунды.
Первые 32 бита делят NTP на эпох. длятся 136 лет, начиная с…
| 2 32 с = 4 294 967 296 с |
| 2 32 с ≈ 136 лет |
или точнее…
| 2 32 с = | 4,294,967,296 с |
| 2 32 с ≈ | 136 лет, 36 дней, 6 часов, |
, но не называйте меня количеством дней.Годы сдвигаются между нормальными годами с 365 днями и високосными с 366 днями в примерно четырехлетнем цикле. Исключения, которые заставили меня написать «примерно», делают это точное число, которое трудно определить. Я предполагаю, что для большинства эпох будет 136 лет и 36 дней плюс дроби в этом цикле, а для исключительных эпох (например, тех, которые содержат 2400 или 2800 лет) будет 136 лет и 37 дней плюс дроби. Но все это пустые домыслы. NTP, вероятно, является самым длинным непрерывно работающим протоколом в Интернете, но было бы поразительно, если бы он просуществовал четыреста лет.
Но все это пустые домыслы. NTP, вероятно, является самым длинным непрерывно работающим протоколом в Интернете, но было бы поразительно, если бы он просуществовал четыреста лет.
Первая эра NTP началась 1 января 1900 года в полночь по среднему времени по Гринвичу (GMT) — предшественнику Всемирного координированного времени (UTC). Конечно, в это время никакие часы NTP не начали тикать буквально. Необходимая технология не была изобретена. (Цифровые компьютеры впервые появились в конце 1930-х годов, а первые атомные часы были построены в 1949 году.) Это просто удобное место для установки нуля для нас, людей, которые привыкли к годам, дням, часам и минутам. Когда UTC вступило в силу в 00:00:00 1 января 1972 года, время NTP составляло 2 272 060 800; первые 32 бита из которых выглядят так…
10000111011011001110010110000000
или со всеми 64 битами, вот так…
10000111011011001110010110000000
Вторые 32 бита обеспечивают точность около четверти наносекунды, поскольку…
2 −32 с = 2. 328 × 10 −10 с 328 × 10 −10 с |
| 2 −32 с ≈ ¼ нс |
Это смехотворный уровень точности, учитывая, что максимальная скорость, с которой любой сигнал может распространяться по сети, равна скорости света. Чтобы воспользоваться преимуществом последнего бита в 64-битном коде NTP, сервер времени должен быть ближе, чем расстояние, пройденное лучом света за 2 −32 с.
| ∆ s = c ∆ t |
| ∆ с = (299 792 458 м / с) (2 −32 с) |
| ∆ с = 0.06980 м |
| ∆ с ≈ 7 см |
Мой любимый сервер NTP — time.nist.gov в Отделе времени и частоты Национального института стандартов и технологий в Боулдере, штат Колорадо. Это примерно 2900 км от моего настольного компьютера в Нью-Йорке. Сигнал, который я получаю, задерживается как минимум на…
.| ∆ t = ∆ s / c |
| ∆ т = (2 900 000 м) / (299 792 458 м / с) |
∆ t = 0. 009673 с 009673 с |
| ∆ t ≈ 10 мс |
Я мог бы повысить точность, переключившись на time-a.nist.gov, расположенный в Гейтерсбурге, штат Мэриленд; который находится всего в 380 км. Этот сигнал будет иметь максимальную задержку всего…
.| ∆ t = ∆ s / c |
| ∆ т = (380 000 м) / (299 792 458 м / с) |
| ∆ t = 0,001268 с |
| ∆ t ≈ 1 мс |
Такое повышение точности бессмысленно, учитывая способ распространения сигналов через Интернет.Данные (например, электронная почта, веб-страницы, потоковое видео и сигналы времени) разбиваются на пакеты, которые могут свободно использовать любой путь, который позволяет сеть. В отличие от классической телефонной сети, где информация пересылается по одному выделенному каналу, пакеты Интернет-сообщения не обязательно должны следовать по одному и тому же пути. Каждый волен вести переговоры о своем собственном путешествии. Путь, по которому следует каждый пакет, определяется архитектурой сети и мгновенным трафиком на каждом узле и через каждую ссылку.Пакеты могут даже теряться или «сбрасываться» по пути. Только после того, как все они прибыли, пакеты снова собираются в исходное сообщение.
Каждый волен вести переговоры о своем собственном путешествии. Путь, по которому следует каждый пакет, определяется архитектурой сети и мгновенным трафиком на каждом узле и через каждую ссылку.Пакеты могут даже теряться или «сбрасываться» по пути. Только после того, как все они прибыли, пакеты снова собираются в исходное сообщение.
Электронный процесс разбиения сообщения на пакеты и их повторной сборки в сообщение требует времени, как и согласование, которое каждый пакет выполняет в соединениях или узлах сети. Общий результат состоит в том, что фактическое время передачи в несколько раз превышает время скорости света. Типичное время пинга в США составляет от 10 до 100 мс.Для NTP на практике это означает отклонение от TAI примерно от 10 до 100 мс. Ошибаясь в сторону осторожности, большинство компаний-разработчиков программного обеспечения заявляют о точности только с точностью до секунды.
| событие | общая эпоха | эра нтп | время нтп |
|---|---|---|---|
| Начало числа юлианского дня с нуля | 1 января 4713 г. до н.э. до н.э. | −49− | 1 795 583 104 |
| начало нашей эры | 1 января 1 CE | −14− | 202 934 144 |
| Начало по григорианскому календарю | 15 октября 1582 | −3− | 2 874 597 888 |
| Начало NTP | 1 января 1900 | 0 | 0 |
| Начало времени Unix | 1 января 1970 года | 0 | 2 208 988 800 |
| UTC синхронизировано с TAI минус 10 с | 1 января 1972 года | 0 | 2,272,060,800 |
| последняя секунда второго тысячелетия | 31 декабря 1999 | 0 | 3,155,673,599 |
| первая секунда третьего тысячелетия | 1 января 2000 | 0 | 3,155,673,600 |
| Время Unix достигает миллиарда секунд | 9 сентября 2001 | 0 | 3 208 988 800 |
| Изменение эры NTP | 7 февраля 2036 г. |



 Примеры векторов включают смещение, скорость и ускорение.
Примеры векторов включают смещение, скорость и ускорение. Эта линия представляет собой сумму векторов.
Эта линия представляет собой сумму векторов. Поскольку смещение содержит две части информации: расстояние от опорной точки и направление от точки, оно хорошо представлено вектором.
Поскольку смещение содержит две части информации: расстояние от опорной точки и направление от точки, оно хорошо представлено вектором.


 ]
]

 До н. Э.)
До н. Э.)