Определитель имеющий два одинаковых ряда равен – 4.Определители. Свойства определителей. | spiruk

4.Определители. Свойства определителей. | spiruk

4.Определители. Свойства определителей.

Квадратной матрице А порядка n можно сопоставить число det А (или |A|, или ), называемое ее определителем, следующим образом:

Определитель матрицы A также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.

Вычисление определителя 2-го порядка иллюстрируется схемой:

Пример 4.1. Найти определители матриц

Решение:

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

Пример 4.2. Вычислить определитель матрицы

Решение:

det А = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.

Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.

Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот. Иными словами,

В дальнейшем строки и столбцы будем просто называть рядами определителя.

Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.

Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

Действительно,

Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одною ряда прибавить соответствующие элементы параллельного ряда, умноженные па любое число.

Пример 4.3. Доказать, что

Решение: Действительно, используя свойства 5, 4 и 3 подучим

Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.

Минором некоторого элемента аij определителя n-го порядка называется определитель n — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, па пересечении которых находится выбранный элемент. Обозначается mij

Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j четное число, и со знаком «минус», если эта сумма нечетная. Обозначается Aij :

Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что

В самом деле, имеем

Свойство 7 содержит в себе способ вычисления определителей высоких порядков.

Пример 4.4. Вычислите определитель матрицы

Решение: Для разложения определителя обычно выбирают гот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю.

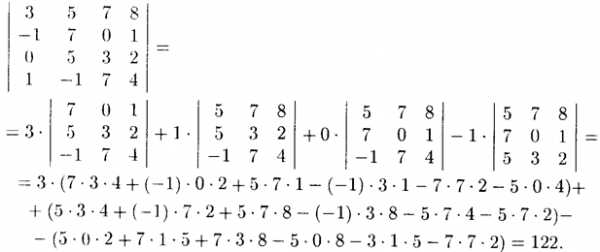
Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например,

Понравилось это:

Нравится Загрузка…

Похожее

spiruk.wordpress.com

. Свойства определителей

СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть

.

СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,

.

СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число kравносильно умножению определителя на это число k. Например,

.

СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).

СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой — вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,

СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,

.

Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.

Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.

СВОЙСТВО 9. Определитель

равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.

Иначе говоря, имеют место следующие равенства:

, ,

, ,

, .

6) Миноры и алгебраические дополнения.

Определение. Минором элемента определителя – го порядка называют определитель – го порядка, который получается из данного определителя вычеркиванием — й строки и – го столбца, на пересечении которых стоит элемент .

Обозначение: .

Определение. Алгебраическим дополнением элемента определителя – го порядка называют его минор, взятый со знаком плюс, если – четное число и со знаком минус в противном случае.

Обозначение: .

Теорема. (О разложении определителя.)

Определитель равен сумме произведений элементов любой строки (или любого столбца) определителя на их алгебраические дополнения:

, ;       (1)

или

, .       (2)

7) Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы

, похожие на обратные по многим свойствам.

8) Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля

Обычно ранг матрицы  обозначается  () или . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. 

Свойства

Теорема (о базисном миноре): Пусть r = rang A M — базисный минор матрицы A, тогда:

• базисные строки и базисные столбцы линейно независимы;

• любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).

Следствия:

• Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.

• Если A — квадратная матрица, и det A = 0 <=> строки и столбцы этой матрицы линейно зависимы.

• Пусть r = rang A, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.

• Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение элементарными преобразованиями. Тогда справедливо утверждение: Если , то их ранги равны для матриц, полученных друг из друга

studfiles.net

Свойства определителей

1. При транспонировании матрицы ее определитель не изменяется: .

Это свойство вытекает из теоремы о разложении определителя . Т.к. разложение определителя по 1-му столбцу тождественно совпадает с разложениемпо 1-й строке.

Это свойство означает полную равноправность строк и столбцов и позволяет все последующие свойства устанавливать лишь для строк, подразумевая, что они справедливы и для столбцов.

2. Свойство антисимметрии при перестановке двух строк (столбцов).

При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

Доказательство. Допустим сначала, что переставлены две соседние строки матрицы: i и i+1. Разложим определитель исходной матрицы Δ по элементам i-й строки, а определитель новой матрицы Δ^΄ — по элементам (i+1)-й строки. Разложения будут отличаться только знаком, т.к. в разложении определителя Δ^΄ каждое алгебраической дополнение A_i+1j будет иметь противоположный знак (множители (-1)^i+j сменятся на множители (-1)^i+1+j). Т.о. Δ^=-Δ^΄.

Если переставить не соседние строки, а, например, i-ю и (i+m)-ю, то эту перестановку можно рассматривать как последовательное смещение i-й строки на m строк вниз (при этом каждый раз знак определителя меняется), а (i+m)-й строки на (m-1) вверх и (m-1) раз меняется знак, т.е. знак поменяется нечетное число раз: (m+m-1=2m-1). Следовательно, Δ =-Δ^΄.

Для столбцов доказательство аналогично.

3. Линейное свойство определителя.

Некоторая строка а=(а₁,а₂,…,а_n) называется линейной комбинацией строк b=(b₁,b₂,…,b_n), c=(c₁,c₂,…,c_n),…, d=(d₁,d₂,…,d_n), с коэффициентами λ₁,λ₂,…,λ_k если она равна сумме произведений этих строк на эти числа:

a=λ₁b+λ₂c+…+λ_kd, т.е. a_j=λ₁b_j+λ₂c_j+…+λ_kd_j j=1,2,…,n

Если в определителе n-го порядка  некоторая i-я строка (a_i1,a_i2,…,a_in) является линейной комбинацией строк (b_i1,b_i2,…,b_in) и (c_i1,c_i2,…,c_in) с коэффициентами  и , то =₁+₂, где ₁ – определитель, у которого i-я строка равна (b_i1,b_i2,…,b_in), а все остальные строки такие же, как и у , а где ₂ – определитель, у которого i-я строка равна (с_i1,с_i2,…,с_in), а все остальные строки такие же, как и у .

=+

Доказательство. Разложим каждый из определителей , ₁, и ₂ по i-й строке по формуле Δ=a_i1A_i1+a_i2A_i2+…+a_inA_in=.Заметим, что алгебраические дополнения A_ij i-й у всех 3-х определителей одинаковы. Следовательно, формула =₁+₂ следует из равенств a_j=λb_j+c_j j=1,2,…,n ч.т.д.

Замечание. Линейное свойство справедливо и для случая, когда i-я строка является линейной комбинацией не 2-х, а нескольких строк.

Рассмотренные 3 свойства являются основными свойствами определителя. Следующие 5 свойств являются логическими следствиями этих свойств.

4. Определитель с двумя одинаковыми строками (столбцами), то равен 0.

Док-во. Переставим равные строки (столбцы) местами. С одной стороны, определитель не изменится, а с другой, по св-ву 2, поменяет знак. Т.е. Δ=-Δ, след-но, Δ=0.

5. Если все элементы какой-либо строки (столбца) определителя умножить на число λ, то и определитель умножится на это число λ.

Доказательство. Вытекает из свойства 3 при =0. Ч.т.д.

Замечание. Т.о., за знак определителя можно выносить общий множитель любой строки или столбца в отличие от матрицы, за знак которой можно выносить только общий множитель всех элементов.

Пример. , но

6. Если все элементы некоторой строки (столбца) определителя равны 0, то и сам определитель равен 0.

Доказательство. Это свойство следует из свойства 5 при =0. ч.т.д.

7. Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен 0.

Доказательство. По свойству 5 коэффициент пропорциональности λ можно вынести за знак определителя, после чего останется определитель с двумя одинаковыми строками: Δ^΄=λΔ, где Δ имеет две одинаковые строки и по свойству 4 равен 0. ч.т.д.

8. Определитель не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

Доказательство. Полученный в результате указанного прибавления определитель, по свойству 3, можно разбить на сумму двух определителей, один из которых равен исходному, а второй равен 0 в силу пропорциональности двух строк (столбцов) и свойства 7.: =+0. ч.т.д.

9. Свойство алгебраических дополнений соседних строк (столбцов).

Сумма произведений элементов какой-либо строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) этого определителя равна 0, т.е. .

Доказательство. Докажем для строк (для столбцов доказательство аналогично). Запишем разложение определителя  по i-й строке:

Δ==a_i1A_i1+a_i2A_i2+…+a_inA_in (7)

Т.к. алгебраические дополнения A_i1, A_i2,…,A_in не зависят от элементов i-й строки a_i1,a_i2,…,а_in, то равенство (70 является тождеством относительно a_i1,a_i2,…,а_in и сохраняется при замене чисел a_i1,a_i2,…,а_in любыми другими n числами. Заменив a_i1,a_i2,…,а_in соответствующими элементами любой (отличной от i-й) k-й строки a_k1,a_k2,…,а_kn, получим слева в (7) определитель с двумя одинаковыми строками a_k1,a_k2,…,а_kn, равный нулю по свойству 4. Таким образом:

a_k1A_i1+a_k2A_i2+…+a_knA_in=0 ik. Ч.т.д.

10. Сумма произведений произвольных чисел с₁,с₂,…,с_n на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы. Полученной из данной заменой элементов этой строки (столбца) на числа с₁,с₂,…,с_n.

Свойство также следует из формулы (7).

studfiles.net

Минор и алгебраическое дополнение

Поиск Лекций

---

Минором m_ij некоторого элемента a_ij определителя n–го порядка называется определитель (n – 1)-го порядка, полученный из исходного определителя путем вычеркивания i-й строки и j-го столбца, на пересечениях которых находится выбранный элемент.

Например, минором элемента a₁₁ определителя третьего порядка является .

Алгебраическим дополнением называется A_ij= (– 1)^i+j m_ij. Если сумма индексов алгебраического дополнения i + j четное число, то алгебраические дополнения и миноры совпадают: A_ij= m_ij, а если – нечетное число, то они отличаются знаком: A_ij = – m_ij.

Свойства определителей

1. Если какой-то ряд состоит из одних нулей, то определитель равен 0.

2. Определитель не изменится, если его строки заменить столбцами, и наоборот.

3. При перестановке двух параллельных рядов определитель меняет знак.

4. Определитель, имеющий два одинаковых ряда, равен нулю.

5. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

6. Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух определителей, с соответствующими слагаемыми этой суммы.

7. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

8. Определитель равен сумме произведений элементам некоторого ряда на соответствующие им алгебраические дополнения.

 

Например, определитель третьего порядка равен:

detA = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ = a₁₁m₁₁– a₁₂m₁₂ + a₁₃m₁₃. (3)

@ Задача 3. Найти .

Решение: Определитель найдем, применяя формулу (3):

 

Ранг матрицы

Наибольший порядок отличных от нуля детерминантов (миноров) прямоугольной матрицы m ´ n, называется рангом матрицы r, причем r £ min(m, n). Для квадратной матрицы ранг r £ n.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

@ Задача 4. Найти ранг матрицы размерности 3´4.

Решение: Ранг матрицы r £ min(3, 4) = 3. Все детерминанты третьего порядка равны нулю, так как две их строки (вторая и третья) одинаковые (отличаются на постоянный множитель). Отличны от нуля только детерминанты второго порядка, поэтому r = 2.

 

 

§1.4. Обратная матрица

 

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля: detA ¹ 0. В противном случае матрица называется вырожденной.

Матрица A^—1 называется обратной матрице А, если выполняется условие

A^—1A = AA^—1 = E.

Только у невырожденных квадратных матриц есть обратные матрицы.

Обратная матрица вычисляется по формуле (detA ¹ 0):

.

Для матрицы A второго порядка обратная матрица равна:

.

@ Задача 1. Найти A^—1, если .

Решение: 1. Находим определитель матрицы:

.

2. Находим обратную матрицу:

.

@ Задача 2. Найти A^—1, если .

Решение: 1. Находим определитель матрицы:

.

2. Вычисляем алгебраические дополнения: , , , , , , , , .

3. Находим обратную матрицу:

.

Рекомендуемые страницы:

Поиск по сайту

poisk-ru.ru

§1.3. Определители и их свойства

Определители

Определителем (детерминантом) квадратной матрицы n-го порядка называется число

.

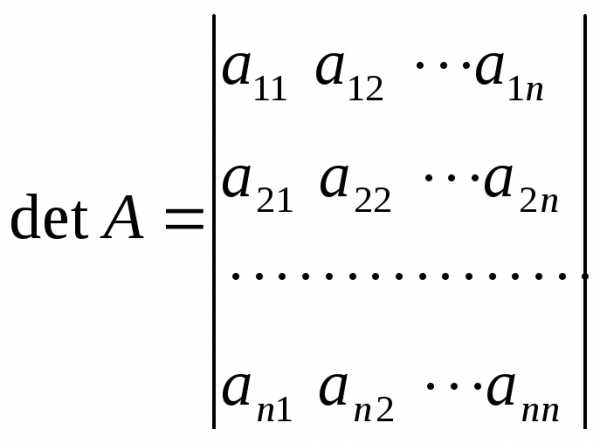þ Обозначения: detA,  и |A|.

Строки и столбцы определителя называются рядами.

Определитель второго порядка вычисляется по правилу (1):

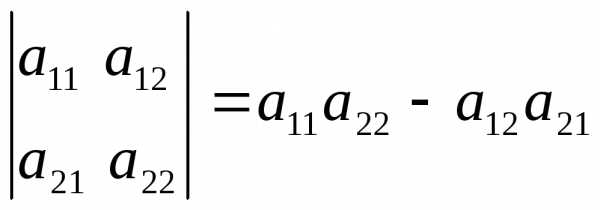. (1)

Определитель третьего порядка вычисляется по правилу (2):

(2).

Правило вычисления определителя третьего порядка следующее. Это алгебраическая сумма шести тройных произведений элементов, стоящих в разных строках и разных столбцах. Со знаком плюс берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали. Со знаком минус берутся произведения, сомножители которых стоят на другой диагонали и в вершинах треугольников с основаниями, параллельными этой диагонали (рис. 1).

(+) (-)

Рис. 1. Правило вычисления определителя третьего порядка

@ Задача 1. Найти .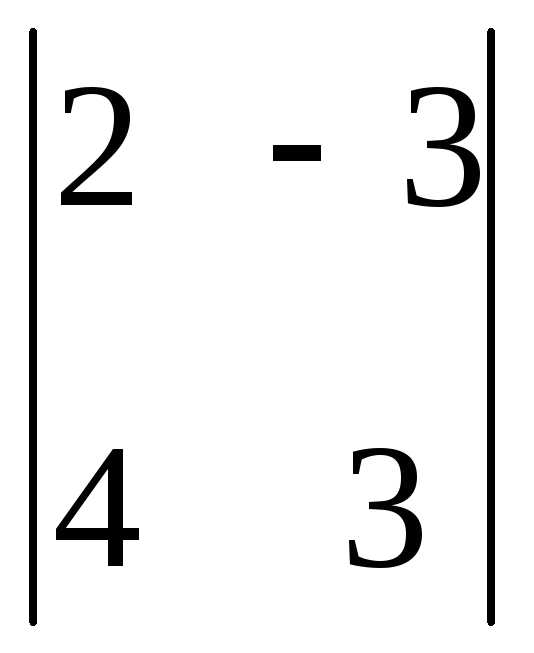

Решение: Определитель второго порядка вычисляется по правилу (1): detA = 2·3 – (–3)·4=18.

@ Задача 2. Найти .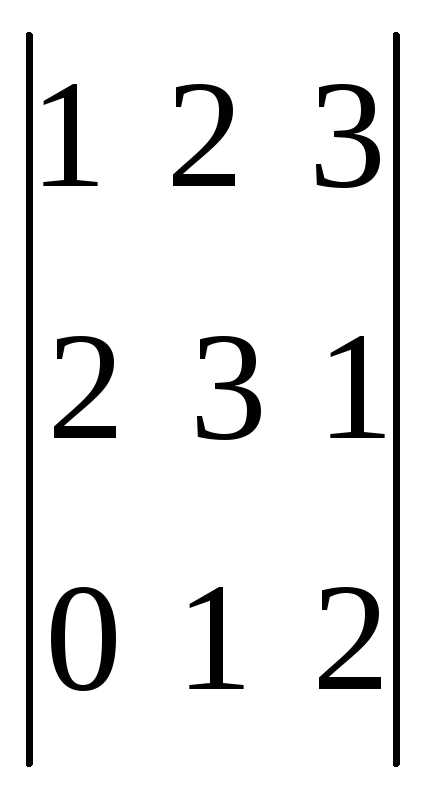

Решение: Определитель третьего порядка вычисляется по правилу (2):

detA = 1·3·2 + 2·1·0 + 3·2·1 – 3·3·0 – 2·2·2 – 1·1·1 = 3.

Минор и алгебраическое дополнение

Минором m_ij некоторого элемента a_ij определителя n–го порядка называется определитель (n – 1)-го порядка, полученный из исходного определителя путем вычеркивания i-й строки и j-го столбца, на пересечениях которых находится выбранный элемент.

Например, минором элемента a₁₁ определителя третьего порядка является .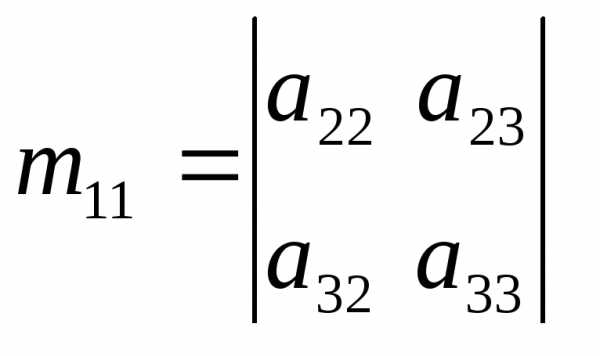

Алгебраическим дополнением называется A_ij = (– 1)^i+j m_ij. Если сумма индексов алгебраического дополнения i + j четное число, то алгебраические дополнения и миноры совпадают: A_ij = m_ij, а если – нечетное число, то они отличаются знаком: A_ij = – m_ij.

Свойства определителей

1. Если какой-то ряд состоит из одних нулей, то определитель равен 0.

2. Определитель не изменится, если его строки заменить столбцами, и наоборот.

3. При перестановке двух параллельных рядов определитель меняет знак.

4. Определитель, имеющий два одинаковых ряда, равен нулю.

5. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

6. Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух определителей, с соответствующими слагаемыми этой суммы.

7. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

8. Определитель равен сумме произведений элементам некоторого ряда на соответствующие им алгебраические дополнения.

Например, определитель третьего порядка равен:

detA = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ = a₁₁m₁₁ – a₁₂m₁₂ + a₁₃m₁₃ . (3)

@ Задача 3. Найти .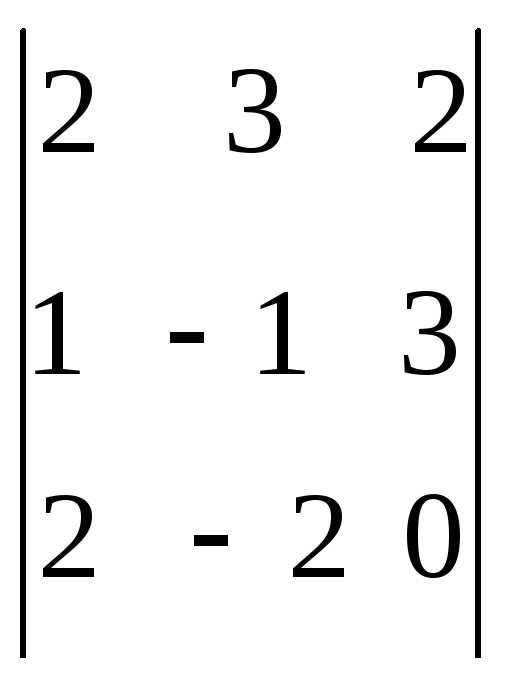

Решение: Определитель найдем, применяя формулу (3):

Ранг матрицы

Наибольший порядок отличных от нуля детерминантов (миноров) прямоугольной матрицы m  n, называется рангом матрицы r, причем r  min(m, n). Для квадратной матрицы ранг r  n.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

@ Задача 4. Найти ранг матрицы 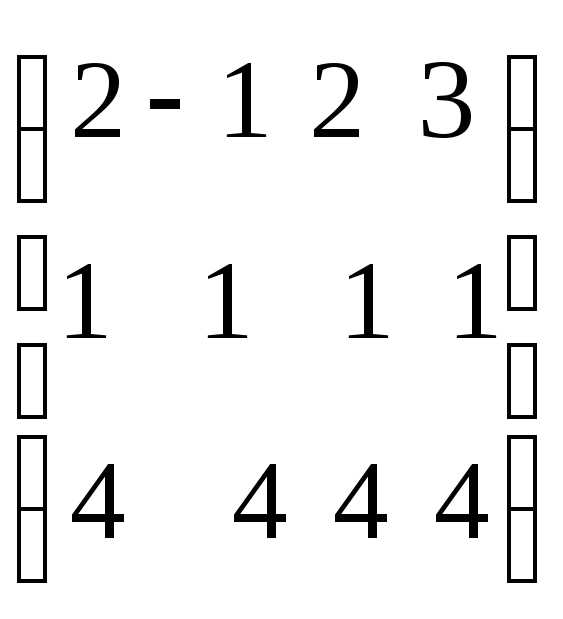размерности3  4.

Решение: Ранг матрицы r  min(3, 4) = 3. Все детерминанты третьего порядка равны нулю, так как две их строки (вторая и третья) одинаковые (отличаются на постоянный множитель). Отличны от нуля только детерминанты второго порядка, поэтому r = 2.

studfiles.net

Определители. Свойства определителей. — КиберПедия

 

 

Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.

Свойство 1 («Равноправность строк и столбцов»). Определитель не изменяется, если его строки заменить столбцами, и наоборот.

Иными словами

, .

В дальнейшем строки и столбцы будем просто называть рядами определителя.

Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.

Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

 

 

Действительно,

.

Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

.

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число.

Пример 2.3. Доказать, что

.

Решение: Действительно, используя свойства 5, 4 и 3 получим

.

Дальнейшие свойства определителя связаны с понятиями минора и алгебраического дополнения.

 

Миноры и алгебраические дополнения элементов определителя.

Разложение определителя по элементам строки или столбца

Минором некоторого элемента определителя n-го порядка называется определитель n – 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается .

Так, если , то , .

Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком «плюс», если сумма – четное число, и со знаком «минус», если эта сумма нечетная. Обозначается .

Так, , .

Свойство 7. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-го порядка. В этом случае свойство 7 означает, что

.

 

В самом деле, имеем

.

Свойство 7 содержит в себе способ вычисления определителей высоких порядков.

 

Пример 2.4. Вычислите определитель матрицы

.

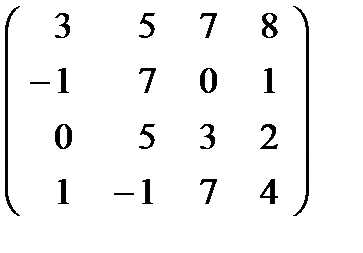Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т.к. соответствующие им слагаемые в разложении будут равны нулю.

 

 

 

 

.

Свойство 8. Сумма произведений какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

Так, например, .

 

cyberpedia.su

Глава 4. Свойства определителей | Решение задач по математике и другим

Свойство 1

При транспонировании матрицы ее определитель не изменяется, т. е.:

Свойство 2

При перестановке двух параллельных рядов (строк либо столбцов) матрицы знак ее определителя изменяется на противоположный. Абсолютное значение определителя при этом не меняется.

(1.4.2)

Свойство 3

Определитель, содержащий два одинаковых ряда, равен нулю:

(1.4.3)

Свойство 4

Определитель, содержащий ряд из нулей, равен нулю:

(1.4.4)

Свойство 5

Общий множитель всех элементов одного ряда определителя можно вынести за знак определителя:

(1.4.5)

Свойство 6

Если все элементы какого–либо ряда определителя представлены в виде суммы двух слагаемых, то такой определитель можно представит в виде суммы двух определителей, у которого элементы рассматриваемого ряда равны соответствующим слагаемым. А остальные элементы у всех трех определителей одни и те же:

(1.4.6)

Свойство 7

Определитель не изменится, если к элементам какого–либо его ряда прибавить соответствующие элементы параллельного ему ряда, умноженного на одно и то же число:

(1.4.7)

Свойство 8

Определитель не изменится, если к элементам какого–либо ряда прибавить соответствующие элементы параллельного ему ряда, умноженные на одно и то же число.

(1.4.8)

Минором Mik элемента Aik определителя называется определитель, который получается из данного после вычеркивания I–ой строки и K–го столбца, на пересечении которых стоит этот элемент.

Пример

DetA=. Найти миноры Mik.

Решение

Минор M11 элемента A11=5 равен:

Минор M32 элемента A32=–1 равен:

Алгебраическим дополнением Aik элемента Aik определителя называется минор этого элемента, взятый со знаком “+”, если I+K – четное число, и со знаком “–“, если I+K – нечетное число, т. е.

Aik =(–1)I+K Mik.

(1.4.9)

Пример

A11 = (–1)1+1 M11 = M11, A12 = (–1)1+2 M12 = – M12, A32 = (–1)3+2 M32 = – M32 и т. д.

Свойство 9

Определитель равен сумме произведений элементов какого–либо его ряда на их алгебраические дополнения, т. е. детерминант матрицы (1.3.3) равен

DetA = A11A11 + A12A12 + A13A13; DetA = A12A12 + A22A22 + A23A23 и т. д.

(1.4.10)

Пример

Вычислить определитель матрицы:

Решение

DetA = A11A11 + A12A12 + A13A13.

Итак, detA = 3×7 + (–2) ×(–10) + 0×(–5) = 41.

Свойство 10

Сумма произведений элементов какого–либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ему ряда равна нулю:

A11A21 + A12A22 + A13A13 = 0, A11A13 + A21A23 + A31A33 = 0 и т. д.

(1.4.11)

< Предыдущая		Следующая >

matica.org.ua

No related posts.