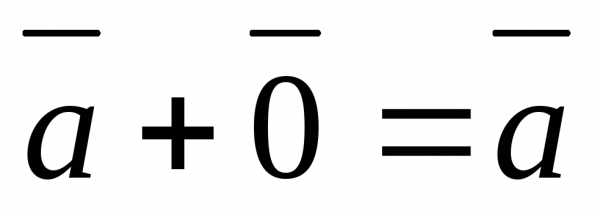]Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы
Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).
Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.
Сложение векторов — элементов линейного пространства
Пусть в линейном пространстве выбран базис и в нём представлены вектора вектора , тогда суммой векторов будет называется следующий вектор: .
Умножение вектора на число
Произведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение — нулевой вектор.
Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .
Из определения произведения вектора на число легко вывести следующие свойства:
если , то . Наоборот, если , то при некотором λ верно равенство ;
всегда °, то есть каждый вектор равен произведению его модуля на орт.
Скалярное произведение
Основная статья: Скалярное произведение
Функция (в другом обозначении ), ставящая любым двум векторам в соответствие число и удовлетворяющая следующим аксиомам:
Линейность по первому аргументу: , где α,β — произвольные числа
Эрмитова симметричность: (в случае если вектора определены над полем действительных чисел, то )
Положительная определённость: тогда и только тогда, когда ,
называется скалярным произведением
Угол ϕ между векторами определяется, как Иногда, когда не известны координаты вектора, для нахождения скалярного произведения удобнее использовать эту формулу.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора с единичным вектором есть ортогональная проекция вектора на направление единичного вектора.
studfiles.net
]Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы
Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).
Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.
Сложение векторов — элементов линейного пространства
Пусть в линейном пространстве выбран базис и в нём представлены вектора вектора , тогда суммой векторов будет называется следующий вектор: .
Умножение вектора на число
Произведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение — нулевой вектор.
Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .
Из определения произведения вектора на число легко вывести следующие свойства:
если , то . Наоборот, если , то при некотором λ верно равенство ;
всегда °, то есть каждый вектор равен произведению его модуля на орт.
Скалярное произведение
Основная статья: Скалярное произведение
Функция (в другом обозначении ), ставящая любым двум векторам в соответствие число и удовлетворяющая следующим аксиомам:
Линейность по первому аргументу: , где α,β — произвольные числа
Эрмитова симметричность: (в случае если вектора определены над полем действительных чисел, то )
Положительная определённость: тогда и только тогда, когда ,
называется скалярным произведением вектора на вектор .
Угол ϕ между векторами определяется, как Иногда, когда не известны координаты вектора, для нахождения скалярного произведения удобнее использовать эту формулу.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора с единичным вектором есть ортогональная проекция вектора на направление единичного вектора.
studfiles.net
Свойства коллинеарных векторов:
1. Нулевой вектор
коллинеарен любому вектору: Если 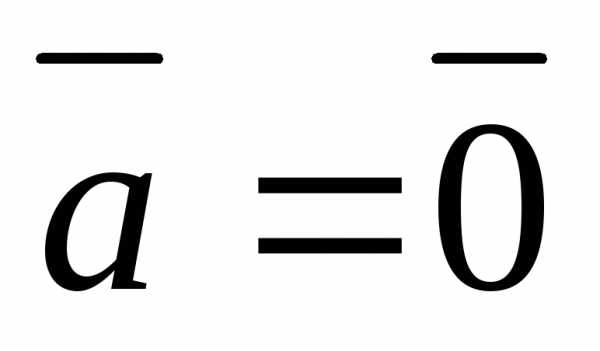 (или
(или 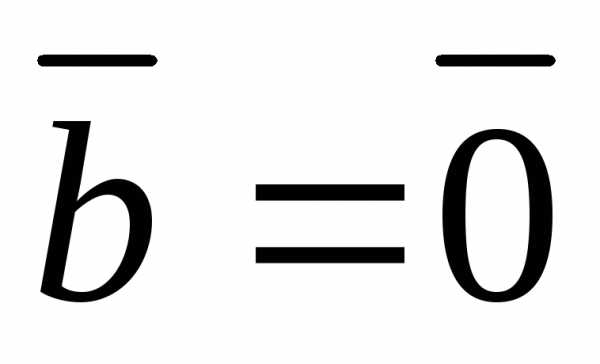 ),
то
),
то 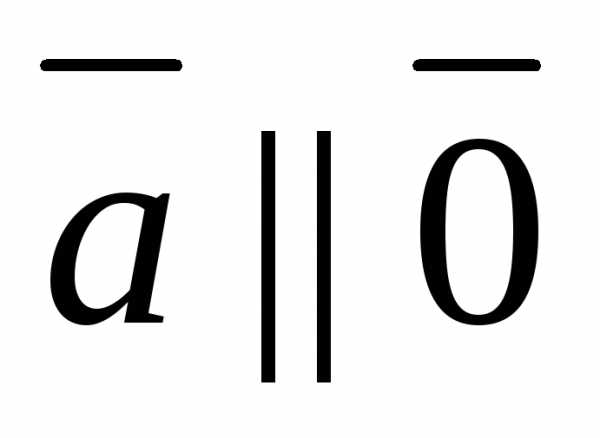 (или
(или  ).
).
2. Нулевой вектор
одинаково направлен с любым вектором,  .
.
3. Любые два коллинеарных вектора можно отложить на одной прямой.
Достаточно отложить векторы от одной точки.
4. На прямой можно указать всего два направления, следовательно, два вектора, отложенных на ней могут иметь либо одно и то же направление, либо противоположное.
Определение 4.
Векторы 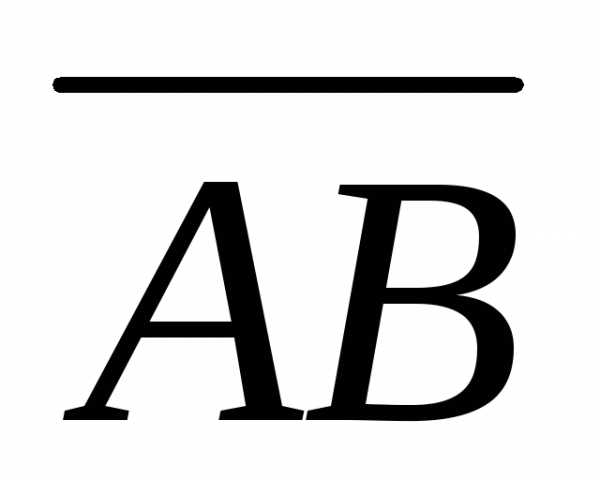 и
и  называются противоположными.
называются противоположными.
Рассмотрим вектор  .
Отложим его от точки А.
.
Отложим его от точки А.
Для вектора 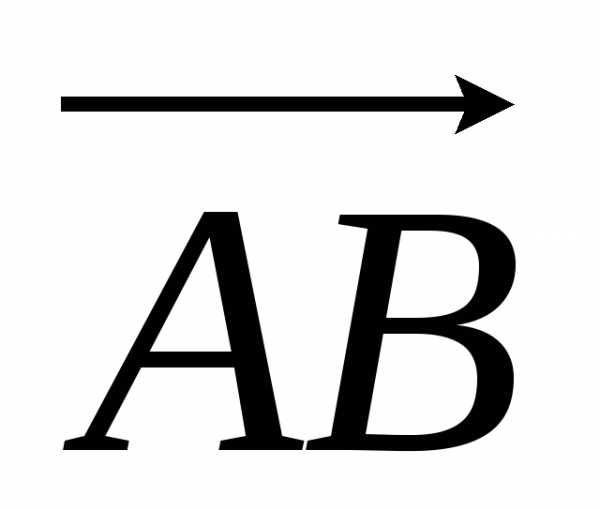 =
= противоположным называется вектор
противоположным называется вектор 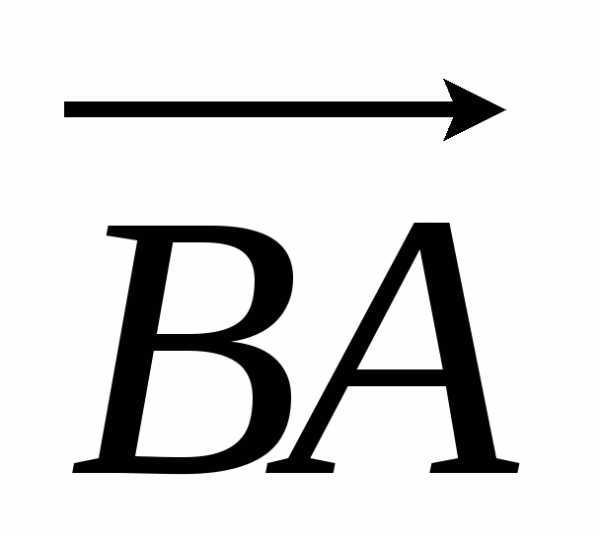
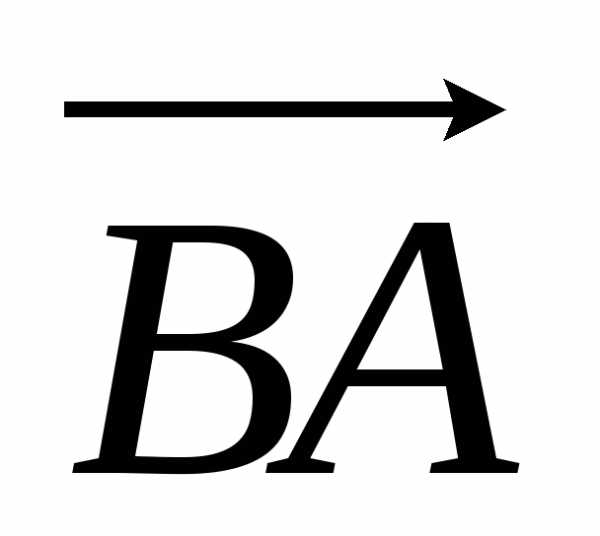 =–
=– .
. Вектор, противоположный 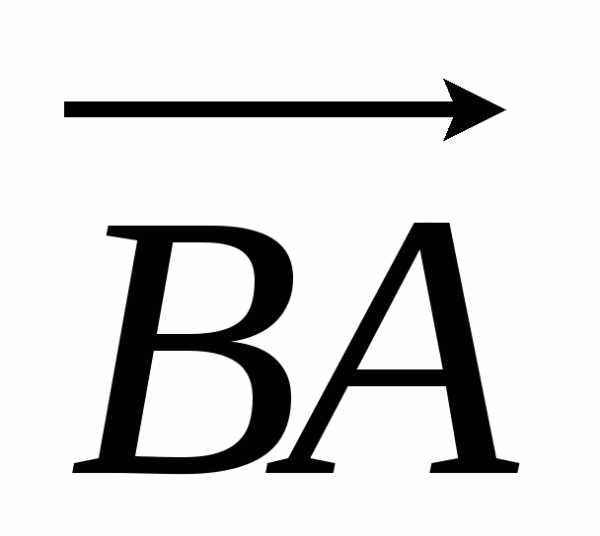 ,
это вектор
,
это вектор  ,
т.е.
,
т.е. 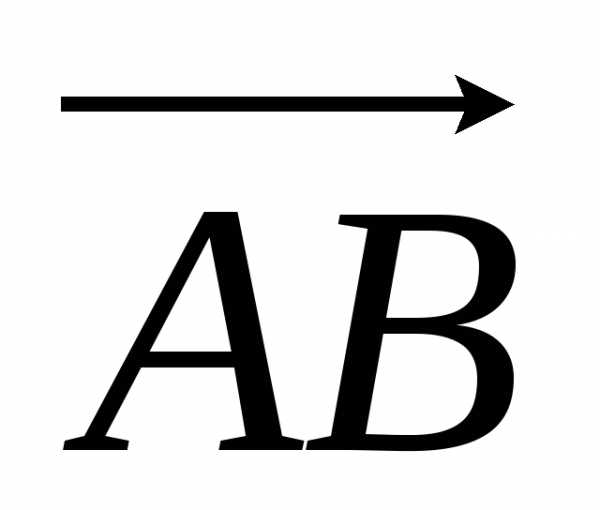 =–(–
=–(– ).
).
Для нулевого
вектора  противоположным является вектор
противоположным является вектор  ,
или
,
или  =–
=–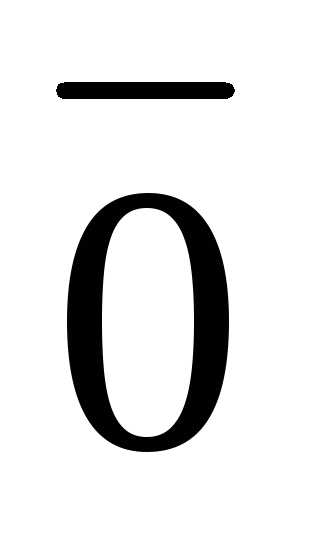 .
.
Определение 5.
Ненулевые векторы 
 называются одинаково
направленными (сонаправленными), если лучи АВ и CD одинаково направлены, обозначается
символом
называются одинаково
направленными (сонаправленными), если лучи АВ и CD одинаково направлены, обозначается
символом  :
:.
Ненулевые векторы  и
и  называются противоположно
направленными,
если лучи АВ и CD противоположно направлены, обозначается
символом
называются противоположно
направленными,
если лучи АВ и CD противоположно направлены, обозначается
символом 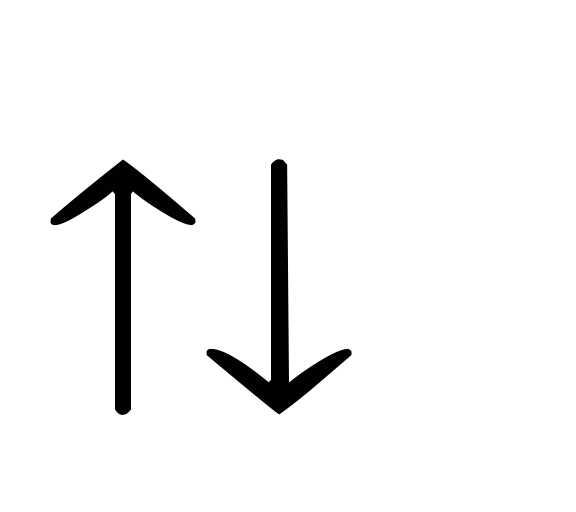 :
:
.
3. Абсолютная величина вектора
Определение 6.
Модулем
(длиной, абсолютной величиной) вектора 
 ,
, 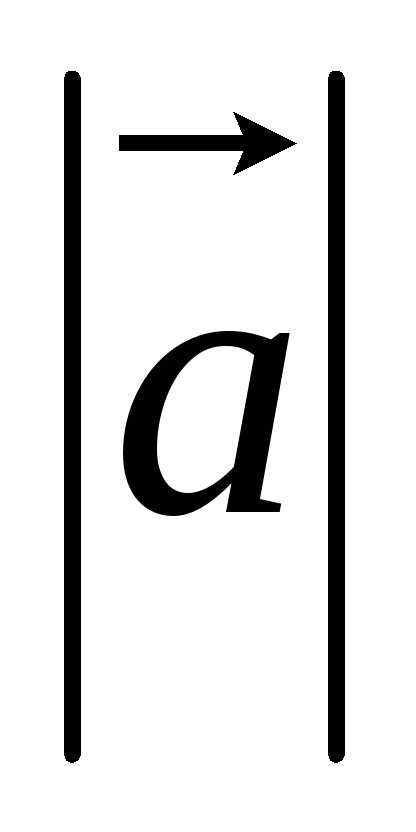 или АВ.
или АВ. Длина нулевого
вектора равна нулю: 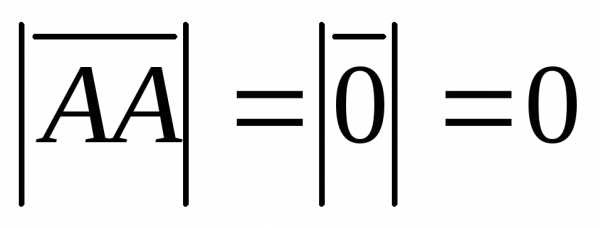 .
.
Определение 7.
Вектор, абсолютная величина которого равна единице, называется единичным.
Единичный вектор
обозначается  ,
, 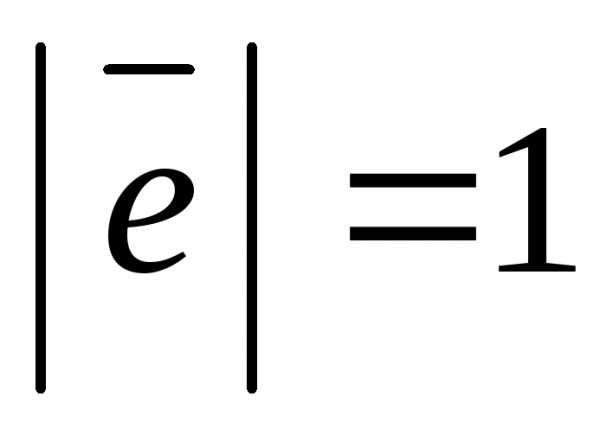 .
.
4. Равенство векторов
Определение 8.
Два вектора  и
и 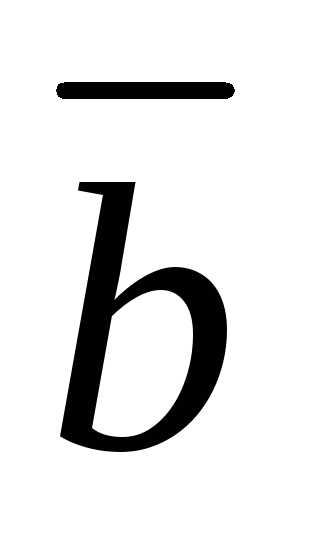 называются равными,
если выполнены следующие условия:
называются равными,
если выполнены следующие условия:
1) они имеют
одинаковое направление, 

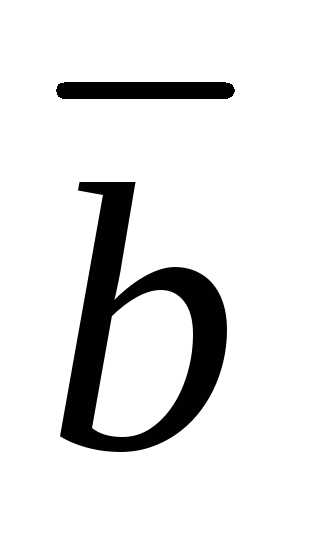 ;
;
2) абсолютные
величины их равны, | |=|
|=| |.
|.
Из определения следует, что два нулевых вектора всегда равны.
Равенство векторов обладает свойствами, аналогичными свойствам равенства чисел.
Свойства равенства векторов:
1. Рефлексивность:
каждый вектор равен самому себе 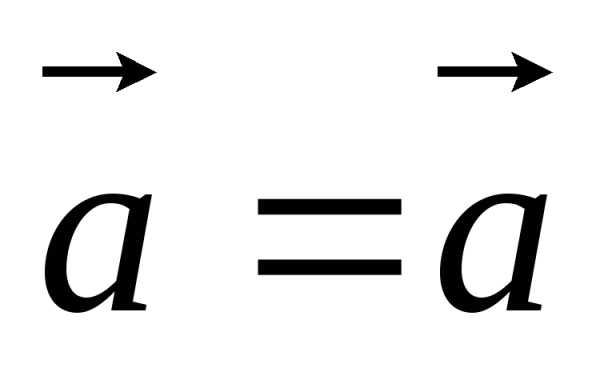 ;
;
2. Симметричность: .
3. Транзитивность: .
Равенство векторов является отношением эквивалентности.
5. Линейные операции над векторами
Линейными операциями над векторами называются сложение векторов и умножение вектора на действительное число.
5.1. Сложение векторов
Определение 9 (Правило треугольника).
Суммой
векторов  и
и 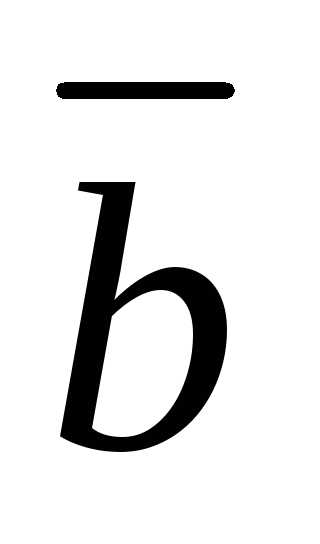 ,
отложенных последовательно, называется
вектор
,
отложенных последовательно, называется
вектор  ,
начало которого совпадает с началом
первого слагаемого вектора, а конец –
с концом второго.
,
начало которого совпадает с началом
первого слагаемого вектора, а конец –
с концом второго.
 ,
,
(7.1)
Сумма векторов существует и определена однозначно.
Свойства сложения:
1.
С=В

2.
С=В, В=А

3.
С=А
4.
Коммутативность
5.
Ассоциативность
Определение 10 (Правило параллелограмма).
Суммой
векторов  и
и 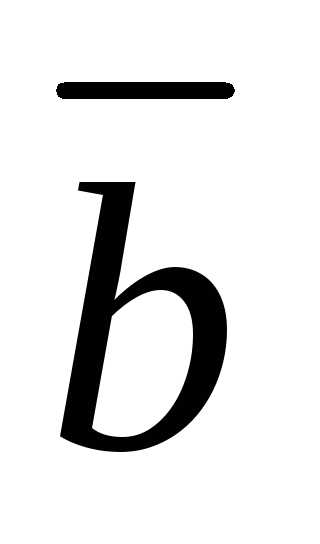 ,
отложенных от общего начала, называется
вектор
,
отложенных от общего начала, называется
вектор  ,
задаваемый диагональю построенного на
них, как на сторонах, параллелограмма,
исходящей из их общего начала. Начало
вектора суммы совпадает с началом
слагаемых векторов, а конец – с
противоположным концом диагонали
параллелограмма.
,
задаваемый диагональю построенного на
них, как на сторонах, параллелограмма,
исходящей из их общего начала. Начало
вектора суммы совпадает с началом
слагаемых векторов, а конец – с
противоположным концом диагонали
параллелограмма.
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух связных (фиксированных) векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Определение 11 (Правило многоугольника).
Суммой n векторов  ,
отложенных последовательно, называется
вектор, начало которого совпадает с
началом первого слагаемого вектора, а
конец – с концом последнего слагаемого
вектора.
,
отложенных последовательно, называется
вектор, начало которого совпадает с
началом первого слагаемого вектора, а
конец – с концом последнего слагаемого
вектора.
studfiles.net
Действия с векторами. Коллинеарность векторов
В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.
Правило сложения векторов по правилу треугольников
Рассмотрим два произвольных ненулевых вектора и :
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор от конца вектора :
Суммой векторов и является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов представляет собой вектор результирующего пути с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.
Кстати, если вектор отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.
Умножение вектора на число
Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».
Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.
Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация: (векторы сонаправлены) или (векторы направлены противоположно).
Произведением ненулевого вектора на число является такой вектор , длина которого равна , причём векторы и сонаправлены при и противоположно направлены при .
Правило умножения вектора на число легче понять с помощью рисунка: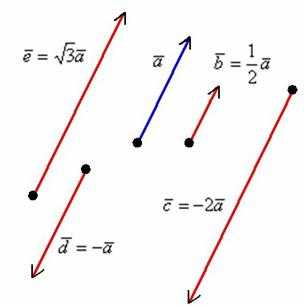
Разбираемся более детально:
1) Направление. Если множитель отрицательный, то вектор меняет направление на противоположное.
2) Длина. Если множитель заключен в пределах или , то длина векторауменьшается. Так, длина вектора в два раза меньше длины вектора . Если множитель по модулю больше единицы, то длина вектора увеличивается в раз.
3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например, . Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному)вектор.
4) Векторы сонаправлены. Векторы и также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.
infopedia.su
Понятие вектора. Равные и коллинеарные векторы.
Ответы на коллоквиум
Понятие вектора. Равные и коллинеарные векторы.
Вектором называется направленный отрезок. Векторы AB и CD называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы AB и CD называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора обозначим | |. Два вектора называютсяравными, если они одинаково направлены и равны по абсолютной величине.
Сложение и вычитание векторов.
Суммой векторов (a1;a2) и (b1;b2) называется вектор (a1+b1;a2+b2)
Разностью векторов (a1;a2) и (b1;b2) называется такой вектор (c1;c2) который в сумме с вектором дает вектор , откуда c1 = a1– b1; c2 = a2– b2.
Суммойтрех векторов называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Умножение вектора на число.
Произведением вектора (a1;a2) на число λ называется вектор (λa1;λa2).
Линейно зависимые и независимые системы векторов.
Скалярным произведением векторов (a1;a2)и (b1;b2) называется число a1b1+a2b2
Скалярное произведение векторов и обозначается .
Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Необходимое и достаточное условие коллинеарности двух векторов.
Два вектора и называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
Нулевой вектор коллинеарен любому вектору.Два ненулевых вектора и коллинеарны, Û когда они пропорциональны т.е. = k , k – скаляр.
Необходимое и достаточное условие компланарности трех векторов.
Три вектора , , называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
Три ненулевых вектора , , компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
= k + l, k ,l– скаляры.
Операции над векторами, заданными своими координатами.
Проекции вектора на координатные оси Ох, Оу, Оz называются координатами вектора. Обозначение: {ax, ay, az}.
Длина вектора:
Расстояние между точками и вычисляется по формуле: .
Действия над векторами в координатной форме.
Даны векторы ={ax, ay, az} и ={bx, by, bz}.
1. ( ± )={ax ± bx, ay ± by, az ± bz}.
2. l ={lax, lay, laz}, где l – скаляр.
Скалярное произведение и его свойства.
Определение: Под скалярным произведением двух векторов и
понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е. = , — угол между векторами и .
Свойства скалярного произведения:
1. × =
2. ( + ) =
3.
4.
5. , где – скаляры.
6. два вектора перпендикулярны (ортогональны), если .
7. тогда и только тогда, когда .
Скалярное произведение в координатной форме имеет вид: , где и .
Векторное произведение и его свойства.
Определение: Под векторным произведением двух векторов и понимается вектор, для которого:
-модуль равен площади параллелограмма, построенного на данных векторах, т.е. , где угол между векторами и
-этот вектор перпендикулярен перемножаемым векторам, т.е.
-если векторы неколлинеарны, то они образуют правую тройку векторов.
Свойства векторного произведения:
1.При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е.
2.Векторный квадрат равен нуль-вектору, т.е.
3.Скалярный множитель можно выносить за знак векторного произведения, т.е.
4.Для любых трех векторов справедливо равенство
5.Необходимое и достаточное условие коллинеарности двух векторов и :
Векторное произведение в координатной форме.
Если известны координаты векторов и , то их векторное произведение находится по формуле:
.
Тогда из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах и , вычисляется по формуле:
Параметрические и каноническое уравнения прямой на плоскости
Векторно-параметрическое уравнение прямой:
где — фиксированная точка, лежащая на прямой;
— направляющий вектор.
В координатах (параметрические уравнения):
Каноническое уравнениепрямой
Ответы на коллоквиум
Понятие вектора. Равные и коллинеарные векторы.
Вектором называется направленный отрезок. Векторы AB и CD называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы AB и CD называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора обозначим | |. Два вектора называютсяравными, если они одинаково направлены и равны по абсолютной величине.
Сложение и вычитание векторов.
Суммой векторов (a1;a2) и (b1;b2) называется вектор (a1+b1;a2+b2)
Разностью векторов (a1;a2) и (b1;b2) называется такой вектор (c1;c2) который в сумме с вектором дает вектор , откуда c1 = a1– b1; c2 = a2– b2.
Суммойтрех векторов называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Умножение вектора на число.
Произведением вектора (a1;a2) на число λ называется вектор (λa1;λa2).
infopedia.su