Разложение подынтегральной функции в ряд маклорена – Приближённые вычисления определённых интегралов с помощью рядов. Первая часть.

Содержание

Приближённые вычисления определённых интегралов с помощью рядов. Первая часть.

Пусть требуется вычислить определенный интеграл $\int\limits_{a}^{b}f(x)dx$ с некоторой наперёд заданной точностью $\varepsilon$. Если непосредственное нахождение первообразной подынтегральной функции $f(x)$ чересчур громоздко, или же интеграл $\int f(x)dx$ вообще не берётся, то в этих случаях можно использовать функциональные ряды. В частности, применяются ряды Маклорена, с помощью которых получают разложение в степенной ряд подынтегральной функции $f(x)$. Именно поэтому в работе нам будет нужен документ с рядами Маклорена.

Степенные ряды, которые мы и станем использовать, сходятся равномерно, поэтому их можно почленно интегрировать по любому отрезку, лежащему внутри интервала сходимости. Схема решения подобных задач на вычисление интегралов с помощью рядов проста:

Разложить подынтегральную функцию в функциональный ряд (обычно в ряд Маклорена).
Произвести почленное интегрирование членов записанного в первом пункте функционального ряда.
Вычислить сумму полученного во втором пункте числового ряда с заданной точностью $\varepsilon$.

Задачи на вычисление интегралов с помощью рядов популярны у составителей типовых расчётов по высшей математике. Поэтому в данной теме мы разберём пять примеров, в каждом из которых требуется вычислить определенный интеграл с точностью $\varepsilon$.

Пример №1

Вычислить $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx$ с точностью до $\varepsilon=10^{-3}$.

Решение

Сразу отметим, что интеграл $\int e^{-x^2}dx$ не берётся, т.е. первообразная подынтегральной функции не выражается через конечную комбинацию элементарных функций. Иными словами, стандартными способами (подстановка, интегрирование по частям и т.д.) первообразную функции $e^{-x^2}$ найти не удастся.

Для таких задач есть два варианта оформления, поэтому рассмотрим их отдельно. Условно их можно назвать «развёрнутый» и «сокращённый» варианты.

Развёрнутый вариант оформления

Запишем разложение функции $e^x$ в ряд Маклорена:

$$e^x=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\ldots$$

Данное разложение верно при всех $x\in{R}$. Подставим $-x^2$ вместо $x$:

$$e^{-x^2}=1-x^2+\frac{\left(-x^2\right)^2}{2}+\frac{\left(-x^2\right)^3}{6}+\ldots=1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots$$

Интегрируем полученное разложение на отрезке $\left[0;\frac{1}{2}\right]$:

$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx=\int\limits_{0}^{\frac{1}{2}}\left(1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots\right)dx=\\ =\left.\left(x-\frac{x^3}{3}+\frac{x^5}{10}-\frac{x^7}{42}+\ldots\right)\right|_{0}^{1/2}= \frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}-\frac{1}{42\cdot{2^7}}+\ldots$$

Получили сходящийся знакочередующийся ряд. Это значит, что если для вычисления приближенного значения заданного интеграла взять $k$ членов полученного ряда, то погрешность не превысит модуля $(k+1)$-го члена ряда.

Согласно условию, точность $\varepsilon=10^{-3}$. Так как $\frac{1}{42\cdot{2^7}}=\frac{1}{5376}<10^{-3}$, то для достижения требуемой точности достаточно ограничиться первыми тремя членами знакочередующегося ряда:

$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}=\frac{443}{960}.$$

Погрешность полученного равенства не превышает $\frac{1}{5376}$.

Однако суммировать обычные дроби – дело утомительное, поэтому чаще всего расчёты ведут в десятичных дробях:

$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}\approx{0{,}5}-0{,}0417+0{,}0031\approx{0{,}461}.$$

Разумеется, в этом случае нужно учитывать погрешность округления. Первое слагаемое (т.е. $0{,}5$) было рассчитано точно, поэтому никакой погрешности округления там нет. Второе и третье слагаемые брались с округлением до четвёртого знака после запятой, посему погрешность округления для каждого из них не превысит $0,0001$. Итоговая погрешность округления не превысит $0+0{,}0001+0{,}0001=0{,}0002$.

Следовательно, суммарная погрешность равенства $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx{0{,}461}$ не превысит $0{,}0002+\frac{1}{5376}<10^{-3}$, т.е. значение интеграла вычислено с требуемой точностью.

Отмечу, что большинство авторов методичек и учебных пособий не учитывают погрешность округления, хоть это и не совсем корректно. В дальнейших примерах данной темы я буду упоминать про эту погрешность, если она возникнет.

Сокращённый вариант оформления

Запишем разложение функции $e^x$ в ряд Маклорена:

$$e^x=\sum\limits_{n=0}^{\infty}\frac{x^n}{n!}$$

Данное разложение верно при всех $x\in{R}$. Подставим $-x^2$ вместо $x$:

$$e^{-x^2}=\sum\limits_{n=0}^{\infty}\frac{\left(-x^2\right)^n}{n!}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{n!}$$

Интегрируем полученный ряд на отрезке $\left[0;\frac{1}{2}\right]$:

$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx=\int\limits_{0}^{\frac{1}{2}}\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{n!}dx= \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!}\int\limits_{0}^{\frac{1}{2}}x^{2n}dx=\\ =\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!}\left.\frac{x^{2n+1}}{2n+1}\right|_{0}^{1/2}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot\left(\frac{1}{2}\right)^{2n+1}}{n!\cdot(2n+1)}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!\cdot(2n+1)\cdot{2^{2n+1}}}$$

Получили знакочередующийся ряд. Запишем несколько первых членов этого ряда (до тех пор, пока записанный член не станет меньше $\varepsilon$):

$$\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!\cdot(2n+1)\cdot{2^{2n+1}}}=\frac{1}{2}-\frac{1}{24}+\frac{1}{320}-\frac{1}{5376}+\ldots$$

Все рассуждения, что были сделаны относительно погрешностей в развёрнутом варианте оформления остаются в силе, т.е. $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}\approx{0{,}461}$.

Чем сокращённый вариант записи лучше развёрнутого?

Во-первых, нам не нужно угадывать, сколько членов ряда взять в изначальном разложении, чтобы вычислить определенный интеграл с заданной точностью. Например, мы записали в самом начале решения:

$$e^{-x^2}=1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots$$

Однако почему мы решили, что нужно взять именно четыре члена ряда? А вдруг нужно взять два члена ряда или пять, или сто? Если бы только шестой член ряда оказался меньше чем $\varepsilon$, – что тогда? А тогда пришлось бы возвращаться в самое начало решения, добавлять ещё пару членов ряда и интегрировать их. А если и этого не хватит, то проделать эту процедуру ещё раз.

Сокращённый вид записи таким недостатком не страдает. Мы получаем числовой ряд, записанный в общем виде, поэтому можем брать столько его членов, сколько потребуется.

Далее, при интегрировании в развёрнутом способе записи мы находили первообразную четыре раза. При интегрировании в сокращённом способе записи, по сути, мы нашли лишь первообразную для $x^{2n}$.

Исходя из вышеперечисленных причин, я предпочитаю именно сокращённый способ записи. В дальнейнем все решения в этой теме будут оформлены в сокращённой форме.

Ответ: $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx{0{,}461}$.

Пример №2

Вычислить определённый интеграл $\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx$ с точностью до $\varepsilon=10^{-3}$, разложив подынтегральную функцию в ряд Маклорена и проинтегрировав почленно.

Решение

Начнём с разложения подынтегральной функции $\frac{1-\cos\frac{5x}{3}}{x}$ в ряд Маклорена. Запишем разложение функции $\cos{x}$ в ряд Маклорена:

$$\cos{x}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{(2n)!}$$

Данное разложение верно при всех $x\in{R}$. Подставим вместо $x$ дробь $\frac{5x}{3}$:

$$\cos{\frac{5x}{3}}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{\left(\frac{5x}{3}\right)}^{2n}}{(2n)!}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}.$$

Теперь разложим $1-\cos\frac{5x}{3}$:

$$ 1-\cos\frac{5x}{3}=1-\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}} $$

Забирая из суммы $\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}$ первый член, получим: $\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=1+\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}$. Следовательно:

$$ 1-\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=1-\left(1+\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}\right)=\\ =-\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}} =\sum\limits_{n=1}^{\infty}\frac{-(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}. $$

Последнее, что остаётся – это разделить на $x$:

$$ \frac{1-\cos\frac{5x}{3}}{x}=\frac{1}{x}\cdot\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n-1}}{3^{2n}\cdot{(2n)!}}. $$

Интегрируем данное разложение на отрезке $\left[0;\frac{1}{5}\right]$:

$$ \int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx=\int\limits_{0}^{\frac{1}{5}}\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n-1}}{3^{2n}\cdot{(2n)!}}dx= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}}{3^{2n}\cdot{(2n)!}}\int\limits_{0}^{\frac{1}{5}}{x}^{2n-1}dx=\\ =\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}}{3^{2n}\cdot{(2n)!}}\cdot\left.\frac{x^{2n}}{2n}\right|_{0}^{1/5}= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{{2n}\cdot 3^{2n}\cdot{(2n)!}} $$

$$\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{{2n}\cdot 3^{2n}\cdot{(2n)!}}=\frac{1}{36}-\frac{1}{7776}+\ldots$$

Так как $\frac{1}{7776}<\varepsilon$, то для вычисления интеграла с точностью $\varepsilon$ достаточно первого члена полученного числового ряда:

$$\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx\approx\frac{1}{36}\approx{0{,}028}.$$

Ответ: $\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx\approx{0{,}028}$.

Продолжение темы вычисления интегралов с помощью рядов Маклорена продолжим во второй части.

math1.ru

ЛЕКЦИЯ 12

Ряды Тейлора и Маклорена.

Ряды Тейлора и Маклорена для основных элементарных функций.

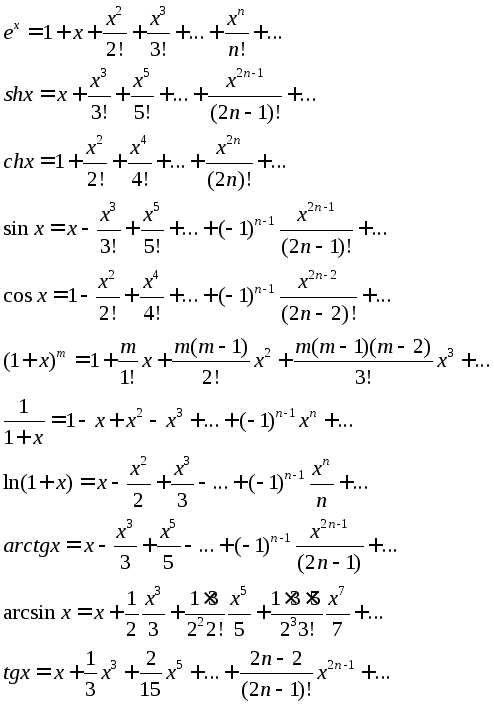
Разложение функций в степенные ряды. Ряд Тейлора

Общая постановка задачи разложения функции в ряд в комплексной области формулируется так же, как и в действительной области. А именно, для заданной функции , определенной в области и удовлетворяющий в ней него которым дополнительным условиям, требуется найти ряд вида который бы сходился в области и его сумма в этой области совпадала с .

Постановка задачи разложения функции в степенной ряд

Для функции , аналитической в области , найти ряд , сходящийся к в круге , принадлежащем области , то есть

Равенство (3.15) означает, что является суммой ряда в круге .

Для решения задачи нужно, очевидно, найти коэффициенты ряда по заданной функции ; найти круг сходимости ряда и установить сходимость ряда именно к . Последнее, напомним, означает, что для точек круга выполняется неравенство для любого и .

Все поставленные вопросы решаются с помощью следующей теоремы.

Теорема Тейлора о разложении функции в степенной ряд

Теорема 3.4. Функция, аналитическая в области , в окрестности каждой точки этой области представляется в виде степенного ряда (3.15), радиус сходимости

которого не меньше, чем расстояние от точки до границы области . Коэффициенты ряда вычисляются по формуле

где — произвольный контур, принадлежащий области и охватывающий точку , в частности, — окружность или по формуле

На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.

Необходимое и достаточное условие разложения функции в ряд Тейлора

Разберем задачу, которая является противоположной той, которая была расмотрена ранее. Предположим, что функцияв т.. Допустим, функцияявляется бесконечно дифференцируемой, если, при этомследовательно для нее ряд Маклорена будет таким:

Если, то его сумма. Определим каковы должны быть условия, чтобы

О: В качестве многочлена Тейлора степенипонимают частичную сумму

Остаточный член ряда Тейлора есть

(30.8)

Т: Если требуется, чтобы бесконечно дифференцируемая в т.была представлена в качестве суммы составленного для нее ряда Тейлора (30.6), необходимо и достаточно выполнение следующго условия

В соответствии с определением сходящегося ряда и используя выражение (30.8), запишем такую цепочку:

— сумма (30.6)

Представим запись остаточного члена, выраженного в форме Лагранжа:

в данном случаерасполагается междуи.

Применение степенных рядов к приближенным вычислениям.

Вычисление значений функций.

Пусть f(x) является суммой ряда Тейлора ( 13 ). Необходимо с погрешностью определить значение функции в точке х1 из области сходимости ряда (x0 – R, x0 + R). Для этого определим номер n при котором значение остаточного члена |Rn(x1)| равно указанной погрешности и вычислим значение многочлена Тейлора Sn(x1)

Вычислить интеграл , где область R ограничена параболами и гиперболами . Замена переменных в двойных интегралах

Пр. Вычислить число е с точностью до 0,001

В разложении ( 14 ) положим х = 1 : е = 1 + 1 + 1/2! + . . . + 1/n! + . . .

Согласно ( 13 ) Rn(1) = exp()/ (n+1)! , а exp() < exp(1) < 3 , т.е. = Rn(1)< 3/(n+1)!

При n = 5 имеем < 3/6! = 1/240 > 0.001 , а при n = 6 < 3/7! = 1/1680 < 0.001

Поэтому е = 2 + ½! + 1/3! + ¼! + 1/5! + 1/6! = 2.7181 с точностью до 0,001.

Применение степенных рядов к приближенным вычислениям.

Вычисление значений функций.

Пр. Вычислить число е с точностью до 0,001

В разложении ( 14 ) положим х = 1 : е = 1 + 1 + 1/2! + . . . + 1/n! + . . .

Согласно ( 13 ) Rn(1) = exp()/ (n+1)! , а exp() < exp(1) < 3 , т.е. = Rn(1)< 3/(n+1)!

При n = 5 имеем < 3/6! = 1/240 > 0.001 , а при n = 6 < 3/7! = 1/1680 < 0.001

Поэтому е = 2 + ½! + 1/3! + ¼! + 1/5! + 1/6! = 2.7181 с точностью до 0,001.

Вычисление определенных интегралов с помощью рядов

Мы уже отмечали, что некоторые интегралы не могут быть вычислены, то есть, выражены в элементарных функциях.

Для их нахождения могут быть использованы разложения подынтегральных функций в степенные ряды, которые сходятся очень быстро.

Рассмотрим несколько примеров:

Пример 1.

Пусть требуется вычислить интеграл .

Здесь первообразная не является элементарной функцией. Поэтому, для вычисления этого интеграла, разложим подынтегральную функцию в ряд, заменяя в разложении e^x показатель x на –x² , итак

e^x=1+ x+ + . . .

Интегрируя обе части этого равенства в пределах от 0 до a, получим:

Получившийся степенной ряд сходится и требуемое его значение можно вычислить с наперед заданной точностью, зная, что погрешность не превосходит по величине первого отбрасываемого члена данного степенного ряда.

Пусть a=1 и нужна точность 0,001, тогда

т. е. необходимо учитывать только шесть первых членов полученного ряда.

studfiles.net

Ряд Маклорена — ПриМат

График функции имеет следующий вид:

Данная функция непрерывна на отрезке [0;0.3], а значит она интегрируема.

Значение данного определённого интеграла — площадь заштрихованной области графика.

Разложим функцию в ряд Маклорена, используя табличное разложение

В данном случае (для достижения нужной точности распишем 4 первых члена ряда)

Меняем подынтегральное выражение на данный степенной ряд

Упрощаем все слагаемые

Почленно интегрируем подынтегральное выражение

Пользуемся формулой Ньютона-Лейбница

Для достижения точности 0.001 нам хватило взять первые два члена ряда.

[свернуть]

ib.mazurok.com

Примеры приближенного вычисления определенных интегралов по формуле Тейлора

График функции имеет следующий вид:

Данная функция непрерывна на отрезке [0;0.3], а значит она интегрируема.

Значение данного определённого интеграла — площадь заштрихованной области графика.

Разложим функцию в ряд Маклорена, используя табличное разложение

В данном случае (для достижения нужной точности распишем 4 первых члена ряда)

Меняем подынтегральное выражение на данный степенной ряд

Упрощаем все слагаемые

Почленно интегрируем подынтегральное выражение

Пользуемся формулой Ньютона-Лейбница

Для достижения точности 0.001 нам хватило взять первые два члена ряда.

[свернуть]

ib.mazurok.com

Разложение в ряд Маклорена некоторых функций

Имеем ;

, и по формуле (5.2) получаем

. (5.3)

Областью сходимости этого степенного ряда является интервал .

Имеем: , , , , , откуда

, , , , и т.д.

Очевидно, что производные четного порядка , а нечетного порядка , , и по формуле (5.2) имеем

(5.4)

Область сходимости ряда .

3. .

Рассматривая аналогично функции , получим:

(5.5)

Область сходимости ряда .

4. , где – любое действительное число.

Имеем , ,

, , …,

, …

При : , , ,

, …, и по формуле (5.2) получаем

(5.6)

Найдем интервал сходимости ряда:

Ряд, составленный из модулей , исследуем с помощью признака Даламбера:

Следовательно, интервал сходимости ряда . На концах интервала при сходимость ряда зависит от конкретных значений .

Ряд (5.6) называется биномиальным. Если – целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при сомножитель равен нулю, следовательно, -йчлен ряда и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма.

Выпишем некоторые разложения функции при различных .

, (5.7)

Если в это разложение подставить вместо , получим:

(5.8)

, (5.9)

, (5.10)

5. .

Получить разложение для этой функции, непосредственно вычисляя коэффициенты с помощью производных, не очень просто, поэтому мы воспользуемся разложением (5.7) и свойством 2) степенных рядов. Интегрируя почленно равенство (5.7) в интервале , где , с учетом того, что , получим

(5.11)

Область сходимости ряда (после выяснения сходимости на концах интервала) есть .

Проделаем то же самое, что и в предыдущем случае, воспользовавшись разложением (5.8):

(5.12)

Область сходимости ряда .

Воспользуемся разложением (5.10), подставив в него вместо :

Интегрируя в интервале , где , получаем:

(5.13)

Область сходимости ряда

Можно доказать, что ряды, приведенные в формулах (5.3) – (5.13), сходятся к функциям, для которых они составлены.

При разложении более сложных функций часто используют готовые разложения (5.3) – (5.13).

Примеры

1) Разложить в ряд Маклорена функцию

Решение. Воспользуемся известной тригонометрической формулой

Разложим в ряд Маклорена функцию , заменяя в разложении (5.5) на :

Тогда

Это и есть разложение в ряд Маклорена функции . Очевидно, что оно справедливо при любом .

2) Разложить в ряд Тейлора по степеням функцию

Решение. Преобразуем данную функцию так, чтобы можно было воспользоваться разложением (5.7):

Полученное разложение справедливо, когда . Отсюда получаем или .

Применение рядов в приближенных вычислениях

Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «не берущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.

Примеры

I. Вычислить приближенно с точностью до 0,0001:

а)

Решение. Для вычисления запишем ряд (5.3) при , принадлежащем области сходимости :

Взяв первые пять членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда, мы допустим погрешность , не превышающую первого отброшенного члена (по абсолютной величине), т.е. .

Итак,

б)

Решение. Воспользуемся разложением (5.11), подставив в него , входящее в область сходимости :

Так как данный числовой ряд не является знакопеременным, то о погрешности нельзя судить по величине первого отбрасываемого члена.

Если в качестве взять сумму первых трех членов, мы допустим погрешность

(здесь мы учли, что сумма сходящегося геометрического ряда в скобках равна )

Итак,

в)

Решение. Для вычисления запишем ряд (5.4) при , принадлежащем области сходимости :

(необходимо взять два члена, так как при этом погрешность ). Итак,

II. Вычислить приближенно с точностью до 0,001 следующие интегралы:

Решение. Так как интеграл «не берущийся», «точное» интегрирование здесь невозможно.

Воспользуемся разложением (5.4). Разделив обе части на , получим

, причем ряд сходится при всех значениях . Интегрируя почленно, получим:

Возьмем первые три члена разложения, т.к. .

Итак,

б)

Решение. Заменив на в разложении (5.3), получим:

Умножая полученный ряд на :

и почленно интегрируя в интервале , принадлежащем интервалу сходимости ряда , имеем:

При этом . Итак, .

Задачи

Разложить в ряд Маклорена следующие функции, указав промежутки сходимости полученных рядов.

86. 87. 88.

89. 90. 91.

92.

Разложить в ряд Тейлора следующие функции и найти область сходимости полученного ряда.

93. по степеням

94 по степеням

95. по степеням

96. по степеням

97. по степеням

98. по степеням

Вычислить приближенно с точностью до 0,0001:

99. 100. 101. 102. 103.

104.

Вычислить приближенно, взяв первые два члена разложения в ряд подынтегральной функции, и оценить допущенные при этом погрешности:

105. 106.

Ответы

В задачах1, 3, 6, 7, 8, 9, 10, 12, 13, 15, 17, 18, 19, 21, 22, 23, 31, 32, 33, 34, 35, 37, 38, 42, 43, 44 – ряды сходятся.

В задачах 2, 4, 5, 11, 14, 16, 20, 24, 25, 26, 27, 28, 29, 30, 36, 39, 40, и 41 – ряды расходятся.

В задачах 45, 46, 47, 49, 50, 51, 55 – ряды абсолютно сходятся.

В задачах 48, 53, 54, 57 – ряды сходятся условно.

В задачах 52, 56, 58, 59 – ряды расходятся.

60.(-1;1],61.[-1/2;1/2),62.{0},63.(-1/3;1/3],64.(-1;1),65.[0;2],66.[-10;10),67.(-∞;∞), 68.(-7;-1), 69. [-4;4), 70. (-2;2), 71. , 72. [1;3), 73. (-1/3;1/3), 74. (-∞;∞), 75. [-1;1], 76. [-1;1), 77. (1;5], 78. (-1/4;1/4), 79. (-1/3;1/3), 80. (-3;1], 81. (-1;1], 82. (-∞;∞), 83. , 84. , 85. [-1/e;1/e),

86. 87.

88. 89.

90. 91.

92. 93.

94. 95.

96. 97.

98.

99. 100. 101.

102. 103. 104.

105. 106. .

Оглавление

§1. Основные понятия. 4

§2. Признаки сходимости знакопостоянных рядов. 7

§3. Признаки сходимости знакопеременных рядов. 22

§4. Степенные ряды.. 27

§5. Ряды Маклорена и Тейлора. 32

§6. Применение рядов в приближенных вычислениях. 39

Ответы.. 43

Подписано в печать 2012 г. Формат 60´84/16. Бумага писчая. Отпечатано на ризографе. Уч. изд. листов 2.
Тираж 600. Заказ №

Московский государственный университет тонких химических технологий им. М.В.Ломоносова

Издательско-полиграфический центр

117571, Москва, просп. Вернадского, 86.

* Напомним, что степенью степенного выражения называется наибольшая из степеней входящих в него слагаемых, само это слагаемое называется старшим, а его коэффициент называется старшим коэффициентом. Например, у степенного выражения старшее слагаемое имеет степень 1,5, а старший коэффициент равен 5.

infopedia.su

Разложение в ряд Маклорена некоторых функций — КиберПедия

Имеем ;

, и по формуле (5.2) получаем

. (5.3)

Областью сходимости этого степенного ряда является интервал .

Имеем: , , , , , откуда

, , , , и т.д.

Очевидно, что производные четного порядка , а нечетного порядка , , и по формуле (5.2) имеем

(5.4)

Область сходимости ряда .

3. .

Рассматривая аналогично функции , получим:

(5.5)

Область сходимости ряда .

4. , где – любое действительное число.

Имеем , ,

, , …,

, …

При : , , ,

, …, и по формуле (5.2) получаем

(5.6)

Найдем интервал сходимости ряда:

Ряд, составленный из модулей , исследуем с помощью признака Даламбера:

Выпишем некоторые разложения функции при различных .

, (5.7)

Если в это разложение подставить вместо , получим:

(5.8)

, (5.9)

, (5.10)

5. .

(5.11)

Область сходимости ряда (после выяснения сходимости на концах интервала) есть .

Проделаем то же самое, что и в предыдущем случае, воспользовавшись разложением (5.8):

(5.12)

Область сходимости ряда .

Воспользуемся разложением (5.10), подставив в него вместо :

Интегрируя в интервале , где , получаем:

(5.13)

Область сходимости ряда

Можно доказать, что ряды, приведенные в формулах (5.3) – (5.13), сходятся к функциям, для которых они составлены.

При разложении более сложных функций часто используют готовые разложения (5.3) – (5.13).

Примеры

1) Разложить в ряд Маклорена функцию

Решение. Воспользуемся известной тригонометрической формулой

Разложим в ряд Маклорена функцию , заменяя в разложении (5.5) на :

Тогда

Это и есть разложение в ряд Маклорена функции . Очевидно, что оно справедливо при любом .

2) Разложить в ряд Тейлора по степеням функцию

Решение. Преобразуем данную функцию так, чтобы можно было воспользоваться разложением (5.7):

Полученное разложение справедливо, когда . Отсюда получаем или .

Применение рядов в приближенных вычислениях

Примеры

I. Вычислить приближенно с точностью до 0,0001:

а)

Решение. Для вычисления запишем ряд (5.3) при , принадлежащем области сходимости :

Итак,

б)

Решение. Воспользуемся разложением (5.11), подставив в него , входящее в область сходимости :

Если в качестве взять сумму первых трех членов, мы допустим погрешность

(здесь мы учли, что сумма сходящегося геометрического ряда в скобках равна )

Итак,

в)

Решение. Для вычисления запишем ряд (5.4) при , принадлежащем области сходимости :

(необходимо взять два члена, так как при этом погрешность ). Итак,

II. Вычислить приближенно с точностью до 0,001 следующие интегралы:

Решение. Так как интеграл «не берущийся», «точное» интегрирование здесь невозможно.

Воспользуемся разложением (5.4). Разделив обе части на , получим

, причем ряд сходится при всех значениях . Интегрируя почленно, получим:

Возьмем первые три члена разложения, т.к. .

Итак,

б)

Решение. Заменив на в разложении (5.3), получим:

Умножая полученный ряд на :

и почленно интегрируя в интервале , принадлежащем интервалу сходимости ряда , имеем:

При этом . Итак, .

Задачи

Разложить в ряд Маклорена следующие функции, указав промежутки сходимости полученных рядов.

86. 87. 88.

89. 90. 91.

92.

Разложить в ряд Тейлора следующие функции и найти область сходимости полученного ряда.

93. по степеням

94 по степеням

95. по степеням

96. по степеням

97. по степеням

98. по степеням

Вычислить приближенно с точностью до 0,0001:

99. 100. 101. 102. 103.

104.

105. 106.

Ответы

В задачах1, 3, 6, 7, 8, 9, 10, 12, 13, 15, 17, 18, 19, 21, 22, 23, 31, 32, 33, 34, 35, 37, 38, 42, 43, 44 – ряды сходятся.

В задачах 2, 4, 5, 11, 14, 16, 20, 24, 25, 26, 27, 28, 29, 30, 36, 39, 40, и 41 – ряды расходятся.

В задачах 45, 46, 47, 49, 50, 51, 55 – ряды абсолютно сходятся.

В задачах 48, 53, 54, 57 – ряды сходятся условно.

В задачах 52, 56, 58, 59 – ряды расходятся.

86. 87.

88. 89.

90. 91.

92. 93.

94. 95.

96. 97.

98.

99. 100. 101.

102. 103. 104.

105. 106. .

Оглавление

§1. Основные понятия. 4

§2. Признаки сходимости знакопостоянных рядов. 7

§3. Признаки сходимости знакопеременных рядов. 22

§4. Степенные ряды.. 27

§5. Ряды Маклорена и Тейлора. 32

§6. Применение рядов в приближенных вычислениях. 39

Ответы.. 43

Московский государственный университет тонких химических технологий им. М.В.Ломоносова

Издательско-полиграфический центр

117571, Москва, просп. Вернадского, 86.

cyberpedia.su

Ряд Маклорена и разложение некоторых функций

Изучающим высшую математику должно быть известно, что суммой некоего степенного ряда, принадлежащего интервалу сходимости данного нам ряда, оказывается непрерывное и безграничное число раз дифференцированная функция. Возникает вопрос: можно ли утверждать, что заданная произвольная функция f(х) — это сумма некоего степенного ряда? То есть при каких условиях ф-ия f(х) может быть изображена степенным рядом? Важность такого вопроса состоит в том, что существует возможность приближенно заменить ф-ию f(х) суммой нескольких первых членов степенного ряда, то есть многочленом. Такая замена функции довольно простым выражением — многочленом — является удобной и при решении некоторых задач математического анализа, а именно: при решении интегралов, при вычислении дифференциальных уравнений и т. д.

Доказано, что для некой ф-ии f(х), в которой можно вычислить производные до (n+1)-го порядка, включая последний, в окрестности (α_{— R; x₀+ R) некоторой точки х = α справедливой является формула:}

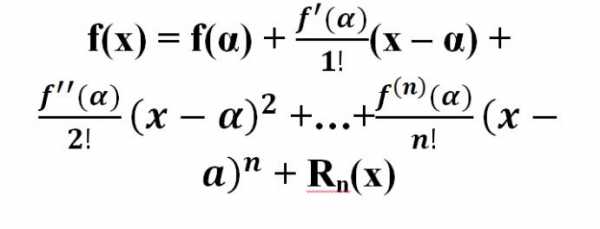Данная формула носит имя известного ученого Брука Тейлора. Ряд, который получают из предыдущего, называется ряд Маклорена:

Правило, которое дает возможность произвести разложение в ряд Маклорена:

Определить производные первого, второго, третьего… порядков.
Высчитать, чему равны производные в х=0.
Записать ряд Маклорена для данной функции, после чего определить интервал его сходимости.
Определить интервал (-R;R), где остаточная часть формулы Маклорена

R_n(х) -> 0 при n -> бесконечности. В случае если таковой существует, в нем функция f(х) должна совпадать с суммой ряда Маклорена.

Рассмотрим теперь ряды Маклорена для отдельных функций.

1. Итак, первой будет f(x) = е^х. Разумеется, что по своим особенностям такая ф-ия имеет производные самых разных порядков, причем f^(k)(х) = e^x, где k равняется всем натуральным числам. Подставим х=0. Получим f^(k)(0) = e⁰=1, k=1,2… Исходя из вышесказанного, ряд е^х^{будет выглядеть следующим образом:}

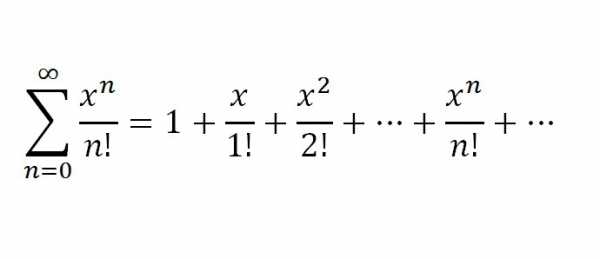2. Ряд Маклорена для функции f(х) = sin х. Сразу же уточним, что ф-ия для всех неизвестных будет иметь производные, к тому же f^‘(х) = cos х = sin(х+п/2), f^»(х) = -sin х = sin(х+2*п/2)…, f^(k)(х) = sin(х+k*п/2), где k равняется любому натуральному числу. То есть, произведя несложные расчеты, можем прийти к выводу, что ряд для f(х) = sin х будет такого вида:

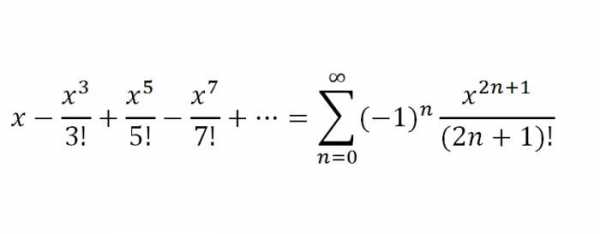3. Теперь попробуем рассмотреть ф-ию f(х) = cos х. Она для всех неизвестных имеет производные произвольного порядка, причем |f^(k)(x)| = |cos(х+k*п/2)|

Итак, мы перечислили важнейшие функции, которые могут быть разложены в ряд Маклорена, однако их дополняют ряды Тейлора для некоторых функций. Сейчас мы перечислим и их. Стоит также отметить, что ряды Тейлора и Маклорена являются важной частью практикума решения рядов в высшей математике. Итак, ряды Тейлора.

1. Первым будет ряд для ф-ии f(х) = ln(1+x). Как и в предыдущих примерах, для данной нам f(х) = ln(1+х) можно сложить ряд, используя общий вид ряда Маклорена. однако для этой функции ряд Маклорена можно получить значительно проще. Проинтегрировав некий геометрический ряд, мы получим ряд для f(х) = ln(1+х) такого образца:

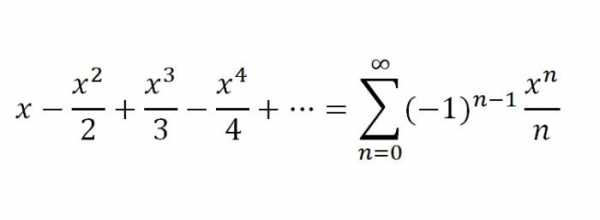
2. И вторым, который будет заключительным в нашей статье, будет ряд для f(х) = arctg х. Для х, принадлежащего промежутку [-1;1] справедливым является разложение:

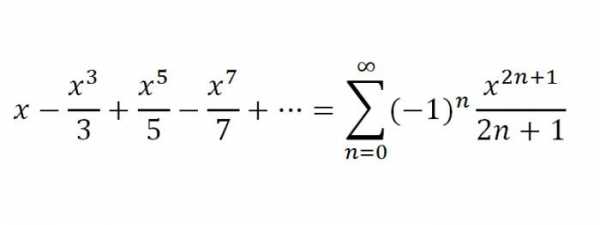
На этом все. В данной статье были рассмотрены наиболее употребляемые ряды Тейлора и Маклорена в высшей математике, в частности, в экономических и технических вузах.

fb.ru

Приближённые вычисления определённых интегралов с помощью рядов. Первая часть.

Развёрнутый вариант оформления

Сокращённый вариант оформления

Чем сокращённый вариант записи лучше развёрнутого?

ЛЕКЦИЯ 12

Теорема Тейлора о разложении функции в степенной ряд

Ряд Маклорена — ПриМат

Примеры приближенного вычисления определенных интегралов по формуле Тейлора

Разложение в ряд Маклорена некоторых функций

Разложение в ряд Маклорена некоторых функций — КиберПедия

Ряд Маклорена и разложение некоторых функций

Добавить комментарий Отменить ответ