7.4. Положительные числовые ряды. Достаточные признаки сходимости
Определение. Числовой ряд (1.1) называется положительным, если все его слагаемые An – положительные числа. Частичная сумма Sn = а1+ а2 + …+ аN такого ряда при любом значении N тоже, естественно, положительна, причем с увеличением номера N она монотонно возрастает. Следовательно, имеются всего две возможности:
1)
2) где S – некоторое положительное число.
В первом случае ряд расходится, во втором сходится. Какая из этих двух возможностей реализуется, зависит, очевидно, от поведения слагаемых ряда при N® ∞. Если эти слагаемые стремятся к нулю, причем делают это достаточно быстро, то ряд будет сходиться. А если они не стремятся к нулю, или стремятся к нему, но недостаточно быстро, то ряд будет расходиться.
Например, у гармонического ряда (1.16) слагаемые хоть и убывают, стремясь к нулю, но делают это довольно медленно. Поэтому гармонический ряд оказался расходящимся. А вот у положительного ряда (1.6) слагаемые стремятся к нулю гораздо быстрее, поэтому он оказался сходящимся.
Еще пример. Ряд вида
(1.18)
Называется Обобщенным гармоническим рядом (при это будет обычный гармонический ряд). Если исследовать его на сходимость – расходимость аналогично тому, как исследовался гармонический ряд (1.16) (с помощью рисунка, подобного рисунку 7.1), то можно установить (попробуйте это сделать самостоятельно), что обобщенный гармонический ряд расходится при (его сумма ) и сходится при (его сумма S – конечное положительное число). И это понятно: при слагаемое обобщенного гармонического ряда убывают медленнее слагаемых гармонического ряда. А так как гармонический ряд расходится (скорость убывания его слагаемых недостаточна для сходимости), то тем более при будет расходиться и обобщенный гармонический ряд (1.18). А при слагаемые ряда (1.18) будут, очевидно, убывать быстрее, чем слагаемые гармонического ряда (1.16). И этой возросшей скорости убывания оказывается достаточно для сходимости ряда (1.18).
Можно эти соображения изложить строже, в виде так называемого Признака сравнения положительных числовых рядов.
Его суть в следующем. Пусть
(1.19)
(1.20)
— два произвольных положительных числовых ряда. И пусть для всех N=1,2,… . То есть (1.20) – ряд с бóльшими членами, чем ряд (1.19). Тогда очевидно, что:
1) Если ряд с бóльшими членами сходится, то и ряд с меньшими членами сходится.
2) Если ряд с меньшими членами расходится (его сумма равна +∞), то и ряд с бóльшими членами тоже расходится (его сумма тем более равна +∞).
3) Если ряд с бóльшими членами сходится (его сумма равна +∞), то про ряд с меньшими членами ничего сказать нельзя.
4) Если ряд с меньшими членами сходится (его сумма – число), то про ряд с бóльшими членами ничего сказать нельзя.
Замечание 1.
Замечание 2. Признак сравнения положительных числовых рядов допускает обобщение. А именно, если существует конечный и отличный от нуля предел
, (1.21)
То есть если
при (1.22)
(Bn эквивалентны Lan при ), то положительные числовые ряды (1.19) и (1.20) сходятся или расходятся одновременно. Данное замечание оставим без доказательства.
Пример 5. Ряд
(1.23)
Расходится (его сумма равна +∞). Действительно, сравнивая этот ряд с гармоническим (1.16), слагаемые которого меньше слагаемых ряда (1.23) для всех N>1, сразу приходим к этому выводу на основании пункта 2 признака сравнения. Его расходимость следует и из того, что это – обобщенный гармонический ряд (1.18) при .
Пример 6. Ряд
(1.24)
— это положительный ряд с меньшим для всех N>1 слагаемыми, чем ряд
(1.25)
Но ряд (1.25) представляет собой сумму бесконечной геометрической прогрессии со знаменателем . Такой ряд, согласно (1.15), сходится и имеет сумму S=1. Но тогда сходится и меньший ряд (1.24), причем его сумма .
Пример 7. Ряд — положительный числовой ряд, у которого слагаемые
при .
Но ряд расходится в силу (1.17). Значит, в соответствии с (1.22), расходится и данный ряд со слагаемыми An.
Признак Даламбера. Этот признак состоит в следующем. Пусть — положительный числовой ряд. Найдем предел Q отношения последующего члена ряда к предыдущему:
(1.26)
Французский математик и механик 19-го века Даламбер доказал, что при Q<1 ряд Сходится; при Q>1 он расходится; при Q=1 вопрос о сходимости — расходимости ряда остается открытым. Доказательство признака Даламбера опускаем.
Пример 8. Исследовать на сходимость – расходимость положительный числовой ряд .
Решение. Применим к этому ряду признак Даламбера. Для этого по формуле (1.26) вычислим Q:
Так как , то данный ряд сходится.
Интегральный признак Коши. Этот признак состоит в следующем. Если члены An положительного ряда монотонно убывают, то этот ряд и несобственный интеграл сходятся или расходятся одновременно. Здесь — непрерывная монотонно убывающая функция, принимающая при X = N значения An членов ряда.
Доказательство интегрального признака Коши, как и признака Даламбера, опустим. Это доказательство, кстати, использует в принципе ту же геометрическую идею, что была применена при доказательстве расходимости гармонического ряда (1.16).
Пример 9. Исследуем на сходимость – расходимость обобщенный гармонический ряд (1.18). При мы получаем гармонический ряд (1.16), который, как мы доказали, расходится. При ряд (1.18) тем более будет расходиться, так как его члены больше членов гармонического ряда. Осталось исследовать случай . Применим к ряду (1.18) при интегральный признак Коши. Для этого вычислим несобственный интеграл
.
В результате получили конечное число . Таким образом, сходится. Но тогда, по интегральному признаку Коши, сходится и ряд (1.18). То есть
(1.27)
| < Предыдущая | Следующая > |
|---|
Признаки сходимости Даламбера и Коши
Ряд вида
называется положительным, если все его члены неотрицательные
Для определения сходимости в литературе собраны правила которые позволяют это быстро определить. Рассмотрим по очереди признаки сходимости числовых рядов
Признак сравнения
Рассмотрим два ряда с положительными членами
Для них выполняются следующие утверждения:
1. Если члены ряда не больше соответствующих членов сходящегося ряда () то ряд сходится.
Если каждый член ряда больше (или ровный) соответствующего члена росходящегося ряда то ряд разбегается.
———————————————
Пример 1.
Исследовать на сходимость ряды
1)
2)
Решение.
1) Сравним заданный ряд
с рядом геометрической прогрессии знаменатель которой равен
Каждый член первого ряда меньше соответствующего член ряда геометрической прогрессии, который сбегается, поскольку
По признаку сравнения первый ряд сходится.
2) Члена данного ряда сравниваем с соответствующими гармонического ряда. Для произвольного выполняется неравенство
Так как гармонический ряд разбежный то в соответствии с признаком сравнения заданный ряд также разбежный.
———————————————
Предельный признак сравнения
Пусть ряды и положительные, а также существует предельная граница
причем , тогда оба ряда или одновременно совпадающие или одновременно разбежные.
———————————————
Пример 2.
Исследовать на сходимость ряд
Решение.
Для сравнения выберем ряд совпадающей геометрической прогрессии. Применяя предельный признак будем иметь
Поскольку оба ряды ведут себя равносильно , а геометрический ряд сходится, то и рассмотренный ряд также сходится.
———————————————
Признак Даламбера
Пусть члены ряда
положительные и отношение -го члена до -го имеет предел при
Если то ряд сходится,
если — ряд расходится.
При надо применять другой признак сходимости, поскольку данный признак не может определить сходится ряд или расходится.
———————————————
Пример 3.
Исследовать на сходимость ряды
1)
2)
3)
Решение.
1) Найдем границу отношения члена до -го при
Поскольку то ряд сходится.
2) Вычислим границу
Ряд сходящийся, так как
3) Применим признак Даламбера
Видим что ряд сходящийся поскольку
——————————————
Радикальный признак Коши
Если для ряда положительными членами существует граница
то при ряд сходится, а при — разбегається.
При нужно применять другой признак сходимости.
——————————————-
Пример 4.
Исследовать на сходимость ряды
1)
2)
Решение.
1) Применим признак Коши
Ряд совпадающий поскольку
2) Вычислим границу
Данный ряд также совпадающий, поскольку
———————————————
Интегральный признак Коши
Пусть задан ряд
причем функцияположительная, непрерывная и монотонно нисходящая функция от переменной . Тогда
1) ряд совпадающий, если несвойственный интеграл
совпадающий;
2) ряд разбежный когда интеграл разбежный.
Под сходимостью интегралу следует понимать его ограниченность, то есть
Рассмотрим примеры применения интегрального признака Коши.
———————————————
Пример 5.
Исследовать на сходимость
1)
2)
3)
Решение.
1) Применим интегральный признак Коши
Ряд совпадающий поскольку интеграл совпадающий.
2) Найдем интеграл
По интегральному признаку Коши ряд разбежный.
3) Вычислим интеграл
Данный ряд совпадающий.
———————————————-
——————————
yukhym.com
Признак сравнения рядов для выяснения их сходимости
Применение признака сравнения заключается в том, что исследуемый ряд сравнивают с рядом, сходимость которого заранее известна.
Непосредственное сравнение членов рядов
Пусть даны два ряда с положительными общими членами и . Пусть для этих рядов выполняется неравенство , то есть члены первого ряда не превосходят соответствующих членов второго ряда.
Тогда из сходимости второго ряда (ряда с бОльшим общим членом) следует сходимость первого ряда, а из расходимости первого ряда (ряда с меньшим общим членом) – расходимость второго ряда.
Предел отношения общих членов рядов
Пусть даны два ряда с положительными общими членами и . Если , то есть предел отношения общих членов ряда равен конечному и отличному от нуля числу, то оба ряда ведут себя одинаково: или оба сходятся, или оба расходятся.
Трудность применения на практике признака сравнения состоит в необходимости иметь «запас» рядов, сходимость (или расходимость) которых известна, а среди них подобрать такой, чтобы выполнялось условие. Для сравнения часто используются:
- геометрический ряд , который сходится, если |q| < 1 и расходится, если |q| ≥ 1;
- обобщённый гармонический ряд , который сходится, если p > 1 и расходится, если p ≤ 1;
- ряд .
Пример 1. Исследовать сходимость ряда
Решение. Члены данного ряда не превосходят соответствующих членов сходящегося геометрического ряда с общим членом
Согласно признаку сравнения, данный ряд также сходится.
Решение. Так как
то члены данного ряда меньше членов
сходящегося ряда. На основании признака сравнения данный ряд также сходится.
Пример 3. Исследовать сходимость ряда
Решение. Сравним данный ряд с гармоническим рядом. Первые их члены совпадают, а остальные члены данного ряда больше соответствующих членов расходящегося гармонического ряда:
поскольку
Согласно признаку сравнения, данный ряд также расходится.
Пример 4. Исследовать сходимость ряда
.
Решение. Так как , а ряд сходится как геометрический ряд с , то по признаку сравнения данный ряд также сходится.
Пример 5. Исследовать сходимость ряда
.
Решение. Выясним значение предела отношения общих членов данного ряда и гармонического ряда :
Так как предел отношения общих членов данного ряда и второго ряда, который расходится, отличен от нуля и не равен бесконечности, то оба ряда ведут себя одинаково. То есть данный ряд так же расходится.
Пример 6. Исследовать сходимость ряда
.
Решение. Выясним значение предела отношения общих членов данного ряда и гармонического ряда :
Так как предел отношения общих членов данного ряда и второго ряда, который расходится, отличен от нуля и не равен бесконечности, то оба ряда ведут себя одинаково. То есть данный ряд так же расходится.
Пример 7. Исследовать сходимость ряда
.
Решение. Выясним значение предела отношения общих членов данного ряда и обобщённого гармонического ряда , который расходится, так как . Искать предел будем, учитывая, что , если , поэтому , если . Итак, предел:
.
Так как предел отношения общих членов данного ряда и второго ряда, который расходится, отличен от нуля и не равен бесконечности, то оба ряда ведут себя одинаково. То есть данный ряд так же расходится.
Всё по теме «Ряды»
function-x.ru
Сходящиеся и расходящиеся числовые ряды. Необходимое условие сходимости — ПриМат
Пусть дана последовательность , где
Символ вида (*) называется числовым рядом и обозначается, при этом называется общим членом ряда. Ряд (*) называется сходящимся, если существует предел , где это n-ая частичная сумма ряда, .
При этом, число называется суммой ряда, и пишут .
Если же предел частичных сумм не существует или бесконечен, то говорят, что ряд (*) расходится и никакой суммы ряду не присваивается.
Пример:
Исследовать на сходимость ряд
Запишем n-ю частичную сумму и с упростим выражение с помощью формулы суммы геометрической прогрессии.
, , при , при . , при . не существует, при .Таким образом, при ряд сходится, а при — расходится.
Если ряд сходится, то необходимо .
Доказательство.
Если ряд сходится, то , следовательно .
Рассмотрим , где , — общий член ряда, . Теорема доказана.
Пример:
Исследовать на сходимость ряд
.Необходимое условие не выполняется: . Следовательно, ряд расходится.
Литература
Сходящиеся и расходящиеся ряды
Лимит времени: 0
Информация
Тест на проверку знаний о сходящихся и расходящихся рядах, а также необходимого условия сходимости.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
ib.mazurok.com
Признак Даламбера сходимости ряда
Исследование сходимости рядов является важным с точки зрения их оценки и необходимым в случае вычисления суммы ряда. Признаков сходимости рядов несколько, популярный и достаточно прост в применении для рядов с положительными членами — признак сходимости Даламбера. Ниже будет разобран ряд примеров на установление сходимости ряда по признаку Даламбера, советую для себя взять максимум полезного.
Напомним что предпосылками для применения признака Даламбера служит наличие степенной зависимости (2, 3, a в степени n) или факториалов в формуле общего члена ряда. Будет это знаменатель или числитель дроби совсем не имеет значения, важно что имеем подобную зависимость, ну или факториал и степенную зависимость в одном наборе. С факториалами у многих на первых порах возникают проблемы но с практикой Вы заметете что ничего сложного в факториалах нет. Надо только расписать факториал подробно до тех пор когда в числителе или знаменателе дроби поучим одинаковые множителе. На словах это звучит не всем понятно, но следующие примеры помогут Вам в этом разобраться. Ну и самые сложные примеры предполагают наличие комбинаций факториалов и степенных зависимостей, два или более факториала, тоже и для степенной фунции, всевозможные цепочки множителей и другие каверзные комбинации. Ниже приведены базовые примеры с которых и начинается практика проверки сходимости ряда по Даламберу.
Пример: 2.5 Исследовать сходимость рядов
а)
Вычисления: Поскольку данный ряд имеет положительные члены то исследовать его на сходимость можем с помощью признака Даламбера:
Если А<1 ряд сходящийся, А>1 — ряд расходящийся и при A=0 следует использовать другие признаки сходимости рядов.
Записываем общий член ряда и следующий, идущий после него
И находим границу их доли
Поскольку граница бесконечна то по признаку Даламбера ряд расходящийся. Если искать суму ряда то она будет бесконечная.
б)
Вычисления: Члены ряда положительные поетому исследуем на сходимость по признаку Даламбера — записываем формулы последовательных членов ряда
И находим предел отношения следующего члена к предыдущему при n стремящемуся к бесконечности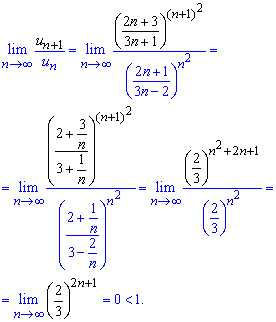
Граница равна нулю так как показатель стремится к бесконечности, а в скобках имеем значение меньше единицы.
По теореме Даламбера A = 0 <1 ряд сходится!
Пример: 2.8 Исследовать ряды на сходимость:
а)
Вычисления: Как Вы уже убедились все примеры которые здесь рассматриваются следует проверять по признаку Даламбера.
В результате упрощения придем ко второму замечательному пределу — экспоненте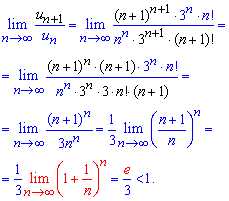
В общем граница меньше единицы следовательно ряд сходится.
б)
Вычисления: Для проверки на сходимость ряда по признаку Даламбера вычисляем предел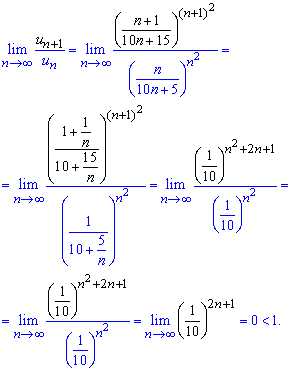
Предел равен 0 (A = 0 <1) следовательно ряд сходится!
Пример: 2.14 Исследовать ряд на сходимость
а)
Вычисления: Находим предел следующего члена ряда к предыдущему
Для удобства чтения формул следующий член ряда выделенный в формулах черным цветом. Хорошо разберитесь как делить факториал на факториал, как показывает статистика множество неверных ответов Вы у Вас выходит в примерах с факториалами.
По признаку Даламбера ряд сходится.
б)
Вычисления: Записываем формулу общего члена ряда и последовавшего за ним
Подставляем их в формулу Даламбера и вычисляем предел 
Граница равна нулю 0 <1, а это значит что данный ряд сходящийся.
Пример: 2.16 Исследовать ряд на сходимость:
а)
Вычисления: По признаку Даламбера проверяем границу общего члена ряда на ограниченность
Превратив множители в числителе и знаменателе дроби сведем функцию в скобках ко второму замечательному пределу
Поскольку граница меньше единицы
то согласно теореме Даламбера ряд сходящийся.
б)
Вычисления: Задан числовой степенной ряд с положительными членами. Найдем предел отношения последующего члена ряда к предыдущему 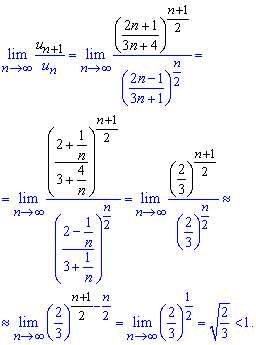
При исчислении границы считаю все моменты Вам понятны, если нет то Вам нужно прочесть статьи с категории «предел функций».
Получили предел меньше единицы,
следовательно ряд сходится за Даламбером .
Пример: 2.26 Исследовать сходимость ряда:
а)
Вычисления: Для применения признака Даламбера выпишем общий член ряда и последующий за ним
Далее подставим их и найдем предел дроби
Предел равен A = 3/2> 1, а это значит что данный ряд расходящийся.
б)
Вычисления: Записываем два последовательных члены положительного ряда
Находим границу для оценки сходимости ряда по теореме Даламбера.
В ходе вычислений получим второй замечательный предел (экспоненту) как в числителе, так и в знаменателе. Результирующая граница больше единицы , следовательно делаем вывод о расхождении ряда.
yukhym.com
