«Сложение и вычитание рациональных чисел»
Цель: содействие развитию самостоятельности учащихся, их умению работать с учётом индивидуальных способов проработки учебного материала, способности анализировать свой ответ и ответ другого учащегося.
Учебный элемент №1.
“Сложение отрицательных чисел”.
Цель: закрепить правило сложения отрицательных чисел при помощи координатной прямой.
Указания учителя:
Вспомните правило сложения чисел при помощи координатной прямой. Для этого прочитайте текст на стр.181 – 183 учебника. Выполните письменно самостоятельную работу.
Задания для самостоятельной работы (на 7 мин.).
С помощью координатной прямой сложите числа.
| 1 вариант | 2 вариант |
| а) 2 и – 5 (1 балл) | а) 8 и – 3 (1 балл) |
| б) – 4 и 6 (1 балл) | б) – 2 и 6 (1 балл) |
| в) – 3 и – 2 (1 балл) | в) – 5 и – 4 (1 балл) |
| г) – 1 и – 4 (1 балл) | г) – 6 и – 2 (1 балл) |
| д) – 1,5 и 3 (2 балла) | д) – 3,5 и 2,5 (2 балла) |
| е) 4 и – 5,5 (2 балла) | е) 4,5 и – 3 (2 балла) |
Указания учителя:
Проверьте и оцените свою работу, правильные
ответы возьмите у учителя. Исправьте ошибки, если
они есть, поставьте количество баллов в
оценочные листы.
Исправьте ошибки, если
они есть, поставьте количество баллов в
оценочные листы.
Если вы набрали 6 баллов или больше, то переходите к следующему учебному элементу. Если меньше, то решайте задание из другого варианта, аналогичных тем, в которой была допущена ошибка, и проставьте набранные баллы в графу “корректирующие задания”.
Ответы к Учебному элементу № 1.
1вариант а) – 3; б) 2; в) – 5; г) – 5; д) 1,5; е) – 1,5
2вариант а) 5; б) 4; в) – 9; г) – 8; д) – 1; е) 1,5
| Оценочный лист учащегося | |||
| Фамилия | |||
| Имя | |||
| Учебные элементы | Количество баллов за основные задания | Корректирующие задания | Общее количество баллов за этап |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| Итоговое количество баллов | |||
| Оценка | |||
Учебный элемент №2
“Сложение отрицательных чисел”
Цель: научиться складывать отрицательные
числа по определению.
Указание учителя:
Прочитайте внимательно данные ниже пояснения. Выполните самостоятельную работу.
Правило сложения отрицательных чисел
Чтобы сложить два отрицательных числа, надо:
1) сложить их модули;
2) поставить перед полученным числом знак “– “.
Например:
1. – 8,7 + (– 3,5) = – (8,7+3,5) = – 12,22. – 2 1/4 + (– 3 1/8) = – (2 1/4 + 3 1/8 ) = – (2 2/8 +3 1/8) = – 5 3/8
Задания самостоятельной работы
Выполните сложение.
| 1 вариант | 2 вариант |
| а) – 35 + (– 9) (1 балл) | а) – 7 + (– 14) (1 балл) |
| б) – 17 + (– 8) (1 балл) | б) – 5 + (– 238) (1 балл) |
| в) – 1,6 + (– 4,7) (2 балла) | в) – 5,6 + (– 2,4) (2 балла) |
| г) – 8,8 + (– 4,2) (2 балла) | г) – 8,8 + (– 4,2) (2 балла) |
| д) – 3/7 + (– 2/3) (3 балла) | д) – 5/9 + (– 1/3) (3 балла) |
| е) – 1 3/8 + (– 2 5/6) (4 балла) | е) – 5 1/12 + (– 3 1/20) (4 балла) |
Указание учителя:
Проверьте и оцените свою работу, правильные
ответы возьмите у учителя. Исправьте ошибки, если
они есть, проставьте количество баллов в
оценочные листы. Если вы набрали 9 баллов, то
переходите к следующему учебному элементу. Если
меньше, то решайте задания другого варианта,
аналогичное тому заданию, в котором ошиблись.
Исправьте ошибки, если
они есть, проставьте количество баллов в
оценочные листы. Если вы набрали 9 баллов, то
переходите к следующему учебному элементу. Если
меньше, то решайте задания другого варианта,
аналогичное тому заданию, в котором ошиблись.
Ответы к Учебному элементу № 2.
1 вариант: а) – 44; б) – 25; в)– 6,3; г) – 13; д) – 1 2/21; е) – 4 5/24
2 вариант: а) – 21; б) – 243; в) – 8; г) – 13; д) – 8/9; е) – 8 2/15
Учебный элемент №3
“Сложение чисел с разными знаками”
Цель: научиться складывать числа с разными знаками.
Указания учителя:
Внимательно прочитайте данные ниже пояснения и выполните задания.
Правило сложения чисел с разными знаками.
Чтобы сложить два числа с разными знаками,
надо:
1) из большего модуля слагаемых вычесть меньший
модуль;
2) поставить перед полученным числом знак того
слагаемого, модуль которого больше.
Обычно сначала определяют и записывают знак суммы, а потом находят разность модулей.
Например:
- 6,1 + (– 4,2) = + (6,1 – 4,2) = 1,9 или короче 6,1+ (– 4,2) = 6,1 – 4,2 = 1,9
- – 3 2/7 + 4 5/7 = 4 5/7 – 3 2/7 = 1 3/7
- 2,7 + (– 3,4 ) = – ( 3,4 – 2,7 ) = – 0,7
- – 8 5/4 + 2 1/3 = – (8 4/5 – 2 1/3) = – (8 12/15 – 2 5/15) = – 6 7/15
Задания для самостоятельной работы
Выполните сложение:
| 1 вариант | 2 вариант |
| а) 26 + (– 6) (2 балла) | а) – 17 + 30 (2 балла) |
| б) – 70 +50 (2 балла) | б) 80 + (– 120) (2 балла) |
| в) – 6,3 + 7,8 (3 балла) | в) 1 + (– 0,39) (3 балла) |
| г) – 9 + 10,2 (3 балла) | г) 0,3 + (– 1,2) (3 балла) |
| д) 5/9 + (– 8/9) (3 балла) | д) 3/4 + (– 2/3 ) (3 балла) |
| е) – 5/8 + 3/4 (3 балла) | е) – 4/5 + 2/3 (3 балла) |
| ж) – 3 3/4 + 2 1/2 (4 балла) | ж) 2 4/7 + (– 3 5/14) (4 балла) |
Указание учителя:
Если набрано 18 баллов, то переходите к
следующему элементу. Если меньше, то перерешайте
соответствующие задания другого варианта.
Если меньше, то перерешайте
соответствующие задания другого варианта.
Ответы к Учебному элементу № 3.
1 вариант: а) 20; б) – 20; в) 1,5; г) 1,2; д) –
3/9 = – 1/3; е) 1/8; ж) – 1 1/4
2 вариант: а) 13; б) – 40; в) 0,16; г) – 0,9; д) 1/12; е) – 2/15; ж) – 1
Учебный элемент №4
“Вычитание”
Цели:
- Научиться вычитать отрицательные числа.
- Закрепить навык вычитания.
Указания учителя:
Внимательно прочитайте данные ниже пояснения и выполните задания.
Вычитание отрицательных чисел имеет тот же
смысл, что и вычитание положительных чисел: по
заданной сумме и одному из слагаемых находят
другое слагаемое. Чтобы найти искомое слагаемое,
можно прибавить к сумме число, противоположное
известному слагаемому.
Например: 8 + 3 = 11, и потому 11 – 8 = 3. Но 11 + (– 8) = 3.
Правило вычитания отрицательных чисел:
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: а – b = а + (– b).
Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.
Например:
- – 18 – 14 = – 18 + (– 14) = – (18 + 14) = – 3
- – 8 + 6 – k = – 8 + 6 + (– k)
Разность двух чисел положительна, если уменьшаемое больше вычитаемого, и отрицательна, если уменьшаемое меньше вычитаемого. Если уменьшаемое и вычитаемое равны, то их разность равна нулю.
Например:
- 25 – 32 = 25 + (– 32 ) = – ( 32 – 25 ) = – 7
- – 5,5 – 2,8 = – 5,5 + (– 2,8) = – (5,5 + 2,8) = – 8,3
- 48 – (– 15) = 48 + 15 = 63
Задача: Чему равна длина отрезка АВ, если А (– 5) и В (9)?
Решение: Длина отрезка АВ показывает, на
сколько единичных отрезков надо переместить
вправо точку А, чтобы она перешла в точку В, т. е.
сколько надо прибавить к числу – 5, чтобы
получилось число 9. Поэтому если обозначить длину
отрезка АВ буквой х, то – 5 + х = 9.
е.
сколько надо прибавить к числу – 5, чтобы
получилось число 9. Поэтому если обозначить длину
отрезка АВ буквой х, то – 5 + х = 9.
х = 9 – (– 5)
х = 9 + 5
х = 14, значит, длина отрезка АВ равна 14 единичным отрезкам.
Чтобы найти длину отрезка на координатной прямой надо из координаты его правого конца вычесть координату его левого конца.
Задания для самостоятельной работы.
| 1 вариант | 2 вариант |
1. Выполните вычитание. |
|
| а) 10 – (– 3) (1 балл) | а) 21 – (– 19) (1 балл) |
| б) 12 – (– 14) (1 балл) | б) 9 – (– 9) (1 балл) |
| в) – 1,4 – 1,4 (2 балла) | в) – 2,5 – 8,5 (2 балла) |
| г) – 5,6 – (– 3,1) (2 балла) | г) 0 – (– 40,6) (2 балла) |
| д) 5/12 – (– 1/12) (3 балла) | д) – 7/15 – (– 2/15) (3 балла) |
| е) – 4/9 – 2/3 (3 балла) | е) – 1 3/8 – 1/4 (3 балла) |
| ж) 1 5/11 – 2 3/22 (4 балла) | ж) – 7 8/9 – (– 9 1/6) (4 балла) |
2. Найдите расстояние между
точками А (а) и В (b), если: Найдите расстояние между
точками А (а) и В (b), если: |
|
| а) а = 2; b =8 (2 балла) | а) а = – 3; b = – 5 (2 балла) |
| б) а = – 1; b = 6 (2 балла) | б) а = 5; b = – 4 (2 балла) |
| в) а = 8,1; b = – 2,5 (3 балла) | в) а = 3,2; b = – 4,7 (3 балла) |
Указания учителя:
Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, если они есть. Поставьте баллы в оценочные листы. Если набрали 21 балл, то можно переходить к следующему учебному элементу. Если набрано менее 21 балла, то нужно решить соответствующие задания из другого варианта.
Ответы к Учебному элементу № 4.
1 вариант: 1а) 13; б) 26; в)– 2,8; г) – 2,5; д) 1/2; е) – 1 1/9; ж) – 15/22. 2а) 6; б) 7; в) 5,6
2 вариант: 1а) 40; б) 18; в) – 11; г) 40,6; д) – 1/3; е) – 1 5/8; ж) 1 5/18.2а) – 2; б) – 9; в) – 7,9
Учебный элемент №5
“Самостоятельный выбор решения”
Указания учителя:
Вы прошли первый уровень усвоения материала. Теперь вам самостоятельно придётся выбрать способ решения того или иного задания. Вспомните все правила сложения и вычитания отрицательных чисел. Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
| 1 вариант | 2 вариант |
| 1. Сравните: | |
| а) – 17 + (– 31) и – 17 (2 балла) | а) – 22 + (– 35) и – 35 (2 балла) |
| 2. Найдите значение выражения х + у + (– 16), если: | |
| а) х = – 17; у = – 29 (3 балла) | а) х = – 9; у = – 7,4 (3 балла) |
3. |
|
| а) х + (– 3) = – 11 (2 балла) | а) – 5 + у = 15 (2 балла) |
| б) т + ( – 12) = 2 (2 балла) | б) 3 + п = – 10 (2 балла) |
4. Решите уравнение и выполните проверку: |
|
| а) – 2 + х = 4,3 (3 балла) | а) 8,1 +у = – 6 (3 балла) |
| б) 5 – х = 1,7 (3 балла) | б) 4 – у = – 2 2/3 (3 балла) |
| в) х + 0,4 = – 1 2/3 (3 балла) | в) у + 7/18 = – 2/3 (3 балла) |
Указания учителя:
Проверьте и оцените свою работу, правильные
ответы возьмите у учителя. Исправьте ошибки, если
они есть. Поставьте баллы в оценочные листы. Если
набрано 15 баллов или больше, то переходите к
следующему учебному элементу, если меньше, то
решайте задания другого варианта, аналогичные
тем заданиям, в которых была допущена ошибка.
Ответы к Учебному элементу № 5.
1 вариант: 1а) < ; 2а) – 6,2; 3а) – 8; б) 14; 4 а) х = 6,3; б) х = 3,3; в) х = – 2 1/15
2 вариант: 1а) <; 2а) – 32,5; 3а) 20; б) – 13; 4а) у = – 14,1; б) у = 6 2/3; в) у = – 1 1/18
Учебный элемент № 6
“Применение знаний в сложной ситуации”
Указание учителя:
МОЛОДЦЫ! Вы освоили решение заданий второго уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях.
Задания для самостоятельной работы.
1.Найдите значение выражения: |
|||
| а) (– 3,25 + (– 1 3/4)) + (– 1 2/3 + (– 1 4/9)) (3 балла) | ж) – 7 – (– 12 + 13) (2 балла) | ||
| б) (– 2/3 + (– 2/15)) + (– 1,85 + (– 1,35)) (3 балла) | з) 4,1 – (– 1,8 + 2,5) (3 балла) | ||
| в) (2/5 + (– 0,5)) + (– 1 1/4) (4 балла) | и) (14,5 – 85) + 55,5 (3 балла) | ||
| г) (0,6 + 2/3) + (– 2 1/15) (4 балла) | к) (– 1 2/3 – 2 1/3) + 2,5 (3 балла) | ||
| д) – 3,7 + (– 5 11/30 + 3 4/15) (4б ) | л) (– 4 2/7 + 3 3/14) – 1 (3 балла) | ||
| е) – 50 + (37 + 30) (2 балла) | м) (– 2 2/5 – (– 3 3/8– 21/4 ) (3 балла) | ||
2. |
|||
| а) 7,8 – х = 9,3 (2 балла) | б) у – (– 17,85) = 12 (2 балла) | в) 5 5/12 + х = – 3 1/3 (3 балла) | |
Указание учителя:
В случае затруднения воспользуйтесь учебником или консультацией учителя.
Проверьте и оцените свои работы. Исправьте ошибки, если они есть; подсчитайте количество баллов. Проставьте количество баллов в оценочные листы. Оцените свои работы.
Ответы к Учебному элементу № 6.
1а) –8 1/9; б) –4; в) – 7/20; г) – 4/5; д) –6; е) 17; ж) –8; з) 3,4; и) – 15; к) –1,5; л) –2 4/7; м) 3 9/40
2а) х = – 1,5; б) у = – 5,85; в) х = – 8 9/12
Z190: модуль сложения и вычитания с гальванической развязкой Seneca.
 КИП-Сервис: промышленная автоматика
КИП-Сервис: промышленная автоматикаГлавная ПЛК, HMI, ввод-вывод Seneca Преобразователи / разветвители сигналов Z190
| Наименование | Тип документа | Размер | Тип файла |
|---|---|---|---|
| Паспорт SENECA для серии Z, K, T, Z-PC, только внесенные в ГРСИ (Формат A4) | Паспорт | 117 KB | |
| Методика поверки преобразователей Seneca серий Z, K, T | Техническое описание | 1 MB | |
| ТО к Z190 | Техническое описание | 237 KB | |
| Seneca: Модули гальванической развязки с универсальными входами/выходами, нормирующие преобразователи сигналов | Каталог | 9 MB | |
| Библиотека EPLAN для модулей Seneca | Библиотека E-PLAN | 1 MB | zip |
| 3D модель Z190 | CAD библиотека | 213 KB | zip |
| Свидетельство об утверждении типа СИ: преобразователи Seneca Z, K, T | Свидетельство об утверждении типа СИ | 11 MB |
Документация и ПО
7 файлов, 23 MB
| Наименование | Наличие | Цена с НДС | |
|---|---|---|---|
Z190 Модуль вычитания или сложения 2-х анал.сигн-в,гальв.разв.1,5кВ вх/вых/пит.Вх.1,2:0/4..20мА,0/1..5В,0/2..10В Вых:0/4..20 мА,0/1..5В,0/2..10В,пит19..40В | Под заказ | 21 673 | Купить |
Процесс выпаривания сиропа при изготовлении сахара происходит под вакуумом. Чтобы знать уровень сиропа в емкости, необходимо учитывать уровень вакуума. Датчики давления имеют разные пределы измерения: -1…0 бар и -1…1 бар. Модуль Z190 не только вычисляет разницу сигналов, но и автоматически учитывает шкалу каждого датчика.
Измерение уровня в резервуарах с вакуумом или поверхностным давлениемИзмерение разницы температур в емкости на разных высотах
- Трехканальная гальваническая развязка ~1500 В AC (питание / вход / выход)
- Каждый вход имеет индивидуальные настройки: тип сигнала (ток и напряжение), верхний предел измерений
- Программируемый DIP-переключателями выход по току 0…20, 4…20 мА (активный или пассивный),
или по напряжению 0…5, 1…5, 0…10, 2…10 В - Два программируемый DIP-переключателями независимых входа по току 0…20, 4…20 мА (активный или пассивный),
или по напряжению 0…5, 1…5, 0…10, 2…10 В
| Параметр | Значение |
|---|---|
| Питание | =19…40 В, ~19…28 В при 50/60 Гц, максимальное потребление: 2,5 Вт |
| Погрешность калибровки | 0,2% |
| Погрешность температурного коэффициента | 0,02%/°С |
| Нелинейность | 0,05% |
| ЭМП | 0,3% |
| Два независимых входа, каждый из которых настраивается: | |
| По току | активный 0…20 мА или 4…20 мА (питание петли =20 В не стабилизированное) пассивный: входное сопротивление 100 Ом |
| По напряжению | 0…5 В, 1…5 В, 0…10 В и 2…10 В (входное сопротивление > 500 кОм) |
| Выходы настраиваются: | |
| По току | активный 0…20 мА или 4…20 мА (сопротивление нагрузки > 600 Ом) пассивный |
| По напряжению | 0…5 В, 1…5 В, 0…10 В и 2…10 В (входное нагрузки > 2 кОм) |
| Условия эксплуатации | |
| Температура | 0…50 °С |
| Влажность | 30…90 % при температуре 40 °C без конденсации |
| Другие характеристики | |
| Защита входа / выходов / источника питания от импульсных перенапряжений |
400 Вт/мс |
| Стандарты | EN50081-2, EN50082-2, EN61010-1 |
Для электрических соединений мы рекомендуем использовать экранированные провода. Экран должен быть заземлен с использованием кабеля, специально выделенного для модуля. Кроме этого, избегайте прокладки проводов рядом с силовыми линиями таких устройств, как инверторы, двигатели, индукционные печи и т.п.
Экран должен быть заземлен с использованием кабеля, специально выделенного для модуля. Кроме этого, избегайте прокладки проводов рядом с силовыми линиями таких устройств, как инверторы, двигатели, индукционные печи и т.п.
Источник питания
Напряжение источника питания должно быть в диапазоне =19…40 В (любой полярности) или ~19…28 В. Напряжение не должно превышать диапазон, это может привести к серьезным повреждениям модуля. Модуль должен быть защищен от источника питания 2-3 подходящим предохранителем.
Вход 1: подключение и настройка DIP-переключателей
Активный по токуПассивный по токуПо напряжениюВход 2: подключение и настройка DIP-переключателей
Активный по токуПассивный по токуПо напряжениюВыход: подключение и настройка DIP-переключателей
Активный по токуПассивный по токуПо напряжению выходИспользуя этот веб-сайт, Вы даете согласие на обработку файлов cookie, пользовательских данных в целях корректного функционирования сайта и проведения статических исследований.
абстрактная алгебра — определение прямой суммы модулей?
спросил
Изменено 8 лет, 5 месяцев назад
Просмотрено 7к раз
$\begingroup$
Я только начал изучать модули и пытаюсь понять определение прямой суммы модулей, но у меня возникли проблемы, так как разные источники дают разные определения, например:
MIT говорит:
Прямая сумма Mλ есть подмножество ограниченных векторов:
$\bigoplus$ $M_{λ}$ := {($m_{λ}$) | $m_{λ}$ = 0 почти для всех λ}
Wolfram MathWorld говорит:
Прямая сумма модулей A и B равна модулю
A $\bigoplus$ B={a$\oplus$b |a $\in$ A,b $\in$ B},
, где все алгебраические операции определены покомпонентно.
[Что такое $\oplus$?]
В моих конспектах лекций написано:
Определить прямую сумму модулей как заданное теоретическое произведение с естественное сложение и умножение на элементы A.
Единственный, который имеет для меня смысл, это последний, но он, кажется, не согласуется с двумя другими сумма
$\endgroup$
3
$\begingroup$
Пусть $A,B$ — $R$-модули. Прямая сумма $A\oplus B= \{(a,b) | a\in A, b\in B \}$ — это модуль относительно покомпонентных операций: $(a_1,b_1)+(a_2,b_2)=(a_1+a_2,b_1+b_2)$ и $r(a,b )=(ra,rb)$.
Это продолжается до прямой суммы конечного числа $R$-модулей. Однако для прямой суммы бесконечного числа $R$-модулей существует дополнительное требование, чтобы элементы имели все компоненты, кроме конечного, равные $0$.
$\endgroup$
$\begingroup$
Для конечного числа слагаемых все совпадает. Тогда $A\oplus B$ — это то, что вы написали, и это верно точно так же для конечного числа слагаемых. Для бесконечного числа слагаемых существуют различия, и нам нужно различать $\oplus M_i$ и $\prod M_i$. Это объясняется в книгах по кольцам и модулям. Хорошим примером является свободный $\mathbb{Z}$-модуль $\oplus_i \mathbb{Z}$, тогда как модуль $\prod_i \mathbb{Z}$ , а не свободен, следовательно, не проективен.
Тогда $A\oplus B$ — это то, что вы написали, и это верно точно так же для конечного числа слагаемых. Для бесконечного числа слагаемых существуют различия, и нам нужно различать $\oplus M_i$ и $\prod M_i$. Это объясняется в книгах по кольцам и модулям. Хорошим примером является свободный $\mathbb{Z}$-модуль $\oplus_i \mathbb{Z}$, тогда как модуль $\prod_i \mathbb{Z}$ , а не свободен, следовательно, не проективен.
$\endgroup$
2
$\begingroup$
Во втором определении $\oplus$ в наборе — это просто символ, а $a\oplus b$ — это просто другой способ записи пары $(a,b)$, который должен объяснить вам, почему это определение то же самое, что и в ваших конспектах лекций. Первое определение немного отличается, потому что оно говорит вам, как определить прямую сумму любого (возможно, бесконечного) набора модулей. Если $\lambda\in\{1,2\}$, то условие в определении пусто, и у вас есть набор пар $(m_1,m_2)$ с $m_i\in M_i$, как и в двух других определения.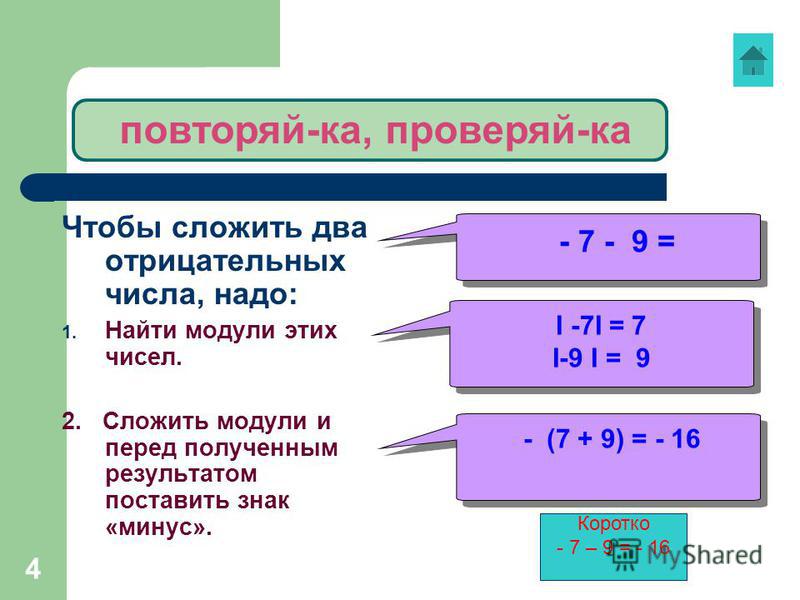 (Это первое определение не обсуждает операции, но опять же они являются «естественными»).
(Это первое определение не обсуждает операции, но опять же они являются «естественными»).
Вы можете определить прямую сумму любого конечного набора модулей индуктивно, используя определения 2 и 3, но первое из них — единственное, которое говорит вам, что делать, если у вас есть бесконечное множество модулей.
$\endgroup$
теория колец — Каково определение прямой суммы подмодулей?
$\begingroup$
Для данного кольца $R$ и $M_1,\ldots,M_n$ $R$-подмодулей $R$-модуля $M$ каково определение этого множества? 9n M_i$$
Откуда я читаю, кажется, что это: $M_1 + \cdots + M_n$ с взаимно непересекающимися $M_i$. Но я во многих местах читал, что это прямое произведение $M_1\times\cdots\times M_n$.
Так что же это? Спасибо за вашу помощь.
- кольцевая
- модули
$\endgroup$
5
$\begingroup$
(«внешняя») прямая сумма модулей $M_i$ — это , определяемый как подмножество декартова произведения $M_i$.
Теперь есть еще одна вещь, называемая «внутренней» прямой суммой подмодулей модуля. Обычно это определяется как подмодули, суммирующиеся со всем модулем и обладающие тем свойством, что каждый компонент тривиально пересекает сумму других. Это означает, что каждый элемент имеет уникальное представление в виде суммы элементов из каждого подмодуля.
Они связаны следующим образом: если вы разложите $M$ как внутреннюю прямую сумму подмодулей $M_i$, внутренняя прямая сумма будет изоморфна «внешней» прямой сумме через отображение $m_1+m_2+\ldots \mapsto (m_1,m_2,\ldots)$.
И наоборот, всякое разложение модуля как прямой суммы других модулей соответствует внутреннему разложению. Вы просто смотрите на изображения компонентов декомпозиции внутри вашего модуля, и они образуют семейство подмодулей, определяющих внутреннюю декомпозицию.
Итак, вы видите, что они в основном одинаковы, просто в одном упор делается на работу с кортежами элементов в декартовом произведении, а другой работает с суммами элементов внутри модуля.
$\endgroup$
7
$\begingroup$
Конечная прямая сумма эквивалентна аналогичному декартовому произведению. Это перестает быть верным для бесконечных сумм/произведений.
Например, $(1,1,1,1,1,\dots) \in \Bbb{Z} \times \Bbb{Z} \times \cdots$, но $(1,1,1, 1,1,\dots) \not\in \Bbb{Z} \oplus \Bbb{Z} \oplus \cdots$, так как элементы в прямой сумме имеют только конечное число ненулевых элементов.
Топология продукта и топология коробки также отражают это различие.
$\endgroup$
3
$\begingroup$
$M_1 + … + M_n$, где $M_i$ взаимно не пересекаются, а $n$ — конечное положительное целое число
точно $M_1 \times … \times M_n$ как множество. Если считать их «оснащенными» поточечными операциями (сложение и умножение с элементами $R$), то они изоморфны как модули $R$.

 2а) – 2; б) –
9; в) – 7,9
2а) – 2; б) –
9; в) – 7,9 Угадайте корень уравнения и
выполните проверку
Угадайте корень уравнения и
выполните проверку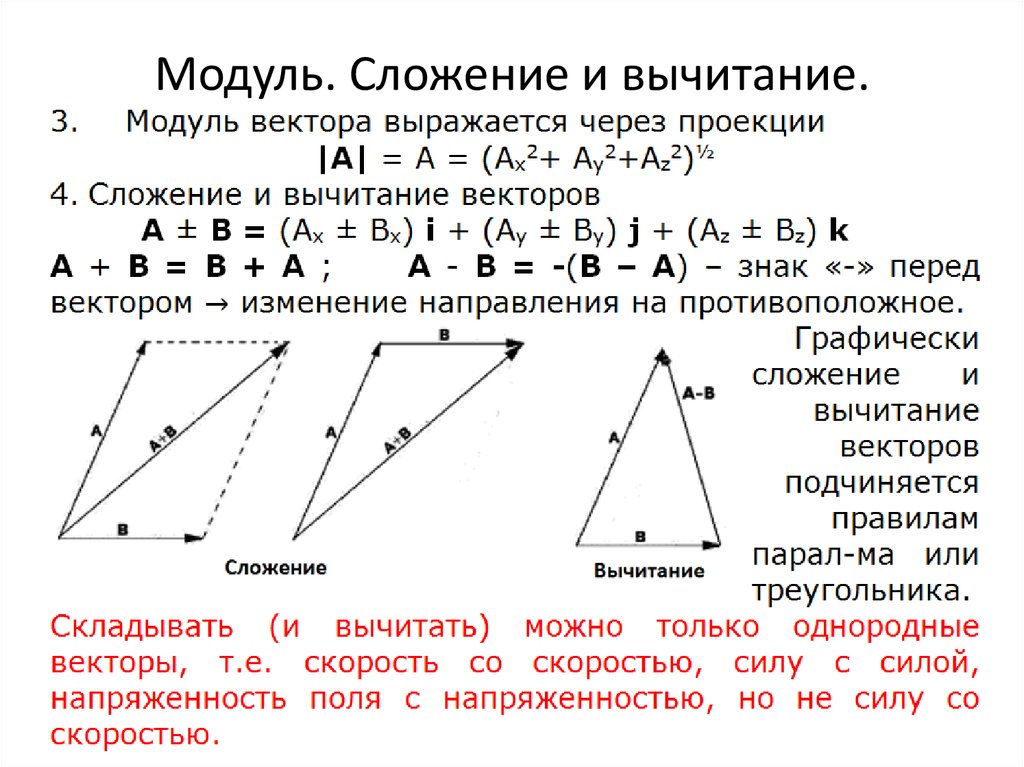 Решите уравнение:
Решите уравнение: