Сложение векторов треугольником: Правило треугольника — урок. Геометрия, 9 класс.

Сложение и вычитание векторов

На уроках геометрии вы уже познакомились с простейшими операциями над векторами: нахождением их суммы и разности. Напомним это.

Сложение векторов. Чтобы найти сумму двух векторов, необходимо: а) параллельным переносом совместить начала векторов; б) дополнить чертёж двумя отрезками так, чтобы получился параллелограмм; в) провести вектор суммы из точки начал векторов в точку соединения дополняющих отрезков (по диагонали параллелограмма).

Проиллюстрируем это правило на примере из § 12-в, когда автомобиль перемещается сначала по вектору AВ1 и затем по вектору В1В2 до поворота на мост (см. чертёж слева). Другими словами, мы ищем вектор суммы или, что то же самое, сумму векторов AВ1 и В1В2.

Сделаем новые чертежи обсуждаемых векторов (см. ниже). На чертеже «а» применим параллельный перенос и переместим вектор В1В2 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним двумя отрезками СВ2 и В1В2 до образования параллелограмма. На чертеже «в» проведём вектор суммы из точки А начал векторов в точку В2 соединения дополняющих отрезков (по диагонали параллелограмма).

Итак, мы нашли вектор суммы или сумму векторов:

Проверим правильность результата: автомобиль, переместившись из точки А в точку В1, затем переместился из точки В1 в точку В2. Иначе говоря, он совершил перемещение «по» вектору АВ2, который мы только что построили, применив правило паралеллограмма.

Вычитание векторов. Чтобы найти разность двух векторов, нужно: а) параллельным переносом совместить начала векторов; б) дополнить чертёж отрезком так, чтобы получился треугольник; в) придать отрезку направление от вычитаемого к уменьшаемому, создав вектор разности.

Проиллюстрируем это правило на том же примере из § 12-в, когда автомобиль подъезжает к середине моста. Для этого из вектора полного перемещения АВ3 вычтем перемещение на третьем этапе, вектор B2В3.

Другими словами, сейчас мы ищем вектор разности:

На чертеже «а» применим параллельный перенос и переместим вектор В2В3 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3.

Контурной стрелкой показан параллельный перенос найденного вектора разности в точку А. Важно: построенный вектор DВ3 равен искомому вектору разности АВ2. Это, по сути, проверка правильности результата, поскольку этот вектор мы уже находили по правилу параллелограмма.

Заметим, что векторы можно складывать и «треугольником», а вычитать «параллелограммом». Но мы рекомендуем запомнить именно правило параллелограмма для суммы векторов и правило треугольника для разности векторов, поскольку в дальнейшем эти правила понадобятся нам именно в таком виде.

Опубликовано в разделах: 9 класс, Введение в кинематику

алгебраическое сложение векторов

алгебраическое сложение векторов

Вы искали алгебраическое сложение векторов? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вектор правило треугольника, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «алгебраическое сложение векторов».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как алгебраическое сложение векторов,вектор правило треугольника,вектор суммы,вектор суммы двух векторов,вектор формулы,вектора вычитание,вектора вычитание и сложение,вектора правило треугольника,вектора сложение,вектора сумма,векторная сумма,векторное сложение,векторное сложение векторов,векторов формула,векторы вычитание,векторы вычитание и сложение,векторы по правилу треугольника,векторы правила треугольника,векторы правило треугольника,векторы сложение,векторы сложение правило треугольника,выполните сложение векторов а и б,вычитание вектора,вычитание векторов,вычитание векторов примеры,вычитание двух векторов,вычитание сонаправленных векторов,вычитания векторов,вычитания векторов примеры,геометрия сложение векторов,геометрия формулы векторов,для того чтобы сложить два вектора нужно,задачи на вычитание и сложение векторов,задачи на сложение векторов,задачи сложение векторов,как производится вычитание векторов,как складывать вектора в геометрии,как сложить 3 вектора,как сложить вектора по координатам,как сложить векторы по координатам,как сложить векторы по правилу треугольника,как сложить три вектора,какие правила сложения векторов вы знаете,какие правила сложения двух и нескольких векторов вы знаете,когда сумма векторов равна 0,когда сумма векторов равна нулю,методы сложения векторов,на рисунке даны векторы а и б какой из векторов c равен сумме этих векторов,определение сложение векторов,определение сумма векторов,определение суммы векторов,по каким правилам можно выполнять сложение векторов,построить сумму векторов,правила вычитания векторов,правила сложения векторов,правила сложения векторов в геометрии,правила треугольника векторы,правило вектора треугольника,правило разности векторов,правило сложение векторов правило треугольника,правило сложения векторов по правилу треугольника,правило сложения векторов треугольника,правило сумма векторов,правило треугольника вектор,правило треугольника векторы,правило треугольника векторы определение,правило треугольника для векторов,примеры вычитание векторов,примеры вычитания векторов,примеры сложение векторов,разница векторов,разность векторов формула,решение векторов сложение и вычитание векторов,складывание векторов,сложение 3 векторов,сложение вектора,сложение векторов,сложение векторов геометрия,сложение векторов задачи,сложение векторов из одной точки,сложение векторов координат,сложение векторов координаты,сложение векторов методом треугольника,сложение векторов определение,сложение векторов параллельных,сложение векторов по координатам формула,сложение векторов по правилу,сложение векторов по правилу треугольника,сложение векторов правило,сложение векторов правило треугольника,сложение векторов примеры,сложение векторов противоположно направленных,сложение векторов треугольником,сложение векторов формула,сложение векторов это,сложение векторы,сложение двух векторов,сложение и вычитание векторов примеры,сложение и вычитание векторов примеры с решением,сложение и вычитание коллинеарных векторов,сложение нескольких векторов,сложение параллельных векторов,сложение противоположно направленных векторов,сложение противоположных векторов,сложение сонаправленных векторов,сложение трех векторов,сложения векторов,способы сложения векторов,сумма 2 векторов,сумма 3 векторов,сумма вектора,сумма векторов,сумма векторов алгебраическая,сумма векторов определение,сумма векторов по правилу треугольника,сумма векторов правило,сумма векторов правило треугольника,сумма векторов треугольника,сумма векторов формула,сумма векторов формула по координатам,сумма векторов формула через координаты,сумма векторов что такое,сумма векторов это,сумма векторов это определение,сумма двух векторов,сумма и вычитание векторов,сумма противоположных векторов,суммы векторов,суммы векторов определение,суммы векторов формула,формула сложения векторов,формула сумма векторов,формула суммы векторов,формулы сложения векторов,чему равна сумма векторов,чему равна сумма противоположных векторов,что такое сумма векторов.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и алгебраическое сложение векторов. Просто введите задачу в окошко и нажмите «решить» здесь (например, вектор суммы).

Решить задачу алгебраическое сложение векторов вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Треугольный закон сложения векторов, вывод Важные концепции JEE

Вектор — это величина или объект, который имеет как величину, так и направление в качестве атрибутов. Обе эти функции необходимы для полного понимания вектора.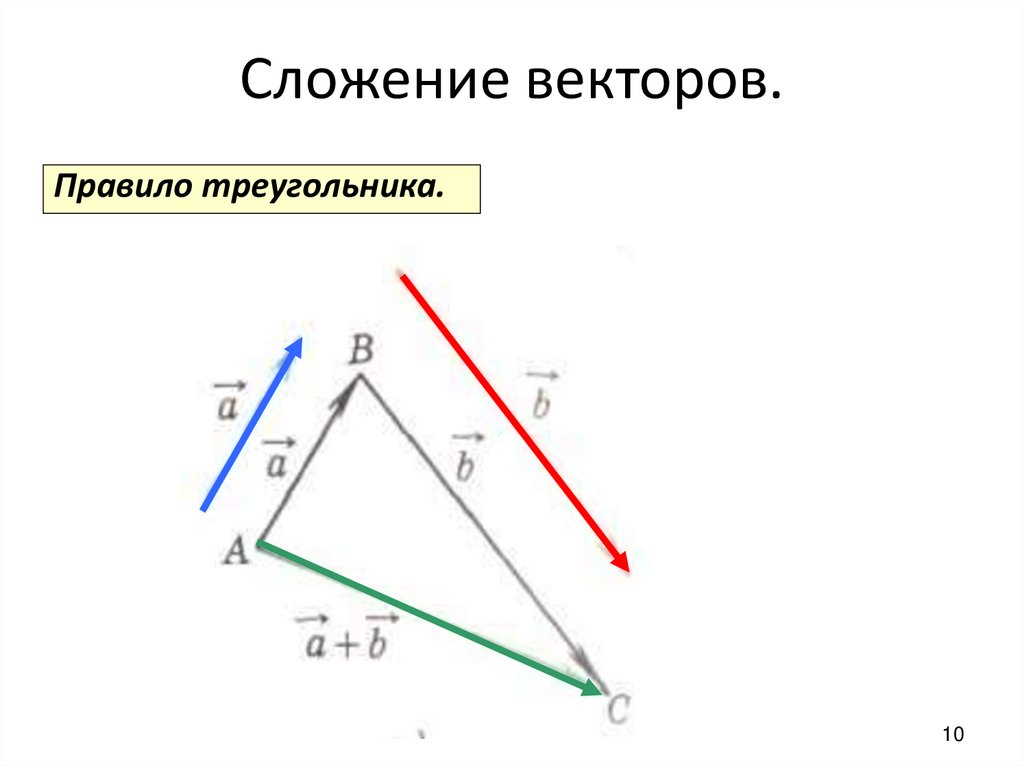 Скаляр, с другой стороны, — это величина, которая имеет только величину и не имеет направления. В физике важны векторы и скаляры. Смещение — фантастический пример векторной величины. Смещение указывает наше расстояние от данной точки, а также нашу ориентацию по отношению к этой точке. Расстояние является примером скаляра и показывает нам, как далеко мы находимся от фиксированного местоположения, но не говорит нам, как туда добраться.

Сложение скаляров может быть выполнено алгебраически, поскольку векторы не являются скалярами и не подчиняются законам скалярной алгебры. Это связано с тем, что векторы имеют как величину, так и направление. Геометрически добавляются векторы. Добавление или композиция векторов происходит при объединении двух или более векторов. Когда два или более вектора соединяются вместе, результирующий вектор является результатом.

Государственный закон треугольника сложения векторов

Существует три закона сложения векторов: 

• Закон векторов треугольника для сложения двух векторов.

• Закон параллелограмма векторов для сложения двух векторов.

• Полигональный закон векторов для сложения более двух векторов.

Сложение и вычитание векторов являются неотъемлемой частью математической физики. Силы являются векторами, и векторная сумма всех отдельных сил, действующих на объект, используется для расчета чистой силы, испытываемой этим объектом. Это использование векторов в ньютоновской механике. Векторы используются почти во всех областях физики, и треугольный закон сложения векторов является важным законом для их сложения. Согласно треугольному закону сложения векторов, если два вектора представлены двумя сторонами треугольника, взятыми по порядку, то сумма их векторов представлена ​​третьей стороной треугольника, взятой в противоположном направлении.

Изображение: Треугольный закон сложения векторов

Сумма, сумма или результат любых двух векторов A и B представлены в виде Из приведенного выше рисунка

P = вектор P

Q = вектор Q

OA = модуль вектора P

AB = модуль вектора Q

R = сумма векторов P и Q с использованием треугольного закона сложения векторов 9{2} \theta=1$

Величина результирующего вектора R определяется уравнением

Чтобы найти направление R, мы берем прямоугольный треугольник OBC,

Из уравнения (2),

Направление результирующего вектора векторов А и В, который в нашем случае равен R, задается как

Примечания к закону сложения векторов треугольника треугольник в том же порядке, равнодействующая представлена ​​третьей стороной треугольника в противоположном порядке.

Величина результирующего вектора определяется как

Где

R = результирующий вектор

P = вектор P

Q = вектор Q

900 02 $\theta=$  Угол между векторами P и Q

$\phi =$ Направление результирующего вектора R

Численные примеры треугольного закона сложения векторов

Пример 1: Необходимо сложить два вектора, имеющие величины 4 и 5 единиц. Векторы, упомянутые в этом вопросе, составляют угол 60 ° друг с другом. Найдите величину и направление результирующего вектора, используя треугольный закон сложения векторов? 9{\ circ}} \\ &\Rightarrow R=\sqrt{16+25+40 \times 0,5} \\ &\Rightarrow R=\sqrt{61} \\ &\Rightarrow R=7,81 \end{align}$

Направление задано как,

Таким образом, равнодействующая заданных векторов равна 7,81 единицы, а направление приблизительно равно 33,66°.

Пример 2: Величина равнодействующей двух векторов, между которыми угол 60°, равна 8 единицам. Один из векторов имеет величину 2 единицы, а направление равнодействующей равно 45°. Найдите модуль второго вектора? 9{\ circ} = \ dfrac {0,866 Q} {2 + 0,5 Q} \\ &\ Стрелка вправо 1 \times (2 + 0,5 Q) = 0,866 Q \\ &\ Стрелка вправо 2 = Q (0,866-0,5) \\ & \Rightarrow \dfrac{2}{0.366}=Q \\ &\Rightarrow Q \simeq 5.46 \end{align}$

Итак, второй вектор примерно равен 5,46 единиц.

Заключение

Закон треугольника сложения векторов — это математическая концепция, которая используется для нахождения суммы двух векторов. Сложение и вычитание векторов являются неотъемлемой частью математической физики. Вектор – это величина, или его еще называют объектом, который имеет как величину, так и направление. Но скаляр — это величина, которая имеет только величину и не имеет направления. Процесс добавления двух или более векторов известен как добавление векторов. Векторы складываются геометрически. Закон треугольника, закон параллелограмма и закон многоугольника — это три закона сложения векторов.

Закон треугольника для сложения векторов гласит, что если два вектора представлены двумя сторонами треугольника, взятыми по порядку, то их векторная сумма представлена ​​третьей стороной треугольника, взятого в противоположном направлении.

Треугольник, параллелограмм и многоугольник Закон векторов

В этой статье мы обсудим сложение векторов как концепцию. Сложение векторов преподается с использованием закона треугольника и закона параллелограмма в дополнение к коммутативным и ассоциативным особенностям сложения векторов.

Треугольный закон сложения векторов

Если два вектора представлены двумя сторонами треугольника по величине и направлению, взятыми в одном порядке, то третья сторона этого треугольника представляет (по величине и направлению) равнодействующую векторов.

 

Треугольный закон сложения векторов — это математическая формула, описывающая, как векторы складываются в треугольник.

Перемещение из точки А в точку В представлено вектором АВ, который может быть записан как при рассмотрении следующего сценария: мальчик путешествует из точки А в точку В, а затем из точки В в точку С. Какова общая сумма вызванного им смещения из точки А в точку С?

 

 

 

Это перемещение обеспечивается вектором AC, где AC — вектор ускорения.

 

АС = АВ + ВС.

В сложении векторов это известно как закон сложения векторов треугольника.

 

Если у вас есть два вектора a и b, вы должны разместить их таким образом, чтобы начальная точка одного вектора совпадала с конечной точкой другого вектора, чтобы сложить их вместе. Это показано на рис. 2 (i) и (ii) ниже, соответственно:

 

 

 

На рис. 2 (ii) показано, что вектор b был перемещен без изменения его величины или направления, так что его начальная точка совпадает с конечной точкой вектора a. Это помогает в формировании треугольника ABC, а третья сторона AC дает нам сумму двух векторов a и b соответственно. В результате на основании рис. 2 (ii) мы можем записать

AB + BC = AC

Ведь теперь мы знаем, что AC = – CA. В результате приведенного выше уравнения мы имеем

 

AB + BC = -CA

Альтернативно, AB + BC + CA = 0,

Альтернативно, AA = 0,

Кроме того, это нулевой вектор, поскольку начальная и конечная точки совпадают, как показано на рис. следующую диаграмму:

 

 

Теперь, как показано на рис. 4 ниже, давайте построим вектор BC ‘, величина которого такая же, как у вектора BC, но направление которого обратно направлению вектора ДО Н.Э. Или

 

до н.э. =– до н.э.

Поэтому, когда мы используем закон сложения векторов треугольника, мы получаем

AC′ = AB + BC′ = AB + (– BC′) = a – b.

Разница между векторами a и b представлена ​​вектором AC′.

Закон сложения векторов параллелограмма

Закон сложения векторов параллелограмма гласит, что если два вектора представлены двумя смежными сторонами параллелограмма по направлению и величине, то равнодействующая этих векторов представлена ​​(по величине и направлению) Диагональ параллелограмма начинается в той же точке, что и два исходных вектора.

 

Закон сложения векторов в виде параллелограмма — это математическая формула, описывающая, как векторы складываются в параллелограмм.

Теперь давайте рассмотрим немного более сложную проблему. Рассмотрим сценарий лодки, плывущей по реке с одного берега на другой в направлении, перпендикулярном течению реки. На эту лодку действуют два вектора скорости:

 

Скорость лодки определяется выходной мощностью двигателя.

Скорость течения реки измеряется в метрах в секунду.

Когда эти две скорости воздействуют на лодку одновременно, лодка начинает двигаться с другой скоростью. Изучите, как мы можем вычислить результирующую скорость лодки, и посмотрите, что у нас получится.

 

Чтобы найти решение, рассмотрим два приведенных ниже вектора a и b, которые являются двумя соседними сторонами параллелограмма с точки зрения их размера и направления, как показано на диаграмме ниже.

 

 

Они представлены по размеру и направлению диагональю параллелограмма, проходящей через их общую точку, которая представляет их сумму, a + b. В векторном сложении это известно как параллелограммный закон сложения векторов.

 

Пожалуйста, имейте в виду, что закон треугольника позволяет нам вывести из рис. 5 следующее:

 

OA +AC = OC.

В качестве альтернативы, OA + OB OC… из-за того, что AC=OB

 

В результате можно сделать вывод, что правила сложения векторов треугольника и параллелограмма аналогичны друг другу по функциональности.

 

 

Изображение, показывающее закон сложения векторов многоугольников многоугольника, взятого в том же порядке, тогда их равнодействующая может быть представлена ​​по величине и направлению замыкающей стороной многоугольника, взятого в обратном порядке.

Заключение

Если два вектора представлены двумя сторонами треугольника по величине и направлению, взятыми в одном порядке, то третья сторона этого треугольника представляет собой (по величине и направлению) равнодействующую векторов. Треугольный закон сложения векторов — это математическая формула, описывающая, как векторы складываются в треугольник. Закон сложения векторов параллелограмма гласит, что если два вектора представлены двумя соседними сторонами параллелограмма по направлению и величине, то равнодействующая этих векторов представлена ​​(по величине и направлению) диагональю параллелограмма, начинающейся в той же точке. как два исходных вектора. Перемещение из точки А в точку В изображается вектором АВ.