Свойства степени с натуральным показателем / Алгебра / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Свойства степени с натуральным показателем
Основное свойство степени
| Для любого числа и любых натуральных чисел и справедливо равенство: . |
Тождество выражает основное свойство степени.
Основное свойство степени распространяется и на произведение трех и более степеней: .
Из основного свойства степеней получаем правило умножения степеней:
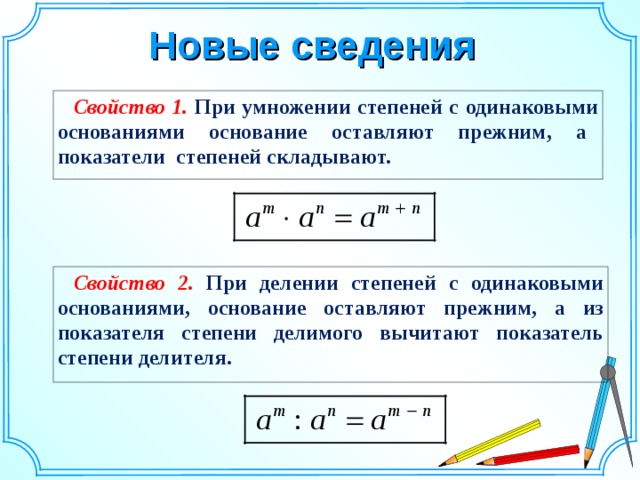
| при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают. |
Примеры:
Частное степеней
Для любого числа |
Правило деления степеней:
| при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. |
Примеры:
Если правило деления применить к частному (т.е. когда ), то получится
.
Степень с нулевым показателем не была определена, но при всяком и любом натуральном справедливо равенство:
.
Получается, можно считать, что при , справедливо равенство:
.
| Степень числа , не равного нулю, с нулевым показателем равна единице. |
Примеры:
Возведение степени в степень
Для любого числа и любых натуральных чисел и справедливо равенство: . |
Правило возведения степени в степень:
| при возведении степени в степень показатели перемножают, а основание оставляют прежним. |
Пример:
.
Возведение произведения в степень
Для любых чисел и и любого натурального числа справедливо равенство: . |
Аналогичное свойство справедливо и для произведения трех и более множителей: .
Правило возведения произведения в степень:
| при возведении произведения в степень каждый множитель возводят в эту степень и полученные результаты перемножают. |
Пример:
.
Советуем посмотреть:
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Тождества
Степень с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 214, Мерзляк, Полонский, Якир, Учебник
Номер 244, Мерзляк, Полонский, Якир, Учебник
Номер 416, Мерзляк, Полонский, Якир, Учебник
Номер 511, Мерзляк, Полонский, Якир, Учебник
Номер 584, Мерзляк, Полонский, Якир, Учебник
Номер 591, Мерзляк, Полонский, Якир, Учебник
Номер 668, Мерзляк, Полонский, Якир, Учебник
Номер 1142, Мерзляк, Полонский, Якир, Учебник
Номер 1147, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 27, Мерзляк, Полонский, Якир, Учебник
Номер 29, Мерзляк, Полонский, Якир, Учебник
Номер 79, Мерзляк, Полонский, Якир, Учебник
Номер 86, Мерзляк, Полонский, Якир, Учебник
Номер 112, Мерзляк, Полонский, Якир, Учебник
Номер 119, Мерзляк, Полонский, Якир, Учебник
Номер 125, Мерзляк, Полонский, Якир, Учебник
Номер 185, Мерзляк, Полонский, Якир, Учебник
Номер 217, Мерзляк, Полонский, Якир, Учебник
Номер 388, Мерзляк, Полонский, Якир, Учебник
Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. 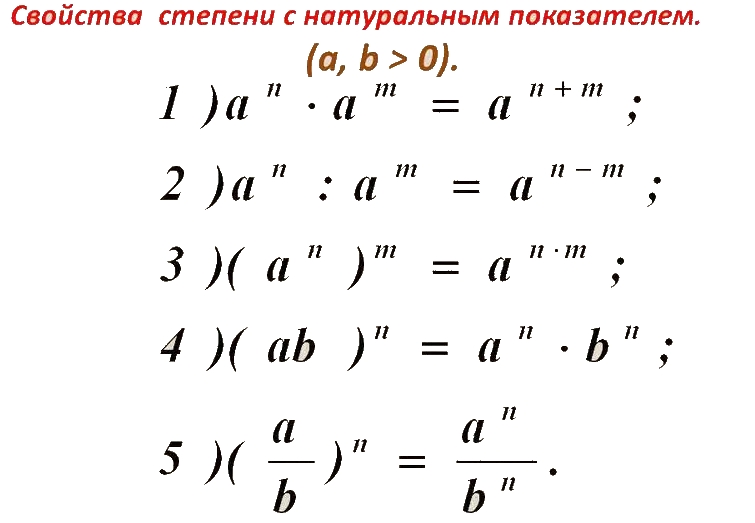 ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ§ 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5.  ОДНОЧЛЕНЫ ОДНОЧЛЕНЫ§ 6. МНОГОЧЛЕНЫ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1.  УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ§ 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2.  ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ§ 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1.  ФОРМУЛЫ ПРИВЕДЕНИЯ ФОРМУЛЫ ПРИВЕДЕНИЯ§ 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5.  РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ§ 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4.  ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИКонтрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ.  ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ§ 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5.  Задачи на проценты Задачи на проценты6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Сложение и вычитание показателей степени — GeeksforGeeks
В математике показатели степени используются для представления большего числа в терминах степени. Он показывает, во сколько раз основание умножается само на себя. Где основанием является любое число или любое математическое выражение. Например, A 3 здесь основание равно A, а степень равна 3, что означает, что A умножится само на себя три раза, то есть A 3 = A x A x A. Общий член показателя степени равен
Y n. = Y × Y × Y ×………n раз
Здесь y известен как основание, а n известен как степень или показатель степени. Типы показателей степени:
- Отрицательная степень: Отрицательные степени — это те степени, которые показывают, во сколько раз обратная величина основания умножается сама на себя.
 Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 .
Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 . - Дробная экспонента: Когда экспонента представлена в виде дроби, такие типы экспоненты известны как дробные экспоненты. Он представлен как 1/n . Например, 3 1/2 , 4 1/3 .
- Десятичный показатель степени: Когда показатель степени представлен десятичными цифрами, такие типы показателей называются десятичными показателями степени. Он представлен как 1.3 . Например, 3 1,5 , 4 12,3 .
Сложение и вычитание показателей степени
Сложение и вычитание — две основные математические операции. Сложение означает нахождение суммы двух цифр, а вычитание — нахождение разницы между двумя цифрами. Но мы не можем напрямую складывать или вычитать показатели степени, мы можем выполнять сложение или вычитание только с коэффициентами или переменными, имеющими одинаковое основание и одинаковую мощность. Мы можем только складывать показатели степени при умножении и вычитать степени степени при делении.
Мы можем только складывать показатели степени при умножении и вычитать степени степени при делении.
Шаги для сложения или вычитания между показателями степени в алгебре:
Чтобы выполнить сложение или вычитание, мы будем следовать тем же шагам:
Шаг 1: основание и показатели совпадают или нет.
Шаг 2: Расположите похожие переменные/члены вместе.
Шаг 3: Теперь выполните сложение или вычитание по мере необходимости между коэффициентами слагаемых.
Пример 1: решить 6x 3 + 12x 3 .
Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
6x 3 + 12x 3 = (6 + 12)x 3
= 18x 3
9 0018 Пример 2: решить 9x 3 -13x 3 .
Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем вычесть коэффициенты двух слагаемых, чтобы получить результат.
9x 3 – 13x 3 = (9 – 13)x 3
= -4x 3
90 018 Шаги для сложения или вычитания между показателями степени в числах:
сложение или вычитание мы будем следовать тем же шагам:
Шаг 1: Перед выполнением любого сложения или вычитания между показателями степени мы должны наблюдать, совпадают ли основание и показатели степени.
Шаг 2: Расположите одинаковые члены основания и степени вместе. Если члены имеют разные основание и показатель степени, то решите их по отдельности.
Шаг 3: Теперь выполните сложение или вычитание по мере необходимости между базой терминов.
Пример 1: решить 6 3 + 6 3 .
Решение:
Здесь одно и то же основание, т.е. 6 и показатели степени двух членов также одинаковы, т.е. 3
Итак, мы решаем их вместе + 6 3 = 2(6) 3
= 2 x 6 x 6 x 6
= 432
Пример 2: решить 9 2 – 13 3 900 04 .
Решение:
Здесь основание и показатели разные
Итак, мы решаем их индивидуально.
9 2 – 13 3 = 9 x 9 -13 x 13 x 13
= 81 – 2197
= -2116
Аналогично Вопросы
Вопрос 1: решить 5x 3 + 3x 3 .
Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
5x 3 + 3x 3 = (5 + 3)x 3
= 8x 3
Итак, 5x 3 9000 4 + 3x 3 = 8x 3
Вопрос 2: Что является результатом выражения -11a 2 + 4a 2 .
Решение:
Здесь основание одинаковое, т. е. a и показатели степени двух слагаемых также одинаковы, т. е. 2
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
-11а 2 + 4а 2 = (-11 + 4)а 2
= (4 – 11)а 2
= -7а 2
Так, -11а 2 + 4a 2 = -7a 2
Вопрос 3: Решите выражение 4x 3 + 4x 2 – 2x 3 + х 2 – х + 1
Решение:
Здесь у нас разные термины (x 3 , x 2 , x), т.
е. основания одинаковые, но разные показатели степени.
Итак, идентифицируйте похожие переменные, сгруппируйте их и выполните сложение/вычитание на основе знаков и расположите в полиномиальном порядке, т.
4x 3 + 4x 2 – 2x 3 + x 2 – x + 1 = (4x 3 – 2x 3 ) + (4x 2 + x 2 )- х + 1
= (4 – 2)х 3 + (4 + 1)х 2 – x + 1
= 2x 3 + 5x 2 – x + 1
Вопрос 4: Каков результат x 3 y + 4x 3 г?
Решение:
Здесь у нас есть 2 разные переменные в 2 терминах x, y и степени x, y в двух терминах одинаковы, т.е. 3,1 соответственно.
Итак, мы можем считать, что эти 2 термина имеют совпадающие переменные, и мы можем добавить/вычесть коэффициент 2 терминов в зависимости от требований.
x 3 y + 4x 3 y = (1 + 4)x 3 y
= 5x 3 y
Вопрос 5: решить x 3 y + 4x 3 y 2 + 4x – x + 1
Решение:
Здесь у нас есть 2 разные переменные в 2 терминах x, y и показатель степени x в 2 терминах одинаковы, т.
е. 3, но показатель степени y не одно и то же, поэтому мы не можем считать два термина одинаковыми и не будем выполнять между ними никаких операций. (осталось как есть)
Но есть еще два члена с той же базовой переменной x и показателем степени, что и 1. Поэтому мы группируем их и выполняем вычисления с их коэффициентами.
x 3 у + 4х 3 у 2 + 4х – х + 1 = 4х 3 у 2 + х 3 у + (4х – х) + 1
= 4х 3 y 2 + x 3 y + (4 – 1)x + 1
= 4x 3 y 2 + x 3 y + 3x + 1
Вопрос 6: Решить х 5 y 2 – x 4 y 4
Решение:
Здесь два члена x 9000 3 5 у 2 , х 4 у 4 и в два термина у нас есть 2 переменные x, y, но показатели переменных не совпадают при сравнении между терминами.
Следовательно, первое слагаемое совершенно не похоже на второе и не может быть вычтено друг из друга.
Оставляем как есть.
х 5 y 2 – x 4 y 4 дальнейшее упрощение невозможно.
6 простых шагов для сложения и вычитания в экспоненте
Вот как складывать и вычитать в экспоненте Когда числа, которые вы добавляете или вычитаете, должны быть равным. Если они уже равны, то можно просто сложить коэффициенты. Если показатели степени не равны, то вы должны сделать их равными, переместив один из десятичных знаков. Самый простой способ сделать десятичные дроби равными — сделать меньшую степень равной большей, переместив десятичную дробь влево. Вы добавляете единицу к показателю степени для каждого пробела, на который вы перемещаете десятичную точку влево. Когда показатели равны, вы можете добавить или вычесть коэффициенты. Последний шаг для Сложение и вычитание в экспоненциальном представлении должно гарантировать, что коэффициент находится между 1 и 10. Если это не так, вы должны переместить десятичную точку так, чтобы она была.
Если это не так, вы должны переместить десятичную точку так, чтобы она была.
Общий базовый стандарт: 8.EE.A.3
Связанные темы: Квадратные корни, кубические корни, иррациональные числа, степени 10, введение в экспоненциальную запись, преобразование чисел в экспоненциальную запись, преобразование чисел из экспоненциальной записи , Умножение в экспоненциальном представлении, Деление в экспоненциальном представлении
Выполнение любого сложения и вычитания в экспоненциальном представлении Пример задачи При сложении и вычитании в экспоненциальном представлении степени чисел, которые вы складываете или вычитаете, должны быть эквивалентны. В том случае, если они эквивалентны, можно просто объединить коэффициенты вместе. Если степени не эквивалентны, вы должны сделать их эквивалентными, переместив один из десятичных знаков так, чтобы степени стали эквивалентными. Как только степени эквивалентны, вы можете либо добавить коэффициенты для добавления научного обозначения, либо вычесть коэффициенты для вычитания научного обозначения. Последним шагом для сложения и вычитания в экспоненциальном представлении является проверка того, что коэффициент находится где-то в диапазоне от 1 до 10. Это самый простой способ решить, как складывать и вычитать экспоненциальное представление.
Последним шагом для сложения и вычитания в экспоненциальном представлении является проверка того, что коэффициент находится где-то в диапазоне от 1 до 10. Это самый простой способ решить, как складывать и вычитать экспоненциальное представление.
- Проверьте, равны ли степени в степени десятков.
- Если степени равны, то вы можете добавить или вычесть коэффициенты.
- Если степени не равны, вы должны сделать их равными, переместив десятичную точку.
- Перемещение десятичной точки влево будет прибавлять к показателю степени для каждой цифры, которую она перемещает влево.
- Когда степени равны, вы можете складывать или вычитать коэффициенты.
- Убедитесь, что ваш коэффициент находится между единицей и десятью, так как он должен быть записан в научной нотации.
Практические задачи на сложение и вычитание
Сложение и вычитание в экспоненциальном представлении
Нажмите «Старт», чтобы начать практический тест!
1 / 5
Добавьте или вычтите следующее в научной записи: 94
Ваш счет
Посмотрите объяснение сложения и вычитания в экспоненциальном представлении видео Посмотрите наше бесплатное видео о том, как решить сложение и вычитание в экспоненциальном представлении . В этом видео показано, как добавить экспоненциальную запись и как вычесть экспоненциальную запись. Вы также можете попробовать решить некоторые практические задачи из нашего бесплатного листа Добавление и вычитание научной нотации , который вы можете получить, отправив свое электронное письмо выше.
В этом видео показано, как добавить экспоненциальную запись и как вычесть экспоненциальную запись. Вы также можете попробовать решить некоторые практические задачи из нашего бесплатного листа Добавление и вычитание научной нотации , который вы можете получить, отправив свое электронное письмо выше.
Посмотрите бесплатное видео о сложении и вычитании в научном представлении на YouTube здесь: Сложение и вычитание в научном представлении
Расшифровка видео:
Это видео о сложении и вычитании в научном не ация. Вы можете бесплатно получить рабочий лист сложения и вычитания научных обозначений, который мы используем в этом видео, нажав на ссылку в описании ниже. Посмотрите это видео, чтобы узнать, как складывать и вычитать экспоненциальные записи.
Первая задача, которую мы собираемся использовать, чтобы показать вам сложение и вычитание экспоненциальной записи, дает нам 9 умножить на 10 до 9 минус 2 умножить на 10 до 9.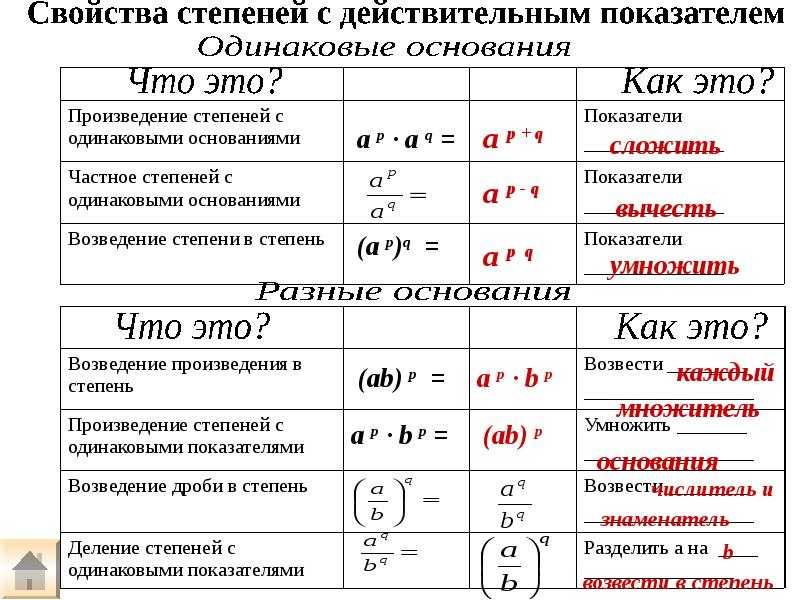 При сложении или вычитании в экспоненциальном представлении вы будете брать коэффициенты каждого числа, которое добавляется или вычитается, и вы собираетесь либо складывать, либо вычитать эти два вместе. В этом случае у нас есть 9 и 2, которые мы в конечном итоге будем складывать или вычитать вместе. Вторая часть добавления или вычитания научной записи, о которой вам нужно знать, заключается в том, что наши степени 10 должны быть равны. Другими словами, показатель степени 10 должен быть одинаковым. Например, если бы это было, скажем, 10 в седьмой степени, мы не могли бы вычесть их, потому что этот показатель равен 9.и этот показатель равен 7. Нам нужно было бы изменить 7 на 9, и когда это было 9, мы могли бы складывать или вычитать, но в случае нашего первого примера у нас есть совпадающие показатели степени.
При сложении или вычитании в экспоненциальном представлении вы будете брать коэффициенты каждого числа, которое добавляется или вычитается, и вы собираетесь либо складывать, либо вычитать эти два вместе. В этом случае у нас есть 9 и 2, которые мы в конечном итоге будем складывать или вычитать вместе. Вторая часть добавления или вычитания научной записи, о которой вам нужно знать, заключается в том, что наши степени 10 должны быть равны. Другими словами, показатель степени 10 должен быть одинаковым. Например, если бы это было, скажем, 10 в седьмой степени, мы не могли бы вычесть их, потому что этот показатель равен 9.и этот показатель равен 7. Нам нужно было бы изменить 7 на 9, и когда это было 9, мы могли бы складывать или вычитать, но в случае нашего первого примера у нас есть совпадающие показатели степени.
Итак, мы собираемся решить эту проблему. При решении этой задачи мы возьмем наши коэффициенты, равные 9 и 2, и вычтем их друг из друга, а затем перепишем нашу степень числа 10 прямо рядом с ним. Мы будем делать 10 раз в 9-й степени, при сложении или вычитании степень 10 должна быть равна. Как только показатель степени равен, вы сохраните показатель степени в своем ответе. Следующим шагом будет фактически пойти дальше и вычесть коэффициент. 9минус 2 равно 7, а затем мы перепишем времена, а затем нашу степень 10, которая равна 10 в 9-й степени. Таким образом, наш ответ в научных обозначениях будет 7 умножить на 10 в 9-й степени, потому что мы не меняем степень 10 в нашем ответе.
Мы будем делать 10 раз в 9-й степени, при сложении или вычитании степень 10 должна быть равна. Как только показатель степени равен, вы сохраните показатель степени в своем ответе. Следующим шагом будет фактически пойти дальше и вычесть коэффициент. 9минус 2 равно 7, а затем мы перепишем времена, а затем нашу степень 10, которая равна 10 в 9-й степени. Таким образом, наш ответ в научных обозначениях будет 7 умножить на 10 в 9-й степени, потому что мы не меняем степень 10 в нашем ответе.
Число 2 очень похоже на число 1. Эта задача покажет вам, как складывать экспоненциальное представление с разными показателями. Нам дано 3 шесть раз по десять до семи плюс две целых один раз по десять до седьмого. Мы знаем, что добавляем, теперь мы собираемся сложить наши коэффициенты вместе, что составляет три целых шесть десятых плюс две целых один десятых. Мы продолжим и напишем, что три целых шесть десятых плюс две целых десятых. Теперь, если вы посмотрите на нашу степень 10, наш показатель степени одинаков для каждой степени 10. 10 в седьмой здесь и десять в седьмой здесь. Нам не нужно менять показатель в степени 10, потому что он уже равен, мы просто перепишем 10 в седьмой степени под нашей задачей. Затем мы продолжим и добавим наши коэффициенты: три целых шесть десятых плюс две целых десятых — это пять целых семь десятых, а затем умножим на 10, а затем уменьшим семерку. Таким образом, наше решение будет пять целых семь десятых в седьмой степени. Все эти задачи можно найти в нашем листе сложения и вычитания с экспоненциальной записью, который можно скачать по ссылке ниже.
10 в седьмой здесь и десять в седьмой здесь. Нам не нужно менять показатель в степени 10, потому что он уже равен, мы просто перепишем 10 в седьмой степени под нашей задачей. Затем мы продолжим и добавим наши коэффициенты: три целых шесть десятых плюс две целых десятых — это пять целых семь десятых, а затем умножим на 10, а затем уменьшим семерку. Таким образом, наше решение будет пять целых семь десятых в седьмой степени. Все эти задачи можно найти в нашем листе сложения и вычитания с экспоненциальной записью, который можно скачать по ссылке ниже.
Число три немного сложнее, потому что оно имеет один дополнительный шаг: семь целых семь целых трижды десять до пятой минус пять целых три десятых до четвертой. Теперь в этом случае мы не можем вычесть их друг из друга, потому что наши показатели степени не совпадают. Вы заметите, что у этого есть четыре, и у этого есть показатель степени пять. Они не равны, что означает, что мы не можем их вычесть, мы должны изменить одно из них на другое, а затем, когда они равны, вы можете их вычесть.
Самый простой способ изменить показатель степени в 10-й степени — это всегда превращать меньший показатель в больший. Что мы собираемся сделать, так это изменить это 4 на 5. Как мы это делаем, мы перемещаем десятичную дробь влево и ставим ее здесь, а затем добавляем единицу к нашему показателю степени. Каждый раз, когда вы перемещаете десятичную дробь влево, вы добавляете единицу к показателю степени. Например, предположим, что мы перемещаем десятичную дробь вместо того, чтобы перемещать ее сразу, мы перемещаем ее один раз два раза, а затем добавляем два к этому показателю степени. Это было бы четыре плюс два, но если бы мы сделали 4 плюс 2, это было бы 6, и мы не пытаемся получить 6, мы пытаемся получить пять, поэтому добавление двух не имеет смысла. Что мы собираемся сделать, так это сдвинуть его влево один раз, а затем добавить один, потому что четыре плюс один равно пяти, и мы пытаемся получить пять. Мы пытаемся сделать показатели равными, поэтому давайте перепишем нашу задачу.

 С. Повторяем и систематизируем школьный курс алгебры и начал анализа.—М.: Просвещение, 1990.— 416 с.
С. Повторяем и систематизируем школьный курс алгебры и начал анализа.—М.: Просвещение, 1990.— 416 с.
 Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 .
Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 .

 е. основания одинаковые, но разные показатели степени.
е. основания одинаковые, но разные показатели степени.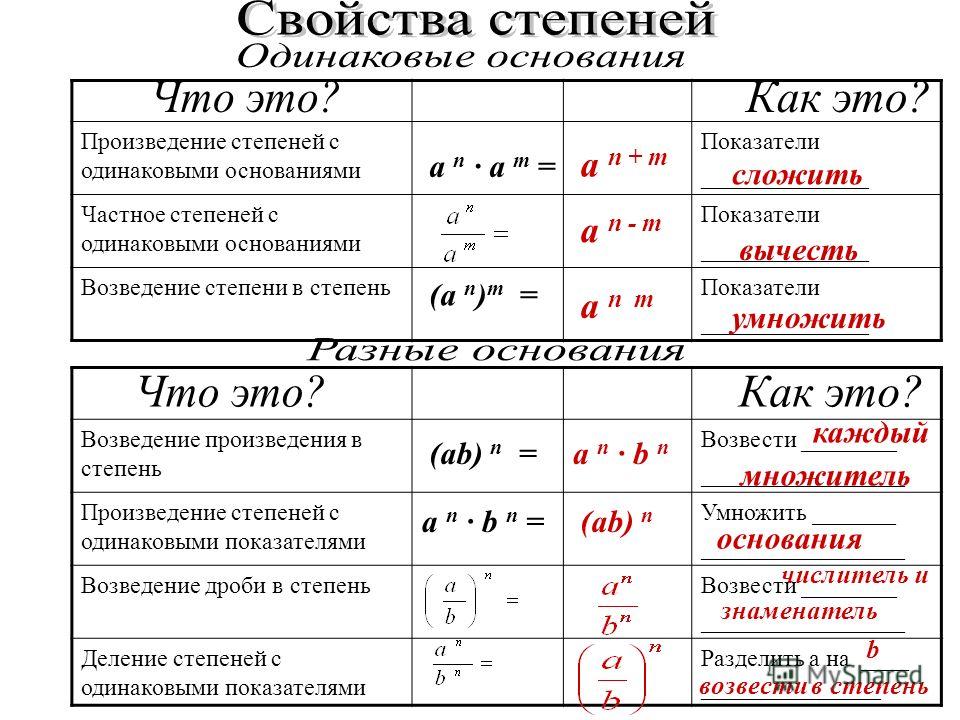 е. 3, но показатель степени y не одно и то же, поэтому мы не можем считать два термина одинаковыми и не будем выполнять между ними никаких операций. (осталось как есть)
е. 3, но показатель степени y не одно и то же, поэтому мы не можем считать два термина одинаковыми и не будем выполнять между ними никаких операций. (осталось как есть)