Сложные задачи 5 класс математика: Сложные задачи по математике для 5 класса

Самые сложные математические задачи в мире

Главная » Новости » Самые сложные математические задачи в мире

Новости

На чтение 6 мин. Просмотров 6.1k.

Трудно определить, какая математическая задача является «самой сложной», поскольку разные задачи могут быть более сложными для разных людей в зависимости от их образования и опыта. Но есть несколько математических задач, над решением которых человечество бьется много лет. Некоторые из самых известных и сложных математических задач:

• Гипотеза Пуанкаре — задача топологии, которую Григорий Перельман решил в 2002 году.
• Гипотеза Римана — проблема теории чисел, которая до сих пор остается нерешенной.
• Гипотеза Коллатца — задача в математике, в которой определяется, всегда ли определенная последовательность чисел сходится к 1.
• Гипотеза Гольдбаха — проблема теории чисел, которая включает в себя определение того, можно ли каждое четное целое число, большее 2, представить в виде суммы двух простых чисел.
• Гипотеза Берча и Суиннертона-Дайера — задача алгебраической геометрии, в которой необходимо определить поведение некоторых эллиптических кривых.

1. Гипотеза Пуанкаре. Эта проблема, предложенная французским математиком Анри Пуанкаре в 1904 году, касалась топологии трехмерных многообразий. Она оставалась нерешенной до 2002 года, пока российский математик Григорий Перельман не решил ее, используя методы дифференциальной геометрии и геометрической топологии. Перельман доказал, что каждое односвязное замкнутое трехмерное многообразие топологически эквивалентно трехмерной сфере.
2. Гипотеза Римана — предложена немецким математиком Бернхардом Риманом в 1859 году. Задача касается распределения простых чисел и имеет далеко идущие последствия в теории чисел. Несмотря на большой прогресс, достигнутый математиками за эти годы, она остается нерешенной. Гипотеза Римана описывает распределение простых чисел, то есть чисел, которые делятся только на 1 и сами на себя. s

   где сумма берется по всем натуральным числам n. Параметр s называется комплексным аргументом функции. Дзета-функция Римана связана с теорией чисел и широко изучается в высшей математике. Она обладает многими интересными свойствами и является предметом многих исследований. Одной из самых известных нерешенных проблем в математике является гипотеза Римана, которая касается поведения дзета-функции на критической линии s = ½.

   Гипотеза Римана считается одной из самых важных нерешенных проблем в математике — она активно изучается уже более 150 лет, в связи с тем, что тесно связана с другими областями математики и имеет значение для распределения простых чисел в долгосрочной перспективе.

3. Гипотеза Коллатца (сиракузская проблема, дилемма 3n+1). Эта простая на вид задача, также известная как дилемма «3n + 1», касается последовательности чисел, полученной путем применения простого правила к каждому числу в последовательности.

   Несмотря на свою кажущуюся простоту, она остается недоказанной и десятилетиями ставит математиков в тупик. Это математическая задача, в которой используется простой рекурсивный процесс. В нем говорится, что если вы возьмете любое положительное целое число и несколько раз примените следующие два шага, вы в конечном итоге достигнете числа 1:

    — Если число четное, разделим его на 2.

    — Если число нечетное, умножим его на 3 и прибавим 1.

   Какое бы вы число не взяли — вы всегда получите в конце 1. Например, если вы начнете с числа 7, вы получите следующую последовательность чисел: 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

   Несмотря на свою простоту, гипотеза Коллатца долгие годы оставалась нерешенной. Математикам удалось доказать, что гипотеза верна для определенных чисел (сейчас доказана ее справедливость для всех чисел вплоть до числа 9 789 690 303 392 599 179 036), но никому не удалось доказать ее для всех натуральных чисел.

   
   В результате гипотеза остается загадкой и вызовом для математиков всего мира.

4. Гипотеза Ходжа. Эта проблема, предложенная британским математиком У. В. Д. Ходжем в 1950-х годах, касается топологии алгебраических многообразий и имеет широкое применение в геометрии и алгебраической геометрии. Остается недоказанной.
5. Гипотеза Бёрча и Свиннертона-Дайера. Эта проблема, предложенная британскими математиками Майклом Атьей и Джоном Хортоном Конвеем в 1960-х годах, касается поведения эллиптических кривых и имеет важные следствия в теории чисел. Также не доказана.
6. Проблема P и NP: эта задача классов, впервые предложенная в 1970-х годах, касается отношения между двумя классами вычислительной сложности: «P» (задачи, которые могут быть быстро решены компьютером) и «NP» (задачи, решение которых может быть проверено с помощью компьютера). Несмотря на значительный прогресс, достигнутый учеными-компьютерщиками, она остается нерешенной.

   Проблема P и NP — это вопрос в информатике, который спрашивает, может ли каждая проблема, решение которой может быть быстро проверено компьютером, быть также быстро решена компьютером.

   Буква P в названии относится к задачам, которые могут быть решены за полиномиальное время, что означает, что время, необходимое для решения задачи, увеличивается не более чем полиномиально в зависимости от размера входных данных.

   NP в названии относится к задачам, для которых предлагаемое решение может быть проверено компьютером за полиномиальное время.

   Проблема P и NP — одна из самых известных нерешенных проблем в информатике, и она имеет большое значение для этой области.

   Если бы было доказано, что P равно NP, это означало бы, что многие проблемы, которые в настоящее время считаются сложными, могут быть решены быстро, что может иметь значительные последствия для таких областей, как криптография и оптимизация. С другой стороны, если бы было доказано, что P не равно NP, это означало бы, что существуют задачи, которые трудно решить или для которых нет эффективного решения.
7. Гипотеза континуума. Эта задача, предложенная немецким математиком Георгом Кантором в конце 19 века, касается размера бесконечных множеств и имеет важное значение в теории множеств. Не доказана.
8. Существование Янга-Миллса и гипотеза о массовом разрыве. Эта гипотеза, предложенная американским физиком Чен Нин Янгом и британским физиком Робертом Миллсом в 1950-х годах, касается поведения субатомных частиц и имеет важные последствия в теоретической физике. Не имеет решения.
9. Гипотеза Римана для функциональных полей: предложена немецким математиком Михаэлем Атьей в 1990-х годах, является вариантом гипотезы Римана, которая касается распределения простых чисел в функциональных полях, а не целых чисел. Доказательства нет.
10. Гипотеза Била (обобщение теоремы Ферма): предложена американским математиком Эндрю Билом в 1990-х годах и касается соотношения между простыми числами и суммами их степеней. Остается недоказанной.

( 7 оценок, среднее 4.71 из 5 )

Задачи для повторения. 5 класс

1. Задачи для повторения

ЗАДАЧИ ДЛЯ
ПОВТОРЕНИЯ
Авторы: Квиндт Ева и Куранова Ирина

2.

Цель урока1.
2.
3.
4.
Решить ряд задач.
Повторить пройденный материал.
Узнать новое.
Вспомнить, то что забыто.

3. Условия

Дорогие одноклассники!!! С этого дня на каждом
уроке математики мы будем решать
интересные задачи и примеры, за которые вы
будете получать баллы. Они записываются в
таблицу. В конце учебного года мы подведем
итоги и у кого будет больше всего баллов тот
получит приз. Какой?! Секрет!!!

4. Начнем с азов. Задача №1

Условие: Старый будильник отстаёт каждый день на
8 мин.
Вопрос: На сколько минут надо его поставить
вперёд в 20-00, чтобы он зазвонил вовремя — в 8-00
следующего утра?
Баллы: 1 балла

5. Ответ на задачу №2

Немного сложнее. Задача №2
Условия: у 28 человек 5 «А» класса на
собрание пришли папы и мамы. Мам
было — 24, пап — 18.
Вопрос: У скольких учеников на
собрание пришли одновременно и папа
и мама?
Баллы: 1 балла
Ответ

6.

Немного сложнее. Задача №2Задача №4
1.
2.
3.
Условия: Вадик написал
название своего родного
города и все его
циклические сдвиги
(таблица 1). Затем,
упорядочив эти «слова»
по алфавиту, он составил
таблицу 2 и выписал её
последний столбец:
ВКСАМО.
Саша сделал то же
самое с названием
своего родного города и
получил МТТЛАРАЕКИС.
Вопрос: Что это за город,
если его название
начинается с буквы С?
Таблица 1 Таблица 2
МОСКВА
АМОСКВ
АМОСКВ
ВАМОСК
ВАМОСК
КВАМОС
КВАМОС
МОСКВА
СКВАМО
ОСКВАМ
ОСКВАМ
СКВАМО

7. Ответ на 3адачу№1

«Десятичные» задания
1.
2.
3.
4.
5.
Что такое 2,43 квадрата? Изобрази на рисунке.
Раздели на 10, 100, 1000 числа 37; 795; 4; 2,3; 65,27;
0,48 и результат запиши в виде десятичной дроби.
Умножь на 10, 100, 1000 числа 4,6; 6,52; 23,095;
0,01999.
Представь: десятичную дробь в виде обыкновенной
дроби и сократи ее:
а) 0,5; 0,2; 0,4; 0,6; 0,8; (5)
б) 0,25; 0,75; 0,05; 0,35; 0,025; (5)
Обыкновенную дробь в виде десятичной:
а) 1/8; 3/8; 5/8; 7/8; 11/8; 125/8; 1/16; 5/16; 9/16;
23/16; (10)
б) 1/500; 3/250; 71/200; 9/125; 27/2500; 1999/2000. 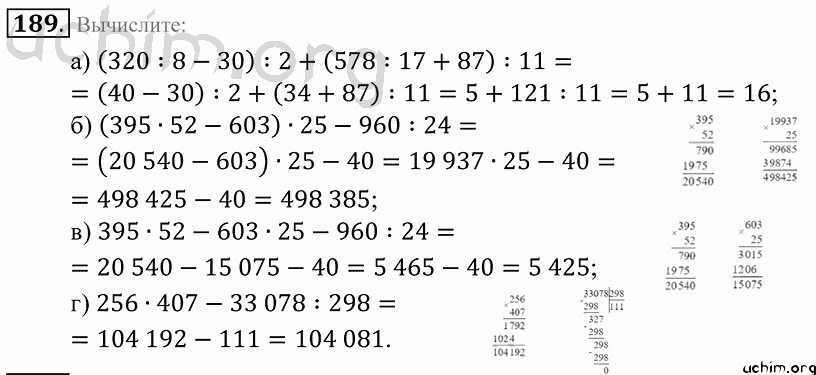(6)

8. Задача №4

Логическая задача
Условие: костюмер одевал клоунов и все
перепутал. Сара, Бим и Бом должны выйти на
арену в красных, синих и зелёных рубашках и
туфлях. Каких цветов будут туфли и рубашка у
Бома, Бима и Сары?
Имя
Рубашки
Туфли
Бим
(один.
)
Бом
—
Сара
Цвета
Ответ
—
К
З
С
Баллы: 2
—
+
—
К
З
С

9. Ответ на задачу №4

Самый сложный уровень. Задача
№5
Условие: таракан Валентин
объявил, что умеет бегать
со скоростью 50 м/мин. Ему
не поверили, и правильно:
на самом деле. Валентин
всё перепутал и думал, что
в метре 60 сантиметров, а в
минуте 100 секунд.
Вопрос: С какой скоростью
(в «нормальных» м/мин)
бегает таракан Валентин?
Баллы: 5 баллов.
ОТВЕТ

10. «Десятичные» задания

Задача №6
Условие: Провод
длиной 60 м. разрезали
на два куска так, что
длина одного из них
оказалась в 5 раз
больше другого.
Задание: Найди длину
каждого куска.
Ответ на
задачу

11. Логическая задача

Задача на нахождение площади
Задание: Найди ширину прямоугольника, если
его площадь равна 342,342 дм2,
а длина 22,23 дм. Запишите ответ в метрах,
сантиметрах.
22,23 дм
Баллы: 2
342, 342 дм2
Ответ
?

12. Ответ на задачку про клоунов

Продолжи ряд
Продолжи ряд на 3 числа и укажи
закономерность:
a) 2,3; 3,8; 5,3…
b) 6,89; 7,04; 7,19…
Баллы:
a) 1
b) 1
c) 2
d) 2
c) 4,53; 7,74; 10,95…
d) 105,83; 87,52; 69,21…

13. Самый сложный уровень. Задача №5

Уравнения
1 вариант
5,7 + x = 8,1
x – 17,2 = 45,7
2,1 * x = 11,97
x / 3,6 = 12,82
Баллы:
1) 1
2) 1
3) 2
4) 2
2 вариант
y + 13,37 = 16,79
y – 13,4 = 21,5
2,4 * y = 38,88
y / 13,54 = 2,7
Ответ

14. Ответ на сложную задачу

Примеры
Составь программу действий и вычисли:
Пример №1
0,81 : 2,7 + 4,5 * 0,12 – 0,69 = ?
Пример №2
102 – ( 155, 4 : 14,8 + 2,1) * 3,5 = ?
Баллы: 4 балла
Ответ

15.

Задача №6Еще одно задание
Представьте числа в виде суммы разрядных слагаемых:
1) 92.571.324
234,09865132
2) 32.672.352
567,08924361
3) 47.876.901
126,07834520
Баллы: 1 за каждое правильное задание.

16. Ответ на задачу №6

Задача №8
Условие: На глобусе проведены 17 параллелей
и 24 меридиана.
Вопрос: На сколько частей разделена
поверхность глобуса?
Баллы: 3

17. Задача на нахождение площади

Задача №9
Условие: Папа может перейти мост за 1 минуту,
мама — за 2, малыш — за 5, а бабушка — за 10
минут. У них есть один фонарик. Мост
выдерживает только двоих.
Вопрос: За какое минимальное кол – во минут
они могут перейти мост?
Баллы: 2
Ответ

18. Ответ на задачу

Выбери числа
Укажите пять целых положительных чисел,
сумма которых равна 20, а произведение:
А) 720 – 2 балла
Б) 240 – 2 балла
В) 420 – 3 балла
Ответ

19. Продолжи ряд

Ответ на задание «Выбери числа»
А) 720 – 2 балла
2 + 3 + 4 + 5 + 6 = 20
2 * 3 * 4 * 5 * 6 = 720
Б) 240 – 2 балла
1 + 2 + 3 + 4 + 10 = 20
1 * 2 * 3 * 4 * 10 = 720
В) 420 – 3 балла
1 + 3 + 4 + 5 + 7 = 20
1 * 3 * 4 * 5 * 7 = 720
Сравни
1)
2)
3)
4)
3
16
7
и
4
16
7
12
12
13 и 13
25
23
3
3
21 и 12
7
7
9
19
32 и 32
14
78
5) 3,2 и 3,4
6) 12,0006 и 12,006
7) 36,334 и 35,335
8) 197,22095 и 236,22075
За каждое задание по 1 баллу

21.

УравненияНайди…
Среди чисел найди: 12;
92 2
98; ; ; 0;
460 79
6
321,098; .
32
1.
2.
3.
4.
5.
1
987 ;
15
1;
13
;
46
21,09;
27
32
;
243
12
;
24
3,0;
Натуральные числа;
Обыкновенные дроби;
Смешанные числа;
Десятичные дроби;
Дроби которые можно сократить.
346;
21
57 ;
23
23
12 ;
56
Баллы:
1–4=1
5=2

22. Ответы на уравнения

Ответ на задание «Найди…»
1.
2.
3.
12; 346; 98; 1; 3,0.
13 2
; .
46 79
23
1
12 ; 987 ;
56
15
21
57 .
23
4.
21,09; 321,098.
5.
12 92
; ;
24 460
27 6
32 ; .
243 32

Электронная книга

Word Problems Workbook для 5-8 классов

Сингапурский математический вызов

Сингапурский математический вызов

352 страницы

5-8 класс / 10-14 лет

Код продукта:

705334-ЕВ

Сейчас: $14,99

Описание

Укрепить стратегии математического мышления учащихся.

Сингапурский математический вызов: задачи со словами для пятого класса и старше содержит 352 страницы инструментов и практики, необходимых для прочной математической основы. Используемый в соответствии со стандартами для класса, этот пошаговый ресурс обучает с помощью сложных текстовых задач, чтобы развить у учащихся навыки начальной геометрии, деления с остатком, группировки, перераспределения, процентов и многого другого.

Сингапурская математика обеспечивает глубокое понимание каждой ключевой математической концепции, является прямым дополнением к текущим учебникам, используемым в Сингапуре, включает введение, объясняющее метод Сингапурской математики, и включает пошаговые решения в ответах.

Особенности:

• Ключ ответа

Спецификации

УПК	044222275686
Авторское право	Техас 8-770-608
ISBN	9781483855615
Информация о продукте	Рабочая тетрадь
Серия	Сингапурский математический конкурс
Темы	Средние классы

Бесплатные ресурсы

Отзывы

Что ученики изучают в 5 классе по математике?

Математика в пятом классе — время осваивать полученные понятия к этому моменту. Студенты также учатся применять эти концепции и механика к более сложным числам. Они учатся и изучают язык математики, а также фактических вычислений. Они учатся активно использовать эти понятия и их математический словарь в решении реальных задач проблемы. Они используют стратегии, чтобы решить, какие шаги предпринять и в каком порядке, решая, как лучше всего использовать имеющиеся у них инструменты.

Числа в математике в пятом классе изменяются от очень больших до очень маленьких. Студенты берут дроби и десятичные дроби до тысячных и целые числа вверх до миллиарда. Учащихся учат упорядочивать эти числа и в при этом научитесь преобразовывать десятичные дроби и дроби. Отрицательные числа введены ситуации, когда могут встречаться отрицательные числа обсуждалось. Географические положения ниже уровня моря и температуры ниже точки замерзания — это отрицательные числа, которые учащиеся смогут относиться к.

Учащиеся пятого класса уточняют округление и оценку навыки. Введены новые стратегии оценки для сравнения ответов и обеспечить разумное решение. Эти навыки оценки также помочь дать ученику уверенность в том, что ответ на трудный проблема правильная.

В этом классе учащиеся учатся находить множители чисел и также для определения, является ли число простым или составным. Они строят о свойствах умножения они уже узнали. Они учатся умножать дроби и десятичные числа. Проблемы со словами становятся все более сложными, и для их решения требуется несколько шагов. Они узнают, что если умножить 2 числа меньше нуля, ответ — число меньше, чем любое из двух исходных чисел. Другие операции включают введение в алгебраические уравнения использование букв или символов для представления чисел в уравнениях. Пятый первоклассники также учатся экстраполировать информацию из диаграмма или график.

Изучая геометрию, ученики учатся измерять окружность. Проблемы потребности в реальных решениях решаются с использованием периметра, площади и объемные уравнения. Учащиеся узнают больше о пространственных отношениях изучая характеристики и отношения между точками, линии, лучи, формы и плоскости. Новые инструменты, такие как транспортиры и компасы представлены.

Дети учатся точно и творчески измерять. Они могут измерить предметы, которые находятся вне досягаемости, путем измерения аналогичного предмета они могут достичь или путем измерения части, которую они могут достичь, и умножения чтобы получить результат. Они учатся определять, является ли необходимо достичь предполагаемого результата или точного решения. Время измеряется в приращениях как меньших, секунд, так и больших, веков. Студенты могут использовать календари, расписания и планировщики для решения задач в реальном времени. Температура может быть преобразована из Фаренгейта в Цельсия.

Пятиклассники используют графики и диаграммы для предоставления информации, которую они можно интерпретировать и сравнивать. Они также создают графики и диаграммы. Они создают сетку с 4 разделами и точками графика с упорядоченными пары целых чисел по горизонтальной оси x и вертикальной оси y.

Предсказание возможных результатов и построение графиков вероятности являются задачами пятиклассник завершает в течение учебного года.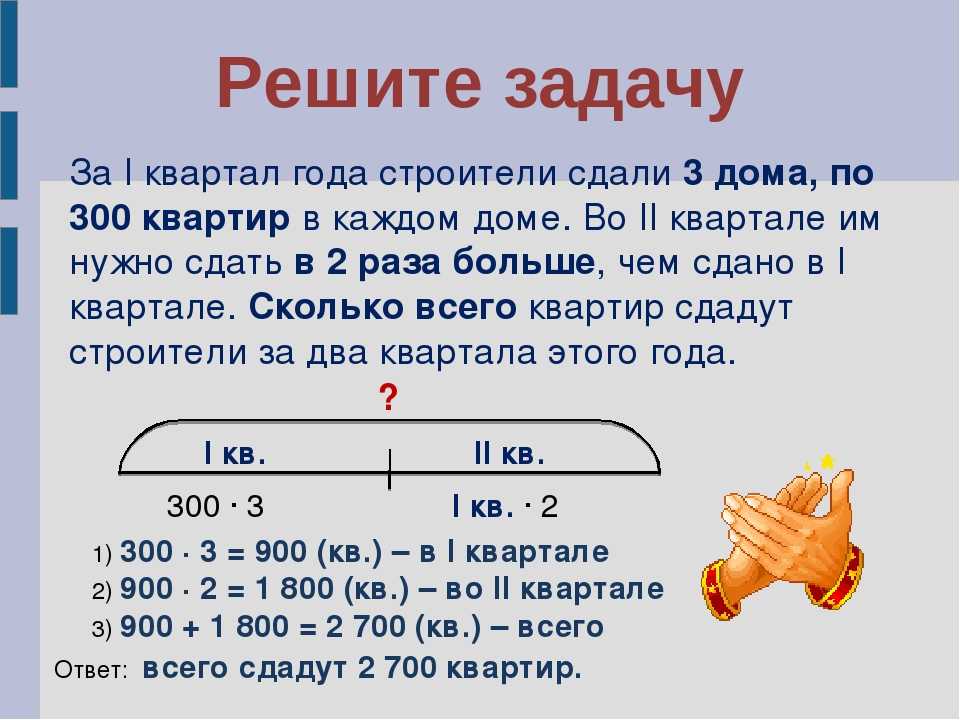

No related posts.