Вертикальные и смежные углы. Н.Никитин Геометрия
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
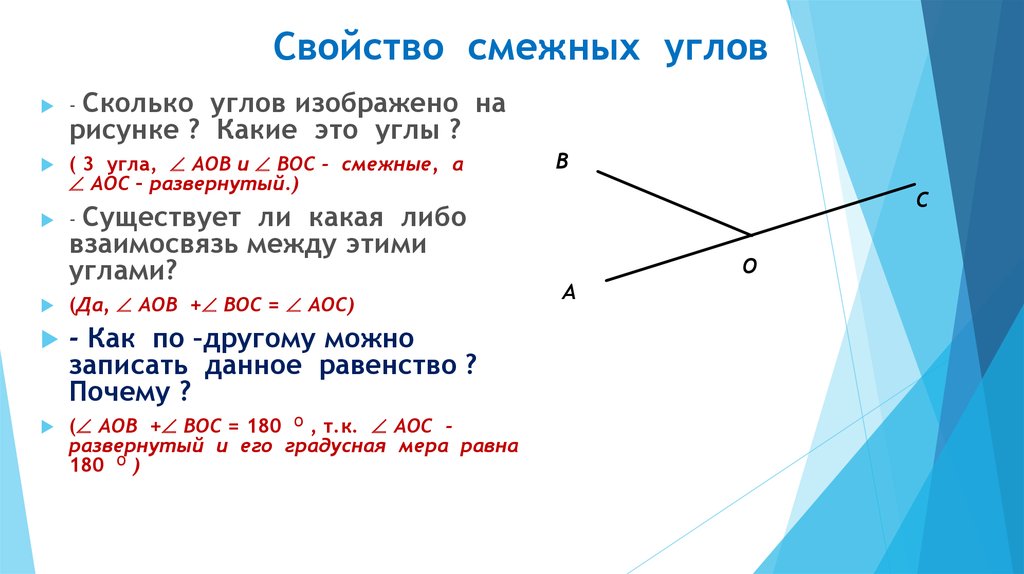
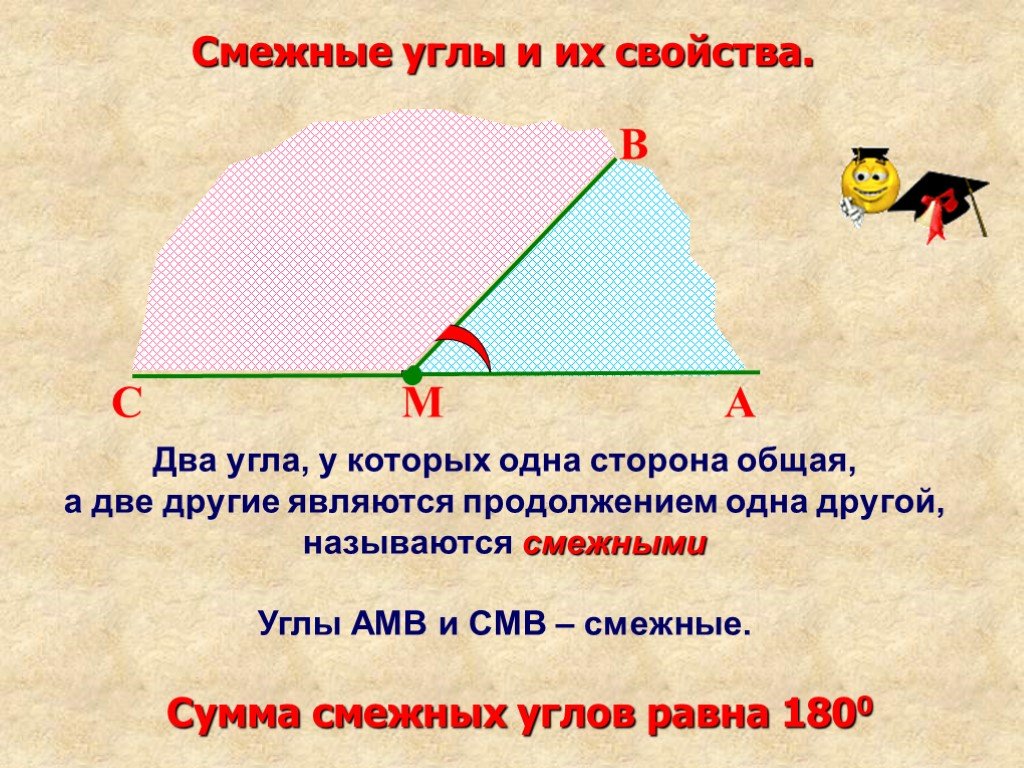
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
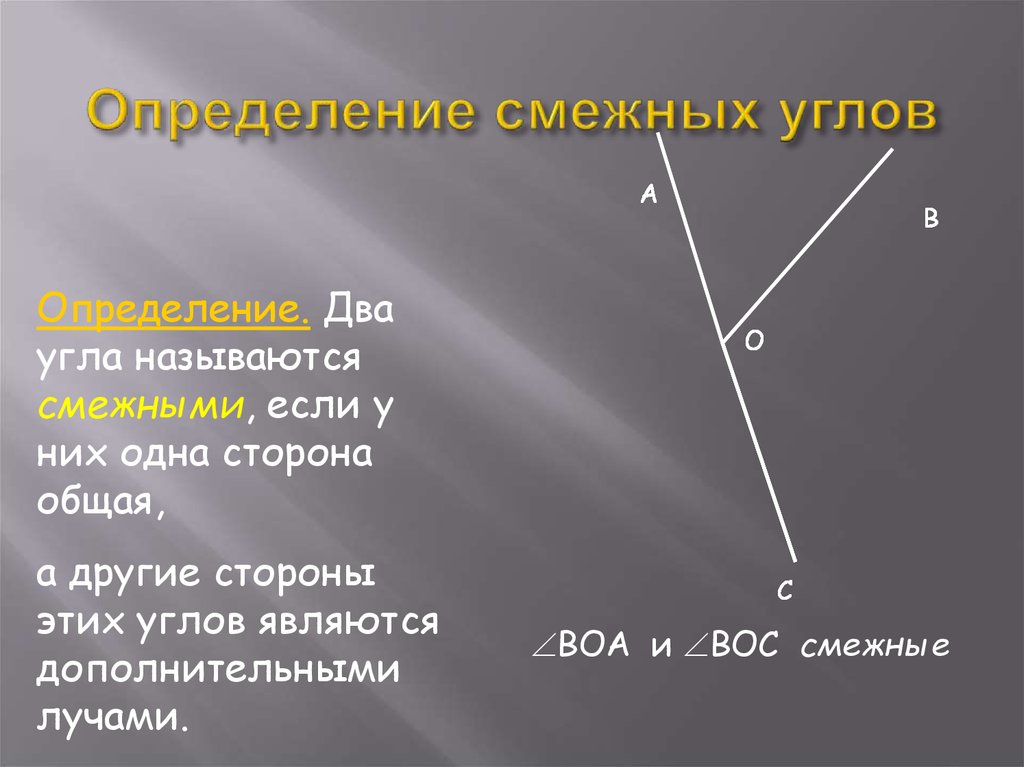
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
по теме: Смежные и вертикальные углы, их свойства.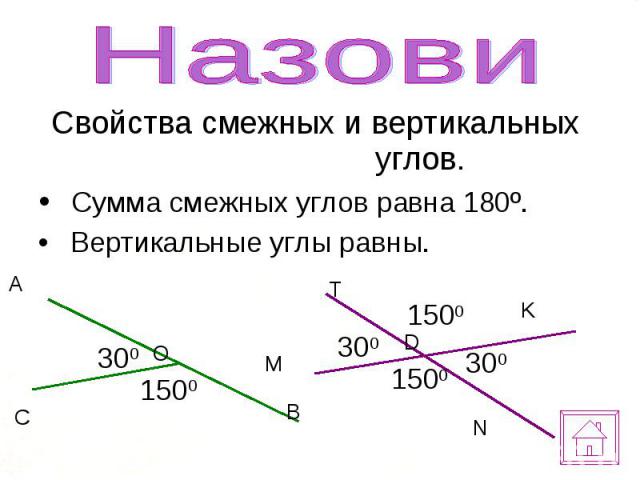
(3 занятия)
В результате изучения темы нужно:
УМЕТЬ:
Понятия: смежных и вертикальных углов, перпендикулярных прямых
Различать понятия смежные и вертикальные углы
Теоремы смежных и вертикальных углов
Решать задачи с использованием свойств смежных и вертикальных углов
Свойства смежных и вертикальных углов
Строить смежные и вертикальные углы, перпендикулярные прямые
ЛИТЕРАТУРА:
1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
2. Геометрия. 7 класс. К.О.Букубаева, А.Т. Миразова. Алматы « Атамұра ». 2012
3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы « Атамұра ». 2012
4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы « Атамұра ». 2012
5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы « Атамұра ». 2012
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях,
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому,
кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
ЗАДАНИЕ №1.
Прочитай определение и выучи (2б):
Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
2) Выучи и запиши в тетрадь теорему: (2б)
Сумма смежных углов равна 180.
Дано:
∠ АОД и ∠ ДОВ –данные смежные углы
ОД — общая сторона
Доказать:
∠ АОД + ∠ ДОВ = 180
Доказательство:
На основе аксиомы III 4:
∠ АОД + ∠ ДОВ = ∠ АОВ.
∠ АОВ — развернутый. Следовательно,
∠ АОД + ∠ ДОВ = 180
Теорема доказана.
3) Из теоремы следует: (2б)
1) Если два угла равны, то смежные с ними углы равны;
2) если смежные углы равны, то градусная мера каждого из них равна 90°.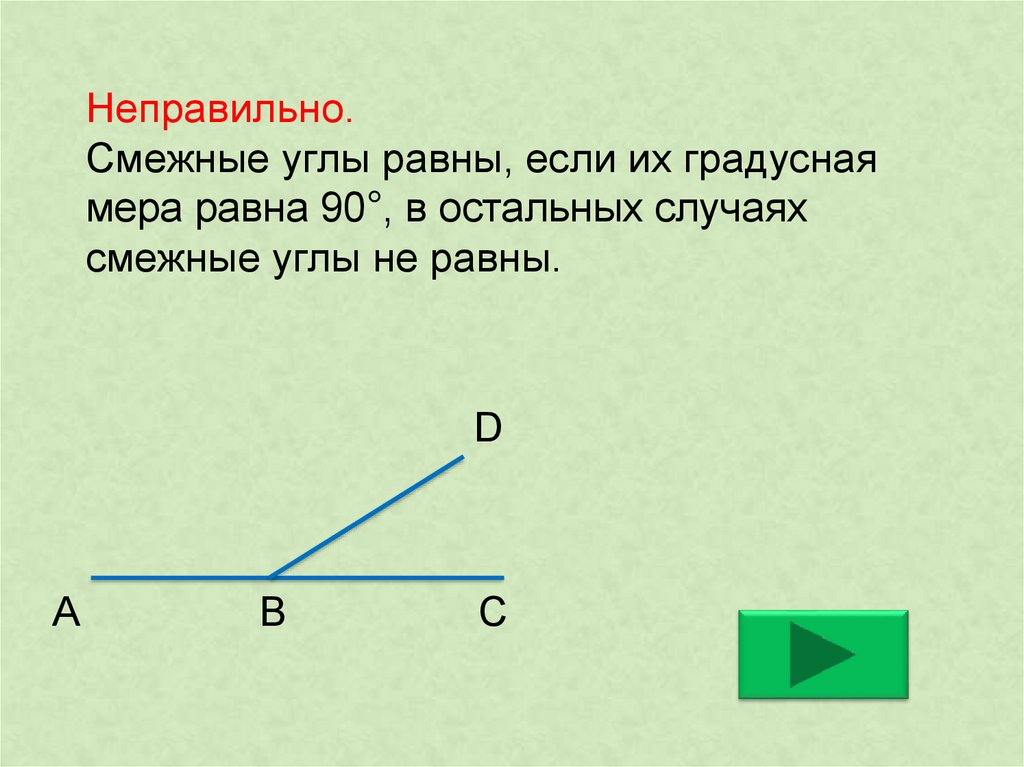
Запомни!
Угол, равный 90°, называется прямым углом.
Угол, меньше 90°, называется острым углом.
Угол, больше 90° и меньше 180°, называется тупым углом.
Прямой угол Острый угол Тупой угол
Так как сумма смежных углов равна 180°, то
1) угол, смежный с прямым углом, прямой;
2) угол, смежный с острым углом, тупой;
3) угол, смежный с тупым углом, острый.
4) Рассмотри образец решения з адачи:
а) Дано: ∠ h k и ∠ kl — смежные; ∠ h k больше ∠ kl на 50° .
Найти: ∠ h k и ∠ kl .
Решение: Пусть ∠ kl = х, тогда ∠ h k = х + 50°. По свойству о сумме смежных углов ∠ kl + ∠ h k = 180°.
х + х + 50° = 180°;
2х = 180° — 50°;
2х = 130°;
х = 65°.
∠ kl = 65°; ∠ h k = 65°+ 50° = 115°.
Ответ: 115° и 65°.
б) Пусть ∠ kl = х, тогда ∠ h k = 3х
х + 3х = 180°; 4х = 180°; х = 45°; ∠ kl = 45°; ∠ hk = 135°.
Ответ: 135° и 45°.
5) Работа с определением смежных углов: (2 б)
6) Найди ошибки в определениях: (2б)
Пройди проверку №1
Задание №2
1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB. (2б)
(2б)
2). Практическая работа на открытие свойства смежных углов: (5б)
Ход работы
1. Построй угол смежный углу а , если а : острый, прямой, тупой.
2. Измерь величины углов.
3.Данные измерений занеси в таблицу.
4. Найди соотношение между величинами углов а и .
5. Сделай вывод о свойстве смежных углов.
Пройди проверку №2
Задание №3
Начертите неразвернутый ∠ АОВ и назовите лучи, являющиеся сторонами этого угла.
Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.
Запишите в тетради: углы ∠ АОВ и ∠ СОД называются вертикальными. (3б)
Выучи и запиши в тетрадь: (4б)
Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.
1 и
Лучи
OF
и
OA
,
OC
и
OE
являются попарно дополнительными лучами.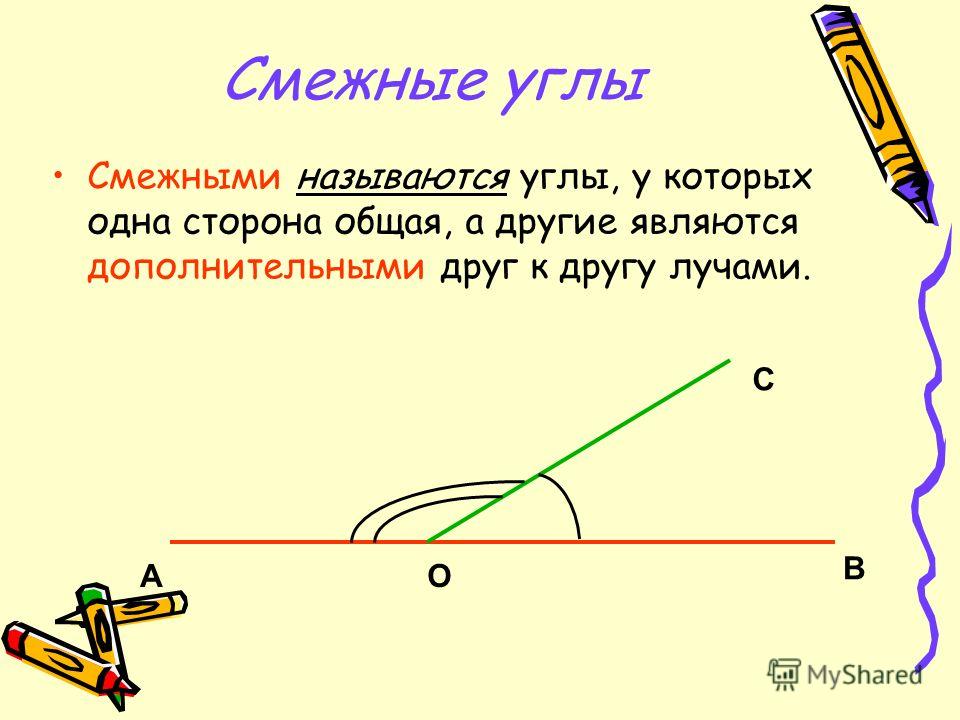
Теорема: Вертикальные углы равны.
Доказательство.
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О. ∠ 1 и ∠ 2 –вертикальные углы.
∠ АОС-развернутый, значит ∠ АОС= 180°. Однако ∠ 1+ ∠ 2= ∠ АОС, т.е.
∠ 3+ ∠ 1= 180°, отсюда имеем:
∠ 1= 180 — ∠ 3. (1)
Также имеем, что ∠ ДОВ= 180°, отсюда ∠ 2+ ∠ 3= 180°, или
Так как в равенствах (1) и (2) прямые части равны, то ∠ 1= ∠ 2.
Теорема доказана.
5). Работа с определением вертикальных углов:(2б)
6) Найди ошибку в определении:(2б).
Пройди проверку №3
Задание №4
1)Практическая работа на открытие свойства вертикальных углов:(5б)
Ход работы:
1.Построй угол β вертикальный углу α , если α :
острый, прямой, тупой.
2.Измерь величины углов.
3.Данные измерений занеси в таблицу
4.Найди соотношение между величинами углов α и β.
5.Сделай вывод о свойстве вертикальных углов.
2)Доказательство свойств смежных и вертикальных углов. (3б)
2) Рассмотри образец решения з адачи.
Задача. Прямые АВ и СД пересекаются в точке О так, что ∠ AOД = 35°. Найдите углы АОС и ВОС.
Решение:
1) Углы АОД и АОС смежные, поэтому ∠ BOC = 180° — 35° = 145°.
2) Углы АОС и ВОС также смежные, поэтому ∠ BOC = 180° — 145° = 35°.
Значит, ∠ BOC = ∠ АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?
3) Решение задач на готовых чертежах: (3б)
1. Найти углы АОВ, АОD, COD.
3) Найти углы BOC, FOA.: (3б)
3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)
Пройди проверку №4
Задание №5
Проверь свои знания, выполнив проверочную работу №1
Задание №6
1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь. (3б)
(3б)
Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.
2) Реши на выбор две задачи:
1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)
2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого.Найдите каждый из углов.(3б)
3.Найдите смежные углы,если их разность и их сумма относятся как 2:9.(3б)
Задание №7
Молодец! Можешь приступать к проверочной работе №2.
Проверочная работа №1.
Реши на выбор любой из вариантов (10б)
Вариант 1
г)
Смежные
д) Начертите (на глаз) угол в 30° и
е) Какие углы называются вертикальными?
Два угла называются вертикальными, если орни равны.
ж) Из точки А провести две прямые, перпендикулярные прямой а
Можно провести только одну прямую.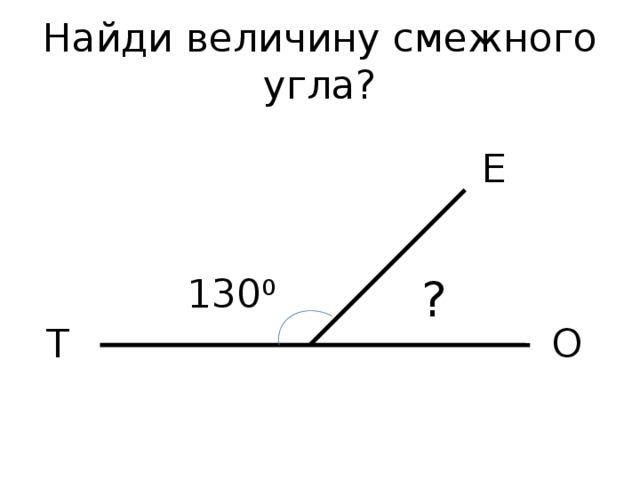
Вариант 2
1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.
Д)
Нет. Они вертикальные
Е) Какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.
2. Назовите вертикальные углы на данном рисунке.
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Проверочная работа №2.
Реши на выбор любой вариант
Вариант I
Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4б)
Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других.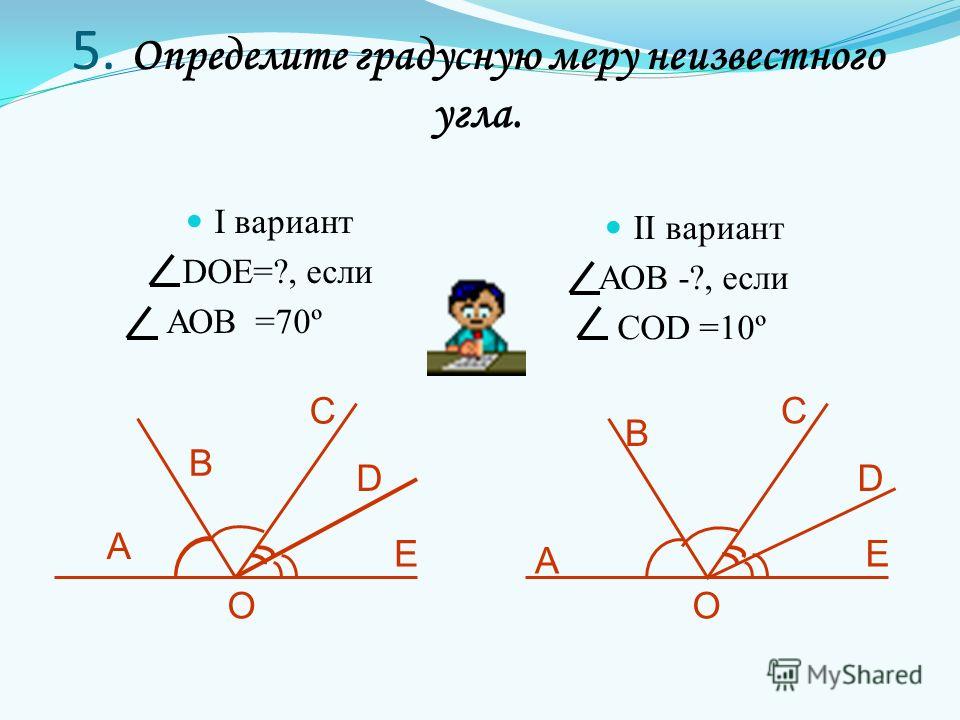 (6б)
(6б)
Вариант II
1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)
2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других.(6б)
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Сумма смежных углов равна 180°
Вертикальные углы — это два угла, у которых стороны одного угла являются продолжение сторон другого.
Вертикальные углы равны.
2. Признаки равенства треугольников:
I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.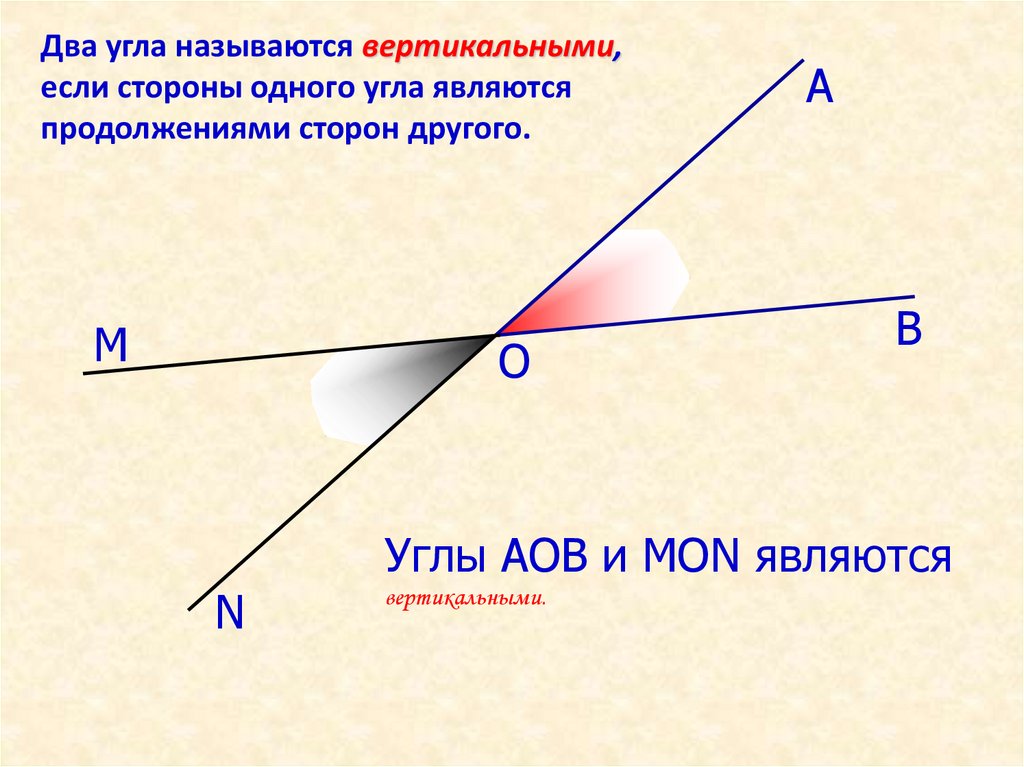
III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
3. Признаки параллельности двух прямых: односторонние углы, накрест лежащие и соответственные:
Две прямые на плоскости называются параллельными , если они не пересекаются.
Накрест лежащие углы: 3 и 5, 4 и 6;
Односторонние углы: 4 и 5, 3 и 6; рис. Стр55
Соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
Теорема : Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Теорема : если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
Теорема : если две параллельные прямые пересечены секущей, то соответственные углы равны
Теорема : если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°
4. Сумма углов треугольника:
Сумма углов треугольника:
Сумма углов треугольника равна 180°
5. Свойства равнобедренного треугольника:
Теорема: В равнобедренном треугольнике углы при основании равны.
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, являетсямедианой и высотой (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90°)
Признак: Если два угла треугольника равны, то треугольник равнобедренный.
6. Прямоугольный треугольник:
Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)
В прямоугольном треугольнике гипотенуза больше катета
1. Сумма двух острых углов прямоугольного треугольника равна 90°
2. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
7.
Сумма углов четырёхугольника равна 2 π = 360°.
Четырёхугольник можно вписать в окружность тогда и только тогда, сумма противоположных углов равна 180°
10. Признаки подобия треугольников:
I признак : если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
III признак : если три стороны одного треугольника порциональны трем сторонам другого, то такие треугольники подобны
11. Формулы:
· Теорема Пифагора: a 2 +b 2 =c 2
· Теорема sin:
· Теорема cos:
· 3 формулы площади треугольника:
· Площадь прямоугольного треугольника: S= S=
· Площадь равностороннего треугольника:
· Площадь параллелограмма: S = ah
· Площадь квадрата: S = a2
· Площадь трапеции:
· Площадь ромба:
· Площадь прямоугольника: S=ab
· Равносторонний треугольник. Высота: h=
Высота: h=
· Тригонометрическая единица: sin 2 a+cos 2 a=1
· Средняя линия треугольника: S=
· Средняя линия трапеции : МК=
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.

Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
На данном уроке мы рассмотрим и уясним для себя понятие смежные углы. Рассмотрим теорему, которая их касается. Введем понятие «вертикальные углы». Рассмотрим опорные факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце занятия рассмотрим несколько задач, посвященных этой теме.
Начнем наш урок с понятия «смежные углы». На рисунке 1 изображен развернутый угол ∠АОС и луч ОВ, который делит данный угол на 2 угла.
Рис. 1. Угол ∠АОС
Рассмотрим углы ∠АОВ и ∠ВОС. Вполне очевидно, что они имеют общую сторону ВО, а стороны АО и ОС являются противолежащими. Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.
Определение: Если два угла имеют общую сторону, а две другие стороны являются дополняющими лучами, то данные углы называются смежными .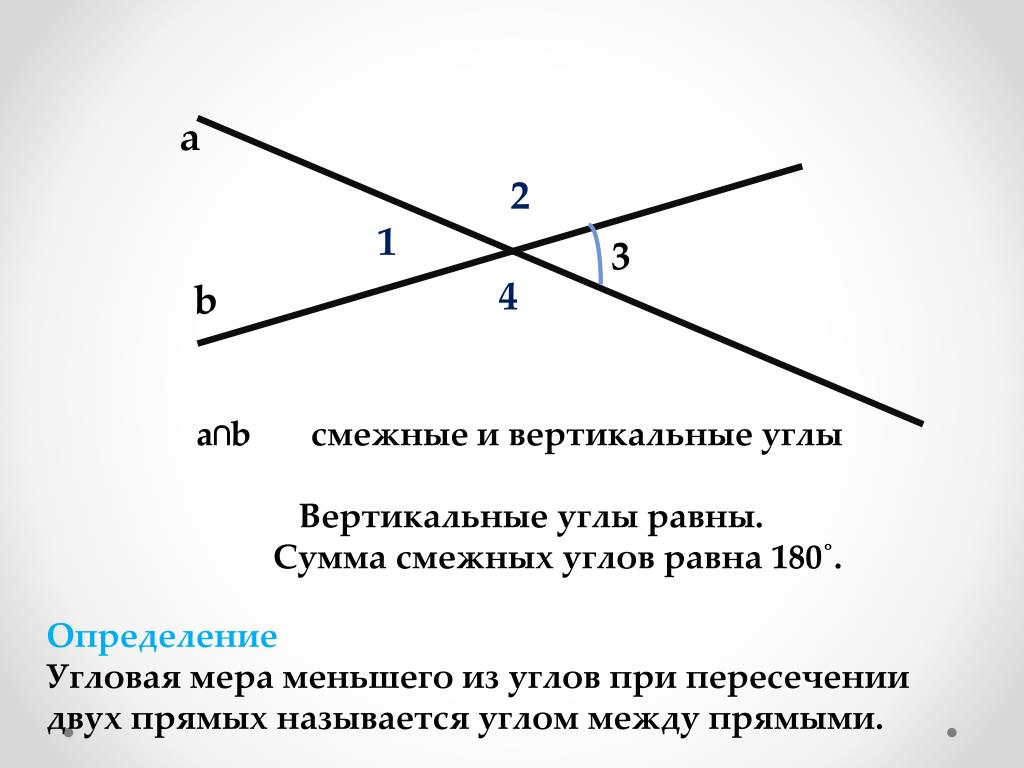
Теорема 1: Сумма смежных углов — 180 о.
Рис. 2. Чертеж к теореме 1
∠МОL + ∠LON = 180 o . Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму — 180 о.
Рассмотрим пересечение двух прямых. На рисунке изображено пересечение двух прямых в точке О.
Рис. 3. Вертикальные углы ∠ВОА и ∠СОD
Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Именно поэтому на рисунке изображено две пары вертикальных углов: ∠АОВ и ∠СОD, а также ∠AOD и ∠ВОС.
Теорема 2: Вертикальные углы равны.
Используем рисунок 3. Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС — ∠ВОС = 180 о — β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD — ∠BОС = 180 о — β.
Из этих соображений мы делаем вывод, что ∠АОВ = ∠СОD = α. Аналогично, ∠AOD = ∠ВОС = β.
Следствие 1: Угол между биссектрисами смежных углов равен 90 о.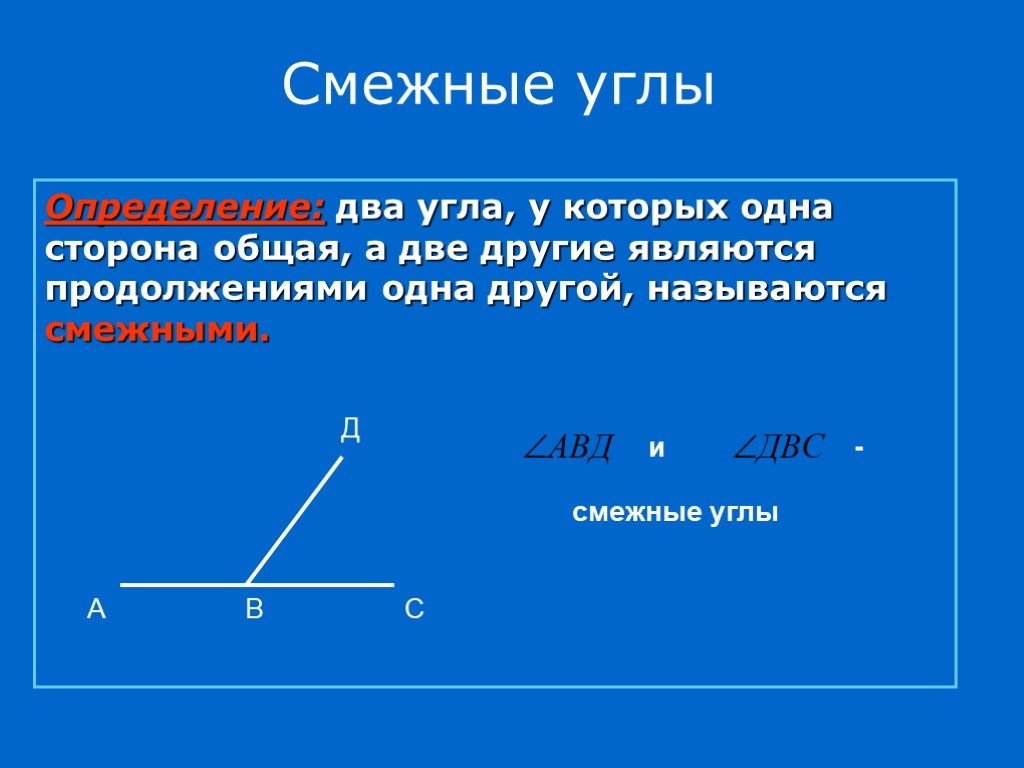
Рис. 4. Чертеж к следствию 1
Поскольку ОL — биссектриса угла ∠ВОА, то угол ∠LOB = , аналогично ∠ВОК = . ∠LOK = ∠LOB + ∠BOK = + = . Сумма углов α + β равна 180 о, поскольку данные углы — смежные.
Следствие 2: Угол между биссектрисами вертикальных углов равен 180 о.
Рис. 5. Чертеж к следствию 2
KO — биссектриса ∠AOB, LO — биссектриса ∠COD. Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Сумма углов α + β равна 180 о, так как данные углы — смежные.
Рассмотрим некоторые задачи:
Найдите угол, смежный с ∠АOС, если ∠АOС = 111 о.
Выполним чертеж к задаче:
Рис. 6. Чертеж к примеру 1
Поскольку ∠АОС = β и ∠СOD = α смежные углы, то α + β = 180 о. То есть 111 о + β = 180 о.
Значит, β = 69 о.
Этот тип задач эксплуатирует теорему о сумме смежных углов.
Один из смежных углов прямой, каким (острым, тупым или прямым) является другой угол?
Если один из углов прямой, а сумма двух углов 180 о, то и другой угол тоже прямой. Эта задача проверяет знания о сумме смежных углов.
Эта задача проверяет знания о сумме смежных углов.
Верно ли, что если смежные углы равны, то они прямые?
Составим уравнение: α + β = 180 о, но поскольку α = β, то β + β = 180 о, значит, β = 90 о.
Ответ: Да, утверждение верно.
Даны два равных угла. Верно ли, что и смежные им углы тоже будут равны?
Рис. 7. Чертеж к примеру 4
Если два угла равны α, то соответствующие им смежные углы будут 180 о — α. То есть они будут равны между собой.
Ответ: Утверждение верно.
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. — М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. — М.: Просвещение.
- \Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Измерение отрезков ().
- Обобщающий урок по геометрии в 7-м классе ().
- Прямая линия, отрезок ().

- № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Найдите два смежных угла, если один из них в 4 раза больше другого.
- Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
- * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?
Смежные углы / Начальные геометрические сведения / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Смежные углы
Смежные углы — это два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
На Рис.1 ОС — общая сторона, ОА и ОВ продолжают друг друга, значит АОС и СОВ — смежные.
Вместе смежные углы составляют развернутый угол, т.е. угол равный 1800. На Рис.1 АОВ = АОС + СОВ = 1800. Значит:
- Зная один из смежных углов, всегда можно найти второй. На Рис.2 СОВ = 350, тогда АОС = 1800 — СОВ = 1800 — 350 = 1450.
- Если один из смежных углов острый, то второй будет тупой и наоборот (Рис.3).
- Если один из смежных углов прямой т.е. равен 900, то второй также будет прямой (Рис.4).
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Длина отрезка
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 55, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 64, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 84, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 152, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 253, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 257, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1059, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Что такое смежные углы? — Определение и примеры
Написано
Малкольм Маккинси
Проверка по фактам
Пол Маззола
Примечание углы.
 Определение
Определение. вершина.
Три признака облегчают выделение смежных углов:
Смежные углы существуют как пары
Они имеют общую вершину
У них общая сторона
Если два угла имеют только общую вершину, то они являются вертикальными углами. Вертикальные углы – это пара противоположных углов, образованных двумя пересекающимися прямыми.
Что такое общая вершина?
Общая вершина является вершиной, которая является общей для двух углов. Вершина — это точка пересечения любых двух линейных построений.
Строка
Отрезок линии
Луч
Вы можете смешивать и сопоставлять их для создания вершин (множественное число от вершины) разными способами:
Что такое общая сторона в геометрии Вы видите вершины в углах многоугольники, как центральные углы в кругах, и когда пересекаются линейные конструкции, такие как параллельные линии и сечения.
Что является общей стороной в геометрии?
Общая сторона – это одна линия, луч или отрезок линии, используемые для создания двух углов, имеющих одну и ту же вершину. Оба угла используют общую сторону и одну другую сторону.
Что такое общая сторона в геометрииСмежные углы всегда парные и никогда не перекрываются.
Посмотрим, как одна вершина квадрата может демонстрировать смежные углы.
Здесь у нас есть простой квадрат, образованный четырьмя сторонами, образующими четыре вершины: ∠W , ∠H , ∠I и ∠Z .
Общая сторона смежных углов примерЕсли мы соединим Точку W с Точкой I , мы построим диагональ WI . Это создает два дополнительных угла в Point W :
omzwi
тнахви
Обратите внимание на оба эти углы. Углы ∠ZWI и ∠HWI являются смежными углами.
Линейные пары
Когда пара смежных углов образует прямую линию или прямой угол, они являются линейной парой. Сумма их углов равна .180° или π радиан.
Сумма их углов равна .180° или π радиан.
Углы, сумма которых равна 180° , называются дополнительными углами. Вот линейная пара. Проверьте, можете ли вы определить общую сторону и общую вершину:
Смежные углы, образующие линейную паруЛуч AT — общий луч обоих углов. Вы определили ∠A как общую вершину?
Параллельные прямые и поперечные
Вот параллельные прямые CP и MN разрезаемые поперечными ИК . Там, где секущая пересекает их, мы имеем точки H и U :
Параллельные прямые и секущуюМало того, что эта конструкция образует восемь пар углов (смежных углов), но все эти пары также являются линейными парами! Какие углы являются смежными углами?
↑CHI и тий
♂ и omchu
onThu . и
omphi и 9
omma и 9
omma
9omma
9 ♂
9 ♂
- .
 ∠PHU
∠PHU ∠CHU and ∠PHU
∠MUK and ∠NUK
∠MUH and ∠NUH
∠MUH и ∠MUK
∠NUH и ∠NUK
Это все примеры смежных углов. Смежные углы могут помочь доказать, что прямые параллельны.
Пример смежных углов
12 мая день рождения Марьям Мирзахани, известного математика, изучавшего особый вид геометрии, называемый гиперболической геометрией. Чтобы отпраздновать ее работу, ваш математический клуб испек торт ко дню рождения и поручил вам разрезать его на восьмые части:
Примеры смежных угловВсе ли углы торта Марьям смежные?
Нет. ∠IMY примыкает к ∠RMI и ∠YMN , но обратите внимание, что ∠RMI не примыкает к ∠YMN , даже если оба угла имеют общую вершину M .
Взаимосвязи углов, такие как смежные углы, должны иметь общую вершину ( Point M ) и общую сторону. ∠RMI не имеет общей стороны с ∠YMN .
∠RMI не имеет общей стороны с ∠YMN .
Сможете ли вы найти линейные пары в торте Марьям? Мы надеемся на это! Для каждого диаметра торта Марьям существует трех линейных пар!
Чтобы увидеть это, мы можем взять только один отрезок линии, YA , в качестве примера. Вы можете создать прямую линию YA with these three linear pairs:
∠YMI and ∠IMA
∠YMR and ∠RMA
∠YMZ and ∠ZMA
Смежные углы — это два угла, имеющие общую вершину и общую сторону. Они появляются во многих местах, но выделяются параллельными линиями, пересекаемыми поперечными линиями.
Что такое смежные углы? Определения и примеры — Блог StudySoup
Смежные углы — это два угла, которые имеют общую сторону, а также общую вершину, но не пересекаются.
Если отсутствует одно из этих свойств, то это просто не смежный угол. Проще говоря, это два угла, которые находятся рядом друг с другом. Давайте разберем общие термины, которые мы используем, когда говорим о них.
Проще говоря, это два угла, которые находятся рядом друг с другом. Давайте разберем общие термины, которые мы используем, когда говорим о них.
Другие важные определения
Прежде чем углубляться в детали, следует помнить о других важных определениях:
•Общая вершина: точка пересечения, которая является общей для двух или более лучей или линий.
•Общая сторона это одна линия, луч или отрезок, используемые для создания двух углов, имеющих одну и ту же вершину. Оба угла используют общую сторону и одну другую сторону.
• Луч — это линия с фиксированной начальной точкой, но неопределенной конечной точкой.
• Отрезок линии — это линия с двумя конечными точками.
Теперь, когда мы определили основную идею того, что они собой представляют, давайте обсудим, как их идентифицировать. Вот шесть основных свойств, которые вам необходимо знать:
Вот шесть основных свойств, которые вам необходимо знать:
• У них общая сторона и вершина.
•Они никогда не пересекаются.
•С обеих сторон общего плеча всегда есть нестандартное плечо.
• Они могут быть дополнительными (сумма мер до 90˚) или дополнительными (сумма мер до 180˚), если они имеют общий угол.
Как определить смежные углыЕсть два свойства, которые помогут вам легко их идентифицировать: Если они имеют общую сторону (плечо) и вершину. Если в двух углах выполняется только одно из этих свойств, то они не являются смежными углами.
Примеры
В реальном мире вы можете увидеть много примеров смежных углов, таких как:
- Два соединенных куска пиццы со средним разделителем, являющимся общей стороной.
- Часовая, минутная и секундная стрелки на часах.
Линейные пары
Одним из наиболее распространенных примеров в геометрии является линейная пара, в которой два угловых измерения складываются в прямой угол (180˙). Вот пример:
Вот пример:
Смежные углы равны?
Иногда они могут совпадать. «Конгруэнтный» означает точно равный по форме, а «примыкающий» означает «рядом с». Таким образом, когда два угла имеют точно такое же измерение угла, они равны. Но, если они не совпадают, они не будут считаться конгруэнтными.
Смежные и несмежные углы могут быть дополнительными, если их сумма составляет 90 градусов. Два угла называются дополнительными, если их сумма равна 90 градусам.
Смежные углы равны 180? Смежные углы могут быть равны 180˙, но не во всех случаях. Как упоминалось выше, дополнительные смежные углы в сумме дают 180˙, но если смежные углы не являются линейными парами, то они не будут составлять в сумме 180˙.
• Нарисуйте и обозначьте два смежных угла, сумма мер которых равна 90˙
• Используйте термины смежные углы, линейная пара или ни один из них, чтобы описать углы 1 и 2 в таком количестве способами, насколько это возможно.