ОглавлениеПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРАПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ Глава 1.  ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗАГлава 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА 2. Недостаточность рациональных чисел для измерения отрезков числовой оси. 3. Упорядочение множества бесконечных десятичных дробей. § 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ) МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ 2. Существование точных граней. § 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ, РАЦИОНАЛЬНЫМИ ЧИСЛАМИ § 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ. ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Существование и единственность суммы и произведения вещественных чисел. § 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Некоторые часто употребляемые соотношения. 3. Некоторые конкретные множества вещественных чисел. § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Аксиоматическое введение множества вещественных чисел. § 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ 2. Операции над множествами. 3. Счетные и несчетные множества. Несчетность сегмента [0, 1].  Мощность множества.4. Свойства операций над множествами. Отображение множеств. Глава 3. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ 2. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности. 3. Основные свойства бесконечно малых последовательностей. 4. Сходящиеся последовательности и их свойства. § 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ 2. Теорема о сходимости монотонной ограниченной последовательности. 4. Примеры сходящихся монотонных последовательностей. § 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ 2. Расширение понятий предельной точки и верхнего и нижнего пределов. 3. Критерий Коши сходимости последовательности. § 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ) ФУНКЦИИ 2. Предел функции по Гейне и по Коши. 4. Арифметические операции над функциями, имеющими предел. 5. Бесконечно малые и бесконечно большие функции. § 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ Глава 4.  НЕПРЕРЫВНОСТЬ ФУНКЦИИ§ 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ 2. Арифметические операции над непрерывными функциями. 3. Сложная функция и ее непрерывность. § 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ 2. Понятие обратной функции. § 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 2. Логарифмическая функция. 3. Степенная функция. 4. Тригонометрические функции. 5. Обратные тригонометрические функции. 6. Гиперболические функции. § 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА 2. Второй замечательный предел. § 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ 2. О точках разрыва монотонной функции. § 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 2. Глобальные свойства непрерывных функций. 3. Понятие равномерной непрерывности функции. 4. Понятие модуля непрерывности функции. § 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА 2. О покрытиях множества системой открытых множеств. 3. Понятие компактности множества. Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 1. ПОНЯТИЕ ПРОИЗВОДНОЙ 2.  Определение производной.3. Геометрический смысл производной. § 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ 2. Дифференцируемость и непрерывность. 3. Понятие дифференциала функции. § 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ 2. Дифференцирование обратной функции. 3. Инвариантность формы первого дифференциала. 4. Применение дифференциала для установления приближенных формул. § 4. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ § 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 3. Производные показательной и обратных тригонометрических функций. 4. Производная степенной функции. 5. Таблица производных простейших элементарных функций. 6. Таблица дифференциалов простейших элементарных функций. 7. Логарифмическая производная. Производная степенно-показательной функции. § 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. n-ые производные некоторых функций. 3.  Формула Лейбница для n-й производной произведения двух функций.4. Дифференциалы высших порядков. § 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ § 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ Глава 6. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ § 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ § 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ § 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА ЛАГРАНЖА) § 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА 2. Условия монотонности функции на интервале. 3. Отсутствие разрывов первого рода и устранимых разрывов у производной. 4. Вывод некоторых неравенств. § 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА КОШИ) § 6. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ) 2. Раскрытие неопределенности вида oo/oo 3. Раскрытие неопределенностей других видов. § 7. ФОРМУЛА ТЕЙЛОРА § 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА. ФОРМУЛА МАКЛОРЕНА 2. Другая запись формулы Тейлора. 3. Формула Маклорена. § 9.  ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ2. Разложение по формуле Маклорена некоторых элементарных функций. § 10. ПРИМЕРЫ ПРИЛОЖЕНИЙ ФОРМУЛЫ МАКЛОРЕНА 2. Доказательство иррациональности числа е. 3. Вычисление значений тригонометрических функций. Глава 7. ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ § 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК 2. Отыскание стационарных точек. 3. Первое достаточное условие экстремума. 4. Второе достаточное условие экстремума. 5. Третье достаточное условие, экстремума. 6. Экстремум функции, недифференцируемой в данной точке. 7. Общая схема отыскания экстремумов. § 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ § 3. ТОЧКИ ПЕРЕГИБА 2. Первое достаточное условие перегиба. 3. Некоторые обобщения первого достаточного условия перегиба. 4. Второе достаточное условие перегиба. 5. Третье достаточное условие перегиба.  § 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ § 6. ГЛОБАЛЬНЫЕ МАКСИМУМ И МИНИМУМ ФУНКЦИИ НА СЕГМЕНТЕ. КРАЕВОЙ ЭКСТРЕМУМ 2. Краевой экстремум. 3. Теорема Дарбу. ДОПОЛНЕНИЕ Алгоритм отыскания экстремальных значений функции, использующий только значения этой функции Глава 8. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Неопределенный интеграл. 3. Основные свойства неопределенного интеграла. 4. Таблица основных неопределенных интегралов. § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование по частям. § 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ в ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Краткие сведения о корнях алгебраических многочленов. 3. Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей. 4. Разложение правильной рациональной дроби на сумму простейших дробей. 5. Интегрируемость рациональной дроби в элементарных функциях. 6. Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений.  § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА ИНТЕГРАЛ РИМАНА: § 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА 2. Основные свойства верхних и нижних сумм. § 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ. КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ 2. Классы интегрируемых функций. § 4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОЦЕНКИ ИНТЕГРАЛОВ. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ 2. Оценки интегралов. § 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ. ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ 2. Основная формула интегрального исчисления. 3. Важные правила, позволяющие вычислять определенные интегралы. 4. Остаточный член формулы Тейлора в интегральной форме. § 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ 2. Неравенство Гёльдера для сумм. 3. Неравенство Минковского для сумм. 4. Неравенство Гёльдера для интегралов. 5. Неравенство Минковского для интегралов. § 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА 2. Критерий интегрируемости Лебега.  ДОПОЛНЕНИЕ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Критерий Коши сходимости несобственного интеграла первого рода. 3. Абсолютная и условная сходимость несобственных интегралов. 4. Замена переменных под знаком несобственного интеграла и формула интегрирования по частям. § 2. Несобственные интегралы второго рода § 3. Главное значение несобственного интеграла ДОПОЛНЕНИЕ 2. Интеграл Стилтьеса 2. Свойства интеграла Стилтьеса. Глава 10. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. ДЛИНА ДУГИ КРИВОЙ 2. Понятие параметризуемой кривой. 3. Длина дуги кривой. Понятие спрямляемой кривой. 4. Критерий спрямляемости кривой. Вычисление длины дуги кривой. 5. Дифференциал дуги. 6. Примеры. § 2. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ 2. Площадь плоской фигуры. 3. Площадь криволинейной трапеции и криволинейного сектора. § 3. ОБЪЕМ ТЕЛА В ПРОСТРАНСТВЕ 2. Некоторые классы кубируемых тел. 3. Примеры. Глава 11.  m.3. Предел функции m переменных. 4. Бесконечно малые функции m переменных. 5. Повторные пределы. § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ 2. Непрерывность функции m переменных по одной переменной. 3. Основные свойства непрерывных функций нескольких переменных. § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Дифференцируемость функции нескольких переменных. 3. Геометрический смысл условия дифференцируемости функции двух переменных. 4. Достаточные условия дифференцируемости. 5. Дифференциал функции нескольких переменных. 6. Дифференцирование сложной функции. 7. Инвариантность формы первого дифференциала. 8. Производная по направлению. Градиент. § 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. Дифференциалы высших порядков. 3. Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме. 4. Формула Тейлора с остаточным членом в форме Пеано. § 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m ПЕРЕМЕННЫХ 2.  Достаточные условия локального экстремума функции m переменных.3. Случай функции двух переменных. ДОПОЛНЕНИЕ 1. Градиентный метод поиска экстремума сильно выпуклой функции 1. Выпуклые множества и выпуклые функции. 2. Существование минимума у сильно выпуклой функции и единственность минимума у строго выпуклой функции. 3. Поиск минимума сильно выпуклой функции. ДОПОЛНЕНИЕ 2. Метрические, нормированные пространства 2. Открытые и замкнутые множества. 3. Прямое произведение метрических пространств. 4. Всюду плотные и совершенные множества. 5. Сходимость. Непрерывные отображения. 6. Компактность. 7. Базис пространства. Топологические пространства Линейные нормированные пространства, линейные операторы ДОПОЛНЕНИЕ 3. Дифференциальное исчисление в линейных нормированных пространствах 2. Формула Лагранжа конечных приращений. 3. Связь между слабой и сильной дифференцируемостью. 4. Дифференцируемость функционалов. 5. Интеграл от абстрактных функций.  6. Формула Ньютона — Лейбница для абстрактных функций. 7. Производные второго порядка. 8. Отображение m-мерного евклидова пространства в n-мерное. 9. Производные и дифференциалы высших порядков. 10. Формула Тейлора для отображений одного нормированного пространства в другое. Исследование на экстремум функционалов в нормированных пространствах 2. Достаточные условия экстремума. Глава 13. НЕЯВНЫЕ ФУНКЦИИ § 1. СУЩЕСТВОВАНИЕ И ДИФФЕРЕНЦИРУЕМОСТЬ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ 2. Вычисление частных производных неявно заданной функции. 3. Особые точки поверхности и плоской кривой. 4. Условия, обеспечивающие существование для функции y=f(x) обратной функции. § 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ 2. Вычисление частных производных функций, неявно определяемых посредством системы функциональных уравнений. 3. Взаимно однозначное отображение двух множеств m-мерного пространства. § 3. ЗАВИСИМОСТЬ ФУНКЦИЙ 2. Функциональные матрицы и их приложения.  § 4. УСЛОВНЫЙ ЭКСТРЕМУМ 2. Метод неопределенных множителей Лагранжа. 3. Достаточные условия. 4. Пример. ДОПОЛНЕНИЕ Отображения банаховых пространств. Аналог теоремы о неявной функции 2. Случай конечномерных пространств. 3. Особые точки поверхности в пространстве n измерений. Обратное отображение. 4. Условный экстремум в случае отображений нормированных пространств. |
Второй замечательный предел, формула и доказат-во
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Пределы Второй замечательный предел
Формула второго замечательного предела
Число – число Эйлера, является основанием натурального логарифма.
Доказательство второго замечательного предела
Для доказательства нам будет необходим бином Ньютона:
где – факториал натурального числа .
Рассмотрим последовательность и применим к ней формулу бинома Ньютона при :
Сокращаем в каждом слагаемом числитель со вторым множителем в знаменателе первого множителя (кроме первых двух слагаемых). В результате получаем:
Оценим преобразованную последовательность сверху. В каждом слагаемом (кроме первого) дроби являются правильными дробям (для натуральных числитель меньше знаменателя), а значит их значение меньше единицы. Заменим каждую из таких дробей единицей, тогда последняя сумма увеличится. То есть
Далее, заменим все числа в знаменателях оставшихся слагаемых на 2, тем самым еще увеличив сумму (так как чем меньше знаменатель, тем дробь больше):
В правой части получилась сумма членов бесконечно убывающей геометрической прогрессии .
Она равна
Поэтому
Таким образом, последовательность ограничена сверху числом 3.
Покажем теперь, что последовательность . Перепишем последовательность следующим образом:
Запишем теперь , для этого в выражении для заменим на :
Каждое из выражений в круглых скобках увеличилось (так как уменьшилось вычитаемое) а, значит, увеличились и все слагаемые, содержащие такие скобки. Число слагаемых также увеличится на одно: добавится положительное слагаемое
Следовательно, при росте номера члены последовательности строго возрастают: .
Тогда, согласно теореме, всякая возрастающая ограниченная сверху последовательности имеет предел
причём число (здесь 3 – число, ограничивающее последовательность ).
Что и требовалось доказать.
Докажем теперь, что второй замечательный предел имеет место для вещественных , то есть докажем следующую теорему.
Доказательство. Рассмотрим два случая:
1. Пусть . Каждое значение заключено между двумя положительными целыми числами
где – целая часть , то есть такое наибольшее целое число, которое не превосходит . Тогда
А тогда
Если , то . Поэтому, согласно тому, что предел , имеем:
А тогда по теореме о пределе промежуточной функции получаем, что и
2. Пусть . Сделаем подстановку , тогда
Из двух этих делаем вывод, что
Теорема доказана.
Следствия из второго замечательного предела
Примеры решения задач
Подобным образом находятся пределы функций вида (при условии, что имеется неопределенность типа )
Замечание. Не любые пределы величин вида вычисляются с помощью сведения ко второму замечательному пределу. Так надо поступать лишь в случае, когда имеем неопределенность типа .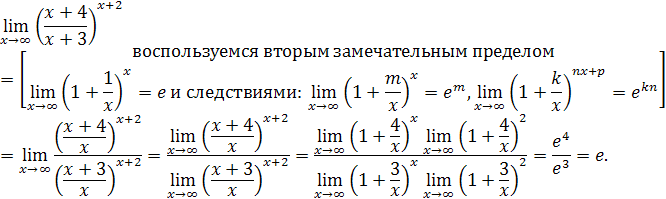
В иных ситуациях можно бывает для вычисления предела обойтись более простыми рассуждениями, а также учесть тот факт, что
| Понравился сайт? Расскажи друзьям! | |||
Чудесные пределы в математике: Часть 2 | Надежда Гут
В предыдущей части мы говорили о некоторых пределах в теории пределов, которые считаются замечательными. Если вы еще не читали, позвольте мне дать вам краткий обзор. Термин «Чудесные пределы» широко известен в постсоветских странах, и таких пределов два. Второй:
Этот лимит представляет собой введение номера e . Вы знаете, показатель степени — это «волшебное» число в математике, поэтому этот предел еще называют чудесным.
На самом деле, мы не можем просто доказать, что предел равен показателю степени, потому что показатель степени является значением этого предела по определению.
Итак, здесь нам нужно доказать , что последовательность (1 + 1/ x ) ˣ имеет предел, когда x приближается к бесконечности . Это доказательство сложнее, чем предыдущее, поэтому, если вы не хотите читать его полностью, можете пропустить эту часть.
Чтобы доказать утверждение, я буду использовать «Теорему о сходимости монотонной ограниченной последовательности действительных чисел» для возрастающей последовательности. В нем указано, что:
Если последовательность действительных чисел является возрастающей и ограниченной сверху, то ее верхняя грань является пределом.
Сначала докажем, что последовательность (1 + 1/ n ) ⁿ ограничивается , когда n стремится к бесконечности, а n является натуральным числом . Это поможет нам получить полное доказательство
По биномиальной теореме мы имеем:
Как вы, возможно, уже знаете, когда n растет, 1/ n уменьшается.
Следовательно, если взять противоположные значения, то последовательность (1–1/ n ), (1–2/ n ) … становится все больше. Вот почему (1 + 1/ n ) ⁿ — возрастающая последовательность, и, следовательно, — монотонная. Итак, мы только что доказали, что последовательность удовлетворяет первой части теоремы.
Теперь нам нужно показать, что эта последовательность ограничена:
Используя формулу суммы геометрической прогрессии, мы получаем следующее неравенство для второго компонента правой части приведенного выше неравенства:
Итак, просуммировав части выражения, получим верхнюю границу последовательности:
И вот мы здесь! Последовательность расположена между 2 и 3 на реальной строке. Итак, он ограничен и монотонен ⇒ у него есть предел (назовем его e )
Это довольно сложно. Нам нужно рассмотреть две ситуации: когда x приближается к +∞ и –∞.
Вы знаете, что любое положительное вещественное число расположено между двумя целыми положительными числами (или 0).
Например, 37,55435 расположено между 37 и 38. В этом примере 37 — это целая часть нашего числа. Обычно мы пишем это как [ х ]. Итак, x всегда удовлетворяет следующему неравенству: [ x ] ≤ x ≤ [ x ] + 1. Поэтому мы можем утверждать, что:
Таким образом, мы получаем, что:
Мы знаем предел из (1 + 1/ n ) ⁿ , давайте использовать его!
По теореме сжатия мы получаем доказательство нашего утверждения, когда x приближается к + бесконечности.
Здесь заменим — x на на . Итак, получаем:
Наконец-то мы здесь! Это очень длинное доказательство, и не доверяйте веб-сайтам, которые пытаются доказать это вкратце, используя натуральные логарифмы и сам показатель степени. Этот предел является введением в экспоненту, и нам нужно действовать так, как будто мы ничего не знаем об этом «загадочном» числе.
Есть много причин, по которым математики так любят показатель степени, но это тема для другой статьи.
Но этот предел прекрасен тем, что знакомит нас с этим числом.
Надеюсь, вам понравилось читать это доказательство (и первую часть тоже)! До встречи в следующих математических статьях!
исчисление — Поиск формулы для конкретных пределов
Вот общий подход к поиску рациональной функции, которая имеет искомое поведение. В частности, я предполагаю, что вы получили следующее:
Значения $f$ в определенных точках равны нулю.
Пределы приближения $f$ к определенным точкам сверху или снизу равны $\pm \infty$; эти точки включают $x \to \pm \infty$, где предел также может быть указан как $0$.
Я предполагаю, что указанная функция не должна иметь других «бесконечностей», кроме указанных, но может иметь и другие нули . Далее мне нужно будет предположить, что пределы при $x \to \pm \infty$ одинаковы, либо оба нули, либо обе бесконечности (возможно, разных знаков), либо задача не может быть решена с помощью рациональных функций. Однако в конце я упомяну способ справиться с этим, используя экспоненты.
- [Выберите точки останова] Запишите точки останова (те, для которых задано поведение ограничения — либо «имеет значение 0», либо «переход к $+\infty$», либо «переход к $-\infty$»). Назовите их $a_1, a_2, \ldots n_k$, в вашем случае это
$$ а_1 = 0\\ а_2 = 2 \\ а_3 = 3, $$ и $k = 3$, потому что точек останова 3, а $$ b_0 = -1\\ б_1 = 1\\ б_2 = 2,5\ б_3 = 4. $$
Нам также понадобится поведение $x \to \pm \infty$, но оставим это на потом.
Для каждой пары точек останова выберите другую точку между ними с дополнительными точками на концах:
\begin{align} б_0 = а_1 — 1 \ b_1 = \frac{1}{2} (a_1 + a_2) \\ \ldots b_{k-1} = \frac{1}{2} (a_{k-1} + a_k) \\ б_{к} = а_к + 1 \end{выравнивание} 9{м_к} $$ Мы собираемся выбрать показатели степени $n_i$ равными $+1, -1,$ или $-2$, а показатели степени $m_i$ равными либо $0$, либо $1$.
(a) Если значение в $a_i$ равно нулю, выберите $n_i = 1$.
(b) Если предел с обеих сторон равен $+\infty$ или с обеих сторон равен $-\infty$, выберите $n_i = -2$.
{-}} = -\infty
$$
Тогда функция должна менять знаки на интервале $[2, 5]$; в этом случае мы устанавливаем показатель степени $m_3$ для $(x — b_3)$ равным $+1$.
С другой стороны, если между контрольными точками нет смены знака, установите показатель степени $m_i$ для этого интервала равным нулю.
Если указано, что ваша функция имеет значение $0$ в каком-то $a_i$, вы должны рассматривать ее как изменение знака в этом месте.
Давайте применим это к вашему примеру:
При $-\infty$ значение равно $0$. Можно предположить, что по мере приближения к $-\infty$ мы приближаемся к нулю сверху, поэтому будем говорить, что значение на первом интервале, $-\infty < x < 0$, положительно на левом конце, но становится отрицательным вблизи $x = 0$ (поскольку предел в 0 равен $-\infty$). Итак, используя правило d, мы выбираем $m_0 = 1$.
При $x = a_1 = 0$ предел с обеих сторон равен $-\infty$, поэтому правило $b$ говорит $n_1 = -2$.
На интервале $0 < x < 2$ (т.
е. от $a_1$ до $a_2$) функция должна перейти от $-\infty$ к $0$; мы сделаем его всегда отрицательным — это самый простой выбор — поэтому $m_1 = 0$. При $x = a_2 = 2$ функция должна быть равна нулю, поэтому правило «a» говорит, что $n_2 = 1$. А правило «знак меняется при нуле» говорит, что справа от $a_2$ функция положительна.
На интервале $2 < x < 3$, т. е. $a_2 < x < a_3$, функция начинается положительной и должна достигать $+\infty$, поэтому мы будем делать ее положительной все время, т. е. выберем $m_2 = 0$. Пределы с противоположных сторон при $x = a_3 = 3$ имеют противоположные знаки, поэтому правило "c" гласит, что $n_2 = -1$. 92 (х-3)}. $$ Остается только один вопрос: корректны ли пределы $f_1$ при $x \to \pm \infty$.
- [Настроить пределы на бесконечность] Пусть $n$ — сумма всех показателей в $f_1$. В нашем случае это $n = 1 + 1 + (-2) + (-1) = -1$.
Сейчас несколько дел.
Случай 1: нет назначенной точки останова с бесконечностью; в этом случае были указаны только нули.