Смежный угл: Смежные и вертикальные углы | Геометрия

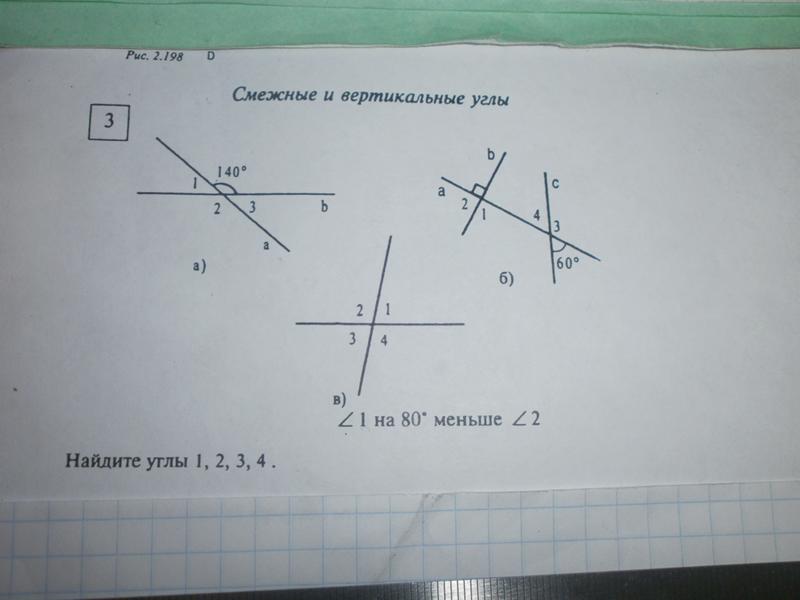
Что такое смежные углы: определение, теорема, свойства

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое смежные углы: определение, теорема, свойства

В данной публикации мы рассмотрим, что из себя представляют смежные углы, приведем формулировку теоремы касательно них (в т.ч. следствия из нее), а также перечислим тригонометрические свойства смежных углов.

• Определение смежных углов
• Теорема о смежных углах
• Тригонометрические свойства смежных углов

Определение смежных углов

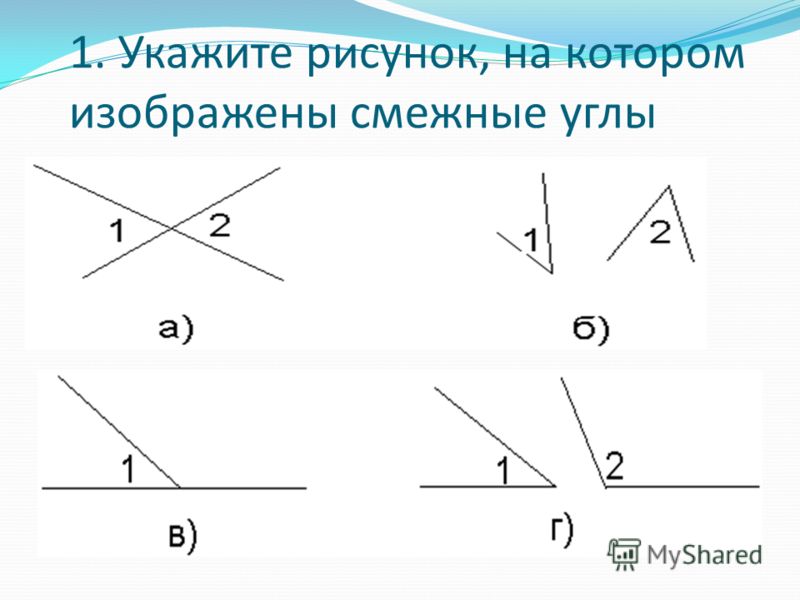
Два прилежащих угла, внешними сторонами образующие прямую, называется смежными. На рисунке ниже это углы α и β.

Если два угла имеют одну общую вершину и сторону, они являются прилежащими. При этом внутренние области этих углов не должны пересекаться.

Принцип построения смежного угла

Одну из сторон угла протягиваем через вершину дальше, в результате чего образуется новый угол, смежный с исходным.

Теорема о смежных углах

Сумма градусов смежных углов равняется 180°.

Смежн. угол 1 + Смежн. угол 2 = 180°

Пример 1
Один из смежных углов равняется 92°, чему равен второй?

Решение, согласно рассмотренной выше теореме, очевидно:
Смежн. угол 2 = 180° – Смежн. угол 1 = 180° – 92° = 88°.

Следствия из теоремы:

• Смежные углы двух равных углов равны между собой.
• Если угол является смежным с прямым (90°), значит он также равен 90°.
• Если угол является смежным с острым, значит он больше 90°, т.е. является тупым (и наоборот).

Пример 2
Допустим, у нас есть угол, смежный с 75°. Он должен быть больше 90°. Давайте проверим это.

Воспользовавшись теоремой, находим значение второго угла:
180° – 75° = 105°.

105° > 90°, следовательно угол является тупым.

Тригонометрические свойства смежных углов

1. Синусы смежных уголов равны, т. е. sin α = sin β.
2. Величины косинусов и тангенсов смежных углов равны, но имеют противоположные знаки (кроме неопределенных значений).
   • cos α = -cos β.
   • tg α = -tg β.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Как определить смежные и вертикальные углы.

Какие углы называются смежными? Чему равна сумма двух смежных углов

В процессе изучения курса геометрии понятия “угол”, “вертикальные углы”, “смежные углы” встречаются достаточно часто. Понимание каждого из терминов поможет разобраться в поставленной задаче и правильно ее решить. Что такое смежные углы и как их определять?

Смежные углы – определение понятия

Термин “смежные углы” характеризует два угла, образованных общим лучом и двумя дополнительными полупрямыми, лежащими на одной прямой. Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.

Смежные углы – основные свойства

1. Исходя из формулировки смежных углов, нетрудно заметить, что сумма таких углов всегда образует развернутый угол, градусная мера которого равна 180°:

• Если μ и η являются смежными углами, то μ + η = 180°.
• Зная величину одного из смежных углов (например, μ), можно легко вычислить градусную меру второго угла (η), используя выражение η = 180° – μ.

2. Данное свойство углов позволяет сделать следующий вывод: угол, являющийся смежным прямому углу, также будет прямым.

3. Рассматривая тригонометрический функции (sin, cos, tg, ctg), основываясь на формулах приведения для смежных углов μ и η справедливо следующее:

• sinη = sin(180° – μ) = sinμ,
• cosη = cos(180° – μ) = -cosμ,
• tgη = tg(180° – μ) = -tgμ,
• ctgη = ctg(180° – μ) = -ctgμ.

Смежные углы – примеры

Пример 1

Задан треугольник с вершинами M, P, Q – ΔMPQ. Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.

• Продлим каждую из сторон треугольника прямой.
• Зная о том, что смежные углы дополняют друг друга до развернутого угла, выясняем, что:

смежным для угла ∠QMP будет ∠LMP,

смежным для угла ∠MPQ будет ∠SPQ,

смежным для угла ∠PQM будет ∠HQP.

Пример 2

Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла?

• Два смежных угла в сумме образуют 180°.
• Если ∠μ = 35°, то смежный ему ∠η = 180° – 35° = 145°.

Пример 3

Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла.

• Обозначим величину одного (меньшего) угла через – ∠μ = λ.
• Тогда, согласно условию задачи, величина второго угла будет равна ∠η = 3λ.
• Исходя из основного свойства смежных углов, μ + η = 180° следует

λ + 3λ = μ + η = 180°,

λ = 180°/4 = 45°.

Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°.

Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач.

угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого известную величину основного угла α₁ = α₂ = 180°-α.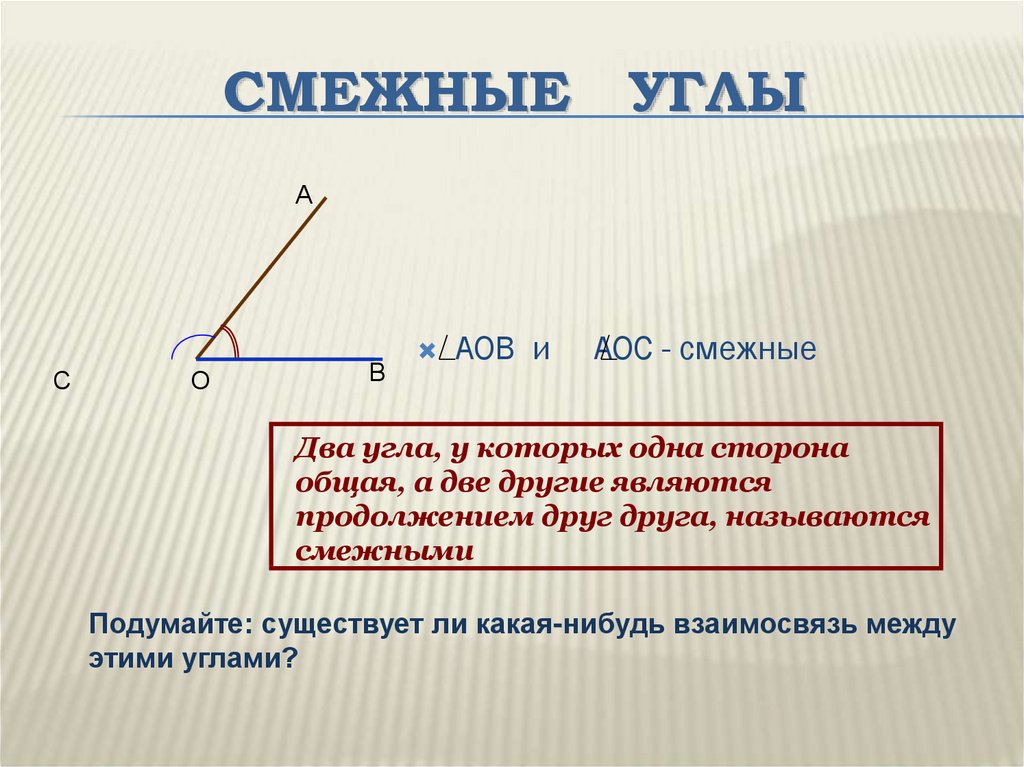

Из этого имеются . Если два угла одновременно являются и смежными, и равными, то они прямые. Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.

Острый угол – это такой, градусная мера которого меньше 90 градусов, но больше 0. Тупой угол имеет градусную меру больше 90 градусов, но меньше 180.

Другое свойство смежных углов формулируется так: если два угла равны, то углы, смежные с ними, также равны. Это , что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам).

Источники:

• Большой Энциклопедический Словарь — Смежные углы
• угол 180 градусов

Слово « » имеет различные толкования. В геометрии угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки – вершины. Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы.

Как и любые фигуры в геометрии, углы можно сравнивать. Равенство углов определяется с помощью движения. Угол нетрудно разделить на две равные части. Разделить на три части немного сложнее, но все же это можно сделать с помощью линейки и циркуля. Кстати, эта задача казалась довольно трудной. Описать, что один угол больше или меньше другого, геометрически несложно.

В качестве единицы измерения углов принят – 1/180

Как найти смежный угол?

Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.

Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.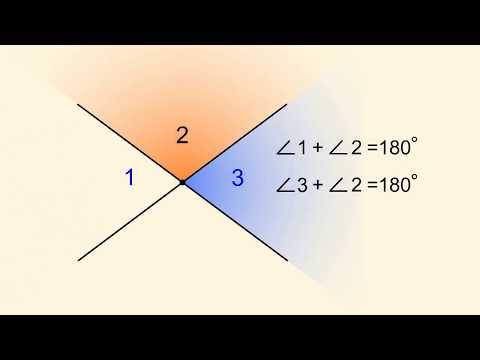

Определение и свойства смежных углов

Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.

К основным свойствам смежных углов относят

• Смежные углы имеют общую вершину и одну сторону;
• Сумма смежных углов равна всегда 180 градусам или числу Пи, если вычисление ведется в радианах;
• Синусы смежных углов всегда равны;
• Косинусы и тангенсы смежных углов равны, но имеют противоположные знаки.

Как найти смежные углы

Обычно даются три вариации задач на нахождение величины смежных углов

• Дана величина основного угла;
• Дано соотношение основного и смежного угла;
• Дана величина вертикального угла.

Каждый вариант задачи имеет свое решение. Рассмотрим их.

Дана величина основного угла

Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.

Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.

Дано соотношение основного и смежного угла

В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла. В этом случае решение будет выглядеть, как уравнение пропорции:

1. Обозначаем долю пропорции основного угла, как переменную «Y».
2. Долю относящуюся к смежному углу обозначаем, как переменную «Х».
3. Количество градусов, которые приходятся на каждую пропорцию, обозначим, например, «a».
4. Общая формула будет выглядеть так — a*X+a*Y=180 или a*(X+Y)=180.
5. Находим общий множитель уравнения «a» по формуле a=180/(X+Y).
6. Затем полученное значение общего множителя «а» умножаем на долю угла, который необходимо определить.

Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах.

Дана величина вертикального угла

Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла.

Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении.

Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах.

Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.

Также вы можете прочесть наши полезные статьи и .

Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.

Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.

Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.

Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.

Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.

Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.

Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т. е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.

Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.

Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».

Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.

Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.

Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.

Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

Два угла размещнные на одной прямой и имеющие одну вершину называются смежными.

Иначе — если сумма двух углов на одной прямой равна 180 градусам и одна сторона у них общая, то это смежные углы.

1 смежный угол + 1 смежный угол = 180 градусов.

Смежные углы -это два угла, у которых одна сторона общая, а две другие стороны в целом образуют прямую линию.

Сумма двух смежных углов всегда равна 180 градусам. К примеру, если один угол 60 градусов, то второй обязательно будет равен 120 градусам (180-60).

Углы АОС и ВОС являются смежными углами, потому что соблюдается все условия характеристики смежных углов:

1.ОС -общая сторона двух углов

2.АО -сторона угла АОС, ОВ -сторона угла ВОС. Вместе эти стороны образуют прямую линию АОВ.

3.Угла два и сумма их равна 180 градусов.

Вспоминая школьный курс геометрии, про смежные углы мы можем сказать следующее:

у смежных углов — одна сторона общая, а другие две стороны принадлежат одной прямой, то есть находятся на одной прямой.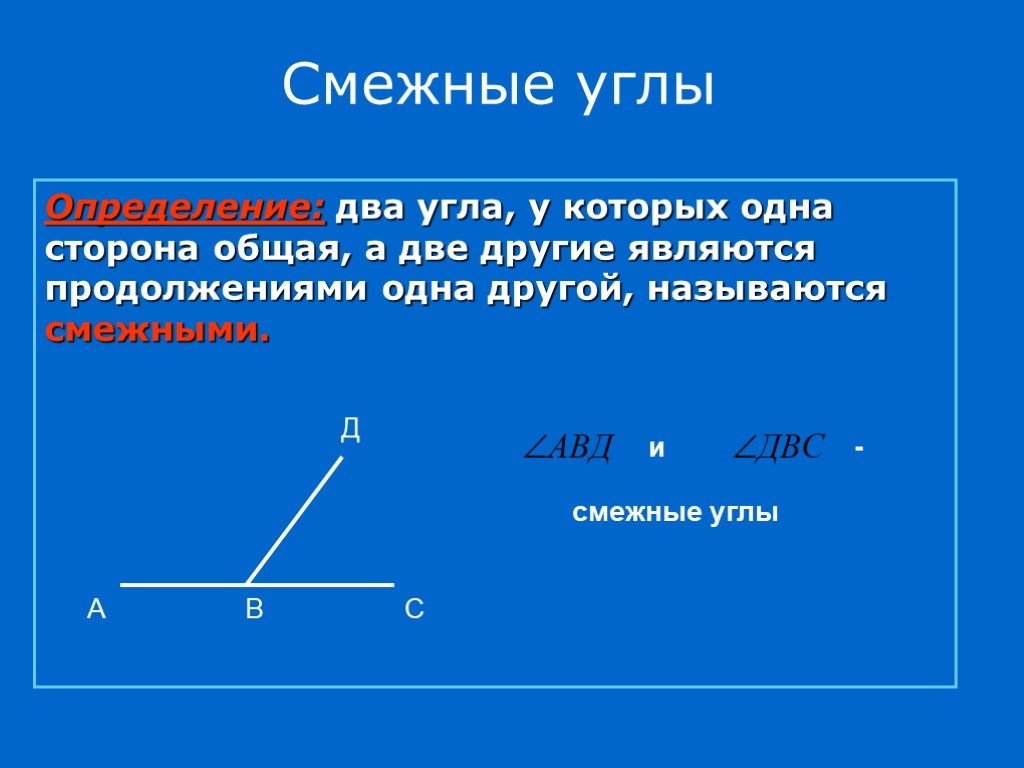 Если по рисунку, то углы СОВ и ВОА — это смежные углы, сумма которых всегда равна 180 , так как они разделяют развернутый угол, а развернутый угол всегда равен 180 .

Смежные углы понятие легкое в геометрии. Смежные углы, угол плюс угол дают 180 градусов в общей сумме.

Два смежных угла — это будет один развернутый угол.

Есть еще несколько свойств. Со смежными углами задачи решать и теоремы доказывать легко.

Смежные углы образуются при проведении луча из произвольной точки прямой. Тогда эта произвольная точка оказывается вершиной угла, луч — общей стороной смежных углов, а прямая от которой проведен луч — двумя оставшимися сторонами смежных углов. Смежные углы могут быть как одинаковыми в случае перпендикуляра, так и отличатся при наклонном луче. Легко понять, что сумма смежных углов равна 180 градусов или попросту прямой линии. По другому этот угол можно объяснить простым примером — вы сперва шли в одном направлении по прямой, потом передумали, решили вернуться назад и развернувшись на 180 градусов отправились по той же прямой в обратном направлении.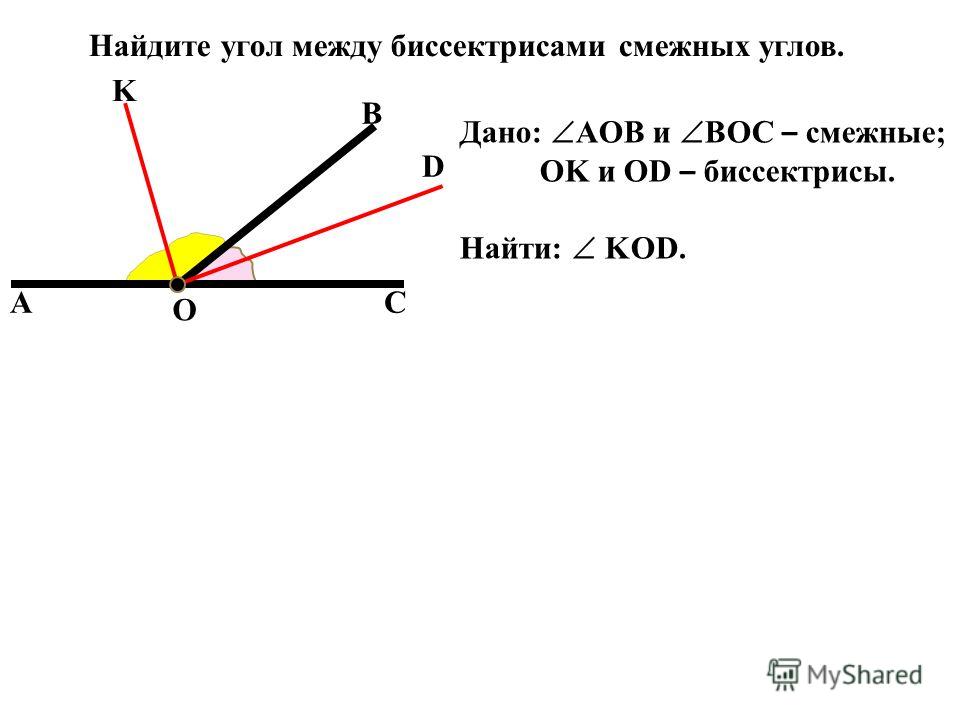

Итак, что же такое смежный угол? Определение:

Смежными называются два угла с общей вершиной и одной общей стороной, причем две другие стороны этих углов лежат на одной прямой.

И небольшой видео урок, где толково показано про смежные углы, вертикальные углы, плюс про перпендикулярные прямые, которые являются частным случаем смежных и вертикальных углов

Смежные углы — это углы, у которых одна сторона общая, а вторая является одной линией.

Смежные углы — это углы, зависящие друг от друга. То есть если общую строну слегка повернуть, то один угол уменьшится на сколько-то градусов и автоматически второй угол увеличится на столько же градусов. Это свойство смежных углов позволяет в Геометрии решать различные задачи и осуществлять доказательства различных теорем.

Общая же сумма смежных углов всегда равна 180 градусов.

Из курса геометрии, (насколько я помню за 6 класс) смежными называются два угла, у которых одна сторона общая, а другие стороны являются дополнительными лучами, сумма смежных углов равна 180. Каждый из двух смежных углов, дополняет другой до развернутого угла. Пример смежных углов:

Смежные углы это два угла с общей вершиной, одна из сторон которых общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.

Что такое смежные углы? [Примеры вопросов]

Определение:

В геометрии два угла смежны , если они имеют общую сторону и общую вершину. Другими словами, смежные углы находятся непосредственно рядом друг с другом и не пересекаются.

Смежные углы Примеры вопросов

Смежные углы Примеры:

В нашем первом примере ∠a смежна с ∠b. Они имеют общую вершину, которая является угловой точкой A. У них также есть общая сторона, линия AD. ∠a и ∠b соприкасаются линией AD, но не пересекаются.

Во втором примере мы видим ∠1, ∠2 и ∠3. Мы видим, что ∠1 и ∠2 смежны, так как имеют общую вершину и общую сторону. То же самое мы видим с ∠2 и ∠3, которые также имеют общую вершину и одну сторону. Рассмотрим ∠1 и ∠3. Хотя они имеют общую вершину, они не смежны, так как не имеют общей стороны.

В нашем последнем примере мы видим два угла, ∠1 и ∠2. Оба угла имеют одну сторону, линию ВС. Однако эти углы не являются смежными, поскольку не имеют общей вершины.

Что такое смежные углы?

Основываясь на нашем определении и приведенных выше примерах, мы можем заключить, что все пары смежных углов имеют два общих свойства: (1) общая вершина и (2) общая сторона. Если в них отсутствует один из этих компонентов, то они не являются смежными. Мы можем классифицировать пары углов как смежные или несмежные, ища эти два свойства.

Существует множество особых отношений между парами углов. Идентификация смежных углов поможет вам распознать другие отношения углов, такие как дополнительные и дополнительные углы.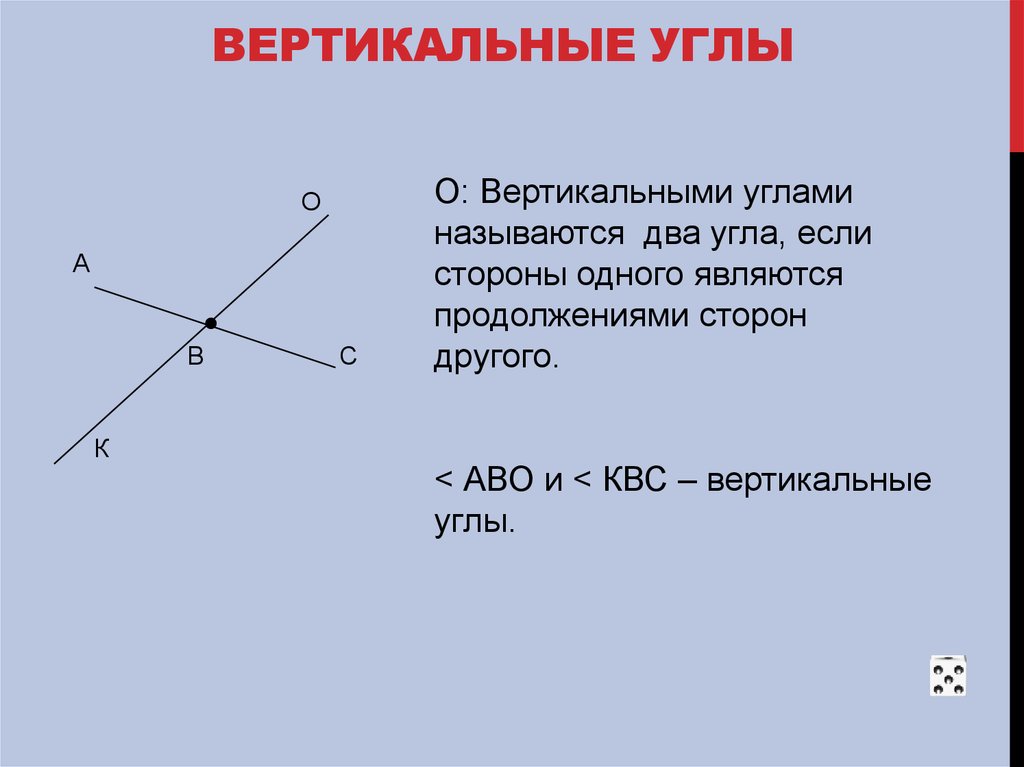

Примеры вопросов по смежным углам

Вот несколько примеров вопросов по смежным углам.

Вопрос №1:

Какое из следующих утверждений верно?

↑1 и ♂4 — смежные

♂3 и грыти. B правильно, потому что ∠3 и ∠4 имеют общую вершину и сторону, две определяющие характеристики смежных углов. A неверно, потому что ∠1 и ∠4 не имеют общей стороны. C неверно, потому что ∠1 и ∠2 имеют общую сторону и вершину. Следовательно, они соседствуют. D неверно, потому что ∠2 и ∠3 не имеют общей стороны.

Скрыть ответ

Вопрос №2:

Какие углы смежные?

↑1 и ♂3

♂5 и ♂3

♂1 и ♂4

♂2 и ♂3

Показать ответ

Ответ:

D — правильный ответ, потому что ♂ и2 и и ∠3 имеют общую сторону и вершину, которые являются двумя необходимыми компонентами смежных углов.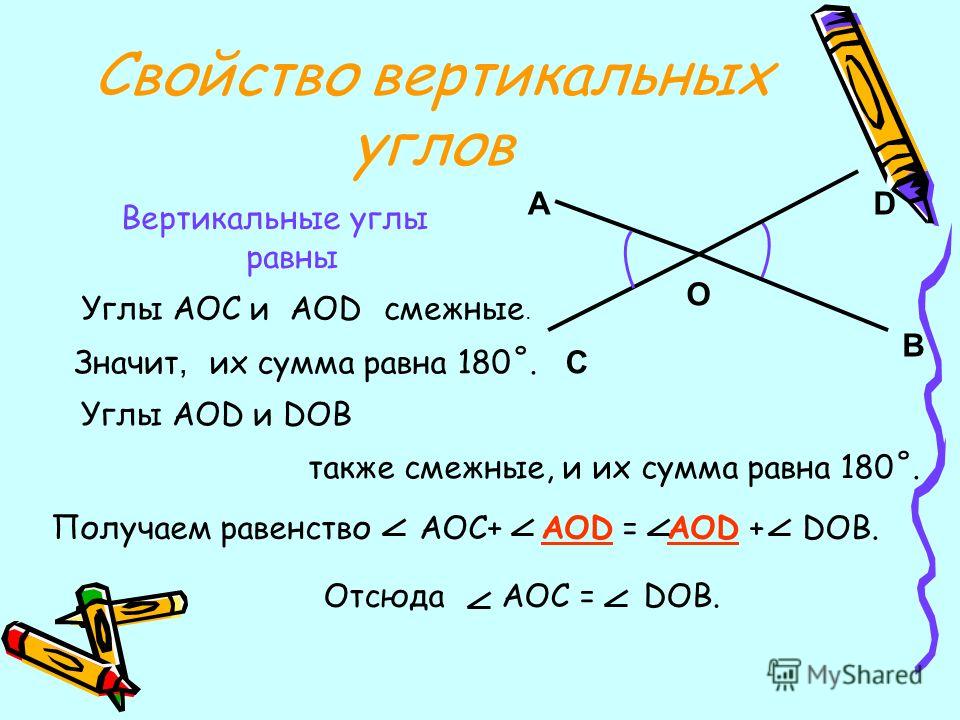

Скрыть ответ

Вопрос №3:

Какие углы равны не рядом?

Показать ответ

Ответ:

C — правильный ответ, потому что ∠a и ∠b хотя и имеют общую сторону, но две разные вершины. Следовательно, они не являются соседними. Варианты A, B и D неверны, поскольку все они показывают пары углов с общими сторонами и общей вершиной.

Скрыть ответ

Вопрос № 4:

Хуан изучает жилки листьев и замечает смежные углы в строении растения. Он рисует приведенную ниже диаграмму и записывает четыре пары смежных углов. Одна из пар смежных углов Хуана неверна. По схеме определите, какая пара углов равна 9.0003 не рядом?

↑gdi и omwdi

omeoe и omeed

omedg и omgdi

♂deo и omwdi

Показать ответ

Ответ:

D. Правильный ответ. ∠WDI не являются смежными углами. У них нет общих сторон и вершин. Варианты A, B и C неверны, потому что в этих вариантах ответа перечислены пары углов с общими сторонами и общей вершиной.

Скрыть ответ

Вопрос №5:

Кейша и Джеймс смотрят на карту городских улиц и замечают множество смежных углов. Джеймс рисует показанное изображение, чтобы проиллюстрировать найденные углы. Кейша указывает, что ∠AOE и ∠COD смежны, потому что у них есть общая вершина и одна сторона. Джеймс не согласен. Он говорит, что эти углы не имеют общей стороны. Кто прав и почему?

Джеймс прав, потому что оба угла имеют одну вершину, но не имеют общей стороны.

Кейша верна, потому что оба угла имеют общую вершину O и прямую AD.

Джеймс неверен, потому что ∠AOE и ∠COD не имеют одной и той же вершины.

Кейша неверна, потому что на карте нет ∠AOE.

Показать ответ

Ответ:

Правильный ответ A, потому что ∠AOE и ∠COD имеют общую вершину в точке O, но не имеют общей стороны. Следовательно, Джеймс прав. B неверно, потому что строка AD не является строкой в ​​∠AOE или ∠COD. C неверно, потому что ∠AOE и ∠COD имеют общую вершину в точке O. D неверно, потому что, хотя Кейша неверна, обоснование, данное в этом варианте ответа, неверно. ∠AOE отображается на карте.

Hide Ответ

Возврат к математическим вопросам

Определение соседних углов и значение

• Верхние определения
• Quiz
• Примеры
• British

.

Сохрани это слово!

Показывает уровень сложности слова.

---

существительное во множественном числе Геометрия.

два угла, имеющие одну вершину и общую сторону.

ВИКТОРИНА

ТЫ ПРОШЕШЬ ИЛИ НАТЯНУСЬ НА ЭТИ ВОПРОСЫ ПО ГРАММАТИКЕ?

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Слова рядом с соседними углами

прил., Adj.A., смежность, смежный, смежный угол, смежные углы, прилагательное, прилагательное, прилагательное придаточное, прилагательное словосочетание, прилагательное местоимение

Dictionary.com Unabridged Основано на словаре Random House Unabridged Dictionary, © Random House, Inc., 2022 г.

Как использовать смежные углы в предложении

• Кто помогает строить конференц-центры и прилегающие к ним отели, чтобы города могли привлечь бизнес-конференций?

  Демократы боятся защищать правительство, но им нужно начать|Майкл Томаски|4 декабря 2014|DAILY BEAST

• Я сижу на турецко-сирийской границе, рядом с городом Кобани, и наблюдаю за сотнями детей рыдать

  Вспоминая Кобани перед осадой|Мустафа Абди, Movements.Org, Продвижение прав человека|8 ноября 2014 г.|DAILY BEAST

• «Фотография оказалась секретным оружием в его революционных пейзажных картинах», — говорится в тексте на соседней стене.

  Разоблачение невидимого Пикассо|Джастин Джонс|3 ноября 2014|DAILY BEAST

• Пожалуй, единственная вещь поблизости, отдающая политикой, — это соседний всплывающий магазин костюмов для Хэллоуина.

  Таинственный человек покупает Кентукки для Республиканской партии|Центр общественной честности|29 октября 2014 г.|DAILY BEAST

• Он хватает телефон умелой рукой, вытягивает длинную руку к потолку и наклоняет ее вниз.

  Уродливая правда о Кори Букере, золотом мальчике из Нью-Джерси|Оливия Нуцци|20 октября 2014 г.|DAILY BEAST

• Башня имеет четыре циферблата, вершины по углам и крутую шиферную крышу, а ее высота составляет 120 футов. .

  Бирмингемский словарь Шоуэлла | Томас Т. Харман и Уолтер Шоуэлл

• Недалеко от него стоял чайный столик, рядом с большим диваном, стоявшим под прямым углом от стены.

  Белла Донна|Роберт Хиченс

• Дорога была построена для перевозки пиломатериалов, и на протяжении шести миль она шла под опасными углами.

  No related posts.