Математический анализ. (Виленкин)
Математический анализ. (Виленкин)
ОглавлениеПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств. 6. Сложение множеств. 7. Разбиение множеств.  8. Вычитание множеств. 9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений. § 2. Уравнения с одним неизвестным 2.  Метод разложения на множители.3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 2. Одночленные иррациональные выражения. 3. Сокращение показателей и приведение корней к общему показателю. 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.  6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений. 6. Метод подстановки. 7. Метод алгебраического сложения уравнений.  8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 3. Основная теорема о симметрических многочленах от двух переменных. 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел. 3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения.  § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа. 7. Функции комплексного переменного и преобразования комплексной плоскости.  § 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 3. Разложение на множители многочленов с действительными коэффициентами. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения. Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2.  3 | |||
| 6 | Risolvere per ? | cos(x)=1/2 | |
| 7 | Risolvere per x | sin(x)=-1/2 | |
| 8 | Преобразовать из градусов в радианы | 225 | |
| 9 | Risolvere per ? | cos(x)=( квадратный корень из 2)/2 | |
| 10 | Risolvere per x | cos(x)=( квадратный корень из 3)/2 | |
| 11 | Risolvere per x | sin(x)=( квадратный корень из 3)/2 | |
| 12 | График | g(x)=3/4* корень пятой степени из x | |
| 13 | Найти центр и радиус | x^2+y^2=9 | |
| 14 | Преобразовать из градусов в радианы | 120 град. 2+n-72)=1/(n+9) |
Как найти кубический корень комплексного числа?
Это важный вопрос, или, по крайней мере, намек на него. К сожалению, я могу ответить на вопрос только в отведенном для этого месте. Ответ придется подождать.
Я никогда не уверен, что такое предварительный расчет. Что осталось после Алгебры I, Алгебры II, Геометрии и Тригонометрии? Но давайте предположим, что пришло время углубиться в то, что на самом деле означает математика, которую мы делали.
Извлечь кубический корень легко, если у нас есть комплексное число в полярных координатах. Я напишу полярную форму как 9circ# — два других кубических корня.
Теоретически эта процедура работает, если нам задано #z# в прямоугольных координатах. Преобразовываем в полярные, берем кубический корень, конвертируем обратно. Это волшебная прогулка по трансцендентному тоннелю.
На практике это немного проблематично. Это большой короткий путь к ответу, но обычно он извлекает стоимость: мы получаем либо приближение, либо результат, выраженный с помощью триггерных функций.
Ни то, ни другое не идеально.
Глубокий вопрос, который мы хотим решить, заключается в том, как выразить #quad root[3]{ a + bi } quad # как # quad x + yi .#
Это связано с удалением радикалов, потому что #i=sqrt{-1}#.
Нас особенно интересует случай, когда #a# и #b# являются целыми, рациональными или квадратичными числами ( #g+h sqrt{d}# для рациональных #g,h,d#, где #d# не является полным квадратом ) и мы хотим знать, есть ли рациональные или поверхностные значения для #x# и #y#.
Меня предупреждают, что это затягивается. Мы едва подошли к делу. Самое острое место, где это всплывает, находится в кубической формуле, которая похожа на квадратичную формулу для кубических уравнений. Простейшая форма называется вдавленной кубической: 93 — 6x = -4#
Применяя формулу,
#x = root[3] { -2 + \sqrt{-4} } + root[3] { -2 — \sqrt{-4} }#
#x = root[3] { -2 + 2i } + root[3] { -2 — 2i }#
Здесь мы должны получить два, но мы получаем сумму двух кубических корней комплексных чисел.
Я хочу показать вам, как их денестировать, что похоже на факторинг.
Но Сократик говорит, что я вас всех запугиваю, поэтому я остановлюсь здесь и продолжу это в одном из будущих ответов. А пока возьмите карандаш и посмотрите, сможете ли вы сделать это выражение равным двум. Другие вопросы для размышления: каковы два других решения? Каждый кубический корень имеет три значения, какие они? Разве это не девять комбинаций для суммы #x#, как это может быть, когда кубик имеет три решения?
Объяснение урока: Кубические корни из единицы
В этом объяснении мы научимся определять кубические корни из единицы с помощью теоремы Муавра.
Кубический (или кубический) корень из единицы является комплексным решением 𝑧 уравнения 𝑧=1. Если рассматривать только вещественные решения
к этому уравнению мы можем применить кубический корень к обеим частям уравнения, чтобы получить 𝑧=√1=1, что означает, что существует только один
вещественное решение. Однако есть и другие решения этого уравнения, которые не являются действительными числами.
Чтобы решить это уравнение алгебраически, мы сначала переставим это
уравнение как 𝑧−1=0. Вспоминая формулу разности кубов
𝑎−𝑏=(𝑎−𝑏)𝑎+𝑎𝑏+𝑏,
мы можем разложить 𝑧−1, чтобы написать
(𝑧−1)𝑧+𝑧+1=0,
Первый множитель 𝑧−1 приводит к действительному корню 𝑧=1, а квадратичный множитель 𝑧+𝑧+1 приводит к комплексные корни, когда мы применяем формулу квадратных корней. Применяя формулу квадратных корней с 𝑎=1, 𝑏=1, и 𝑐=1, мы имеем 𝑧=−𝑏±√𝑏−4𝑎𝑐2𝑎=−1±√1−42=−12±√32𝑖.
Это дает нам два других комплекснозначных решения уравнения 𝑧=1. Таким образом, мы получили три кубических корня из единицы.
Определение: кубические корни из единицы в декартовой форме
Кубические корни из единицы являются комплексными решениями уравнения 𝑧=1. Три кубических корня из единицы в декартовой форме равны 𝑧∈1,−12+√32𝑖,−12−√32𝑖.
Действительный корень 1 называется тривиальным кубическим корнем из единицы, а нетривиальные корни −12+√32𝑖
и −12−√32𝑖 называются комплексными кубическими корнями из единицы.
Из декартовой формы кубических корней из единицы видно, что два комплексных кубических корня из единицы являются комплексно-сопряженными друг другу.
Хотя этот метод можно использовать для нахождения кубических корней из единицы, его нельзя обобщить для получения более высоких корней из единицы, которые являются решениями уравнение 𝑧=1 для 𝑛>3. Другой метод получения кубических корней из единицы основан на теореме Муавра. и этот метод можно легко обобщить, чтобы найти более высокие корни из единицы. Напомним теорему де Муавра для кубических корней.
Теорема: Теорема де Муавра для кубических корней √𝑟𝜃+2𝜋𝑘3+𝑖𝜃+2𝜋𝑘3косин для 𝑘=0,1 и 2,
В первом примере мы применим теорему де Муавра для корней, чтобы найти полярную форму кубических корней из единицы.
Пример 1. Кубические корни из единицы
Найдите все значения 𝑧, для которых 𝑧=1.
Ответ
В этом примере нам нужно найти все решения уравнения 𝑧=1.
Если мы хотим вычислить только действительные решения, мы можем применить
кубический корень в обеих частях уравнения, чтобы получить 𝑧=1.
Чтобы извлечь кубический корень и найти комплексные решения этого уравнения, мы будем использовать полярную форму комплексного числа. Напомним, что мы можем выразить комплекс число с модулем 𝑟 и аргументом 𝜃 в полярной форме как 𝑟(𝜃+𝑖𝜃).коссин
Мы знаем, что теорема Муавра позволяет нам извлекать корни комплексного числа в его полярной форме. В частности, напомним теорему Муавра для кубических корней: учитывая комплексное число в полярной форме 𝑟 (𝜃 + 𝑖𝜃) косинус, кубические корни этого комплексного числа равны √𝑟𝜃+2𝜋𝑘3+𝑖𝜃+2𝜋𝑘3косин для 𝑘=0,1 и 2.
Следовательно, чтобы извлечь кубический корень из правой части уравнения, который равен 1, мы можем начать с выражения 1 в полярной форме. Мы знаем, что модуль 1
равно 1, а поскольку 1 находится на положительной вещественной оси диаграммы Аргана, мы также знаем, что аргумент 1 равен
0 радиан.
Мы можем записать полярную форму числа 1, используя 𝑟=1
и 𝜃=0:
1=1(0+𝑖0).косинус
Применяя теорему де Муавра к кубическим корням из 1 в полярной форме, мы получаем √12𝜋𝑘3+𝑖2𝜋𝑘3=2𝜋𝑘3+𝑖2𝜋𝑘3коссинкоссин для 𝑘=0,1 и 2. Отсюда имеем 𝑘=0∶0+𝑖0=1,𝑘=1∶2𝜋3+𝑖2𝜋3,𝑘=2∶4𝜋3+𝑖4𝜋3.cossincossin
Напомним, что по аргументу комплексного числа соглашение, должно лежать в стандартном диапазоне ]−𝜋,𝜋]. Первые два кубических корня имеют аргументы 0 и 2𝜋3, которые находятся в этом диапазоне, но аргумент последнего корня равен 4𝜋3, который не лежит в этом диапазоне. Поскольку этот аргумент превышает верхнюю границу 𝜋, мы можем получить эквивалентный аргумент, вычитая полный оборот 2𝜋 радиана от этого значения: 4𝜋3−2𝜋=4𝜋3−6𝜋3=−2𝜋3.
Заметим, что этот эквивалентный аргумент −2𝜋3 лежит в стандартном диапазоне ]−𝜋,𝜋],
поэтому мы можем использовать этот аргумент, чтобы записать третий корень из единицы
коссин−2𝜋3+𝑖−2𝜋3.
Следовательно, кубические корни из единицы равны 1,2𝜋3+𝑖2𝜋3,−2𝜋3+𝑖−2𝜋3.cossincossin
В предыдущем примере мы нашли полярную форму кубических корней из единицы, применяя теорему де Муавра. Напомним, что экспоненциальная форма комплексное число с модулем 𝑟 и аргументом 𝜃 равно 𝑟𝑒, что означает полярное и экспоненциальное формы комплексного числа связаны тождеством 𝑟(𝜃+𝑖𝜃)=𝑟𝑒.коссин
Используя полярную форму кубических корней из единицы, полученную в предыдущем примере, мы также можем записать экспоненциальную форму корней из единицы.
Определение: кубические корни из единицы в полярной и экспоненциальной формах
Три кубических корня из единицы в полярной форме 𝑧∈1,2𝜋3+𝑖2𝜋3,−2𝜋3+𝑖−2𝜋3.cossincossin
Три кубических корня из единицы в экспоненциальной форме равны В частности, корни
Приведенные выше выражения для кубических корней из единицы дают модули и аргументы комплексных чисел.
Мы видим, что модули всех кубических корней из единицы
равны 1, что означает, что все они лежат на единичной окружности диаграммы Аргана. Первый корень, 1, лежит на положительной прямой, а два других корня
симметричны относительно действительной оси, о чем мы можем судить по тому, что их аргументы имеют противоположные знаки. Нарисуем кубические корни из единицы на диаграмме Аргана.
На приведенной выше диаграмме Аргана мы видим, что угол между двумя линиями от начала координат до двух комплексных кубических корней из единицы равен 𝜃=2𝜋−2𝜋3−2𝜋3=2𝜋3.
Другими словами, три кубических корня можно получить, начав с точки (1,0) на диаграмме Аргана и вращая 2𝜋3 радиана против или по часовой стрелке по единичной окружности. Мы можем связать геометрическое вращение на диаграмме Аргана со степенью комплексных чисел, используя теорему де Муавра.
Теорема: Теорема де Муавра для целых степеней
Пусть 𝑧=𝑟𝑒 — ненулевое комплексное число в экспоненциальной форме.
Тогда для любого целого числа 𝑛
𝑧=𝑟𝑒.
В частности, эта теорема говорит нам, что если мы возводим в квадрат комплексное число с модулем 1, мы удваиваем аргумент комплексного числа. Что касается приведенной выше диаграммы Аргана, мы можем видеть, что возведение в квадрат комплексного кубического корня из единицы приведет к другому комплексному корню из единицы.
В следующем примере мы продемонстрируем этот факт с помощью явных вычислений.
Пример 2: Произведения кубических корней из единицы
Пусть 𝑧=𝑒 и 𝑧=𝑒 — комплексные кубические корни из единицы.
- Оценить 𝑧. Как это соотносится с 𝑧?
- Оценить 𝑧. Как это соотносится с 𝑧?
Ответ
В этом примере нам нужно взять степени комплексных чисел в экспоненциальной форме. Начнем с того, что вспомним теорему де Муавра для целых степеней: 𝑟𝑒=𝑟𝑒.
Мы применим эту теорему, чтобы взять квадраты 𝑧 и 𝑧 в каждой из следующих частей.
В частности, эта теорема говорит
Нам известно, что если мы возводим комплексное число в квадрат по модулю 1, мы удваиваем аргумент комплексного числа.
Часть 1
Применяя теорему Муавра для целых степеней, мы можем написать (𝑧)=𝑒=𝑒=𝑒.
Напомним, что аргумент комплексного числа по соглашению должен лежать в стандартном диапазоне ] −𝜋,𝜋], в то время как аргумент 𝑧 выше равен 4𝜋3. Поскольку этот аргумент превышает верхнюю границу 𝜋, мы можем получить эквивалентный аргумент, вычитая полный оборот 2𝜋 радиан от этого значения: 4𝜋3−2𝜋=4𝜋3−6𝜋3=−2𝜋3.
Заметим, что этот эквивалентный аргумент −2𝜋3 лежит в стандартном диапазоне ]−𝜋,𝜋], поэтому мы можем записать экспоненциальную форму 𝑧, 𝑧=𝑒, что то же самое, что 𝑧.
Мы также можем понять это тождество, наблюдая за диаграммой Аргана. Помните, что по теореме де Муавра возведение в квадрат комплексного числа с
модуль 1 эквивалентен удвоению аргумента комплексного числа на единичной окружности.
Следовательно, когда мы возводим в квадрат 𝑒,
мы получаем комплексное число с модулем 1 и аргументом
2×2𝜋3=4𝜋3.
Мы уже заметили, что это эквивалентно аргументу −2𝜋3, 𝑒, который является аргументом для 𝑧. Это приводит к следующей схеме.
Следовательно, 𝑧=𝑒 (т.е. 𝑧=𝑧).
Часть 2
Аналогично, применяя теорему Муавра для целых степеней, можно записать (𝑧)=𝑒=𝑒=𝑒.
Мы можем видеть, что аргумент 𝑧 выше равен −4𝜋3, что делает не лежать в стандарте диапазон ]−𝜋,𝜋]. Поскольку этот аргумент ниже нижней границы −𝜋, мы можем получить эквивалент аргумент, добавляя полный оборот 2𝜋 радиан к этому значению: −4𝜋3+2𝜋=−4𝜋3+6𝜋3=2𝜋3.
Этот эквивалентный аргумент 2𝜋3 лежит в стандартном диапазоне ]−𝜋,𝜋]; следовательно, экспоненциальная форма
из 𝑧 записывается как
𝑧=𝑒,
что то же самое, что 𝑧.
Как и в предыдущей части, мы можем визуализировать эту связь с помощью диаграммы Аргана. Если мы удвоим аргумент
из 𝑧, мы получаем
−2𝜋3×2=−4𝜋3,
что эквивалентно аргументу 𝑧. Это приводит к диаграмме Аргана ниже.
Следовательно, 𝑧=𝑒 (т.е. 𝑧=𝑧).
В предыдущем примере мы получили, что квадрат комплексного кубического корня из единицы приводит к другому комплексному корню, как мы и ожидали, исходя из диаграммы Аргана. Мы также знаем, что два комплексных корня из единицы являются комплексно-сопряженными друг другу. Это приводит к следующему свойству.
Свойство: Квадрат комплексных кубических корней из единицы
Пусть 𝜔 комплексный кубический корень из единицы. Затем, 𝜔=𝜔.
Рассмотрим пример, в котором мы можем применить это свойство для упрощения выражения, включающего 𝜔.
Пример 3. Использование свойств кубических корней из единицы
Вычислите 𝜔−𝜔, где 𝜔 — комплексный кубический корень из единицы.
Ответ
Напомним, что комплексный кубический корень из единицы удовлетворяет 𝜔=𝜔.
Следовательно, выражение в скобках 𝜔−𝜔 можно записать в виде 𝜔−𝜔.
Напомним также, что любое комплексное число 𝑧 удовлетворяет условию 𝑧−𝑧=2𝑖𝑧.Im
Следовательно, 𝜔−𝜔=2𝑖𝑧.Im
Комплексные кубические корни из единицы равны −12+√32𝑖 и −12−√32𝑖, что значит Im𝜔=±√32.
Подставляя это значение выше, получаем 𝜔−𝜔=2𝑖×±√32=±𝑖√3.
Следовательно, 𝜔−𝜔=±𝑖√3.
Поскольку мы берем четную степень числа ±𝑖√3, знак этого числа можно игнорировать. Распределяя мощность, мы имеем ±𝑖√3=𝑖√3.
Используя правила показателей степени, мы можем написать 𝑖√3=𝑖√3=(−1)3=−2187.
Следовательно, если 𝜔 — комплексный кубический корень из единицы, 𝜔−𝜔=−2187.
В предыдущем примере мы использовали свойство, состоящее в том, что если мы возводим в квадрат комплексный кубический корень из единицы, мы получаем другой комплексный кубический корень из единицы, который является сопряженным
исходного корня.
Мы уже знаем по определению, что получаем 1, когда возводим в куб комплексный кубический корень из единицы. Следовательно, мы можем заметить, что 3 является наименьшим положительным
целая степень комплексного кубического корня из единицы, которая приводит к ответу 1. С другой стороны, этого нельзя сказать о кубическом корне из единицы 1,
так как 1=1, а также 1=1. Это приводит к важному определению, которое мы сейчас сформулируем.
Определение: примитивные кубические корни из единицы
Примитивный кубический корень из единицы — это кубический корень из единицы 𝜔, для которого 𝑘=3 — наименьшее натуральное число для что 𝜔=1.
Как мы заметили, оба комплексных кубических корня из единицы также являются примитивными кубическими корнями из единицы, в то время как кубический корень из единицы с действительным знаком не является примитивным кубическим корнем из единицы.
корень единства. Не всегда все комплексные корни из единицы являются первообразными корнями из единицы, но это верно для кубических корней из единицы.
Рассмотрим другие степени примитивного кубического корня из единицы. Для общей целочисленной степени 𝑛 можно написать 𝑛=3𝑘+𝑎 для некоторых целых чисел 𝑘 и 𝑎=0,1,2. Это соотношение также подразумевает, что 𝑎≡𝑛(3)mod. Используя правила показателей, мы можем написать 𝜔=𝜔=𝜔𝜔=𝜔𝜔=(1)𝜔=𝜔.
Это приводит к следующему свойству для примитивных кубических корней из единицы.
Свойство: целые степени примитивных кубических корней из единицы
Пусть 𝜔 — примитивный кубический корень из единицы. Для любого целого числа 𝑛 имеем 𝜔=𝜔,𝑎≡𝑛(3).где мод
Рассмотрим несколько примеров, где мы можем применить это свойство для вычисления различных степеней примитивного кубического корня из единицы.
Пример 4. Вычисление степени кубического корня из единицы
Запишите 𝜔 в его простейшей форме, где 𝜔 — примитивный кубический корень из единицы.
Ответ
Напомним, что для любого примитивного кубического корня из единицы 𝜔 любая целая степень удовлетворяет свойству
𝜔=𝜔,𝑎≡𝑛(3).
wheremod
В этом примере нам нужно взять примитивный кубический корень из единицы в 11-й степени; следовательно, 𝑛=11. Поскольку 11=3×3+2, у нас есть 2≡11(3).mod
Это говорит нам о том, что 𝑎=2. Подставляя это значение в указанное выше свойство, мы имеем 𝜔=𝜔.
Мы также можем применить это свойство для отрицательных целых степеней, как мы увидим в следующем примере.
Пример 5: Упрощение выражений, использующих кубические корни из единицы
Запишите 𝜔 в простейшей форме, где 𝜔 — примитивный кубический корень из единицы.
Ответ
Напомним, что для любого примитивного кубического корня из единицы 𝜔 любая целая степень удовлетворяет свойству 𝜔=𝜔,𝑎≡𝑛(3).где мод
В этом примере нам нужно взять -149-ю степень примитивного кубического корня из единицы; следовательно, 𝑛=−149. Мы заметили −149=−150+1=3×(−50)+1, что приводит к −149≡1(3).mod
Это говорит нам о том, что 𝑎=1.
Подставляя это значение в указанное выше свойство, мы имеем
𝜔=𝜔=𝜔.
В предыдущих двух примерах мы вычисляли целые степени примитивных кубических корней из единицы. Рассмотрим другое свойство примитивных кубических корней из единицы. Если 𝜔 — примитивный кубический корень из единицы, мы знаем, что 𝜔=1, что означает 𝜔−1=0,
Используя упомянутую ранее формулу разности кубов, мы можем записать это уравнение как (𝜔−1)𝜔+𝜔+1=0.
Мы знаем, что 1 не является примитивным кубическим корнем из единицы; следовательно, мы должны иметь 𝜔+𝜔+1=0.
Это приводит к полезному свойству, которое можно использовать для упрощения полиномиального выражения в 𝜔.
Свойство: Примитивные кубические корни из единицы
Примитивный кубический корень из единицы 𝜔 должен удовлетворять 𝜔+𝜔+1=0.
Рассмотрим несколько примеров, где мы будем применять это свойство для упрощения полиномиальных выражений в 𝜔.
Пример 6.
Вычисление отрицательных степеней выражения, содержащего кубические корни из единицыВычислить 1+𝜔, где 𝜔 — примитивный кубический корень из единицы.
Ответ
Напомним, что примитивный кубический корень из единицы 𝜔 удовлетворяет 𝜔+𝜔+1=0.
Левая часть этого уравнения напоминает выражение, данное в скобках. Мы можем изменить это уравнение, чтобы написать 1+𝜔=−𝜔.
Подставляя это выражение, 1+𝜔=(−𝜔).
Поскольку −133 — нечетная степень, мы можем вынести знак минус и записать (−𝜔)=−𝜔.
Теперь нам нужно вычислить мощность 𝜔. Напомним, что для любого примитивного кубического корня из единицы 𝜔 любая целая степень удовлетворяет свойству 𝜔=𝜔,𝑎≡𝑛(3).wheremod
Нам нужно взять примитивный кубический корень из единицы в степени −133; следовательно, 𝑛=−133. Мы заметили
−133=−135+2=3×(−45)+2,
что приводит к
−133≡2(3).
mod
Это говорит нам о том, что 𝑎=2. Подставляя это значение в указанное выше свойство, мы имеем 𝜔=𝜔.
Подставляя это выражение выше, мы имеем 1+𝜔=−𝜔.
В предыдущем примере мы применили тождество 𝜔+𝜔+1=0, которое верно для любого примитивного (или комплексного) кубического корня из единицы. Ключом к сокращению выражений в 𝜔 является определение частей данного выражение, напоминающее левую часть этого уравнения. Иногда сходство не сразу видно из данного выражения, и нам нужно манипулировать данным выражением, прежде чем мы сможем увидеть, как применить это тождество.
В следующем примере мы будем манипулировать данным выражением, прежде чем применять это тождество, чтобы сократить данное выражение в 𝜔.
Пример 7. Вычисление выражений с кубическими корнями из единицы
Вычислить −8𝜔+15+5𝜔+1𝜔, где 𝜔 представляет собой комплексный кубический корень из единицы.
Ответ
Начнем с того, что вспомним, что комплексный кубический корень из единицы 𝜔 удовлетворяет тождеству
𝜔+𝜔+1=0.
В этом примере мы применим это тождество для вычисления данного выражения.
Во-первых, заметим, что в знаменателе дроби в первом наборе скобок стоит член 𝜔+1. Мы можем изменить личность для комплексных корней из единицы написать 𝜔+1=−𝜔.
Это означает, что выражение в первом наборе скобок может быть записано как −8𝜔+1=−8−𝜔=8𝜔.
Теперь рассмотрим выражение во втором наборе скобок. Здесь первые два члена равны 5+5𝜔, что можно записать как 5(1+𝜔). Используя то же тождество, мы можем заменить 1+𝜔 на −𝜔, чтобы написать это выражение как −5𝜔. Затем, 5+5𝜔+1𝜔=−5𝜔+1𝜔.
Мы можем сложить эти два числа, сделав общий знаменатель 𝜔. Это дает −5𝜔+1𝜔=−5𝜔𝜔+1𝜔=−5𝜔+1𝜔.
Поскольку 𝜔 — кубический корень из единицы, мы знаем, что 𝜔=1. Это уменьшает выражение во втором наборе скобок до 5+5𝜔+1𝜔=−4𝜔.
Перемножив эти выражения, получим
−8𝜔+15+5𝜔+1𝜔=8𝜔×−4𝜔=−32𝜔.
Наконец, поскольку 𝜔=1, данное выражение равно −32.
В нашем последнем примере мы упростим полиномиальное выражение от 𝜔, используя это тождество.
Пример 8: вычисление выражений, включающих кубические корни из единицы
где 𝜔 — нетривиальный кубический корень из единицы.
Ответ
Напомним, что кубических корней из единицы три. Среди трех кубических корней из единицы 1 называется тривиальным корнем из единицы, а два других корня называются нетривиальными, или комплексными, корнями из единицы. Для кубических корней из единицы мы также знаем, что комплексный корень из единицы также является примитивным корнем из единицы. Напомним свойства примитивных кубических корней из единицы, которые мы будем использовать для упрощения данного выражения. Любой примитивный кубический корень из единство 𝜔 удовлетворяет 𝜔=𝜔,𝑎≡𝑛(3)𝑛,𝜔+𝜔+1=0.где мод для любого целого числа
Начнем с замены высших степеней 𝜔 их эквивалентными степенями от 0 до 2, используя первое свойство для целых степеней.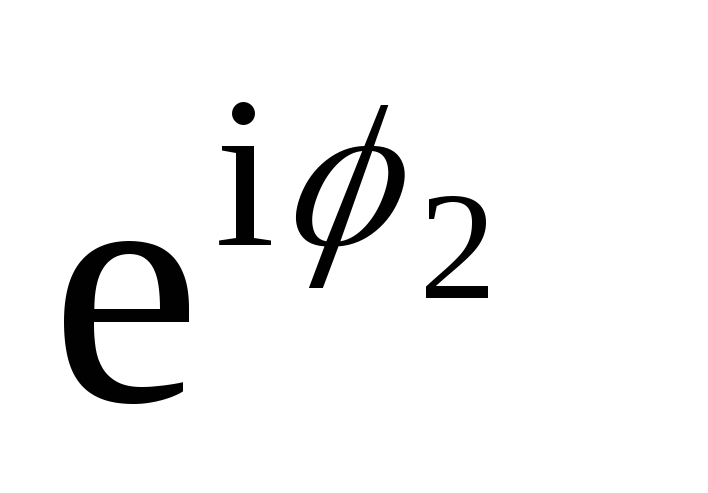
В данном выражении имеем 𝜔, что означает 𝑛=4. Поскольку мы знаем, что 4=1×3+1,
мы получаем 4≡1(3)mod, что приводит к 𝑎=1. Это дает
𝜔=𝜔=𝜔.
Тогда данное выражение можно записать в виде 9−𝜔+9𝜔+6+6𝜔+6𝜔.
Мы можем переставить члены в первом наборе скобок, чтобы написать 9−𝜔+9𝜔=−𝜔+9(𝜔+1).
Из второго свойства первообразных кубических корней из единицы мы можем переписать уравнение, чтобы записать 𝜔+1=−𝜔. Это означает −𝜔+9(𝜔+1)=−𝜔+9−𝜔=−10𝜔.
Следовательно, 9−𝜔+9𝜔=−10𝜔=100𝜔=100𝜔, где мы использовали тождество 𝜔=𝜔 для последнего равенства. Это упрощает первый член в данном выражении.
Теперь рассмотрим второй член, который равен 6+6𝜔+6𝜔. Поскольку 6 является общим делителем в скобках, мы можем записать этот термин как 61+𝜔+𝜔.
По свойству примитивных кубических корней из единицы мы знаем, что 𝜔+𝜔+1=0. Это значит, что
61+𝜔+𝜔=0.