Примеры интегрирования: Примеры решений неопределенных интегралов

alexxlab / / Разное

Примеры на интегрирование

Примеры на интегрирование функций подобного состава заданий задают студентам 1, 2 курсов. Это в основном задания для математиков, экономистов, статистов, программистов. Данные интегралы задавали на контрольной работе в ЛНУ им. И. Франка, другие ВУЗы Украины также практикует подобные здания на контрольных по интегрированию. Чтобы формулы в задачах и ответах не повторялись условия заданий выписывать не будем. Всем и так известно что в задачах нужно или «Найти интеграл», или «Вычислить интеграл».

Пример 18. Для раскрытия иррациональности в знаменателе дроби необходимо в подобных примерах выполнять такую замену переменных — «икс» в наименьшей степени. В результате придем к интегралу от дробной функции

дальше выполняем деления числителя на знаменатель и упрощение

Таким образом без громоздких расписаний дробей придем к интегралу


Пример 19. Корневую функцию обозначаем за новую переменную в квадрате (для удобства вычислений). Далее находим дифференциал переменной, подставляем в неопределенный интеграл и выполняем упрощение.

В результате замены получим дробь которая разделяется на два интеграла. Второй интеграл равен разнице логарифмов


Пример 20. Следующие интегралы касаются исключительно тригонометрических функций, а именно их произведения, квадратов, кубов, рациональных функций. Первый из приведенных интегралов нужно свести к синусу. Для этого косинус в 5 степени расписываем на произведение косинуса в 4 степени на косинус, который вносим под дифференциал


Для упрощения вводим замену переменных и приходим к интегрированию полинома

После интегрирования возвращаемся к замене и вместо t везде записываем sin(x).


Пример 21. Для вычисления интеграла нужно снизить степень синуса. Таким образом используем тригонометрические формулы, понижаем степень первой, а дальше находим интеграл по табличным формулам.


Пример 22. Нужно найти интеграл от произведения двойного синуса на тройной косинус.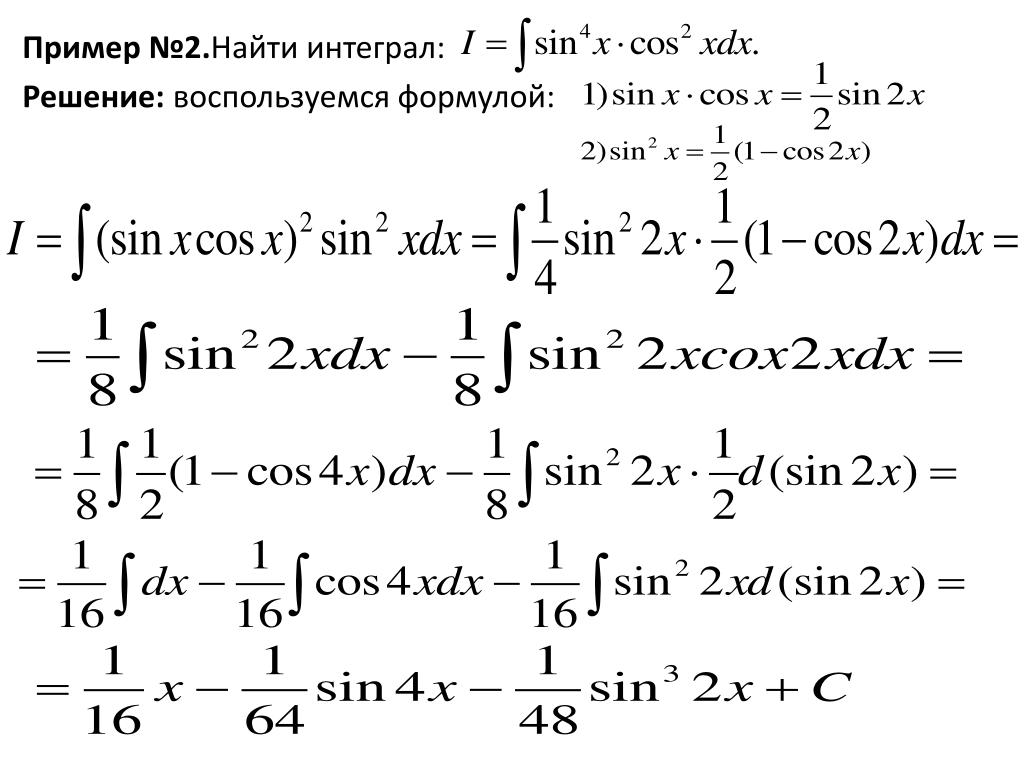 Под дифференциал ничего внести не удастся, поскольку имеем различные переменные. Для упрощения распишем произведение тригонометрических функций через разницу синусов


Пример 23. Данный интеграл без универсальной тригонометрической замены переменных найти не удастся. Поэтому пусть тангенс половины угла равный t, тогда синус превратится по формуле

После раскрытия скобок в знаменателе получим квадратный трехчлен

Для сведения такой дроби к табличному арктангенсу в знаменателе сначала выделяем квадратный трехчлен

Не забываем в конце вернуться к выполненной в начале замены. Это важно при тестах и контрольных.


Пример 24. Здесь можем использовать универсальную тригонометрическую замену, а может пойти другим путем. Вынесем в знаменателе синус в квадрате за скобки и перегруппируем слагаемые в скобках, чтобы по тригонометрическим формулам получить котангенс. Его и обозначим за новую переменную u, вычисляем также дифференциал du и подставляем все в интеграл

В результате интегрирования получим табличную формулу арктангенса


Пример 25. Необходимо вычислить интеграл от тангенса в квадрате от тройного аргумента. Сначала расписываем тангенс как часть синуса к косинусу. Далее синус в квадрате расписываем через косинус. После деления числителя на знаменатель получим два интеграла которые без труда находим по формулам интегрирования

Как только Вы изучите приведенные схемы и методики сведения интегралов под то или иное правило, научитесь видеть в примерах табличные интегралы и преобразования, которые в несколько шагов позволят Вам найти интеграл — тогда контрольная работа, или «срезы» для Вас не будут препятствием в обучении. Для этого нужно решить с десяток различных интегралов к каждому из приведенных типов. Все остальные после этого будут для Вас подобными, а схема их вычислений очевидной и понятной. Если в обучении встречаются сложные интегралы или сомневаетесь в собственных силах помните — мы всегда готовы оказать помощь. Это предложение актуально не только для студентов стационарной формы обучения, но и для заочников и школьников. В 11 классе в обучении с недавних времен школьникам также приходится иметь дело с интегралами.

Готовые решения контрольной по интеграции

  • < Предыдущие ответы
  • Контрольная работа по интегрированию № 2
  • Контрольная работа по интегрированию № 3

Примеры интегрирования функций

Ниже приведены примеры интегрирования, каторые охватывают значительную часть разнообразных способов нахождения неопределенного интеграла. Такого типа примеры интегрирования функций Вы чаще всего увидите на 1,2 курсах учебы из высшей математики. Ниже приведены ответы одновременно и объясняют методику взятия интегралов, и служат инструкцией по их вычислению. Чтобы сэкономить время и место самих условий до примеров мы не выписывали.

Пример 1. Если бы перед интегралом имели множителем «икс», то его можно было бы внести под дифференциал и провести замену переменных.
Однако интеграл более сложен, потому выражения в скобках подносим к кубу, а дальше выполняем интегрирование каждого из слагаемых.


Пример 2. Задана дробная функция в знаменателе которой содержится иррациональность. Чтобы от нее избавиться функцию под корнем обозначим за новую переменную, дальше находим ее дифференциал и подставляем в интеграл. После незначительных манипуляций с показателями вычисляем интеграл, и вместо переменной подставляем выполненную замену.


Пример 3. Кто часто вычисляет интегралы или хорошо знает теорию интегралов, то в этом и подобных заданиях за новую переменную выбирает логарифм. При дифференцировании логарифма получаем единицу разделенную на «икс», который значительно упрощает дальнейшее интегрирование.
Напоследок не забывайте в примерах на замену переменных перейти к начальной переменной «икс».


Пример 4. Выполняем интегрирование частями, для этого синус вносим под дифференциал

После первого раза опять получим интеграл, который вычисляем интегрированием частями.


Пример 5. Имеем задание под правило интегрирования частями u*dv. За переменную выбираем экспоненту, а синус вносим под дифференциал.

После повторного интегрирования частями придем к рекуррентной формуле, из которой и определяем интеграл.


Пример 6. В этом интеграле квадратный трехчлен, который стоит в знаменателе надо возвести к сумме или разнице квадратов.

Дальше за формулами интегрирования получим арктангенс.


Пример 7. Интегрирование произведения тригонометрических функций дается не всем студентам, и здесь нужно учитывать как степени, так и сам вид функций.
В этом примере один косинус нужно внести под дифференциал и свести задание к интегрированию функции от синуса.


Сам интеграл не сложен и находится по правилу степенных функций .


Пример 8. Если имеем синусы или косинусы в показателях больше единицы, то за тригонометрическими формулами их надо расписать вплоть до первой степени. Дальше применяют формулы интегрирования синусов или косинусов.


Пример 9. Чтобы найти интеграл от дробной функции сначала разделим числитель на знаменатель, и полученную в остатке дробь распишем на самые простые дроби. После этого, используя формулы интегрирования, вычисляем значение каждого из интегралов.


Пример 10. Имеем интеграл от дробной функции

Записываем ее через самые простые дроби первого и второго типов.

Дальше возводим дроби под общий знаменатель и из условия равенства числителей складываем систему линейных уравнений для вычисления неизвестных постоянных.


После ее решения возвращаемся к дроби, подставляем сталые и выполняем интегрирование.


Пример 11. Имеем интеграл от дробной иррациональной функции. Для раскрытия иррациональности выполняем следующую замену переменных под интегралом

В результате придем к дробной рациональной функции под интегралом, которую расписав на простые дроби легко проинтегрировать.


Пример 12. В этом задании чтобы избавиться иррациональности под интегралом необходимо использовать одну известную схему.
Она заключается в том, что проведя следующую замену переменных придем к рациональной функции от косинуса.


После интегрирования возвращаемся к выполненной замене и на этом вычислению можно завершить.
Однако, если иметь под рукой тригонометрические формулы то ответ можно упростить и записать в более компактном виде.


Пример 13. Имеем в знаменателе рациональную функцию от косинуса и синуса. Такие интегралы следует находить через универсальную тригонометрическую замену t=tg (x/2)

После подстановки формул синус и косинуса через тангенс половины кута подинтегральная функция превратится к дробной, в знаменателе которой будем иметь квадратный трехчлен. Его возводим к квадрату выражения, которое содержит переменную и интегрируем по правилу степенных функций .

После интегрирования не забываем, что наше t=tg (x/2) и подставляем его в формулу интеграла.


На этом подборка примеров завершается, больше примеров Вы найдете в категории интегрирования.
Для увеличения базы готовых интегралов присылайте интересные примеры на Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. или заказывайте у нас решение контрольных и расчетных работ.

Интеграция в математике: определение, способы расчета и примеры

В этой статье

  1. Что такое математическая интеграция?

  2. Ключевые формулы интегрирования

  3. Как вычислять интегралы

  4. 4 примера интеграции

Что такое интеграция в математике?

Что означает интегрирование в математике? Интеграция есть обратный процесс дифференциации. Интегрирование некоторой функции f(x)f(x)f(x) дает другую функцию, F(x)F(x)F(x). При дифференцировании эта функция F(x)F(x)F(x) возвращает исходную функцию f(x)f(x)f(x). По этой причине неопределенный интеграл часто называют первообразной. Точно так же мы также называем интеграцию антидифференцированием.

Чтобы освежить свои знания об интегралах, прочтите это руководство для начинающих по интегралам.

Давайте рассмотрим обозначения для интегрирования. Неопределенный интеграл действительнозначной функции f (x) f (x) f (x) по действительной переменной x записывается как:

∫f(x)dx=F(x)+C\int f(x)dx = F(x) + C∫f(x)dx=F(x)+C

  • Символ ∫\ int∫ называется знаком интеграла.

  • Функция f(x)f(x)f(x) называется подынтегральной функцией. Мы хотим найти первообразную этой функции.

  • Буквы dxdxdx обозначают дифференциал dxdxdx. Дифференциал dxdxdx указывает на то, что мы интегрируем нашу функцию по переменной x.

  • F(x)F(x)F(x) — первообразная функция, полученная в результате взятия интеграла.

  • Заглавная буква C представляет некоторую постоянную величину, называемую константой интегрирования.

Почему константа интегрирования ставится в конце каждого неопределенного интеграла?

Для каждого f(x)f(x)f(x) мы добавляем C к его первообразной F(x)F(x)F(x), чтобы включить все первообразные f(x)f(x) ф(х).

2 + C = F(x)∫(2x)dx=x2+C=F(x). 92+100F(x)=x2+100, тогда F’(x)=2xF’(x) = 2xF’(x)=2x

Какую бы константу мы ни поставили в конце первообразной функции F(x)F(x)F(x), производная F’(x)F’(x)F’(x) всегда одна и та же; и F’(x)F’(x)F’(x) всегда равна исходной функции f(x)f(x)f(x).

Поскольку существует бесконечное число функций F(x)F(x)F(x), производная которых равна f(x)f(x)f(x), включение C дает нам способ выразить общее форма первообразной F (x) F (x) F (x), представляя семейство бесконечно многих функций.

Чтобы подробнее рассказать об первообразных производных, один из наших инструкторов, доктор Тим Шартье, расскажет о них более подробно:

Ключевые формулы интегрирования

Давайте рассмотрим наиболее важные правила интегрирования и некоторые стандартные интегралы. Хотя есть много правил, которые нужно запомнить, не отчаивайтесь. Многие следуют аналогичной схеме. Стоит потратить время, чтобы ознакомиться с ними всеми.

В следующих свойствах предположим, что fff и ggg — непрерывные функции. 9{-1}x + C∫1+x2dx​=tan−1x+C

∫sin⁡(ax)dx=−cos⁡(ax)a+C\int \sin{(ax)}dx = \frac{-\cos{(ax)}}{a}+C∫sin(ax) dx=a−cos(ax)​+C для некоторого действительного числа a

∫cos⁡(ax)dx=sin⁡(ax)a+C\int \cos{(ax)}dx = \frac{\sin{(ax)}}{a}+C∫cos(ax)dx= asin(ax)​+C для некоторого действительного числа a

Правило абсолютного значения

∫∣x∣dx=x∣x∣2+C\int |x|dx = \frac{x |x|}{2} + C∫∣x∣dx=2x∣x∣​+C

Д-р Тим Шартье объясняет эти правила подробнее здесь:

Как вычислять интегралы

Мы узнаем, как интегрировать, используя 4 разных метода. 4} dx∫x4x3−2x​dx. Обратите внимание, что, упростив и используя правило суммы, мы получаем: 9{2}}+C∫x4x3−2x​dx=ln∣x∣+x21​+C.

2. Интеграция по частям

Мы используем интегрирование по частям для вычисления интеграла от произведения функций.

Вот формула интегрирования по частям:

∫udv=uv−∫vdu\int udv = uv — \int vdu∫udv=uv−∫vdu

Интегрирование по частям включает в себя выбор одной функции под интегралом для представления u и одной функции для представления dv.

Вот несколько простых шагов:

1. Выберите uuu и dvdvdv, чтобы разделить заданную функцию на произведение функций.

2. Разделите uuu, чтобы найти dududu, и объедините dvdvdv, чтобы найти vvv.

3. Подставьте uuu, vvv и dududu в формулу интегрирования по частям.

4. Решите и упростите там, где это необходимо.

Как правило, вы выбираете uuu как термин, который легче всего различать, и выбираете dvdvdv как термин, который легче всего интегрировать.

Вместе сделаем один пример. Допустим, мы хотим вычислить ∫xcos⁡(3x)dx\int x \cos (3x) dx∫xcos(3x)dx.

Шаг 1

Давайте выберем dv=cos⁡(3x)dxdv = \cos (3x)dxdv=cos(3x)dx, поскольку у нас есть простая формула для интегрирования этой функции с использованием приведенных выше правил тригонометрии. Тогда u=xu = xu=x, так как это то, что осталось.

Шаг 2

Дифференцируя u, мы имеем dudx=d(x)dx=1\frac{du}{dx}=\frac{d(x)}{dx}=1dxdu=dxd(x)=1. После умножения обеих частей на дифференциал dxdxdx мы находим, что du=1dxdu = 1dxdu=1dx.

Теперь давайте интегрируем dvdvdv, чтобы найти vvv. Одна из приведенных выше тригонометрических формул дает нам простой ответ на этот вопрос. Итак, v = ∫dv = ∫cos⁡(3x)dx=sin⁡(3x)3v = \int dv = \int \cos (3x) dx = \frac{\sin{(3x)}}{3}v= ∫dv=∫cos(3x)dx=3sin(3x)​.

Шаг 3

Используя формулу интегрирования по частям, имеем:

∫udv=uv−∫vdu\int udv = uv — \int vdu∫udv=uv−∫vdu

∫xcos⁡(3x)dx=x⋅sin⁡(3x)3−∫sin⁡(3x) 3dx\int x \cos (3x) dx = x \cdot \frac{\sin{(3x)}}{3} — \int \frac{\sin{(3x)}}{3}dx∫xcos(3x )dx=x⋅3sin(3x)​−∫3sin(3x)​dx

=xsin⁡(3x)3−13⋅∫sin⁡(3x)dx= \frac{x\sin{(3x)}} {3} — \frac{1}{3} \cdot \int \sin{(3x)}dx=3xsin(3x)​−31​⋅∫sin(3x)dx

=xsin⁡(3x)3− 13⋅−cos⁡(3x)3= \frac{x\sin{(3x)}}{3} — \frac{1}{3} \cdot \frac{-\cos{(3x)}}{3 }=3xsin(3x)−31⋅3−cos(3x)​

=xsin⁡(3x)3+cos⁡(3x)9+C= \frac{x\sin{(3x)}}{3} + \frac{\cos{(3x)}}{9}+ C=3xsin(3x)​+9cos(3x)​+C

Итак, ∫xcos⁡(3x)dx=xsin⁡(3x)3+cos⁡(3x)9+C\int x \cos (3x) dx = \frac{x\sin{(3x)}}{3} + \frac{{\cos{(3x)}}}{9}+C∫xcos(3x)dx=3xsin(3x)​+9cos(3x) +С.

3. U-замена

U-подстановка распутывает цепное правило для производных. По этой причине u-подстановка также называется правилом обратной цепочки и используется для интеграции составных функций.

Если вы можете распознать как функцию, так и ее производную внутри одного и того же интеграла, это хороший признак того, что вы можете использовать u-подстановку. Функция, в которой вы можете использовать u-подстановку, будет выглядеть так:

∫f(g(x))g'(x)dx\int f(g(x))g'(x)dx∫f(g(x))g'(x)dx

Мы хотим подставим вместо подынтегрального выражения u=g(x)u = g(x)u=g(x) и du=g'(x)du = g'(x)du=g'(x) так, чтобы оно выглядело так:

∫f(g(x))g'(x)dx=f(u)du\int f(g(x))g'(x)dx = f(u)du∫f(g(x) )g'(x)dx=f(u)du 92+5}+C∫(4x)e2x2+5dx=e2x2+5+C.

4. Интегрирование неполными дробями

Этот метод полезен для интегрирования рациональных функций. Рациональная функция — это функция, которая записывается как отношение двух полиномиальных функций. 2+92+9x+4} = \frac{2x}{(2x+1)(x+4)}2×2+9x+42x​=(2x+1)(x+4)2x​

=A2x+1+ Bx+4= \frac{A}{2x+1} + \frac{B}{x+4}=2x+1A​+x+4B​

=A(x+4)(2x+1)( x+4)+B(2x+1)(2x+1)(x+4)=\frac{A(x+4)}{(2x+1)(x+4)}+\frac{B( 2x+1)}{(2x+1)(x+4)}=(2x+1)(x+4)A(x+4)​+(2x+1)(x+4)B(2x+ 1)​

=Ax+4A+2Bx+B(2x+1)(x+4)=\frac{Ax+4A+2Bx+B}{(2x+1)(x+4)}=(2x +1)(x+4)Ax+4A+2Bx+B​

Теперь мы собираем члены x с одной стороны числителя и собираем постоянные члены с другой стороны числителя. Это позволяет нам отразить структуру исходного числителя подынтегрального выражения 2x+02x+02x+0.

2x(2x+1)(x+4)=(Ax+2Bx)+(4A+B)(2x+1)(x+4)\frac{2x}{(2x+1)(x+4) )} = \frac{(Ax+2Bx)+(4A+B)}{(2x+1)(x+4)}(2x+1)(x+4)2x​=(2x+1)(x +4)(Ax+2Bx)+(4A+B)​

Теперь мы можем найти A и B, составив два уравнения:

числитель новой рациональной функции.

Это уравнение уравнивает постоянные члены в числителе исходного подынтегрального выражения с постоянными членами в числителе новой рациональной функции. 92+9x+4} dx = \int (\frac{-2}{7(2x+1)}+\frac{8}{7(x+4)})dx∫2×2+9x+42x​dx= ∫(7(2x+1)−2​+7(x+4)8​)dx

=−27∫12x+1dx+87∫1x+4dx=\frac{-2}{7}\int \ frac{1}{2x+1}dx + \frac{8}{7}\int \frac{1}{x+4}dx=7−2​∫2x+11​dx+78​∫x+41 ​dx

= −2ln⁡(2x+1)2⋅7+8ln⁡(x+4)7+C=\frac{-2 \ln{(2x+1)}}{2 \cdot 7} + \frac{8 \ln{(x+4)}}{7} + C=2⋅7−2ln(2x+1)​+78ln(x+4)​+C

= −17ln⁡(2x+ 1)+87ln⁡(x+4)=-\frac{1}{7}\ln{(2x+1)} + \frac{8}{7} \ln{(x+4)}=-71 ​ln(2x+1)+78​ln(x+4)

=87ln⁡(x+4)−17ln⁡(2x+1)+C=\frac{8}{7} \ln{(x +4)} -\frac{1}{7}\ln{(2x+1)} + C=78​ln(x+4)−71​ln(2x+1)+C 93} + C=3×3−lnx​−9×31​+C

Пример 3

Вычислить ∫sin⁡(ln⁡x)xdx\int \frac{\sin{(\ln x)}}{x}dx∫xsin(lnx)​dx.

Решение : Мы можем решить эту проблему с помощью u-замены. Пусть u=ln⁡xu = \lnxu=lnx. Тогда du=1xdu = \frac{1}{x}du=x1​.

∫sin⁡(ln⁡x)xdx=∫sin⁡udu\int \frac{\sin{(\ln x)}}{x}dx = \int \sin{u}du∫xsin(lnx)​ dx=∫sinudu

=−cos⁡u+C=-\cos{u}+C=−cosu+C

=−cos⁡(ln⁡x)+C=-\cos{(\ln x) } + C=−cos(lnx)+C 92+10x+3} = \frac{x+1}{(x+3)(3x+1)}3×2+10x+3x+1​=(x+3)(3x+1)x+1​

=Ax+3+B3x+1= \frac{A}{x+3} + \frac{B}{3x+1}=x+3A​+3x+1B​

=A(3x+1) +B(x+3)(x+3)(3x+1)=\frac{A(3x+1)+B(x+3)}{(x+3)(3x+1)}=(x +3)(3x+1)A(3x+1)+B(x+3)​

=3Ax+A+Bx+3B(x+3)(3x+1)=\frac{3Ax+A+ Bx+3B}{(x+3)(3x+1)}=(x+3)(3x+1)3Ax+A+Bx+3B​

=3Ax+Bx+A+3B(x+3) (3x+1)=\frac{3Ax+Bx+A+3B}{(x+3)(3x+1)}=(x+3)(3x+1)3Ax+Bx+A+3B​

Теперь составим наши два уравнения.

Один представляет термины x, а другой представляет константы. 92+10x+3}dx=\int(\frac1{4(x+3)}+\frac1{4(3x+1)})dx∫3×2+10x+3x+1​dx=∫(4(x +3)1​+4(3x+1)1​)dx

=14∫1x+3dx+14∫13x+1dx=\frac{1}{4}\int \frac{1}{x+3 }dx+\frac{1}{4}\int \frac{1}{3x+1}dx=41​∫x+31​dx+41​∫3x+11​dx

=14ln⁡(x+3 )+112ln⁡(3x+1)+C=\frac{1}{4} \ln{(x+3)}+\frac{1}{12} \ln{(3x+1)} + C= 41​ln(x+3)+121​ln(3x+1)+C

Исследуйте отмеченные наградами курсы For-Credit от Outlier

Outlier (от соучредителя MasterClass) собрал воедино некоторые из лучшие в мире преподаватели, гейм-дизайнеры и режиссеры для создания будущего онлайн-колледжа.

Ознакомьтесь с этими родственными курсами:

Исчисление I

Изучите курс

Исчисление I

Математика изменений.

Изучить курс

Введение в статистику

Изучить курс

Введение в статистику

Как данные описывают наш мир.

Изучить курс

Введение в микроэкономику

Изучить курс

Введение в микроэкономику

Почему маленькие решения имеют большое влияние.

Исследуйте курс

интеграция в предложение | Примеры предложений из Кембриджского словаря

Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.

То есть существует общность эффекта, согласующаяся с ролью этого региона в интеграции звука и значения.

Из Кембриджского корпуса английского языка