Собственный вектор матрицы онлайн: Собственные числа матрицы онлайн

Решение высшей математики онлайн

‹— Назад

В разделе «Матрица линейного преобразования» мы выяснили, что каждое линейное преобразование -мерного линейного пространства в фиксированном базисе задается матрицей. Если меняется базис, то, как правило, меняется и матрица. Возникает вопрос, нельзя ли найти базис, в котором матрица линейного преобразования имеет наиболее простой вид. В общем случае выбрать такой базис довольно сложно. Это связано с нахождением нормальной жордановой формы матрицы, изложение которого можно найти в более обстоятельных учебниках по линейной алгебре, например, в [4], [5]. Следующая теорема отвечает на этот вопрос в более простом случае.

        Теорема 19.2   Пусть  — линейное преобразование -мерного линейного пространства. Матрица линейного преобразования имеет диагональный вид

(19. 5)

тогда и только тогда, когда векторы базиса являются собственнными векторами преобразования , соответствующими собственным числам .

        Доказательство.     Пусть преобразование имеет линейно независимых собственных векторов , соответствующих собственным числам . Так как векторы линейно независимы, то они образуют базис. Найдем матрицу преобразования в этом базисе. Ее первый столбец является координатным столбцом вектора . Так как  — собственный вектор, то

Координатный столбец этого вектора . Второй столбец матрицы является координатным столбцом вектора . Так как  — собственный вектор, то

Координатный столбец этого вектора . Вычисляя аналогично остальные столбцы, получаем, что матрица линейного преобразования в базисе имеет вид  (19.5). Первая часть теоремы доказана.

Пусть в некотором базисе матрица линейного преобразования имеет вид (19.5). Найдем образ вектора . Этот вектор имеет координатный столбец , его образ имеет координатный столбец

Следовательно,  — собственное число преобразования , а  — соответствущий ему собственный вектор. Аналогично находим, что любой базисный вектор является собственным вектором преобразования , соответствующим собственному числу .     

        Следствие 19.2   Если у матрицы порядка существует набор из линейно независимых собственнных векторов, соответствующих собственным числам , то матрица подобна диагональной матрице с числами на диагонали.

        Теорема 19.3   Пусть собственные векторы преобразования соответствуют собственным числам , среди которых нет равных друг другу. Тогда система векторов является линейно независимой.

        Доказательство.     Воспользуемся методом математической индукции по числу векторов. Если , то утверждение теоремы следует из того, что собственный вектор — ненулевой.

Пусть утверждение верно для системы векторов . Составим линейную комбинацию векторов и приравняем ее к нулю

(19.6)

К обеим частям применим преобразование

По определению линейного преобразования получим

Так как  — собственные векторы, то

Умножим равенство (19. 6) на и вычтем из последнего равенства. Получим

Так как по предположению индукции векторы линейно независимы, то

По условию , следовательно, . Подставим эти значения в (19.6), получим . Получили, что из равенства (19.6) следует , то есть векторы линейно независимы.     

        Следствие 19.3   Если матрица порядка имеет попарно различных собственных чисел, то она подобна диагональной матрице.

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Нежное введение в собственные разложения, собственные значения и собственные векторы для машинного обучения

  Перевод   Ссылка на автора

Матричные разложения являются полезным инструментом для сокращения матрицы до ее составных частей, чтобы упростить ряд более сложных операций.

Возможно, наиболее используемый тип разложения матриц — это разложение, которое разбивает матрицу на собственные векторы и собственные значения. Эта декомпозиция также играет роль в методах, используемых в машинном обучении, таких как метод анализа основных компонентов или PCA.

В этом уроке вы узнаете собственное разложение, собственные векторы и собственные значения в линейной алгебре.

После завершения этого урока вы узнаете:

• Что такое собственное разложение и роль собственных векторов и собственных значений.
• Как рассчитать собственное разложение в Python с помощью NumPy.
• Как подтвердить вектор является собственным вектором и как восстановить матрицу из собственных векторов и собственных значений.

Давайте начнем.

Обзор учебника

Этот урок состоит из 5 частей; они есть:

1. Собственное разложение матрицы
2. Собственные векторы и собственные значения
3. Расчет собственного разложения
4. Подтвердите собственный вектор и собственное значение
5. Восстановить оригинальную матрицу

Собственное разложение матрицы

Собственное разложение матрицы — это тип разложения, который включает в себя разложение квадратной матрицы на набор собственных векторов и собственных значений.

Один из наиболее широко используемых видов разложения матриц называется собственным разложением, в котором мы разлагаем матрицу на набор собственных векторов и собственных значений.

— страница 42, Глубокое обучение, 2016

Вектор является собственным вектором матрицы, если он удовлетворяет следующему уравнению.

A . v = lambda . v

Это называется уравнением собственных значений, где A — матрица исходного квадрата, которую мы разлагаем, v — собственный вектор матрицы, а лямбда — строчная греческая буква и представляет скаляр собственного значения.

Или без точечной записи.

Av = lambdav

Матрица может иметь один собственный вектор и собственное значение для каждого измерения родительской матрицы. Не все квадратные матрицы могут быть разложены на собственные векторы и собственные значения, а некоторые могут быть разложены только таким способом, который требует комплексных чисел. Можно показать, что родительская матрица является произведением собственных векторов и собственных значений. -1 является обратной матрицей, состоящей из собственных векторов.

Однако мы часто хотим разложить матрицы на их собственные значения и собственные векторы. Это может помочь нам проанализировать определенные свойства матрицы, так же как разложение целого числа на его основные факторы может помочь нам понять поведение этого целого числа.

— страница 43, Глубокое обучение, 2016

Эйген это не имя, например метод не назван в честь «Eigen»; eigen (произносится как eye-gan) — это немецкое слово, которое означает «собственный» или «врожденный», как принадлежащее родительской матрице.

Операция декомпозиции не приводит к сжатию матрицы; вместо этого он разбивает его на составные части, чтобы упростить выполнение определенных операций над матрицей. Как и другие методы матричной декомпозиции, собственная декомпозиция используется в качестве элемента для упрощения вычисления других более сложных матричных операций.

Почти все векторы меняют направление, когда они умножаются на A. Некоторые исключительные векторы x находятся в том же направлении, что и Ax. Это «собственные векторы». Умножьте собственный вектор на A, и вектор Ax будет числом лямбда-раз, умноженным на исходную x. […] Лямбда с собственным значением сообщает, растянут ли специальный вектор x, сжимается ли он, перевернут ли или не изменяется — когда он умножается на A.

— страница 289, Введение в линейную алгебру, Пятое издание, 2016.

Собственное разложение также может быть использовано для вычисления главных компонентов матрицы в методе анализа основных компонентов или PCA, который может использоваться для уменьшения размерности данных в машинном обучении.

Собственные векторы и собственные значения

Собственные векторы являются единичными векторами, что означает, что их длина или величина равна 1,0. Их часто называют правыми векторами, что означает вектор-столбец (в отличие от вектора-строки или левого вектора). Правый вектор — это вектор, как мы его понимаем.

Собственные значения — это коэффициенты, применяемые к собственным векторам, которые дают векторам их длину или величину. Например, отрицательное собственное значение может инвертировать направление собственного вектора как часть его масштабирования.

Матрица, которая имеет только положительные собственные значения, упоминается как положительно определенная матрица, тогда как, если все собственные значения являются отрицательными, она упоминается как отрицательно определенная матрица.

Разложение матрицы по ее собственным значениям и собственным векторам дает ценную информацию о свойствах матрицы Определенные матричные вычисления, такие как вычисление мощности матрицы, становятся намного проще, когда мы используем собственное разложение матрицы.

— страница 262, Руководство по линейной алгебре, 2017

Расчет собственного разложения

Собственное разложение вычисляется на квадратной матрице с использованием эффективного итерационного алгоритма, о котором мы не будем вдаваться в подробности.

Часто сначала находят собственное значение, а затем определяют собственный вектор для решения уравнения в виде набора коэффициентов.

Собственное разложение можно рассчитать в NumPy с помощью функции eig ().

В приведенном ниже примере сначала определяется квадратная матрица 3 × 3. Собственное разложение вычисляется по матрице, возвращающей собственные значения и собственные векторы.

# eigendecomposition
from numpy import array
from numpy.linalg import eig
# define matrix
A = array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(A)
# calculate eigendecomposition
values, vectors = eig(A)
print(values)
print(vectors)

При выполнении примера сначала печатается определенная матрица, за которой следуют собственные значения и собственные векторы. Более конкретно, собственные векторы являются собственными векторами с правой стороны и нормированы на единицу длины.

[[1 2 3]
 [4 5 6]
 [7 8 9]]

[  1.61168440e+01  -1.11684397e+00  -9.75918483e-16]

[[-0.23197069 -0.78583024  0.40824829]
 [-0.52532209 -0.08675134 -0.81649658]
 [-0. 8186735   0.61232756  0.40824829]]

Подтвердите собственный вектор и собственное значение

Мы можем подтвердить, что вектор действительно является собственным вектором матрицы.

Мы делаем это, умножая собственный вектор-кандидат на собственный вектор и сравнивая результат с собственным значением.

Сначала мы определим матрицу, затем вычислим собственные значения и собственные векторы. Затем мы проверим, являются ли первые вектор и значение собственными значением и собственным вектором для матрицы. Мы знаем, что это так, но это хорошее упражнение.

Собственные векторы возвращаются в виде матрицы с теми же размерами, что и у родительской матрицы, где каждый столбец является собственным вектором, например, первый собственный вектор — векторы [:, 0]. Собственные значения возвращаются в виде списка, где индексы значений в возвращенном массиве соединяются с собственными векторами по индексу столбца, например, первое собственное значение в значениях [0] связано с первым собственным вектором в векторах [:, 0].

# confirm eigenvector
from numpy import array
from numpy.linalg import eig
# define matrix
A = array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# calculate eigendecomposition
values, vectors = eig(A)
# confirm first eigenvector
B = A.dot(vectors[:, 0])
print(B)
C = vectors[:, 0] * values[0]
print(C)

В этом примере исходная матрица умножается на первый собственный вектор и сравнивается с первым собственным вектором, умноженным на первое собственное значение.

Выполнение примера выводит результаты этих двух умножений, которые показывают один и тот же результирующий вектор, как и следовало ожидать.

[ -3.73863537  -8.46653421 -13.19443305]

[ -3.73863537  -8.46653421 -13.19443305]

Восстановить оригинальную матрицу

Мы можем повернуть процесс вспять и восстановить исходную матрицу, учитывая только собственные векторы и собственные значения.

Во-первых, список собственных векторов должен быть преобразован в матрицу, где каждый вектор становится строкой. Собственные значения должны быть расположены в диагональной матрице. Для этого можно использовать функцию NumPy diag ().

Далее нам нужно вычислить обратную матрицу собственных векторов, чего мы можем достичь с помощью функции inv () NumPy. Наконец, эти элементы должны быть умножены вместе с функцией dot ().

# reconstruct matrix
from numpy import diag
from numpy import dot
from numpy.linalg import inv
from numpy import array
from numpy.linalg import eig
# define matrix
A = array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(A)
# calculate eigenvectors and eigenvalues
values, vectors = eig(A)
# create matrix from eigenvectors
Q = vectors
# create inverse of eigenvectors matrix
R = inv(Q)
# create diagonal matrix from eigenvalues
L = diag(values)
# reconstruct the original matrix
B = Q.dot(L).dot(R)
print(B)

В примере снова вычисляются собственные значения и собственные векторы и используются их для восстановления исходной матрицы.

При выполнении примера сначала печатается исходная матрица, а затем матрица, восстановленная из собственных значений и собственных векторов, соответствующих исходной матрице.

[[1 2 3]
 [4 5 6]
 [7 8 9]]

[[ 1.  2.  3.]
 [ 4.  5.  6.]
 [ 7.  8.  9.]]

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Создайте 5 примеров, используя каждую операцию со своими собственными данными.
• Реализуйте каждую матричную операцию вручную для матриц, определенных как списки списков.
• Найдите документы по машинному обучению и найдите 1 пример каждой используемой операции.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

• Раздел 6.1. Собственные значения и собственные векторы. Руководство по линейной алгебре, 2017
• Глава 6 Собственные значения и собственные векторы, Введение в линейную алгебру, Пятое издание, 2016.
• Раздел 2.7 Собственное разложение, Глубокое обучение, 2016
• Глава 5. Собственные значения, собственные векторы и инвариантные подпространства. Линейная алгебра сделано правильно Третье издание, 2015.
• Лекция 24, Проблемы собственных значений, Численная линейная алгебра, 1997.

API

• API numpy.linalg.eig ()
• API numpy.diag ()
• API numpy.dot ()
• API numpy.linalg.inv ()

статьи

• eigen в Викисловарь
• Собственные значения и собственные векторы
• Собственное разложение матрицы
• Алгоритм собственных значений
• Матричная декомпозиция

Резюме

В этом уроке вы обнаружили собственное разложение, собственные векторы и собственные значения в линейной алгебре.

В частности, вы узнали:

• Что такое собственное разложение и роль собственных векторов и собственных значений.
• Как рассчитать собственное разложение в Python с помощью NumPy.
• Как подтвердить вектор является собственным вектором и как восстановить матрицу из собственных векторов и собственных значений.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Онлайн-калькулятор: Калькулятор собственных векторов

  Исследование  Математика  Алгебра

Этот онлайн-калькулятор вычисляет собственные векторы квадратной матрицы до 4-й степени.

Это последний калькулятор, посвященный собственным векторам и собственным значениям. Первым из них был калькулятор характеристического полинома, который выводит характеристическое уравнение, подходящее для дальнейшей обработки. Второй калькулятор — калькулятор собственных значений решает это уравнение для нахождения собственных значений (используя аналитические методы, поэтому он работает только до 4-й степени), а калькулятор ниже вычисляет собственные векторы для каждого найденного собственного значения. Некоторые теории можно найти под калькулятором.

Калькулятор собственных векторов

5 6 3 -1 0 1 1 2 -1

Квадратная матрица

Точность вычислений

Знаки после запятой: 2

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

Как найти собственные векторы

Позвольте мне повторить определение собственных векторов и собственных значений из калькулятора собственных значений.

Существуют векторы, для которых матричное преобразование дает вектор, параллельный исходному вектору.

,

где — некоторое скалярное число.

Эти векторы называются собственными векторами матрицы A, а эти числа называются собственными значениями матрицы A.

Мы используем приведенное выше уравнение в следующей форме: собственные значения путем решения характеристического уравнения

.

После того, как мы нашли собственные значения, мы можем найти собственные векторы. Мы должны подставить каждое конкретное собственное значение в уравнение и решить его для против . Это означает, что нам просто нужно решить следующую систему линейных уравнений (в матричной форме):

Это однородная система линейных уравнений, и даже более того, ее уравнения НЕ являются независимыми. То есть система имеет бесконечно много решений. Это потому, что у нас есть семейство собственных векторов (включая нулевой вектор) или собственных пространств для каждого собственного значения. Итак, когда вас просят найти собственные векторы для матрицы, вам действительно нужно подобрать какое-то «красивое» решение системы линейных уравнений, полученное для каждого собственного значения, то есть какой-то выборочный собственный вектор с возможным отсутствием дробей и небольшими положительными целыми числами.

В большинстве случаев собственное значение дает однородную систему с одной независимой переменной.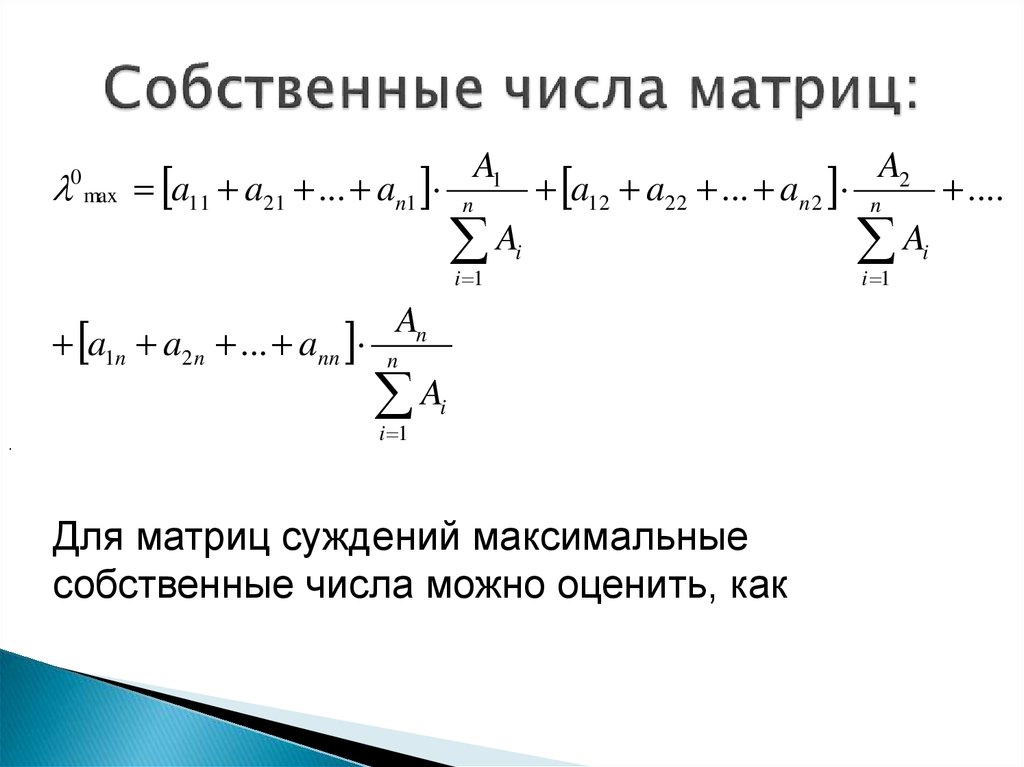 Однако в некоторых случаях собственное значение имеет кратность более 1 (например, в случае двойных корней). В таких случаях однородная система будет иметь более одной независимой переменной, и у вас будет несколько линейно независимых собственных векторов, связанных с таким собственным значением — по одному для каждой независимой переменной.

URL скопирован в буфер обмена

Похожие калькуляторы

• • Калькулятор собственных значений
• • Характеристический полином
• • Решение неоднородной системы линейных уравнений с помощью обратной матрицы
• • Модульная обратная матрица
• • Калькулятор обратной матрицы
• • Раздел алгебры (110 калькуляторов)

2 9 алгебра собственный вектор Алгебра характеристическое уравнение собственное значение собственный вектор Математическая матрица

  PLANETCALC, Калькулятор собственных векторов

 Тимур  2020-12-11 12:18:53

Как найти собственные значения, собственные векторы и собственные пространства — Криста Кинг Математика

Что такое собственные векторы и собственные значения?

Любой вектор ???\vec{v}??? который удовлетворяет ???T(\vec{v})=\lambda\vec{v}??? является собственным вектором преобразования ???T???, а ???\lambda??? это собственное значение, связанное с собственным вектором ???\vec{v}???.

Преобразование ???Т??? является линейным преобразованием, которое также может быть представлено как ???T(\vec{v})=A\vec{v}???.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Первое, что вы хотите отметить относительно ???T(\vec{v})=\lambda\vec{v}???, это то, что ???\lambda??? является константой, которая действует как скаляр на ???\vec{v}???, мы говорим, что преобразование ???\vec{v}???, ???T(\vec{v })???, на самом деле просто масштабированная версия ???\vec{v}???.

Можно также сказать, что собственные векторы ???\vec{v}??? это векторы, которые не меняют направление, когда мы применяем матрицу преобразования ???T???. Итак, если мы применим ???T??? в вектор ???\vec{v}???, а результат ???T(\vec{v})??? параллельно исходному ???\vec{v}???, то ???\vec{v}??? является собственным вектором. 9\циркуляр??? никогда не будет удовлетворять ???T(\vec{v})=\lambda\vec{v}???.

Но в домене могут быть и другие векторы, которые остаются на той же линии при преобразовании и могут просто увеличиваться или уменьшаться на ???T???. Это векторы, которые будут удовлетворять ???T(\vec{v})=\lambda\vec{v}???, что означает, что это собственные векторы для ???T???. И это имеет смысл, потому что ???T(\vec{v})=\lambda\vec{v}??? буквально читается как «преобразованная версия ???\vec{v}??? такое же, как исходное ???\vec{v}???, но увеличенное или уменьшенное на ???\lambda???».

Чтобы действительно идентифицировать собственный вектор, нужно сравнить диапазон ???\vec{v}??? с размахом ???T(\vec{v})???. Диапазон любого одиночного вектора ???\vec{v}??? всегда будет линия. Если при преобразовании ???T??? диапазон остается таким же, что ???T(\vec{v})??? имеет тот же диапазон, что и ???\vec{v}???, тогда вы знаете ???\vec{v}??? является собственным вектором. Векторы ???\vec{v}??? и ???T(\vec{v})??? могут быть разной длины, но их пролеты одинаковы, потому что они лежат на одной линии.

Причина, по которой мы заботимся об идентификации собственных векторов, заключается в том, что они часто являются хорошими базисными векторами для подпространства, а мы всегда заинтересованы в поиске простого базиса, с которым легко работать.

Нахождение собственных значений

Потому что мы сказали, что ???T(\vec{v})=\lambda\vec{v}??? и ???T(\vec{v})=A\vec{v}???, должно быть верно, что ???A\vec{v}=\lambda\vec{v}???. Что означает, что собственные векторы — это любые векторы ???\vec{v}??? которые удовлетворяют ???A\vec{v}=\lambda\vec{v}???.

Мы также знаем, что будет ???2??? собственные векторы, когда ???A??? ???2\times2???, то будет ???3??? собственные векторы, когда ???A??? есть ???3\times3???, а что будет ???n??? собственные векторы, когда ???A??? равно ???n\times n???.

Пока ???\vec{v}=\vec{O}??? будет удовлетворять ???A\vec{v}=\lambda\vec{v}???, мы на самом деле не включаем это как собственный вектор. Причина в том, что, во-первых, это не дает нам никакой интересной информации, а во-вторых, потому что ???\vec{v}=\vec{O}??? не позволяет определить соответствующее собственное значение ???\lambda???.

Нас интересуют только векторы ???\vec{v}??? которые не равны нулю. Если мы переработаем ???A\vec{v}=\lambda\vec{v}???, мы могли бы записать его как

???\vec{O}=\lambda\vec{v}-A\ век{в}???

???\vec{O}=\lambda I_n\vec{v}-A\vec{v}???

???(\lambda I_n-A)\vec{v}=\vec{O}???

Поймите, что это просто произведение матрицы на вектор, равное нулевому вектору. Потому что ???\лямбда I_n-A??? просто матрица. Собственное значение ???\лямбда??? действует как скаляр на единичной матрице ???I_n???, что означает ???\lambda I_n??? будет матрица. Если из ???\lambda I_n??? вычесть матрицу ???A???, то все равно получится просто другая матрица, поэтому ???\lambda I_n-A??? является матрицей. Итак, сделаем замену ???B=\lambda I_n-A???.

???B\vec{v}=\vec{O}???

Записав таким образом, мы увидим, что любой вектор ???\vec{v}??? который удовлетворяет ???B\vec{v}=\vec{O}??? будет находиться в нулевом пространстве ???B???, ???N(B)???. Но мы уже сказали, что ???\vec{v}??? должен был быть ненулевым, что сразу говорит нам о том, что в нулевом пространстве должен быть хотя бы один вектор, отличный от нулевого. Всякий раз, когда мы знаем, что в нулевом пространстве есть вектор, отличный от нулевого вектора, мы заключаем, что матрица ???B??? (матрица ???\lambda I_n-A???) имеет линейно зависимые столбцы, и что ???B??? необратим, и что определитель ???B??? равно ???0???, ???|B|=0???.

Что означает, что мы могли бы придумать эти правила:

???A\vec{v}=\lambda\vec{v}??? для ненулевых векторов ???\vec{v}??? тогда и только тогда, когда ???|\lambda I_n-A|=0???.

???\лямбда??? является собственным значением ???A??? тогда и только тогда, когда ???|\lambda I_n-A|=0???.

Помня об этих правилах, у нас есть все необходимое, чтобы найти собственные значения для конкретной матрицы.

Как найти собственные значения, собственные векторы и собственные пространства

Пройти курс

Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого.

🙂

Нахождение собственных значений преобразования

Пример

Нахождение собственных значений матрицы преобразования ???A???.

Нам нужно найти определитель ???|\lambda I_n-A|???.

Тогда определитель полученной матрицы равен 92-4\лямбда+3=0???

Чтобы найти ???\лямбда???, мы всегда пытаемся разложить на множители, но если многочлен нельзя разложить на множители, мы можем либо дополнить квадрат, либо использовать формулу квадрата. Это можно учесть.

???(\лямбда-3)(\лямбда-1)=0???

???\лямбда=1??? или ???\лямбда=3???

Таким образом, предполагая ненулевые собственные векторы, мы говорим, что ???A\vec{v}=\lambda\vec{v}??? можно решить для ???\lambda=1??? и ???\лямбда=3???.

Причина, по которой мы заботимся об идентификации собственных векторов, заключается в том, что они часто являются хорошими базисными векторами для подпространства, а мы всегда заинтересованы в поиске простого базиса, с которым легко работать.

Мы хотим отметить пару важных моментов, оба из которых иллюстрируются этим последним примером.

Во-первых, сумма собственных значений всегда будет равна сумме элементов матрицы, расположенных по диагонали. В матрице ???А??? из примера значения по диагонали были ???2??? и???2???. Их сумма равна ???4???, что означает, что сумма собственных значений будет ???4??? также. Сумма элементов по диагонали называется следом матрицы, поэтому можно сказать, что след всегда будет равен сумме собственных значений.

???\text{Trace}(A)=\text{сумма }A\text{собственных значений}???

Поймите, что это также означает, что для ???n\times n??? матрица ???A???, как только мы найдем ???n-1??? собственных значений, у нас уже будет значение ???n???го собственного значения.

Во-вторых, определитель ???A???, ???|A|???, всегда будет равен произведению собственных значений. В последнем примере ???|A|=(2)(2)-(1)(1)=4-1=3???, а произведение собственных значений было ???\lambda_1\lambda_2= (1)(3)=3???.

???\text{Det}(A)=|A|=\text{произведение собственных значений }A\text{}???

Нахождение собственных векторов

После того, как мы нашли собственные значения для матрицы преобразования, нам нужно найти связанные с ними собственные векторы. Для этого мы начнем с определения собственного пространства для каждого собственного значения матрицы.

Собственное пространство ???E_\lambda??? для конкретного собственного значения ???\лямбда??? множество всех собственных векторов ???\vec{v}??? которые удовлетворяют ???A\vec{v}=\lambda\vec{v}??? для этого конкретного собственного значения ???\lambda???.

Как мы знаем, мы смогли переписать ???A\vec{v}=\lambda\vec{v}??? как ???(\lambda I_n-A)\vec{v}=\vec{O}???, и мы узнали, что ???\lambda I_n-A??? просто матрица. Таким образом, собственное пространство — это просто нулевое пространство матрицы ???\lambda I_n-A???.

???E_\lambda=N(\lambda I_n-A)???

Чтобы найти матрицу ???\lambda I_n-A???, мы можем просто подставить собственное значение в значение, которое мы нашли ранее для ???\lambda I_n-A???. Давайте вернемся к предыдущему примеру и найдем собственные векторы, связанные с ???\lambda=1??? и ???\лямбда=3???.

Пример

Для матрицы преобразования ???A??? мы нашли собственные значения ???\lambda=1??? и ???\лямбда=3???. Найдите собственные векторы, связанные с каждым собственным значением.

С ???\лямбда=1??? и ???\lambda=3???, у нас будет два собственных пространства, заданных как ???E_\lambda=N(\lambda I_n-A)???. С

получаем

Следовательно, собственные векторы в собственном пространстве ???E_1??? удовлетворит

???v_1+v_2=0???

???v_1=-v_2???

Таким образом, вместо ???v_1=-v_2??? мы заменим ???v_2=t??? и скажем, что

???\begin{bmatrix}v_1\\ v_2\end{bmatrix }=t\begin{bmatrix}-1\\ 1\end{bmatrix}???

Что означает, что ???E_1??? определяется как

???E_1=\text{Span}\Big(\begin{bmatrix}-1\\ 1\end{bmatrix}\Big)???

И собственные векторы в собственном пространстве ???E_3??? удовлетворит

???v_1-v_2=0???

???v_1=v_2???

И с ???v_1=v_2??? мы заменим ???v_2=t??? и скажем, что

???\begin{bmatrix}v_1\\ v_2\end{bmatrix} =t\begin{bmatrix}1\\ 1\end{bmatrix}???

Что означает, что ???E_3??? определяется как

???E_3=\text{Span}\Big(\begin{bmatrix}1\\ 1\end{bmatrix}\Big)???

Если мы объединим эти два последних примера (в первом, где мы нашли собственные значения, и во втором, где мы нашли соответствующие собственные векторы), мы можем нарисовать картину решения. Для собственного значения ???\lambda=1??? мы получили

???E_1=\text{Span}\Big(\begin{bmatrix}-1\\ 1\end{bmatrix}\Big)???

Мы можем нарисовать остовный собственный вектор ???\vec{v}=(-1,1)???,

, а затем сказать, что собственное пространство для ???\lambda=1??? это набор всех векторов, которые лежат вдоль линии, созданной ???\vec{v}=(-1,1)???.

Тогда для собственного значения ???\lambda=3??? мы получили

???E_3=\text{Span}\Big(\begin{bmatrix}1\\ 1\end{bmatrix}\Big)???

Мы можем добавить к нашему эскизу остовный собственный вектор ???\vec{v}=(1,1)???,

, а затем сказать, что собственное пространство для ???\lambda=3??? это набор всех векторов, которые лежат вдоль линии, созданной ???\vec{v}=(1,1)???.

Другими словами, мы знаем, что для любого вектора ???\vec{v}??? вдоль любой из этих строк, когда вы применяете преобразование ???T??? к вектору ???\vec{v}???, ???T(\vec{v})??? будет вектором вдоль той же линии, его можно просто увеличить или уменьшить.

No related posts.