Все формулы по математике с 1 по 4 класс: Математические формулы 1-4 класс

Математика 4 класса – какие задания и темы нужно учить?

Заключительный класс начальной школы – очень ответственный для каждого ученика. Подросшие школьники вот-вот перейдут в среднюю школу, где их ждет довольно большая нагрузка по всем предметам. Кроме того, добавится много новых уроков, вытекающих из уже пройденного материала. Именно поэтому важно, как малыш закончит начальную школу – усвоит ли программу, научится ли успевать выполнять задания, сможет ли терпеливо изучать то, что не сильно заинтересовало с первого урока. Помощниками в это время, несомненно, должны выступать родители. Понимание, поддержка и помощь в сложных ситуациях – то, что нужно ребенку для результативного обучения в школе.

На первый взгляд может показаться, что имеют значение только лишь старшие классы, ведь не за горами и выпускные экзамены. Но начальная школа закладывает фундамент, без которого успешная учеба в дальнейшем вряд ли сложится. Родителям стоит много внимания уделить успеваемости детей в начальной школе по всем предметам. Математика 4 класса – одна из тех дисциплин, на которых основывается все школьное образование.

1 и 2 четверть – что проходят в первом полугодии

Математика за четвертый класс включает в себя много нового материала, по сравнению с предыдущими годами. В 1-2 четверти в основном проходят трехзначные числа. Школьники постепенно расширяют свои знания, учась складывать, вычитать, умножать большие числа в столбик. В том числе, проводятся математические действия с остатком.

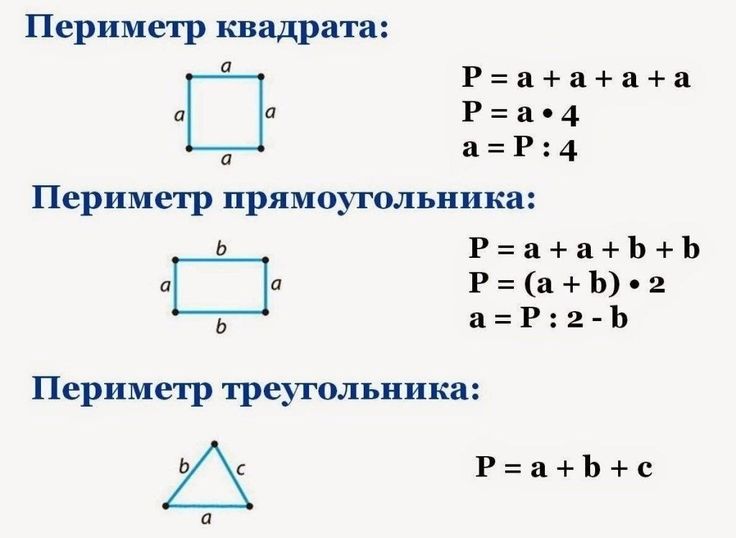
Когда дети хорошо усвоили работу с трехзначными числами и легко решают задачи с их использованием, начинается новый этап – знакомство с классом тысяч, миллионов и миллиардов. Кроме того, ребята узнают, что такое многочлен, и как с ним выполнять математические действия. Если первая четверть больше посвящена арифметике, то вторая постепенно заполняется геометрией. Ученики все больше погружаются в изучение геометрических фигур, учатся находить периметр и площадь. Также вторая четверть наполнена многочисленными задачами, нацеленными, в том числе, и на изучение времени, циферблата и долей.

Независимо от тем на протяжении всего времени изучения математики школьники тренируют навыки устного и письменного счета разной сложности. Ведь умение считать – основа математики.

3-4 четверть – темы второго полугодия

Второе полугодие 4 класса более сложное и ответственное. Ведь это последний этап, когда происходит подготовка к средней школе. Особое внимание в 3-4 четверти уделяется следующим темам:

• изучение пропорций;
• решение задач на нахождение скорости, времени, расстояния; применение этих понятий в жизни;
• деление на круглые, многозначные числа;
• деление с остатком;
• чтение и анализ данных;
• обучение составлению таблиц и диаграмм.

Математика 4 класса в 3-4 четверти обучает детей очень важным навыкам, которые пригодятся ребятам на протяжении всей жизни. Они учатся находить информацию, вычленять главное в многочисленных данных, а также проводить обратное действие – переводить данные в таблицы.

Четвертый класс помогает детям набраться опыта в математике во всех направлениях, которые пригодятся ребенку на протяжении всего обучения этой дисциплине. Родителям необходимо следить за тем, чтобы малыш преуспевал в каждой теме, ведь как в алгебре, так и в геометрии все связано между собой, а темы вытекают одна из другой.

Задачи по математике в 4 классе, которые нужно уметь решать

Конечно, важное место в 4 классе занимают задачи по математике. Школьники решают легкие и сложные, на одно действие и несколько, с геометрическими фигурами и сложными числами. Задания включают в себя задачи на:

• пропорциональное деление;
• нахождение скорости, пути, времени движения с разными точками старта или с одной, в одном направлении или в разном;
• нахождение неизвестного по двум разностям;
• увеличение или уменьшение числа в несколько раз;
• увеличение или уменьшение числа на несколько единиц;
• нахождение неизвестного вычитаемого, слагаемого, уменьшаемого и других компонентов примера.

Усердно занимаясь и вникая в школьную программу, ребенок будет лучше подготовлен к обучению в старших классах, где математическая нагрузка в разы выше, а времени на понимание материала – меньше. Поэтому очень важно уделять должное внимание каждой теме в начальной школе.

Как выучить математику в начальной школе на отлично?

Изначальная цель – знать математику на отлично – неверная. Ведь основная задача ребенка – вникнуть в предмет, понять его, научиться применять свои знания в повседневной жизни, а не просто получать пятерки. Для этого недостаточно выучить формулы и запомнить последовательность решения задач – нужно подходить к обучению осознанно.

Важно замотивировать школьника на изучение предмета, сделать так, чтобы ему самому было интересно учиться. Добиться этого можно с помощью внедрения элементов игры в привычные уроки. Именно на этом принципе основана Амаматика – методика обучения математике для учеников 1-5 класса.

Программа не только учит решать задания из школьной программы, но и прививает ребенку знания из смежных областей. Развитие логики и пространственного мышления, изучение арифметики, геометрии, основ программирования и финансовой грамотности, решение логических и нестандартных задач – курс комплексно совершенствует способности школьника.

Большое количество развивающих игр и интерактивный формат подачи материала делает обучение не только эффективным, но и увлекательным. Запишитесь на Амаматику и начните развивать навыки ребенка уже сейчас.

Формула в математике – основные правила

4.6

Средняя оценка: 4.6

Всего получено оценок: 80.

4.6

Средняя оценка: 4.6

Всего получено оценок: 80.

Формула – это одно из важнейших понятий в математике. Основные формулы облегчают расчет и экономят время при решении уравнений. Поговорим о том, что такое формула, откуда они берутся и выделим основные формулы математики.

Что это такое?

Формула – это всегда равенства. С левой стороны находится выражение, которое можно преобразовать, а с правой результат преобразования. 2)$$ – разность кубов это произведение разности чисел на квадрат суммы этих чисел.

Как показывает практика, последние две формулы проще запомнить в словесной форме. К тому же эти формулы часто встречаются при решении простых уравнений. Поэтому, дабы не бежать каждый раз в интернет – проще их запомнить.

Что мы узнали?

Мы дали определение понятию формулы, привели основные формулы математики и обозначили, что формулой можно пользоваться в обе стороны от знака равенства.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 80.

---

А какая ваша оценка?

2 \) — Это, наверное, знаковая и одна из фундаментальных формул алгебры, представляющая собой квадрат двух переменных, сложенных вместе!

Важные математические формулы

Когда мы говорим о формулах, мы ожидаем сложных выражений, чисел и показателей степени! Формулы на самом деле облегчают учащимся решение и понимание математических понятий, обычно вводимых им с младших классов. 2 \) где c — длина гипотенузы, a и b — длины двух других сторон прямоугольного треугольника. – Эта формула, созданная великим Пифагором, греческим математиком, упоминает соотношение между гипотенузой, наибольшей стороной прямоугольного треугольника, и длинами двух других сторон. 9{\circ} \), где n — количество сторон. — Предыдущая формула говорила о прямоугольном треугольнике, который является многоугольником. На самом деле все замкнутые фигуры с тремя и более сторонами являются многоугольниками. А сумма внутренних углов многоугольника вычисляется по приведенной формуле.

Форма наклона точки: \( y-y_1=m(x-x_1) \), где m — уклон, а \( (x_1,~y_1) \) — координаты точки, проходящей через линию. — Многоугольники состоят из прямых линий, и когда мы говорим о линиях, есть способ представить прямую линию в виде одного из четырех основных типов уравнений, и это уравнение представляет наклон и одну точку на линии. 9n \) – Уходя от геометрии, мы имеем формулу, которая не позволяет нам повторять умножение. Представление выражения, указывающего на многократное умножение, облегчает жизнь многим учащимся.

Простые проценты: \( I=Prt \) где P — основная сумма, r — процентная ставка (в десятичной форме), t — период времени. – Продолжая тему увеличения числа в геометрической прогрессии, мы также можем рассмотреть вопрос о том, как заставить деньги расти с помощью простых процентов.

\( \text{Среднее}=\frac{\text{Сумма всех значений данных}}{\text{Количество значений данных}} \) — И когда нам нужно вычислить среднее значение набора чисел или значений, нам просто нужна сумма всех значений и разделить ее на количество значений. Эта формула определенно имеет статистическую значимость!

Расширение: при расширении координаты фигуры \( (x,~y) \) становятся \( (kx,~ky) \), где k — масштабный коэффициент. – Важное значение в координатной геометрии имеет понятие расширения, которое заключается в увеличении или уменьшении размера геометрической формы с заданным коэффициентом масштабирования.

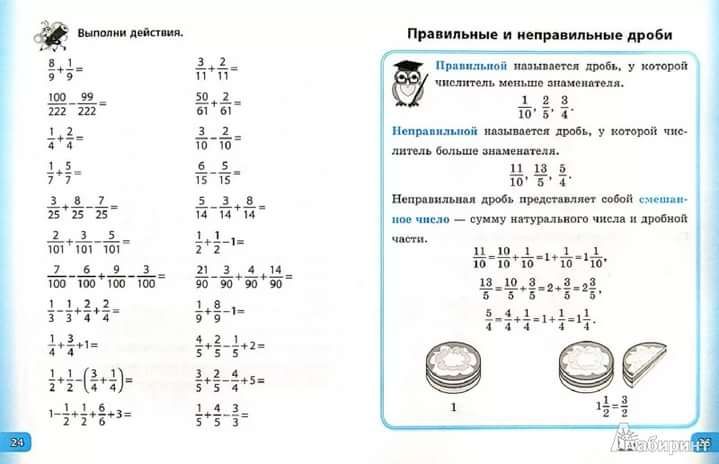
Преимущества математических формул

• Математика как предмет не изолирована от множества других предметов. На самом деле математика связана с такими отраслями науки, как физика, химия и биология. Мало того, что математика помогает поддерживать теории по этим предметам, прогнозы, сделанные исследователями и учеными, основаны на математических моделях.

 

• Говоря о математических моделях, многие сценарии реальной жизни решаются с помощью правил и символов. Все эти правила и символы в совокупности дают нам формулы. В обучении уравнениям и формулам происходит переход от заучивания одного, и один дает два, к вычитанию «x» из «y», что дает нам «z».

 

• Разница здесь в том, что по мере того, как учащийся переходит из одного класса в другой, сложность формул, которые учащийся изучает, постепенно увеличивается. Именно уроки в классе и математические формулы, которые вводятся в большем количестве, позволяют учащимся расшифровывать окружающую их действительность.

 

• Формулы облегчают изучение математики, а также практику. Постоянное взаимодействие с формулами на нашем веб-сайте обязательно сделает учащихся более острыми и сосредоточенными на всем, что они делают изо дня в день.

 

• Свободное запоминание формул обязательно поможет учащимся старших классов и в колледже. Поскольку формулы, введенные в школе, являются основой для более сложных формул в старших классах и колледже.

 

• От колледжа до карьеры, с ними определенно связаны формулы. Не простые, такие как определение площади квадрата или определение скорости автомобиля, а те, которые могли бы помочь человеку на Марсе, или построить следующее по высоте здание, или даже исследовать самые глубокие части океана!

Часто задаваемые вопросы

Для чего нужны формулы в математике?

Формулы обеспечивают метод решения задач, а также делают учащегося сообразительным, сосредоточенным и готовым к решению реальных проблем.

Можно ли решать математические задачи без формул?

Конечно, математические задачи можно решить и без формул. Однако процесс получения решения проблемы может включать гораздо больше шагов по сравнению с применением формулы к той же проблеме и ее решением за меньшее количество шагов.

Сколько лет формулам, которые используются в математике?

Несмотря на то, что математика началась с подсчета чисел, сложные формулы были известны многим древним цивилизациям, поскольку они были необходимы для строительства памятников, измерения земли, отслеживания торговли и так далее. Однако Пифагор и его формула для гипотенузы или даже Евклид — пара греческих математиков, чьи формулы стали знаменитыми!

Есть только формулы для геометрии и алгебры?

Будь то алгебра, геометрия или арифметика, для всех этих разделов математики существуют формулы.

Нужно ли запоминать формулы?

Чтобы укоренить эти формулы, нужно понять концепцию и понять, почему окончательная форма формулы такова, как она написана. 2 \), предложенное Эйнштейном. Евклид, Эйлер и Пифагор — другие математики, в честь которых названы формулы.

Используются ли формулы для быстрого решения математических задач?

Формулы обеспечивают прямой путь решения проблем, а не ярлыки. Несмотря на то, что могут быть альтернативные методы решения проблем, использование формулы и подстановка значений в выражение может быть более быстрым и эффективным способом получения решения.

В каждом классе есть фиксированное количество формул?

Не существует фиксированного количества формул для каждого класса, так как количество формул может варьироваться в зависимости от математических понятий, относящихся к конкретному классу, начиная с четвертого класса.

В младших классах нет формул?

Применение формул начинается с 4 класса, так как в младших классах знакомство с формулами с неизвестными может показаться учащимся сложным для восприятия.

Ознакомьтесь с другими нашими курсами

Учебная программа по математике в начальных и неполных средних классах – Энциклопедия TIMSS 2015

Home/Страны/Норвегия/Учебная программа по математике в начальных и неполных средних классах

Далее следует краткий обзор учебной программы по математике для 1–10 классов.

В первом предложении учебного плана говорится: «Математика является частью нашего глобального культурного наследия». ⁸ После представления математики как возможного источника радости в учебной программе делается упор на широкий спектр математических приложений и утилит. Далее вводятся некоторые конкретные и практические, а также абстрактные и теоретические аспекты математики, которые играют важную роль в преподавании и изучении предмета.

Учебная программа по математике организована по предметным областям. Предметами для 1–4 классов являются числа, геометрия, измерение и статистика. Предметами для 5–7 классов являются числа и алгебра, геометрия, измерения, статистика и вероятность. Предметами для учащихся 8–10 классов являются числа и алгебра; Геометрия; Измерение; Статистика, Вероятность и Комбинаторика; и Функции.

Учебная программа определяет пять основных областей навыков по всем предметам и для всех классов. Для математики эти области навыков включают следующее:

• Устные навыки — Создание смысла путем слушания, вопросов, разговоров, рассуждений и обсуждения математических вопросов; развитие коммуникативных навыков, переход от простого неформального языка к точной терминологии и недвусмысленному понятийному языку
• Навыки письма — выражение открытий, идей, направлений мысли и решений; составление подходящих эскизов, рисунков, таблиц, графиков и диаграмм; и развитие способности использовать формальный, символический язык и формулировать всесторонние аргументы о сложных отношениях
• Навыки чтения — понимание текстов, содержащих математические выражения, графики, диаграммы, таблицы, символы, формулы и логические рассуждения; и понимание сложных текстов с расширенным символическим языком и понятиями
• Численность — применение символического языка, математических понятий и различных стратегий при решении проблем и исследованиях в практических, повседневных ситуациях и в чисто математических контекстах; распознавание математических аспектов ситуаций и проблем, их анализ и оценка обоснованности решений; переход от базового понимания чисел к анализу и решению сложных проблем с использованием различных стратегий и методов; и научиться больше использовать различные инструменты в расчетах, моделировании и общении
• Цифровые навыки — применение цифровых инструментов для расчета, исследования, визуализации, моделирования, моделирования и презентации; и критическая оценка источников, анализов, результатов и утилит

В приложении 1 представлены краткие сведения о компетенциях, которыми должны обладать учащиеся по математике с 1 по 4 классы, с 5 по 7 классы и с 8 по 10 классы соответственно.