Сочетание без повторений: формула, определение, примеры решения задач из комбинаторики

Сочетания без повторений

Лекция №1 Основы комбинаторики

Основы комбинаторики

Комбинаторика – это область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из конечного числа заданных объектов. Другими словами, это раздел математики, в котором изучаются задачи выбора элементов из заданного конечного множества и размещения этих элементов в каком-либо порядке, при этом используются два основных правила комбинаторики – правило суммы и правило произведения.

Правило суммы. Если объект А может быть выбран m способами, а объект B – n способами, причем выборы объектов взаимно исключают друг друга, то выбор «либо A, либо B» может быть осуществлен m + n способами.

Правило суммы можно распространить на выбор любого конечного числа объектов.

Пример 1. На полке в книжном шкафу стоят 25 книг, среди которых учебники: 5 книг по математике, 4 книги по физике, 6 книг по химии, остальные книги – художественная литература. Сколькими способами можно выбрать учебник с этой полки?

Решение: Взять любую из 5 книг по математике можно 5 способами, книгу по физике – 4 способами, книгу по химии – 6 способами. Выбор одной книги не влияет на выбор другой книги. Значит, по правилу суммы учебник с полки можно выбрать 5 + 4 + 6 = 15 способами.

Правило произведения. Если объект А может быть выбран m способами и после каждого из этих выборов объект B может быть выбран n способами, то выбор пары А, B может быть осуществлен m×n способами.

Правило произведения можно распространить на выбор любого конечного числа объектов, т.е. пусть необходимо один за другим выполнить какие-то

к действий. Если первое действие можно выполнить n₁ способом, после чего второе действие можно выполнить п₂ способами, после чего третье действие можно выполнить n₃ способами и т. д. до к-го действия, которое можно выполнить п_к способами, то все к действий вместе могут быть выполнены n₁× п₂× n₃×п_к способами.

Пример 2. Сколько трехзначных чисел можно составить из цифр 2, 4, 5, если цифры в числе не повторяются?

Решение: На месте сотен поставим любую из трех цифр. Это можно сделать тремя способами. После каждого такого выбора на месте десятков можно поставить любую из двух оставшихся цифр (т.е. двумя способами), так как цифры в числе не повторяются. Наконец, на месте единиц можно поставить оставшуюся одну цифру (т.е. одним способом). Применяя правило произведения два раза получим: 3

×2×1 = 6 способов, и соответственно, шесть трехзначных чисел.

Пример 3. Бросают две игральные кости разного цвета. Сколько существует результатов опыта? Каждая кость может упасть независимо от другой шестью способами.

Ответ: 6*6=36.

Пример 4. У велосипедистов есть суеверие: в нагрудном номере не должно быть цифры 8. Сколько человек участвовало в соревновании, если были розданы все трехзначные номера, не содержащие цифры 8. Ответ: . 9×9×9=729

Пример 5. В урне 4 красных, 3 белых и 6 синих шаров. Сколькими способами можно достать последовательно 3 шара так, чтобы первым был вынут красный шар, вторым − белый, третьим − синий? Ответ:4 ×3 ×6=72.

Графической иллюстрацией правила произведения является специальная схема, условно называемая «дерево». Для рассмотренного примера соответствующая схема будет выглядеть так:

2

4

5

5

4

245

254

Рассмотрим пример на применение этих двух правил.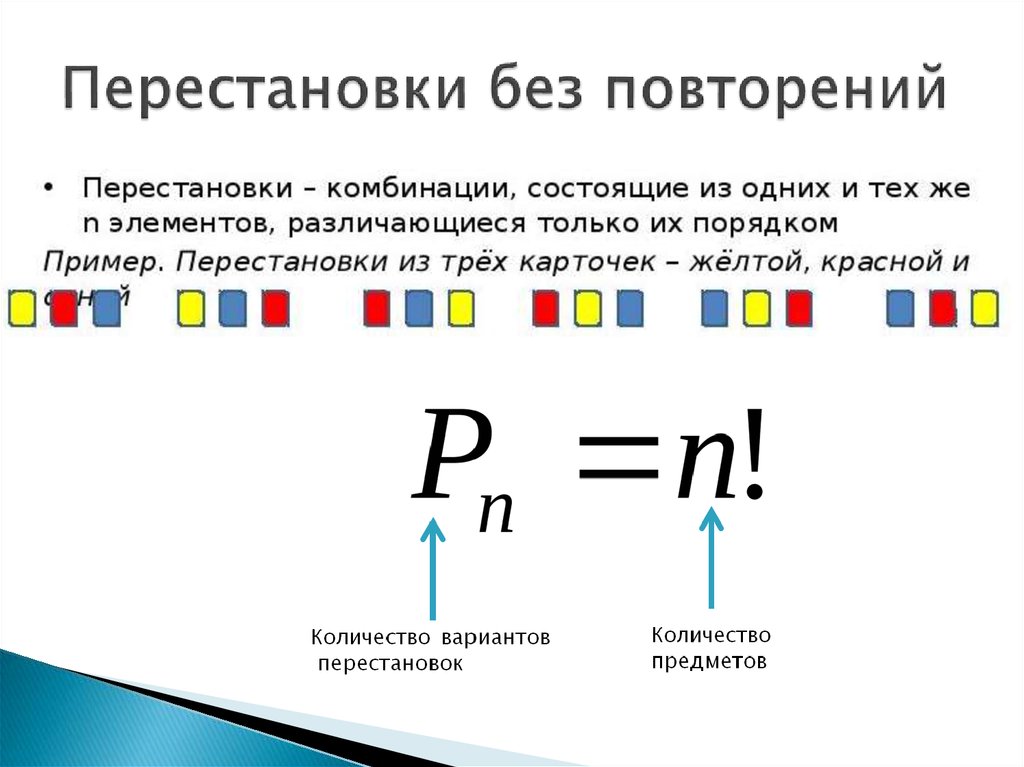

Пример 6. Сколько различных «слов» (т.е. последовательностей букв), состоящих не менее чем из пяти различных букв, можно образовать из букв слова «рисунок»?

Решение: Слово «рисунок» состоит из семи различных букв. Применяя правило произведения соответствующее число раз, можно подсчитать, что существует:

N1 = 7 × 6× 5× 4 × 3 = 2520 «слов» из пяти букв (выбираемых из букв слова «рисунок»), N2 = 7 × 6× 5× 4× 3× 2 = 5040 «слов» из шести букв, N3 = 7× 6 × 5× 4 × 3× 2× 1 = 5040 «слов» из семи букв. Тогда по правилу суммы, существует N = N1 + N2 + N3 = 2520 + 5040 + 5040 = 12 600 «слов», состоящих не менее чем из пяти букв слова «рисунок».

Существуют следующие комбинации: перестановки, размещения, сочетания.

Перестановки

А. Перестановки без повторений (n различных объектов).

Упорядоченные множества из n элементов называются

перестановками из n элементов. Таким образом, перестановки из n элементов отличаются только порядком следования элементов.

Перестановками из n элементов называют различные упорядочения данного конечного множества, состоящего из n элементов.

Перестановками называют комбинации, состоящие из одних и тех же n-различных элементов и отличающиеся только порядком расположения.

P_n = n! = 1 × 2× 3 ×…× n

Факториал – произведение всех натуральных чисел от 1 до n включительно называют «n-факториал».

Факториал нуля равен единице: 0!=1.

Пример 7. Сколькими способами можно расставить 6 различных книг на одной полке?

Решение: Искомое число способов равно P₆ = 6! = 1 × 2× 3 ×4× 5 × 6 = 720. Действительно, первую книгу можно выбрать шестью способами, вторую — пятью способами и т.д., последнюю — одним способом. По правилу умножения общее число способов равно 6- 5-4• 3• 2-1 = 720.

Пример 8. Сколькими способами можно расположить на полке 10 различных книг? Ответ: 10! .

B. Перестановки c повторениями.

В том случае, если некоторые переставляемые объекты совпадают, то число перестановок будет меньше. Предположим, что имеется k различных типов объектов и известно, что имеется n₁ элементов 1-го типа, n₂ элементов 2-го типа, …, n_kэлементов k-го типа. При этом n₁+ n₂ +… + n_k =n.

Перестановки такого типа будем называть n-перестановками с повторениями и обозначать P(n₁, n₂ ,…, n_k).

P(n₁, n₂ ,…, n_k)= n!/ (n₁! ×n₂! ×…×n_k!)

Перестановка п элементов, среди которых k₁элемент первого типа, k₂элементов второго типа, …, k_m элементов m-го типа (k₁ + k₂ + … + k_m = п), причем элементы разных типов различны, называется перестановкой с повторениями п элементов, среди которых k₁ элементов первого типа, k₂ элементов второго типа, …, k_m элементов m-го типа

Пример 9. Сколько различных последовательностей букв можно составить, переставляя буквы в слове «криминалистика».

Решение: Так как в слове «криминалистика» 14 букв, то п = 14. Элементов первого типа (буквы «к») 2 штуки (k1 = 2). Далее: k2 = 1 (буква «р»), k3 = 4 (буква «и»), k4 = 1 (буква «м»), k5 = 1 (буква «н»), k6 = 2 (буква «а»), k7 = 1 (буква «л»), k8 = 1 (буква «с»), k9 = 1 (буква «т»). Следовательно, количество всех слов: Р(2, 1, 4, 1, 1, 2, 1, 1, 1) = 14! /(2!4!2!)=

Размещения

А. Размещения без повторений

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком следования.

Упорядоченные подмножества из n элементов по k элементов каждое, называются размещениями из n элементов по k элементов (или кратко: размещениями из n по k). Таким образом, размещения отличаются либо составом элементов, либо их порядком.

Пусть дано множество, состоящее из п элементов. Размещением из п элементов по к (к < п) элементов называется упорядоченное подмножество, содержащее к различных элементов данного множества Все эти подмножества отличаются друг от друга или составом элементов, или порядком их распределения. Но число элементов во всех этих подмножествах равно к.

Размещениями из n по m называются всевозможные упорядоченные подмножества, содержащие

m элементов из данных n. Обозначаются и вычисляются по формуле:

Пример 10. Сколько можно составить четырехзначных чисел, содержащих различные цифры из 5 цифр.

Решение: Четырехзначное число – это упорядоченная последовательность цифр, т. е. имеем дело с размещениями без повторений: А₅⁴=5!/(5-4)!=5!/1!=5432=120.

Пример 11. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами может быть составлено расписание на 1 день?

Решение:

Пример 12. Сколькими способами можно выбрать 3 из 10 различных шаров?

Ответ: А₁₀³=720.

B. Размещения с повторениями

Размещением с повторениями из m элементов по k элементов называется такое упорядоченное множество, которое содержит k элементов, причем один и тот же элемент может входить в это множество несколько раз (от нуля до k). Число всех размещений с повторениями из m по k равно m^k , т.е. Ā^k_m = m^k

Размещениями с повторениями из n элементов по k элементов называются упорядоченные множества, каждое из которых содержит k необязательно различных элементов из данного множества n элементов. Число размещений с повторениями вычисляется по формуле:

Пример 13. Сколько различных пятизначных чисел можно составить при помощи цифр 1, 2, 3?

Решение. Согласно предыдущему, искомое число равно Ā⁵₃ =3⁵=243

Пример 14. Кодовый замок имеет на диске 12 букв. Секретное слово состоит из 5 букв. Сколько неудачных попыток можно сделать? Общее число комбинаций Ā⁵₁₂ =12⁵=248832. Число неудачных попыток 248832-1=248831.

Пример 15. В стену здания вмонтированы 8 гнезд для флажков. В каждое гнездо вставляется либо голубой, либо красный флажок. Сколько различных случаев распределения флажков на здание.

Решение: Так как порядок расположения элементов важен и не все элементы используются в данном соединении, то это размещение. А так как всего 8 гнезд, а флажков 2 вида (голубой и красный), то они будут повторяться, т.е. это размещение с повторением.

Сочетания

Определение. Подмножества из n элементов по k элементов каждое, отличающиеся хотя бы одним элементом, называются сочетаниями из n элементов по k элементов (или кратко: сочетания из n по k). Таким образом, сочетания отличаются только составом элементов. Число сочетаний из n по k обозначается: C^k_n.

Пусть дано множество, состоящее из п элементов. Сочетанием из п элементов по к (0 < к < п) элементов называется любое подмножество, которое содержит к различных элементов данного множества. Таким образом, различными подмножествами считаются только те, которые отличаются составом элементов. Подмножества, отличающиеся друг от друга лишь порядком следования элементов, не считаются различными. Число всех возможных сочетаний из п элементов по к обозначается C^k_n. Так как число перестановок из к равно k!, то число размещений из п элементов по к — А^k_n будет в к! раз больше, чем число сочетаний из п

элементов по к — С^k_n , т.е. А^k_n =n! × C^k_n.

Отсюда: C^k_n= А^k_n /k!= n!/(n—k)! ×k!

Пусть имеются n различных элементов. k- сочетаниями без повторений из n элементов называют k-расстановки, составленные из этих элементов, и отличающиеся друг от друга составом, но не порядком элементов. Число k-сочетаний без повторений из n различных элементов обозначается С^k_n.

Сочетаниями из n по m называются всевозможные подмножества данных n элементов, состоящие из m элементов. Для подсчета их числа используются следующие обозначение и формула:

Сочетанием называют комбинации, составленные из n –различных элементов по m элементов, которые отличаются только составом элементов и не зависят от порядка следования.

Пример 16. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Решение: Так как порядок выбранных четырех человек не имеет значения, то это можно сделать C⁴₂₅ способами: C⁴₂₅ = 25!/(25-4)! ×4!=12650

Пример 17. Сколькими способами можно выбрать при игре в спортлото 6 из 49 номеров?

Ответ: C⁶₄₉=69919080

Пример 18. В кондитерской продавалось 4 вида пирожных: наполеоны, эклеры, песочные, слоеные. Сколькими способами можно купить 7 пирожных?

Ответ: C⁴₇=

Сочетанием с повторениями из m элементов по k элементов (или короче: сочетанием с повторениями из m по k) называется множество, содержащее k элементов, причем каждый элемент принадлежит к одному из m типов. Число всех вышеупомянутых сочетаний с повторениями из m по k обозначается Ĉ^k_m (обратите внимание на отличие от обозначения числа сочетаний из n по k – черта сверху).Число сочетаний с повторениями из т по k равно:

Пусть имеется n различных типов предметов. Сколько k-расстановок можно составить, которые отличаются друг от друга составом, но не порядком входящих элементов? Такие k -расстановки называются k-сочетаниями с повторениями из n типов предметов. Число k -сочетаний с повторениями из n типов предметов обозначается Ĉ^k_m.

Сочетания из n элементов, в каждое из которых входит m элементов, причем один и тот же элемент может повторяться в каждом сочетании любое число раз, но не более m, называются сочетаниями с повторениями. Число сочетаний с повторениями вычисляется по формуле:

Пример 19. На почте продаются открытки 10 сортов. Сколько вариантов существует для покупки 12 открыток.

Решение: Порядок расположения элементов не имеет значения, следовательно, это сочетание. А так как открытки в наборе могут повторяться, то это сочетание с повторениями.

.

Таким образом, из 10 открыток можно выбрать набор из12 штук 293930 способами.

Пример 20.Число различных бросаний двух одинаковых кубиков равно

Пример 21. Напишем все сочетания с повторениями из трех элементов А, В, С по 3. Сколько их?

Вот они: ААА ВВВ ССС, АВВ ВСС, АСС ВВС, ААВ, ААС, АСВ. Их 10 штук, т.е.Ĉ³₃.=10.

Свойства сочетаний

1) С^k_n = С^n—k_n

2) С^k_n = С^k-1_n-1+ С^k_n-1

3) С⁰_n + С¹_n + С²_n + …+ Сⁿ_n = 2ⁿ

4) С^k_n * С^m—k_n—k= С^k_m+ С^m_n

Все сочетания легко вычисляются, если записать их в виде треугольной таблицы (треугольника Паскаля ):

1 С_о°

1 1 C₁⁰ С₁¹

1 2 1 С₂⁰ С₂¹ С₂²

1 3 3 1 С₃⁰С₃¹ С₃²С₃³

1 4 6 4 1 С₄⁰ С₄¹С₄²С₄³С₄⁴

1 5 10 10 5 1 С₅⁰С₅¹С₅²С₅³С₅⁴С₅⁵

На основании данной таблицы можно увидеть справедливость указанных выше свойств сочетаний.

При определении вида комбинации удобно пользоваться схемой:

КОМБИНАТОРНЫЕ ЗАДАЧИ

Задача 1. Максимально возможное количество матчей, которое можно организовать в высшей лиге футбольного дивизиона страны не должно превышать 160 в один круг. Сколько (максимально) команд можно включить в состав высшей лиги.

Решение. Обозначим возможное количество команд через n, тогда число сыгранных матчей равно C²_n . По условию C²_n ≤ 160. Пусть C²_n = 160, тогда:

n!/(n-2)!* 2!=160. Тогда n=18,4;-17,4.

Число команд должно быть натуральным числом, поэтому n = 18.

Ответ. 18 команд.

Задача 2. Имеется 4 сорта чая, 5 сортов конфет и 6 сортов печенья. Сколькими способами можно организовать чаепитие-дегустацию на трех человек, если каждый может выпить одну чашку чая определенного сорта с одной конфетой и одним печеньем?

Решение. Используя правило произведения, подсчитаем, что:

1) число способов распределить сорта чая для трех дегустаторов равно 4³;

2) число способов распределить по одной конфете определенного сорта для трех дегустаторов равно 5³;

3) число способов распределить по одному печенью определенного для трех дегустаторов равно 6³.

Применяя еще раз правило произведения, мы получим, что число способов организовать данное чаепитие-дегустацию равно 4³* 5³* 6³= 1 728 000.

Задача 3. В соревнованиях принимают участие 16 команд Сколькими способами могут распределиться три первых места, т е необходимо найти число всех подмножеств, состоящих из трех элементов, отличающихся составом (номерами команд) или порядком их размещения (подмножества № 1, № 2, № 3 и № 2, № 1, № 3 являются разными). Таким образом, имеем дело с размещением. Тогда искомое число равно A³₁₆=3360

Задача 4. В отделении 10 солдат. Необходимо составить наряд из 4-х человек. Сколько существует способов составления такого наряда?

Решение. Поскольку порядок, в котором мы выбираем участников наряда, не важен, то мы имеем дело с сочетаниями их 10 по 4. Итак, C⁴₁₀=210

Задача 5. Сколько существует четырехзначных чисел, состоящих из различных цифр?

Решение. Ноль не может быть первой цифрой, следовательно, есть 9 возможностей выбрать первую цифру. Далее может следовать любая упорядоченная тройка оставшихся цифр, а для этого есть A³₉ способов. Итого, получаем 9* A³₉=4536

Задача 6. Сколькими способами можно раскрасить диаграмму из 4 столбцов четырехцветной ручкой так, чтобы каждый столбец был окрашен в определенный цвет.

Решение: Порядок расположения элементов имеет значение и в диаграмме 4 столбца, а ручка тоже четырехцветная, т. е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска столбцов не повторяется (в условии сказано, что столбцы имеют разные цвета), то это перестановка без повторения. Итак, P_n= n! = 4! = 1234 = 24 Ответ: столбцы можно закрасить 24 способами.

Задача 7. Имеется 5 кружков: 3 белых и 2 черных. Сколько различных узоров можно получить, располагая кружки в ряд.

Решение: Порядок расположения элементов имеет значение и в узоре 5 кружков, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска кружков повторяется (в условии сказано, что 3 белых и 2 черных), то это перестановка с повторением. Итак,

Ответ: узор можно составить 10 способами.

Задача 8. Сколько словарей надо издать, чтобы можно было непосредственно выполнить перевод с любого из 5 языков на любой из 5 языков.

Решение: Порядок имеет значение (так как русско-английский и англо-русский словари различны) и не все элементы присутствуют в соединении (а только 2 из 5), значит, это размещение. Так как языки различны, то это размещение без повторения. Итак, . Ответ: надо составить 20 словарей.

Задача 9. На железнодорожной станции имеется 5 светофоров. Сколько может быть дано различных комбинаций их сигналов, если каждый светофор имеет 3 состояния.

Решение: Порядок имеет значение и не все элементы присутствуют в соединении, значит, это размещение. Так как цвета повторяются, то это размещение с повторением. Итак, . Ответ: может быть дано 243 различных комбинаций цветов.

Задача 10. 12 человек играли в городки. Сколькими способами они могут разбиться на команды по 4 человека в каждой.

Решение: Порядок расположения игроков в команде не имеет значения, следовательно, это сочетание. А так как игроки не повторяются (все члены команды различные люди), то это сочетание без повторения. Итак, .

Ответ: игроки могут разбиться на команды по 4 человека в каждой 495 способами.

Задача 11. В цветочном магазине продаются цветы 6 видов. Сколько можно составить букетов из 10 цветов в каждом (букеты отличающиеся лишь расположением цветов считать одинаковыми).

Решение: Порядок расположения цветов в букете не имеет значения, следовательно, это сочетание. А так как цветы повторяются, то это сочетание с повторением. Итак, . Ответ: букеты можно составить 3003 способами.

Задача 12. В группе 25 студентов, из которых 5 отличников, 11 хорошистов и остальные троечники. Сколькими способами можно выбрать группу для выполнения лабораторной работы, состоящей из 3 хорошистов, 1 отличника и 1 троечника.

Решение: Сначала узнаем сколькими способами можно выбрать 3 хорошистов из 11 человек. Порядок расположения студентов не важен, значит, это сочетание. А так как люди в группе не повторяются, то это соединение – сочетание без повторения. Итак, одного хорошиста можно выбрать способами. Аналогично рассуждая, приходим к тому, что 1 отличника можно выбрать способами и одного троечника можно выбрать способами. Так как команда для выполнения лабораторной работы выбирается одновременно, т.е. 5 хорошистов, затем 1 отличник, затем 1 троечник, то, применив правило произведения, получим: способами. Ответ: группу для выполнения лабораторной работы можно составить 3300 способами.

Задача 13: Имеется 4 чашки, 5 блюдец, 6 ложек (все чашки, блюдца, ложки различны). Сколькими способами можно накрыть стол к чаю на 3 человека, если каждый получает 1 чашку, 1 блюдце и 1 ложку.

Решение: Выберем для 3 человек чашки из 4 имеющихся. Порядок расположения элементов имеет значение, и не все элементы входят в соединение, значит, это размещение. Но так чашки не повторяются, то это размещение без повторения. Итак, из 4 чашек 3 можно выбрать способами. Аналогично рассуждая, получим, что из 5 блюдец 3 можно выбрать способами, а из 6 ложек 3 можно выбрать способами. Так блюдце, чашка и ложка входят в набор одновременно, то стол можно накрыть способами. Ответ: стол можно накрыть 172800 способами.

Задача 14. Группу из 20 студентов можно разместить в аудитории по 2 человека за каждой партой. Порядок их размещения имеет значения.

Решение. Количество возможных вариантов размещений вычисляется по формуле:

Задача 15. Найти количество трехзначных чисел с неповторяющимися цифрами, которые можно составить из цифр: 1, 2, 3, 4, 5.

Решение. Количество трехзначных чисел в данном примере определяется по формуле размещений (3) и равно:

Задача 16. Группу из 20 студентов следует рассадить в аудитории по 2 человека за каждой партой. Порядок их размещения не имеет значения. Определить количество возможных вариантов сочетаний.

Решение. Количество возможных вариантов сочетаний вычисляется по формуле 4):

Задача 17. Флаг государства может комбинироваться из трёх полос разного цвета. Определить число комбинаций из пяти разных цветов, которые можно получить, выбирая из них три полосы разного цвета.

Решение. Если учитывать порядок в комбинации, то число вариантов равно:

Если же порядок в комбинации не имеет значения, то количество разных вариантов равно:

Комбинаторика в Excel

Комбинаторика в Excel

Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».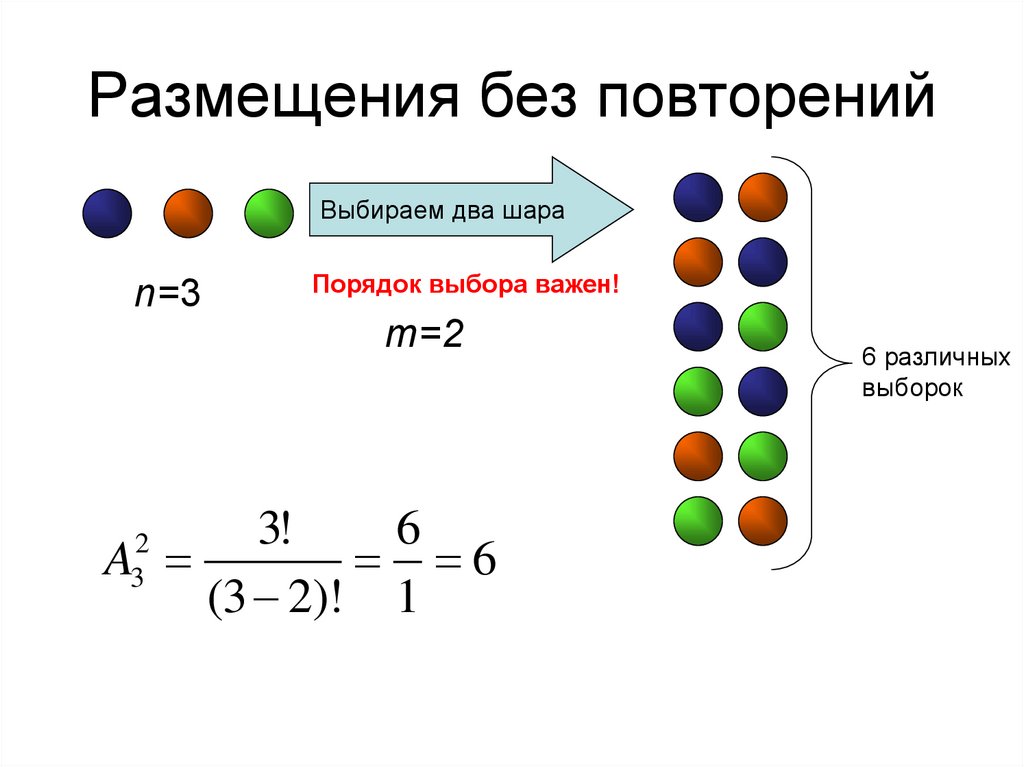 Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:

1. Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
2. Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
3. Важен ли порядок элементов в выборке?
4. После выбора элемента мы его возвращаем назад?

Рис. 1. Дерево решений, какую формулу комбинаторики использовать

Скачать заметку в формате Word или pdf, примеры в формате Excel

Перестановки без повторений

Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.

Рис. 2. Перестановки (картинка взята здесь)

Если все n элементы разные, то число перестановок обозначается P_n от perturbation.

С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!

Например

По определению: 1! = 1; 0! = 1.

Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).

Рис. 3. Расчет числа перестановок без повторений с помощью факториала

Перестановки с повторениями

Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).

Рис. 4. Перестановки с повторениями (картинка найдена здесь)

В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n₁ раз, второй – n₂ раз, третий – n₃ раз, …, k-й – n_k раз (где n₁ + n₂ + … + n_k = n) называется перестановкой с повторениями из n элементов.

Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?

Решение. Буквы а и н повторяются 2 раза, а буква м один раз.

Размещение без повторений

Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается  от arrangement.

Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):

Рис. 5. Размещение без повторений (картинка из презентации)

Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).

Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)

Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу

Размещение с повторениями

Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.

Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).

Рис. 7. Размещение с повторениями

В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:

В Excel используется функция ПЕРЕСТА(n;k).

Задача. Сколько различных номеров можно составить в одном коде региона?

Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).

Рис. 8. Номер автомобиля

Решение. Можно воспользоваться формулой для размещения с повторениями:

Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.

Сочетания без повторений

Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).

Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):

Рис. 9. Сочетания без повторений из 4 по 2

Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями

где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:

Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

В Excel используется функция =ЧИСЛКОМБ(n;m).

Сочетания с повторениями

Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.

Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).

Рис. 11. Сочетания с повторениями

В общем случае, число сочетаний с повторениями:

Для нашего примера с фруктами

В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.

Комбинация без повторения Python с примерами кода

Комбинация без повторения Python с примерами кода

В этой статье мы рассмотрим несколько примеров того, как решить проблему Python «Комбинация без повторения».

 импортировать itertools как есть
список (it.combinations ([1,2,3,4,5], 4))
#[(1, 2, 3, 4), (1, 2, 3, 5), (1, 2, 4, 5), (1, 3, 4, 5), (2, 3, 4, 5) )]
 

Решение ранее упомянутой проблемы Комбинация без повторения Python также может быть найдено в другом методе, который будет обсуждаться ниже с некоторыми примерами кода.

 >>> импортировать itertools как есть
>>> список(it.combinations([1,2,3,4,5], 4))
[(1, 2, 3, 4), (1, 2, 3, 5), (1, 2, 4, 5), (1, 3, 4, 5), (2, 3, 4, 5) ]
 

Мы представили множество наглядных примеров, чтобы показать, как можно решить проблему Python «Комбинация без повторения», а также объяснили, как это сделать.

Как составить комбинацию без повторений?

Выполните следующие действия:

• Определите соответствующие значения. Нам нужны комбинации из 4 чисел; следовательно, наши выборки имеют размер r = 4,
• В формулу сочетаний без повторений введите значения: C ( n , r ) = n !
• Вот оно! Так вы подсчитываете количество комбинаций без повторений.

Как получить уникальные комбинации в Python?

Как получить все уникальные комбинации двух списков в Python

• список1 = [«а», «б», «в»]
• список2 = [1, 2]
• все_комбинации = []
• list1_permutations = itertools. перестановки (список1, длина (список2))
• для each_permutation в list1_permutations:
• заархивировано = заархивировано (каждая_перестановка, список2)
• все_комбинации.
• печать (все_комбинации)

Как получить все возможные комбинации списка в Python без Itertools?

Чтобы создать комбинации без использования itertools, переберите список один за другим, зафиксируйте первый элемент списка и создайте комбинации с оставшимся списком. Точно так же выполните итерацию со всеми элементами списка один за другим путем рекурсии оставшегося списка. 21 июня 2022 г.

Что такое Permute в Python?

Перестановка, также называемая «порядковым номером» или «порядком», представляет собой перестановку элементов упорядоченного списка S во взаимно-однозначное соответствие с самим S. Строка длины n содержит n! перестановка. Примеры: Ввод: str = ‘ABC’ Вывод: ABC ACB BAC BCA CAB CBA.11-Jul-2022

Сколько комбинаций из 4 предметов не имеют повторов?

Количество возможных комбинаций из 4 чисел без повторения равно 15. Формула, которую мы используем для расчета количества комбинаций из n элементов, когда повторение не разрешено, равна 2n — 1.

Как рассчитать уникальные комбинации?

Формула для комбинаций обычно n! / (r! (n — r)!), где n — общее количество возможностей начать, а r — количество сделанных выборов. В нашем примере у нас есть 52 карты; следовательно, n = 52,24 апреля 2017 г.

Как сгенерировать все возможные комбинации одного списка?

Чтобы перечислить все возможные комбинации на листе Excel, выполните следующую процедуру;

• Шаг 1: Откройте лист. Сначала вам нужно открыть лист с данными, из которых вы хотите составить все возможные комбинации.
• Шаг 2: Выберите ячейку для результата.
• Шаг 3: Перетащите формулу в другие ячейки.

Как объединить все комбинации в Python?

product() вызывается для поиска всех возможных комбинаций элементов. И zip() используется для объединения всех этих комбинаций, преобразования каждого элемента в список и добавления их в нужный список комбинаций. 16 июня 2021 г.

Как вывести все возможные комбинации строки в Python?

Чтобы найти все возможные перестановки заданной строки, вы можете использовать модуль itertools, который имеет полезный метод под названием permutations(iterable[ r]). Этот метод возвращает последовательные перестановки элементов в итерируемом объекте в виде кортежей. 30 сентября 2019 г.

Как вывести все комбинации строки?

Используя метод поиска с возвратом, можно вывести все перестановки заданной строки. Поиск с возвратом — это алгоритм поиска всех возможных решений путем изучения всех возможных путей. 11 января 2022 г.

python — Функция для поиска всех комбинаций без повторения, которые в сумме составляют число

спросил 1 год, 2 месяца назад

Изменено 1 год, 2 месяца назад

Просмотрено 399 раз

Я ищу функцию, которая найдет все уникальные комбинации из списка, который в сумме дает число. Я не могу позволить себе бросить все перестановки списка, так как списки будут очень длинными, а время имеет существенное значение.

the_list = [7,6,5,5,4,3,2,1] stop_sum = 11

Итак, если найдена комбинация (7, 3, 1), я не хочу, чтобы (1, 3, 7) была найдена.

В настоящее время я делаю это с помощью рекурсивной функции, такой как внизу, но этого недостаточно, когда списки содержат более 300 номеров. (все целые числа).

 the_list = [7,6,5,5,4,3,2,1]
стоп_сумма = 11
уникальные_комбо = []
def combo_find(C, S, B=[]):
    для i, a в перечислении (C):
        если а > S:
            Продолжать
        B.append(a) # B+[a] все еще может быть возможным списком
        if a == S: # Найдена работающая последовательность
            последовательность = отсортировано (кортеж (B))
            если последовательность не в unique_combos:
                unique_combos.append (последовательность)
        combo_find(C[i + 1:], S - a, B)
        B.pop() # удалить [a] из списка возможных
the_list.sort()
combo_find(the_list, stop_sum)
печать (уникальные_комбо)
 

У кого-нибудь есть идеи, как сделать это умнее/быстрее?

• python
• функция
• рекурсия
• комбинации
• перестановка

3

Следующее должно быть достаточно производительным при использовании некоторого кэширования:

 from functools import lru_cache
определение combo_find (C, S):
    С. сортировать()
    @lru_cache(Нет)
    запись защиты (пул, с):
        если не с:
            возвращаться [[]]
        если с < 0:
            возвращаться []
        я, результат = 0, []
        в то время как я < len (бассейн):
            crnt = пул[i]
            для комбо в rec(pool[i+1:], s-crnt):
                результат.append([crnt] + комбо)
            # использовать первое из последовательных равенств или ни одно из них!
            # это позволяет избежать дубликатов, но позволяет использовать все вхождения без проверки принадлежности
            в то время как я < len(pool) и pool[i] == crnt:
                я += 1
        вернуть результат
    return rec(tuple(C), S) # tuplify, чтобы аргументы можно было хэшировать
>>> combo_find([7,6,5,5,4,3,2,1], 11)
[[1, 2, 3, 5], [1, 3, 7], [1, 4, 6], [1, 5, 5], [2, 3, 6], [2, 4, 5] , [4, 7], [5, 6]]
 

2

Вы можете написать решить как функцию над вашими числами, n и суммой запроса, q . Этот алгоритм не требует сортировки n и может быть оптимизирован, если вы сделаете сортировку обязательной. Алгоритм написан с использованием индуктивных рассуждений —

1. Если сумма запроса q равна нулю, мы уже знаем ответ. Выдайте пустое решение {} и вернитесь.
2. (индуктивная) q не равно нулю. Если q отрицательное или n не имеет оставшихся чисел для проверки, то решение выходит за пределы или не может быть достигнуто. Возвращаться.
3. (индуктивный) q положительный, а n имеет по крайней мере один номер для проверки. Для каждого решения подзадачи добавьте первые n , если они еще не существуют в решении, затем уступите. Дополнительно попытайтесь решить тот же запрос q , пропустив первые n .

 определение решения (n, q):
 # 1. решение найдено, вернуть пустой набор
 если q == 0: возврат (набор доходности())
 # 2.
No related posts.