Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
04.15
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Вычисление объемов тел вращения.
Применение интегралаПохожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Вычисление объемов тел вращения
Применение интегралаУ
O
Постановка
задачи
y=f(x)
a
b
х
Пусть функция y = f(x) определена, неотрицательна и
непрерывна на отрезке [a; b],
тогда график кривой у=f(x) на [a; b], ось OX,
прямые x = a, x = b образуют криволинейную трапецию.
Рассмотрим тело, образованное вращением этой
криволинейной трапеции вокруг оси OX и найдем его
объем.
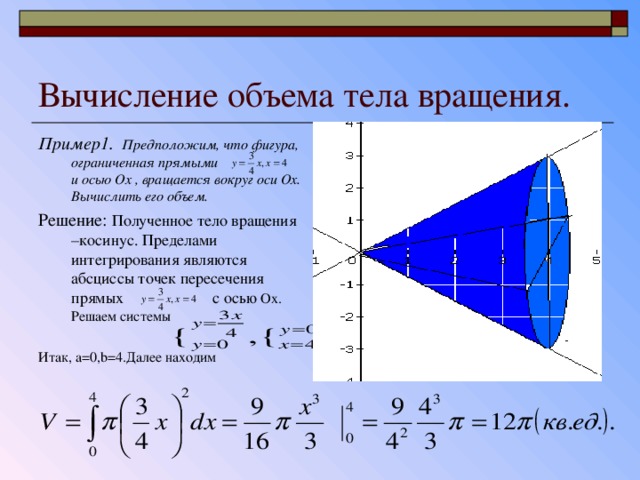
Разобьем отрезок [a;b] на n частей произвольным
образом, через каждую точку деления проведем
плоскость, перпендикулярную к оси ОХ и найдём
площади полученных поперечных сечений.
У
O
y=f(x)
х
Очевидно, что любое поперечное
сечение тела вращения – круг. Радиус
круга равен значению функции в хс
Площадь этого круга – S(x) = π· f 2 (xс)
Построим на каждом промежутке
цилиндрическое тело, образующая которого
параллельна оси ОХ,
а основанием является сечение — круг.
y
y=f(x)
f(xс)
Радиус круга равен
значению функции в хс
Площадь этого круга –
S(x) = π f 2 (xс)
r
xс
Объём цилиндра –
V=S(x)∙ Δx
Объем каждого цилиндра с основанием
S(x) и высотой Δx равен S(x)∙ Δx , а объем
всего ступенчатого тела равен сумме
объёмов всех цилиндров.
n
VCT S ( xk ) xk
k 1
Предел полученной интегральной суммы,
который существует в силу непрерывности
функции S(x), при n → ∞ называется объемом
заданного тела и равен определенному
интегралу:
b
V lim VCT S ( x) x
n
a
Предел полученной интегральной суммы, при n → ∞
равен определенному интегралу:
n
b
k 1
a
V lim S ( x) x S ( x) x
n
Тогда объем тела вращения вокруг оси ОХ:
b
b
b
a
a
a
V S ( x) x f 2 ( x) x f 2 ( x) x
Если тело образовано вращением криволинейной
трапеции, образованной функцией у=f(x) на отрезке
[a;b],вокруг оси ОХ, то его объём можно найти по
формуле:
y=f(x)
b
y
V f ( x) x
2
x
a
b
V f 2 ( x) x
Задача.
a
Пусть тело образовано вращением параболы у=х2
на отрезке [0;2] вокруг оси ОХ.
Найдите объём тела вращения.
у
2
у=х2
2
V S ( x) x ( х ) x
2 2
0
5 2
2
2
О
0
х
х
х x
5
0
4
0
32
(куб .ед.)
5
b
V f 2 ( x) x
Задача.
a
Пусть тело образовано вращением функции у=0,5x
на отрезке [0;4] вокруг оси ОХ.
Найдите объём тела вращения.
y
y 0,5 х
4
V (0,5х) x
2
O
4
x
0
0,25x
3
3
4
0
16
( кв.ед.)
3
9. Рассмотрим конус и найдём его объём
bРассмотрим конус и найдём
его объём
y
y
V f 2 ( x) x
a
r
x
h
r
O
h
2
x
r
V x x
h
0
h
1 2
V r h
3
2
r x
2
h 3
3
h
0
r 2 h
3
10. Рассмотрим усечённый конус и найдём его объём
bV f 2 ( x) x
Рассмотрим усечённый
конус и найдём его объём
y
y
R r
x r
h
R
h
R r
V
x r x
h
0
2
h
r
O
x
R r
x r
h
h
R r
3
h
3( R r )
a
R
3
r
3
3 h
0
1
3
h( R Rr r )
2
2
11.
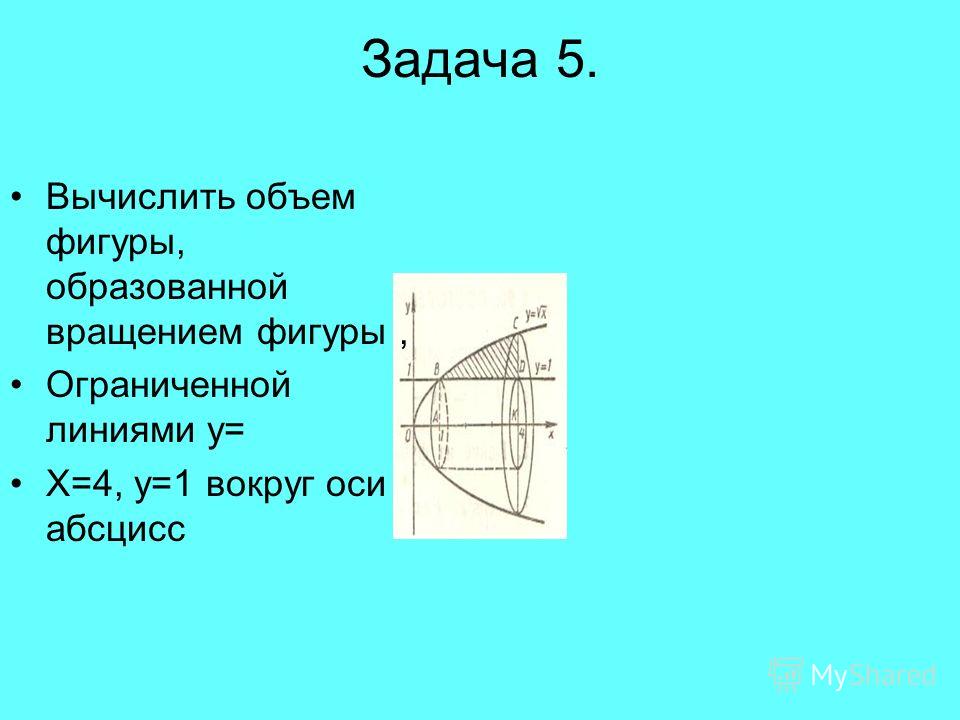*** Найдите объём тела, если его поверхность получена вращением фигуры образованной графиками функций:у 0,5x 2 1, на [ 3; 2]у 6 x 12 3, на [2; 8]
у 4 x 4 , на [4; 8]
12. Вычисление определённых интегралов
bV f 2 ( x) x
a
V Vоснования Vчаши Vвыемки
2
2
Vоснования 0,5 x 2 1 x (0,25x 4 x 2 1) x
30 125 куб .ед.
3
3
8
Vчаши
2
8
2
8
6 x 12 3 x (6 x 12 6 6 x 12 9) x
2
306 куб .ед.
2
8
Vвыем ки 4 4 x 4 x 16(4 x 4) x 128 куб .ед.
2
4
Vкубка 208 125 654.4куб .ед
4
Решите задачу
Вычислить объем тела, образованного вращением вокруг
оси ОХ фигуры, ограниченной линиями
English Русский Правила
исчисление — Нахождение объема вращением треугольника
Задавать вопрос
спросил
Изменено 3 года, 3 месяца назад
Просмотрено 3к раз
$\begingroup$
Следующая задача взята из книги «Исчисление и аналитический геометр» Томаса и Финни.
2 \\
v &= \pi \left( 8 — \frac{8}{3} — \left( 4 — \frac{1}{3} \right) \right)
= \pi \left( 8 — \frac{8}{3} — 4 + \frac{1}{3} \right) \\
v &= \pi ( 4 — \ frac{7}{3 } ) \\
v &= \frac{5\pi}{3} \\
\конец{выравнивание*}
Ответ книги: $\frac{4\pi}{3}$. Что я сделал не так? 92=\pi\left(\frac{8}{3}-2-\left(\frac{1}{3}-1\right)\right)=\pi\left(\frac{2}{3) }+\frac{2}{3}\right)=\frac{4\pi}{3}.$$
Думаю, ошибка в том, что вы вращались вокруг оси $x$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
интегрирование — Нахождение объема тела путем вращения двух отрезков вокруг оси x
спросил
Изменено 7 лет, 10 месяцев назад
Просмотрено 113 раз
9t\times sin(t))$$ Я понятия не имею, с чего начать, и даже не знаю, как это сделать, мне не нужен прямой ответ, но, пожалуйста, дайте мне направление, что делать, чтобы решить эту проблему , я не очень понимаю вопрос.