Сокращение квадратных уравнений: Сокращение квадратных уравнений. Квадратные уравнения

Квадратные уравнения и неравенства. Алгоритмы решения квадратного уравнения и неравенства. Формулы дискриминанта и корней квадратного уравнения. Теорема Виета. Примерно 7 класс (13 лет)

		Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Квадратные уравнения и неравенства. Алгоритмы решения квадратного уравнения и неравенства. Формулы дискриминанта и корней квадратного уравнения. Теорема Виета. Примерно 7 класс (13 лет) Поделиться:    Квадратные уравнения и неравенства. Алгоритм решения квадратного уравнения. Формулы дискриминанта и корней квадратного уравнения. Решение неполных квадратных уравнений. Теорема Виета. Алгоритм решения квадратного неравенства. Примерно 7 класс (13 лет) Алгоритм решения квадратного уравнения Перевести все слагаемые в левую часть уравнения, упростить ее, получив уравнение вида: Вычислить дискриминант D. Если D≥0, вычислить корни уравнения. Если D<0, записать ответ:»корней нет» Формулы дискриминанта и корней квадратного уравнения В общем случае: Если b-четное, удобнее считать: Решение неполных квадратных уравнений Теорема Виета Алгоритм решения квадратного неравенства Привести неравенство к виду: ax2+bx+c>0 или ax2+bx+c<0; Найти нули функции y=ax2+bx+c; На оси Ox найти промежутки, где y>0 и где y<0; Выбрать нужные промежутки. Таблица квадратов, пригодится: Справочно: Таблицы квадратов чисел от 1. Таблица квадратных корней. Натуральных чисел от 1 до 30 и от 1 до 100. Таблица квадратов больших чисел. Удобная расчетная таблица 1,00 — 9,99. Таблица квадратов — таблица квадратных корней натуральных чисел от 1 до 99 (от 1 до 9, от 10 до 99 ). Таблица квадратных корней. Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

10 квадратных уравнений

10 квадратных уравнений

Вы искали 10 квадратных уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 ac, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз.

И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «10 квадратных уравнений».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 10 квадратных уравнений,4 ac,a c b квадратное уравнение,b a c квадратное уравнение,алгебра квадратные уравнения,если d 0,если d 0 то уравнение имеет один корень,как в алгебре решать квадратные уравнения,как найти х в уравнении квадратном,как решается квадратное уравнение,как решать квадратное уравнение,как решать квадратные,как решать квадратные приведенные уравнения,как решать квадратные уравнения,как решать уравнения квадратные 9 класс,как решать уравнения с квадратом,как решаются квадратные уравнения,как решить квадратное уравнение,как решить квадратное уравнение без дискриминанта,как решить квадратное уравнение без с,как решить квадратное уравнение через дискриминант,как упростить квадратное уравнение,кв уравнение,квадрат уравнения,квадратичное уравнение,квадратичные уравнения,квадратне рівняння приклади,квадратні рівняння приклади,квадратного уравнения решения,квадратное,квадратное решить,квадратное уравнение,квадратное уравнение в квадрате,квадратное уравнение как решать,квадратное уравнение примеры с решением,квадратное уравнение решение,квадратное уравнение с,квадратные,квадратные уравнение,квадратные уравнения,квадратные уравнения 10 класс,квадратные уравнения 8 класс примеры с решением,квадратные уравнения 9 класс примеры с решением,квадратные уравнения алгебра,квадратные уравнения как решать,квадратные уравнения математика,квадратные уравнения примеры для решения,квадратные уравнения примеры с решением,квадратные уравнения простые,квадратные уравнения решать,квадратные уравнения решение,квадратные уравнения решения,квадратные уравнения решенные,квадратные уравнения решить,квадратные уравнения с ответами,квадратные уравнения с решением,квадратные уравнения с решениями,квадратный уравнения,квадратных,квадратных уравнений,квадратных уравнений формула решения,когда квадратное уравнение имеет один корень,линейные и квадратные уравнения как решать,математика квадратные уравнения,математика решение квадратных уравнений,математика уравнения квадратные,правила квадратных решения уравнений,пример квадратного уравнения с решением,примеры для решения квадратные уравнения,примеры квадратных уравнений с решением,примеры с ответами квадратных уравнений,примеры с решением квадратных уравнений,простые квадратные уравнения,решаем квадратное уравнение,решаем уравнение квадратное,решать квадратные уравнения,решение квадратного уравнения,решение квадратного уравнения с,решение квадратного уравнения формулы,решение квадратные уравнения,решение квадратных,решение квадратных уравнение,решение квадратных уравнений,решение квадратных уравнений без дискриминанта,решение квадратных уравнений примеры,решение квадратных уравнений примеры и подробное решение,решение квадратных уравнений примеры решение,решение квадратных уравнений формула,решение квадратных уравнений формулы,решение уравнений 8 класс примеры и их решение,решение формулы квадратного уравнения,решения квадратного уравнения,решения квадратные уравнения,решения квадратных уравнений,решения квадратных уравнений формулы,решения уравнения квадратного,решите квадратное уравнение,решите уравнение квадратное уравнение,решить квадратное уравнение,решить квадратные уравнения,решить уравнения квадратные,с квадратное уравнение,с решение квадратного уравнения,сокращение квадратного уравнения,составить квадратное уравнение,таблица квадратных уравнений,упрощение квадратных уравнений,уравнения алгебра квадратные,уравнения квадратные решения,уравнения математика квадратные,уравнения по математике квадратные уравнения,уравнения с квадратом как решать,формула для решения квадратного уравнения,формула решение квадратных уравнений,формула решения квадратного уравнения,формула решения квадратных уравнений,формула решения уравнения,формулы решение квадратного уравнения,формулы решения квадратного уравнения,формулы решения квадратных уравнений.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 10 квадратных уравнений. Просто введите задачу в окошко и нажмите «решить» здесь (например, a c b квадратное уравнение).

Решить задачу 10 квадратных уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

10 СПОСОБОВ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

• Главная
• Список секций
• Математика
• 10 СПОСОБОВ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

• Авторы
• Файлы работы
• Наградные документы

Улевский С. А. 1

---

1МБОУ ЕСОШ №11

Автор работы награжден дипломом победителя II степени

Диплом школьника

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Оглавление

Введение 3

1. Методы и способы решения квадратных уравнений 4

1.1. Решение квадратных уравнений по общей формуле. 5

1.2.Разложение левой части на множители. 5

1.3.Метод выделения полного квадрата 5

1.4.Решение уравнений с помощью теоремы Виета 6

1.5.Решение уравнений с использованием свойств коэффициентов. 6

1.6. Решение уравнений способом «переброски». 7

1.7. Геометрический способ решения квадратных уравнений 7

1. 8. Графическое решение квадратного уравнения. 7

1.9. Решение уравнения при помощи циркуля и линейки.. 8

1.10.Решение квадратных уравнений с помощью номограммы. 8

Заключение . 8

Приложение 1 9

Приложение 2 9

Литература 10

Введение

Теория уравнений занимает ведущее место в алгебре и математике в целом. Значимость ее заключается не только в теоретическом значении для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.

В школьной программе рассматривается только 3 способа их решения. Готовясь к предстоящим экзаменам, я заинтересовался другими способами их этих уравнений. Поэтому я выбрал тему «10 способов решения квадратных уравнений».

Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, что также пригодится и при решении более сложных задач, в том числе и при сдаче экзаменов.

Цель работы: изучить различные способы решения квадратных уравнений, научиться решать квадратные уравнения.

Задачи:

— рассмотреть стандартные и нестандартные методы решения квадратных уравнений;

— выявить наиболее удобные способы решения квадратных уравнений;

— научиться решать квадратные уравнения различными способами.

Объект исследования: квадратные уравнения.

Предмет исследования: способы решения квадратных уравнений.

Методы исследования:

1. Методы решения квадратных уравнений

Квадратным уравнением называется уравнение вида ,где х-переменная, a, b и с-некоторые числа, при этом а≠0. Корень такого уравнения – это значение переменной, обращающее квадратный трёхчлен в ноль, то есть значение, обращающее квадратное уравнение в тождество. Коэффициенты квадратного уравнения имеют собственные названия: коэффициент а называют первым или старшим, коэффициент b называют вторым или коэффициентом при х, с называется свободным членом этого уравнения.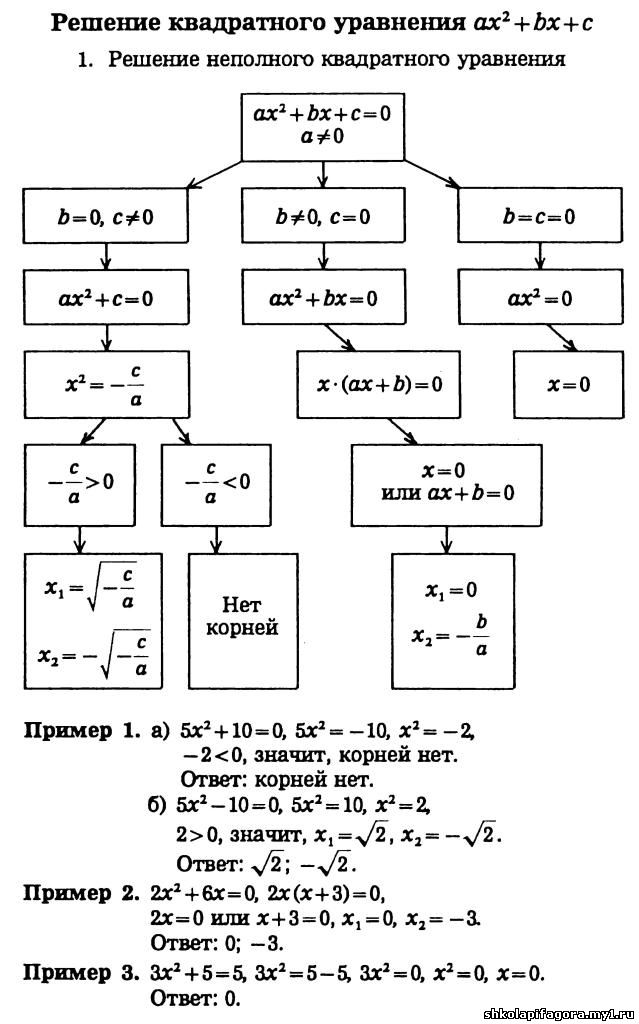

Полным квадратным уравнением называют такое, все коэффициенты которого отличны от нуля (a, b, c≠0).

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент а: , р=b/a, q=c/a.

Неполные квадратные уравнения бывают трёх видов:

1) , где с ≠ 0;

2) , где b ≠ 0;

3) .

В рамках данной работы мы будем рассматривать способы решения только полных квадратных уравнений.

1.1. Решение квадратных уравнений по общей формуле

Для решения квадратных уравнений применяется способ нахождения корней через дискриминант. Для нахождения дискриминанта используется следующая формула . После нахождения D мы используем формулу для нахождения корней уравнения .

Стоит заметить, что если:

D>0 – уравнение имеет два корня;

D=0– уравнение имеет один корень;

DАС, или

), окружность Рис. 4

Пересекает ось абсцисс в двух точках .К (х₁ ; 0) и N (х₂ ;0), где х₁ и х₂ – корни квадратного уравнения .

— если радиус окружности равен ординате центра (AB = AС, или

, окружность касается оси абсцисс в точке С(х₁ ; 0), где х₁ – корень квадратного уравнения.

— если радиус окружности меньше ординаты центра (AB

Просмотров работы: 2976

Изучение уравнений, сводящихся к квадратным уравнениям, с примерами

• Автор Sushma_P
• Последнее изменение 20-07-2022

• Автор Сушма_П
• Последнее изменение 20-07-2022

Уравнения, сводимые к квадратным уравнениям : В этой статье мы обсудим уравнения, которые не являются квадратными, но сводятся к квадратным уравнениям. Эти уравнения могут быть легко решены, если мы преобразуем их в квадратную форму, которую в противном случае трудно решить. Кроме того, мы обсудим, как кубическое уравнение сводится к квадратному уравнению для их решения. 92\), переменную подстановки, а затем использовать эти решения и определение подстановки, чтобы найти реальные решения уравнения. В большинстве случаев все, что требуется, чтобы определить, можно ли привести его к квадратичной форме, — это проверить, что один из показателей в два раза больше другого. {2}+b x+c=0\) называется квадратным уравнением, где \(a, b, c\) — действительные числа, а \(a \neq 0\). 9{2}+b x+c=0 \), где \(a, b, c, \in R\) и \(a \neq 0\).

Коэффициент \(a\) называется старшим коэффициентом, поскольку он является коэффициентом высшей степени, а \(c\) является абсолютным или постоянным членом \(f(x)\). Квадратный полином, приравненный к нулю, становится квадратным уравнением. Квадратное уравнение будет иметь два корня. Значения \(х\), которые удовлетворяют уравнению, называются корнями уравнения, а именно \((\альфа, \бета)\). Корни квадратного уравнения могут быть как действительными, так и мнимыми. 92) +к

Уравнения, приводимые к квадратному уравнению

Основной метод состоит в том, чтобы проверить, приводятся ли уравнения к квадратной форме, а затем использовать метод подстановки, чтобы преобразовать их в квадратные уравнения. Мы решаем новое уравнение, чтобы найти значение переменной, а затем подставляем его обратно в исходное уравнение, чтобы получить нужное решение. {2}+4x+3x+12\вправо]+1=0\) 9{2}+10 г+25=0\)

Тип VI: Иррациональные уравнения, сводимые к квадратным уравнениям:

\(\sqrt{a x+b}=x+k\) или \(\sqrt{a x+b}+\sqrt{c x+d}=k\) или \(\sqrt{a x+ b}+\sqrt{c x+d}=\sqrt{e x+f}\).

Метод: В этом типе уравнения мы возводим данное уравнение в квадрат с обеих сторон, чтобы получить уравнение в квадратичной форме. В приведенном ниже примере объясняется метод.

Пример: \(\sqrt{4-x}+\sqrt{9+x}=5\)

Данное уравнение можно записать в виде: 9{2}+6 x+x+3\вправо)\)
\( \стрелка вправо \влево( {x – 2} \вправо)\влево\{ {2x\влево( {x + 3} \вправо) + 1 \left( {x + 3} \right)} \right\}\)
\(\Rightarrow(x-2)(2 x+1)(x+3)\)
Следовательно, решения равны \(x =2, x=-\frac{1}{2}\) и \(x=-3\).

Резюме

В этой статье изучалось определение и стандартная форма квадратного уравнения. Эта статья написана исключительно для уравнений, которые не имеют квадратной формы, но могут быть сведены к квадратным уравнениям. Мы выучили шесть типов уравнений.

Некоторые формы представляют собой биквадратные уравнения, уравнения взаимности и иррациональные уравнения, сводимые к квадратным уравнениям. Кроме того, мы узнали определение кубического уравнения и решили кубические уравнения, сводя их к квадратным уравнениям.

Часто задаваемые вопросы по уравнениям, сводимым к квадратным уравнениям

Ответы на наиболее часто задаваемые вопросы по уравнениям и квадратным уравнениям здесь:

Q.1: Как факторизовать квадратное уравнение?
А: Чтобы разложить квадратное уравнение на множители, сначала запишите данное уравнение в стандартной форме квадратного уравнения. Затем используйте квадратичную формулу, чтобы найти факторы данного уравнения. Также уравнение можно решить методом расщепления среднего члена. Чтобы найти множители, приравняйте множители нулю и решите линейное уравнение.

Q.2: Какова стандартная форма квадратного уравнения?
A: Квадратные уравнения — это уравнения хотя бы с одной переменной в квадрате. {2}+bx+c=0\), где \(a, b\) — коэффициенты, а \(c\) — константа.

Q.3: Каково использование квадратного уравнения?
A: На самом деле квадратные уравнения используются в нашей повседневной жизни. Некоторые реальные приложения вычисляют площадь для определения продуктов, прибыли или определения скорости транспортного средства. Мы можем сформулировать квадратное уравнение для заданных данных в реальных примерах и решить их, чтобы найти неизвестное значение.

Q.4: Почему мы изучаем квадратные уравнения?
A: Квадратичные функции являются важной и уникальной частью школьной программы. Значения этих уравнений легко вычисляются. Они продвинуты к линейным функциям и дают значительный отход от привязанности к прямым линиям. 9{2}+10 х+9=0\). Квадратное уравнение, которое можно решить любым методом и подставить обратно значение, чтобы найти фактические корни уравнения.

Пройдите бесплатные пробные тесты, относящиеся к квадратным уравнениям

Уравнения, приводимые к квадратным в форме

Онлайн-заметки Пола
Дом / Алгебра / Решение уравнений и неравенств / Уравнения, приводимые к квадратным по форме

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-9: Уравнения, приводимые к квадратному виду

В этом разделе мы рассмотрим уравнения, называемые квадратичный в форме или сводимый к квадратному в форме . Это означает, что мы будем рассматривать уравнения, и если мы посмотрим на них в правильном свете, то сможем сделать их похожими на квадратные уравнения. В этот момент мы можем использовать методы, которые мы разработали для квадратных уравнений, чтобы помочь нам с решением фактического уравнения.

Обычно лучше всего показать процесс на примере, так что давайте сделаем это.

Пример 1 Решить \({x^4} — 7{x^2} + 12 = 0\) 92}\]

Другими словами, здесь мы можем заметить, что переменная часть первого члена ( т. е. игнорирует коэффициент) есть не что иное, как переменная часть второго члена в квадрате. Также обратите внимание, что все, что нам действительно нужно было здесь заметить, это то, что показатель степени первого члена был вдвое больше показателя степени второго члена.

Это, наряду с тем фактом, что третий член является константой, означает, что это уравнение приводится к квадратному виду. Мы решим это, сначала определив, 92}\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}x = \pm \sqrt 4 = \pm 2\end{align*}\]

Итак, у нас есть четыре решения исходного уравнения: \(x = \pm 2\) и \(x = \pm \sqrt 3 \).

Итак, основной процесс состоит в том, чтобы проверить, что уравнение приводится к квадратному по форме, а затем сделать быструю замену, чтобы превратить его в квадратное уравнение. Мы решаем новое уравнение относительно \(u\), переменной из подстановки, а затем используем эти решения и определение подстановки, чтобы получить решения уравнения, которые нам действительно нужны.

В большинстве случаев для проверки приводимости к квадратичной форме все, что нам действительно нужно сделать, это проверить, что один из показателей степени в два раза больше другого. Есть одно исключение, которое мы увидим здесь, когда перейдем к набору примеров.

Кроме того, как только вы станете «хорошо» в них, вам часто не нужно делать замену. Мы сделаем их, чтобы убедиться, что работа понятна. Однако во многих случаях эти проблемы можно решить без замены.

9{\ гидроразрыва {1} {3}}} = \ гидроразрыва {1} {2} \ конец {выравнивание *} \]

Два решения этого уравнения: \(y = 1\) и \(y = \frac{1}{2}\).

c \(z — 9\sqrt z + 14 = 0\) Показать решение

Здесь немного сложнее увидеть, что он квадратичен по форме, но это так. Чтобы увидеть это, вспомним, что показатель степени квадратного корня равен половине, тогда мы можем заметить, что показатель степени первого члена в два раза больше показателя степени второго члена. Таким образом, это уравнение фактически приводится к квадратному виду. 92} = — 2\hspace{0.5in} \Rightarrow \hspace{0.25in}t = \pm \sqrt { — 2} = \pm \sqrt 2 \,\,i\end{align*}\]

В этом случае мы получаем четыре решения, два из которых комплексные. Получение сложных решений из них на самом деле более распространено, чем можно предположить из этого набора примеров. Проблема в том, что для получения некоторых сложных решений требуются знания, которые мы не рассматриваем (и не будем) в этом курсе. Так что не так часто они появляются. 92} — и — 4 = 0\]

Это значение не учитывается, поэтому нам нужно применить к нему квадратичную формулу. Из квадратичной формулы решения:

\[u = \frac{{1 \pm \sqrt {33} }}{4}\]

Теперь, чтобы вернуться к \(x\), нам понадобятся десятичные значения для них, поэтому

\[u = \frac{{1 + \sqrt {33}}}}{4} = 1,68614\hspace{0,5 дюйма}\hspace{0,25 дюйма}u = \frac{{1 — \sqrt {33}}}{ 4} = — 1,18614\] 9{\ гидроразрыва {1} {5}}} = — 1,03473 \ конец {выравнивание *} \]

Нам пришлось использовать калькулятор, чтобы получить окончательный ответ для них. Это одна из причин того, что на уроках алгебры не так уж много таких заданий. Работа и/или ответы, как правило, немного запутаны.

По-Шен Лох | Квадратичный метод: подробное объяснение

В последнее время я систематически думал о том, как объяснить школьные математические понятия более вдумчиво и интересно, создавая свои Daily Challenge уроков. Однажды ночью в сентябре 2019 года, во время мозгового штурма различных способов осмысления квадратичной формулы, я с удивлением придумал простой метод исключения догадок и проверок из факторинга, которого я никогда раньше не видел.

Альтернативный метод решения квадратных уравнений

1. Если найти и с суммой и произведением, то и они все корни
2. Сумма двух чисел, когда они равны
3. Их произведение равно
4. Квадратный корень всегда дает действительный
5. Таким образом работают пески и все корни

Известные сотни лет назад (Виэт)
Известные тысячи лет назад (вавилоняне, греки)

Отдельные этапы этого метода были отдельно открыты древними математиками. Комбинацию этих шагов мог придумать каждый, но после того, как эта веб-страница была выпущена в открытый доступ, единственной предыдущей ссылкой на аналогичный последовательный метод решения квадратных уравнений была хорошая статья учителя математики Джона Сэвиджа. , опубликовано в Учитель математики в 1989 году. Его подход частично совпадал почти во всех расчетах, с педагогической разницей в выборе знака, но имел разницу в логике, поскольку (возможно, из-за дружелюбного стиля письма, который оставляет некоторую логику для интерпретации) он по-видимому, использует дополнительный (верный, но значительно более продвинутый) факт, что каждое квадратичное число может быть разложено на два линейных множителя или имеет некоторые обратные направления импликации, которые технически неверны. В частности, мой подход к избеганию дополнительного предположения в «Завершении квадрата» не был достигнут методом Сэвиджа. На соответствующей рабочей странице сравнивается метод, описанный Сэвиджем, с методом, который предложил я. Поскольку я до сих пор не видел ни одной ранее существовавшей книги или статьи, в которой этот тип метода излагается таким образом, чтобы он подходил для начинающих (избегая углубленных знаний) и четко и последовательно обосновывал все шаги, я решил поделиться им, чтобы предоставить версия, на которую можно безопасно ссылаться.

Объяснение квадратичного метода на примере

Приведенная ниже презентация основана на подходе, изложенном в моей первоначально опубликованной статье, но идет дальше. Он использует мое соглашение о знаках и мои собственные логические шаги (в отличие от версии Сэвиджа), чтобы быть логически обоснованным, а также потому, что я думаю, что мой выбор полезен для понимания более глубокой связи между квадратичным уравнением и его решениями. Он также показывает чистое сведение задачи от решения стандартного квадратичного уравнения к классической задаче, решаемой вавилонянами и греками. Это видео представляет собой самостоятельный практический урок, в котором рассматривается множество примеров с объяснением каждого логического шага. Обсуждение текста ниже идет немного глубже и включает комментарии, которые могут быть полезны учителям.

Обзор: Умножение и неумножение

Давайте начнем с обзора фактов, которые обычно учат при введении квадратных уравнений. Во-первых, мы используем распределительное правило для умножения (также называемое FOIL):

Ключевой вывод состоит в том, что in получается при сложении вместе and, а the получается при умножении вместе and.

Вот еще один пример:

Так как у нас были оба условия «и», то условия «и» сократились, что дало нам разницу в квадратах. Это пригодится позже.

Причина, по которой полезно знать, что происходит при умножении, заключается в том, что если мы можем сделать это в обратном порядке, мы сможем решать квадратные уравнения. Например, предположим, что мы хотим найти все такие, что мы уже знаем, что это то же самое (имеет точно такие же решения), как и единственный способ умножить два числа на ноль, если одно (или оба) равны нулю. (Формальное обоснование этого 90 568 свойства нулевого произведения 90 569 использует основную аксиому, что вы можете делить на любое ненулевое число: предположим для противоречия, что и то, и другое не равно нулю. Тогда, разделив обе части уравнения на, мы получим противоречие.)

Так вот, работают именно те, где(что есть) или(что есть). Обратите внимание, что решения — это числа, из которых мы вычитаем, т. е. не и, а и. Важно, что это все решения.

Обзор: настройка для факторинга

Давайте попробуем обратный процесс для примера. Было бы здорово, если бы мы могли разложить его на нечто подобное. Студенты еще не узнали, что всегда можно найти такую ​​факторизацию, но наш подход также докажет им, что это всегда возможно! Согласно предыдущему разделу, если нам удалось разложить на множители, то все, что окажется в этих пробелах, будет решениями. Но что будет работать в этих пустых местах? Два числа, у которых есть сумма и произведение. Наиболее часто изучаемый метод состоит в том, чтобы найти эти числа путем угадывания и проверки. Это может разочаровать, особенно когда есть отрицательные числа, которые нужно попробовать, и когда продукт имеет много возможных разложений на множители (имеет массу возможностей).

Как указано в соответствующей работе, версия Сэвиджа имеет аналогичные вычисления, за исключением того, что он ищет факторизацию в математически эквивалентной форме. Затем числа в пробелах являются отрицательными значениями решений, поэтому после нахождения факторизации Сэвидж отрицает числа в качестве последнего шага. С образовательной точки зрения, я думаю, что немного выгоднее чисто свести стандартную квадратичную задачу к задаче на сумму и произведение (без необходимости возвращаться и помнить об отрицании в конце), потому что тогда можно получить представление о прямая связь между коэффициентами и суммой и произведением корней.

Чтобы сделать это еще более естественным для новичка, я бы посоветовал ввести понятие факторинга с начальным примером, который имеет отрицательный коэффициент, так что факторизация уже естественна и удобна. Кроме того, тогда еще более прозрачно наблюдать за решениями через свойство нулевого произведения, потому что отрицание не требуется.

Проницательность: Факторинг без угадывания

Вот способ определения чисел, который работает без каких-либо угадываний! Сумма двух чисел равна их среднему значению. Таким образом, мы можем попытаться найти числа, которые плюс некоторая сумма и минус та же сумма. Все, что нам нужно сделать, это выяснить, существует ли такое, что работает как два числа и может существовать.

При поиске двух чисел формы и они автоматически суммируются. Итак, нам просто нужно их умножить на. Мы хотим выяснить, существует ли такое, которое удовлетворяет: Мы уже видели подобный шаблон, где у нас есть сумма двух чисел, умноженная на их разность. Ответ всегда разность их квадратов! Итак, переписав левую часть в эквивалентной форме, мы хотим выяснить, существует ли такое, что это интересно! Есть одиночка, а все остальное просто число! Это означает, что мы можем закончить поиск валидности, следуя своему чутью, вместо того, чтобы требовать каких-либо новых методов.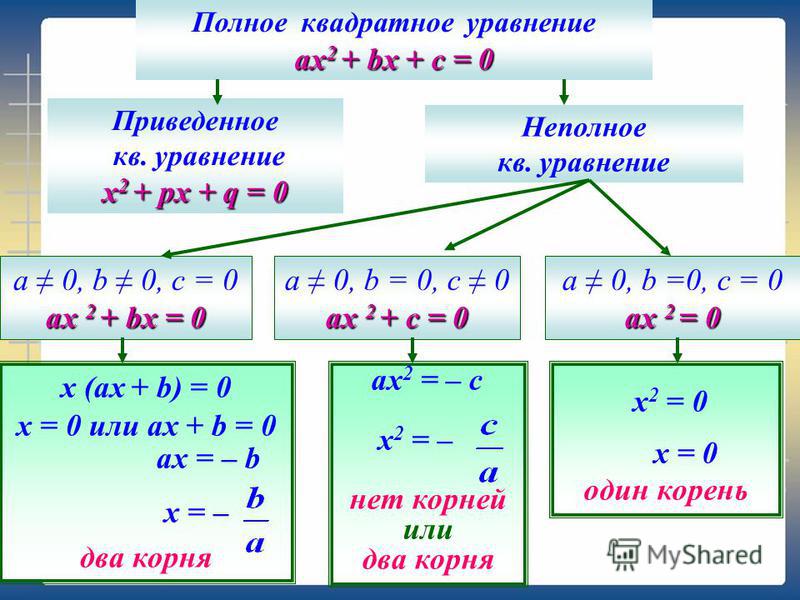 Мы хотим: что мы можем получить от Итак, выбор существует! (В качестве альтернативы мы могли бы выбрать, но это в конечном итоге дало бы тот же результат.) Следовательно, прослеживая логику вверх, мы знаем, что и обязательно будут два числа, у которых есть сумма и произведение. Тот факт, что эти числа удовлетворяют отношениям суммы и произведения, означает, что факторизация существует, а это также означает, что мы нашли полный набор решений: или.

Обратите внимание, что в этом подходе нам нужно только существование одного конкретного числа, квадрат которого равен другому конкретному числу. В этом примере очевидно, что это число, квадрат которого равен . Когда у нас есть одно такое число, мы уже можем следовать нашим логическим шагам и вывести полный набор решений исходного квадратичного уравнения. Напротив, на соответствующем шаге завершения квадрата нам потребуется полный список всех чисел, которые возводятся в квадрат. Понятно, что и должно быть в списке, но сложнее ответить, почему это полный список (особенно когда в качестве вариантов разрешены комплексные числа).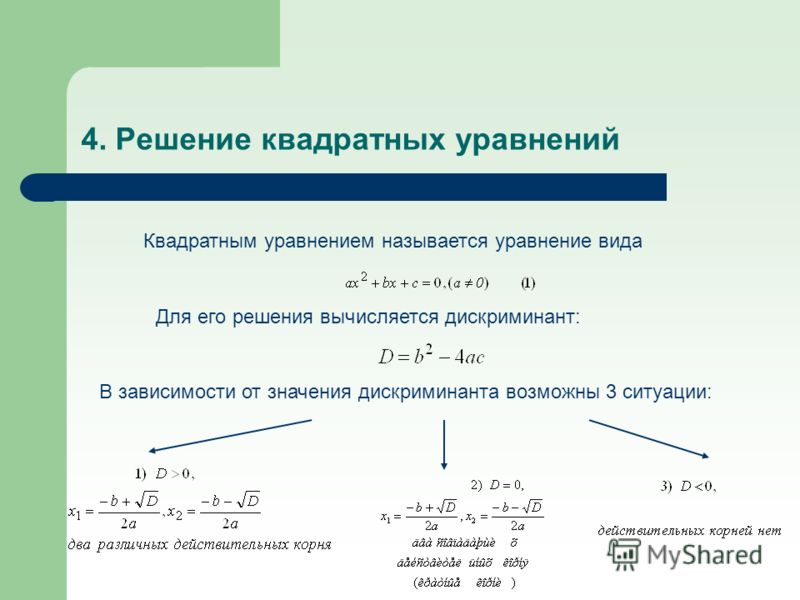 Эта деталь обсуждается более подробно здесь.

Как я отметил в своей полной статье, хотя я (как и многие другие) самостоятельно придумал способ нахождения двух чисел по их сумме и произведению, вавилоняне и греки уже знали этот трюк за тысячи лет до этого. Однако математика была недостаточно развита, чтобы они могли использовать этот трюк самостоятельно для решения общих квадратных уравнений. В частности, они не работали с полиномиальным факторингом или отрицательными числами (не говоря уже о недействительных комплексных числах). Для более подробного обсуждения посетите соответствующую рабочую страницу.

Пример использования: квадратное число, которое нельзя легко разложить на множители

Теперь, когда угадывание исключено, мы действительно можем решить любое квадратное число с помощью этого метода. Рассмотрим этот пример: Во-первых, давайте очистим его, умножив обе части на, чтобы получить уравнение, набор решений которого идентичен: Как и раньше, , если мы можем найти два числа с суммой и произведением, тогда факторизация будет существовать, и эти два числа будут решения. Разделив сумму пополам, чтобы получить среднее значение, мы видим, что все будет готово, если мы сможем найти что-то такое, что числа вида и дают произведение. Эти два уравнения эквивалентны друг другу: мы можем удовлетворить уравнению дна, выбрав. Важно отметить, что математическое изобретение комплексных чисел позволяет нам извлекать квадратный корень из отрицательного числа, так что у нас есть правильный выбор. (Вот почему нам не нужна Основная теорема алгебры, и, фактически, именно поэтому этот подход доказывает эту теорему для многочленов степени 2.) Итак, действительно есть два числа с суммой и произведением, и они естьи, которые есть. Тот факт, что эти числа удовлетворяют отношениям суммы и произведения, означает, что факторизация существует, и поэтому мы нашли решения: Мы решили задачу, и нам вообще не понадобилось использовать заученную формулу! Этот метод работает для любого квадратного уравнения, не требуя запоминания, и каждый шаг имеет простое математическое обоснование.

Доказательство квадратной формулы

Если кто-то хочет вывести квадратную формулу, этот метод также предоставляет альтернативное простое доказательство.

Для общего квадратного уравнения вышеизложенное показывает, что достаточно найти два числа с суммой и произведением, после чего факторизация будет существовать, и они будут корнями. Итак, мы хотели бы выяснить, существует ли такое, что эти два числа будут работать. Они автоматически суммируются. Их произведение точно тогда, когда выполняются эти два эквивалентных уравнения: Поскольку квадратный корень всегда существует (распространяясь на комплексные числа, если необходимо), выбирая квадратный корень из for, мы можем удовлетворить последнее уравнение. Таким образом, у этих двух чисел есть сумма и произведение, и все они являются решениями.

Вышеприведенной формулы уже достаточно для решения любого квадратного уравнения, потому что вы можете умножить или разделить обе части на число так, что ничего не будет впереди. Однако просто для того, чтобы убедиться, что эта формула та самая, которую все привыкли запоминать (что уже не нужно, в свете нашего метода), мы можем показать, как получить формулу для самого общего квадратного уравнения при . Нам просто нужно сначала разделить на, чтобы получить эквивалентное уравнение. Затем, подставив информацию for и for в приведенные выше решения, мы получим, что решения таковы:

Резюме

Этот метод состоит из двух основных шагов, начиная с общего квадратного уравнения в стандартной форме.

1. Из-за полиномиального разложения, если мы можем найти два числа с суммой и произведением, то это полный набор решений.
2. Используйте древний вавилонско-греческий трюк (распространенный на комплексные числа), чтобы найти эти два числа в любых обстоятельствах.

Для того чтобы эти шаги были математически обоснованными как завершенный метод, важно, чтобы при любых обстоятельствах на шаге 2 были найдены два числа для использования в шаге 1, даже если они не являются действительными комплексными числами.