примеры, таблица простых чисел, решето Эратосфена
В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.
Простые и составные числа – определения и примеры
Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.
Определение 1Простыми числами называют целые числа, которые больше единицы и имеют два положительных делителя, то есть себя и 1.
Определение 2Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.
Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Простые числа – это натуральные числа, имеющие только два положительных делителя.
Определение 4Составное число – это натуральное число, имеющее более двух положительных делителей.
Любое число, которое больше 1 является либо простым, либо составным. Из свойства делимости имеем, что 1 и число а всегда будут делителями для любого числа а, то есть оно будет делиться само на себя и на 1. Дадим определение целых чисел.
Определение 5Натуральные числа, которые не являются простыми, называют составными.
Простые числа: 2, 3, 11, 17, 131, 523. Они делятся только сами на себя и на 1. Составные числа: 6, 63, 121, 6697. То есть число 6 можно разложить на 2 и 3, а 63 на 1, 3, 7,9, 21, 63, а 121 на 11, 11, то есть его делители будут 1, 11, 121.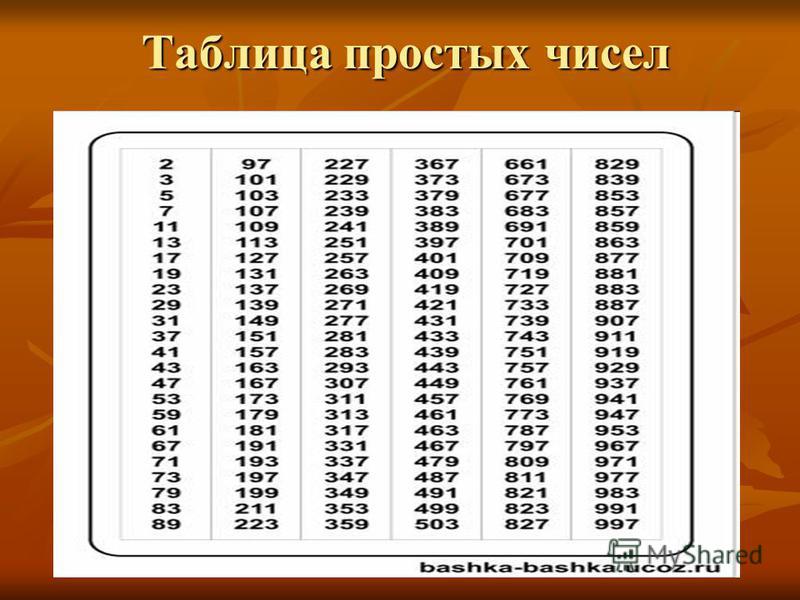 Число 6697 разложится на 37 и 181. Заметим, что понятия простых чисел и взаимно простых чисел – разные понятия.
Число 6697 разложится на 37 и 181. Заметим, что понятия простых чисел и взаимно простых чисел – разные понятия.
Таблица простых чисел
Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:
Таблица для всех существующих натуральных чисел нереальна, так как их существует бесконечное множество. Когда числа достигают размеров 10000 или 1000000000, тогда следует задуматься об использовании решета Эратосфена.
Рассмотрим теорему, которая объясняет последнее утверждение.
Теорема 1Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Доказательство 1Возьмем, что а является натуральным числом, которое больше 1, b является наименьшим отличным от единицы делителем для числа а. Следует доказать, что b является простым числом при помощи метода противного.
Допустим, что b – составное число. Отсюда имеем, что есть делитель для b, который отличен от 1 как и от b. Такой делитель обозначается как b1. Необходимо, чтобы условие 1<b1<b
Такой делитель обозначается как b1. Необходимо, чтобы условие 1<b1<b
Из условия видно, что а делится на b, b делится на b1, значит, понятие делимости выражается таким образом: a=b·q и b=b1·q1, откуда a= b1·(q1·q), где q и q1являются целыми числами. По правилу умножения целых чисел имеем, что произведение целых чисел – целое число с равенством вида a=b1·(q1·q). Видно, что b1– это делитель для числа а. Неравенство 1<b1<b не соответствует, потому как получим, что b является наименьшим положительным и отличным от 1 делителем а.
Теорема 2Простых чисел бесконечно много.
Доказательство 2Предположительно возьмем конечное количество натуральных чисел n и обозначим как p1, p2, …, pn. Рассмотрим вариант нахождения простого числа, отличного от указанных.
Примем на рассмотрение число р, которое равняется p1, p2, …, pn+1. Оно не равняется каждому из чисел, соответствующих простым числам вида p1, p2, …, pn.
Если это было бы не так, тогда, исходя из свойства делимости произведения p1, p2, …, pn, получим, что оно делилось бы на pn+1. Заметим, что на выражение pn+1делится число р равняется сумме p1, p2, …, pn+1. Получим, что на выражение pn+1должно делиться второе слагаемое этой суммы, которое равняется 1, но это невозможно.
Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.
Так как простых чисел очень много, то таблицы ограничивают числами 100, 1000, 10000 и так далее.
Решето Эратосфена
При составлении таблицы простых чисел следует учитывать то, что для такой задачи необходима последовательная проверка чисел, начиная с 2 до 100.
Рассмотрим пошагово.
Если начать с числа 2, то оно имеет только 2 делителя: 2 и 1, значит, его можно занести в таблицу. Также и с числом 3. Число 4 является составным, следует разложить его еще на 2 и 2. Число 5 является простым, значит, можно зафиксировать в таблице. Так выполнять вплоть до числа 100.
Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.
Способ при помощи решета Эратосфена считают самым удобным. Рассмотрим на примере таблиц, приведенных ниже. Для начала записываются числа 2, 3, 4, …, 50.
Теперь необходимо зачеркнуть все числа, которые кратны 2. Произвести последовательное зачеркивание. Получим таблицу вида:
Далее вычеркиваем все числа, кратные 3. Получаем таблицу вида:
Переходим к вычеркиванию чисел, кратных 5. Получим:
Получим:
Вычеркиваем числа, кратные 7, 11. В конечном итоге таблица получает вид
Перейдем к формулировке теоремы.
Теорема 3Наименьший положительный и отличный от 1 делитель основного числа а не превосходит a, где a является арифметическим корнем заданного числа.
Доказательство 3Необходимо обозначить b наименьший делитель составного числа а. Существует такое целое число q, где a=b·q, причем имеем, что b≤q. Недопустимо неравенство вида b>q, так как происходит нарушение условия. Обе части неравенства b≤q следует умножить на любое положительное число b, не равное 1. Получаем, что b·b≤b·q, где b2≤a и b≤a.
Из доказанной теоремы видно, что вычеркивание чисел в таблице приводит к тому, что необходимо начинать с числа , которое равняется b2 и удовлетворяет неравенству b2≤a. То есть, если вычеркнуть числа, кратные 2, то процесс начинается с 4, а кратных 3 – с 9 и так далее до 100.
Составление такой таблицы при помощи теоремы Эратосфена говорит о том, что при вычеркивании всех составных чисел, останутся простые, которые не превосходят n. В примере, где n=50, у нас имеется, что n=50. Отсюда и получаем, что решето Эратосфена отсеивает все составные числа, которые по значению не больше значения корня из 50. Поиск чисел производится при помощи вычеркивания.
В примере, где n=50, у нас имеется, что n=50. Отсюда и получаем, что решето Эратосфена отсеивает все составные числа, которые по значению не больше значения корня из 50. Поиск чисел производится при помощи вычеркивания.
Данное число простое или составное?
Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.
Пример 1Доказать что число 898989898989898989 является составным.
Решение
Сумма цифр заданного числа равняется 9·8+9·9=9·17. Значит, число 9·17 делится на 9, исходя из признака делимости на 9. Отсюда следует, что оно составное.
Такие признаки не способны доказать простоту числа. Если нужна проверка, следует производить другие действия. Самый подходящий способ – это перебор чисел. В течение процесса можно найти простые и составные числа. То есть числа по значению не должны превосходить a. То есть число а необходимо разложить на простые множители. если это будет выполнено, тогда число а можно считать простым.
если это будет выполнено, тогда число а можно считать простым.
Определить составное или простое число 11723.
Решение
Теперь необходимо найти все делители для числа 11723. Необходимо оценить 11723.
Отсюда видим, что 11723<200, то 2002=40 000, а 11 723<40 000. Получаем, что делители для 11 723 меньше числа 200.
Для более точной оценки числа 11723 необходимо записать выражение 1082=11 664, а
При разложении получим, что 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107 – это все простые числа. Весь данный процесс можно изобразить как деление столбиком. То есть разделить 11723 на 19. Число 19 является одним из его множителей, так как получим деление без остатка. Изобразим деление столбиком:
Отсюда следует, что 11723 является составным числом, потому как кроме себя и 1 имеет делитель 19.
Ответ: 11723 является составным числом.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000
Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000| Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000. Простые числа список. Поделиться: | |
Вы сейчас находитесь в каталоге: Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000. Простые числа список. |
|
Ниже приведена таблица простых чисел от 2 до 10000 (1229 штук). Таблица простых чисел от 2 до 1000. Таблица простых чисел от 2 до 1000 выделена серым. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1009 | 1013 | 1019 | 1021 | 1031 | 1033 | 1039 | 1049 | 1051 | 1061 | 1063 | 1069 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1087 | 1091 | 1093 | 1097 | 1103 | 1109 | 1117 | 1123 | 1129 | 1151 | 1153 | 1163 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1171 | 1181 | 1187 | 1193 | 1201 | 1213 | 1217 | 1223 | 1229 | 1231 | 1237 | 1249 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1259 | 1277 | 1279 | 1283 | 1289 | 1291 | 1297 | 1301 | 1303 | 1307 | 1319 | 1321 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1327 | 1361 | 1367 | 1373 | 1381 | 1399 | 1409 | 1423 | 1427 | 1429 | 1433 | 1439 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1447 | 1451 | 1453 | 1459 | 1471 | 1481 | 1483 | 1487 | 1489 | 1493 | 1499 | 1511 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1523 | 1531 | 1543 | 1549 | 1553 | 1559 | 1567 | 1571 | 1579 | 1583 | 1597 | 1601 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1607 | 1609 | 1613 | 1619 | 1621 | 1627 | 1637 | 1657 | 1663 | 1667 | 1669 | 1693 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1697 | 1699 | 1709 | 1721 | 1723 | 1733 | 1741 | 1747 | 1753 | 1759 | 1777 | 1783 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1787 | 1789 | 1801 | 1811 | 1823 | 1831 | 1847 | 1861 | 1867 | 1871 | 1873 | 1877 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1879 | 1889 | 1901 | 1907 | 1913 | 1931 | 1933 | 1949 | 1951 | 1973 | 1979 | 1987 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1993 | 1997 | 1999 | 2003 | 2011 | 2017 | 2027 | 2029 | 2039 | 2053 | 2063 | 2069 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2081 | 2083 | 2087 | 2089 | 2099 | 2111 | 2113 | 2129 | 2131 | 2137 | 2141 | 2143 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2153 | 2161 | 2179 | 2203 | 2207 | 2213 | 2221 | 2237 | 2239 | 2243 | 2251 | 2267 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2269 | 2273 | 2281 | 2287 | 2293 | 2297 | 2309 | 2311 | 2333 | 2339 | 2341 | 2347 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2351 | 2357 | 2371 | 2377 | 2381 | 2383 | 2389 | 2393 | 2399 | 2411 | 2417 | 2423 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2437 | 2441 | 2447 | 2459 | 2467 | 2473 | 2477 | 2503 | 2521 | 2531 | 2539 | 2543 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2549 | 2551 | 2557 | 2579 | 2591 | 2593 | 2609 | 2617 | 2621 | 2633 | 2647 | 2657 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2659 | 2663 | 2671 | 2677 | 2683 | 2687 | 2689 | 2693 | 2699 | 2707 | 2711 | 2713 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2719 | 2729 | 2731 | 2741 | 2749 | 2753 | 2767 | 2777 | 2789 | 2791 | 2797 | 2801 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2803 | 2819 | 2833 | 2837 | 2843 | 2851 | 2857 | 2861 | 2879 | 2887 | 2897 | 2903 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2909 | 2917 | 2927 | 2939 | 2953 | 2957 | 2963 | 2969 | 2971 | 2999 | 3001 | 3011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3019 | 3023 | 3037 | 3041 | 3049 | 3061 | 3067 | 3079 | 3083 | 3089 | 3109 | 3119 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3121 | 3137 | 3163 | 3167 | 3169 | 3181 | 3187 | 3191 | 3203 | 3209 | 3217 | 3221 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3229 | 3251 | 3253 | 3257 | 3259 | 3271 | 3299 | 3301 | 3307 | 3313 | 3319 | 3323 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3329 | 3331 | 3343 | 3347 | 3359 | 3361 | 3371 | 3373 | 3389 | 3391 | 3407 | 3413 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3433 | 3449 | 3457 | 3461 | 3463 | 3467 | 3469 | 3491 | 3499 | 3511 | 3517 | 3527 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3529 | 3533 | 3539 | 3541 | 3547 | 3557 | 3559 | 3571 | 3581 | 3583 | 3593 | 3607 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3613 | 3617 | 3623 | 3631 | 3637 | 3643 | 3659 | 3671 | 3673 | 3677 | 3691 | 3697 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3701 | 3709 | 3719 | 3727 | 3733 | 3739 | 3761 | 3767 | 3769 | 3779 | 3793 | 3797 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3803 | 3821 | 3823 | 3833 | 3847 | 3851 | 3853 | 3863 | 3877 | 3881 | 3889 | 3907 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3911 | 3917 | 3919 | 3923 | 3929 | 3931 | 3943 | 3947 | 3967 | 3989 | 4001 | 4003 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4007 | 4013 | 4019 | 4021 | 4027 | 4049 | 4051 | 4057 | 4073 | 4079 | 4091 | 4093 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4099 | 4111 | 4127 | 4129 | 4133 | 4139 | 4153 | 4157 | 4159 | 4177 | 4201 | 4211 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4217 | 4219 | 4229 | 4231 | 4241 | 4243 | 4253 | 4259 | 4261 | 4271 | 4273 | 4283 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4289 | 4297 | 4327 | 4337 | 4339 | 4349 | 4357 | 4363 | 4373 | 4391 | 4397 | 4409 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4421 | 4423 | 4441 | 4447 | 4451 | 4457 | 4463 | 4481 | 4483 | 4493 | 4507 | 4513 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4517 | 4519 | 4523 | 4547 | 4549 | 4561 | 4567 | 4583 | 4591 | 4597 | 4603 | 4621 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4637 | 4639 | 4643 | 4649 | 4651 | 4657 | 4663 | 4673 | 4679 | 4691 | 4703 | 4721 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4723 | 4729 | 4733 | 4751 | 4759 | 4783 | 4787 | 4789 | 4793 | 4799 | 4801 | 4813 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4817 | 4831 | 4861 | 4871 | 4877 | 4889 | 4903 | 4909 | 4919 | 4931 | 4933 | 4937 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4943 | 4951 | 4957 | 4967 | 4969 | 4973 | 4987 | 4993 | 4999 | 5003 | 5009 | 5011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5021 | 5023 | 5039 | 5051 | 5059 | 5077 | 5081 | 5087 | 5099 | 5101 | 5107 | 5113 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5119 | 5147 | 5153 | 5167 | 5171 | 5179 | 5189 | 5197 | 5209 | 5227 | 5231 | 5233 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5237 | 5261 | 5273 | 5279 | 5281 | 5297 | 5303 | 5309 | 5323 | 5333 | 5347 | 5351 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5381 | 5387 | 5393 | 5399 | 5407 | 5413 | 5417 | 5419 | 5431 | 5437 | 5441 | 5443 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5449 | 5471 | 5477 | 5479 | 5483 | 5501 | 5503 | 5507 | 5519 | 5521 | 5527 | 5531 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5557 | 5563 | 5569 | 5573 | 5581 | 5591 | 5623 | 5639 | 5641 | 5647 | 5651 | 5653 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5657 | 5659 | 5669 | 5683 | 5689 | 5693 | 5701 | 5711 | 5717 | 5737 | 5741 | 5743 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5749 | 5779 | 5783 | 5791 | 5801 | 5807 | 5813 | 5821 | 5827 | 5839 | 5843 | 5849 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5851 | 5857 | 5861 | 5867 | 5869 | 5879 | 5881 | 5897 | 5903 | 5923 | 5927 | 5939 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5953 | 5981 | 5987 | 6007 | 6011 | 6029 | 6037 | 6043 | 6047 | 6053 | 6067 | 6073 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6079 | 6089 | 6091 | 6101 | 6113 | 6121 | 6131 | 6133 | 6143 | 6151 | 6163 | 6173 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6197 | 6199 | 6203 | 6211 | 6217 | 6221 | 6229 | 6247 | 6257 | 6263 | 6269 | 6271 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6277 | 6287 | 6299 | 6301 | 6311 | 6317 | 6323 | 6329 | 6337 | 6343 | 6353 | 6359 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6361 | 6367 | 6373 | 6379 | 6389 | 6397 | 6421 | 6427 | 6449 | 6451 | 6469 | 6473 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6481 | 6491 | 6521 | 6529 | 6547 | 6551 | 6553 | 6563 | 6569 | 6571 | 6577 | 6581 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6599 | 6607 | 6619 | 6637 | 6653 | 6659 | 6661 | 6673 | 6679 | 6689 | 6691 | 6701 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6703 | 6709 | 6719 | 6733 | 6737 | 6761 | 6763 | 6779 | 6781 | 6791 | 6793 | 6803 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6823 | 6827 | 6829 | 6833 | 6841 | 6857 | 6863 | 6869 | 6871 | 6883 | 6899 | 6907 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6911 | 6917 | 6947 | 6949 | 6959 | 6961 | 6967 | 6971 | 6977 | 6983 | 6991 | 6997 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7001 | 7013 | 7019 | 7027 | 7039 | 7043 | 7057 | 7069 | 7079 | 7103 | 7109 | 7121 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7127 | 7129 | 7151 | 7159 | 7177 | 7187 | 7193 | 7207 | 7211 | 7213 | 7219 | 7229 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7237 | 7243 | 7247 | 7253 | 7283 | 7297 | 7307 | 7309 | 7321 | 7331 | 7333 | 7349 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7351 | 7369 | 7393 | 7411 | 7417 | 7433 | 7451 | 7457 | 7459 | 7477 | 7481 | 7487 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7489 | 7499 | 7507 | 7517 | 7523 | 7529 | 7537 | 7541 | 7547 | 7549 | 7559 | 7561 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7573 | 7577 | 7583 | 7589 | 7591 | 7603 | 7607 | 7621 | 7639 | 7643 | 7649 | 7669 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7673 | 7681 | 7687 | 7691 | 7699 | 7703 | 7717 | 7723 | 7727 | 7741 | 7753 | 7757 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7759 | 7789 | 7793 | 7817 | 7823 | 7829 | 7841 | 7853 | 7867 | 7873 | 7877 | 7879 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7883 | 7901 | 7907 | 7919 | 7927 | 7933 | 7937 | 7949 | 7951 | 7963 | 7993 | 8009 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8011 | 8017 | 8039 | 8053 | 8059 | 8069 | 8081 | 8087 | 8089 | 8093 | 8101 | 8111 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8117 | 8123 | 8147 | 8161 | 8167 | 8171 | 8179 | 8191 | 8209 | 8219 | 8221 | 8231 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8233 | 8237 | 8243 | 8263 | 8269 | 8273 | 8287 | 8291 | 8293 | 8297 | 8311 | 8317 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8329 | 8353 | 8363 | 8369 | 8377 | 8387 | 8389 | 8419 | 8423 | 8429 | 8431 | 8443 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8447 | 8461 | 8467 | 8501 | 8513 | 8521 | 8527 | 8537 | 8539 | 8543 | 8563 | 8573 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8581 | 8597 | 8599 | 8609 | 8623 | 8627 | 8629 | 8641 | 8647 | 8663 | 8669 | 8677 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8681 | 8689 | 8693 | 8699 | 8707 | 8713 | 8719 | 8731 | 8737 | 8741 | 8747 | 8753 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8761 | 8779 | 8783 | 8803 | 8807 | 8819 | 8821 | 8831 | 8837 | 8839 | 8849 | 8861 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8863 | 8867 | 8887 | 8893 | 8923 | 8929 | 8933 | 8941 | 8951 | 8963 | 8969 | 8971 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8999 | 9001 | 9007 | 9011 | 9013 | 9029 | 9041 | 9043 | 9049 | 9059 | 9067 | 9091 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9103 | 9109 | 9127 | 9133 | 9137 | 9151 | 9157 | 9161 | 9173 | 9181 | 9187 | 9199 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9203 | 9209 | 9221 | 9227 | 9239 | 9241 | 9257 | 9277 | 9281 | 9283 | 9293 | 9311 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9319 | 9323 | 9337 | 9341 | 9343 | 9349 | 9371 | 9377 | 9391 | 9397 | 9403 | 9413 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9419 | 9421 | 9431 | 9433 | 9437 | 9439 | 9461 | 9463 | 9467 | 9473 | 9479 | 9491 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9497 | 9511 | 9521 | 9533 | 9539 | 9547 | 9551 | 9587 | 9601 | 9613 | 9619 | 9623 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9629 | 9631 | 9643 | 9649 | 9661 | 9677 | 9679 | 9689 | 9697 | 9719 | 9721 | 9733 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9739 | 9743 | 9749 | 9767 | 9769 | 9781 | 9787 | 9791 | 9803 | 9811 | 9817 | 9829 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9833 | 9839 | 9851 | 9857 | 9859 | 9871 | 9883 | 9887 | 9901 | 9907 | 9923 | 9929 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9931 | 9941 | 9949 | 9967 | 9973 | конец таблички 🙂 ! | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Справка проекта:
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0.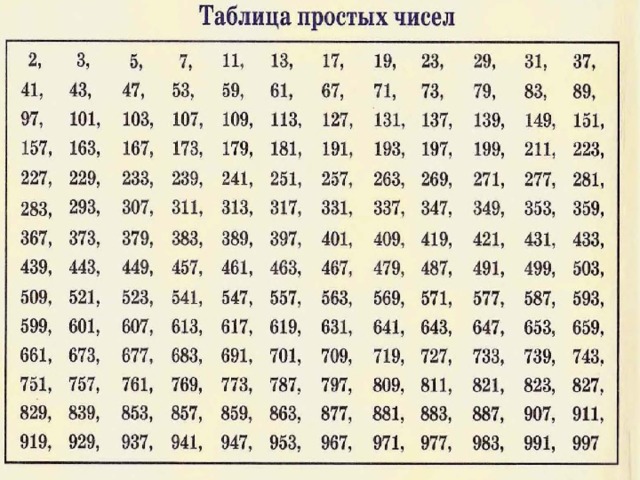 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Что такое простое число? Объяснение для учителей, родителей и детей
Простое число — это число, которое можно разделить только само на себя и на 1 без остатка. Здесь мы подробно объясним, что это значит, дадим вам список простых чисел, которые дети должны знать в начальной и средней школе, и предоставим вам несколько практических вопросов и примеров.
Здесь мы подробно объясним, что это значит, дадим вам список простых чисел, которые дети должны знать в начальной и средней школе, и предоставим вам несколько практических вопросов и примеров.
Простое число — это целое число больше 1, имеющее только два делителя — само себя и 1.
Простое число нельзя разделить ни на какие другие положительные целые числа без остатка, десятичной дроби или дроби.
Примером простого числа является 13. Его делителями являются только 1 и 13. При делении простого числа на другое натуральное число остаются числа. Например, 13 ÷ 6 = 2, остаток 1.
15 не является примером простого числа, потому что оно делится на 5 и 3, а также само по себе, а 1.
15 является примером составного числа. число, потому что оно имеет более двух делителей.
Простые числа часто рассматриваются математиками в качестве «кирпичиков» в теории чисел. Основная теорема арифметики гласит, что составное число можно представить в виде произведения простых чисел.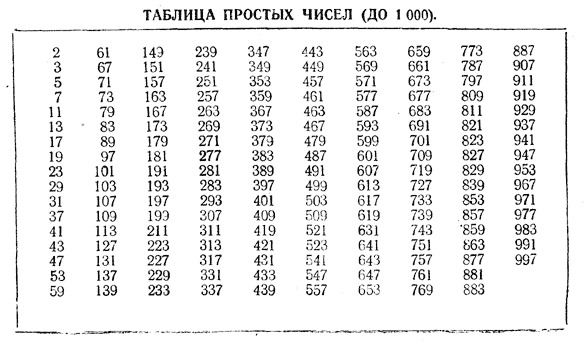
См. также: Правила делимости
Примеры простых чисел
Как определить, является ли заданное число простым или составным, на основе свойств простых чисел.
Какие простые числа?- Меньше 20 есть 8 простых чисел: 2, 3, 5, 7, 11, 13, 17 и 19.
- Первые 10 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
- Существует 25 простых чисел от 1 до 100.
- Простые числа включают большие числа и могут продолжаться далеко за пределы 100.
- Например, 21 577 — простое число.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67 , 71, 73, 79, 83, 89, 97
Обратите внимание, что этот список простых чисел содержит только нечетные числа, за исключением числа 2.
Наименьшее простое число 2 — наименьшее простое число. Кроме того, это единственное четное простое число — все остальные четные числа могут делиться как минимум сами на себя, на 1 и 2, то есть у них будет как минимум 3 делителя.
Греческий математик Евклид (один из самых известных математиков классической эпохи) записал доказательство того, что среди множества простых чисел нет наибольшего простого числа. Тем не менее, многие ученые и математики все еще пытаются найти его в рамках Великого Интернет-поиска простых чисел Мерсенна.
наибольшее известное простое число (по состоянию на ноябрь 2020 г.) равно 2 82 589 933 − 1, число, состоящее из 24 862 048 цифр при записи по основанию 10. , имеющий 23 249 425 цифр.
К тому времени, как вы это прочтете, он может стать еще больше, но вы можете следить за его развитием в Википедии.
Часто задаваемые вопросы о простых числах
Что такое простое число в математике?
Простое число — это число, которое можно разделить только на себя и на 1 без остатка.
Какие простые числа от 1 до 100?
Простые числа от 1 до 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Почему 1 не простое число?
1 не является простым числом, потому что оно имеет только один делитель, а именно 1. Простые числа должны иметь ровно два делителя.
Почему 2 простое число?
2 — простое число, потому что его единственными делителями являются 1 и оно само.
Является ли 51 простым числом?
51 не является простым числом, потому что оно имеет 3 и 17 в качестве делителей, а также само себя и 1. Другими словами, 51 имеет четыре делителя.
БЕСПЛАТНЫЙ набор математических игр и заданий для 5-го класса
17 занимательных математических игр и заданий для учащихся 5-го класса, которые можно выполнять самостоятельно или с партнером.
Одним из наиболее важных применений простых чисел является кибербезопасность — обеспечение большей безопасности информации, передаваемой через Интернет.
Чтобы зашифровать (защитить) такие вещи, как данные кредитной карты, медицинские записи и даже некоторые службы обмена сообщениями, такие как WhatsApp, инженеры-программисты создают алгоритмы, используя простые числа.
Перемножая два очень больших простых числа (некоторые компании используют простые числа, состоящие из сотен цифр!), мы получаем еще большее число, исходные делители которого (два очень больших простых числа) известны только нам. Затем мы используем это еще большее число для шифрования нашей информации.
Если кто-то еще хочет узнать, какую информацию мы посылаем, он должен выяснить, каковы были наши первоначальные факторы. С такими длинными простыми числами, как те, которые мы использовали, им могут потребоваться годы или даже десятилетия постоянных проб и ошибок, прежде чем они найдут хотя бы одно.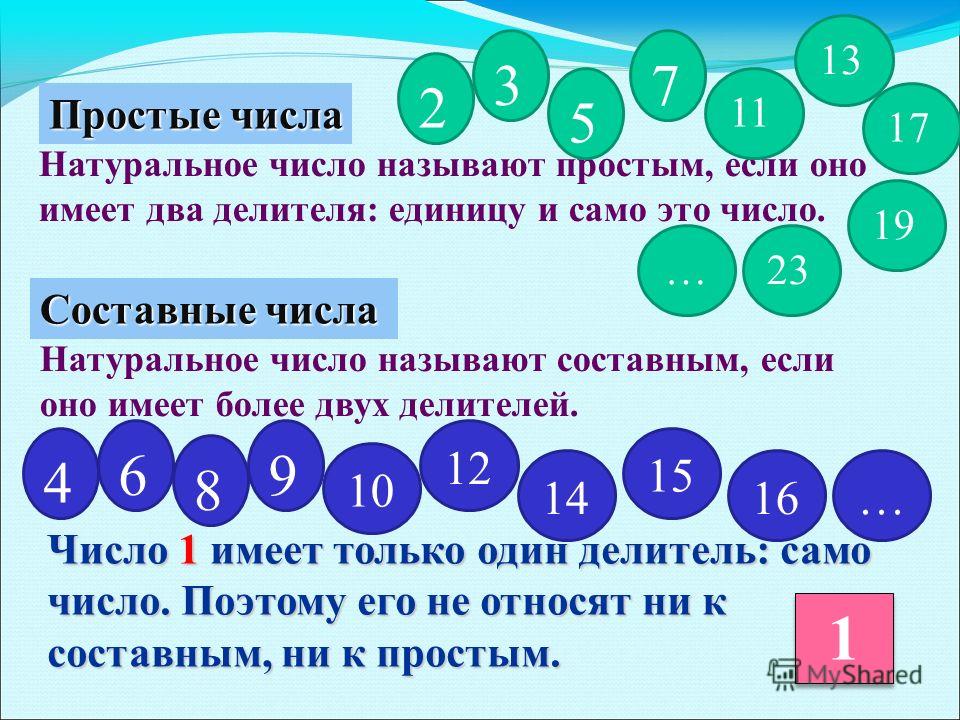 Такая криптография с открытым ключом обеспечивает безопасность нашей информации.
Такая криптография с открытым ключом обеспечивает безопасность нашей информации.
Хотите знать, как объяснить своим детям другие ключевые слова по математике? Ознакомьтесь с нашим словарем Primary Math Dictionary или попробуйте эти основные математические термины:
- Что такое кубическое число: объяснение для основных родителей и детей
- Что такое наименьшее общее кратное: объяснение для основных родителей и детей
- Что такое наивысший общий делитель: объяснение для основных родителей и детей
1) Квадратное число и простое число имеют в сумме 22. Какие это два числа?
A: 9 и 13
2) Эмма думает о двух простых числах. Она складывает два числа вместе. Ее ответ — 36. Напишите все возможные пары простых чисел, которые могла придумать Эмма.
А: 3 и 33; 5 и 31; 7 и 29; 13 и 23; 17 и 19
3) Обведите два простых числа – 29, 59, 39, 69, 29
A: 29 и 59
4) Запишите три простых числа, при умножении которых получается 231.
27 A: 3 x 7 x 11
ЗАДАЧА: Чен выбирает простое число. Он умножает его на 10, а затем округляет до ближайшей сотни. Его ответ — 400. Напишите все возможные простые числа, которые мог выбрать Чен.
A: 37, 41 или 43.
Онлайн-центр Third Space Learning Maths Hub содержит сотни математических ресурсов для учителей начальной школы и родителей, которые можно использовать в школе и дома. Регистрация на бесплатных математических ресурсах выполняется быстро, легко и доступна для всех сотрудников вашей школы. Чтобы получить доступ к премиум-ресурсам, вашей школе потребуется премиум-подписка Maths Hub. Кроме того, доступ ко всем ресурсам премиум-класса включен бесплатно для школ, подписавшихся на наше онлайн-обучение по математике.
Рабочие листы с простыми числами
- Готовые уроки 5-го класса Умножение и деление (осенний блок 4) Слайды и рабочие листы
- Готовые уроки 6-го класса 4 Операции (осенний блок 2) Слайды и рабочие листы
- Год Рабочий лист 5 рабочих примеров: умножение и деление 1
- Рабочий лист 6 рабочих примеров: четыре операции
Видео с простыми числами
- Как учить простые и составные числа
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Содержание этой статьи изначально было написано учителем начальных классов Софи Бартлетт, а затем было отредактировано и адаптировано для школ США учителем математики начальных классов Кэти Китон.
Объяснение простых и составных чисел
Очень важно понимать разницу между простыми и составными числами в математике. В то время как составных числа — это числа с более чем двумя делителями. Они просто противоположны простым числам. Простые числа — это те, которые имеют только два делителя, то есть 1 и само число. Простое число всегда натуральное число. Все натуральные числа, не являющиеся простыми, попадают в категорию составных чисел. Итак, составные числа делятся более чем на два числа. В этой статье мы узнаем следующее:
Все натуральные числа, не являющиеся простыми, попадают в категорию составных чисел. Итак, составные числа делятся более чем на два числа. В этой статье мы узнаем следующее:
- Что такое простые и составные числа?
- Разница между простыми и составными числами
- Свойства простых и составных чисел
- Как определить простые и составные числа
- Факты о простых и составных числах
- Список составных чисел
- Таблица простых и составных чисел
Что такое простые числа?
Простое число — это положительное целое число. У него ровно два делителя: 1 и само число. Итак, если n — простое число, его делители будут равны 1 и самому n. Мы также можем определить простое число как число, которое является целым положительным числом и не является произведением любых двух других положительных целых чисел, кроме самого числа и 1. 9(82 589 933) — 1 — самое большое простое число за последнее время. Математики все еще находят больше.
Простые числа, разность которых равна двум, являются простыми числами-близнецами. Например, 3 и 5, 5 и 7, 11 и 13 — это наборы простых чисел-близнецов. Другими словами, это два последовательных простых числа, между которыми находится только одно число.
Взаимно простые числа — это два числа, у которых есть только 1 в качестве общего делителя. Например, 2 и 3, 4 и 5, 3 и 7, 4 и 9.являются взаимно простыми числами.
Свойства простых чисел
Ниже приведены некоторые свойства простых чисел:
- Каждое простое число больше 1 делится хотя бы на одно простое число.
- Каждое положительное целое число, четное и превышающее 2, можно представить в виде суммы двух простых чисел.
- 2 — единственное четное простое число.
- Все простые числа нечетные, кроме 2.
- Два простых числа взаимно просты друг с другом.

- Каждое составное число можно разложить на простые множители.
Список простых чисел
Ниже приведен список простых чисел от 1 до 100. Учащиеся могут понять концепцию простых чисел из этого списка и создать список, превышающий 100, для практики.
| Список простых чисел |
| 2, 3, 5, 7, 1, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
Что такое составные числа?
В отличие от простого числа, составное число — это число, имеющее более двух делителей.
Мы можем определить составные числа как числа, которые могут быть получены путем умножения двух наименьших положительных целых чисел и содержат по крайней мере еще один делитель в дополнение к числу «1» и самому себе. Все четные числа больше 2 входят в число многих примеров составных чисел.
Итак, все ли четные числа составные?
Нет, 2 — четное простое число. На самом деле, это единственное четное число, которое является простым. Следовательно, мы не можем сказать, что все четные числа являются составными числами.
На самом деле, это единственное четное число, которое является простым. Следовательно, мы не можем сказать, что все четные числа являются составными числами.
Типы составных чисел
Композитные номера составляют два типа:
- Нечетные составные номера
- Даже составные номера
нечетные составные номера
Все нечетные числа больше 1, которые не являются первичными, являются нечетными композитными числами
. .
Примерами нечетных составных чисел являются 9, 15, 21 и другие.
Четные составные числа
Четные составные числа включают все четные целые числа, не являющиеся простыми числами.
Примерами четных составных чисел являются 4, 6, 8, 10 и другие.
Свойства составных чисел
Составные числа имеют следующие свойства:
- Каждое составное число имеет более двух делителей
- Делители составных чисел без остатка
- Составные числа тоже являются своими факторами.

- 4 — наименьшее составное число
- Каждое составное число имеет как минимум два простых числа в качестве сомножителей.
- Составное число также делится на другие составные числа.
Список составных чисел
Вот список всех составных чисел от 1 до 100. Учащиеся могут понять концепцию составных чисел из этого списка и создать список, превышающий 100, для практики.
| Список составных номеров |
| 4. 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100 |
Как найти составные числа?
Вы должны найти делители числа, чтобы определить, является ли оно составным. Если множителей больше двух, то число составное. Мы можем выполнить тест на делимость, чтобы определить, является ли число простым или составным.
В тесте на делимость мы делим число на общие множители, такие как 2, 3, 5, 7, 11 и 13. Если эти множители не могут полностью разделить число, то это число является простым числом. Например, 22 делится на 2, что означает, что оно имеет делитель 2, отличный от 1 и 22. Следовательно, 22 — составное число.
Как найти простые числа?
Существует два метода, помогающих определить, являются ли данные числа простыми или составными.
Метод 1:
Любое простое число, кроме 2 и 3, можно записать в виде 6n + 1 или 6n – 1, где n — натуральное число.
Например:
6(1) – 1 = 5
6(1) + 1 = 7
Метод 2:
Для определения числа больше 40 как простого числа мы можем использовать по следующей формуле:
n2 + n + 41, где n= 0, 1, 2, ….и выше.
Например:
(0)2 + 0 + 41 = 41
(1)2 + 1 + 41 = 43
(2)2 + 2 + 41 = 47
Разница между простыми и составными числами
Существует множество различий между простыми и составными числами. В следующих таблицах перечислены некоторые ключевые различия между ними.
В следующих таблицах перечислены некоторые ключевые различия между ними.
| Простые числа | Составные числа |
| У них есть 2 множителя. Единица и само число. | У них более двух факторов. |
| Можно записать в виде произведения двух чисел. | Их можно записать как произведение двух или более чисел |
| Пример: Делители 7 равны 1 и 7. | Пример: Делители 6 равны 1, 2, 3 и 6 |
Таблица простых и составных чисел
Ранее математики использовали числовые таблицы для записи всех простых чисел или простых факторизаций. Решето Эратосфена представляло собой список простых чисел. Этот метод обеспечивает карту-карту Эратосфена. На следующей диаграмме простые числа до 100 показаны в цветных прямоугольниках. Все числа, кроме цветных прямоугольников, являются составными числами.
На следующей диаграмме простые числа до 100 показаны в цветных прямоугольниках. Все числа, кроме цветных прямоугольников, являются составными числами.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Что такое простые числа? Определение, схема, примеры и факты
Что такое простые числа?
Простые числа — это числа больше 1. Они имеют только два делителя: 1 и само число. Это означает, что эти числа нельзя разделить ни на какое другое число, кроме 1 и самого числа, не оставляя остатка.
Они имеют только два делителя: 1 и само число. Это означает, что эти числа нельзя разделить ни на какое другое число, кроме 1 и самого числа, не оставляя остатка.
Числа, имеющие более двух делителей, называются 9.0003 составные числа .
Примеры и не примеры простых чисел
Разница между простым и составным числом
Решето Эратосфена
числа.
Выполните указанные шаги, чтобы определить простые числа от 1 до 100.
Шаг 1: Создайте сто графиков.
Шаг 2: Оставьте 1, так как это не простое и не составное число.
Шаг 3: Обведите число 2 и зачеркните все числа, кратные ему, поскольку они не являются простыми.
Шаг 4: Обведите следующее незачеркнутое число, равное 3, и вычеркните все его кратные числа. Не обращайте внимания на ранее зачеркнутые числа, такие как 6, 12, 18 и так далее.
Шаг 5: Продолжайте процесс обведения следующего незачеркнутого числа и вычеркивания его кратных до тех пор, пока все числа в таблице не будут либо обведены, либо зачеркнуты, кроме 1.
Итак, из таблицы видно, что 2, 3 , 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 — простые числа.
Существует 25 простых чисел от 1 до 100.
Термины, относящиеся к простым числам
Взаимопростые числа: Два числа называются взаимно простыми, если они имеют только один общий делитель, то есть 1 , Эти числа не обязательно должны быть простыми числами. Например, 9 и 10 взаимно просты. Давайте проверим.
Обратите внимание, что пары любых двух простых чисел всегда взаимно просты. Это потому, что из их двух множителей общий множитель может быть только 1. Итак, (3, 5), (11, 19) являются некоторыми примерами взаимно простых чисел.
Простые числа-близнецы: Пара простых чисел называется простыми числами-близнецами, если между ними есть только одно составное число. Например, (3, 5), (5, 7), (11, 13), (17, 19) и т. д.
Список простых чисел от 1 до 100
2, 3, 5, 7, 11 , 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Есть 25 простых чисел от 1 до 100.
Список простых чисел от 1 до 200
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199
Всего 46 простых чисел. от 1 до 200.
Список простых чисел от 1 до 1000
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59 , 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317 , 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467 , 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641 , 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811 , 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997. Факты о простых числах
Факты о простых числах
- 2 — наименьшее простое число.
- 2 — единственное четное простое число.
- 2 и 3 — единственные последовательные простые числа.
- За исключением 0 и 1, целое число является либо простым, либо составным числом.
- Все нечетные числа не являются простыми числами. Например, 21, 39 и т. д.
- Ни одно простое число больше 5 не оканчивается на 5.
- Решето Эратосфена — один из первых методов нахождения простых чисел.
- Простые числа встречаются реже по мере увеличения числа.
- Не существует самого большого простого числа. Самое большое известное простое число (по состоянию на сентябрь 2021 г.) — 282 589 933 − 1, число, состоящее из 24 862 048 цифр при записи по основанию 10. К тому времени, когда вы будете это читать, оно может быть еще больше.
Решенные примеры
Пример 1. Классифицируйте данные числа как простые или составные.
13, 48, 49, 23, 74, 80, 71, 59, 45, 47
Solution:
| Prime Numbers | Composite Numbers |
| 13 , 23, 71, 59, 47 | 48, 49, 74, 80, 45 |
Пример 2: Представьте 21 в виде суммы двух нечетных простых чисел.
Решение:
21 = 19 + 2
Пример 3. Какие простые числа находятся между 20 и 30?
Решение:
Простые числа от 20 до 30 — это 23 и 29.
Пример 4. Какое самое большое простое число от 80 до 90?
Решение:
Основные числа от 80 до 90 составляют 83 и 89.
Таким образом, 89 — наибольшее основное число от 80 до 90,
Практические задачи на основных числах
83
61 61
71
81
Правильный ответ: 81
Делители числа 81 — это 1, 3, 9, 27 и 81. Остальные числа имеют только 2 делителя — 1 и самих себя.
23
29
31
37
Правильный ответ: 29
2, 3, 5, 7, 11, 13, 17, 19 и 23 — первые 9 простых чисел, а 1 0 2 9 .
1
2
3
4
Правильный ответ: 3
Простые числа между 40 и 50: 41, 43 и 47.

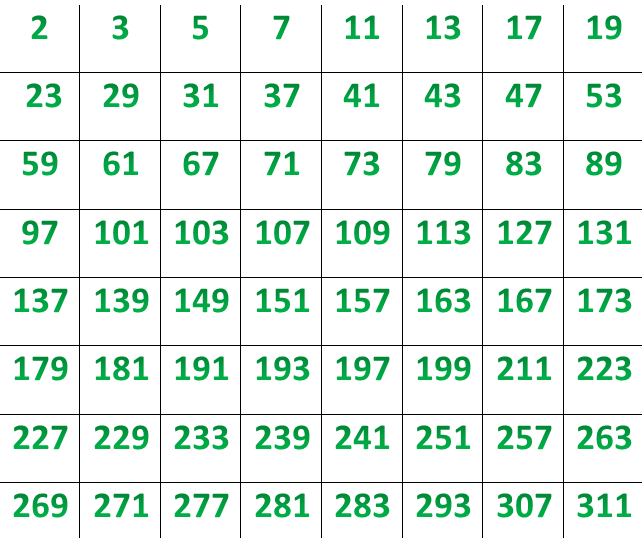 Единица не включена, извините. Некоторые считают, что единица не включена поскольку… она и не может там быть. «Простым числом называются числа имеющие два делителя: единицу и само число.» А число 1 имеет только один делитель, оно не относится ни к простым, ни к составным числам. (толковое замечание от Ольги 21.09.12) Мы, тем не менее помним, что простые числа вводятся иногда и так: «Простым числом называются числа которые делятся нацело на единицу и само себя.» В этом случае единица, очевидно, является простым числом.
Единица не включена, извините. Некоторые считают, что единица не включена поскольку… она и не может там быть. «Простым числом называются числа имеющие два делителя: единицу и само число.» А число 1 имеет только один делитель, оно не относится ни к простым, ни к составным числам. (толковое замечание от Ольги 21.09.12) Мы, тем не менее помним, что простые числа вводятся иногда и так: «Простым числом называются числа которые делятся нацело на единицу и само себя.» В этом случае единица, очевидно, является простым числом.
