Признак параллельности прямых через внутренние односторонние углы. Параллельные прямые, признаки и условия параллельности прямых
Страница 1 из 2
Вопрос 1. Докажите, что две прямые, параллельные третьей, параллельны.
Ответ. Теорема 4.1. Две прямые, параллельные третьей, параллельны.
Доказательство. Пусть прямые a и b параллельны прямой c. Допустим, что a и b не параллельны (рис. 69). Тогда они не пересекаются в некоторой точке C. Значит, через точку C проходят две прямые, параллельные прямой c. Но это невозможно, так как через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной. Теорема доказана.
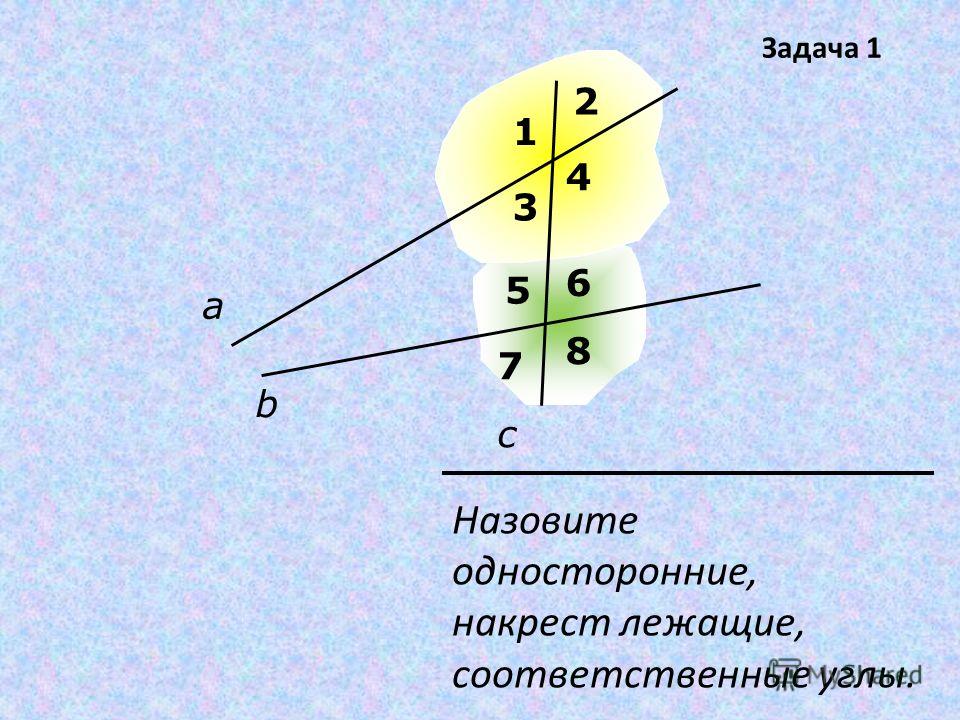
Вопрос 2. Объясните, какие углы называются внутренними односторонними. Какие углы называются внутренними накрест лежащими?
Ответ. Пары углов, которые образуются при пересечении прямых AB и CD секущей AC, имеют специальные названия.
Если точки B и D лежат в одной полуплоскости относительно прямой AC, то углы BAC и DCA называются внутренними односторонними (рис. 71, а).
71, а).
Рис. 71
Вопрос 3. Докажите, что если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны, а сумма внутренних односторонних углов каждой пары равна 180°.
Ответ. Секущая AC образует с прямыми AB и CD две пары внутренних односторонних и две пары внутренних накрест лежащих углов. Внутренние накрест лежащие углы одной пары, например угол 1 и угол 2, являются смежными внутренним накрест лежащим углам другой пары: угол 3 и угол 4 (рис. 72).
Рис. 72
Поэтому если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны.
Пара внутренних накрест лежащих углов, например угол 1 и угол 2, и пара внутренних односторонних углов, например угол 2 и угол 3, имеют один угол общий – угол 2, а два других угла смежные: угол 1 и угол 3.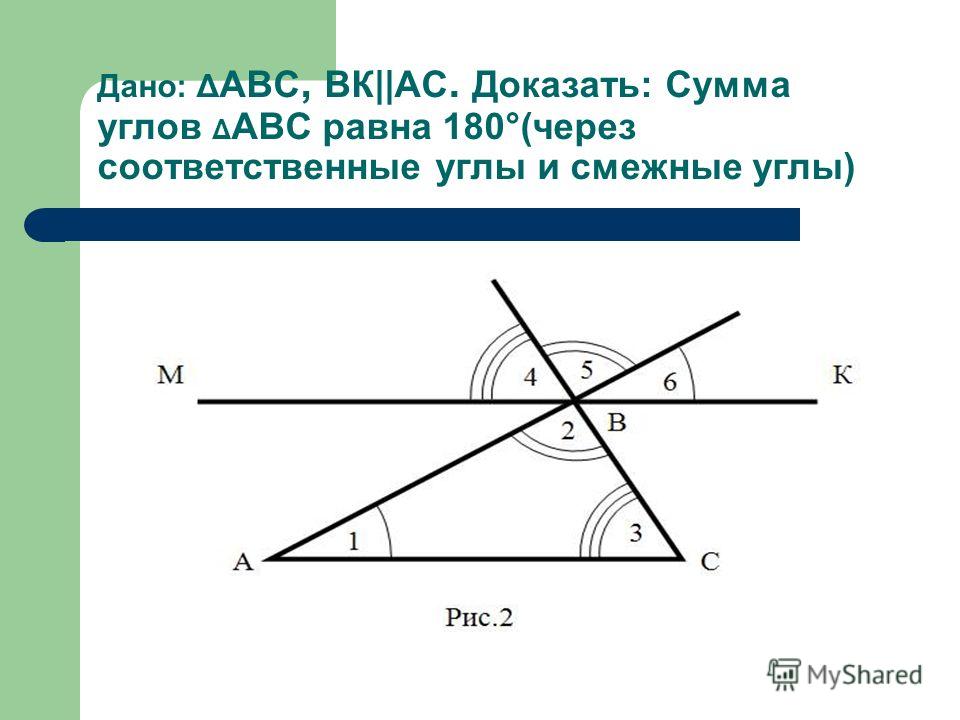
Поэтому если внутренние накрест лежащие углы равны, то сумма внутренних углов равна 180°. И обратно: если сумма внутренних накрест лежащих углов равна 180°, то внутренние накрест лежащие углы равны. Что и требовалось доказать.
Вопрос 4. Докажите признак параллельности прямых.
Ответ. Теорема 4.2 (признак параллельности прямых). Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Доказательство. Пусть прямые a и b образуют с секущей AB равные внутренние накрест лежащие углы (рис. 73, а). Допустим, прямые a и b не параллельны, а значит, пересекаются в некоторой точке C (рис. 73, б).
Рис. 73
Секущая AB разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник BAC 1 , равный треугольнику ABC, с вершиной C 1 в другой полуплоскости. По условию внутренние накрест лежащие углы при параллельных a, b и секущей AB равны. Так как соответствующие углы треугольников ABC и BAC 1 с вершинами A и B равны, то они совпадают с внутренними накрест лежащими углами.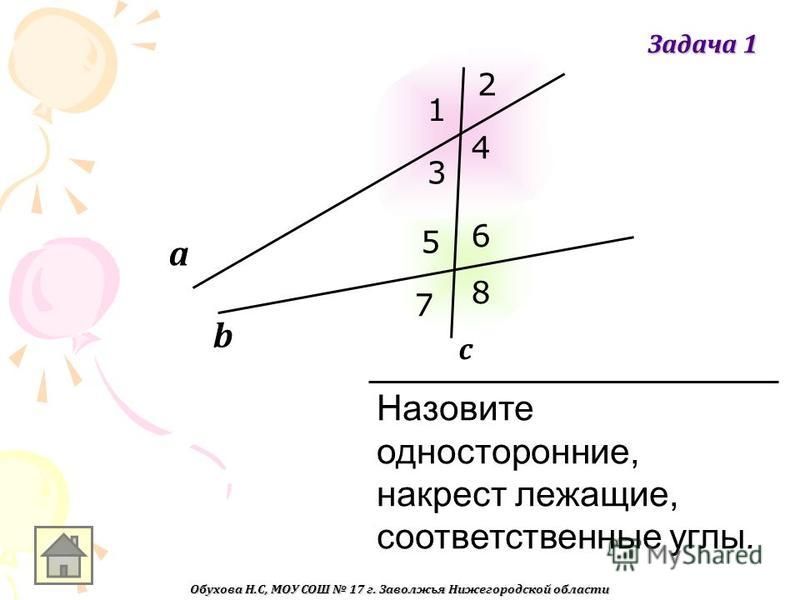
Если у прямых a и b и секущей AB сумма внутренних односторонних углов равна 180°, то, как мы знаем, внутренние накрест лежащие углы равны. Значит, по доказанному выше, прямые a и b параллельны. Теорема доказана.
Вопрос 5. Объясните, какие углы называются соответственными. Докажите, что если внутренние накрест лежащие углы равны, то соответственные углы тоже равны, и наоборот.
Ответ. Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей. Что и требовалось объяснить.
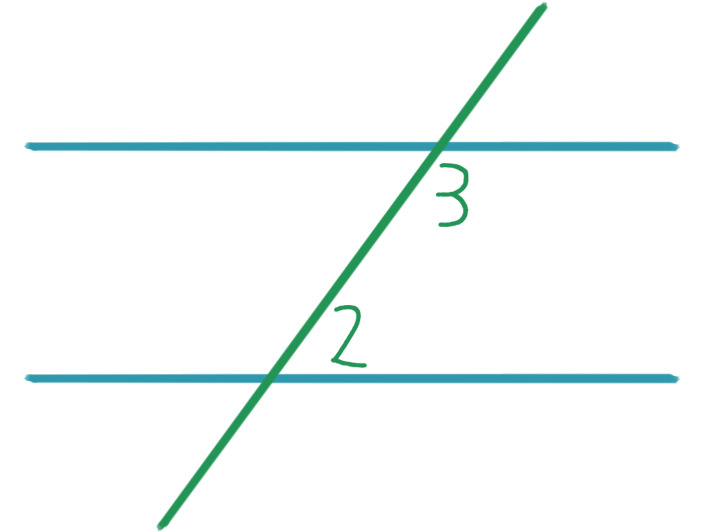 Углы 1 и 2 равны как внутренние накрест лежащие. А углы 2 и 3 равны как вертикальные. Получаем: \(\angle\)1 = \(\angle\)2 и \(\angle\)2 = \(\angle\)3. По свойству транзитивности знака равенства следует, что \(\angle\)1 = \(\angle\)3. Аналогично доказывается и обратное утверждение.
Углы 1 и 2 равны как внутренние накрест лежащие. А углы 2 и 3 равны как вертикальные. Получаем: \(\angle\)1 = \(\angle\)2 и \(\angle\)2 = \(\angle\)3. По свойству транзитивности знака равенства следует, что \(\angle\)1 = \(\angle\)3. Аналогично доказывается и обратное утверждение.Отсюда получается признак параллельности прямых по соответственным углам. Именно: прямые параллельны, если соответственные углы равны. Что и требовалось доказать.
Вопрос 6. Докажите, что через точку, не лежащую на данной прямой, можно провести параллельную ей прямую. Сколько прямых, параллельных данной, можно провести через точку, не лежащую на этой прямой?
Ответ. Задача (8). Даны прямая AB и точка C, не лежащая на этой прямой. Докажите, что через точку C можно провести прямую, параллельную прямой AB.
Решение. Прямая AC разбивает плоскость на две полуплоскости (рис. 75). Точка B лежит в одной из них. Отложим от полупрямой CA в другую полуплоскость угол ACD, равный углу CAB.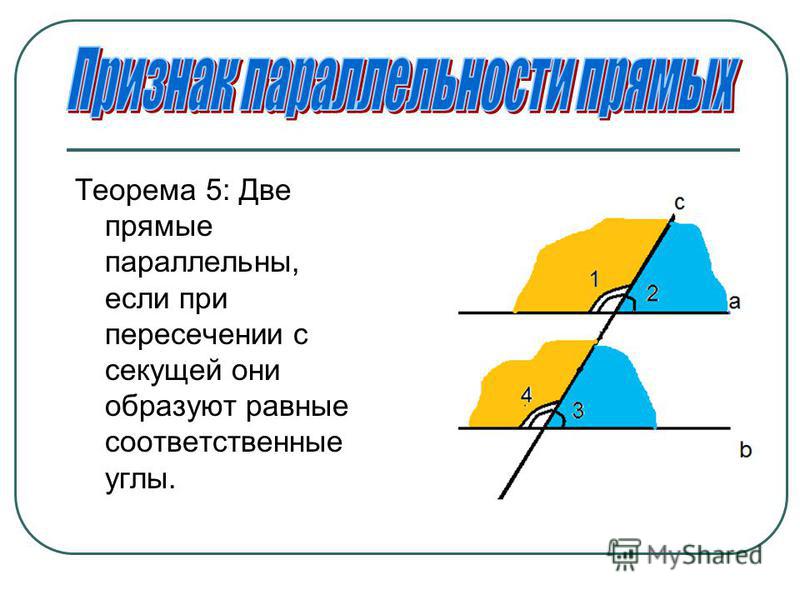 Тогда прямые AB и CD будут параллельны. В самом деле, для этих прямых и секущей AC углы BAC и DCA внутренние накрест лежащие. А так как они равны, то прямые AB и CD параллельны. Что и требовалось доказать.
Тогда прямые AB и CD будут параллельны. В самом деле, для этих прямых и секущей AC углы BAC и DCA внутренние накрест лежащие. А так как они равны, то прямые AB и CD параллельны. Что и требовалось доказать.
Сопоставляя утверждение задачи 8 и аксиомы IX (основного свойства параллельных прямых), приходим к важному выводу: через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.
Вопрос 7. Докажите, что если две прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
Ответ. Теорема 4.3 (обратная теореме 4.2). Если две параллельные прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
Доказательство. Пусть a и b – параллельные прямые и c – прямая, пересекающая их в точках A и B. Проведём через точку A прямую a 1 так, чтобы внутренние накрест лежащие углы, образованные секущей c с прямыми a 1 и b, были равны (рис.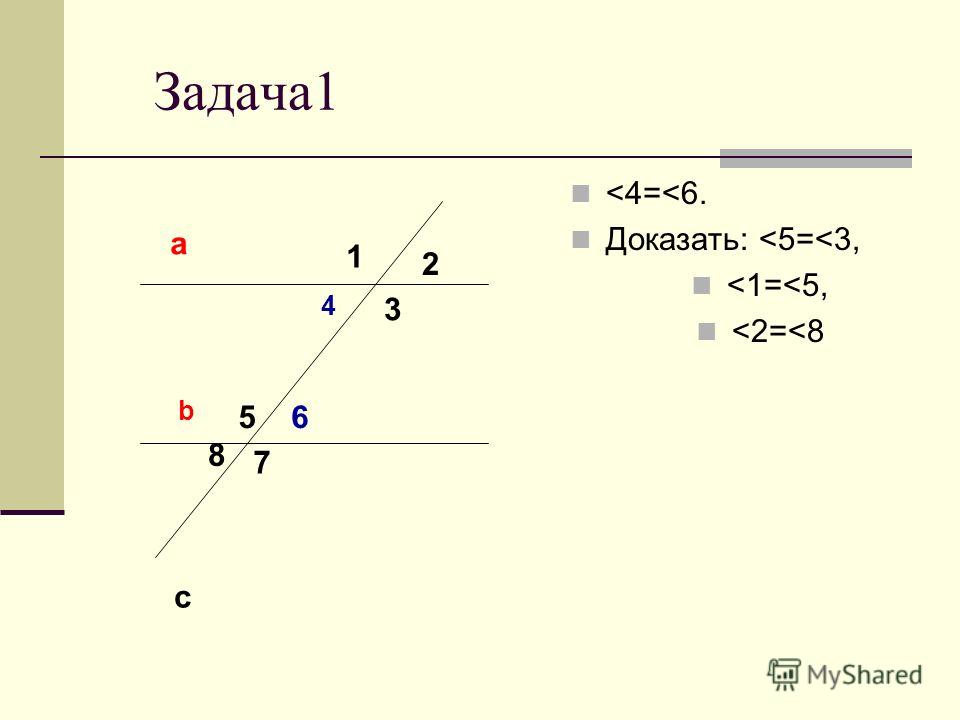 76).
76).
По признаку параллельности прямых прямые a 1 и b параллельны. А так как через точку A проходит только одна прямая, параллельная прямой b, то прямая a совпадает с прямой a 1 .
Значит, внутренние накрест лежащие углы, образованные секущей с
Вопрос 8. Докажите, что две прямые, перпендикулярные третьей, параллельны. Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Ответ. Из теоремы 4.2 следует, что две прямые, перпендикулярные третьей, параллельны.
Предположим, что две какие-либо прямые перпендикулярны третьей прямой. Значит, эти прямые пересекаются с третьей прямой под углом, равным 90°.
Из свойства углов, образованных при пересечении параллельных прямых секущей, следует, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Вопрос 9. Докажите, что сумма углов треугольника равна 180°.
Ответ.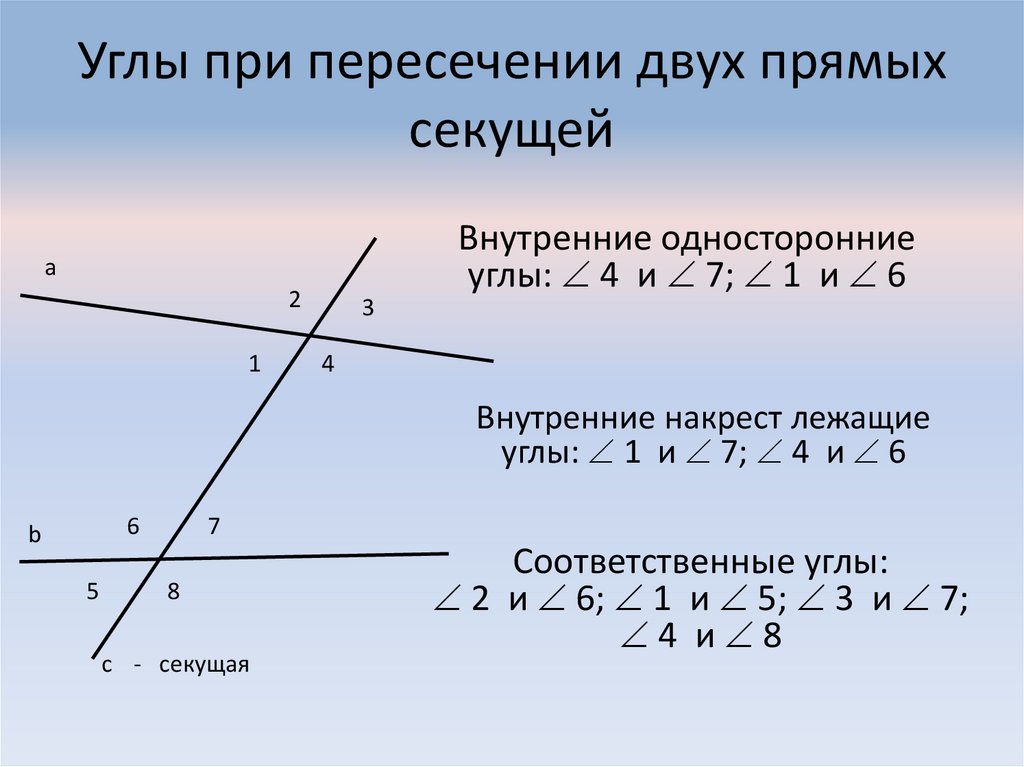 Теорема 4.4. Сумма углов треугольника равна 180°.
Теорема 4.4. Сумма углов треугольника равна 180°.
Доказательство. Пусть ABC – данный треугольник. Проведём через вершину B прямую, параллельную прямой AC. Отметим на ней точку D так, чтобы точки A и D лежали по по разные стороны от прямой BC (рис. 78).
А сумма всех трёх углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD и секущей AB, то их сумма равна 180°. Теорема доказана.
Вопрос 10. Докажите, что у любого треугольника по крайней мере два угла острые.
Ответ. Действительно, допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть два угла, каждый из которых не меньше 90°. Сумма этих двух углов уже не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°.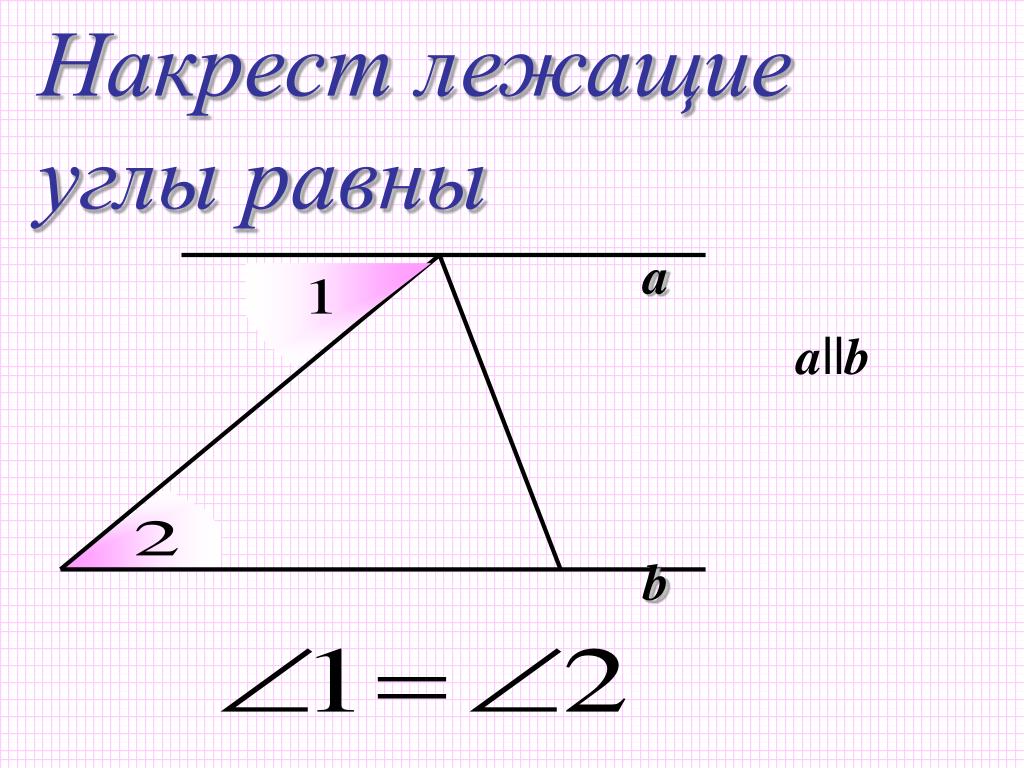
Признаки параллельности двух прямых
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Следствие 1 .
Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.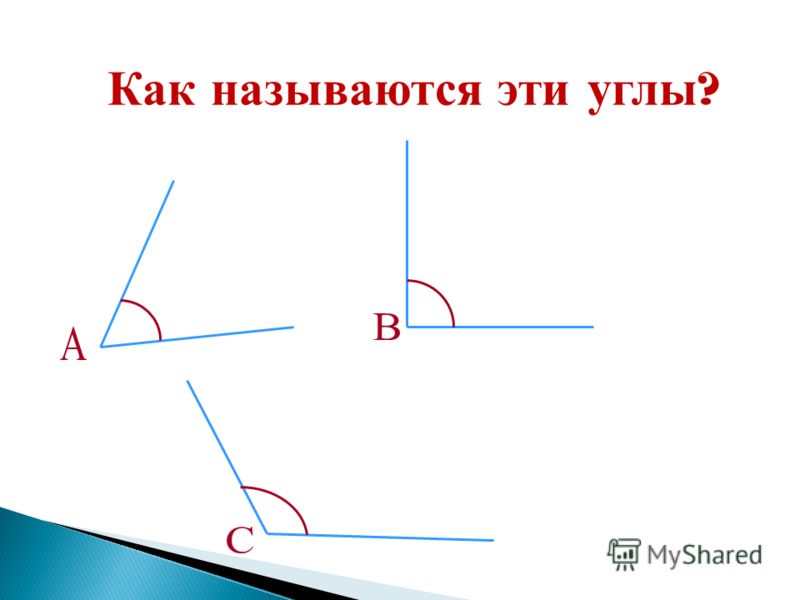 2).
2).Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной .
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
сумма односторонних углов равна 180°.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Они не пересекаются, сколько бы их ни продолжали. Параллельность прямых на письме обозначают так: AB || С E
Возможность существования таких прямых доказывается теоремой.
Теорема.
Через всякую точку, взятую вне данной прямой, можно провести параллельную этой прямой .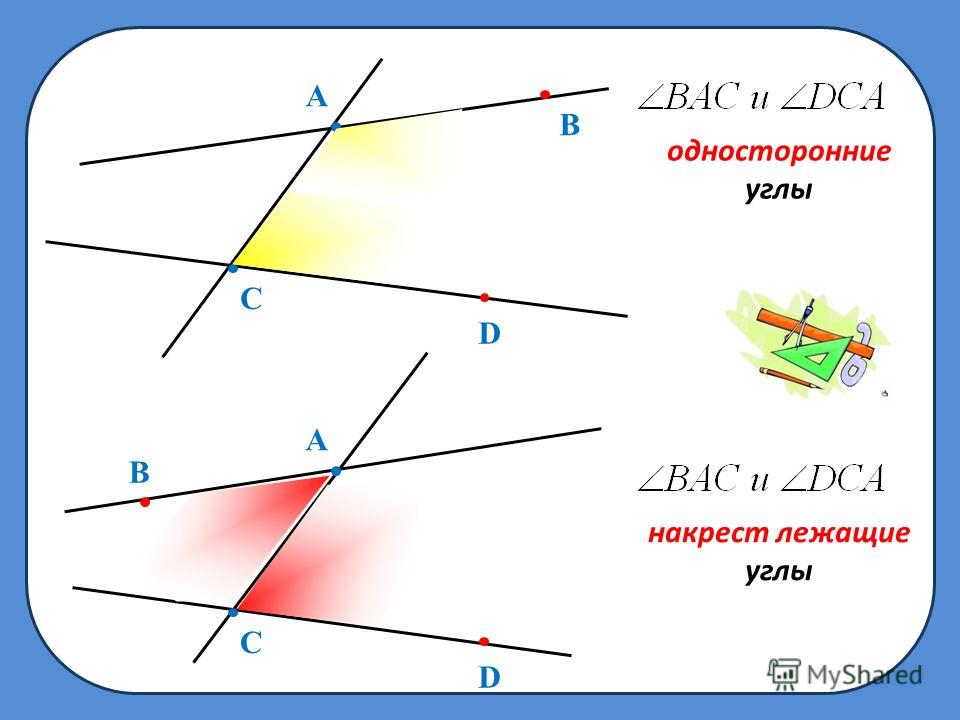 С D , что возможно. Прямая CE параллельна AB .
С D , что возможно. Прямая CE параллельна AB .
Для доказательства допустим противное, т.е., что CE пересекается с AB в некоторой точке M . Тогда из точки M к прямой С D мы имели бы два различных перпендикуляра M D и MС , что невозможно. Значит, CE не может пересечься с AB , т.е. С E параллельна AB .
Следствие.
Два перпендикуляра (С E и DB ) к одной прямой (С D ) параллельны.
Аксиома параллельных линий.
Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой.
Так, если прямая С D , проведенная через точку С параллельна прямой AB , то всякая другая прямая С E , проведенная через ту же точку С , не может быть параллельна AB , т.е. она при продолжении пересечется с AB .
Доказательство этой не вполне очевидной истины оказывается невозможным. Ее принимают без доказательства, как необходимое допущение (postulatum).
Следствия.
1. Если прямая (С E ) пересекается с одной из параллельных (СВ ), то она пересекается и с другой (AB ), потому что в противном случае через одну и ту же точку С проходили бы две различные прямые, параллельные AB , что невозможно.
2. Если каждая из двух прямых (A и B ) параллельны одной и той же третьей прямой (С ) , то они параллельны между собой.
Действительно, если предположить, что A и B пересекаются в некоторой точке M , то тогда через эту точку проходили бы две различные прямые, параллельные С , что невозможно.
Теорема .
Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой параллельной . С D .
С D .
Перпендикуляр E F , пересекаясь с AB , непременно пересечет и С D . Пусть точка пересечения будет H .
Предположим теперь, что С D не перпендикулярна к EH . Тогда какая-нибудь другая прямая, например HK , будет перпендикулярна к EH и, следовательно через одну и ту же точку H будут проходить две прямые параллельные AB : одна С D , по условию, а другая HK по доказанному раньше. Так как это невозможно, то нельзя допустить, что СВ была не перпендикулярна к EH .
Класс: 2
Цель урока:
- сформировать понятие о параллельности 2-х прямых, рассмотреть первый признак параллельности прямых;
- выработать умение применять признак при решении задач.
Задачи:
- Образовательные: повторение и закрепление изученного материала,
формирование понятия о параллельности 2-х прямых, доказательство 1-го
признака параллельности 2-х прямых.

- Воспитательные: воспитывать умение аккуратно вести записи в тетради и соблюдать правила построения чертежей.
- Развивающие задачи: развитие логического мышления, памяти, внимания.
Оборудование урока:
- мультимедийный проектор;
- экран, презентации;
- чертёжные инструменты.
Ход урока
I. Организационный момент.
Приветствие, проверка готовности к уроку.
II. Подготовка к активной УПД.
Этап 1.
На первом уроке геометрии мы рассматривали взаимное расположение 2-х прямых на плоскости.
Вопрос. Сколько общих точек могут иметь две прямые?
Ответ. Две прямые могут иметь либо одну общую точку, либо не имеют не
одной общей точки.
Вопрос. Как будут расположены относительно друг друга 2-е прямые, если
они имеют одну общую точку?
Ответ. Если прямые имеют одну общую точку, то они пересекаются
Вопрос. Как расположены 2-е прямые относительно друг друга, если они
не имеют общих точек?
Ответ. То в этом случае данные прямые не пересекаются.
То в этом случае данные прямые не пересекаются.
Этап 2.
На прошлом уроке Вы получили задание сделать презентацию, где мы встречаемся с непересекающимися прямыми в нашей жизни и в природе. Сейчас мы посмотрим эти презентации и выберем из них лучшие. (В жюри вошли учащиеся, которым в силу низкого интеллекта сложно создать свои презентации.)
Просмотр презентаций, выполненных учащимися: «Параллельность прямых в природе и жизни», и выбор из них лучших.
III. Активная УПД (объяснение нового материала).
Этап 1.
Рисунок 1
Определение. Две прямые на плоскости, которые не пересекаются, называются параллельными.
На данной таблице изображены различные случаи расположения 2-х параллельных прямых на плоскости.
Рассмотрим, какие отрезки будут параллельными.
Рисунок 2
1) Если прямая a параллельна b, то и отрезки AB и CD параллельны.
2) Отрезок может быть параллелен прямой. Так отрезок MN параллелен прямой a.
Рисунок 3
3) Отрезок AB параллелен лучу h. Луч h параллелен лучу k.
4) Если прямая a перпендикулярна прямой c, и прямая b перпендикулярна прямой c, то прямые a и b параллельны.
Этап 2.
Углы, образованные двумя параллельными прямыми и секущей.
Рисунок 4
Две параллельные прямые пересекаются третьей прямой в двух точках. При этом образуются восемь углов, обозначенных на рисунке числами.
Некоторые пары этих углов имеют специальные названия (см. рисунок 4).
Существует три признака, параллельности двух прямых , связанных с этими углами. На этом уроке мы рассмотрим первый признак .
Этап 3.
Повторим материал, необходимый для доказательства этого признака.
Рисунок 5
Вопрос. Как называются углы, изображённые на рисунке 5?
Ответ. Углы AOC и COB называются смежными.
Вопрос. Какие углы называются смежными? Дайте определение.
Ответ. Два угла называются смежными, если у них одна сторона является
общей, а две другие являются продолжениями друг друга.
Два угла называются смежными, если у них одна сторона является
общей, а две другие являются продолжениями друг друга.
Вопрос. Каким свойством обладают смежные углы?
Ответ. Смежные углы в сумме дают 180 градусов.
AOC + COB
= 180°
Вопрос. Как называются углы 1 и 2?
Ответ. Углы 1 и 2 называются вертикальными.
Вопрос. Какими свойствами обладают вертикальные углы?
Ответ. Вертикальные углы равны между собой.
Этап 4.
Доказательство первого признака параллельности.
Теорема. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Рисунок 6
Дано: а и b – прямые
AB – секущая
1 =
2
Доказать: a//b.
1-ый случай.
Рисунок 7
Если 1 и 2 прямые, то a перпендикулярен AB, и b перпендикулярен AB, то а//b.
2-ой случай.
Рисунок 8
Рассмотрим случай, когда
1 и
2 не
прямые Разделим отрезок AB пополам точкой O.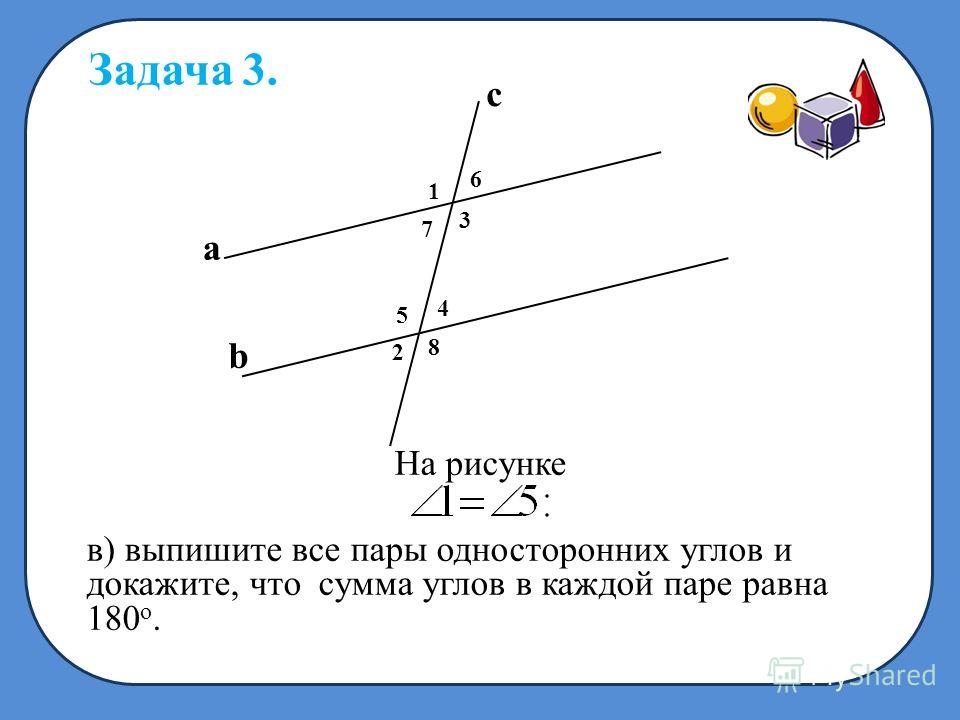
Вопрос. Какими будут отрезки AO и OB по длине?
Ответ. Отрезки AO и OB равны по длине.
1) Из точки O проведём перпендикуляр к прямой а, ОН перпендикулярен a.
Вопрос. Каким будет угол 3?
Ответ. Угол 3 будет прямым.
2) От точки А на прямой b отложим циркулем отрезок АН 1 = ВН.
3) Проведём отрезок ОН 1 .
Вопрос. Какие треугольники образовались в результате доказательства?
Ответ. Треугольник ОНВ и треугольник ОН 1 А.
Докажем, что они равны.
Вопрос. Какие углы равны по условию теоремы?
Ответ. Угол 1 равен углу 2.
Вопрос. Какие стороны равны по построению.
Ответ. АО = ОВ и АН 1 = ВН
Вопрос. По какому признаку равны треугольники?
Ответ. Треугольники равны по двум сторонам и углу между ними (первый признак
равенства треугольников).
Вопрос. Каким свойством обладают равные треугольники?
Ответ. В равных треугольниках против равных сторон лежат равные углы.
Вопрос. Какие углы будут равны?
Ответ. 5 =
6,
3 =
4.
Вопрос. Как называются
5 и
6?
Ответ. Эти углы называются вертикальными.
Из этого следует, что точки: Н 1 , О, Н лежат на одной прямой.
Т.к.
3 – прямой, а
3 =
4, то
4 – прямой.
Вопрос. Как расположены прямые а и b по отношению к прямой НН 1 ,
если углы 3 и 4 прямые?
Ответ. Прямые а и b перпендикулярны HH 1 .
Вопрос. Что мы можем сказать о двух перпендикулярах к одной прямой?
Ответ. Два перпендикуляра одной прямой параллельны.
Итак, а//b. Теорема доказана.
Сейчас я повторю все доказательство сначала, а Вы внимательно меня послушаете постараетесь все понять запомнить.
IV. Закрепление нового материала.
Работа по группам с разным уровнем развития интеллекта, с последующей проверкой на экране и на доске. У доски работают 3 ученика (по одному из каждой группы).
№1 (для учащихся со сниженным уровнем интеллектуального развития).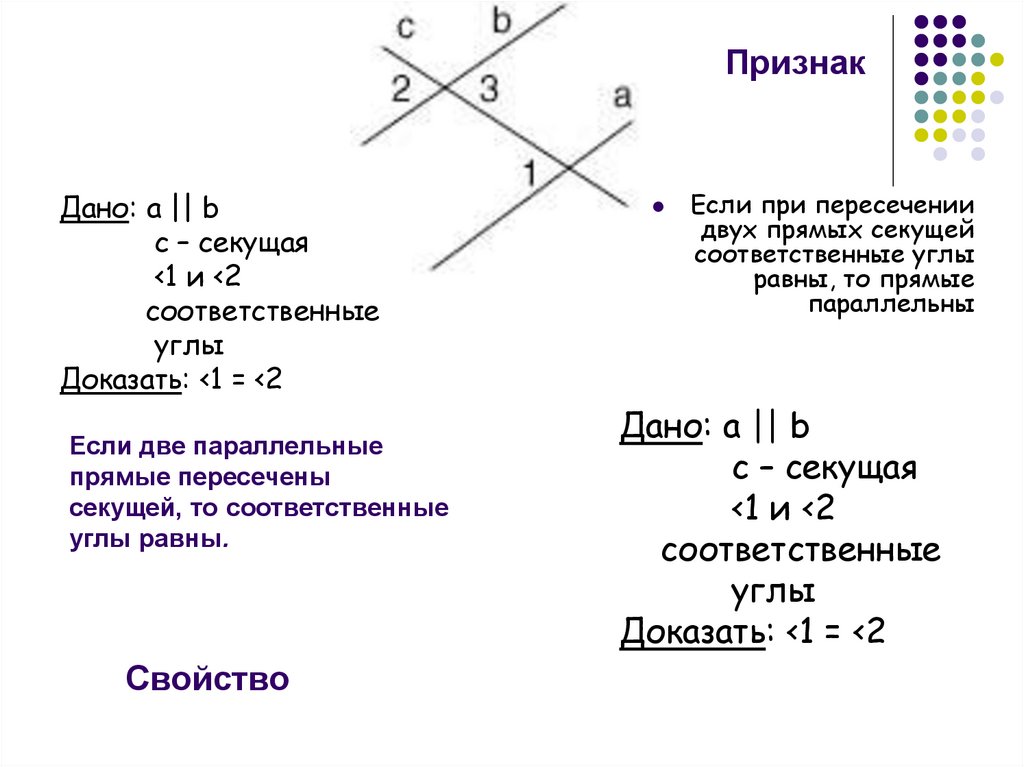
Дано: а и b прямые
с – секущая
1 = 37°
7 = 143°
Доказать: а//b.
Решение.
7 =
6
(вертикальные)
6 = 143°
1 +
4 = 180° (смежные)
4 =180°
– 37° = 143°
4 =
6 = 143°,
а они накрест лежащие
а//b 5 = 48°,
3 и
5 –
накрест лежащие углы, они равны
a//b.
Рисунок 11
V. Итог урока.
Итог урока проводится с использованием рисунков 1-8.
Производится оценка деятельности учащихся на уроке (каждый ученик получает соответствующий смайлик).
Домашнее задание: учить – стр. 52-53; решить №186 (б, в).
Параллельность – очень полезное свойство в геометрии. В реальной жизни параллельные стороны позволяют создавать красивые, симметричные вещи, приятные любому глазу, поэтому геометрия всегда нуждалась в способах эту параллельность проверить. О признаках параллельных прямых мы и поговорим в этой статье.
Определение для параллельности
Выделим определения, которые необходимо знать для доказательства признаков параллельности двух прямых.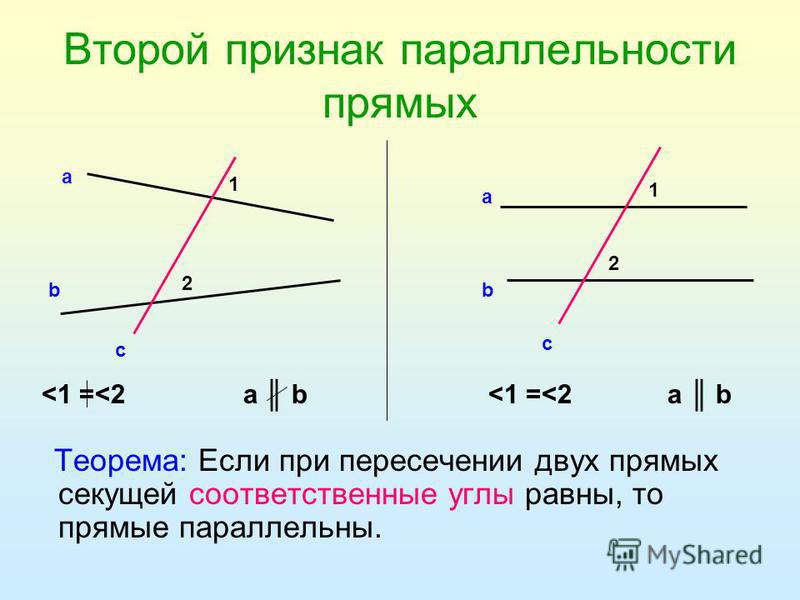
Прямые называют параллельными, если они не имеют точек пересечения. Кроме того, в решениях обычно параллельные прямые идут в связке с секущей линией.
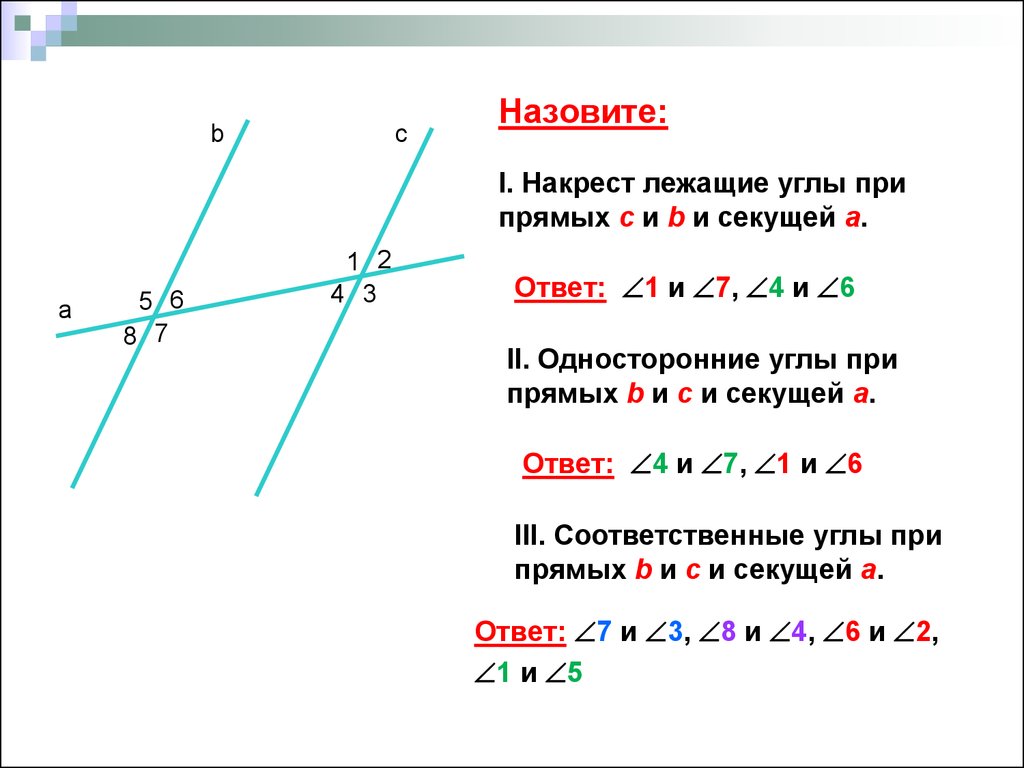
Секущей прямой называется прямая, которая пересекает обе параллельные прямые. В этом случае образуются накрест лежащие, соответственные и односторонние углы. Накрест лежащими будут пары углов 1 и 4; 2 и 3; 8 и 6; 7 и 5. Соответственными будут 7 и 2; 1 и 6; 8 и 4; 3 и 5.
Односторонними 1 и 2; 7 и 6; 8 и 5; 3 и 4.
При правильном оформлении пишется: «Накрест лежащие углы при двум параллельных прямых а и b и секущей с», потому что для двух параллельных прямых может существовать бесконечное множество секущих, поэтому необходимо указывать, какую именно секущую, вы имеете в виду.
Также для доказательства понадобится теорема о внешнем угле треугольника, которая гласит, что внешний угол треугольника равен сумме двух углов треугольника несмежных с ним.
Признаки
Все признаки параллельных прямых завязаны на знание свойств углов и теорему о внешнем угле треугольника.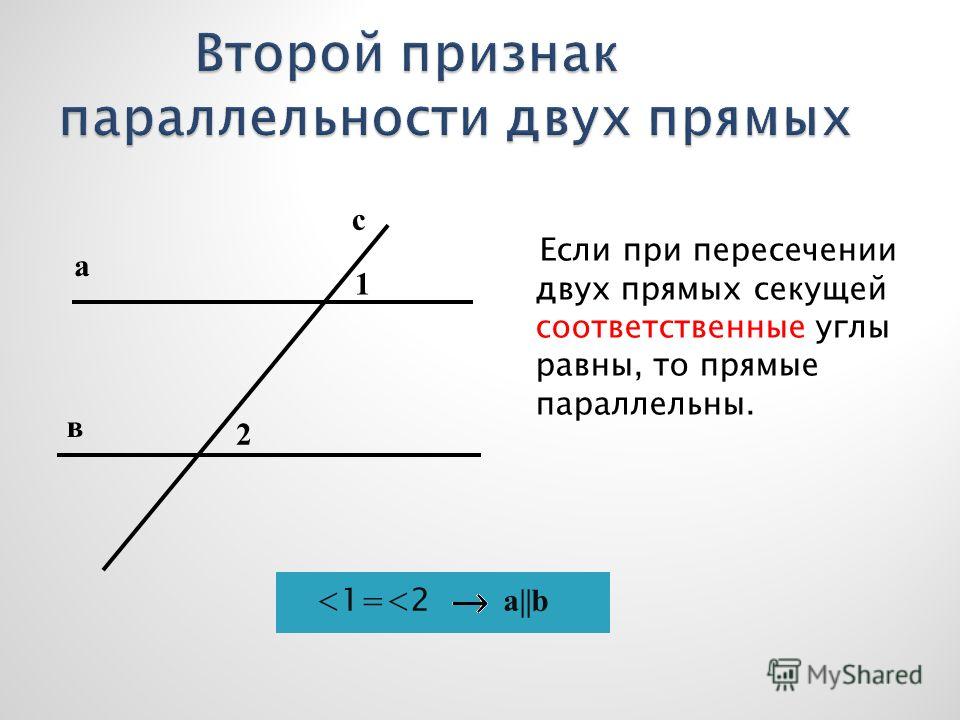
Признак 1
Две прямые параллельны, если накрест лежащие углы равны.
Рассмотрим две прямые а и b с секущей с. Накрест лежащие углы 1 и 4 равны. Предположим, что прямые не параллельны. Значит прямые пересекаются и должна быть точка пересечения М. Тогда образуется треугольник АВМ с внешним углом 1. Внешний угол должен быть равен сумме углов 4 и АВМ как несмежных с ним по теореме о внешнем угле в треугольнике. Но тогда получится, что угол 1 больше угла 4, а это противоречит условию задачи, значит, точки М не существует, прямые не пересекаются, то есть параллельны.
Рис. 1. Рисунок к доказательству.
Признак 2
Две прямые параллельны, если соответственные углы при секущей равны.
Рассмотрим две прямые а и b с секущей с. Соответственные углы 7 и 2 равны. Обратим внимание на угол 3. Он является вертикальным для угла 7. Значит, углы 7 и 3 равны. Значит, углы 3 и 2 также равны, так как
Рис. 2. Рисунок к доказательству.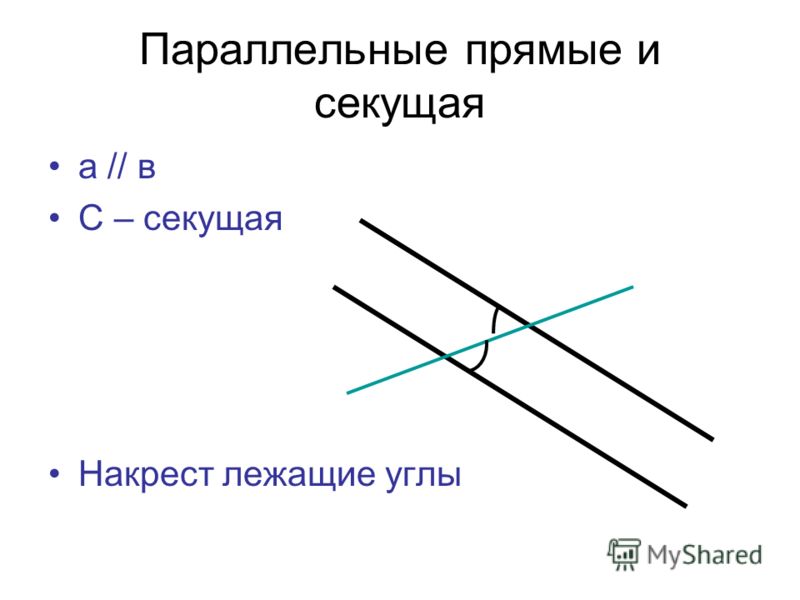
Признак 3
Две прямые параллельны, если сумма односторонних углов равна 180 градусам.
Рис. 3. Рисунок к доказательству.
Рассмотрим две прямые а и b с секущей с. Сумма односторонних углов 1 и 2 равна 180 градусов. Обратим внимание на углы 1 и 7. Они являются смежными. То есть:
$$
$$
Вычтем из первого выражения второе:
$$(
$$(
$$
$$
$
Что мы узнали?
Мы в подробностях разобрали, какие углы получаются при рассечении параллельных прямых третьей линией, выделили и подробно расписали доказательство трех признаков параллельности прямых.
Тест по теме
Оценка статьи
Средняя оценка: 4.1 . Всего получено оценок: 220.
Если смежные углы. Смежные и вертикальные углы, их свойства
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разнообразные положения (рис. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 54°, то второй угол будет равен:
180° — 54° = l26°.
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.
Таким же образом можно вычислить, чему равны ∠3 и ∠4.
∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;
∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.
Доказательство можно провести следующим образом (рис. 78):
78):
∠a + ∠c = 180°;
∠b + ∠c = 180°;
(так как сумма смежных углов равна 180°).
∠a + ∠c = ∠b + ∠c
(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b , т. е. вертикальные углы равны между собой.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
∠1 + ∠2 + ∠3 + ∠4 = 180°.
На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
Другие материалы
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.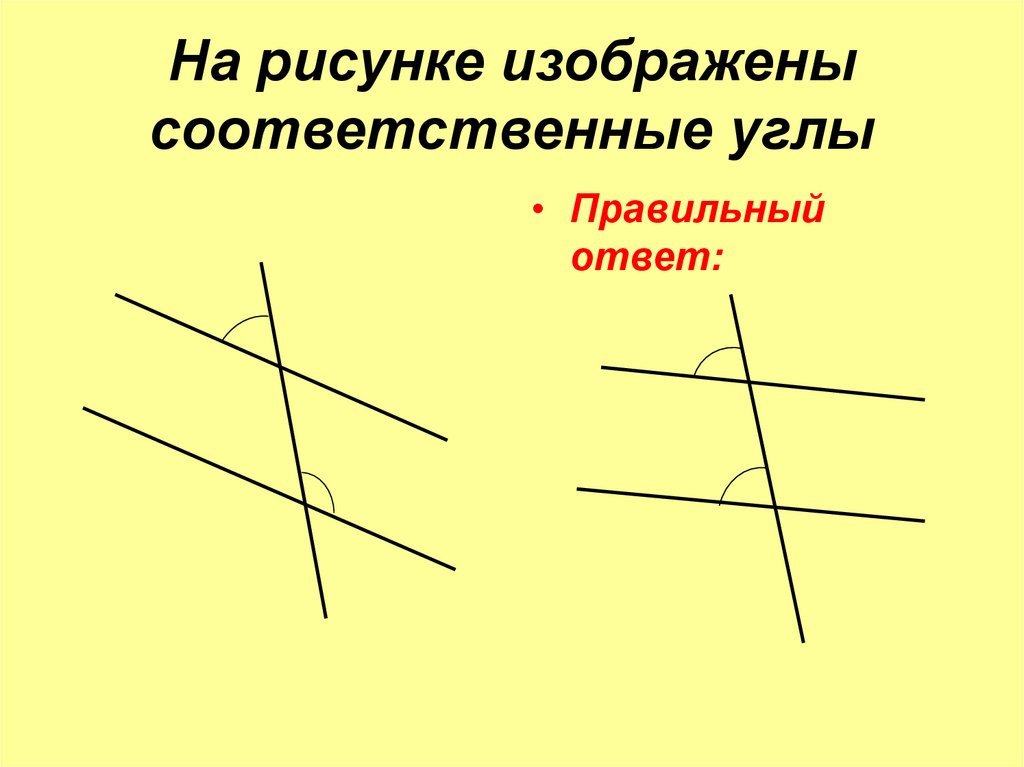
Сумма смежных углов равна 180°
Вертикальные углы — это два угла, у которых стороны одного угла являются продолжение сторон другого.
Вертикальные углы равны.
2. Признаки равенства треугольников:
I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
3. Признаки параллельности двух прямых: односторонние углы, накрест лежащие и соответственные:
Две прямые на плоскости называются параллельными , если они не пересекаются.
Накрест лежащие углы: 3 и 5, 4 и 6;
Односторонние углы: 4 и 5, 3 и 6; рис. Стр55
Стр55
Соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
Теорема : Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Теорема : если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
Теорема : если две параллельные прямые пересечены секущей, то соответственные углы равны
Теорема : если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°
4. Сумма углов треугольника:
Сумма углов треугольника равна 180°
5. Свойства равнобедренного треугольника:
Теорема: В равнобедренном треугольнике углы при основании равны.
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, являетсямедианой и высотой (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90°)
Признак: Если два угла треугольника равны, то треугольник равнобедренный.
Сумма углов четырёхугольника равна 2 π = 360°.
Четырёхугольник можно вписать в окружность тогда и только тогда, сумма противоположных углов равна 180°
10. Признаки подобия треугольников:
I признак : если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
III признак : если три стороны одного треугольника порциональны трем сторонам другого, то такие треугольники подобны
11. Формулы:
· Теорема Пифагора: a 2 +b 2 =c 2
· Теорема sin:
· Теорема cos:
· 3 формулы площади треугольника:
· Площадь прямоугольного треугольника: S= S=
· Площадь равностороннего треугольника:
· Площадь параллелограмма: S = ah
· Площадь квадрата: S = a2
· Площадь трапеции:
· Площадь ромба:
· Площадь прямоугольника: S=ab
· Равносторонний треугольник.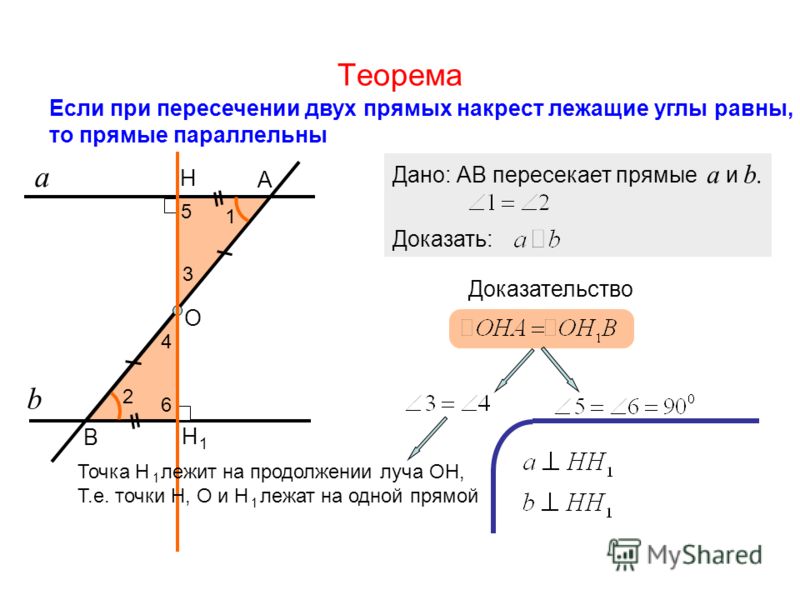 Высота: h=
Высота: h=
· Тригонометрическая единица: sin 2 a+cos 2 a=1
· Средняя линия треугольника: S=
· Средняя линия трапеции : МК=
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
На данном уроке мы рассмотрим и уясним для себя понятие смежные углы. Рассмотрим теорему, которая их касается. Введем понятие «вертикальные углы». Рассмотрим опорные факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце занятия рассмотрим несколько задач, посвященных этой теме.
Начнем наш урок с понятия «смежные углы». На рисунке 1 изображен развернутый угол ∠АОС и луч ОВ, который делит данный угол на 2 угла.
Рис. 1. Угол ∠АОС
Рассмотрим углы ∠АОВ и ∠ВОС. Вполне очевидно, что они имеют общую сторону ВО, а стороны АО и ОС являются противолежащими. Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.
Определение: Если два угла имеют общую сторону, а две другие стороны являются дополняющими лучами, то данные углы называются смежными .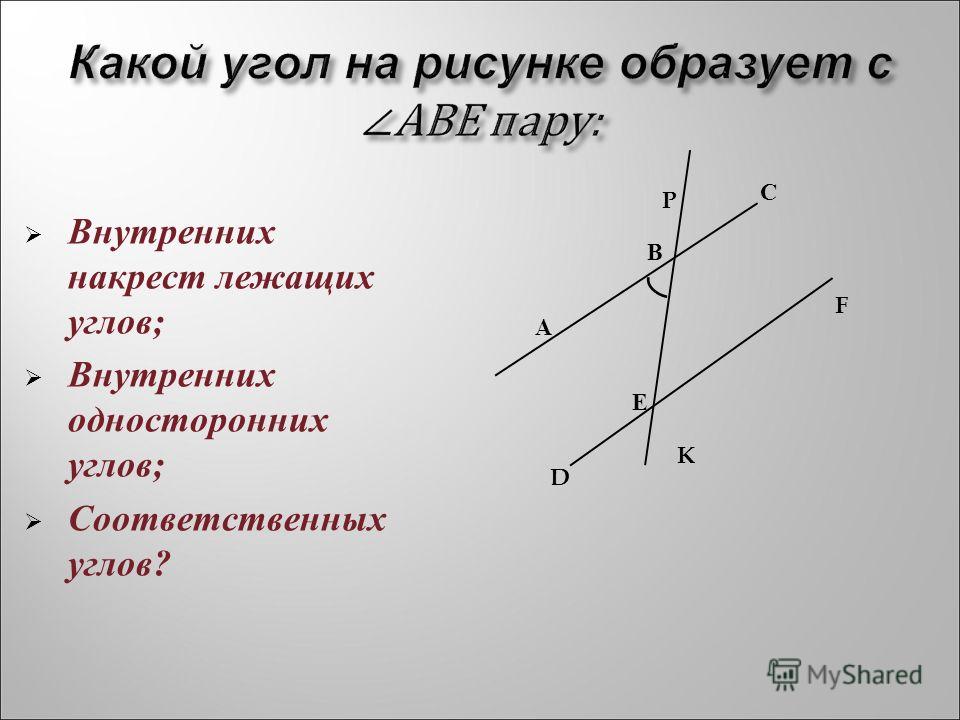
Теорема 1: Сумма смежных углов — 180 о.
Рис. 2. Чертеж к теореме 1
∠МОL + ∠LON = 180 o . Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму — 180 о.
Рассмотрим пересечение двух прямых. На рисунке изображено пересечение двух прямых в точке О.
Рис. 3. Вертикальные углы ∠ВОА и ∠СОD
Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Именно поэтому на рисунке изображено две пары вертикальных углов: ∠АОВ и ∠СОD, а также ∠AOD и ∠ВОС.
Теорема 2: Вертикальные углы равны.
Используем рисунок 3. Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС — ∠ВОС = 180 о — β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD — ∠BОС = 180 о — β.
Из этих соображений мы делаем вывод, что ∠АОВ = ∠СОD = α. Аналогично, ∠AOD = ∠ВОС = β.
Следствие 1: Угол между биссектрисами смежных углов равен 90 о.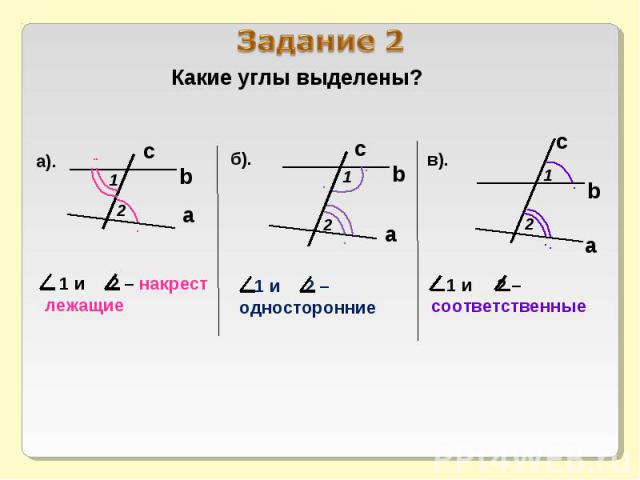
Рис. 4. Чертеж к следствию 1
Поскольку ОL — биссектриса угла ∠ВОА, то угол ∠LOB = , аналогично ∠ВОК = . ∠LOK = ∠LOB + ∠BOK = + = . Сумма углов α + β равна 180 о, поскольку данные углы — смежные.
Следствие 2: Угол между биссектрисами вертикальных углов равен 180 о.
Рис. 5. Чертеж к следствию 2
KO — биссектриса ∠AOB, LO — биссектриса ∠COD. Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Сумма углов α + β равна 180 о, так как данные углы — смежные.
Рассмотрим некоторые задачи:
Найдите угол, смежный с ∠АOС, если ∠АOС = 111 о.
Выполним чертеж к задаче:
Рис. 6. Чертеж к примеру 1
Поскольку ∠АОС = β и ∠СOD = α смежные углы, то α + β = 180 о. То есть 111 о + β = 180 о.
Значит, β = 69 о.
Этот тип задач эксплуатирует теорему о сумме смежных углов.
Один из смежных углов прямой, каким (острым, тупым или прямым) является другой угол?
Если один из углов прямой, а сумма двух углов 180 о, то и другой угол тоже прямой. Эта задача проверяет знания о сумме смежных углов.
Эта задача проверяет знания о сумме смежных углов.
Верно ли, что если смежные углы равны, то они прямые?
Составим уравнение: α + β = 180 о, но поскольку α = β, то β + β = 180 о, значит, β = 90 о.
Ответ: Да, утверждение верно.
Даны два равных угла. Верно ли, что и смежные им углы тоже будут равны?
Рис. 7. Чертеж к примеру 4
Если два угла равны α, то соответствующие им смежные углы будут 180 о — α. То есть они будут равны между собой.
Ответ: Утверждение верно.
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. — М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. — М.: Просвещение.
- \Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Измерение отрезков ().
- Обобщающий урок по геометрии в 7-м классе ().
- Прямая линия, отрезок ().

- № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Найдите два смежных угла, если один из них в 4 раза больше другого.
- Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
- * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?
по теме: Смежные и вертикальные углы, их свойства.
(3 занятия)
В результате изучения темы нужно:
УМЕТЬ:
Понятия: смежных и вертикальных углов, перпендикулярных прямых
Различать понятия смежные и вертикальные углы
Теоремы смежных и вертикальных углов
Решать задачи с использованием свойств смежных и вертикальных углов
Свойства смежных и вертикальных углов
Строить смежные и вертикальные углы, перпендикулярные прямые
ЛИТЕРАТУРА:
1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
2. Геометрия. 7 класс. К.О.Букубаева, А.Т. Миразова. Алматы « Атамұра ». 2012
3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы « Атамұра ». 2012
4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы « Атамұра ». 2012
5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы « Атамұра ». 2012
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях,
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому,
кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
ЗАДАНИЕ №1.
Прочитай определение и выучи (2б):
Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
2) Выучи и запиши в тетрадь теорему: (2б)
Сумма смежных углов равна 180.
Дано:
∠ АОД и ∠ ДОВ –данные смежные углы
ОД — общая сторона
Доказать:
∠ АОД + ∠ ДОВ = 180
Доказательство:
На основе аксиомы III 4:
∠ АОД + ∠ ДОВ = ∠ АОВ.
∠ АОВ — развернутый. Следовательно,
∠ АОД + ∠ ДОВ = 180
Теорема доказана.
3) Из теоремы следует: (2б)
1) Если два угла равны, то смежные с ними углы равны;
2) если смежные углы равны, то градусная мера каждого из них равна 90°.
Запомни!
Угол, равный 90°, называется прямым углом.
Угол, меньше 90°, называется острым углом.
Угол, больше 90° и меньше 180°, называется тупым углом.
Прямой угол Острый угол Тупой угол
Так как сумма смежных углов равна 180°, то
1) угол, смежный с прямым углом, прямой;
2) угол, смежный с острым углом, тупой;
3) угол, смежный с тупым углом, острый.
4) Рассмотри образец решения з адачи:
а) Дано: ∠ h k и ∠ kl — смежные; ∠ h k больше ∠ kl на 50° .
Найти: ∠ h k и ∠ kl .
Решение: Пусть ∠ kl = х, тогда ∠ h k = х + 50°. По свойству о сумме смежных углов ∠ kl + ∠ h k = 180°.
х + х + 50° = 180°;
2х = 180° — 50°;
2х = 130°;
х = 65°.
∠ kl = 65°; ∠ h k = 65°+ 50° = 115°.
Ответ: 115° и 65°.
б) Пусть ∠ kl = х, тогда ∠ h k = 3х
х + 3х = 180°; 4х = 180°; х = 45°; ∠ kl = 45°; ∠ hk = 135°.
Ответ: 135° и 45°.
5) Работа с определением смежных углов: (2 б)
6) Найди ошибки в определениях: (2б)
Пройди проверку №1
Задание №2
1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB.(2б)
2). Практическая работа на открытие свойства смежных углов: (5б)
Ход работы
1. Построй угол
смежный углу а , если а : острый, прямой, тупой.
2. Измерь величины углов.
3.Данные измерений занеси в таблицу.
4. Найди соотношение между величинами углов а и .
5. Сделай вывод о свойстве смежных углов.
Пройди проверку №2
Задание №3
Начертите неразвернутый ∠ АОВ и назовите лучи, являющиеся сторонами этого угла.
Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.
Запишите в тетради: углы ∠ АОВ и ∠ СОД называются вертикальными. (3б)
Выучи и запиши в тетрадь: (4б)
Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.
1 и
Лучи OF и OA , OC и OE являются попарно дополнительными лучами.
Теорема: Вертикальные углы равны.
Доказательство.
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и
b
пересекаются в точке О. ∠
1 и
∠
2 –вертикальные углы.
∠
1 и
∠
2 –вертикальные углы.
∠ АОС-развернутый, значит ∠ АОС= 180°. Однако ∠ 1+ ∠ 2= ∠ АОС, т.е.
∠ 3+ ∠ 1= 180°, отсюда имеем:
∠ 1= 180 — ∠ 3. (1)
Также имеем, что ∠ ДОВ= 180°, отсюда ∠ 2+ ∠ 3= 180°, или ∠ 2= 180°- ∠ 3. (2)
Так как в равенствах (1) и (2) прямые части равны, то ∠ 1= ∠ 2.
Теорема доказана.
5). Работа с определением вертикальных углов:(2б)
6) Найди ошибку в определении:(2б).
Пройди проверку №3
Задание №4
1)Практическая работа на открытие свойства вертикальных углов:(5б)
Ход работы:
1.Построй угол β вертикальный углу α , если α :
острый, прямой, тупой.
2.Измерь величины углов.
3.Данные измерений занеси в таблицу
4.Найди соотношение между величинами углов α и β.
5.Сделай вывод о свойстве вертикальных углов.
2)Доказательство свойств смежных и вертикальных углов. (3б)
2) Рассмотри образец решения з адачи.
Задача. Прямые АВ и СД пересекаются в точке О так, что ∠ AOД = 35°. Найдите углы АОС и ВОС.
Решение:
1) Углы АОД и АОС смежные, поэтому ∠ BOC = 180° — 35° = 145°.
2) Углы АОС и ВОС также смежные, поэтому ∠ BOC = 180° — 145° = 35°.
Значит, ∠ BOC = ∠ АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?
3) Решение задач на готовых чертежах: (3б)
1. Найти углы АОВ, АОD, COD.
3) Найти углы BOC, FOA.: (3б)
3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)
Пройди проверку №4
Задание №5
Проверь свои знания, выполнив проверочную работу №1
Задание №6
1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь. (3б)
(3б)
Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.
2) Реши на выбор две задачи:
1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)
2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого.Найдите каждый из углов.(3б)
3.Найдите смежные углы,если их разность и их сумма относятся как 2:9.(3б)
Задание №7
Молодец! Можешь приступать к проверочной работе №2.
Проверочная работа №1.
Реши на выбор любой из вариантов (10б)
Вариант 1
г)
Смежные
д) Начертите (на глаз) угол в 30° и
е) Какие углы называются вертикальными?
Два угла называются вертикальными, если орни равны.
ж) Из точки А провести две прямые, перпендикулярные прямой а
Можно провести только одну прямую.
Вариант 2
1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.
Д)
Нет. Они вертикальные
Е) Какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.
2. Назовите вертикальные углы на данном рисунке.
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Проверочная работа №2.
Реши на выбор любой вариант
Вариант I
Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4б)
Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других. (6б)
(6б)
Вариант II
1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)
2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других.(6б)
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Угол. Свойства смежных и вертикальных углов. Смежные и вертикальные углы. Перпендикулярные прямые
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.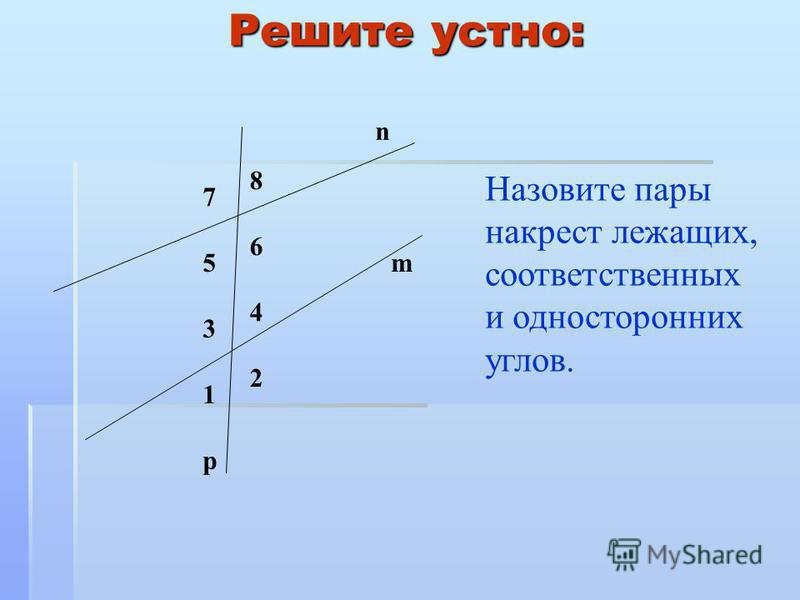
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т.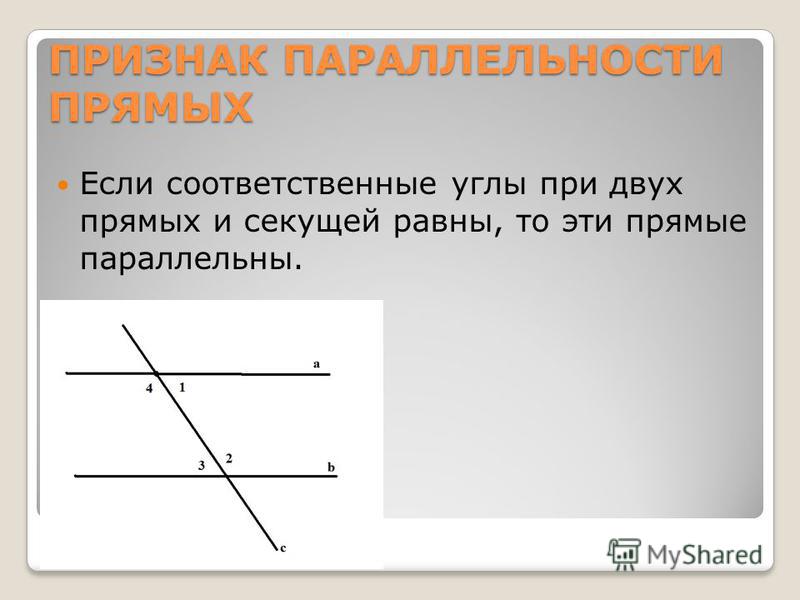 е. 1 1 / 8 d .
е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).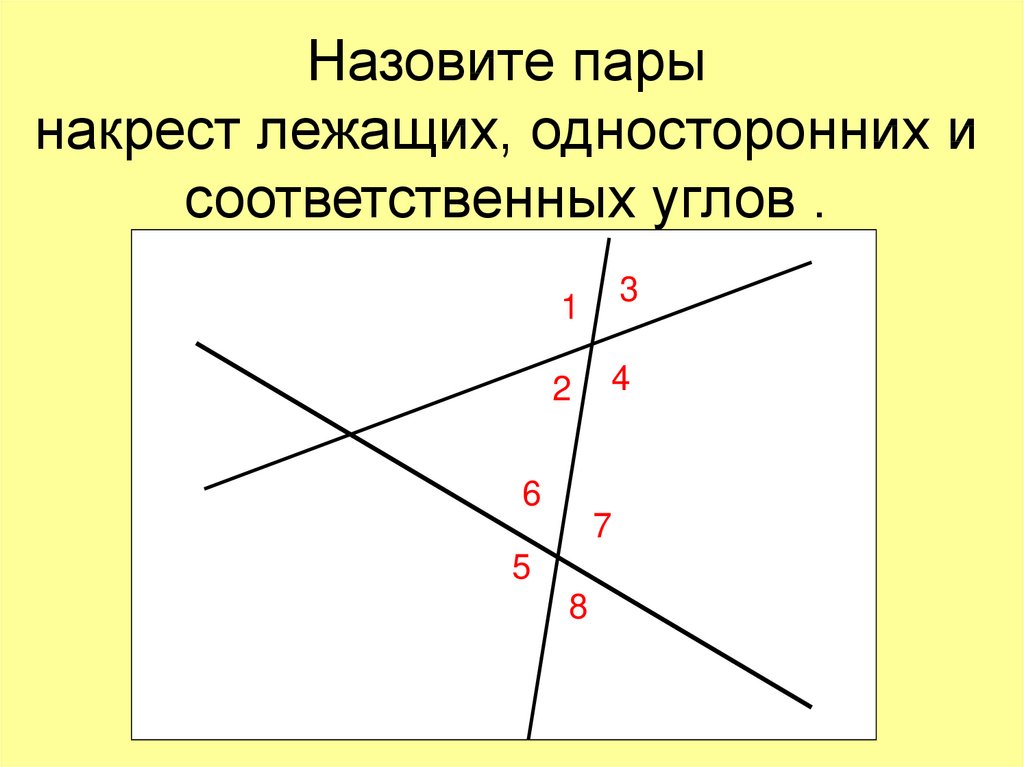
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
по теме: Смежные и вертикальные углы, их свойства.
(3 занятия)
В результате изучения темы нужно:
УМЕТЬ:
Понятия: смежных и вертикальных углов, перпендикулярных прямых
Различать понятия смежные и вертикальные углы
Теоремы смежных и вертикальных углов
Решать задачи с использованием свойств смежных и вертикальных углов
Свойства смежных и вертикальных углов
Строить смежные и вертикальные углы, перпендикулярные прямые
ЛИТЕРАТУРА:
1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
2. Геометрия. 7 класс. К.О.Букубаева, А.Т. Миразова. Алматы « Атамұра ». 2012
3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы «
Атамұра
». 2012
К.О.Букубаева. Алматы «
Атамұра
». 2012
4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы « Атамұра ». 2012
5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы « Атамұра ». 2012
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях,
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому,
кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
ЗАДАНИЕ №1.
Прочитай определение и выучи (2б):
Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
2) Выучи и запиши в тетрадь теорему: (2б)
Сумма смежных углов равна 180.
Дано:
∠ АОД и ∠ ДОВ –данные смежные углы
ОД — общая сторона
Доказать:
∠ АОД + ∠ ДОВ = 180
Доказательство:
На основе аксиомы III 4:
∠
АОД +
∠
ДОВ =
∠
АОВ.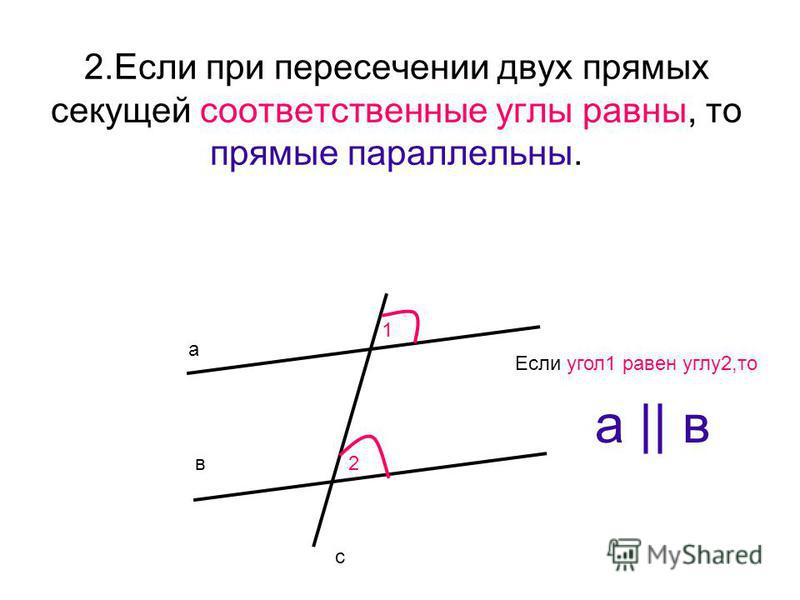
∠ АОВ — развернутый. Следовательно,
∠ АОД + ∠ ДОВ = 180
Теорема доказана.
3) Из теоремы следует: (2б)
1) Если два угла равны, то смежные с ними углы равны;
2) если смежные углы равны, то градусная мера каждого из них равна 90°.
Запомни!
Угол, равный 90°, называется прямым углом.
Угол, меньше 90°, называется острым углом.
Угол, больше 90° и меньше 180°, называется тупым углом.
Прямой угол Острый угол Тупой угол
Так как сумма смежных углов равна 180°, то
1) угол, смежный с прямым углом, прямой;
2) угол, смежный с острым углом, тупой;
3) угол, смежный с тупым углом, острый.
4) Рассмотри образец решения з адачи:
а) Дано: ∠ h k и ∠ kl — смежные; ∠ h k больше ∠ kl на 50° .
Найти: ∠ h k и ∠ kl .
Решение: Пусть ∠ kl = х, тогда ∠ h k = х + 50°. По свойству о сумме смежных углов ∠ kl + ∠ h k = 180°.
х + х + 50° = 180°;
2х = 180° — 50°;
2х = 130°;
х = 65°.
∠ kl = 65°; ∠ h k = 65°+ 50° = 115°.
Ответ: 115° и 65°.
б) Пусть ∠ kl = х, тогда ∠ h k = 3х
х + 3х = 180°; 4х = 180°; х = 45°; ∠ kl = 45°; ∠ hk = 135°.
Ответ: 135° и 45°.
5) Работа с определением смежных углов: (2 б)
6) Найди ошибки в определениях: (2б)
Пройди проверку №1
Задание №2
1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB.(2б)
2). Практическая работа на открытие свойства смежных углов: (5б)
Ход работы
1. Построй угол смежный углу а , если а : острый, прямой, тупой.
2. Измерь величины углов.
3.Данные измерений занеси в таблицу.
4. Найди соотношение между величинами углов а и .
5. Сделай вывод о свойстве смежных углов.
Пройди проверку №2
Задание №3
Начертите неразвернутый
∠
АОВ и назовите лучи, являющиеся сторонами этого угла.
Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.
Запишите в тетради: углы ∠ АОВ и ∠ СОД называются вертикальными. (3б)
Выучи и запиши в тетрадь: (4б)
Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.
1 и
Лучи OF и OA , OC и OE являются попарно дополнительными лучами.
Теорема: Вертикальные углы равны.
Доказательство.
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О. ∠ 1 и ∠ 2 –вертикальные углы.
∠ АОС-развернутый, значит ∠ АОС= 180°. Однако ∠ 1+ ∠ 2= ∠ АОС, т.е.
∠ 3+ ∠ 1= 180°, отсюда имеем:
∠ 1= 180 — ∠ 3. (1)
Также имеем, что ∠ ДОВ= 180°, отсюда ∠ 2+ ∠ 3= 180°, или ∠ 2= 180°- ∠ 3. (2)
Так как в равенствах (1) и (2) прямые части равны, то
∠
1=
∠
2.
Теорема доказана.
5). Работа с определением вертикальных углов:(2б)
6) Найди ошибку в определении:(2б).
Пройди проверку №3
Задание №4
1)Практическая работа на открытие свойства вертикальных углов:(5б)
Ход работы:
1.Построй угол β вертикальный углу α , если α :
острый, прямой, тупой.
2.Измерь величины углов.
3.Данные измерений занеси в таблицу
4.Найди соотношение между величинами углов α и β.
5.Сделай вывод о свойстве вертикальных углов.
2)Доказательство свойств смежных и вертикальных углов. (3б)
2) Рассмотри образец решения з адачи.
Задача. Прямые АВ и СД пересекаются в точке О так, что ∠ AOД = 35°. Найдите углы АОС и ВОС.
Решение:
1) Углы АОД и АОС смежные, поэтому ∠ BOC = 180° — 35° = 145°.
2) Углы АОС и ВОС также смежные, поэтому ∠ BOC = 180° — 145° = 35°.
Значит,
∠
BOC
=
∠
АОД = 35°, причем эти углы являются вертикальными.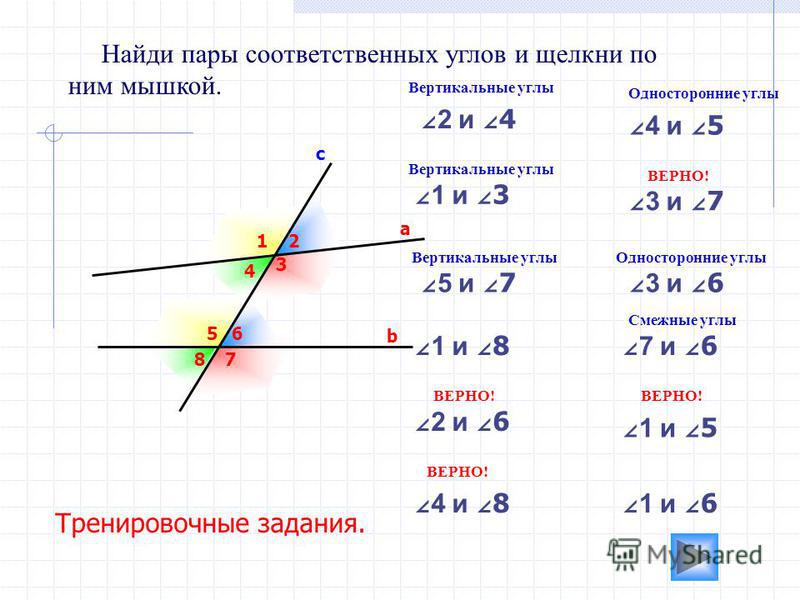 Вопрос: верно ли утверждение, что любые вертикальные углы равны?
Вопрос: верно ли утверждение, что любые вертикальные углы равны?
3) Решение задач на готовых чертежах: (3б)
1. Найти углы АОВ, АОD, COD.
3) Найти углы BOC, FOA.: (3б)
3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)
Пройди проверку №4
Задание №5
Проверь свои знания, выполнив проверочную работу №1
Задание №6
1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь. (3б)
Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.
2) Реши на выбор две задачи:
1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)
2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого.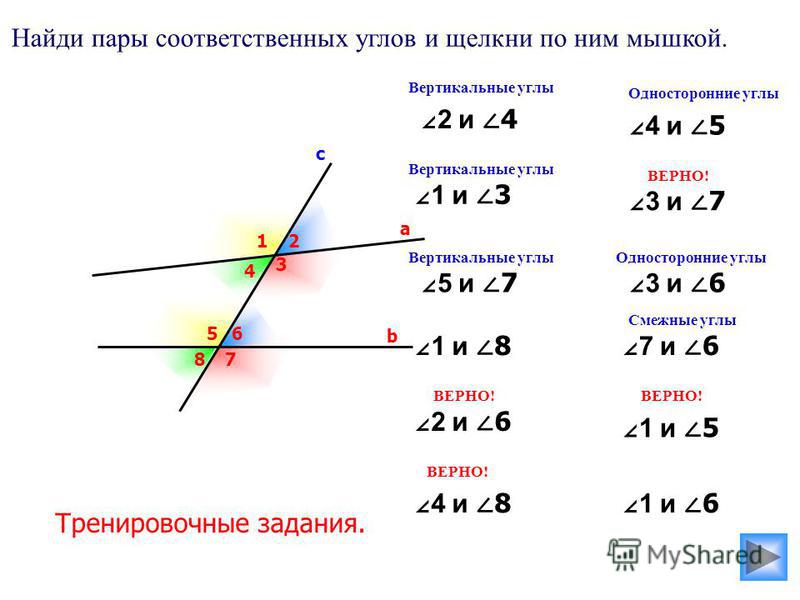 Найдите каждый из углов.(3б)
Найдите каждый из углов.(3б)
3.Найдите смежные углы,если их разность и их сумма относятся как 2:9.(3б)
Задание №7
Молодец! Можешь приступать к проверочной работе №2.
Проверочная работа №1.
Реши на выбор любой из вариантов (10б)
Вариант 1
г)
Смежные
д) Начертите (на глаз) угол в 30° и
е) Какие углы называются вертикальными?
Два угла называются вертикальными, если орни равны.
ж) Из точки А провести две прямые, перпендикулярные прямой а
Можно провести только одну прямую.
Вариант 2
1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.
Д)
Нет. Они вертикальные
Е) Какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.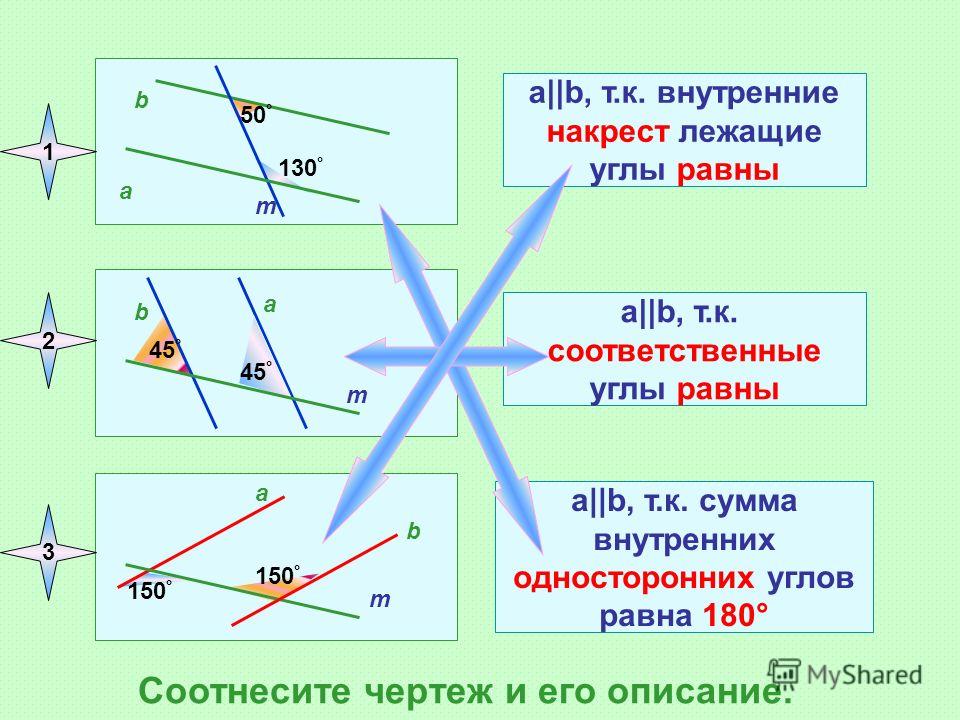
2. Назовите вертикальные углы на данном рисунке.
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Проверочная работа №2.
Реши на выбор любой вариант
Вариант I
Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4б)
Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других.(6б)
Вариант II
1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)
2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других.(6б)
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
На данном уроке мы рассмотрим и уясним для себя понятие смежные углы. Рассмотрим теорему, которая их касается. Введем понятие «вертикальные углы». Рассмотрим опорные факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце занятия рассмотрим несколько задач, посвященных этой теме.
В конце занятия рассмотрим несколько задач, посвященных этой теме.
Начнем наш урок с понятия «смежные углы». На рисунке 1 изображен развернутый угол ∠АОС и луч ОВ, который делит данный угол на 2 угла.
Рис. 1. Угол ∠АОС
Рассмотрим углы ∠АОВ и ∠ВОС. Вполне очевидно, что они имеют общую сторону ВО, а стороны АО и ОС являются противолежащими. Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.
Определение: Если два угла имеют общую сторону, а две другие стороны являются дополняющими лучами, то данные углы называются смежными .
Теорема 1: Сумма смежных углов — 180 о.
Рис. 2. Чертеж к теореме 1
∠МОL + ∠LON = 180 o . Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму — 180 о.
Рассмотрим пересечение двух прямых. На рисунке изображено пересечение двух прямых в точке О.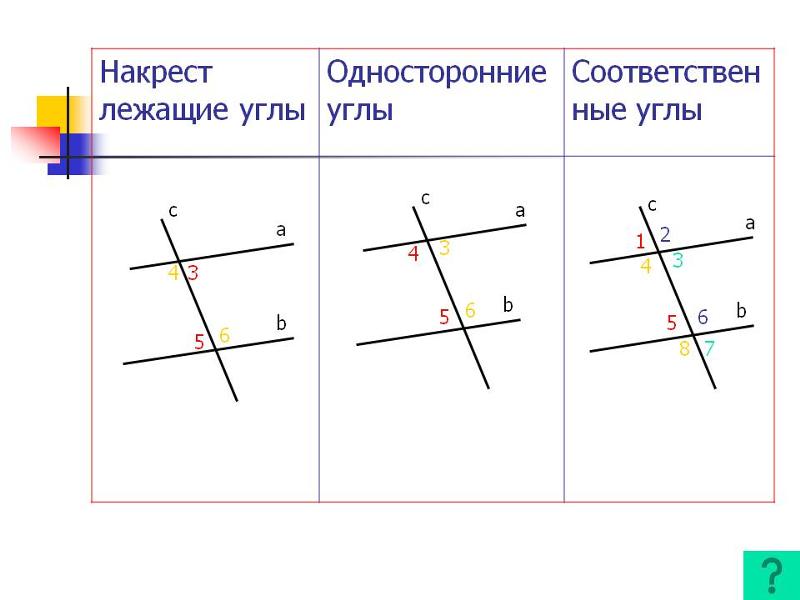
Рис. 3. Вертикальные углы ∠ВОА и ∠СОD
Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Именно поэтому на рисунке изображено две пары вертикальных углов: ∠АОВ и ∠СОD, а также ∠AOD и ∠ВОС.
Теорема 2: Вертикальные углы равны.
Используем рисунок 3. Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС — ∠ВОС = 180 о — β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD — ∠BОС = 180 о — β.
Из этих соображений мы делаем вывод, что ∠АОВ = ∠СОD = α. Аналогично, ∠AOD = ∠ВОС = β.
Следствие 1: Угол между биссектрисами смежных углов равен 90 о.
Рис. 4. Чертеж к следствию 1
Поскольку ОL — биссектриса угла ∠ВОА, то угол ∠LOB = , аналогично ∠ВОК = . ∠LOK = ∠LOB + ∠BOK = + = . Сумма углов α + β равна 180 о, поскольку данные углы — смежные.
Следствие 2: Угол между биссектрисами вертикальных углов равен 180 о.
Рис. 5. Чертеж к следствию 2
KO — биссектриса ∠AOB, LO — биссектриса ∠COD. Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Сумма углов α + β равна 180 о, так как данные углы — смежные.
Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Сумма углов α + β равна 180 о, так как данные углы — смежные.
Рассмотрим некоторые задачи:
Найдите угол, смежный с ∠АOС, если ∠АOС = 111 о.
Выполним чертеж к задаче:
Рис. 6. Чертеж к примеру 1
Поскольку ∠АОС = β и ∠СOD = α смежные углы, то α + β = 180 о. То есть 111 о + β = 180 о.
Значит, β = 69 о.
Этот тип задач эксплуатирует теорему о сумме смежных углов.
Один из смежных углов прямой, каким (острым, тупым или прямым) является другой угол?
Если один из углов прямой, а сумма двух углов 180 о, то и другой угол тоже прямой. Эта задача проверяет знания о сумме смежных углов.
Верно ли, что если смежные углы равны, то они прямые?
Составим уравнение: α + β = 180 о, но поскольку α = β, то β + β = 180 о, значит, β = 90 о.
Ответ: Да, утверждение верно.
Даны два равных угла. Верно ли, что и смежные им углы тоже будут равны?
Рис. 7. Чертеж к примеру 4
Если два угла равны α, то соответствующие им смежные углы будут 180 о — α. То есть они будут равны между собой.
То есть они будут равны между собой.
Ответ: Утверждение верно.
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. — М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. — М.: Просвещение.
- \Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Измерение отрезков ().
- Обобщающий урок по геометрии в 7-м классе ().
- Прямая линия, отрезок ().
- № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Найдите два смежных угла, если один из них в 4 раза больше другого.
- Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
- * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Сумма смежных углов равна 180°
Вертикальные углы — это два угла, у которых стороны одного угла являются продолжение сторон другого.
Вертикальные углы равны.
2. Признаки равенства треугольников:
I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
3. Признаки параллельности двух прямых: односторонние углы, накрест лежащие и соответственные:
Две прямые на плоскости называются параллельными , если они не пересекаются.
Накрест лежащие углы: 3 и 5, 4 и 6;
Односторонние углы: 4 и 5, 3 и 6; рис. Стр55
Стр55
Соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
Теорема : Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Теорема : если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
Теорема : если две параллельные прямые пересечены секущей, то соответственные углы равны
Теорема : если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°
4. Сумма углов треугольника:
Сумма углов треугольника равна 180°
5. Свойства равнобедренного треугольника:
Теорема: В равнобедренном треугольнике углы при основании равны.
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, являетсямедианой и высотой (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90°)
Признак: Если два угла треугольника равны, то треугольник равнобедренный.
Сумма углов четырёхугольника равна 2 π = 360°.
Четырёхугольник можно вписать в окружность тогда и только тогда, сумма противоположных углов равна 180°
10. Признаки подобия треугольников:
I признак : если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
III признак : если три стороны одного треугольника порциональны трем сторонам другого, то такие треугольники подобны
11. Формулы:
· Теорема Пифагора: a 2 +b 2 =c 2
· Теорема sin:
· Теорема cos:
· 3 формулы площади треугольника:
· Площадь прямоугольного треугольника: S= S=
· Площадь равностороннего треугольника:
· Площадь параллелограмма: S = ah
· Площадь квадрата: S = a2
· Площадь трапеции:
· Площадь ромба:
· Площадь прямоугольника: S=ab
· Равносторонний треугольник. Высота: h=
Высота: h=
· Тригонометрическая единица: sin 2 a+cos 2 a=1
· Средняя линия треугольника: S=
· Средняя линия трапеции : МК=
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12
Признак параллельности прямых по соответственным углам. Признаки и свойства параллельных прямых
1. Если две прямые параллельны третьей прямой, то они являются параллельными:
Если a ||c и b ||c , то a ||b .
2. Если две прямые перпендикулярны третьей прямой, то они параллельны:
Если a ⊥c и b ⊥c , то a ||b .
Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.
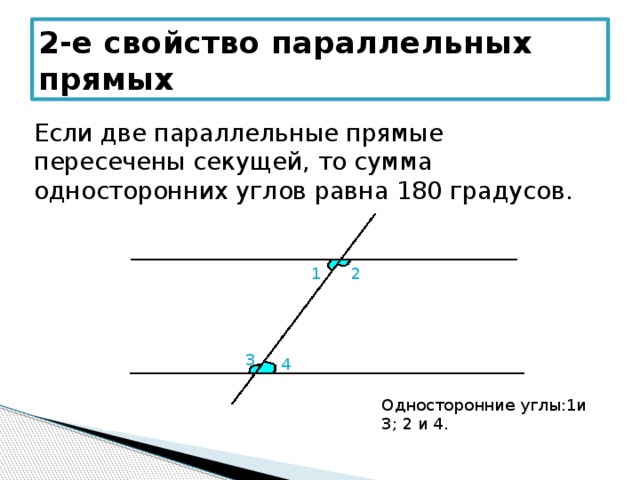
3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:
Если ∠1 + ∠2 = 180°, то a ||b .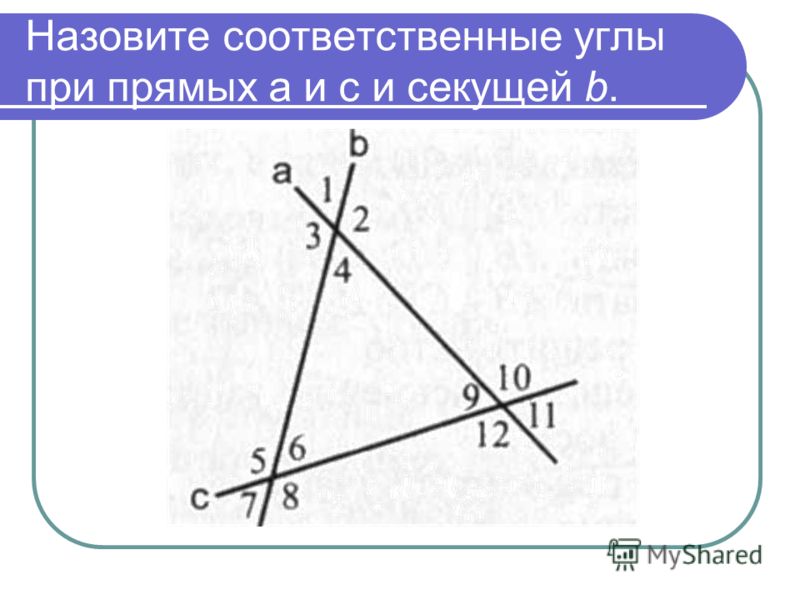
4. Если соответственные углы равны, то прямые параллельны:
Если ∠2 = ∠4, то a ||b .
5. Если внутренние накрест лежащие углы равны, то прямые параллельны:
Если ∠1 = ∠3, то a ||b .
Свойства параллельных прямых
Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.
1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:
Если a ||b , то ∠1 + ∠2 = 180°.
2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:
Если a ||b , то ∠2 = ∠4.
3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:
Если a ||b , то ∠1 = ∠3.
Следующее свойство является частным случаем для каждого предыдущего:
4.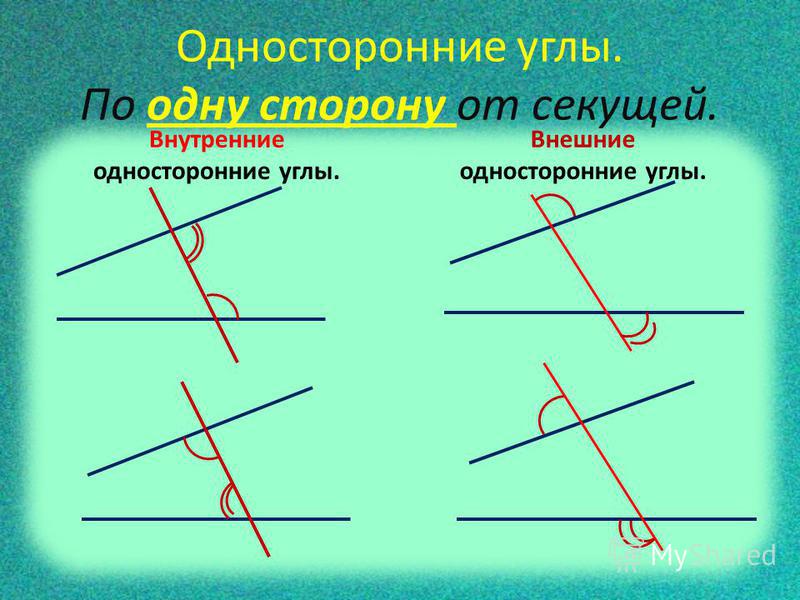 Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:
Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:
Если a ||b и c ⊥a , то c ⊥b .
Пятое свойство — это аксиома параллельности прямых:
5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
Страница 1 из 2
Вопрос 1. Докажите, что две прямые, параллельные третьей, параллельны.
Ответ. Теорема 4.1. Две прямые, параллельные третьей, параллельны.
Доказательство. Пусть прямые a и b параллельны прямой c. Допустим, что a и b не параллельны (рис. 69). Тогда они не пересекаются в некоторой точке C. Значит, через точку C проходят две прямые, параллельные прямой c. Но это невозможно, так как через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной. Теорема доказана.
Вопрос 2. Объясните, какие углы называются внутренними односторонними. Какие углы называются внутренними накрест лежащими?
Какие углы называются внутренними накрест лежащими?
Ответ. Пары углов, которые образуются при пересечении прямых AB и CD секущей AC, имеют специальные названия.
Если точки B и D лежат в одной полуплоскости относительно прямой AC, то углы BAC и DCA называются внутренними односторонними (рис. 71, а).
Если точки B и D лежат в разных полуплоскостях относительно прямой AC, то углы BAC и DCA называются внутренними накрест лежащими (рис. 71, б).
Рис. 71
Вопрос 3. Докажите, что если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны, а сумма внутренних односторонних углов каждой пары равна 180°.
Ответ. Секущая AC образует с прямыми AB и CD две пары внутренних односторонних и две пары внутренних накрест лежащих углов. Внутренние накрест лежащие углы одной пары, например угол 1 и угол 2, являются смежными внутренним накрест лежащим углам другой пары: угол 3 и угол 4 (рис. 72).
Рис. 72
72
Поэтому если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны.
Пара внутренних накрест лежащих углов, например угол 1 и угол 2, и пара внутренних односторонних углов, например угол 2 и угол 3, имеют один угол общий – угол 2, а два других угла смежные: угол 1 и угол 3.
Поэтому если внутренние накрест лежащие углы равны, то сумма внутренних углов равна 180°. И обратно: если сумма внутренних накрест лежащих углов равна 180°, то внутренние накрест лежащие углы равны. Что и требовалось доказать.
Вопрос 4. Докажите признак параллельности прямых.
Ответ. Теорема 4.2 (признак параллельности прямых). Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Доказательство. Пусть прямые a и b образуют с секущей AB равные внутренние накрест лежащие углы (рис. 73, а). Допустим, прямые a и b не параллельны, а значит, пересекаются в некоторой точке C (рис. 73, б).
73, б).
Рис. 73
Секущая AB разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник BAC 1 , равный треугольнику ABC, с вершиной C 1 в другой полуплоскости. По условию внутренние накрест лежащие углы при параллельных a, b и секущей AB равны. Так как соответствующие углы треугольников ABC и BAC 1 с вершинами A и B равны, то они совпадают с внутренними накрест лежащими углами. Значит, прямая AC 1 совпадает с прямой a, а прямая BC 1 совпадает с прямой b. Получается, что через точки C и C 1 проходят две различные прямые a и b. А это невозможно. Значит, прямые a и b параллельны.
Если у прямых a и b и секущей AB сумма внутренних односторонних углов равна 180°, то, как мы знаем, внутренние накрест лежащие углы равны. Значит, по доказанному выше, прямые a и b параллельны. Теорема доказана.
Вопрос 5. Объясните, какие углы называются соответственными. Докажите, что если внутренние накрест лежащие углы равны, то соответственные углы тоже равны, и наоборот.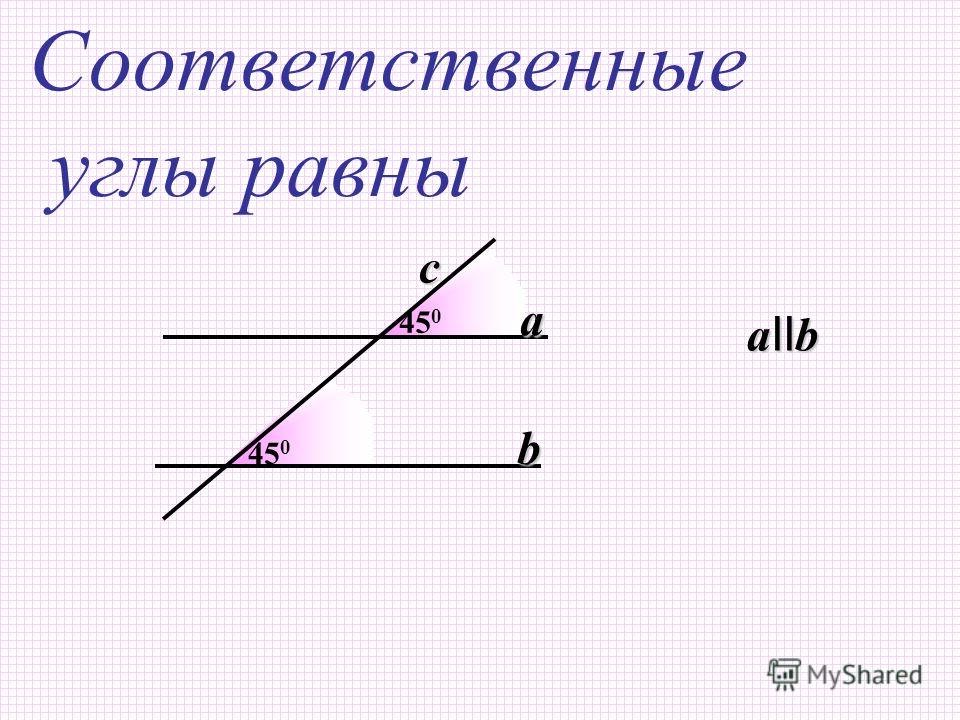
Ответ. Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей. Что и требовалось объяснить.
Из равенства внутренних накрест лежащих углов следует равенство соответственных углов, и наоборот. Допустим, у нас есть две параллельные прямые (так как по условию внутренние накрест лежащие углы равны) и секущая, которые образуют углы 1, 2, 3. Углы 1 и 2 равны как внутренние накрест лежащие. А углы 2 и 3 равны как вертикальные. Получаем: \(\angle\)1 = \(\angle\)2 и \(\angle\)2 = \(\angle\)3. По свойству транзитивности знака равенства следует, что \(\angle\)1 = \(\angle\)3. Аналогично доказывается и обратное утверждение.
Отсюда получается признак параллельности прямых по соответственным углам. Именно: прямые параллельны, если соответственные углы равны. Что и требовалось доказать.
Вопрос 6. Докажите, что через точку, не лежащую на данной прямой, можно провести параллельную ей прямую.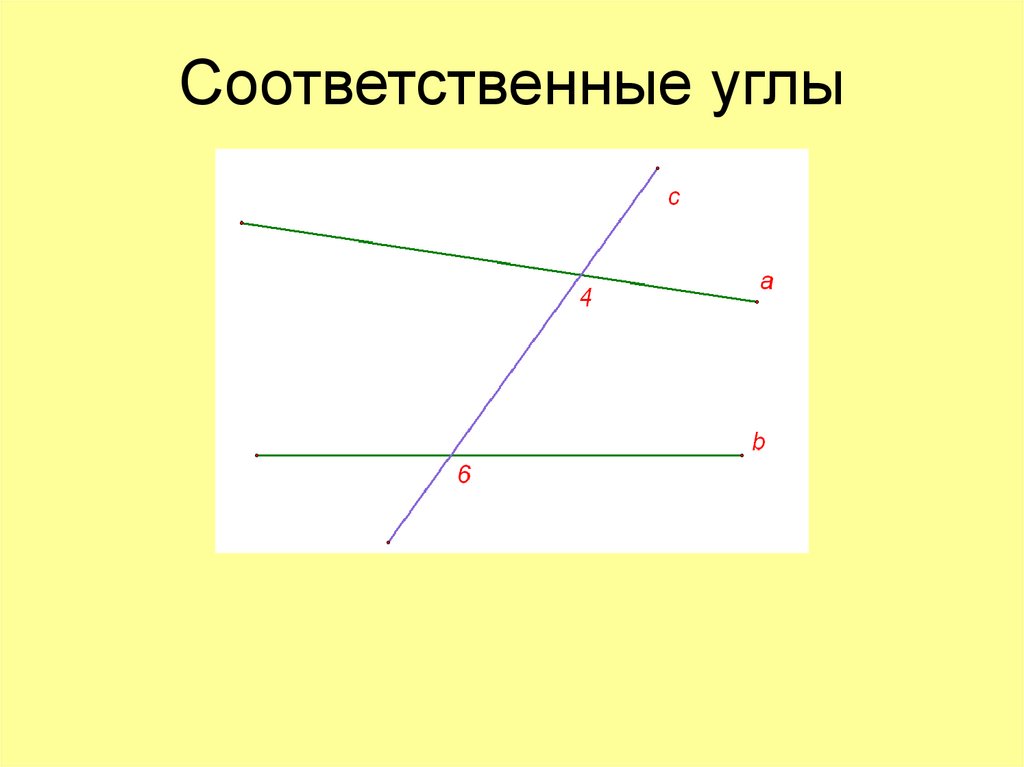 Сколько прямых, параллельных данной, можно провести через точку, не лежащую на этой прямой?
Сколько прямых, параллельных данной, можно провести через точку, не лежащую на этой прямой?
Ответ. Задача (8). Даны прямая AB и точка C, не лежащая на этой прямой. Докажите, что через точку C можно провести прямую, параллельную прямой AB.
Решение. Прямая AC разбивает плоскость на две полуплоскости (рис. 75). Точка B лежит в одной из них. Отложим от полупрямой CA в другую полуплоскость угол ACD, равный углу CAB. Тогда прямые AB и CD будут параллельны. В самом деле, для этих прямых и секущей AC углы BAC и DCA внутренние накрест лежащие. А так как они равны, то прямые AB и CD параллельны. Что и требовалось доказать.
Сопоставляя утверждение задачи 8 и аксиомы IX (основного свойства параллельных прямых), приходим к важному выводу: через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.
Вопрос 7. Докажите, что если две прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
Ответ. Теорема 4.3 (обратная теореме 4.2). Если две параллельные прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
Доказательство. Пусть a и b – параллельные прямые и c – прямая, пересекающая их в точках A и B. Проведём через точку A прямую a 1 так, чтобы внутренние накрест лежащие углы, образованные секущей c с прямыми a 1 и b, были равны (рис. 76).
По признаку параллельности прямых прямые a 1 и b параллельны. А так как через точку A проходит только одна прямая, параллельная прямой b, то прямая a совпадает с прямой a 1 .
Значит, внутренние накрест лежащие углы, образованные секущей с
параллельными прямыми a и b, равны. Теорема доказана.
Вопрос 8. Докажите, что две прямые, перпендикулярные третьей, параллельны. Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Ответ. Из теоремы 4.2 следует, что две прямые, перпендикулярные третьей, параллельны.
Предположим, что две какие-либо прямые перпендикулярны третьей прямой. Значит, эти прямые пересекаются с третьей прямой под углом, равным 90°.
Из свойства углов, образованных при пересечении параллельных прямых секущей, следует, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Вопрос 9. Докажите, что сумма углов треугольника равна 180°.
Ответ. Теорема 4.4. Сумма углов треугольника равна 180°.
Доказательство. Пусть ABC – данный треугольник. Проведём через вершину B прямую, параллельную прямой AC. Отметим на ней точку D так, чтобы точки A и D лежали по по разные стороны от прямой BC (рис. 78).
Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и C равна углу ABD.
А сумма всех трёх углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD и секущей AB, то их сумма равна 180°. Теорема доказана.
Теорема доказана.
Вопрос 10. Докажите, что у любого треугольника по крайней мере два угла острые.
Ответ. Действительно, допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть два угла, каждый из которых не меньше 90°. Сумма этих двух углов уже не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°. Что и требовалось доказать.
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Yandex.RTB R-A-339285-1 Определение 1
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.
Определение 2
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.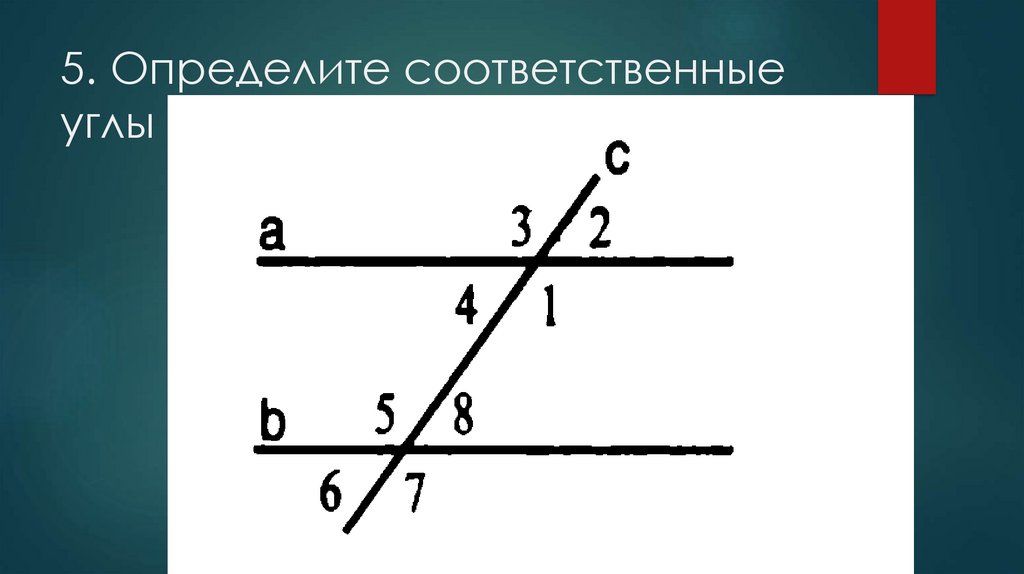
Чтобы обозначить параллельность прямых, общепринято использовать символ ∥ . Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b . Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b , или прямая b параллельна прямой а.
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Аксиома
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Теорема 1
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10 — 11 классов).
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых.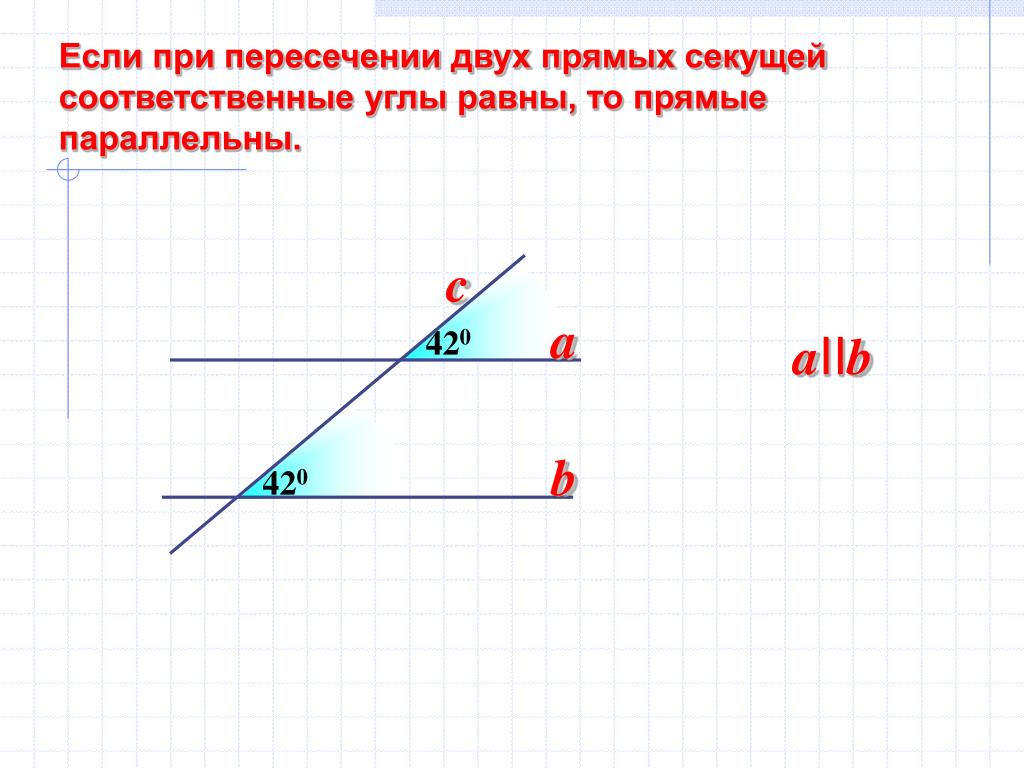 Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Определение 3
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:
Продемонстрируем их на иллюстрации:
Теорема 2
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:
Доказательство указанных условий присутствует в программе геометрии за 7 — 9 классы.
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
Теорема 3
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
Теорема 4
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.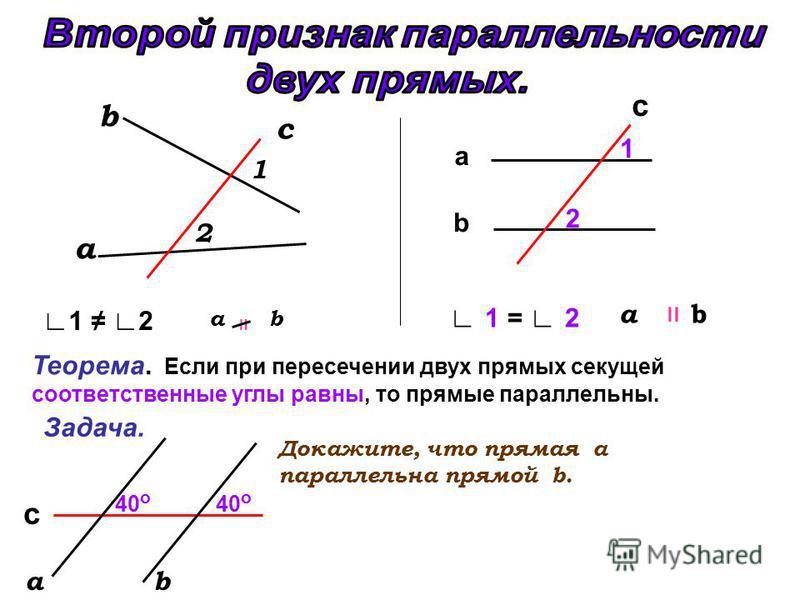
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
Теорема 5
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
Теорема 6
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Проиллюстрируем:
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Теорема 7
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a → = (a x , a y) и b → = (b x , b y) являются направляющими векторами прямых a и b ;
и n b → = (n b x , n b y) являются нормальными векторами прямых a и b , то указанное выше необходимое и достаточное условие запишем так: a → = t · b → ⇔ a x = t · b x a y = t · b y или n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y или a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.
Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.
- Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A 1 x + B 1 y + C 1 = 0 ; прямая b — A 2 x + B 2 y + C 2 = 0 . Тогда нормальные векторы заданных прямых будут иметь координаты (А 1 , В 1) и (А 2 , В 2) соответственно. Условие параллельности запишем так:
A 1 = t · A 2 B 1 = t · B 2
- Прямая a описывается уравнением прямой с угловым коэффициентом вида y = k 1 x + b 1 . Прямая b — y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты (k 1 , — 1) и (k 2 , — 1) соответственно, а условие параллельности запишем так:
k 1 = t · k 2 — 1 = t · (- 1) ⇔ k 1 = t · k 2 t = 1 ⇔ k 1 = k 2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
- Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x — x 1 a x = y — y 1 a y и x — x 2 b x = y — y 2 b y или параметрическими уравнениями прямой на плоскости: x = x 1 + λ · a x y = y 1 + λ · a y и x = x 2 + λ · b x y = y 2 + λ · b y .
Тогда направляющие векторы заданных прямых будут: a x , a y и b x , b y соответственно, а условие параллельности запишем так:
a x = t · b x a y = t · b y
Разберем примеры.
Пример 1
Заданы две прямые: 2 x — 3 y + 1 = 0 и x 1 2 + y 5 = 1 . Необходимо определить, параллельны ли они.
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y — 1 = 0
Мы видим, что n a → = (2 , — 3) — нормальный вектор прямой 2 x — 3 y + 1 = 0 , а n b → = 2 , 1 5 — нормальный вектор прямой x 1 2 + y 5 = 1 .
Полученные векторы не являются коллинеарными, т.к. не существует такого значения t , при котором будет верно равенство:
2 = t · 2 — 3 = t · 1 5 ⇔ t = 1 — 3 = t · 1 5 ⇔ t = 1 — 3 = 1 5
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Пример 2
Заданы прямые y = 2 x + 1 и x 1 = y — 4 2 . Параллельны ли они?
Решение
Преобразуем каноническое уравнение прямой x 1 = y — 4 2 к уравнению прямой с угловым коэффициентом:
x 1 = y — 4 2 ⇔ 1 · (y — 4) = 2 x ⇔ y = 2 x + 4
Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2 x + 1 , например, (0 , 1) , координаты этой точки не отвечают уравнению прямой x 1 = y — 4 2 , а значит прямые не совпадают.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Нормальный вектор прямой y = 2 x + 1 это вектор n a → = (2 , — 1) , а направляющий вектором второй заданной прямой является b → = (1 , 2) . Скалярное произведение этих векторов равно нулю:
Скалярное произведение этих векторов равно нулю:
n a → , b → = 2 · 1 + (- 1) · 2 = 0
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Теорема 8
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a → = (a x , a y , a z) и b → = (b x , b y , b z) являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t , чтобы выполнялось равенство:
a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z
Пример 3
Заданы прямые x 1 = y — 2 0 = z + 1 — 3 и x = 2 + 2 λ y = 1 z = — 3 — 6 λ . Необходимо доказать параллельность этих прямых.
Необходимо доказать параллельность этих прямых.
Решение
Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a → и b → заданных прямых имеют координаты: (1 , 0 , — 3) и (2 , 0 , — 6) .
1 = t · 2 0 = t · 0 — 3 = t · — 6 ⇔ t = 1 2 , то a → = 1 2 · b → .
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Признаки параллельности двух прямых
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Следствие 1 . Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.2).
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное)
тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной .
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис. 4).
4).
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
сумма односторонних углов равна 180°.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Углы, образованные при пересечении двух прямых секущей
Introduction
These Website Standard Terms and Conditions written on this webpage shall manage your use of this website. These Terms will be applied fully and affect to your use of this Website. By using this Website, you agreed to accept all terms and conditions written in here. You must not use this Website if you disagree with any of these Website Standard Terms and Conditions.
Minors or people below 18 years old are not allowed to use this Website.
Intellectual Property Rights
Other than the content you own, under these Terms, Buckle LLC and/or its licensors own all the intellectual property rights and materials contained in this Website.
You are granted limited license only for purposes of viewing the material contained on this Website.
Restrictions
You are specifically restricted from all of the following
- publishing any Website material in any other media;
- selling, sublicensing and/or otherwise commercializing any Website material;
- publicly performing and/or showing any Website material;
- using this Website in any way that is or may be damaging to this Website;
- using this Website in any way that impacts user access to this Website;
- using this Website contrary to applicable laws and regulations, or in any way may cause harm to the Website, or to any person or business entity;
- engaging in any data mining, data harvesting, data extracting or any other similar activity in relation to this Website;
- using this Website to engage in any advertising or marketing.
Certain areas of this Website are restricted from being access by you and Buckle LLC may further restrict access by you to any areas of this Website, at any time, in absolute discretion. Any user ID and password you may have for this Website are confidential and you must maintain confidentiality as well.
Any user ID and password you may have for this Website are confidential and you must maintain confidentiality as well.
Your Content
In these Website Standard Terms and Conditions, “Your Content” shall mean any audio, video text, images or other material you choose to display on this Website. By displaying Your Content, you grant Buckle LLC a non-exclusive, worldwide irrevocable, sub licensable license to use, reproduce, adapt, publish, translate and distribute it in any and all media.
Your Content must be your own and must not be invading any third-party’s rights. Buckle LLC reserves the right to remove any of Your Content from this Website at any time without notice.
No warranties
This Website is provided “as is,” with all faults, and Buckle LLC express no representations or warranties, of any kind related to this Website or the materials contained on this Website. Also, nothing contained on this Website shall be interpreted as advising you.
Limitation of liability
In no event shall Buckle LLC, nor any of its officers, directors and employees, shall be held liable for anything arising out of or in any way connected with your use of this website whether such liability is under contract. Buckle LLC, including its officers, directors and employees shall not be held liable for any indirect, consequential or special liability arising out of or in any way related to your use of this Website.
Indemnification
You hereby indemnify to the fullest extent Buckle LLC from and against any and/or all liabilities, costs, demands, causes of action, damages and expenses arising in any way related to your breach of any of the provisions of these Terms.
Severability
If any provision of these Terms is found to be invalid under any applicable law, such provisions shall be deleted without affecting the remaining provisions herein.
Variation of Terms
Buckle LLC is permitted to revise these Terms at any time as it sees fit, and by using this Website you are expected to review these Terms on a regular basis.
Assignment
The Buckle LLC is allowed to assign, transfer, and subcontract its rights and/or obligations under these Terms without any notification. However, you are not allowed to assign, transfer, or subcontract any of your rights and/or obligations under these Terms.
Entire Agreement
These Terms constitute the entire agreement between Buckle LLC and you in relation to your use of this Website, and supersede all prior agreements and understandings.
Governing Law & Jurisdiction
These Terms will be governed by and interpreted in accordance with the laws of the State of New York, and you submit to the non-exclusive jurisdiction of the state and federal courts located in New York for the resolution of any disputes.
2 прямые параллельны накрест лежащие. Параллельные прямые
Цели занятия: На этом занятии вы познакомитесь с понятием «параллельные прямые», узнаете, как можно убедиться в параллельности прямых, а также, какими свойствами обладают углы, образованные параллельными прямыми и секущей.
Параллельные прямые
Вы знаете, что понятие «прямая» относится к числу так называемых неопределяемых понятий геометрии.
Вы уже знаете, что две прямые могут совпадать, то есть иметь все общие точки, могут пересекаться, то есть иметь одну общую точку. Пересекаются прямые под разными углами, при этом углом между прямыми считают наименьших из углов, которые ими образованы. Частным случаем пересечения можно считать случай перпендикулярности, когда угол, образованный прямыми, равен 90 0 .
Но две прямые могут и не иметь общих точек, то есть не пересекаться. Такие прямые называются параллельными .
Поработайте с электронным образовательным ресурсом « ».
Чтобы познакомиться с понятием «параллельные прямые», поработайте в материалами видеоурока
Таким образом, теперь вы знаете определение параллельных прямых.
Из материалов фрагмента видеоурока вы узнали о различных видах углов, которые образуются при пересечении двух прямых третьей.
Пары углов 1 и 4; 3 и 2 называют внутренними односторонними углами (они лежат между прямыми a и b ).
Пары углов 5 и 8; 7 и 6 называют внешними односторонними углами (они лежат вне прямых a и b ).
Пары углов 1 и 8; 3 и 6; 5 и 4; 7 и 2 называют односторонними углами при прямых a и b и секущей c . Как вы видите, из пары соответственных углов один лежит между прямым a и b , а другой вне их.
Признаки параллельности прямых
Очевидно, что пользуясь определением сделать вывод о параллельности двух прямых невозможно. Поэтому для того чтобы сделать заключение о том, что две прямые параллельны, пользуются признаками .
Один из них вы уже можете сформулировать, познакомившись с материалами первой части видеоурока:
Теорема 1 . Две прямые, перпендикулярные третьей, не пересекаются, то есть параллельны.
С другими признаками параллельности прямых на основе равенства определенных пар углов вы познакомитесь, поработав с материалами второй части видеоурока «Признаки параллельности прямых».
Таким образом, вы должны знать еще три признака параллельности прямых.
Теорема 2 (первый признак параллельности прямых) . Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Рис. 2. Иллюстрация к первому признаку параллельности прямых
Еще раз повторите первый признак параллельности прямых, поработав с электронным образовательным ресурсом « ».
Таким образом, при доказательстве первого признака параллельности прямых используется признак равенства треугольников (по двум сторонам и углу между ними), а также признак параллельности прямых как перпендикулярных одной прямой.
Задание 1.
Запишите формулировку первого признака параллельности прямых и ее доказательство в свои тетради.
Теорема 3 (второй признак параллельности прямых) . Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Еще раз повторите второй признак параллельности прямых, поработав с электронным образовательным ресурсом « ».
При доказательстве второго признака параллельности прямых используется свойство вертикальных углов и первый признак параллельности прямых.
Задание 2.
Запишите формулировку второго признака параллельности прямых и ее доказательство в свои тетради.
Теорема 4 (третий признак параллельности прямых) . Если при пересечении двух прямых секущей сумма односторонних углов равна 180 0 , то прямые параллельны.
Еще раз повторите третий признак параллельности прямых, поработав с электронным образовательным ресурсом « ».
Таким образом, при доказательстве первого признака параллельности прямых используется свойство смежных углов и первый признак параллельности прямых.
Задание 3.
Запишите формулировку третьего признака параллельности прямых и ее доказательство в свои тетради.
Для того чтобы потренироваться в решении простейших задач, поработайте с материалами электронного образовательного ресурса « ».
Признаки параллельности прямых используются при решении задач.
Теперь рассмотрите примеры решения задач на признаки параллельности прямых, поработав с материалами видеоурока «Решение задач по теме «Признаки параллельности прямых».
А теперь проверьте себя, выполнив задания контрольного электронного образовательного ресурса « ».
Тот, кто хочет поработать с решением более сложных задач, может поработать с материалами видеоурока «Задачи на признаки параллельности прямых».
Свойства параллельных прямых
Параллельные прямые обладают набором свойств.
Вы узнаете, какие это свойства, поработав с материалами видеоурока «Свойства параллельных прямых».
Таким, образом, важным фактом, который вы должны знать, является аксиома параллельности.
Аксиома параллельности . Через точку, не лежащую на данной прямой, можно провести прямую , параллельную данной, и притом только одну.
Как вы узнали из материалов видеоурока, опираясь на эту аксиому, можно сформулировать два следствия.
Следствие 1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую параллельную прямую .
Следствие 2. Если две прямые параллельны третьей, то они параллельны между собой.
Задание 4.
Запишите формулировку сформулированных следствий и их доказательства в свои тетради.
Свойства углов, образованных параллельными прямыми и секущей являются теоремами, обратными соответствующим признакам.
Так, из материалов видеоурока вы узнали свойство накрест лежащих углов.
Теорема 5 (теорема , обратная первому признаку параллельности прямых) . При пересечении двух параллельных прямых секущей накрест лежащие углы равны.
Задание 5.
Еще раз повторите первое свойство параллельных прямых, поработав с электронным образовательным ресурсом « ».
Теорема 6 (теорема , обратная второму признаку параллельности прямых) . При пересечении двух параллельных прямых соответственные углы равны.
Задание 6.
Запишите формулировку данной теоремы и ее доказательство в свои тетради.
Еще раз повторите второе свойство параллельных прямых, поработав с электронным образовательным ресурсом « ».
Теорема 7 (теорема , обратная третьему признаку параллельности прямых) . При пересечении двух параллельных прямых сумма односторонних углов равна 180 0 .
Задание 7.
Запишите формулировку данной теоремы и ее доказательство в свои тетради.
Еще раз повторите третье свойство параллельных прямых, поработав с электронным образовательным ресурсом « ».
Все свойства параллельных прямых также используются при решении задач.
Рассмотрите типичные примеры решения задач, поработав с материалами видеоурока «Параллельные прямые и задачи на углы между ними и секущей».
Параллельность – очень полезное свойство в геометрии. В реальной жизни параллельные стороны позволяют создавать красивые, симметричные вещи, приятные любому глазу, поэтому геометрия всегда нуждалась в способах эту параллельность проверить. О признаках параллельных прямых мы и поговорим в этой статье.
Определение для параллельности
Выделим определения, которые необходимо знать для доказательства признаков параллельности двух прямых.
Прямые называют параллельными, если они не имеют точек пересечения. Кроме того, в решениях обычно параллельные прямые идут в связке с секущей линией.
Секущей прямой называется прямая, которая пересекает обе параллельные прямые. В этом случае образуются накрест лежащие, соответственные и односторонние углы. Накрест лежащими будут пары углов 1 и 4; 2 и 3; 8 и 6; 7 и 5. Соответственными будут 7 и 2; 1 и 6; 8 и 4; 3 и 5.
Накрест лежащими будут пары углов 1 и 4; 2 и 3; 8 и 6; 7 и 5. Соответственными будут 7 и 2; 1 и 6; 8 и 4; 3 и 5.
Односторонними 1 и 2; 7 и 6; 8 и 5; 3 и 4.
При правильном оформлении пишется: «Накрест лежащие углы при двум параллельных прямых а и b и секущей с», потому что для двух параллельных прямых может существовать бесконечное множество секущих, поэтому необходимо указывать, какую именно секущую, вы имеете в виду.
Также для доказательства понадобится теорема о внешнем угле треугольника, которая гласит, что внешний угол треугольника равен сумме двух углов треугольника несмежных с ним.
Признаки
Все признаки параллельных прямых завязаны на знание свойств углов и теорему о внешнем угле треугольника.
Признак 1
Две прямые параллельны, если накрест лежащие углы равны.
Рассмотрим две прямые а и b с секущей с. Накрест лежащие углы 1 и 4 равны. Предположим, что прямые не параллельны. Значит прямые пересекаются и должна быть точка пересечения М. Тогда образуется треугольник АВМ с внешним углом 1. Внешний угол должен быть равен сумме углов 4 и АВМ как несмежных с ним по теореме о внешнем угле в треугольнике. Но тогда получится, что угол 1 больше угла 4, а это противоречит условию задачи, значит, точки М не существует, прямые не пересекаются, то есть параллельны.
Тогда образуется треугольник АВМ с внешним углом 1. Внешний угол должен быть равен сумме углов 4 и АВМ как несмежных с ним по теореме о внешнем угле в треугольнике. Но тогда получится, что угол 1 больше угла 4, а это противоречит условию задачи, значит, точки М не существует, прямые не пересекаются, то есть параллельны.
Рис. 1. Рисунок к доказательству.
Признак 2
Две прямые параллельны, если соответственные углы при секущей равны.
Рассмотрим две прямые а и b с секущей с. Соответственные углы 7 и 2 равны. Обратим внимание на угол 3. Он является вертикальным для угла 7. Значит, углы 7 и 3 равны. Значит, углы 3 и 2 также равны, так как
Рис. 2. Рисунок к доказательству.
Признак 3
Две прямые параллельны, если сумма односторонних углов равна 180 градусам.
Рис. 3. Рисунок к доказательству.
Рассмотрим две прямые а и b с секущей с. Сумма односторонних углов 1 и 2 равна 180 градусов. Обратим внимание на углы 1 и 7. Они являются смежными. То есть:
Они являются смежными. То есть:
$$
$$
Вычтем из первого выражения второе:
$$(
$$(
$$
$$
$
Что мы узнали?
Мы в подробностях разобрали, какие углы получаются при рассечении параллельных прямых третьей линией, выделили и подробно расписали доказательство трех признаков параллельности прямых.
Тест по теме
Оценка статьи
Средняя оценка: 4.1 . Всего получено оценок: 220.
Определение 1
Прямую $с$ называют секущей для прямых $а$ и $b$, если она пересекает их в двух точках.
Рассмотрим две прямые $a$ и $b$ и секущую прямую $с$.
При их пересечении возникают углы, которые обозначим цифрами от $1$ до $8$.
У каждого из этих углов есть название, которое часто приходиться употреблять в математике:
- пары углов $3$ и $5$, $4$ и $6$ называются накрест лежащими ;
- пары углов $1$ и $5$, $4$ и $8$, $2$ и $6$, $3$ и $7$ называют соответственными ;
- пары углов $4$ и $5$, $5$ и $6$ называют односторонними .
 {\circ}$.
{\circ}$. - Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A 1 x + B 1 y + C 1 = 0 ; прямая b — A 2 x + B 2 y + C 2 = 0 . Тогда нормальные векторы заданных прямых будут иметь координаты (А 1 , В 1) и (А 2 , В 2) соответственно. Условие параллельности запишем так:
- Прямая a описывается уравнением прямой с угловым коэффициентом вида y = k 1 x + b 1 .
 Прямая b — y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты (k 1 , — 1) и (k 2 , — 1) соответственно, а условие параллельности запишем так:
Прямая b — y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты (k 1 , — 1) и (k 2 , — 1) соответственно, а условие параллельности запишем так: - Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x — x 1 a x = y — y 1 a y и x — x 2 b x = y — y 2 b y или параметрическими уравнениями прямой на плоскости: x = x 1 + λ · a x y = y 1 + λ · a y и x = x 2 + λ · b x y = y 2 + λ · b y .
- Острый угол: угол, значение которого лежит между 0° и 90°, острый угол.
- Тупой угол: Угол, значение которого лежит в пределах от 90° до 180°, является тупым углом.
- Прямой угол: угол, значение которого равно 90°, прямой угол.
- Прямой угол: угол, значение которого равно 180°, является прямым углом.
- Дополнительные углы: Когда сложение двух углов равно 180°, такие углы называются дополнительными углами. Два прямых угла всегда являются дополнительными углами.

- Дополнительные углы: когда сумма двух углов равна 90°, эти углы являются дополнительными углами.
- Смежные углы: Смежными углами называются углы, имеющие общую вершину и общее плечо.
- Вертикально противоположные углы: Если две линии делятся пополам, углы, образующиеся напротив друг друга в точке деления пополам, являются вертикально противоположными углами.
- ∠p = ∠w
- ∠q = ∠x
- ∠г = ∠у
- ∠s = ∠z
- Два соответствующих угла не могут быть соседними углами.
- Два соответствующих угла не могут быть последовательными внутренними углами, так как они не соприкасаются.
- Углы, лежащие против поперечной, являются альтернативными углами.
- Два соответствующих угла будут равны, когда поперечная линия пересечет две параллельные.

- Внутренний и внешний углы соответствуют друг другу тем, что находятся на одной и той же поперечной стороне.
- Дополнительные соответствующие углы (когда сумма равна 180 градусам)
- Дополнительные соответствующие углы (когда сумма равна 90 градусов)
- Обычно окна имеют решетки в виде квадратных коробок или ромбовидных блоков.
 Они образуют соответствующие углы.
Они образуют соответствующие углы. - Мост на гигантском столбе стоит крепко, потому что столбы соединены таким образом, что соответствующие углы равны.
- Железнодорожные пути профессионально спроектированы таким образом, чтобы соответствующие углы были равными.
- Внутренний угол — это угол, лежащий между двумя прямыми, пересекающими поперечную.
- Внешний угол — это угол, который находится выше верхней линии или ниже нижней линии, когда две линии пересекают секущую.
- «Верхняя левая» пара углов : оба угла лежат слева от трансверсали, верхний угол — внешний, а нижний угол — внутренний.
- «Верхний правый» пара углов : оба угла справа от секущей, верхний угол — внешний, а нижний угол — внутренний.
- «Нижняя левая» пара углов : оба угла слева от секущей, верхний угол внутренний, а нижний угол внешний.
- «Нижняя правая» пара уголков : оба угла лежат справа от поперечной, верхний угол внутренний, а нижний угол внешний.
- Углы a и e являются соответствующими углами (пара «верхний левый»)
- Углы d и h являются соответствующими углами (пара «верхний правый»)
- Углы b и f — соответствующие углы («нижняя левая» пара)
- Углы c и g — соответствующие углы («нижняя правая» пара)
- x = y
- x + y = 90
- x = y
- x + y = 90 [Первое уравнение]
- x + x = 90 [y = x, по второму уравнению]
- 2x = 90
- 51 2X = 90
- 51 2x
- 5199999999999999999999999999999999999999999999999999999999999999999999999009н.
 Это также говорит нам о том, что y = 45, поскольку x = y. Итак, если соответствующие углы комплементарны и прямые, пересекающие секущую, параллельны, то оба угла должны иметь градусную меру 45 градусов. Прямые L и M — параллельные прямые, а прямая N — поперечная. Соответствующие углы x и y конгруэнтны, и поскольку один равен 45, другой равен 45, поэтому они дополняют друг друга (сумма их углов равна 9).0 градусов).
Это также говорит нам о том, что y = 45, поскольку x = y. Итак, если соответствующие углы комплементарны и прямые, пересекающие секущую, параллельны, то оба угла должны иметь градусную меру 45 градусов. Прямые L и M — параллельные прямые, а прямая N — поперечная. Соответствующие углы x и y конгруэнтны, и поскольку один равен 45, другой равен 45, поэтому они дополняют друг друга (сумма их углов равна 9).0 градусов).Соответствующие углы дополняют друг друга?
Соответствующие углы могут быть дополнительными, если сумма их величин составляет 180 градусов. Если два угла равны x и y, то мы имеем уравнение:
- x + y = 180
В частном случае параллельных прямых мы знаем из нашего предыдущего обсуждения, что два соответствующих угла конгруэнтны ( равный). То есть у нас есть уравнение:
- x = y
Когда мы объединяем эти два уравнения подстановкой, мы получаем:
- x + y = 180 [first equation]
- x + x = 180 [y = x, by the second equation]
- 2x = 180
- x = 90
Это также говорит нам о том, что y = 90, поскольку x = y.
 Итак, если соответствующие углы дополнительные и прямые, пересекающие секущую, параллельны, то оба угла должны иметь меру 90 градусов (оба прямые).
Итак, если соответствующие углы дополнительные и прямые, пересекающие секущую, параллельны, то оба угла должны иметь меру 90 градусов (оба прямые).Обратите внимание, что это также говорит нам о том, что секущая перпендикулярна двум прямым, и все пары соответствующих углов равны 90 градусов.
Прямые L и M — параллельные прямые, а прямая N — поперечная. Поскольку N перпендикулярно L и M, у нас есть углы 90 градусов. Соответствующие углы x и y конгруэнтны, а так как один равен 90, то другой равен 90, а значит, они дополнительные (сумма их углов равна 180 градусам).Являются ли соответствующие углы прямыми углами?
Соответствующие углы являются прямыми углами (90 градусов) в упомянутом ранее случае: когда две прямые, пересекающие секущую, параллельны, а секущая перпендикулярна этим прямым.
Как решать соответствующие углы
Чтобы решить соответствующие углы, вам могут понадобиться факты о:
- сумме соответствующих углов (в сумме они дают 180, когда линии, пересекающие поперечные, параллельны)
- дополнительные углы (прямой угол равен 180 градусам и состоит из двух смежных углов, когда секущая пересекает прямую)
Пример 1.
 Решение соответствующих углов без переменных
Решение соответствующих углов без переменныхРассмотрим приведенную ниже диаграмму, на которой показан угол x и соответствующий ему угол y. Мы хотим найти значение y.
Прямые L и M — параллельные прямые, а прямая N — поперечная. Мы знаем, что х и у — соответствующие углы, а х = 40 градусов, и мы хотим найти у.Если прямые L и M параллельны, то трансверсаль T дает нам соответствующие углы при x и y. Это означает, что:
- x = y
Поскольку x = 40 градусов, мы знаем, что y также равно 40 градусам. Итак, у = 40,
Пример 2. Решение соответствующих углов без переменных (с использованием дополнительных углов)
Рассмотрим приведенную ниже диаграмму, на которой показан угол x и соответствующий ему угол y. Мы хотим найти значение y.
Прямые L и M — параллельные прямые, а прямая N — поперечная. Мы знаем, что х и у — соответствующие углы, а угол, примыкающий к х, равен 150 градусам, и мы хотим найти у.Если прямые L и M параллельны, то трансверсаль T дает нам соответствующие углы при x и y.
 Это означает, что:
Это означает, что:- x = y
Если мы сможем найти x, то получим и значение y. Мы не знаем х, но знаем, что угол, прилежащий к х, равен 150 градусам.
Так как х и смежный с ним угол являются дополнительными, они в сумме дают 180, что дает нам уравнение: известно, что у тоже 30 градусов, так как х и у соответствующие углы. Итак, у = 30,
Пример 3. Решение соответствующих углов с помощью переменных
Рассмотрим приведенную ниже диаграмму, на которой показан угол 3x + 20 и соответствующий ему угол 5x – 10. Мы хотим найти значение x и найти меру обоих углов.
Прямые L и M — параллельные прямые, а прямая N — поперечная. Мы знаем, что 3x + 20 и 5x — 10 — соответствующие углы, и мы хотим найти меру угла.Если прямые L и M параллельны, то поперечная T дает нам соответствующие углы при 3x + 20 и 5x – 10. Это означает, что:
- 3x + 20 = 5x – 10
- 30 = 2x
- 15 = x
 Используя первый, находим:
Используя первый, находим:- Верхний угол = 3x + 20
- Верхний угол = 3(15) + 20
- Верхний угол = 65
- Нижний угол = 5x – 10
- Нижний угол = 5(15) – 10
- Нижний угол = 65
Угол соответствует 5 градусам.
Пример 4. Решение соответствующих углов с помощью переменных (с использованием дополнительных углов)
Рассмотрим приведенную ниже диаграмму, на которой показан угол 3x + 20 и соответствующий ему угол y. Мы хотим найти значение y.
Прямые L и M — параллельные прямые, а прямая N — поперечная. Мы знаем, что 3x + 30 и y — соответствующие углы, а угол, примыкающий к y, равен 7x — 30, и мы хотим найти y.Если прямые L и M параллельны, то трансверсаль T дает нам соответствующие углы при 3x + 20 и y. Это означает, что:
- y = 3x + 20
Мы не знаем y, но знаем, что угол, прилежащий к y, равен 7x – 30.

Поскольку y и прилежащий к нему угол являются дополнительными, они суммируем 180, что дает нам уравнение:
- y + (7x – 30) = 180
- y = 210 – 7x
Объединяя оба наших уравнения, мы получаем:
- y = 3x + 20 [since y and 3x + 20 are corresponding angles]
- 210 – 7x = 3x + 20 [substitute y = 210 – 7x]
- 190 = 10x
- 19 = x
Поскольку x = 19, мы можем решить для обоих углов. Верхний угол:
- Верхний угол = 3x + 20
- Верхний угол = 3(19) + 20
- Верхний угол = 77
- Нижний угол = y
- Нижний угол = 210 — 7x
- Нижний угол = 210 — 7 (19)
- Нижний угол = 77 99
- Нижний угол = 77 99
- .
 65 градусов для обоих соответствующих углов. Итак, y = 77.
65 градусов для обоих соответствующих углов. Итак, y = 77.Заключение
Теперь вы знаете о соответствующих углах и о том, когда они равны. Вы также знаете о некоторых особых случаях, например, когда соответствующие углы прямые (90 градусов) и как решить для углов.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
~Джонатон
Почему углы равны и доказательства | Хацуди
В математике мы изучаем плоские формы. Одной из важных тем является вертикальный угол, соответствующий угол и альтернативный угол. Эти три угла часто встречаются в задачах, связанных с фигурами. Следовательно, это концепция, которую вы должны понять.
Итак, что такое вертикальные углы, соответствующие углы и альтернативные углы? И каковы их свойства?
Ключом к этим трем углам является идея, что углы одинаковы.
 Если вы задумаетесь, почему углы равны, вы сможете глубже понять математику. Доказательство простое, поэтому давайте также поймем, почему углы равны.
Если вы задумаетесь, почему углы равны, вы сможете глубже понять математику. Доказательство простое, поэтому давайте также поймем, почему углы равны.В этом разделе мы объясним свойства вертикальных углов, соответствующих углов и альтернативных углов, которые важны для плоских фигур, включая причины. 9
- 1.1 Доказательство того, что углы одинаковы и чередующиеся углы имеют одинаковые углы
- 2.2 Причина, по которой углы одинаковы
- 2.3 Существуют четыре модели чередующихся углов
- 3 Упражнения: вертикальный, соответствующий и альтернативный углы
- 4 Изучите правило равенства углов на плоских фигурах
Вертикальный угол на плоских фигурах имеет одинаковый угол
Из видов углов на плоских фигурах мы узнаем о вертикальном угле. Что такое вертикальные углы? Вертикальные углы — это углы, которые обращены друг к другу при пересечении двух прямых.
Например, ниже приведены вертикальные углы.
Углы, находящиеся в таком соотношении, называются вертикальными углами.
 Важно помнить, что вертикальные углы всегда равны. Помните, что если есть два вертикальных угла, ∠A и ∠B, то ∠A = ∠B.
Важно помнить, что вертикальные углы всегда равны. Помните, что если есть два вертикальных угла, ∠A и ∠B, то ∠A = ∠B.Доказательство того, что углы одинаковы
Итак, почему вертикальные углы равны? Это доказательство можно объяснить математическими знаниями, которые мы уже изучили.
Например, предположим, что у нас есть ∠A и ∠B со следующим соотношением.
Угол прямой составляет 180°. Следовательно, угол ∠A можно рассчитать следующим образом.
- $180°-120°=60°$
Таким же образом можно рассчитать ∠B следующим образом.
- $180°-120°=60°$
В этом расчете мы приняли 120°. Даже если предположить, что углы разные, ∠A и ∠B всегда будут одним и тем же углом. Таким образом, мы можем доказать, что вертикальные углы всегда одинаковы.
Понимание связи между соответствующими углами и альтернативными углами
Как только вы поймете, что такое вертикальные углы, вам нужно узнать о соответствующих углах.
 Соответственные углы – это углы, образованные пересечением двух прямых. Углы, которые имеют следующее соотношение, являются соответствующими углами.
Соответственные углы – это углы, образованные пересечением двух прямых. Углы, которые имеют следующее соотношение, являются соответствующими углами.Попробуйте понять соответствующие углы изображения; углы, которые находятся в одном и том же положении для двух прямых, являются соответствующими углами.
На плоских фигурах мы также узнаем о альтернативных углах. Углы со следующим соотношением являются альтернативными углами.
Когда есть соответствующие углы, есть и альтернативные углы. Очень трудно объяснить соответствующие углы и альтернативные углы в предложении. Итак, давайте воспользуемся изображением выше, чтобы вспомнить, что это за углы.
В параллельных прямых соответствующие и альтернативные углы имеют одинаковые углы
Важным случаем соответствующих и альтернативных углов является случай, когда две прямые параллельны. Когда две прямые параллельны, мы имеем следующее.
- Соответственные углы равны.
- Альтернативные углы равны.

Если две прямые не параллельны, то соответствующие углы не равны. Аналогично, противоположные углы не равны. Даже если прямые не параллельны, соответствующие углы и альтернативные углы все равно существуют. Однако для того, чтобы соответствующие углы и альтернативные углы были одинаковыми соответственно, две линии должны быть параллельны.
— Соответствующий угол и альтернативный угол равны
Если мы это поймем, мы увидим, что когда две прямые параллельны, соответствующий угол и альтернативный угол равны. Это связано с тем, что соответствующий угол и альтернативный угол являются отношениями вертикального угла.
Итак, поймите, что для параллельных прямых и соответствующий угол, и альтернативный угол являются одним и тем же углом.
-Символ параллельности ||
Символ параллелизма ||. Например, в случае $l||m$ это означает, что прямые $l$ и $m$ параллельны.
Причина, по которой углы одинаковы
Итак, если две прямые параллельны, почему соответствующие углы и противоположные углы имеют одинаковые углы? Давайте подумаем об этой причине.
 Думая об этой причине, используйте треугольную линейку.
Думая об этой причине, используйте треугольную линейку.Если мы переместим треугольную линейку и нарисуем линию, мы можем провести две параллельные линии. Это следующее.
В результате мы можем создать соответствующие углы для двух параллельных прямых. Поскольку мы используем одну и ту же треугольную линейку, соответствующие углы одинаковы. Таким образом, мы можем видеть, что соответствующие углы одинаковы для параллельных прямых. Мы можем понять, почему соответствующие углы одинаковы, рисуя фигуры без необходимости доказывать их числами.
Кроме того, как упоминалось выше, альтернативные углы и соответствующие углы являются отношениями вертикальных углов. Следовательно, если две прямые параллельны, мы можем понять, что противоположные углы равны.
Есть четыре схемы чередующихся углов
Любой может легко понять соответствующие углы. С другой стороны, когда впервые узнаешь об альтернативных углах, их трудно различить. Итак, давайте попробуем запомнить различные схемы чередующихся углов.
 В частности, мы должны разделить чередующиеся углы на четыре шаблона.
В частности, мы должны разделить чередующиеся углы на четыре шаблона.При понимании альтернативных углов мы можем разделить их на следующие четыре типа.
Под разными углами все они имеют Z-образную форму. В некоторых случаях это может быть открытая буква Z или сжатая буква Z. Но в любом случае форма буквы Z представляет собой альтернативный угол.
Упражнения: вертикальные, соответствующие и альтернативные углы
Q:. Если $l||m$, ответьте на углы от a до d.
A1: Ответы.
(a, b, c)
Ответьте на вертикальный, соответствующий и альтернативный углы соответственно.
- a: 60° (вертикальный угол)
- b: 60° (соответствующий угол)
- c: 110° (альтернативный угол)
(d)
В расширенных вопросах вам будет задано найти угол д. Ничего не делая, нельзя ответить на угол d. Итак, давайте добавим параллельные линии следующим образом.

Складывая линии таким образом, мы можем найти угол d. Используя соответствующий угол и альтернативный угол, мы знаем, что один угол равен 40°, а другой равен 70°. Таким образом, сложив два угла, мы получим d = 110 °.
При ответе на угол на плоской фигуре часто бывает необходимо добавить параллельные линии для решения задачи. Когда вам дается формулировка проблемы, вместо того, чтобы не добавлять строки, активно пытайтесь добавлять строки. Есть много проблем, на которые можно ответить, просто нарисовав параллельные линии.
Изучите правило равенства углов на плоских фигурах
Задачи на углы часто задают в математике. При изучении углов основными являются вертикальные углы, соответствующие углы и альтернативные углы. Если вы не понимаете этих понятий, вы не сможете решить последующие математические задачи.
Рассматривая свойства углов, мы видим следующее.
- Вертикальный угол: Углы всегда равны.
- Соответствующий угол: если прямые параллельны, то углы равны.

- Альтернативный угол: Если прямые параллельны, углы равны.
Помимо вычисления углов, мы также используем вертикальные углы, соответствующие углы и альтернативные углы во многих ситуациях в математике, таких как доказательства конгруэнтности или подобия. Итак, убедитесь, что вы понимаете значение и характеристики этих углов.
Соответствующие углы | Что?, Определение, Теорема, Примеры
Что я узнаю из этой статьи?
Прочитав эту статью, вы сможете:
- правильно определять соответствующие углы;
- знать соответствующую теорему об углах;
- определить соответствующие углы на основе рисунков;
- доказать соответствующую теорему об углах;
- доказать обращение соответствующей теоремы; и
- применяют теоремы при решении задач, связанных с соответствующими углами.
Что такое соответствующие углы?
Когда другая линия, называемая поперечной линией, пересекает две различные линии, углы в углах, образованных в точке пересечения, называются соответствующими углами.
 Соответствующие углы находятся на пересечении двух или более прямых линий, находящихся в одном и том же относительном положении.
Соответствующие углы находятся на пересечении двух или более прямых линий, находящихся в одном и том же относительном положении.Соответственные углы, образованные непараллельными прямыми
Если существуют хотя бы две непараллельные прямые, которые не равны, то соответствующие углы между ними не имеют отношения и не равны.
Например, прямая 1 и прямая 2 являются непараллельными прямыми, разделенными поперечной линией, прямой 3.
Таким образом, мы можем сказать, что ∠1 и ∠2 являются соответствующими углами. Однако меры этих углов не связаны друг с другом.
Соответствующие углы, образованные параллельными прямыми
Когда две параллельные прямые пересекаются с третьей прямой (поперечной линией), углы, находящиеся в одном и том же относительном положении на каждом пересечении, называются соответствующими углами.
Скажем, например,
На рисунке выше показаны соответствующие углы. Таким образом, интерпретируя рисунок:
- Линия 1 и Линия 2 параллельны;
- Линия 3 пересекается с линиями 1 и 3;
- Углы 1 и 2 имеют одинаковое относительное положение.

Таким образом, мы можем заключить, что углы 1 и 2 являются соответствующими углами.
Какие существуют теоремы о соответствующих углах?
Есть две теоремы о соответствующих углах.
Теорема о соответствующем угле
Теорема о соответствующем угле утверждает, что
Если прямая пересекает две параллельные прямые, то соответствующие углы в этих двух пересечениях равны.
Скажем, например,
На рисунке, поскольку мы знаем, что линия 1 ∥ линия 2 и линия 3 являются поперечными линиями, то ∠1 соответствует ∠2. Следовательно, мы можем сказать, что угол, который существует между ними, равен. Таким образом, если ∠1=60°, то ∠2=60°.
Обратная теорема о соответствующем угле
Обратная теорема о соответствующем угле утверждает, что
Если соответствующие углы в двух областях пересечения конгруэнтны, то две прямые называются параллельными.
Обратите внимание:
- Пара соответствующих углов лежит по одну сторону от поперечной линии.

- Один внешний угол и один внутренний угол составляют соответствующую пару углов.
- Не все соответствующие углы равны. Если секущая пересекает две параллельные прямые, то соответствующие углы равны. Когда секущая пересекает непараллельные прямые, образующиеся углы неконгруэнтны и не связаны между собой.
- Смежные углы образуются при перпендикулярном пересечении секущей двух параллельных прямых.
- Если прямые параллельны, то внешние углы по одну сторону от секущей являются дополнительными. Точно так же, если две прямые параллельны, внутренние углы являются дополнительными.
Какие доказательства теорем о соответствующих углах?
Доказательство теоремы о соответствующем угле
Предположим, что прямые A и прямые B параллельны.
Докажите, что соответствующие углы равны.
Предположим, что прямая A параллельна прямой B. Если отдельная прямая M пересекается с прямыми A и B, то мы можем обозначить углы α, β и γ, как показано на рисунке.

По определению соответствующих углов мы можем сказать, что γ соответствует β.
Поскольку α и γ лежат на одной прямой, по постулату линейной пары мы можем заключить, что сумма α и γ равна 180°. Таким образом, γ=180°-α.
Поскольку β и α образуют внутренний и внешний углы параллельных прямых, отсюда также следует, что β является дополнительным к α. Таким образом, мы можем сделать вывод, что β=180°-α. Тогда у нас будет
γ=180°-α; и β=180°-α.
Следовательно, γ=β.
Следовательно, соответствующие углы равны друг другу.
Доказательство обратной теоремы о соответствующих углах
Предположим, что соответствующие углы равны.
Докажите, что прямая P и прямая Q параллельны.
Предположим, что две различные прямые P и Q пересекаются поперечной линией T и при условии, что соответствующие углы равны, тогда мы можем обозначить углы как α и β, как показано на рисунке.
Согласно постулату линейной пары, мы можем обозначить каждую пару соответствующих углов как α или β.
 Поскольку для каждой пары углов α и β сумма равна 180 °, а внутренние углы равны. Таким образом, согласно теореме, обратной той же теореме о внутреннем углу, прямая P и прямая Q параллельны.
Поскольку для каждой пары углов α и β сумма равна 180 °, а внутренние углы равны. Таким образом, согласно теореме, обратной той же теореме о внутреннем углу, прямая P и прямая Q параллельны.Следовательно, $\overleftrightarrow{P} ∥ \overleftrightarrow{Q}$.
Как найти соответствующие углы?
Если две параллельные прямые пересечь поперечной линией, то каждая точка пересечения образует четыре угла. Таким образом, если каждый из четырех углов в первой области пересечения будет иметь еще один с тем же относительным положением во втором пересечении.
Давайте посмотрим на образец ниже.
На данном рисунке углы, соответствующие друг другу,
- ∠1 и ∠2, где оба угла расположены в верхней правой части линий 1 и 2;
- ∠2 и ∠6, где оба угла расположены в нижней правой части линий 1 и 2;
- ∠3 и ∠7, где оба угла расположены в верхней левой части линий 1 и 2; и
- ∠4 и ∠8, где оба угла расположены в верхней левой части линий 1 и 2.

Пример #1Определите соответствующие углы на рисунке.
Решение
На данном рисунке, где прямые S и прямые T параллельны друг другу, они пересекаются поперечной линией Q. Таким образом, по соответствующей теореме об углах,
Создавая углы из точки пересечения линии S и линии Q, а также линии T и линии Q, мы будем иметь следующие углы, соответствующие друг другу.
- ∠1 соответствует ∠6;
- ∠2 соответствует ∠5;
- ∠3 соответствует ∠8; а
- ∠4 соответствует ∠7.
Пример #2Определите соответствующие углы на рисунке ниже.
Решение
На рисунке видно, что поперечная B пересекается с прямыми A и C, которые не параллельны. Таким образом, соответствующие углы равны:
- ∠1 соответствует ∠5;
- ∠2 соответствует ∠8;
- ∠3 соответствует ∠7; а
- ∠4 соответствует ∠6.

Хотя они могут соответствовать друг другу, измерения их углов не имеют отношения друг к другу.
Пример #4
Рассмотрим окно ниже. Определите соответствующие углы, которые могут быть образованы внутри окна. Сколько пар соответствующих углов внутри окна?
Решение
По определению соответствующих углов мы можем назвать каждую пару соответствующих углов в окнах как:
Таким образом,
- ∠A соответствует ∠B;
- ∠C соответствует ∠D;
- ∠E соответствует ∠F;
- ∠G соответствует ∠H;
- ∠I соответствует ∠J;
- ∠K соответствует ∠L;
- ∠M соответствует ∠N; а
- ∠O соответствует ∠P
Следовательно, внутри окна 8 пар соответствующих углов.
Решение задач на соответствующие углы
Чтобы решить задачи на соответствующие углы:
- Определить соответствующие углы.
- Используйте теорему о соответствующих углах, которая утверждает, что соответствующие углы равны.

Пример #1
Определите угловую меру ∠1, если линия 1 ∥ линия 2 и пересекается поперечной линией.
Решение
Как указано в задаче, существуют прямые 1 и 2, которые параллельны друг другу и пересекаются поперечной линией, прямой 3. Приведенная цифра говорит о том, что ∠2=55°. Таким образом, по соответствующей теореме об углах ∠1=55°.
Следовательно, ∠1=55°.
Пример #2
Какова мера ∠2 и значение x на основе данной цифры?
Решение
На основании рисунка можно сказать, что ∠1 и ∠2 соответствуют друг другу. Таким образом,
∠1=∠2. Путем замены∠1=∠2
60=3x+10
3x=60-10
3x=50
x=16,67Следовательно, значение x равно 16,67, а мера ∠2=60°.
Пример №3
Рассмотрим рисунок ниже. Определите значение x и угловые меры ∠2 и ∠4, если дороги параллельны друг другу.
Решение:
Как указано в задаче, две дороги параллельны друг другу.
 Таким образом, ∠1 соответствует ∠2, а ∠3 соответствует ∠4.
Таким образом, ∠1 соответствует ∠2, а ∠3 соответствует ∠4.Шаг 1: Найдите угловую меру ∠2. По теореме о соответствующих углах, если два угла соответствуют друг другу и линии между ними параллельны, то они конгруэнтны. Таким образом, если ∠1=110°, то ∠2=110°.
Шаг 2: Найдите значение x в ∠4=13x+5. Поскольку ∠3 соответствует ∠4, то∠3 = 4
70 = 13x + 5
13x = 70-5
13x=65
13x/13 = 65/13
x = 5Следовательно, мера угла ∠2=110° и ∠4=70°. Значение x равно 5.
Каково значение соответствующих углов?
Многочисленные применения соответствующих углов остаются незамеченными, например:
- Окна оснащены горизонтальными и вертикальными решетками, образующими несколько квадратов. Каждой вершине квадрата соответствует один из углов.
- Мосты поддерживаются столбами. Каждый столб соединен таким образом, что углы соответствующих столбов равны.

- Железнодорожные пути спроектированы таким образом, что все соответствующие углы на пути равны.
Рекомендуемые рабочие листы
Тупоугольные треугольники (на тему магазина игрушек) Рабочие листы по математике
Разносторонние треугольники (на тему летнего лагеря) Рабочие листы по математике
Параллельные линии, разрезанные поперечной Рабочие листы по математике для 8-го классаПросмотреть все рабочие листы
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Доказательство конгруэнтности соответствующих углов с помощью жестких движений
CCSS-M.G-CO.C.9. Докажите теоремы о прямых и углах. Теоремы включают в себя: вертикальные углы конгруэнтны; , когда секущая пересекает параллельные прямые, чередующиеся внутренние углы конгруэнтны и соответствующие углы конгруэнтны ; точки на серединном перпендикуляре к отрезку равноудалены от концов отрезка.

Доказав, что вертикальные углы конгруэнтны, мы обратили внимание на углы, образованные параллельными прямыми, пересеченными секущей.
Мои ученики приходят в школу геометрии, имея опыт работы с отношениями измерения углов, когда параллельные прямые пересекаются секущими. Но они не думали о том, почему.
Мы понимаем Евклида 5 th Постулат (формулировка ниже из «Разруби узел»):
Если прямая линия, пересекающая две прямые, делает внутренние углы с одной и той же стороны меньше двух прямых, то две прямые, если их продолжить бесконечно, пересекутся на той стороне, на которой это углы, меньшие двух прямых углов.
Мы используем программу динамической геометрии для изучения параллельных прямых и поперечных:
И затем традиционно мы допускаем конгруэнтность соответствующих углов, когда параллельные прямые пересекаются поперечными, как постулат в нашей дедуктивной системе. Студентам понятно, что соответствующие углы равны.
 Затем, как только мы допустили это, не так уж плохо доказать, что альтернативные внутренние углы конгруэнтны, когда параллельные прямые пересекаются секущей.
Затем, как только мы допустили это, не так уж плохо доказать, что альтернативные внутренние углы конгруэнтны, когда параллельные прямые пересекаются секущей.Но мы задаемся вопросом, должны ли мы вводить соответствующие углы в качестве постулата. Можем ли мы использовать жесткие движения, чтобы показать, что соответствующие углы конгруэнтны?
Один студент предложил построить середину X отрезка BE. Затем мы провели параллель между прямыми m и n через X. Это не очень помогло нам показать, что соответствующие углы конгруэнтны. (изображение вверху слева)
Другой студент предложил перевести линию м с помощью вектора BE. Так что мы действительно перевели больше, чем просто строку м . Мы действительно перевели верхний полуплан, образованный линией м . Мы использовали снимок верхней части диаграммы (линия м и выше) и транслировали его с помощью вектора BE. На рисунке справа мы можем видеть, что m отображается в n , а трансверсаль — в себя, и поэтому мы заключаем (нижнее левое изображение), что ∠CBA конгруэнтна ∠DEB: если две параллельные прямые разрезать секущей соответствующие углы равны.

Если соответствующие углы конгруэнтны, то доказательство конгруэнтности альтернативных внутренних (или внешних) углов или последовательных внутренних (или внешних) дополнительных углов, когда две параллельные прямые пересекаются секущей, следует с использованием комбинации конгруэнтных вертикальных углов, переходных и/или замещающих , Конгруэнтные добавки.
Но можем ли мы доказать, что параллельные внутренние углы конгруэнтны, если параллельные прямые пересекаются секущей с использованием жестких движений?
Несколько студентов предложили нам сделать такой же перевод (перевести «верхнюю» параллельную линию на «нижнюю» параллельную линию). ∠2≅∠2’ из-за перевода (и потому что они соответствуют), и мы можем сказать, что ∠2’≅∠3, так как мы уже доказали, что вертикальные углы конгруэнтны. ∠2≅∠3 с использованием транзитивного свойства конгруэнтности. Мы заключаем, что при пересечении двух параллельных прямых секущей внутренние смежные углы равны.
Другая команда предложила построить середину M отрезка XY (верхнее изображение).
 Они повернули данные линии и поперечные на 180˚ относительно М (нижнее изображение). ∠2 было перенесено на ∠3, а ∠3 было перенесено на ∠2. Мы заключаем, что при пересечении двух параллельных прямых секущей внутренние смежные углы равны.
Они повернули данные линии и поперечные на 180˚ относительно М (нижнее изображение). ∠2 было перенесено на ∠3, а ∠3 было перенесено на ∠2. Мы заключаем, что при пересечении двух параллельных прямых секущей внутренние смежные углы равны.Другая команда построила ту же самую среднюю точку, что и выше, с линией, параллельной данным линиям, проходящей через эту среднюю точку. Они отразили всю диаграмму об этой линии, которая создала линию красным цветом. Они использовали углы при основании равнобедренного треугольника, чтобы показать, что альтернативные внутренние углы конгруэнтны.
Примечание 1: Мы по-прежнему постулируем, что через точку, не лежащую на прямой, проходит ровно одна прямая, параллельная данной прямой. Это то, что учебники, которые я использовал в прошлом, называли параллельным постулатом . И мы постулируем, что расстояние между параллельными прямыми постоянно.
Примечание 2. На самом деле мы не доказали, что углы при основании равнобедренного треугольника равны.
 Но ученики определенно знают, что это правда, из своей работы в средней школе. Доказательство скоро будет.
Но ученики определенно знают, что это правда, из своей работы в средней школе. Доказательство скоро будет.Примечание 3: Многие из этих же идей покажут, что последовательные (или односторонние) внутренние углы являются дополнительными. Мы можем использовать жесткие движения, чтобы изображения двух последовательных внутренних углов образовывали линейную пару.
После урока коллега предложил иллюстративную задачу по математике на конгруэнтные углы, образованные параллельными прямыми и поперечной, которая помогла мне обдумать обоснованность аргументов, выдвинутых моими учениками. По мере того, как путешествие продолжается, я нахожу задачи, комментарии и решения по IM своим собственным учебником — динамичным ресурсом для учащихся, молодых и старых.
Теги: CCSS-M.G-CO.C.9, Геометрия Nspired, Иллюстративная математика, Параллельные линии, пересекаемые секущей, Доказательство конгруэнтности альтернативных внутренних углов с использованием жестких движений, Доказательство конгруэнтности соответствующих углов с использованием жестких движений, Жесткие движения, TI -Nspire Technology
√ Соответствующие углы (теорема и примеры)
Угол образован двумя лучами, имеющими общую конечную точку.
 Есть несколько видов углов. Они здесь.
Есть несколько видов углов. Они здесь.Содержание
Тип угла
В общем, существует несколько видов углов:
1. Острый угол (менее 90°)
Подробнее о острый угол .
2. Прямой угол (90°)
3. Тупой угол (больше 90°, но меньше 180°)
Подробнее о тупой угол .
4. Прямой угол (180°)
5. Угол отражения (более 180°)
Узнайте больше о Угол отражения .
Если две параллельные прямые пересечены другой прямой (поперечной), то существуют углы, имеющие одинаковую меру (одинаковую величину), которые называются соответствующими углами .
Теорема о соответствующих ангелахТеорема о соответствующих углах утверждает, что
«Если секущая пересекает две параллельные прямые, их соответствующие углы равны»
На основании теоремы существует восемь углов, которые можно использовать для решения задач с углами
Подробнее смотрите на рисунке.

Судя по рисунку, линии a параллельны линиям b и пересекаются линией c , поэтому существуют углы, имеющие одинаковую меру (одинаковую величину), которые называются соответствующими углами.
На основании теоремы существуют:
1. Чередующиеся внутренние углы
Пара чередующихся внутренних углов одинаковой величины. Судя по рисунку, альтернативные внутренние углы: ∠a 4 = ∠b 2 и ∠a 4 = ∠b 2 .
2. Альтернативные внешние углы
Пара альтернативных внешних углов одинаковой величины. Судя по рисунку, альтернативные внутренние углы: ∠a 1 = ∠b 3 и ∠a 2 = ∠b 4 .
3. Последовательные внутренние углы
Сумма пары последовательных внутренних углов равна 180°. Это ∠a 4 + ∠b 1 = 180° и ∠a 3 + ∠b 2 = 180°.

4. Смежные внешние углы
Сумма пары последовательных внешних углов равна 180°. Это ∠a 1 + ∠b 4 = 180° и ∠a 2 + ∠b 3 = 180°.
5. Соответствующие углы
Пара соответствующих углов имеет одинаковую меру. Судя по картинке, они ∠a 1 = ↑B 1 , ♂ 2 = ♂ 2 , ♂ 3 = ♂ 3 и ♂ 4 = тна .
6. Вертикальные углы
Пара вертикальных углов одинаковой величины. На основе картинки они являются ♂ 1 = ♂ 3 , секрета ∠б 4 . Его также называют ∠a 1 , противоположным ∠a 9.1367 3.
Примеры соответствующих углов- Найдите a, b и c!
Ответ
Используя теорему о соответствующих углах,
- ∠x имеет одинаковую меру с противоположными углами, поэтому это x (вертикальные углы).

- ∠x (по предыдущей причине) и ∠(x+40)° – это последовательные внутренние углы, поэтому сумма составляет 180 °.
х + 40 o + х = 180 o
2x + 40 o = 180 O
2x = 140 O
x = 70 O
- TAPOSE ONPOSE OF RT (x+40) ° SO, так что это так же, что это так, что это так, и такая же показатель = 7011111. о + 40 о = 110 о
- Сумма ∠b и ∠a равна 180°. Это потому, что они являются дополнительными углами.
Кроме того, ∠b можно найти, исходя из того, что ∠b дополняет ∠(x+40)° , так что сумма равна 180°, или исходя из того, что ∠b и ∠x являются альтернативными внутренними углами, поэтому они имеют такая же мера.
2. Найдите х!
Ответ
Проведя еще одну линию между двумя параллельными линиями на картинке, вы легко решите эту задачу. Назовите это линиями a, b и c.
- Так как ∠y является дополнительным углом к ∠30° , поэтому ∠y = 150° (мы предполагаем, что ∠y есть)
- Сосредоточьтесь на линиях b и c, поэтому мы имеем:
(Используя альтернативные внутренние углы и последовательные внутренние углы)
- Сосредоточьтесь на линиях a и b (используя последовательные внутренние углы)
- Теперь посмотрите на x.
 это сумма углов при вершине и основании линии b.
это сумма углов при вершине и основании линии b.
x = 45 o + 30 o = 75 o
3. Значения двух соответствующих углов равны p – 15° и 3p – 5°. Определить величину каждого соответствующего угла.
Ответ
Сначала определите угол p.
Соответствующий угол означает их сумму 180°
p – 15° + 3p – 5° = 180°
4p – 20° = 180°
4p = 200 °
P = 50 °
Затем величина каждого соответствующего углов:
- P — 15 ° = 50 ° — 15 ° = 35 °
- 3P — 5 = 3 (50 ° = 35 °
- 3P — 5 = 3 (50 ° ) – 5° = 145°.
4. Посмотрите на схему.
Определить угол b + 2d – e.
Ответ
- Известный угол равен 135°, пусть он равен x.
Тогда b + x = 180° (дополнительный угол)
B + 135 ° = 180 °
B = 45 °
- Сумма B и D составляет 180 ° (последовательный внутренний угол)
B + D = 180 °
45 ° + D = 180 °
d = 135° (чередующийся внутренний угол с x)
- e дополняет d.
 Это также альтернативный внутренний угол. Следовательно, e = b = 45°.
Это также альтернативный внутренний угол. Следовательно, e = b = 45°. - Итак, b + 2d – e = 45° + 2(135°) – 45° = 270°.
5. Есть две линии, m и n. Они параллельны. Они пересекаются прямой линией с именем k. Если наименьший угол 2х+10, а самый большой 11х-25. Определить значение х.
Ответ
Исходя из задачи, схема линий
Существует только два вида углов. Пусть «а» — наименьший угол, а «b» — наибольший угол. Почему? Помните о соответствующих углах.
A = 2x + 10
B = 11x-25
A + B = 180 ° (дополнительный угол)
Затем
2x + 10 + 11x-25 = 180 °
13x-15 = 180 °
13x = 195°
x = 15°
значит, значение x равно 15°.
6. Посмотрите на фигуру
Если AC//DE, определите x.
Ответ
Первый шаг — фокус на РEDB. Это дополнительный угол РАДЭ, тогда он равен 180° – 65° = 115°.
Далее сосредоточьтесь на ∆DBE.

Согласно III-му признаку параллельности прямых $a \parallel b$. Утверждение доказано.
Пример 3
Дано : $\bigtriangleup ABC=\bigtriangleup ADB$.
Доказать : $AC \parallel BD$, $AD \parallel BC$.
Доказательство :
У рассматриваемых рисунков сторона $АВ$ – общая.
Т.к. треугольники $АВС$ и $ADB$ равны, то $AD=CB$, $AC=BD$, а также соответствующие углы равны $∠1=∠2$, $∠3=∠4$, $∠5=∠6$.
Пара углов $3$ и $4$ – накрест лежащие для прямых $АС$ и $BD$ и соответствующей секущей $АВ$, поэтому согласно I-му признаку параллельности прямых $AC \parallel BD$.
Пара углов $5$ и $6$ – накрест лежащие для прямых $AD$ и $BC$ и соответствующей секущей $АВ$, поэтому согласно I-му признаку параллельности прямых $AD \parallel BC$.
Видеоурок «Признаки параллельности двух прямых» содержит доказательство теорем, которые описывают признаки, означающие параллельность прямых. При этом в видео описывается 1) теорема о параллельности прямых, при которых секущей созданы равные углы, 2) признак, означающий параллельность двух прямых — по равным образованным соответственным углам, 3) признак, означающий параллельность двух прямых в случае, когда при их пересечении секущей односторонние углы в сумме составляют 180°. Задача данного видеоурока — ознакомить учеников с признаками, означающими параллельность двух прямых, знание которых необходимо для решения многих практических задач, наглядно представить доказательство данных теорем, формировать навыки в доказательстве геометрических утверждений.
Задача данного видеоурока — ознакомить учеников с признаками, означающими параллельность двух прямых, знание которых необходимо для решения многих практических задач, наглядно представить доказательство данных теорем, формировать навыки в доказательстве геометрических утверждений.
Преимущества видеоурока связаны с тем, что при помощи анимации, голосового сопровождения, возможности выделения цветом, он обеспечивает высокую степень наглядности, может послужить заменой подачи стандартного блока нового учебного материала учителем.
Начинается видеоурок с выведения на экран названия. Перед описанием признаков параллельности прямых ученики знакомятся с понятием секущей. Дается определение секущей как прямой, которая пересекает другие прямые. На экране изображены две прямые a и b, которые пересекаются прямой с. Построенная прямая с выделена синим цветом, акцентируя внимание на том, что они является секущей данных прямых а и b. Для того чтобы рассматривать признаки параллельности прямых необходимо более детально ознакомиться с областью пересечения прямых. Секущая в точках пересечения с прямыми образует 8 углов ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, ∠8, анализируя соотношения которых можно вывести признаки параллельности данных прямых. Отмечается, что углы ∠3 и ∠5, а также ∠2 и ∠4 называются накрест лежащими. Дается подробное объяснение при помощи анимации расположения накрест лежащих углов как углов, которые лежат между параллельными прямыми, и примыкают к прямым, располагаясь накрест. Затем дается понятие односторонних углов, в число которых входят пары ∠4 и ∠5, а также ∠3 и ∠6. Также указываются пары соответственных углов, которых на построенном изображении 4 пары — ∠1-∠5, ∠4-∠8, ∠2-∠6, ∠3-∠7.
Секущая в точках пересечения с прямыми образует 8 углов ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, ∠8, анализируя соотношения которых можно вывести признаки параллельности данных прямых. Отмечается, что углы ∠3 и ∠5, а также ∠2 и ∠4 называются накрест лежащими. Дается подробное объяснение при помощи анимации расположения накрест лежащих углов как углов, которые лежат между параллельными прямыми, и примыкают к прямым, располагаясь накрест. Затем дается понятие односторонних углов, в число которых входят пары ∠4 и ∠5, а также ∠3 и ∠6. Также указываются пары соответственных углов, которых на построенном изображении 4 пары — ∠1-∠5, ∠4-∠8, ∠2-∠6, ∠3-∠7.
В следующей части видеоурока рассматриваются три признака параллельности любых двух прямых. На экран выводится первое описание. Теорема утверждает, что при равенстве накрест лежащих углов, образуемых секущей, данные прямые будут параллельны. Утверждение сопровождается рисунком, на котором изображены две прямые а и b и секущая АВ. Отмечается, что образуемые накрест лежащие углы ∠1 и ∠2 равны между собой. Данное утверждение требует доказательства.
Данное утверждение требует доказательства.
Наиболее просто доказываемый частный случай — когда данные образуемые накрест лежащие углы являются прямыми. Это означает, что секущая является перпендикуляром к прямым, а по уже доказанной теореме в этом случае прямые а и b не будут пересекаться, то есть являются параллельными. Доказательство для данного частного случая описывается на примере изображения, построенного рядом с первым рисунком, выделяя важные детали доказательства при помощи анимации.
Для доказательства в общем случае необходимо проведение дополнительного перпендикуляра из середины отрезка АВ на прямую а. Далее на прямой b откладывается отрезок ВН 1 , равный отрезку АН. Из полученной при этом точки Н 1 проводится отрезок, соединяющий точки О и Н 1 . Далее рассматриваются два треугольника ΔОНА и ΔОВН 1 , равенство которых доказывается по первому признаку равенства двух треугольников. Стороны ОА и ОВ равны по построению, так как точка О отмечалась как середина отрезка АВ. Стороны НА и Н 1 В также равны по построению, так как мы откладывали отрезок Н 1 В, равный НА. А углы ∠1=∠2 по условию задачи. Так как образованные треугольники равны между собой, то и соответствующие оставшиеся пары углов и сторон также равны между собой. Из этого следует, что и отрезок ОН 1 является продолжением отрезка ОН, составляя один отрезок НН 1 . При этом отмечается, что так как построенный отрезок ОН — перпендикуляр к прямой а, то соответственно и отрезок НН 1 является перпендикулярным к прямым а и b. Данный факт означает, используя теорему о параллельности прямых, к которым построен один перпендикуляр, что данные прямые а и b являются параллельными.
Стороны НА и Н 1 В также равны по построению, так как мы откладывали отрезок Н 1 В, равный НА. А углы ∠1=∠2 по условию задачи. Так как образованные треугольники равны между собой, то и соответствующие оставшиеся пары углов и сторон также равны между собой. Из этого следует, что и отрезок ОН 1 является продолжением отрезка ОН, составляя один отрезок НН 1 . При этом отмечается, что так как построенный отрезок ОН — перпендикуляр к прямой а, то соответственно и отрезок НН 1 является перпендикулярным к прямым а и b. Данный факт означает, используя теорему о параллельности прямых, к которым построен один перпендикуляр, что данные прямые а и b являются параллельными.
Следующая теорема, требующая доказательства — признак равенства параллельных прямых по равенству соответственных углов, образованных при пересечении секущей. Утверждение указанной теоремы выведено на экран и может быть предложено под запись учениками. Доказательство начинается с построения на экране двух параллельных прямых а и b, к которым построена секущая с. Выделенная на рисунке синим цветом. Секущей образованы соответственные углы ∠1 и ∠2, которые по условию равны между собой. Также отмечаются смежные углы ∠3 и ∠4. ∠2 по отношению к углу ∠3 является вертикальным углом. А вертикальные углы всегда равны. К тому же углы ∠1 и ∠3 являются накрест лежащими между собой — их равенство (по уже доказанному утверждению) означает, что прямые а и b параллельны. Теорема доказана.
Выделенная на рисунке синим цветом. Секущей образованы соответственные углы ∠1 и ∠2, которые по условию равны между собой. Также отмечаются смежные углы ∠3 и ∠4. ∠2 по отношению к углу ∠3 является вертикальным углом. А вертикальные углы всегда равны. К тому же углы ∠1 и ∠3 являются накрест лежащими между собой — их равенство (по уже доказанному утверждению) означает, что прямые а и b параллельны. Теорема доказана.
Последняя часть видеоурока посвящена доказательству утверждения о том, что если сумма односторонних углов, которые образованы при пересечении двух некоторых прямых секущей прямой, будет равняться 180°, в этом случае данные прямые будут параллельны между собой. Доказательство демонстрируется, используя рисунок, на котором изображены прямые а и b, пересекающиеся с секущей с. Образованные пересечением углы отмечены аналогично предыдущему доказательству. По условию, сумма углов ∠1 и ∠4 равна 180°. При этом известно, что сумма углов ∠3 и ∠4 равна 180°, так как они являются смежными. Это означает, что углы ∠1 и ∠3 равны между собой. Данный вывод дает право утверждать, что прямые а и b параллельны. Теорема доказана.
Это означает, что углы ∠1 и ∠3 равны между собой. Данный вывод дает право утверждать, что прямые а и b параллельны. Теорема доказана.
Видеоурок «Признаки параллельности двух прямых» может быть использован учителем в качестве самостоятельного блока, демонстрирующего доказательства названных теорем, заменяющего объяснение учителя или сопровождающего его. А подробное объяснение дает возможность использовать материал для самостоятельного изучения учениками и поможет в объяснении материала при дистанционном обучении.
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Определение 1
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.
Определение 2
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.
Чтобы обозначить параллельность прямых, общепринято использовать символ ∥ . Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b . Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b , или прямая b параллельна прямой а.
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Аксиома
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Теорема 1
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10 — 11 классов).
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Определение 3
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:
Теорема 2
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:
Доказательство указанных условий присутствует в программе геометрии за 7 — 9 классы.
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
Теорема 3
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
Этот признак доказывается на основе аксиомы параллельности, указанной выше.
Теорема 4
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
Теорема 5
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
Теорема 6
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Проиллюстрируем:
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т. д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Теорема 7
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a → = (a x , a y) и b → = (b x , b y) являются направляющими векторами прямых a и b ;
и n b → = (n b x , n b y) являются нормальными векторами прямых a и b , то указанное выше необходимое и достаточное условие запишем так: a → = t · b → ⇔ a x = t · b x a y = t · b y или n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y или a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.
A 1 = t · A 2 B 1 = t · B 2
k 1 = t · k 2 — 1 = t · (- 1) ⇔ k 1 = t · k 2 t = 1 ⇔ k 1 = k 2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
Тогда направляющие векторы заданных прямых будут: a x , a y и b x , b y соответственно, а условие параллельности запишем так:
a x = t · b x a y = t · b y
Разберем примеры.
Пример 1
Заданы две прямые: 2 x — 3 y + 1 = 0 и x 1 2 + y 5 = 1 . Необходимо определить, параллельны ли они.
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y — 1 = 0
Мы видим, что n a → = (2 , — 3) — нормальный вектор прямой 2 x — 3 y + 1 = 0 , а n b → = 2 , 1 5 — нормальный вектор прямой x 1 2 + y 5 = 1 .
Полученные векторы не являются коллинеарными, т.к. не существует такого значения t , при котором будет верно равенство:
2 = t · 2 — 3 = t · 1 5 ⇔ t = 1 — 3 = t · 1 5 ⇔ t = 1 — 3 = 1 5
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Пример 2
Заданы прямые y = 2 x + 1 и x 1 = y — 4 2 . Параллельны ли они?
Решение
Преобразуем каноническое уравнение прямой x 1 = y — 4 2 к уравнению прямой с угловым коэффициентом:
x 1 = y — 4 2 ⇔ 1 · (y — 4) = 2 x ⇔ y = 2 x + 4
Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2 x + 1 , например, (0 , 1) , координаты этой точки не отвечают уравнению прямой x 1 = y — 4 2 , а значит прямые не совпадают.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Нормальный вектор прямой y = 2 x + 1 это вектор n a → = (2 , — 1) , а направляющий вектором второй заданной прямой является b → = (1 , 2) . Скалярное произведение этих векторов равно нулю:
n a → , b → = 2 · 1 + (- 1) · 2 = 0
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Теорема 8
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a → = (a x , a y , a z) и b → = (b x , b y , b z) являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t , чтобы выполнялось равенство:
a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z
Пример 3
Заданы прямые x 1 = y — 2 0 = z + 1 — 3 и x = 2 + 2 λ y = 1 z = — 3 — 6 λ . Необходимо доказать параллельность этих прямых.
Решение
Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a → и b → заданных прямых имеют координаты: (1 , 0 , — 3) и (2 , 0 , — 6) .
1 = t · 2 0 = t · 0 — 3 = t · — 6 ⇔ t = 1 2 , то a → = 1 2 · b → .
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
соответствующих углов | Решенные примеры
Прежде чем перейти к соответствующим углам, давайте вспомним, что такое параллельные прямые, поперечные прямые и непараллельные прямые. Параллельные прямые — это две или более прямых, которые никогда не пересекаются и не встречаются в двухмерной плоскости. В то время как непараллельные прямые пересекаются и встречаются в одной точке. Поперечная линия проходит через две другие прямые, независимо от их параллельности.
Соответствующие углы — это углы, образованные в соответствующих углах с поперечной линией. При пересечении двух параллельных прямых какой-либо другой прямой, т. е. поперечной, образуются соответствующие углы. Например, углы p и w являются соответствующими углами на данном рисунке. Это углы, занимающие относительное положение на пересечении с секущей. Если эти прямые параллельны, то соответствующие образующиеся углы также равны. Эти соответствующие углы являются типом пары углов. Они могут иметь как альтернативные внутренние углы, так и альтернативные внешние углы.
Это углы, занимающие относительное положение на пересечении с секущей. Если эти прямые параллельны, то соответствующие образующиеся углы также равны. Эти соответствующие углы являются типом пары углов. Они могут иметь как альтернативные внутренние углы, так и альтернативные внешние углы.
Типы углов:
Различные типы углов могут образовываться при пересечении двух или более линий. Кратко обсудим их:
Поняв, что такое соответствующие углы, давайте разберемся с их типами. Мы знаем, что поперечная линия может пересекать две параллельные или непараллельные прямые. Таким образом, эти углы бывают двух видов:
1. Соответственные углы, включающие параллельные прямые и секущие При пересечении поперечной прямой двух заданных параллельных прямых соответствующие углы, образующиеся, имеют одинаковую меру. Например, две параллельные прямые на рисунке пересекаются секущей. Она образует восемь углов с поперечной линией. Итак, углы при пересечении первой прямой с секущей имеют равные соответствующие углы, образованные пересечением второй прямой с секущей. Следовательно,
Итак, углы при пересечении первой прямой с секущей имеют равные соответствующие углы, образованные пересечением второй прямой с секущей. Следовательно,
Здесь
∠p = ∠s, ∠q = ∠r, ∠w = ∠z и ∠x = ∠y — пары вертикально противоположных углов.
2. Соответствующие углы, включая непараллельные прямые и секущиеПри пересечении поперечной прямой двух непараллельных прямых соответствующие углы не будут иметь отношения и будут неравны. Они будут соответствующими, но не равными.
Они бывают двух типов в зависимости от суммы. Это:
Эта теория соответствующих углов утверждает, что если поперечная линия пересекает две параллельные прямые, соответствующие углы равны. При этом соответствующие углы всегда будут равны, если поперечная прямая пересекает две прямые, параллельные друг другу.
Соответствующие углы в треугольнике В треугольнике углы конгруэнтной пары сторон двух конгруэнтных или одинаковых треугольников являются соответствующими углами. Следовательно, эти углы имеют одинаковую величину или равны.
Это предложение или теорема о соответствующих углах гласит:
«Когда две параллельные прямые пересекают поперечную прямую, тогда углы в областях пересечения равны и являются соответствующими углами».
Теорема о соответствующих углах, обратнаяТеорема о соответствующих углах работает наоборот. Таким образом, мы можем сформулировать формулировку обратной теоремы так:
«Если углы области пересечения конгруэнтны и являются соответствующими углами, то прямые параллельны». Если секущая пересекается, то две прямые параллельны. Тогда она образует обратную соответствующую теорему об углах.
Применение соответствующих угловСоответствующие углы имеют широкий спектр применений, которые мы часто игнорируем. Рассмотрим несколько практических применений соответствующих углов.
Пример 1: Если два соответствующих угла равны 6x + 12 и 70. Найдите значение x?
Решение: Пусть два угла равны соответственным углам.
6x + 12 = 70
6x = 70 – 12
6x = 58
x = 9,67
Пример 2: Два соответствующих угла равны 8y + 17 и 6. угол?
Решение: Даны значения соответствующих углов:
8y – 15 и 6y + 7
Теперь найдем значения обеих переменных x и y.
Мы знаем, что это конгруэнтные соответственные углы.
8y – 15 = 6y + 7
8y – 6y = 15 + 7
2y = 22
y = 11
Величина каждого соответствующего угла,
81 – 15 73
6 лет + 7 = 6(11) + 7 = 73
Пример 3: Дано:
∠1 = 5x + 1 и ∠3 = 6x – 3 — два соответствующих угла.
Найдите значение x.
Решение: Поскольку это соответствующие углы, они будут конгруэнтны, поскольку прямые помогают быть параллельными.
Теперь мы приравняем оба угла и найдем x.
∠1 = 5x + 1 и ∠3 = 6x – 3,
5x + 1 = 6x – 3
1 + 3 = 6x – 5x
4 = x
Следовательно, значение x равно 03.
Пример 4: Когда два соответствующих угла равны ∠2 = 6x + 4 и ∠6 = 5x + 12. Найдите значение x.
Решение: Так как это соответствующие углы, то они будут конгруэнтны, так как прямые называются параллельными по своей природе.
Теперь приравняем оба угла и найдем x
∠2 = 6x + 4 и ∠6 = 5x + 12 = 8
Следовательно, значение x равно 8.
Пример 5: Когда два соответствующих угла равны ∠7 = 5x + 6 и ∠3 = 9х – 10. Найдите значение х.
Решение: Поскольку они являются соответствующими углами, а прямые по своей природе параллельны, они должны быть конгруэнтны.
Приравняйте данные выражения ∠7 = 5x + 6 и ∠3 = 9x – 10 и найдите значение x.
5x + 6 = 9x – 10
6 + 10 = 9x – 5x
16 = 4x
x = 16/4
x = 4
Соответствующее значение x0 соответствует 03. Углы (7 вещей, которые нужно знать) – JDM Educational
Соответствующие углы могут помочь нам найти меру углов или значение переменных в геометрии, особенно когда мы имеем дело с двумя параллельными линиями.
Итак, что вам нужно знать о соответствующих углах? Соответственные углы лежат по одну сторону от секущей, но по разные стороны от двух прямых, пересекающих эту секущую (один угол внутренний, другой внешний). Если прямые параллельны, то соответствующие углы равны, а если секущие перпендикулярны, то они прямые.
Конечно, нам также может понадобиться использовать дополнительные углы (для смежных углов), чтобы помочь нам найти соответствующие углы.
В этой статье мы поговорим о соответствующих углах, о том, как они выглядят и когда они дополняют друг друга. Мы также рассмотрим несколько примеров того, как находить значения соответствующих углов.
Мы также рассмотрим несколько примеров того, как находить значения соответствующих углов.
Начнем.
Что такое соответствующие углы?
Соответствующие углы означают пару углов, лежащих по одну сторону от секущей, но по разные стороны от двух прямых, пересекающих эту секущую (один угол внутренний, другой угол внешний).
Прямая n — это секущая, пересекающая прямые l и m. Углы а и b являются соответствующими углами: они лежат по одну сторону (правую сторону) от секущей (прямая n), причем один внутренний (а лежит между прямыми l и m), а другой внешний (b ниже линия м).Секущей называется прямая, пересекающая две другие прямые.
Запомните разницу между внутренними и внешними углами:
 Углы a, d, f и g являются внешними углами (a и d лежат выше линии l, а f и g ниже линии m).
Углы a, d, f и g являются внешними углами (a и d лежат выше линии l, а f и g ниже линии m).При пересечении секущей двух прямых имеется четыре пары соответствующих углов:
| Angle Pair | Side Of Transversal | Upper Angle | Lower Angle |
|---|---|---|---|
| Top Left | left | exterior | interior |
| Top Right | справа | снаружи | внутри |
| Bottom Left | left | interior | exterior |
| Bottom Right | right | interior | exterior |
angle orientation (interior or exterior ) для
четыре пары соответствующих углов.

Каждый из этих ящиков выглядит немного иначе.
Как выглядит соответствующий угол?
Соответствующие углы выглядят немного по-разному в зависимости от того, на какую из четырех пар вы смотрите. Вы можете увидеть каждый из четырех случаев ниже:
Соответствующие углы конгруэнтны?
Соответствующие углы конгруэнтны (равны друг другу), если две прямые, пересекающие секущую, параллельны. Помните, что параллельные прямые никогда не пересекаются (у них одинаковый наклон, но разные точки пересечения по оси Y).
Если соответствующие углы равны x и y, то мы имеем уравнение:
Обратите внимание, что каждая пара соответствующих углов имеет два конгруэнтных угла в этом частном случае параллельных прямых.
Если две прямые, пересекающие секущую, параллельны, то пары соответствующих углов конгруэнтны (имеют одинаковую меру). Здесь две прямые параллельны (обе горизонтальны), поэтому пары углов 1 и 3 конгруэнтны (2 и 4, 5 и 7, & 6 и 8 также конгруэнтны пары).Дополнительны ли соответствующие углы?
Соответствующие углы могут быть дополнительными, если сумма их величин составляет 90 градусов. Если два угла равны x и y, то мы имеем уравнение:
В частном случае параллельных прямых мы знаем из нашего предыдущего обсуждения, что два соответствующих угла конгруэнтны ( равный). То есть у нас есть уравнение:
Когда мы объединяем эти два уравнения подстановкой, мы получаем: