Внеклассный урок — Система уравнений второй степени. Способы решения. Системы уравнений второй степени.
Система уравнений второй степени. Способы решенияСистема уравнений второй степени – это система уравнений, в которой есть хотя бы одно уравнение второй степени.
Систему из двух уравнений, в которой одно уравнение второй степени, а второе уравнение первой степени, решают следующим образом:
1) в уравнении первой степени одну переменную выражают через другую; 2) подставляют полученное выражение в уравнение второй степени, благодаря чему получается уравнение с одной переменной; 3) решают получившееся уравнение с одной переменной; 4) находят соответствующие значения второй переменной. |
Пример: Решим систему уравнений
│x2 – 3xy – 2y2 = 2
│x + 2y = 1
Решение:
Следуем правилу:
1) Второе уравнение является уравнением первой степени. В ней выражаем переменную x через y:
В ней выражаем переменную x через y:
x = 1 – 2y
2) в первом уравнении вместо x подставляем полученное выражение 1 – 2y:
(1 – 2y)2 – 3(1 – 2y)y – 2y2 = 2.
Раскрываем скобки и упрощаем:
8y2 – 7y + 1 = 2.
Приравниваем уравнение к нулю и решаем получившееся квадратное уравнение:
8y2 – 7y + 1 – 2 = 0
8y2 – 7y – 1 = 0.
3) Решив квадратное уравнение, найдем его корни:
y1 = – 0,125
y2 = 1.
4) Осталось найти значения x. Для этого в одно из двух уравнений системы просто подставляем значение y. Второе уравнение проще, поэтому выберем его.
Итак, подставляем значения y в уравнение x + 2y = 1 и получаем:
1) х + 2(-0,125) = 1
х – 0,25 = 1
х = 1 + 0,25
х1 = 1,25.
2) х + 2 · 1 = 1
х + 2 =1
х = 1 – 2
х2 = –1.
Ответ:
x1 = 1,25, y1 = – 0,125
x2 = –1, y2 = 1.
Способы решения системы уравнений с двумя уравнениями второй степени.
1. Замена системы уравнений равносильной совокупностью двух систем.
Пример: Решим систему уравнений
│x2 – 9y2 – x + 3y = 0
│x2 – xy + y = 7
Здесь нет уравнений первой степени, поэтому решать их вроде бы сложнее. Но в первом уравнении многочлен можно разложить на линейные множители и применить метод группировки:
x2 – 9y2 – x + 3y = (x – 3y)(x + 3y) – (x – 3y) = (x – 3y)(x + 3y) – 1(x – 3y) = (x – 3y)(x + 3y – 1).
(Пояснение-напоминание: x – 3y встречается в выражении дважды и является общим множителем в многочлене (x – 3y)(x + 3y) – 1(x – 3y). По правилу группировки, мы умножили его на сумму вторых множителей и получили равносильное уравнение).
В результате наша система уравнений обретает иной вид:
│(x – 3y)(x + 3y – 1) = 0
│x2 – xy + y = 7
Первое уравнение равно нулю только в том случае, если x – 3y = 0 или x + 3y – 1 = 0.
Значит, нашу систему уравнений мы можем записать в виде двух систем следующего вида:
│x – 3y = 0
│x2 – xy + y = 7
и
│x + 3y – 1 = 0
│x2 – xy + y = 7
Мы получили две системы, где первые уравнения являются уравнениями первой степени. Мы уже можем легко решить их. Понятно, что решив их и объединив затем множество решений этих двух систем, мы получим множество решений исходной системы. Говоря иначе, данная система равносильна совокупности двух систем уравнений.
Мы уже можем легко решить их. Понятно, что решив их и объединив затем множество решений этих двух систем, мы получим множество решений исходной системы. Говоря иначе, данная система равносильна совокупности двух систем уравнений.
Итак, решаем эти две системы уравнений. Очевидно, что здесь мы применим метод подстановки, подробно изложенный в предыдущем разделе.
Обратимся сначала к первой системе.
В уравнении первой степени выразим х через у:
х = 3у.
Подставим это значение во второе уравнение и преобразим его в квадратное уравнение:
(3у)2 – 3у · у + у = 7,
9у2 – 3у2 + у = 7,
6у2 + у = 7,
6у2 + у – 7 = 0
Как решается квадратное – см.раздел «Квадратное уравнение». Здесь мы сразу напишем ответ:
7
у1 = 1, у2 = – ——.
6
Теперь подставим полученные значения у в первое уравнение первой системы и решим его:
1) х – 3 · 1 = 0,
х1 = 3.
7
2) х – 3 · (– ——) = 0,
6
7
х + —— = 0,
2
7
х2 = – ——
2
Итак, у нас есть первые ответы:
х1 = 3, у1 = 1;
7 7
х2 = – ——, у2 = – ——.
2 6
Переходим ко второй системе. Не будем производить вычисления – их порядок точно такой же, что и в случае с уравнениями первой системы. Поэтому сразу напишем результаты вычислений:
х3 = –2, у3 = 1.
х4 = –2,5, у4 = – 0,5.
Таким образом, исходная система уравнений решена.
Ответ:
1 1
(–3 — ; –1 — ), (3; 1), (2,5; –0,5), (–2; 1).
2 6
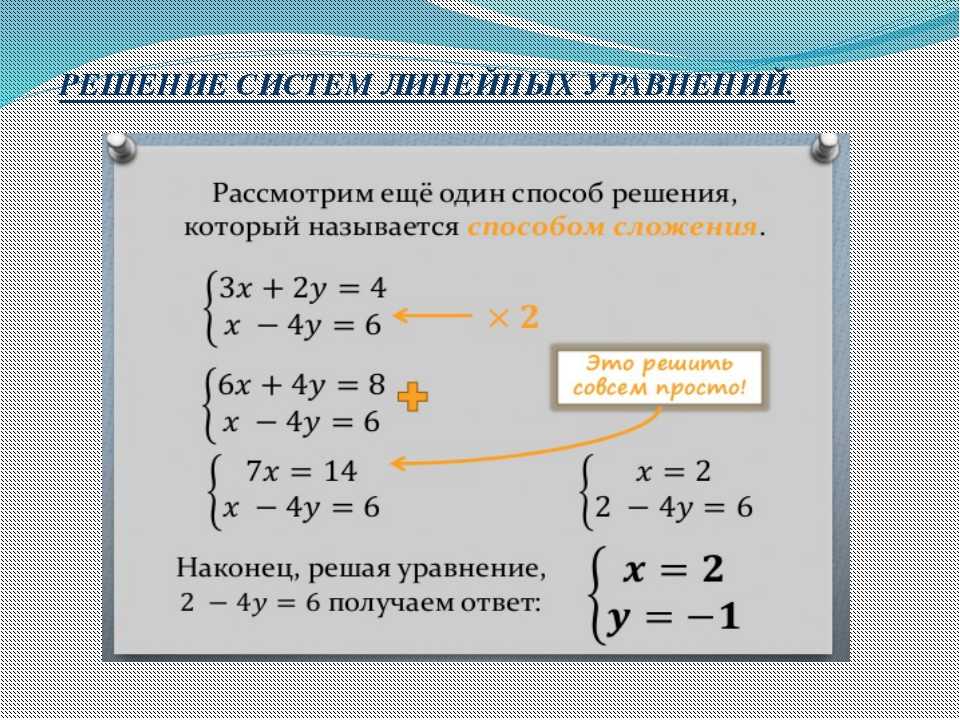
2. Решение способом сложения.
Пример 2: Решим систему уравнений
│2x2 + 3y = xy
│x2 – y = 3xy
Решение.
Второе уравнение умножим на 3:
3x2 – 3y = 9xy
Зачем мы умножили уравнение на 3? Благодаря этому мы получили равносильное уравнение с числом -3y, которое встречается и в первом уравнении, но с противоположным знаком. Это поможет нам буквально при следующем шаге получить упрощенное уравнение (они будут взаимно сокращены).
Сложим почленно левые и правые части первого уравнения системы и нашего нового уравнения:
2x2 + 3y + 3x2 – 3y = xy + 9xy
Сводим подобные члены и получаем уравнение следующего вида:
5x2 = 10xy
Упростим уравнение еще, для этого сокращаем обе части уравнения на 5 и получаем:
x2 = 2xy
Приравняем уравнение к нулю:
x2 – 2xy = 0
Это уравнение можно представить в виде x(x – 2y) = 0.
Здесь мы получаем ситуацию, с которой уже сталкивались в предыдущем примере: уравнение верно только в том случае, если x = 0 или x – 2y = 0.
Значит, исходную систему опять-таки можно заменить равносильной ей совокупностью двух систем:
│x = 0
│x2 – y = 3xy
и
│x = 2y
│x2 – y = 3xy
Обратите внимание: во второй системе уравнение x – 2y = 0 мы преобразовали в x = 2y.
Итак, в первой системе мы уже знаем значение x. Это ноль. То есть x1 = 0. Легко вычислить и значение y: это тоже ноль. Таким образом, первая система имеет единственное решение: (0; 0).
Решив вторую систему, мы увидим, что она имеет два решения: (0; 0) и (–1; –0,5).
Таким образом, исходная система имеет следующие решения: (0; 0) и (–1; –0,5).
Пример решен.
3. Решение методом подстановки.
Решение методом подстановки.
Этот метод был применен в начале раздела. Здесь мы выделяем его в качестве одного из способов решения. Приведем еще один пример.
Пример. Решить систему уравнений
│х + у = 9
│у2 + х = 29
Решение.
Первое уравнение проще, поэтому выразим в нем х через у:
х = 9 – у.
Теперь произведем подстановку. Подставим это значение х во второе уравнение, получим квадратное уравнение и решим его:
у2 + 9 – у = 29
у2 – у – 20 = 0
D = b2 – 4ас = 1 – 4 · 1 · (–20) = 81
√D = 9
–b + √D 1 + 9
у1 = ———— = ——— = 5
2a 2
–b – √D 1 – 9
у2 = ———— = ——— = –4
2a 2
Осталось найти значения х. Первое уравнение проще, поэтому им и воспользуемся:
1) х + 5 = 9
х = 9 – 5
х1 = 4
2) х – 4 = 9
х = 9 + 4
х2 = 13
Ответ: (4; 5), (13; –4).
Решение систем уравнений в MathCad 13, 14, 15 на примерах. Универсальные методы Given
Для решения уравнений в Mathcad можно воспользоваться двумя способами. Эти способы были частично рассмотрены в разделе «Решение уравнений»:
- Метод Given — Find
- Метод Solve
Использование метода
Given — Find:В рабочем поле mathcad записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения системы уравнений численными методами.
Затем указывается начальное приближение для искомых переменных. Это нужно для увеличения скорости и точности решения системы. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю для всех переменных, при этом, если окажется, что система имеет несколько решений, то есть риск не определить все корни. Поэтому лучше всегда задавать приближение

Далее вводятся уравнения. Их можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)
Когда уравнения записаны вводится функция Find(x, y, z,…) (где х, y, z,… — переменные). Это функция, которая возвращает результат решения системы. Значение функции Find() можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах (см. рис. 3). При решении систем уравнений в mathcad результатом всегда будет являтся матрица значений
 3. Ввод функции Find()
3. Ввод функции Find()Для того чтобы увидеть результат решения системы уравнений, после Find(x, y, z,…) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 4).
В зависимости от сложности системы через определенное время MathCad выведет результат. На рис. 5 можно рассмотреть синтаксис и результат решения системы уравнений. Обратите внимание, что можно присваивать результат решения системы матричной переменной и можно работать с отдельными ее элементами
Mathcad позволяет решать системы уравний в символьном виде. Обычно это полезно, когда требуется получить не точное значение переменных, а их выражения через константы. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно
 рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот метод
рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот методИспользование метода
Solve:Как показывает практика, методом solve иногда удается решить системы уравнений, которые не поддаются решению с помощью функции Find()
Синтаксис следующий: на панели matrix нажимаем иконку Matrix or Vector и в появившемся окне указываем количество уравнений входящих в систему. В нашем примере их будет три (см. рис. 7)
Заполняем систему, вводя последовательно все уравнения используя логический символ «ровно» из панели Boolean. Каждый элемент матрицы-столбца содержит одно уравнение (см. рис. 8)
рис. 8)
Когда все уравнения введены, убедитесь, что курсор ввода находится в вашей матрице и затем нажмите кнопку «solve» из панели Symbolic. Появится служебное слово (функция) solve. Далее поставте запятую и введите последовательно все переменные, относительно которых необходимо решить систему уравнений (см. рис. 9)
Уведите курсор в свободное поле mathcad и дождитесь окончания решения системы. Обратите внимание, что мы не вводили начальные приближения. Даный метод их назначает автоматически. Обратите так же внимание, что для решения системы в символьном виде синтаксис аналогичен (см. рис. 10)
Как показывает моя инженерная практика, решение систем в символьном виде сопряжено с большими вычислительными трудностями.То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями
mathtype
|
||||||||
| Use matrices to format |
| a system of equations |
| or inequalities |
| Используйте матрицы |
| для формата систем |
| уравнений и неравенств |



 (This must be done in the Matrix
dialog when you first build the matrix. The
Align Right option in the Format menu is not
what you want.)
(This must be done in the Matrix
dialog when you first build the matrix. The
Align Right option in the Format menu is not
what you want.)
 (Это
делается в диалоге
Матрица, когда Вы создаёте
черновик матрицы. Опция
Правое Выравнивание в
меню Формат в этом случае
«отдыхает»)
(Это
делается в диалоге
Матрица, когда Вы создаёте
черновик матрицы. Опция
Правое Выравнивание в
меню Формат в этом случае
«отдыхает») Ячейки в
первой строке верхнего
примера: » 3x + «, » 4y + «, » z = » и «17».
Ячейки в
первой строке верхнего
примера: » 3x + «, » 4y + «, » z = » и «17». В случае,
когда оператора после
переменной нет (третье
уравнение), вставляйте
пробел вместо переменной, чтобы
он сместился вправо.
Удерживайте нажатой
клавишу Ctrl, когда Вы нажимаете
spacebar, чтобы вставить пробел. (Используйте
клавишу Команда и spacebar на Макинтоше.)
В случае,
когда оператора после
переменной нет (третье
уравнение), вставляйте
пробел вместо переменной, чтобы
он сместился вправо.
Удерживайте нажатой
клавишу Ctrl, когда Вы нажимаете
spacebar, чтобы вставить пробел. (Используйте
клавишу Команда и spacebar на Макинтоше.) Установите
интервал для столбца
матрицы в позицию 25 % и
щелкните ОК.
Установите
интервал для столбца
матрицы в позицию 25 % и
щелкните ОК.
 Выравнивание в таком
случае будет идеальным..
Выравнивание в таком
случае будет идеальным..
Copyright © 2000-2002 by Design
Science, Inc. All rights reserved.
All rights reserved.
Решение системы уравнений способом уравнивания коэффициентов
58. Способ сложения и вычитания или способ уравнения коэффициентов. Решим совместно следующие 2 уравнения:
7x + 5y = 47 и 7x – 5y = 9 (1)
Мы видим, что в левой части одного уравнения входит член +5y, а в левой части другого — член –5y. Если бы пришлось эти части сложить между собою, то эти члены уничтожились бы. И этого достигнуть легко: из данных двух уравнений составим вытекающее из них новое, для чего сложим и левые части обоих уравнений между собою, и правые части между собою – результаты этих сложений, очевидно, должны быть равны между собою, т. е. получим:
14x = 56
(члены +5y и –5y взаимно уничтожились). Отсюда получим x = 4. Умножим затем обе части второго уравнения на –1; получим:
7x + 5y = 47
–7x + 5y = –9
и теперь опять сложим левые части между собою и правые между собою (говорят: сложим эти 2 уравнения по частям).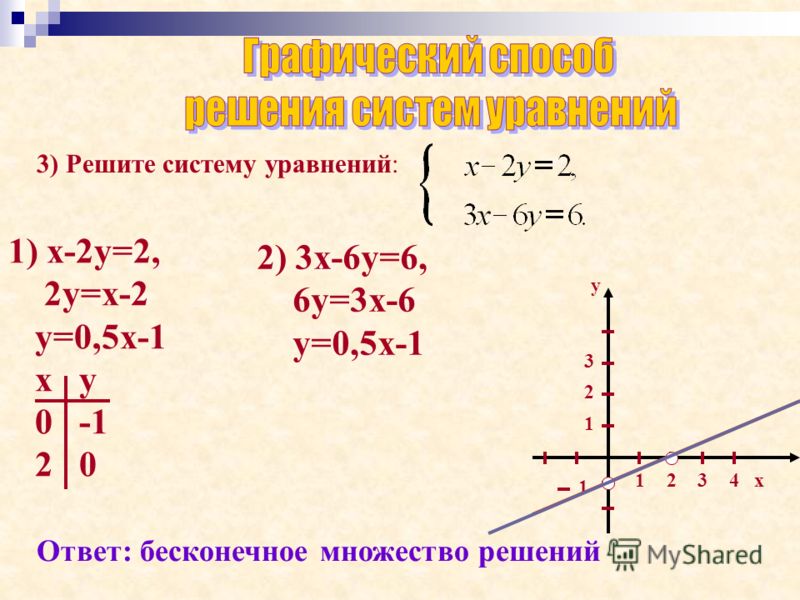 Получим, так как члены +7x и –7x взаимно уничтожаются:
Получим, так как члены +7x и –7x взаимно уничтожаются:
10y = 38, откуда y = 3,8
Мы могли бы взамен этого сделать и так: вернемся к уравнениям (1) и вычтем по частям (т. е. из левой части левую часть и из правой части правую часть) из первого уравнения второе. Тогда надо у всех членов 2-го уравнения переменить знаки — результат получится тот же самый.
В разобранном примере абсолютные величины коэффициентов при каждом неизвестном в каждом уравнении были равны; рассмотрим теперь пример, когда абсолютные величины этих коэффициентов неравны.
3x + 4y = 23 и 9x + 10y = 65.
Рассматривая эти уравнения, мы видим, что коэффициенты при x не равны, но что их легко сделать равными, если обе части первого уравнения умножим на 3. Сделав это, получим:
9x + 12y = 69
9x + 10y = 65
Теперь вычтем по частям из первого уравнения второе (надо у всех членов 2-го уравнения переменить знаки). Получим:
2y = 4, откуда y = 2.
Рассматривая данные уравнения, мы теперь приходим к возможности уравнять коэффициенты при y, для чего можно поступить по разному: 1) обе части 1-го уравнения умножить на 2 ½ — тогда получим:
7 ½ x + 10y = 57 ½
9x + 10y = 65
Вычтем теперь из 2-го уравнения по частям 1-е, для чего переменим знаки у всех членов 1-го уравнения (мы вычитаем из 2-го первое, а не наоборот, только для того, чтобы в левой части коэффициент при x получился положительный), получим:
1 ½ x = 7 ½, откуда x = 7 ½ : 1 ½ = 5.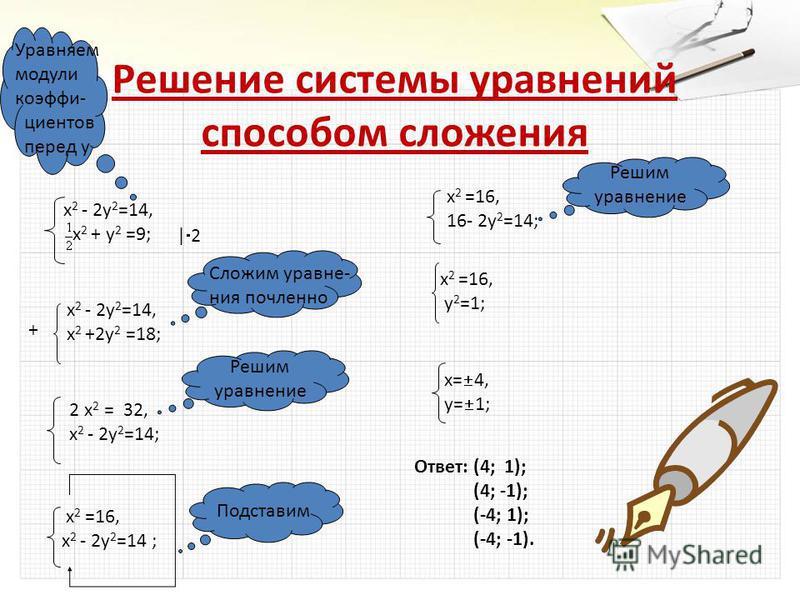
2) Обе части 2-го уравнения умножим на 2/5, — получим:
3x + 4y = 23 (первое оставляем без изменения).
3 3/5 x + 4y = 26
Вычитая по частям из 2-го уравнения первое, получим:
3/5 x = 3, откуда x = 3 : 3/5 = 5.
3) Если не желаем иметь дело с дробными коэффициентами, то найдем общее наименьшее кратное для коэффициентов при y, т. е. для чисел 4 и 10 – оно есть 20 и, умножением обеих частей 1-го уравнения и обеих частей 2-го, сведем дело к тому, чтобы в каждом уравнении коэффициентом при y служило это общее наименьшее кратное. В нашем примере для этого умножим обе части 1-го уравнения на 5 и обе части 2-го уравнения на 2. Получим:
15x + 20y = 115
18x + 20y = 130.
Опять вычтем по частям из 2-го уравнения первое, — получим:
3x = 15, откуда x = 5.
Заметим еще, что когда одно неизвестное определено, можно подстановкою получить другое. Так, мы сначала нашли y = 2. Подставим это значение в 1-ое уравнение:
3x + 4 · 2 = 23
или
3x = 23 – 8 = 15, откуда x = 5.
Коротко выполним еще один пример:
6x – 15y = 32 | · 3 | · 2
4x + 9y = 34 | · 5 | · 3
Сбоку мы отметили, что надо обе части 1-го уравнения умножить на 3 и обе части 2-го на 5 — мы имеем в виду уравнять абсолютные величины коэффициентов при y. Получим:
18x – 45y = 96.
20x + 45y = 170.
Сложим эти уравнения по частям, получим:
38x = 266 и x = 7.
Теперь умножим обе части 1-го уравнения на 2 и обе части второго на 3 (отмечено сбоку). Получим:
12x – 30y = 64
12x + 27y = 102.
Вычтем по частям из 2-го уравнения первое; получим:
57y = 38 и y = 38/57 = 2/3.
Примем этот способ к решению двух уравнений с двумя неизвестными в общем виде:
ax + by = m | · d | · c
cx + dy = n | · b | · a
Сначала умножим, как отмечено, обе части 1-го уравнения на d и обе части 2-го на b. Получим:
adx + bdy = md
cbx + =bdy = nb.
Вычтем по частям из 1-го уравнения второе, получим:
adx – cbx = md – nb.
Вынесем в левой части x за скобки, получим:
(ad – cb)x = md – nb,
откуда
x = (md – nb) / (ad – cb).
Уравняем теперь коэффициенты при x, для чего обе части 1-го уравнения умножим на c и обе части второго на a. Получим:
acx + bcy = mc
acx + ady = na.
Вычтем по частям из 2-го уравнения первое, получим:
ady – bcy = na – mc,
откуда
(ad – bc) y = na – mc
и
y = (na – mc) / (ad – bc).
Мы вычитали здесь из 2-го уравнения первое, а не наоборот, с целью получить тот же знаменатель ad – bc, какой получился при определении x – a.
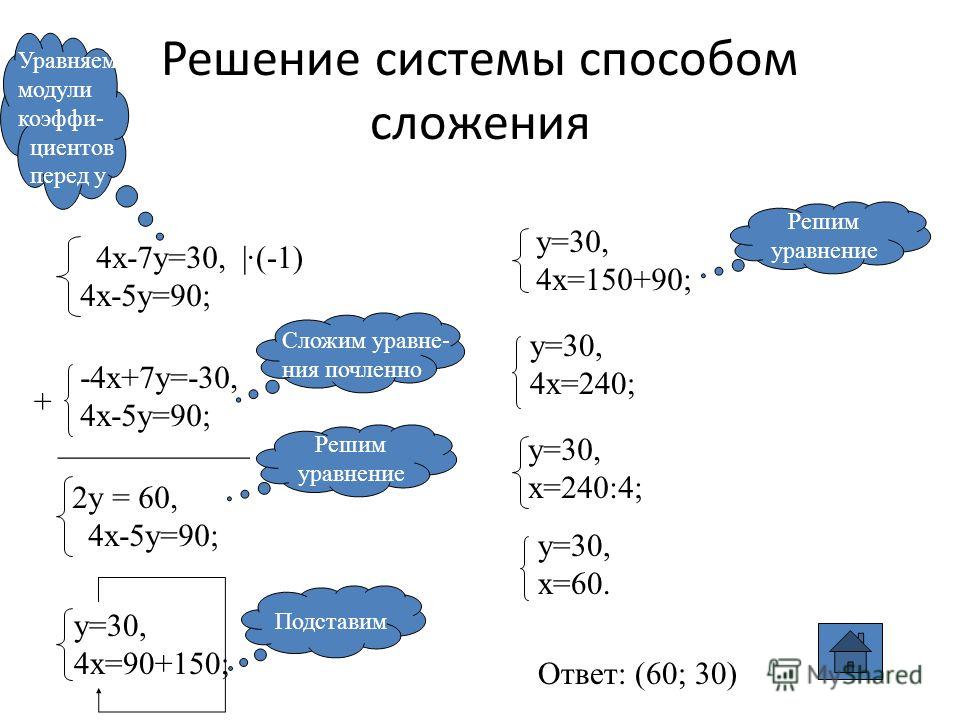
Решение систем уравнений способом сложения
Репетиторы ❯ Математика ❯ Решение систем уравнений способом сложения
Автор: Валентина Галиневская
●
27.07.2015
●
Раздел: Математика
Очень часто ученики затрудняются с выбором способа решения систем уравнений.
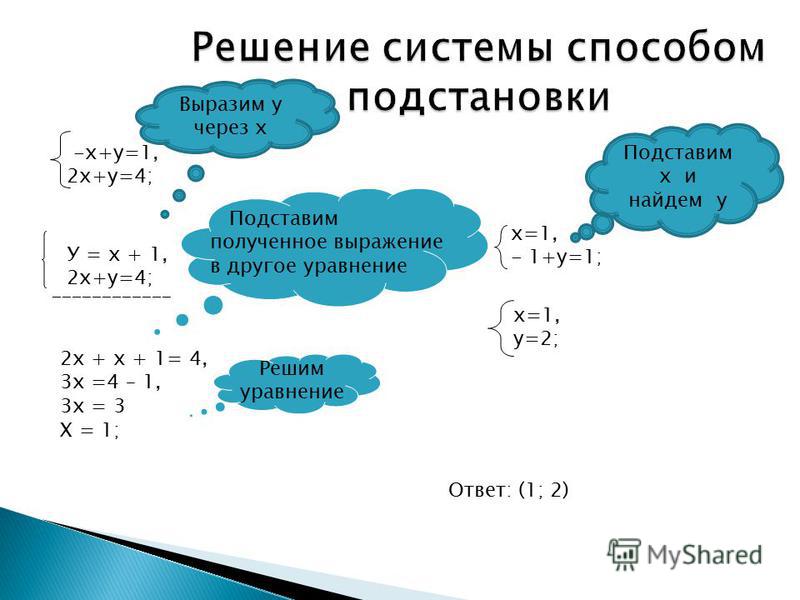
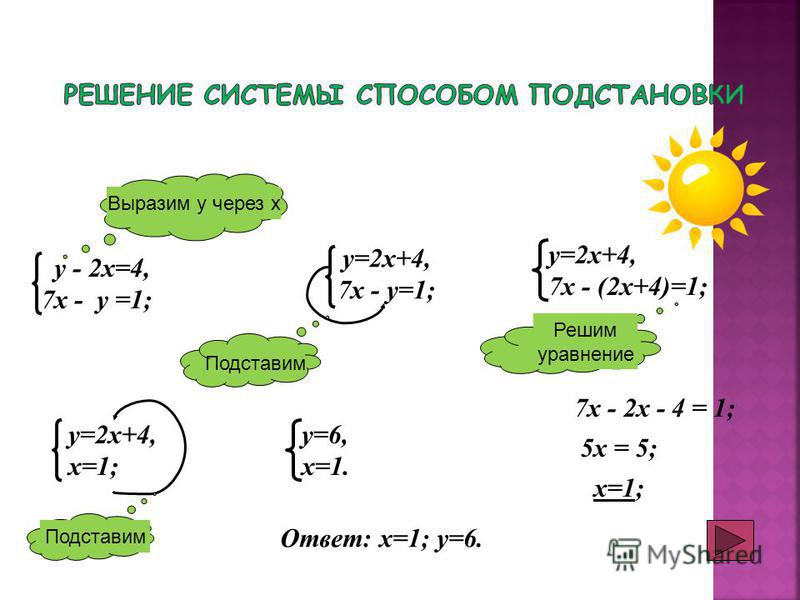
В данной статье мы рассмотрим один из способов решения систем – способ подстановки.
Если находят общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что данные уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурной скобкой, например
Замечаем, что при х = 15 , а у = 5 оба уравнения системы верны. Эта пара чисел и есть решение системы уравнений. Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как же решать системы способом подстановки? Если коэффициенты при каком – нибудь неизвестном в обоих уравнениях равны по абсолютной величине (если же не равны , то уравниваем), то, складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определяем одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы ( в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Затем решаем это уравнение. Определяем одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы ( в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Пример 1. Решите систему уравнений
Здесь коэффициенты при у по абсолютному значению равны между собой, но противоположны по знаку. Давайте попробуем почленно сложить уравнения системы.
Полученное значение х=4, подставляем в какое–нибудь уравнение системы (например в первое) и находим значение у:
2 *4 +у = 11, у = 11 – 8, у = 3.
Наша система имеет решение х = 4, у = 3. Или же ответ можно записать в круглых скобках, как координаты точки, на первом месте х , на втором у.
Ответ: (4; 3)
Пример 2. Решить систему уравнений
Уравняем коэффициенты при переменной х, для этого умножим первое уравнение на 3, а второе на (-2), получим
Будьте внимательны при сложении уравнений
Тогда у = — 2. Подставим в первое уравнение вместо у число (-2), получим
Подставим в первое уравнение вместо у число (-2), получим
4х + 3( -2) = — 4. Решаем это уравнение 4х = — 4 + 6, 4х = 2, х = ½.
Ответ: (1/2; — 2)
Пример 3. Решите систему уравнений
Умножим первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система решений не имеет, так ка 0 не равен (-13).
Ответ: решений нет.
Пример 4. Решите систему уравнений
Замечаем, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и мы получаем систему, которая состоит из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения одинаковы (мы получили всего одно уравнение с двумя переменными). Как же представить решение этой системы? Давайте выразим переменную у из уравнения х + у = 5. Получим у = 5 – х.
Тогда ответ запишется так: (х; 5-х), х – любое число.
Мы рассмотрели решение систем уравнений способом сложения. Если остались вопросы или что – то непонятно запишитесь на урок и мы с вами устраним все проблемы.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Система уравнений
Рассмотрим, что же такое система уравнений с двумя переменными, а также равносильные системы уравнений.
Например, нам даны два уравнения, которые имеют две переменные f(x;y) = 0 и g (x;y) = 0.
Решить систему уравнений – это значит найти абсолютно все общие решения двух данных уравнений, которые имеют две переменные. Каждая пара значений данных переменных, которые обращают каждое уравнение нашей системы в верное равенство и будут решением системы уравнений. Проще говоря, решить систему уравнений – это значит найти абсолютно все ее решение, или же доказать, что этих решений не существует.
Уравнения, которые образуют систему, как правило, объединяют фигурной скобкой.
Если две системы уравнений имеют одни и те же решения, то такие системы называются равносильными. Тоже касается и тех систем, которые не имеет решений. Для того, чтобы решить систему уравнений, в большинстве случаев пользуются «способом замены», то есть заменяют данную систему уравнений на более «удобную» или легкую, но, при этом. обязательно равносильную. Что касается возможности такой замены, то она обуславливается двумя теоремами:
- Допустим, дана система двух уравнений, которые имеют две переменные.
 Если оставить одно уравнений системы и не изменять его, а второе уравнение системы заменять равносильными, то мы получим систему, которая будет равносильна данной. Следствием данной теоремы является то, что, если каждое уравнение заданной системы заменять равносильными, то получим систему, которая будет равносильна данной.
Если оставить одно уравнений системы и не изменять его, а второе уравнение системы заменять равносильными, то мы получим систему, которая будет равносильна данной. Следствием данной теоремы является то, что, если каждое уравнение заданной системы заменять равносильными, то получим систему, которая будет равносильна данной. - Допустим, дана система двух уравнений, которые имеют две переменные. Если оставить одно уравнение системы и не изменять его, а второе уравнение заменить разностью или суммой обоих уравнений системы, то полученная система уравнений будет равносильна данной.
Решение уравнения первой степени ax = b
| x = | b a |
(a ≠ 0) |
Решение системы двух уравнений первой степени
| { | ax + by = c |
| dx + ey = f |
| { | x = | ce — fb | (ae — db ≠ 0) |
| ae — db | |||
| y = | af — dc | ||
| ae — db |
либо через определители
| x = | | | c b f e |
| | ; | y = | | | a c d f |
| | |
| | | a b d e |
| | | | a b d e |
| |
Формула корней квадратного уравнения
| ax2 + bx + c = 0 |
| ax2 + bx + c = 0 |
| x1,2 = | -b ± | √ | b2 — 4ac |
| 2a | |||
Формула приведенного квадратного уравнения
| x2 + px + q = 0 |
| x1,2 = | — | p 2 |
± | 1 2 |
√ | p2— 4q |
Теорема Виета для квадратного уравнения
| ax2 + bx + c = 0 |
| x1 + x2 = — | b a |
; x1 * x2 = | c a |
Теорема Виета для приведенного квадратного уравнения
| x2 + px + q = 0 |
| x1 + x2 = -p; x1 * x2 = q |
Теорема Виета для приведенного кубического уравнения
| x3 + px2 + qx + r = 0 |
| x1 + x2 + x3 = -p; |
| x1x2 * x2x3 * x1x3 = q; |
| x1x2x3 = -r |
Разложение на множители квадратного трехчлена
| ax2 + bx + c = a(x — x1)(x — x2), | где x1 и x2 — корни уравнения ax2 + bx + c = 0 |
Выделение квадрата двучлена из квадратного трехчлена
| ax2 + bx + c = a(x + | b 2a | )2 + | 4ac — b2 4a |
Решение биквадратного уравнения
| ax4 + bx2 + c = 0 |
| x1,2 = ± | √ | -b + √b2 — 4ac |
| 2a | ||
| x3,4 = ± | √ | -b — √b2 — 4ac |
| 2a | ||
Формула действительного корня неполного кубического уравнения
| y3 + py + q = 0 |
| y = 3√ |
| + 3√ |
|
Системы уравнений — Руководство по исследованиям и практике
Введение
Системы уравнений (или «одновременные уравнения») включают решение двух или более уравнений, содержащих два или более неизвестных.
Понимание проблемы
Что делает системы уравнений трудными для учителей?
Аспекты систем уравнений, которые вызывают затруднения у учащихся, усложняют их обучение. Тем не менее, у учителей есть дополнительные сложности, связанные с определением хода учебной программы для поддержки обучения учащихся. В очень простом (читай: не соответствующем стандартам) учебнике по математике вы можете увидеть только три шага в прогрессии: (1) линии графика и найти точку пересечения, (2) решить с помощью метода подстановки и (3) решить методом исключения.
Если мы посмотрим на стандарты, как и в большинстве других тем, мы можем ожидать прогресса в обучении, который строит процедурную беглость с концептуальным пониманием. Системы уравнений впервые появляются в 8 классе:
8.EE.C.8. Анализируйте и решайте пары одновременных линейных уравнений.
8.EE.C.8.a. Объясните, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, поскольку точки пересечения удовлетворяют обоим уравнениям одновременно.
8.EE.C.8.b. Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения в виде графика. Решите простые случаи путем проверки. Например, 3 x + 2 y = 5 и 3 x + 2 y = 6 не имеют решения, потому что 3 x + 2 y не могут быть одновременно 5 и 6. Стандарты 8-го класса представляют некоторые проблемы. Результат доказательства требует, чтобы учащиеся «анализировали и решали», и ограничивает системы линейными уравнениями. Часть (а) итоговых данных посвящена концептуальному пониманию того, что значит быть решением системы уравнений, а часть (б) содержит подробные сведения о процедурном аспекте их решения. Здесь интерпретация стандартов становится неясной. Если мы соберем воедино формулировку в Части (b), то в ней действительно говорится «решить… алгебраически», что некоторые могли бы интерпретировать как решение с использованием методов замены и исключения, которые являются формальными, абстрактными подходами, ожидаемыми ближе к концу обучения. прогресс. Однако в части (b) также говорится, что учащиеся должны «оценивать решения, рисуя графики» и «решать простые случаи путем проверки», оба из которых являются менее формальными методами, которые человек ожидает на более раннем этапе обучения. Стандарты для 8-го класса не упоминают замены и исключения, и неясно, должны ли они быть частью учебной программы 8-го класса.
прогресс. Однако в части (b) также говорится, что учащиеся должны «оценивать решения, рисуя графики» и «решать простые случаи путем проверки», оба из которых являются менее формальными методами, которые человек ожидает на более раннем этапе обучения. Стандарты для 8-го класса не упоминают замены и исключения, и неясно, должны ли они быть частью учебной программы 8-го класса.
Системы уравнений также встречаются в стандартах средней школы:
HS.A-REI.C.5. Докажите, что для данной системы двух уравнений с двумя переменными замена одного уравнения суммой этого уравнения и кратного другого дает систему с теми же решениями.
HS.A-REI.C.6. Решайте системы линейных уравнений точно и приблизительно (например, с помощью графиков), ориентируясь на пары линейных уравнений с двумя переменными.
HS.A-REI.C.7. Решить простую систему, состоящую из линейного уравнения и квадратного уравнения с двумя переменными, алгебраически и графически. Например, найти точки пересечения линии y = −3 x и окружность x 2 + y 2 = 3.
Опять же, здесь нет явных упоминаний о методах замены и исключения, но тщательная интерпретация может дать некоторые руководство здесь. HS.A-REI.C.5, по сути, описывает метод исключения, но не для того, чтобы учащиеся могли решить его, а для того, чтобы доказать, что метод работает. (См. пример и пояснение к отдельной задаче по иллюстративной математике A-REI.C.5.) HS.A-REI.C.6 направляет учащихся к точному и приблизительному решению систем линейных уравнений. Язык здесь очень похож на часть 8.EE.C.8.b, но более прямой и недвусмысленный. HS.A-REI.C.7 также предлагает учащимся решать системы уравнений, но включать нелинейные уравнения.
Таким образом, если обучение системам уравнений от 8 до старшей школы начинается с концептуального понимания того, что представляет собой решение системы уравнений, и заканчивается процедурной беглостью решения систем, включающих как линейные, так и нелинейные уравнения, как выглядит середина этой прогрессии? Стандарты описывают некоторые строительные блоки, но не говорят достаточно, чтобы действительно помочь учителям и разработчикам учебных программ увидеть все возможности учебных программ.
Рекомендации
Сосредоточьтесь на двух эффективных методах обучения NCTM
Два эффективных метода обучения NCTM особенно важны при обучении системам уравнений: (#3) использовать и соединять математические представления и (#6) развивать процедурную беглость на основе концептуального понимания .
3. Использовать и соединять математические представления. Учителя обычно думают о множественных представлениях как об уравнениях, таблицах и графиках. Но если вы посмотрите более внимательно на эту практику в Принципы действий (NCTM, 2014, стр. 25), обсуждаемые типы представлений: контекстуальные , физические , символические , вербальные и визуальные . Эта эффективная педагогическая практика призывает учителей вводить формы представления, которые могут быть полезны учащимся, и сосредоточивать внимание учащихся на структуре или существенных чертах математических идей, которые появляются независимо от представления. Хотя это можно и нужно делать с помощью уравнений, таблиц и графиков, существует гораздо более широкий набор представлений и моделей, которые могут быть полезны при изучении систем уравнений.
Хотя это можно и нужно делать с помощью уравнений, таблиц и графиков, существует гораздо более широкий набор представлений и моделей, которые могут быть полезны при изучении систем уравнений.
6. Развивайте процедурную беглость благодаря концептуальному пониманию. Формальные процедуры решения систем уравнений с использованием методов подстановки и исключения должны строиться на фундаменте концептуального понимания, на создание которого могут уйти месяцы или даже годы. Это концептуальное понимание должно включать использование неформальных стратегий рассуждений, которые учителя могут помочь учащимся связать со значениями и свойствами более формальных операций, таких как замена и исключение.
Вместе эти две практики заложили основу для построения учебной программы по изучению систем уравнений.
Введение и объяснение с помощью неформальных, контекстуальных ситуаций для достижения понимания
Идея о том, что изучение математики должно основываться в первую очередь на контекстуальных, неформальных ситуациях, распространена во многих теориях, программах и учебных материалах, но, вероятно, наиболее тесно связана с Реалистичным Математическое образование , теория и подход, зародившиеся в Нидерландах в конце 19 века. 60-х и 1970-х годов, и все еще развивается сегодня (van den Heuvel-Panhuizen & Wijers, 2005). Одним из учебных ресурсов, в котором был принят этот подход для Соединенных Штатов, был Mathematics in Context , серия модулей для 5–8 классов, включающая один модуль «Сравнение величин» (Kindt, Abels, Dekker, Meyer, Pligge, & Burrill, 2006). ), которые были сосредоточены на использовании неформальных контекстов и «доформальных» представлений и моделей для развития концептуального понимания систем уравнений. Приведенные ниже примеры задач взяты из этого модуля, который больше не печатается.
60-х и 1970-х годов, и все еще развивается сегодня (van den Heuvel-Panhuizen & Wijers, 2005). Одним из учебных ресурсов, в котором был принят этот подход для Соединенных Штатов, был Mathematics in Context , серия модулей для 5–8 классов, включающая один модуль «Сравнение величин» (Kindt, Abels, Dekker, Meyer, Pligge, & Burrill, 2006). ), которые были сосредоточены на использовании неформальных контекстов и «доформальных» представлений и моделей для развития концептуального понимания систем уравнений. Приведенные ниже примеры задач взяты из этого модуля, который больше не печатается.
Перетягивание каната
Перетягивание каната. © Британская энциклопедия.
В задании «перетягивание каната» учащимся предлагается обосновать два известных равных условия (четыре быка = пять лошадей и один слон = бык и две лошади) и использовать эти знания, чтобы ответить на вопрос: «Какие животные будут выиграть перетягивание каната внизу?» где слон и три лошади тянут против четырех волов.
Учащиеся, даже учащиеся 6-го класса и младше, могут решать подобные задачи без использования каких-либо математических символов или формальных процедур. Скорее всего, они придумают следующие подходы:
- Заменив слона слева на быка и двух лошадей, мы получим пять лошадей и быка, тянущего против четырех волов. Тогда, заменив четырех быков справа на пять лошадей, мы получим пять лошадей и быка, тянущего против пяти лошадей. Поскольку у обеих сторон одинаковое количество лошадей, левая сторона выиграет в перетягивании каната, потому что она тоже тянет быка.
- Заменив слона слева на быка и двух лошадей, мы получим пять лошадей и быка, тянущего против четырех волов. Если мы удалим быка слева и одного из быков справа, которые должны тянуть одинаково, это даст нам пять лошадей, тянущих против трех быков. Поскольку мы знаем, что пять лошадей тянут так же, как четыре вола, мы знаем, что левая сторона выиграет в перетягивании каната, потому что у правой стороны только три быка.

- Замена четырех волов с правой стороны пятью лошадьми дает нам слона и трех лошадей, тянущихся против пяти лошадей. Если мы удалим трех лошадей слева и трех лошадей справа, которые должны тянуть одинаково, это даст нам одного слона, тянущего против двух лошадей. Поскольку мы знаем, что слон тянет так же, как вол и две лошади, левая сторона выиграет в перетягивании каната, потому что на правой стороне только две лошади и нет быка.
Задание на перетягивание каната не только представляет учащимся контекст, который мог бы быть реальным в их сознании, но также представляет концепцию равенства как относительную, а не операционную, что может стать серьезным камнем преткновения для учащихся. . Представления баланса (например, весы для нахождения массы объектов, когда сковорода или поднос слева уравновешиваются с одним справа) также усиливают реляционную концепцию равенства. Не вводя формальных символических представлений, учителя могут помочь учащимся с этими типами заданий, сосредоточив внимание на акте замены и заставляя учеников объяснить свои рассуждения о том, что можно заменить чем и почему.
Зонтики и колпачки
Зонтики и колпачки. © Британская энциклопедия.
Другим типом задач для построения концептуального понимания систем уравнений являются «комбинационные» задачи. Это могут быть комбинации длины и ширины, высоты и веса, или комбинации продуктов, которые составляют общую цену. Задача «Зонты и кепки» из «Математика в контексте » — одна из таких задач, в которой учащимся сообщается, что два зонта и кепка стоят 80 долларов, а один зонт и две кепки — 76 долларов. Студенты должны захотеть ответить на вопрос: «Сколько стоит один зонт? Сколько стоит одна шляпа?» Как и в случае с перетягиванием каната, учащиеся могут рассуждать об этом задании без введения формальных математических символов и представлений. Стратегии решения могут включать:
- Сравнение двух комбинаций, чтобы сделать вывод, что зонт стоит на 4 доллара больше, чем шляпа, затем угадывание и проверка с разными ценами, пока не будут найдены цены, которые подходят для обеих комбинаций.

- Складываем первую комбинацию со второй, чтобы получить три зонта и три шляпы за 156 долларов, а затем рассуждаем, что один зонт и одна шляпа должны стоить 52 доллара. В сочетании с пониманием того, что зонтик стоит на 4 доллара больше, чем шляпа, зонтик должен стоить 28 долларов, а шляпа — 24 доллара.
- Наблюдение закономерности от первой комбинации ко второй, которая включает в себя удаление зонтика, добавление шляпы и вычитание 4 долларов. Если следовать шаблону до третьей комбинации, эта комбинация будет иметь три шляпы по цене 72 доллара, что означает, что каждая шляпа стоит 24 доллара. Точно так же, если следовать шаблону в обратном направлении, новая комбинация, показанная сверху, будет иметь три зонтика по 84 доллара, что означает, что каждый зонтик стоит 28 долларов.
Свечи. © Британская энциклопедия.
Эти задания на комбинирование цен вовлекают учащихся в реальный для них контекст, который можно обосновать. Такие задачи, как задача со свечами, написаны, чтобы вовлечь учащихся непосредственно в рассуждения другого ученика. В то время как задача «перетягивание каната» позволила сформировать концептуальное понимание метода замещения, эти задачи по сочетанию цен открывают больше возможностей для развития концептуального понимания метода исключения, а также идеи о том, что «равные, добавленные к равным, равны» и « равные, вычтенные из равных, равны», которые являются общими понятиями № 2 и № 3 из Евклида 9.0018 Элементы , Книга I.
В то время как задача «перетягивание каната» позволила сформировать концептуальное понимание метода замещения, эти задачи по сочетанию цен открывают больше возможностей для развития концептуального понимания метода исключения, а также идеи о том, что «равные, добавленные к равным, равны» и « равные, вычтенные из равных, равны», которые являются общими понятиями № 2 и № 3 из Евклида 9.0018 Элементы , Книга I.
Вовлечение учащихся в использование предварительных формальных моделей и представлений
Одной из основных особенностей обучения реалистичной математике являются концепции прогрессивной формализации и эмерджентного моделирования . Прогрессивная формализация (Webb, Boswinkel, Dekker, 2008) — это идея о том, что учащиеся должны начинать обучение с неформальных, контекстуальных представлений, затем переходить к «доформальным» представлениям и моделям, которые помогают навести концептуальное понимание на беглость процедур, а затем, наконец, на формальную математику. , который обычно символичен и зависит от процедурной беглости. Эмерджентное моделирование (Гравемейер, 19 лет)97) заключается в том, что модели, которые учащиеся первоначально используют, представляют собой моделей неформального контекста, но по мере того, как их рассуждения и использование модели становятся более изощренными, они становятся моделями для рассуждений с обобщаемой математической идеей. Хотя это похоже на конкретно-репрезентативно-абстрактные (CRA) точки зрения на прогресс обучения учащихся, они не совсем одинаковы. CRA подразумевает, что обучение должно начинаться с конкретного, но если это «конкретное» манипулятивное действие похоже на алгебраические плитки, которые являются физическими манипуляциями, учащиеся могут не иметь достаточного понимания плиток или контекста для их использования, чтобы сделать их «реальными» в своих занятиях. умы. При прогрессивной формализации и эмерджентном моделировании сначала появляется неформальный контекст, а затем могут быть введены «конкретные» репрезентации, чтобы рассуждать с контекстом.
, который обычно символичен и зависит от процедурной беглости. Эмерджентное моделирование (Гравемейер, 19 лет)97) заключается в том, что модели, которые учащиеся первоначально используют, представляют собой моделей неформального контекста, но по мере того, как их рассуждения и использование модели становятся более изощренными, они становятся моделями для рассуждений с обобщаемой математической идеей. Хотя это похоже на конкретно-репрезентативно-абстрактные (CRA) точки зрения на прогресс обучения учащихся, они не совсем одинаковы. CRA подразумевает, что обучение должно начинаться с конкретного, но если это «конкретное» манипулятивное действие похоже на алгебраические плитки, которые являются физическими манипуляциями, учащиеся могут не иметь достаточного понимания плиток или контекста для их использования, чтобы сделать их «реальными» в своих занятиях. умы. При прогрессивной формализации и эмерджентном моделировании сначала появляется неформальный контекст, а затем могут быть введены «конкретные» репрезентации, чтобы рассуждать с контекстом.
Комбинированные диаграммы и записи в блокнотах
Нотации в блокнотах. © Британская энциклопедия.
Таблица комбинаций. © Британская энциклопедия.
Предварительные представления систем уравнений включают такие представления, как комбинированные диаграммы и запись в тетрадях. Комбинированная диаграмма, показанная здесь, соответствует задаче с зонтами и кепками, при этом количество кепок отображается по горизонтальной оси, а количество зонтов — по вертикальной оси. Такое размещение двух переменных в двух измерениях может помочь учащимся связать свое понимание систем с двумя переменными с построением графика в координатной плоскости. Учащиеся должны работать над заполнением комбинированной таблицы, а также распознавать и объяснять найденные закономерности. Например, каждое движение по диагонали вниз и вправо снижает цену на 4 доллара и представляет собой удаление одного зонта и добавление одной крышки. Каждое движение по диагонали вверх и вправо добавляет зонтик и кепку и увеличивает цену на 52 доллара.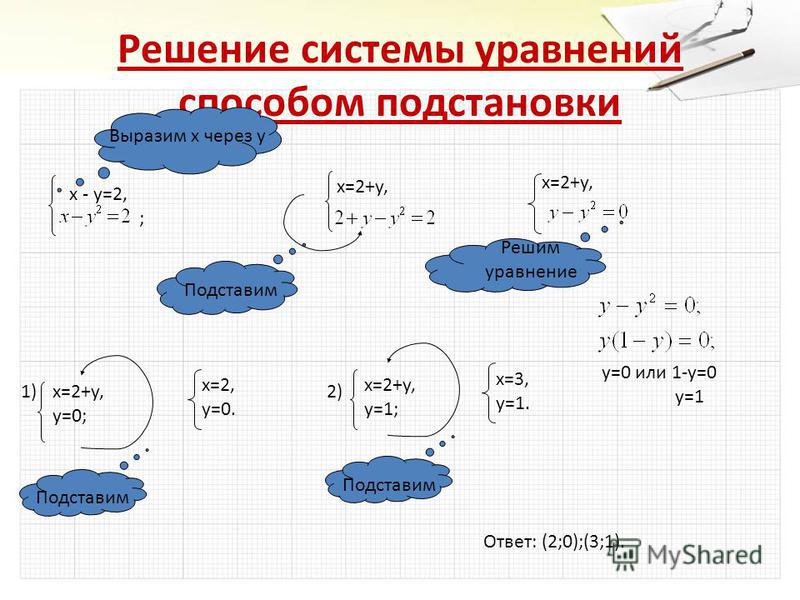 Эти два диагональных движения на диаграмме комбинаций соответствуют действиям по вычитанию и сложению двух комбинаций вместе. Эти диагональные движения можно продолжать до тех пор, пока учащиеся не окажутся на левом или нижнем краях, после чего они считают только зонты или только кепки и могут найти цену за единицу. Это может быть связано с необходимостью сведения задачи системы уравнений к одной из переменных, чтобы ее можно было решить.
Эти два диагональных движения на диаграмме комбинаций соответствуют действиям по вычитанию и сложению двух комбинаций вместе. Эти диагональные движения можно продолжать до тех пор, пока учащиеся не окажутся на левом или нижнем краях, после чего они считают только зонты или только кепки и могут найти цену за единицу. Это может быть связано с необходимостью сведения задачи системы уравнений к одной из переменных, чтобы ее можно было решить.
Записная книжка — еще одно предформальное представление. Показанная здесь запись в блокноте соответствует задаче со свечами и использует столбцы для упорядочения количества высоких свечей, количества коротких свечей и стоимости каждой комбинации. Одним из преимуществ записи в блокноте является то, что она может легко вместить более двух переменных, что является ограничением комбинированных диаграмм. Нотация в тетради побуждает учащихся выполнять операции над строкой, например умножать строку на 2, чтобы создать новую строку (удвоить количество свечей, удвоить стоимость), или вычесть одну строку из другой, чтобы «исключить» одну из переменных (например, вычитание строки 3 из строки 1 в этом примере, что исключает высокие свечи). Еще одним преимуществом нотной записи является то, что работа организована по вертикали, подобно работе, показанной при алгебраическом решении систем уравнений, и учащиеся могут аннотировать каждую новую строку пояснениями операций, которые они использовали для ее вычисления.
Еще одним преимуществом нотной записи является то, что работа организована по вертикали, подобно работе, показанной при алгебраическом решении систем уравнений, и учащиеся могут аннотировать каждую новую строку пояснениями операций, которые они использовали для ее вычисления.
План многолетнего обучения системам уравнений
В то время как прогресс обучения системам уравнений, описанным в стандартах, неясен, особенно в каких алгебраических методах следует внедрять и осваивать и когда, ясно, что прогресс должен охватывать несколько лет. Кроме того, «Эффективные методы преподавания» напоминают нам об использовании и соединении математических представлений, а также о построении процедурной беглости на основе концептуального понимания. В совокупности эти рекомендации убедительно свидетельствуют о том, что формальные обобщенные методы замены и исключения не следует ожидать от учащихся 8-х классов.
Учащимся 8-х классов рекомендуется начинать с неформальных контекстов, а затем соединять их с предформальными представлениями. Чтобы соответствовать требованиям 8.EE.C.8, некоторые контексты должны поддаваться легкому представлению в виде таблиц и графиков, поскольку эти представления также можно использовать для развития понимания наряду с другими предварительными формальными представлениями, такими как комбинированные диаграммы и записи в тетради. . Для решения простых случаев путем проверки их неформальное представление, скорее всего, поначалу облегчит их понимание. Например, две рубашки и две шляпы по цене 100 долларов и те же две рубашки и две шляпы по цене 9 долларов.0 означает отсутствие решения, потому что две рубашки и две шляпы не могут одновременно быть двумя разными ценами. Такого рода рассуждения можно распространить на «простые случаи», указанные в 8.EE.C.8.b, в виде системы 2 S + 2 H = 100 и 2 S + 2 . H = 90.
Чтобы соответствовать требованиям 8.EE.C.8, некоторые контексты должны поддаваться легкому представлению в виде таблиц и графиков, поскольку эти представления также можно использовать для развития понимания наряду с другими предварительными формальными представлениями, такими как комбинированные диаграммы и записи в тетради. . Для решения простых случаев путем проверки их неформальное представление, скорее всего, поначалу облегчит их понимание. Например, две рубашки и две шляпы по цене 100 долларов и те же две рубашки и две шляпы по цене 9 долларов.0 означает отсутствие решения, потому что две рубашки и две шляпы не могут одновременно быть двумя разными ценами. Такого рода рассуждения можно распространить на «простые случаи», указанные в 8.EE.C.8.b, в виде системы 2 S + 2 H = 100 и 2 S + 2 . H = 90.
Учащимся старших классов рекомендуется продолжать использовать неформальные контексты, чтобы помочь в рассуждениях учащихся, и установить прочные связи между доформальными моделями и формальными представлениями и методами. Даже после того, как учащиеся хорошо освоятся с формальными методами замены и исключения, они все равно могут найти полезными предварительные формальные модели. Одним из примеров этого будет, когда их попросят решить системы, включающие нелинейные функции, как это предусмотрено в HS.A-REI.C.7.
Даже после того, как учащиеся хорошо освоятся с формальными методами замены и исключения, они все равно могут найти полезными предварительные формальные модели. Одним из примеров этого будет, когда их попросят решить системы, включающие нелинейные функции, как это предусмотрено в HS.A-REI.C.7.
Ссылки
Алибали, М.В., Кнут, Э.Дж., Хаттикудур, С., Макнил, Н.М., и Стивенс, А.С. (2007). Продольное исследование понимания учениками средней школы знака равенства и эквивалентных уравнений. Математическое мышление и обучение, 9 (3), 221–247. https://doi.org/10.1080/10986060701360902
Gravemeijer, K. (1997). Решение текстовых задач: пример моделирования? Обучение и инструкции, 7 (4), 389–397. https://doi.org/10.1016/S0959-4752(97)00011-X
Киндт, М., Абельс, М., Деккер, Т., Мейер, М.Р., Плигге, М.А., и Беррилл, Г. (2006). Сравнение количества. В Висконсинском центре исследований в области образования и Институте Фройденталя (редакторы), Mathematics in Context (2-е изд. , стр. 49). Британская энциклопедия.
, стр. 49). Британская энциклопедия.
НКТМ. (2014). Принципы действий: Обеспечение математического успеха для всех . Национальный совет учителей математики.
ван ден Хойвель-Панхуизен, М., и Вийерс, М. (2005). Математические стандарты и учебные программы в Нидерландах. ЗДМ, 37 (4), 287–307. https://doi.org/10.1007/BF02655816
ван Реувейк, М. (2001). От неформальной к формальной, прогрессивной формализации пример «решения систем уравнений». В H. Chick, K. Stacey, J. Vincent и J. Vincent (Eds.), Будущее преподавания и изучения алгебры: 12-я учебная конференция ICMI (стр. 613–620). http://repository.unimelb.edu.au/10187/2812
Уэбб, Д. К., Босвинкель, Н., и Деккер, Т. (2008). Под верхушкой айсберга: использование представлений для поддержки понимания учащихся. Преподавание математики в средней школе, 14 (2), 110–113. https://doi.org/10.5951/MTMS.14.2.0110
Математическое видео для детей «Решение систем уравнений»
ЧТО ТАКОЕ СИСТЕМА УРАВНЕНИЙ?
Система уравнений — это набор уравнений, которые нам нужно рассмотреть вместе. Решением системы уравнений является набор значений переменных, который является решением каждого уравнения в системе.
Решением системы уравнений является набор значений переменных, который является решением каждого уравнения в системе.
Для лучшего понимания систем уравнений…
ЧТО ТАКОЕ СИСТЕМА УРАВНЕНИЙ?. Система уравнений — это набор уравнений, которые нам нужно рассмотреть вместе. Решением системы уравнений является набор значений переменных, который является решением каждого уравнения в системе. Чтобы лучше понять системы уравнений…
ДАВАЙТЕ РАЗБИРАЕМ!
Составьте систему уравнений для представления продаж барбекю.
Система уравнений — это два или более уравнений, которые используют одни и те же переменные. Например: x + y = 5 и 2x + 3y = 8 — это два уравнения с одними и теми же переменными, x и y. Они представляют собой систему уравнений. Вот еще один пример. Адесина купила 1 куриное крылышко и 1 бургер за 8 долларов. Эйприл купила 6 куриных крылышек и 2 гамбургера за 24 доллара. Сколько стоит каждый бургер и каждое куриное крылышко? Вы можете написать систему уравнений для решения. Пусть c — стоимость одного куриного крылышка, а b — стоимость одного бургера. Тогда c + b = 8 и 6c + 2b = 24. Эти два уравнения образуют систему уравнений, которую вы можете решить, чтобы найти ответ. Попробуйте сами: У вас в банке несколько десятицентовиков и пятицентовиков. Всего 8 монет. Общая стоимость монет составляет 60 центов. Напишите систему линейных уравнений, чтобы представить количество десятицентовиков и количество пятицентовых монет в банке.
Пусть c — стоимость одного куриного крылышка, а b — стоимость одного бургера. Тогда c + b = 8 и 6c + 2b = 24. Эти два уравнения образуют систему уравнений, которую вы можете решить, чтобы найти ответ. Попробуйте сами: У вас в банке несколько десятицентовиков и пятицентовиков. Всего 8 монет. Общая стоимость монет составляет 60 центов. Напишите систему линейных уравнений, чтобы представить количество десятицентовиков и количество пятицентовых монет в банке.
Составьте систему уравнений для представления продаж барбекю. Система уравнений — это два или более уравнений, которые имеют одни и те же переменные. Например: x + y = 5 и 2x + 3y = 8 — это два уравнения с одними и теми же переменными, x и y. Они представляют собой систему уравнений. Вот еще один пример. Адесина купила 1 куриное крылышко и 1 бургер за 8 долларов. Эйприл купила 6 куриных крылышек и 2 гамбургера за 24 доллара. Сколько стоит каждый бургер и каждое куриное крылышко? Вы можете написать систему уравнений для решения. Пусть c — стоимость одного куриного крылышка, а b — стоимость одного бургера. Тогда c + b = 8 и 6c + 2b = 24. Эти два уравнения образуют систему уравнений, которую вы можете решить, чтобы найти ответ. Попробуйте сами: у вас есть несколько центов в банке. Всего 8 монет. Общая стоимость монет составляет 60 центов. Напишите систему линейных уравнений, чтобы представить количество десятицентовиков и количество пятицентовых монет в банке.
Пусть c — стоимость одного куриного крылышка, а b — стоимость одного бургера. Тогда c + b = 8 и 6c + 2b = 24. Эти два уравнения образуют систему уравнений, которую вы можете решить, чтобы найти ответ. Попробуйте сами: у вас есть несколько центов в банке. Всего 8 монет. Общая стоимость монет составляет 60 центов. Напишите систему линейных уравнений, чтобы представить количество десятицентовиков и количество пятицентовых монет в банке.
Используйте подстановку, чтобы найти стоимость товаров для барбекю.
Вы можете решать системы уравнений с помощью подстановки. Для этого перестройте одно уравнение, чтобы изолировать одну переменную. Затем подставьте значение этой переменной в другое уравнение. Для примера с барбекю выберите любое из двух уравнений, чтобы переставить их. Перестановка c+b=8 выглядит проще всего. Выберите одну переменную и изолируйте ее с одной стороны: b=8-c. Затем замените b на 8-c в другом уравнении, 6c+2b=24. Это дает нам 6c+28-c=24. Решите это уравнение, чтобы найти значение c: 6c+16-2c=24, 4c+16=24, 4c=8 и, наконец, c=2. Теперь мы знаем, что куриное крылышко стоит 2 доллара. Мы можем оценить одно из исходных уравнений при этом значении, чтобы найти другую стоимость. Неважно, какое уравнение мы используем! Используя первое уравнение, c+b=8, подставьте c = 2 и найдите b, что равно 6. Итак, мы знаем, что гамбургер стоит 6 долларов, а куриное крылышко — 2 доллара. Чтобы проверить это решение, подставьте c = 2 и b = 6 в оба уравнения и убедитесь, что обе части равны. Поскольку они есть, мы знаем, что у нас есть правильный ответ. Попробуйте сами: Решите систему уравнений, которую вы составили для задачи о монетах, используя подстановку.
Теперь мы знаем, что куриное крылышко стоит 2 доллара. Мы можем оценить одно из исходных уравнений при этом значении, чтобы найти другую стоимость. Неважно, какое уравнение мы используем! Используя первое уравнение, c+b=8, подставьте c = 2 и найдите b, что равно 6. Итак, мы знаем, что гамбургер стоит 6 долларов, а куриное крылышко — 2 доллара. Чтобы проверить это решение, подставьте c = 2 и b = 6 в оба уравнения и убедитесь, что обе части равны. Поскольку они есть, мы знаем, что у нас есть правильный ответ. Попробуйте сами: Решите систему уравнений, которую вы составили для задачи о монетах, используя подстановку.
Используйте замену для определения стоимости товаров для барбекю. Вы можете решать системы уравнений с помощью подстановки. Для этого перестройте одно уравнение, чтобы изолировать одну переменную. Затем подставьте значение этой переменной в другое уравнение. Для примера с барбекю выберите любое из двух уравнений, чтобы переставить их. Перестановка c+b=8 выглядит проще всего. Выберите одну переменную и изолируйте ее с одной стороны: b=8-c. Затем замените b на 8-c в другом уравнении, 6c+2b=24. Это дает нам 6c+28-c=24. Решите это уравнение, чтобы найти значение c: 6c+16-2c=24, 4c+16=24, 4c=8 и, наконец, c=2. Теперь мы знаем, что куриное крылышко стоит 2 доллара. Мы можем оценить одно из исходных уравнений при этом значении, чтобы найти другую стоимость. Неважно, какое уравнение мы используем! Используя первое уравнение, c+b=8, подставьте c = 2 и найдите b, что равно 6. Итак, мы знаем, что гамбургер стоит 6 долларов, а куриное крылышко — 2 доллара. Чтобы проверить это решение, подставьте c = 2 и b = 6 в оба уравнения и убедитесь, что обе части равны. Поскольку они есть, мы знаем, что у нас есть правильный ответ. Попробуйте сами: решите систему уравнений, которую вы написали для задачи о монетах, используя подстановку.
Выберите одну переменную и изолируйте ее с одной стороны: b=8-c. Затем замените b на 8-c в другом уравнении, 6c+2b=24. Это дает нам 6c+28-c=24. Решите это уравнение, чтобы найти значение c: 6c+16-2c=24, 4c+16=24, 4c=8 и, наконец, c=2. Теперь мы знаем, что куриное крылышко стоит 2 доллара. Мы можем оценить одно из исходных уравнений при этом значении, чтобы найти другую стоимость. Неважно, какое уравнение мы используем! Используя первое уравнение, c+b=8, подставьте c = 2 и найдите b, что равно 6. Итак, мы знаем, что гамбургер стоит 6 долларов, а куриное крылышко — 2 доллара. Чтобы проверить это решение, подставьте c = 2 и b = 6 в оба уравнения и убедитесь, что обе части равны. Поскольку они есть, мы знаем, что у нас есть правильный ответ. Попробуйте сами: решите систему уравнений, которую вы написали для задачи о монетах, используя подстановку.
Решите системы уравнений с помощью графика.
Эмили выгуливает собак и зарабатывает 8 долларов в день. Вы можете представить деньги, которые зарабатывает Эмили, используя линейное уравнение с наклоном 8, y = 8x, где x представляет собой количество отработанных дней, а y представляет собой сумму денег, которую она зарабатывает. Амари работает на роликовом катке. Он зарабатывает 5 долларов в день и уже накопил 15 долларов. Вы можете представить это с помощью линейного уравнения y=5x+15, где 5 показывает его дневную ставку, x представляет количество отработанных дней, а 15 показывает, сколько он уже сэкономил. Вы хотите узнать, сколько дней они проработают, прежде чем Эмили и Амари получат одинаковую сумму денег. Начертите оба линейных уравнения на одной координатной плоскости. График Амари проходит через точки (0, 15) и (1, 20). График Эмили проходит через точки (0, 0) и (1, 8). Точка пересечения двух прямых называется точкой пересечения и является решением системы уравнений. Это потому, что это точка, которая делает оба уравнения верными одновременно. Эта точка равна (5, 40), поэтому на 5-й день и у Эмили, и у Амари есть по 40 долларов. Попробуйте сами: Нарисуйте линии y=3x+2 и y=4x-2, отметьте их точки пересечения и оцените их координаты.
Амари работает на роликовом катке. Он зарабатывает 5 долларов в день и уже накопил 15 долларов. Вы можете представить это с помощью линейного уравнения y=5x+15, где 5 показывает его дневную ставку, x представляет количество отработанных дней, а 15 показывает, сколько он уже сэкономил. Вы хотите узнать, сколько дней они проработают, прежде чем Эмили и Амари получат одинаковую сумму денег. Начертите оба линейных уравнения на одной координатной плоскости. График Амари проходит через точки (0, 15) и (1, 20). График Эмили проходит через точки (0, 0) и (1, 8). Точка пересечения двух прямых называется точкой пересечения и является решением системы уравнений. Это потому, что это точка, которая делает оба уравнения верными одновременно. Эта точка равна (5, 40), поэтому на 5-й день и у Эмили, и у Амари есть по 40 долларов. Попробуйте сами: Нарисуйте линии y=3x+2 и y=4x-2, отметьте их точки пересечения и оцените их координаты.
Решите системы уравнений с помощью графика. Эмили выгуливает собак и зарабатывает 8 долларов в день. Вы можете представить деньги, которые зарабатывает Эмили, используя линейное уравнение с наклоном 8, y = 8x, где x представляет собой количество отработанных дней, а y представляет собой сумму денег, которую она зарабатывает. Амари работает на роликовом катке. Он зарабатывает 5 долларов в день и уже накопил 15 долларов. Вы можете представить это с помощью линейного уравнения y=5x+15, где 5 показывает его дневную ставку, x представляет количество отработанных дней, а 15 показывает, сколько он уже сэкономил. Вы хотите узнать, сколько дней они проработают, прежде чем Эмили и Амари получат одинаковую сумму денег. Начертите оба линейных уравнения на одной координатной плоскости. График Амари проходит через точки (0, 15) и (1, 20). График Эмили проходит через точки (0, 0) и (1, 8). Точка пересечения двух прямых называется точкой пересечения и является решением системы уравнений. Это потому, что это точка, которая делает оба уравнения верными одновременно. Эта точка равна (5, 40), поэтому на 5-й день и у Эмили, и у Амари есть по 40 долларов.
Вы можете представить деньги, которые зарабатывает Эмили, используя линейное уравнение с наклоном 8, y = 8x, где x представляет собой количество отработанных дней, а y представляет собой сумму денег, которую она зарабатывает. Амари работает на роликовом катке. Он зарабатывает 5 долларов в день и уже накопил 15 долларов. Вы можете представить это с помощью линейного уравнения y=5x+15, где 5 показывает его дневную ставку, x представляет количество отработанных дней, а 15 показывает, сколько он уже сэкономил. Вы хотите узнать, сколько дней они проработают, прежде чем Эмили и Амари получат одинаковую сумму денег. Начертите оба линейных уравнения на одной координатной плоскости. График Амари проходит через точки (0, 15) и (1, 20). График Эмили проходит через точки (0, 0) и (1, 8). Точка пересечения двух прямых называется точкой пересечения и является решением системы уравнений. Это потому, что это точка, которая делает оба уравнения верными одновременно. Эта точка равна (5, 40), поэтому на 5-й день и у Эмили, и у Амари есть по 40 долларов. Попробуйте сами: начертите линии y=3x+2 и y=4x-2, отметьте их точку пересечения и оцените ее координаты.
Попробуйте сами: начертите линии y=3x+2 и y=4x-2, отметьте их точку пересечения и оцените ее координаты.
Многие профессии требуют решения систем уравнений.
Пилоты используют системы уравнений для определения расхода топлива и стоимости полетов. Центры реабилитации диких животных используют системы уравнений для определения стоимости ухода за различными животными. Химики используют системы уравнений для расчета количества ингредиентов, необходимых для их реакций. Попробуйте сами: Как вы можете использовать системы уравнений в жизни или в карьере?
Многие профессии требуют решения систем уравнений. Пилоты используют системы уравнений для определения расхода топлива и стоимости поездок. Центры реабилитации диких животных используют системы уравнений для определения стоимости ухода за различными животными. Химики используют системы уравнений для расчета количества ингредиентов, необходимых для их реакций. Попробуйте сами: можете ли вы придумать, как вы можете использовать системы уравнений в своей жизни или в карьере?
СЛОВАРЬ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
Линейное уравнение
Уравнение, которое на графике представляет собой прямую линию.
Решение уравнения
Набор значений переменных в уравнении, которые приводят к истинному числовому уравнению.
Система уравнений
Два или более уравнений с одинаковыми переменными.
Решение системы уравнений
Набор значений переменных в уравнениях, которые приводят к истинному числовому уравнению для всех уравнений в системе.
Метод подстановки для решения систем уравнений
Метод решения систем уравнений, при котором одно уравнение переставляется и подставляется в другое уравнение.
Графический метод решения систем уравнений
Метод решения систем уравнений, при котором оба уравнения строятся в виде графика на координатной плоскости, а пересечение оценивается визуально.
Точка пересечения
Точка пересечения двух графиков и решение системы уравнений
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВОПРОСЫ ДЛЯ ОБСУЖДЕНИЯ
Что такое система уравнений?
Система уравнений — это набор уравнений, которые используют одни и те же переменные.
Какой метод замены?
Метод подстановки — это метод решения системы уравнений. В этом методе одно уравнение устанавливается равным одной переменной, а затем подставляется в другое уравнение.
Какой метод построения графика?
Графический метод — это метод оценки решения системы уравнений. В этом методе два линейных уравнения строятся на одной координатной плоскости. Точка пересечения двух прямых и есть решение системы.
Имеет ли значение, какую переменную вы переставляете в методе подстановки?
Нет, я получаю один и тот же ответ независимо от того, какую переменную я переставляю или какое уравнение переставляю первым. Может быть одна переменная, которую легче решить первой, и в этом случае я могу сначала решить ее, но мне это не нужно.
Когда вы проверяете решение системы уравнений, нужно ли вам проверять решение всех уравнений в системе?
Да; возможно, что точка находится на одной прямой, а не на другой. Решение системы должно быть на обеих линиях, поэтому мне нужно проверить оба уравнения.
Вернуться к уроку
Система уравнений
Системы уравнений — это наборы уравнений, решением которых является точка (точки) пересечения между уравнениями. Большинство систем уравнений, которые вы видите в алгебре, представляют собой наборы двух линейных уравнений в стандартной форме Ax + By = C.
Для решения систем линейных уравнений обычно используются три метода: построение графика, метод подстановки и метод исключения. метод. Эти методы можно применять и к более сложным системам нелинейных уравнений.
Метод построения графиков
Решение систем уравнений с помощью графиков выполняется путем построения графика каждого уравнения в системе и определения точки (точек) пересечения. Может быть проще изобразить уравнения в виде графиков, преобразовав стандартную форму каждого уравнения в форму пересечения наклона.
Пример
|
Метод подстановки
Решение систем уравнений методом подстановки включает замену переменной в одном уравнении на эквивалент этой переменной, рассчитанный с использованием другого уравнения. См. пример ниже.
См. пример ниже.
Первым шагом метода подстановки является нахождение переменной в одном уравнении.
Вы можете решить, какую переменную решать, изучив каждый коэффициент. Переменные с коэффициентами, равными 1, найти проще всего, потому что вам не придется ни на что делить. Переменные с коэффициентами, которые плохо делятся на другие коэффициенты, создают беспорядочные дроби.
Пример
| 3x + y = 31 | → | у = -3х + 31 |
| 2x — 5y = 15 | → | -5у = 15 — 2х |
Затем подставьте эквивалент переменной, которую вы только что нашли, в соответствующую переменную в другом уравнении.
y = -3x + 31
2x — 5y = 15
2x — 5(-3x + 31) = 15
Теперь, поскольку в уравнении осталась только одна переменная, вы можете решить ее!
2x — 5 (-3x + 31) = 15
2x + 15x — 155 = 15
17x = 170
x = 10
Чтобы найти оставшуюся переменную, вы можете подставить ее значение в любое из исходных уравнений.
x = 10
2(10) — 5y = 15
-5y = -5
y = 1
Теперь у вас есть значения обеих координат! Решением системы уравнений является (10, 1).
Вы можете проверить свои ответы, подставив значения x и y в исходные уравнения и упростив их. Если оба уравнения возвращают верные утверждения, как показано ниже, то вы успешно использовали метод подстановки!
| х = 10 | г = 1 |
| 3x + у = 31 | 2х — 5у = 15 |
| 3(10) + (1) = 31 | 2(10) — 5(1) = 15 |
| 31 = 31 | 15 = 15 |
Метод исключения
Для решения систем уравнений методом исключения необходимо исключить одну переменную. Прежде чем начать, очень важно, чтобы оба уравнения были в стандартной форме Ax + By = C. Это организует системы уравнений, выравнивая каждый член в одном уравнении с соответствующим членом в другом.
При использовании метода исключения постарайтесь представить систему уравнений как один большой столбец сложения, за исключением того, что здесь нет переноса, и вы можете только складывать и вычитать соответствующие переменные и константы.
Пример
| 6x + 2y | = 18 | |
| + | 5x + 4y | = 22 |
Цель исключения — исключить переменную. Это означает, что когда у вас есть уравнения, выстроенные в ряд по столбцу и переменной, как в приведенном выше примере, вы хотите, чтобы сумма столбца переменной равнялась 0. Для этого вам нужно умножить один, а иногда и оба, из уравнения в системе на константу, которая создаст коэффициент, который имеет такое же значение, но противоположный знак от соответствующей переменной в другом уравнении.
Чтобы решить, какое уравнение использовать и на какую константу его умножить, мы можем проверить каждую пару переменных. Спросите себя: «На что я могу умножить эту переменную, чтобы исключить переменную в другом уравнении?»
В примере 6x и 5x труднее манипулировать, чтобы компенсировать, чем 2y и 4y. Вы можете умножить верхнее уравнение на (или нижнее на, но это затруднит работу с остальной частью любого уравнения. Вы также можете умножить верхнее уравнение на 5, а нижнее на -6, но это также даст числа с которыми сложнее работать, чем с вариантом, представленным ниже.
Вы также можете умножить верхнее уравнение на 5, а нижнее на -6, но это также даст числа с которыми сложнее работать, чем с вариантом, представленным ниже.
Использование 2y и 4y приводит к относительно простому уравнению, поскольку вы можете умножить первое уравнение на -2, чтобы сократить 4y во втором уравнении, как показано ниже.
| -2(6х + 2у | = | 18) | |
| + | 5x + 4y | = | 22 |
| -12x — 4г | = | -36 | |
| + | 5x + 4y | = | 22 |
Примечание. Не забудьте умножить все уравнение на константу, включая правую часть знака равенства. Если вы не умножите все уравнение, оно уже не будет одним и тем же уравнением!
Теперь вы можете добавить каждый столбец:
| -12x — 4г | = | -36 | |
| + | 5x + 4y | = | 22 |
| -7x + 0 | = | -14 |
Тогда найдите x!
| -7x | = -14 |
Затем подставьте значение x в одно из исходных уравнений, чтобы найти значение y.
| 5(2) + 4 года | = 22 |
| 4 года | = 12 |
Теперь у вас есть значения обеих координат. Таким образом, решением системы уравнений является (2, 3).
Затем вы можете проверить правильность своего решения, подставив значения x и y в исходные уравнения.
| х = 2 | г = 3 |
| 6х + 2у = 18 | 5х + 4у = 22 |
| 6(2) + 2(3) = 18 | 5(2) + 4(3) = 22 |
| 12 + 6 = 18 | 10 + 12 = 22 |
| 18 = 18 | 22 = 22 |
Системы линейных уравнений не имеют решения (параллельные прямые), одно решение (пересекающиеся прямые) или бесконечные решения (одинаковые прямые).
Все вышеперечисленные примеры имели одно решение. Давайте рассмотрим другие случаи.
Когда система линейных уравнений не имеет решения, прямые параллельны друг другу и поэтому никогда не пересекаются.
Каждый метод, который вы попробуете, приведет к устранению обеих переменных, а его упрощение оставит вас с утверждением, которое не соответствует действительности.
Пример
| -15x + 3г | = 9 |
| -5х + у | = 2 |
Сначала методом подстановки:
| у = 5х + 2 |
| -15х + 3(5х + 2) | = 9 |
| -15х + 15х + 6 | = 9 |
Результат, полученный методом подстановки, дает ложное утверждение, поскольку 6 ≠ 9.
Метод исключения:
| -15x + 3г | = 9 | |
| + | (-3)(-5х + у | = 2) |
| -15x + 3г | = 9 | |
| + | 15x — 3 года | = 6 |
| 0 + 0 | ≠ | 3 |
Результат, полученный с помощью метода исключения, также дает ложное утверждение, поскольку 0 ≠ 3
Использование графического метода:
Поскольку линии параллельны, они имеют одинаковый наклон и никогда не пересекаются.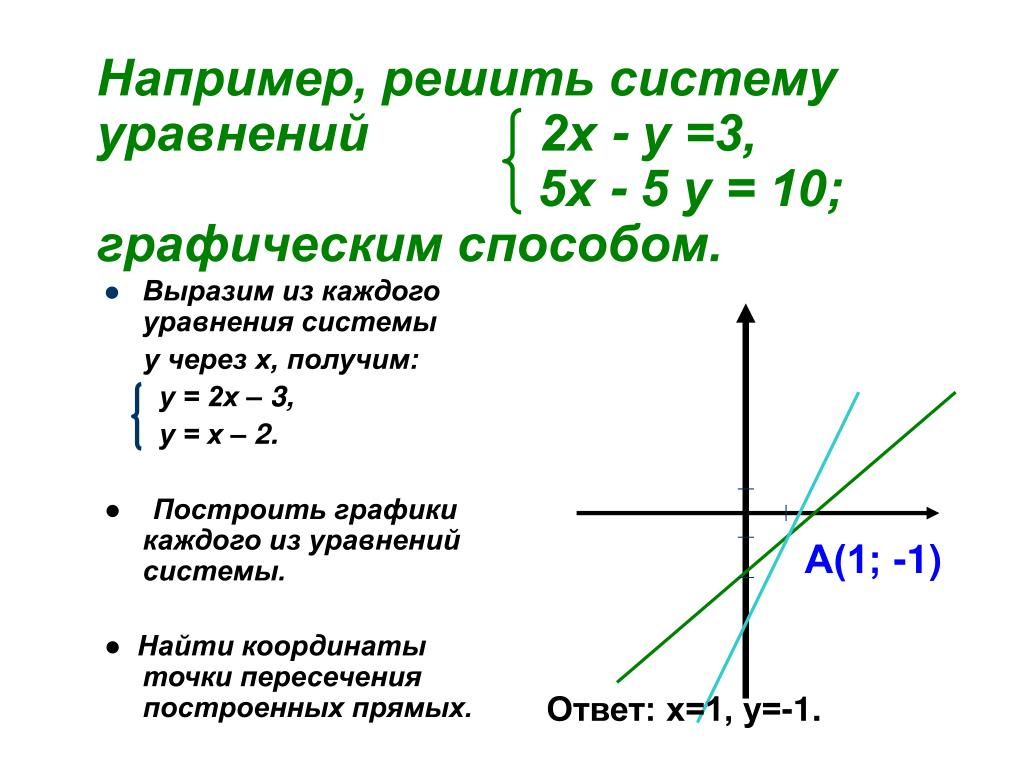 Следовательно, система уравнений не имеет решения.
Следовательно, система уравнений не имеет решения.
Используя эти знания, можно распознавать системы линейных уравнений, в которых нет решения, поскольку коэффициенты каждого набора переменных будут кратны друг другу, и обе пары будут иметь одинаковый множитель (число, которое вы умножаете на получить кратность). Если константы не кратны или не имеют того же множителя, что и коэффициенты, то система не будет иметь решения.
С другой стороны, если вы можете умножить одно из уравнений в системе на константу, чтобы получить в точности другое уравнение, это означает, что уравнения описывают одну и ту же прямую и что система будет иметь бесконечные решения. Системы линейных уравнений с бесконечными решениями сокращают обе переменные, что дает верное утверждение. Это связано с тем, что одинаковые линии имеют одинаковый наклон и точку пересечения по оси Y и будут пересекаться в каждой точке.
Пример
| -15x + 3г | = 9 |
| -5х + у | = 3 |
Метод замены:
| у = 5х + 3 |
| -15х + 3(5х + 3) | = 9 |
| -15х + 15х + 9 | = 9 |
Поскольку результатом использования метода подстановки является истинное утверждение, 9= 9 система уравнений имеет бесконечные решения.
Метод исключения:
| -15x + 3г | = 9 | |
| + | (-3)(-5х + у | = 3) |
| -15x + 3г | = 9 | |
| + | 15x — 3 года | = -9 |
| 0 + 0 | = | 0 |
Подобно методу подстановки, поскольку результатом метода исключения является другое верное утверждение, 0 = 0, система уравнений имеет бесконечные решения.
Метод построения графика:
График из двух уравнений позволяет нам увидеть, что выглядит только одна линия. Это потому, что система уравнений определяет одну и ту же линию, подтверждая, что существует бесконечное количество решений.
Системы линейных уравнений
Цели
- Узнайте, что такое система линейных уравнений.
- Узнайте, как система линейных уравнений соответствует векторному уравнению.

- Узнайте, что означает решение системы линейных уравнений.
- Понимать решения систем линейных уравнений геометрически в измерениях 2 и 3.
- Словарь: система линейных уравнений , согласованная система , несовместимая система .
Основная часть линейной алгебры — понимание решений систем линейных уравнений.
Определение
Уравнение с неизвестными x,y,z,… называется линейным , если обе части уравнения представляют собой сумму (постоянных) кратных x,y,z,… плюс необязательная константа.
Например,
3x+4y=2z-x-z=100
— это линейные уравнения, но
3x+yz=3sin(x)−cos(y)=2
нет.
Обычно мы переносим неизвестные в левую часть уравнения, а константы — в правую.
Система линейных уравнений представляет собой набор нескольких линейных уравнений, таких как
Ax+2y+3z=62x−3y+2z=143x+y−z=−2. (2.1.1)
(2.1.1)
Определение (наборы решений)
- Решение системы уравнений представляет собой список чисел x,y,z,…, которые делают все уравнения истинными одновременно.
- Набор решений системы уравнений представляет собой совокупность всех решений.
- Решить систему означает найти все решения с формулами, включающими некоторое количество параметров.
В предыдущей главе мы столкнулись с векторными уравнениями. Получается, что векторные уравнения — это просто системы линейных уравнений в другой записи. Мы приведем два примера, чтобы показать, что это так.
Пример
Пример
Система линейных уравнений может не иметь решения. Мы уже видели пример этого в векторной записи (пример в разделе 1.2). Вот еще один пример: не существует чисел x и y, для которых одновременно верны следующие два уравнения:
Сх+2у=3х+2у=-3.
В этом случае набор решений пуст , и говорят, что система несовместима .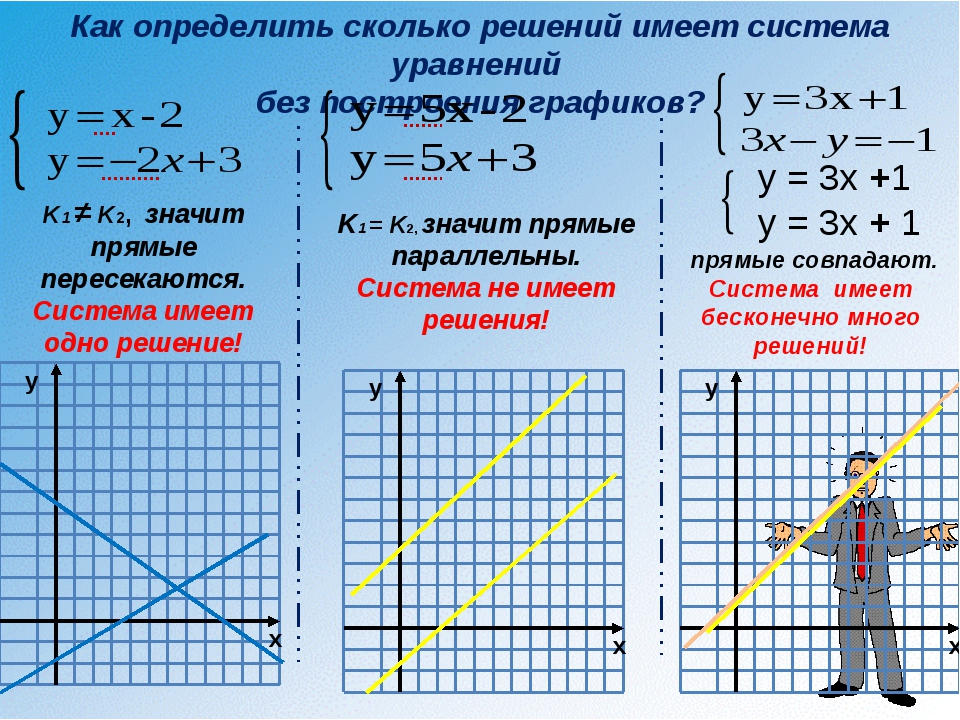
Определение
Система линейных уравнений называется несовместимо , если не имеет решений. Оно называется -непротиворечивым , если оно имеет хотя бы одно решение.
Это определение точно соответствует определению для векторных уравнений (определение в разделе 1.2). Система линейных уравнений непротиворечива в точности тогда, когда непротиворечиво связанное с ней векторное уравнение.
Перед обсуждением того, как решить приведенную ниже систему линейных уравнений, полезно посмотреть на некоторые изображения того, как эти наборы решений выглядят геометрически.
Одно уравнение с двумя переменными
Рассмотрим линейное уравнение x+y=1. Мы можем переписать это как y=1−x, что определяет линию на плоскости: наклон равен −1, а точка пересечения с осью x равна 1.
Определение (линии)
Для наших целей линия — это луч, который является прямым и бесконечным в обоих направлениях.
Одно уравнение с тремя переменными
Рассмотрим линейное уравнение x+y+z=1. Это неявное уравнение для самолета в космосе.
Определение (плоскости)
Плоскость представляет собой плоский лист, бесконечный во всех направлениях.
Два уравнения с двумя переменными
Теперь рассмотрим систему двух линейных уравнений
Сх-3у=-32х+у=8.
Каждое уравнение индивидуально определяет линию на плоскости, показанную ниже.
Решением системы обоих уравнений является пара чисел (x,y), которая делает оба уравнения верными одновременно. Другими словами, это как точка, лежащая одновременно на обеих прямых. На картинке выше видно, что есть только одна точка пересечения прямых: следовательно, эта система имеет ровно одно решение. (Это решение (3,2), как может убедиться читатель.)
Обычно две линии на плоскости пересекаются в одной точке, но, конечно, это не всегда так. Рассмотрим теперь систему уравнений
Сх-3у=-3х-3у=3.
Они определяют параллельных линий на плоскости.
Тот факт, что линии не пересекаются, означает, что система уравнений не имеет решения. Конечно, это легко увидеть алгебраически: если x−3y=−3, то не может быть и так, что x−3y=3.
Есть еще одна возможность. Рассмотрим систему уравнений
Cx-3y=-32x-6y=-6.
Второе уравнение кратно первому, поэтому эти уравнения определяют ту же прямую на плоскости.
В этом случае существует бесконечно много решений системы уравнений.
Два уравнения с тремя переменными
Рассмотрим систему двух линейных уравнений
Бх+у+г=1х-г=0.
Каждое уравнение индивидуально определяет плоскость в пространстве. Решениями системы обоих уравнений являются точки, лежащие на обеих плоскостях. На картинке ниже мы видим, что плоскости пересекаются по прямой. В частности, эта система имеет бесконечно много решений.
Рисунок 13. Плоскости, определяемые уравнениями x+y+z=1 и x−z=0, пересекаются по красной линии, которая является набором решений системы обоих уравнений.
Согласно этому определению, решение системы уравнений означает запись всех решений в терминах некоторого числа параметров. Мы дадим систематический способ сделать это в разделе 2.3; пока мы даем параметрические описания в примерах предыдущего пункта.
строк
Рассмотрим линейное уравнение x+y=1 из этого примера. В этом контексте мы называем x+y=1 числом 9.0018 неявное уравнение линии. Мы можем записать ту же строку в параметрической форме следующим образом:
(x,y)=(t,1−t)для любого t∈R.
Это означает, что каждая точка на прямой имеет вид (t,1−t) для некоторого действительного числа t. В этом случае мы называем t параметром , так как он параметризует точек на линии.
t=0t=1t=−1Теперь рассмотрим систему двух линейных уравнений
Вх+у+г=1х-г=0
этого примера. В совокупности они образуют неявные уравнения для линии в R3. (Для определения линии в пространстве необходимы как минимум два уравнения. ) Эта линия также имеет параметрическую форму с одним параметром t:
) Эта линия также имеет параметрическую форму с одним параметром t:
(х, у, г) = (т, 1-2т, т).
Рисунок 16. Плоскости, определяемые уравнениями x+y+z=1 и x−z=0, пересекаются по желтой линии, которая параметризуется выражением (x,y,z)=(t,1−2t,t). Переместите ползунок, чтобы изменить параметризованную точку.Обратите внимание, что в каждом случае параметр t позволяет нам использовать R до метка точек на линии. Однако ни одна из прямых не совпадает с числовой прямой R: действительно, каждая точка первой строки имеет две координаты, например точка (0,1), а каждая точка второй строки имеет три координаты, например (0,1 ,0).
Самолеты
Рассмотрим линейное уравнение x+y+z=1 из этого примера. Это неявное уравнение плоскости в пространстве. Эта плоскость имеет уравнение в параметрической форме : мы можем записать каждую точку на плоскости как
(x,y,z)=(1−t−w,t,w)для любого t,w∈R.
В данном случае нам нужны два параметра t и w для описания всех точек на плоскости.
Обратите внимание, что параметры t,w позволяют нам использовать R2 для меток точек на плоскости. Однако эта плоскость , а не , как и плоскость R2: действительно, каждая точка на этой плоскости имеет три координаты, как и точка (0,0,1).
При наличии единственного решения, как в этом примере, нет необходимости использовать параметры для описания набора решений.
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
Как решать системы уравнений (видео и практические вопросы)
TranscriptFAQsPractice
Привет, ребята! Добро пожаловать в это видео по системам уравнений.
Система уравнений представляет собой группу из двух или более уравнений , и каждое из уравнений в группе имеет по крайней мере одну неизвестную переменную.
Когда задана система уравнений, цель состоит в том, чтобы найти значение для каждой из неизвестных переменных.
В этом видео мы обсудим два инструмента, которые помогут вам найти неизвестные переменные: замену и исключение.
Подстановка
Подстановка — это способ решения системы путем избавления от всех переменных, кроме одной, и решения этого уравнения.
Подстановку лучше всего использовать, когда у вас есть переменная с коэффициентом 1 или -1. Причина в том, что если она имеет коэффициент 1 или -1, то вам не нужно отменять умножение или деление, вам просто нужно отменить сложение или вычитание, чтобы изолировать переменную.
Есть три шага, которые необходимо выполнить, чтобы иметь возможность решить систему с помощью подстановки.
- Найдите ваши \(x\) или \(y\) в одном уравнении.
- Подставьте ваши \(x\) или \(y\), которые вы решили, в другое уравнение, затем решите.
- Используйте число, полученное при решении для другой переменной или переменных, в зависимости от того, сколько уравнений у вас есть.
Итак, приступим!
Пример
\(4x+3y=2\)
\(x-9y=-19\)
В этом примере мы можем видеть, что наше второе уравнение имеет переменную с 1 в качестве коэффициента . Итак, это позволяет нам найти \(x\). Теперь вы можете решить для любой из переменных. Просто всегда будет легче решить тот, у которого коэффициент 1 или -1.
Теперь, чтобы сделать это, мы просто добавляем \(9y\) к обеим сторонам.
\(x= 9y -19\)
Итак, мы сделали то, что говорит нам наш первый шаг, и нашли решение для одной из наших переменных. Шаг второй теперь говорит нам подставить переменную, для которой мы решили, в наше другое уравнение, а затем решить. Итак, мы собираемся подставить наш \(x\) в \(4x+3y = 2\). Поскольку мы знаем, что \(x=9y -19\), мы подставим это значение в наше значение \(x\) и затем решим.
Итак, мы собираемся подставить наш \(x\) в \(4x+3y = 2\). Поскольку мы знаем, что \(x=9y -19\), мы подставим это значение в наше значение \(x\) и затем решим.
\(4(9y-19)+3y=2\)
Теперь, когда у нас есть одна переменная, мы можем найти значение этой переменной, поэтому в этом случае \ (у\).
Давайте перепишем это, умножив наши 4 на все, что находится в скобках.
\(36y – 76 + 3y = 2\)
Теперь мы можем добавить наши 76 к обеим сторонам. Вы можете сделать это несколькими способами. Если вы хотите сначала сложить свои \(y\) вместе, сделайте это. Я просто делаю то, что проще на мой взгляд.
Когда я добавляю свои 76 к обеим сторонам и складываю свои \(y\) вместе, я получаю \(39y= 78\).
Теперь я делю обе части на 39.
\(y=2\)
Используйте число, полученное при решении, чтобы найти другую переменную или переменные.
Теперь все, что нам нужно сделать, это взять наше значение \(y\) и подставить его в одно из наших исходных уравнений. Неважно какой! Вы можете подставить его в первое или второе уравнение, но я подключу его ко второму уравнению просто так.
Получается:
\(x -9(2) = -19\)
\(x – 18 = -19\)
\(x=-1\)
Готово! Мы нашли значение обеих наших переменных с помощью подстановки.
Теперь давайте посмотрим, как решить систему с помощью исключения.
Исключение
Причина, по которой этот инструмент называется исключением, заключается в том, что вы складываете два уравнения, чтобы исключить одну из ваших переменных.
Пример 1
\(3x – 4y = -27\)
\(7x + 4y = 57\)
Просто взглянув на него, мы можем сказать, что наши \(y\)s будут отменяет. Итак, как только мы сложим два уравнения вместе. У нас есть \(10x = 30\).
И мы можем разделить обе части на 10: \(x=3\)
Мы можем взять наше значение \(x\) и подставить его в любое из наших исходных уравнений. Я включу его в наш первый здесь. Итак, имеем:
Я включу его в наш первый здесь. Итак, имеем:
\(3(3) – 4y = -27\)
Итак, и тогда я перепишу это:
\(9 – 4y = -27\)
Теперь нам нужно переместить 9 на другую сторону, вычитая 9.
\(-4y=-36\)
Затем мы делим обе части на -4 здесь.
\(y=9\)
Итак, мы решили и нашли обе наши переменные. Это был хороший пример, чтобы узнать, как работает исключение, но не всегда наши условия могут быть отменены так легко. Пример 2 нам нужно немного манипулировать, чтобы заставить их делать то, что мы от них хотим.
Итак, что мы можем сделать, чтобы наши условия были отменены? Ну, есть пара вещей, но проще всего, как мне кажется, умножить наше первое уравнение на 2. Это позволит нам сократить наши \(y\)s, потому что мы будем добавлять \( -6\) и \(+6\). Итак, давайте сделаем это.
У нас есть это уравнение (\(9x – 3y = -57\)) все умножается на 2, поэтому давайте перепишем его и получим:
\(2(9x – 3y = -57)\)
\ (18x – 6y = -114\)
Теперь нам нужно взять это и добавить к другому нашему уравнению, чтобы наши \(y\) сокращались. Так что это даст нам \(20x = -80\).
Так что это даст нам \(20x = -80\).
Теперь нам нужно разделить обе стороны на 20, что дает нам \(x=-4\).
Итак, теперь, когда мы знаем, что \(x=-4\), мы можем подставить наши \(-4\), где наши \(x\) находятся в любом из исходных уравнений.
Подключу ко второму. Итак, мы имеем:
\(2(-4) + 6y = 34\)
Я упрощу это и перепишу.
\(-8 + 6y =34\)
Теперь я сдвину свои 8 в обе стороны: \(6y=42\).
Теперь мы разделим обе части на 6 здесь: \(y=7\)
Итак, наш окончательный ответ на эту задачу таков:
\(x=-4 \text{ и } y=7\)
Я надеюсь, что это видео о том, как решить систему уравнений с помощью замены и исключения, было полезным.
Увидимся в следующий раз!
Часто задаваемые вопросы
Q
Как вы решаете системы уравнений?
A
Система уравнений — это набор или набор уравнений, которые используют одни и те же переменные. Цель решения систем уравнений состоит в том, чтобы определить место пересечения линий при построении уравнений. Упорядоченная пара \((x, y)\) этой точки пересечения считается решением системы. Обычно существует четыре метода решения систем уравнений: подстановка, исключение, построение графиков и матрицы. Выбор метода зависит от структуры уравнений. Например, если уравнения уже представлены в форме пересечения наклона \((y=mx+b)\), то удобным вариантом является метод построения графика.
Цель решения систем уравнений состоит в том, чтобы определить место пересечения линий при построении уравнений. Упорядоченная пара \((x, y)\) этой точки пересечения считается решением системы. Обычно существует четыре метода решения систем уравнений: подстановка, исключение, построение графиков и матрицы. Выбор метода зависит от структуры уравнений. Например, если уравнения уже представлены в форме пересечения наклона \((y=mx+b)\), то удобным вариантом является метод построения графика.
Q
Какие существуют четыре метода решения систем уравнений?
A
При решении систем уравнений у вас есть несколько вариантов выбора метода. Выбранный вами метод будет зависеть от структуры уравнений. Конечно, целью является выбор наиболее удобной и эффективной стратегии. Чем больше вы работаете с системами, тем более натренированным ваш глаз станет в выборе наилучшего метода. Четыре метода на выбор включают замену, исключение, график и матрицы. Все подходы совершенно разные, но все стратегии в конечном итоге приведут к одной и той же цели — найти упорядоченную пару \((x, y)\) в месте пересечения линий.
Q
Почему мы используем системы уравнений?
A
Системы уравнений имеют множество полезных практических применений. Например, всякий раз, когда вам даются два неизвестных значения, а также информация, которая связывает два неизвестных значения, можно составить систему уравнений, чтобы найти два неизвестных. Например, допустим, плата за вход в парк развлечений составляет \(20 долларов США\) для детей и \(30 долларов США\) для взрослых. Предположим также, что сегодня в парк вошли \(215\) человек, и что общая сумма входных билетов, собранных сегодня, составила \($3{,}500\). Мы можем найти количество проданных билетов для детей и взрослых, составив систему уравнений. У нас есть два неизвестных значения, и у нас достаточно информации, связывающей эти два значения, чтобы составить наши уравнения. Чтобы решить эту проблему, нам сначала нужно выбрать стратегию (подстановка, исключение, построение графика или матрицы). Решение систем уравнений — это навык, который имеет множество полезных применений. Вот почему процесс решения систем считается основной ветвью алгебры.
Вот почему процесс решения систем считается основной ветвью алгебры.
Q
Чем уравнение отличается от системы уравнений?
A
Линейное уравнение может быть построено путем подстановки значений для \(x\), а затем вычисления соответствующих значений \(y\). Эти \(x\)- и \(y\)-координаты можно изобразить на графике, и в конечном итоге они образуют линию. Когда существует более одного уравнения и они используют одни и те же переменные, уравнения называются «системой».
Пример системы уравнений:
\(y=2x+5\)
\(3y=4x-8\)
Q
В каких профессиях используются системы уравнений?
A
Самое интересное в обучении решению систем уравнений заключается в том, что этот навык можно применить практически в любой профессии! Каждый раз, когда вы сталкиваетесь со сценарием, в котором у вас есть два неизвестных значения и достаточно информации для сравнения двух значений, создание и решение системы уравнений позволит вам определить количество каждого значения. Это часто полезно в сфере финансов, бизнеса и продаж. В частности, карьеры, которые включают расчеты с затратами, доходами и прибылью.
Это часто полезно в сфере финансов, бизнеса и продаж. В частности, карьеры, которые включают расчеты с затратами, доходами и прибылью.
Q
Как системы уравнений используются в реальной жизни?
A
Решение систем уравнений является ценным навыком для изучения из-за его многочисленных применений в реальном мире. Каждый раз, когда у нас есть два неизвестных значения и достаточно информации для сравнения двух значений, мы можем найти неизвестные, составив систему уравнений. Помните, что решение системы уравнений — это значение каждой переменной, при котором оба уравнения верны. Этот навык находит применение во многих сферах нашей повседневной жизни. Например, мы можем использовать систему уравнений, чтобы определить, сколько калорий мы сжигаем, используя различные тренажеры в тренажерном зале. Если мы используем гребной тренажер в течение \(30\) минут и беговую дорожку в течение \(20\) минут и сжигаем в общей сложности \(430\) калорий, это можно представить как уравнение № 1: \(30r +20w=430\). Если мы пойдем в спортзал на следующий день и будем использовать гребной тренажер в течение \(50\) минут и беговую дорожку в течение \(10\) минут, сжигая в общей сложности \(600\) калорий, это можно представить как уравнение № 2: \(50r+10w=600\). У нас есть два неизвестных значения (сколько калорий мы сжигаем в минуту на каждой машине), и у нас достаточно информации для сравнения обоих значений. Это означает, что мы можем решить задачу, составив и решив систему уравнений.
Если мы пойдем в спортзал на следующий день и будем использовать гребной тренажер в течение \(50\) минут и беговую дорожку в течение \(10\) минут, сжигая в общей сложности \(600\) калорий, это можно представить как уравнение № 2: \(50r+10w=600\). У нас есть два неизвестных значения (сколько калорий мы сжигаем в минуту на каждой машине), и у нас достаточно информации для сравнения обоих значений. Это означает, что мы можем решить задачу, составив и решив систему уравнений.
Q
Как вы решаете системы уравнений путем замены?
A
Решение систем уравнений методом замены состоит из трех основных шагов.
Шаг 1: Решите одно уравнение для одной из переменных.
Шаг 2: Подставьте это выражение в другое уравнение и найдите отсутствующую переменную.
Шаг 3: Подставьте этот ответ в одно из уравнений, чтобы найти другую переменную.
Q
Что такое метод замены с примером?
A
Следующая система уравнений может быть решена в три шага.
\(2x+y=1\)
\(x-2y=8\)
Шаг 1: Решите одно уравнение для одной из переменных.
Найдите уравнение с коэффициентом \(1\) или \(-1\). Это ускоряет процесс решения. \(x-2y=8\) имеет коэффициент \(1\) для \(x\), поэтому давайте решим для \(x\). Когда \(2y\) добавляется к обеим частям уравнения, \(x-2y=8\) становится \(x=8+2y\).
Шаг 2: Подставьте это выражение в другое уравнение и найдите отсутствующую переменную.
\(x=8+2y\) было решено для \(x\), так что подставьте это выражение в другое уравнение для \(x\). \(2x+y=1\) становится \(2(8+2y)+y=1\).
Теперь у нас есть уравнение только с y -переменной. На данный момент мы можем решить для y . Сначала мы распределяем, поэтому \(2(8+2y)+y=1\) становится \(16+4y+y=1\). Теперь мы объединяем подобные термины. \(16+4y+y=1\) становится \(16+5y=1\). Теперь вычтите \(16\) с обеих сторон, разделите на \(5\), и мы увидим, что \(y=-3\).
Шаг 3: Подставьте этот ответ в одно из исходных уравнений, чтобы найти другую переменную.
Теперь, когда мы знаем \(y=-3\), мы можем найти \(x\). Подставьте \(-3\) вместо \(y\) в любом уравнении. Воспользуемся первым уравнением \(2x+y=1\). Когда \(-3\) подставляется вместо \(y\), уравнение принимает вид \(2x+(-3)=1\). Когда мы находим \(x\), мы видим, что \(x=2\).
Мы знаем, что \(x=2\) и \(y=-3\). Это означает, что упорядоченная пара \((2, -3)\) является решением системы уравнений. Это место, где линии будут пересекаться друг с другом при построении графика.
Q
Как вы делаете исключение в алгебре?
A
Системы уравнений можно решать методом исключения. Этот метод следует трем основным шагам. Шаг 1: Измените уравнения так, чтобы одна переменная сокращалась при сложении или вычитании уравнений. Шаг 2: Сложите или вычтите уравнения, чтобы исключить одну переменную. Найдите оставшуюся переменную. Шаг 3: Подставьте найденную переменную обратно в одно из исходных уравнений, чтобы найти другую переменную.
Например, следующую систему можно решить методом исключения.
\(3x-4y=-5\)
\(5x+8y=-1\)
Шаг 1: Измените уравнения так, чтобы одна переменная сокращалась при сложении или вычитании уравнений.
В этом случае мы можем умножить первое уравнение на \(2\), чтобы \(y\)-переменные сокращались при сложении уравнений. \(3x-4y=-5\) становится \(6x-8y=-10\).
Шаг 2: Сложите или вычтите уравнения, чтобы исключить одну переменную. Найдите оставшуюся переменную.
\(6x-8y=-10\)
\(5x+8y=-1\)
При сложении уравнений получается \(11x=-11\). Теперь мы можем найти \(x\), разделив обе части уравнения на \(11\). \(х=-1\).
Шаг 3: Подставьте найденную переменную обратно в одно из исходных уравнений, чтобы найти другую переменную. Подставим \(-1\) вместо \(x\) в первом уравнении \(3x-4y=-5\). Теперь уравнение принимает вид \(3(-1)-4y=-5\), что упрощается до \(y=\frac{1}{2}\).
\(x=-1\) и \(y=\frac{1}{2}\), что означает, что решением системы уравнений является упорядоченная пара \((-1, \frac{1} {2})\). Если бы два исходных уравнения были изображены в виде графика, эта упорядоченная пара оказалась бы там, где пересекались бы две линии.
Если бы два исходных уравнения были изображены в виде графика, эта упорядоченная пара оказалась бы там, где пересекались бы две линии.
Q
Как решить систему \(3×3\) методом исключения?
A
Иногда в системе может быть более двух уравнений. Например, следующая система состоит из трех уравнений.
\(x+2y-z=2\)
\(2x-3y+z=-1\)
\(5x-y-2z=-3\)
Процесс решения системы трех уравнений будет быть таким же, как процесс для двух уравнений. Однако наша первая цель — перейти от трех уравнений к двум. Это может быть достигнуто путем сложения или вычитания двух уравнений. Сложим первые два уравнения.
| \(\фантом{00}x+2y-z=2\) | ||
| \(+\) | \(2x-3y+z=-1\) | \(3x-y=1\) |
Переменная \(z\) выпала, и теперь у нас есть только два уравнения, что означает, что мы на правильном пути. Однако нам нужно включить в смесь третье уравнение. Давайте сделаем это, умножив второе уравнение на \(2\), а затем добавив это к третьему уравнению.
Давайте сделаем это, умножив второе уравнение на \(2\), а затем добавив это к третьему уравнению.
Второе уравнение становится \(4x-6y+2z=-2\), и когда мы добавляем его к третьему уравнению, мы получаем \(9x-7y=-5\) (Выпавшие \(z\)s !).
На данный момент мы просто решаем систему из двух уравнений с двумя переменными.
\(3x-y=1\) (Умножьте это уравнение на \(-7\), чтобы \(y\)-переменные были исключены при сложении уравнений)
| \ (-21x+7y=-7\) | ||
| \(+\) | \(\фантом{0}9x-7y=-5\) | |
| \(-12x=-12\) |
Теперь подставим \(1\) для \(x\ ) в любом из уравнений.
\(3(1)-y=1\)
\(y=2\)
Наконец, подставьте \(x=1\) и \(y=2\) в любое из уравнений и найдите \(г\). Если эти значения подставить в первое уравнение, \(x+2y-z=2\) станет \((1)+2(2)-z=2\), что упрощается до \(z=3\).
Помните, когда у вас есть система с тремя уравнениями и тремя переменными, основная идея состоит в том, чтобы перейти к двум уравнениям с двумя переменными и, в конечном итоге, к одному уравнению с одной переменной. Чем больше вы будете практиковать эти задачи на устранение, тем легче они будут становиться!
Чем больше вы будете практиковать эти задачи на устранение, тем легче они будут становиться!
Q
Вы умеете вычитать системы уравнений?
A
При решении системы уравнений методом исключения уравнения можно сложить или вычесть , чтобы исключить переменную. Например, если вы заметили, что в обоих уравнениях одна и та же переменная с одинаковым знаком, то наиболее эффективным методом, вероятно, будет исключение с помощью вычитания.
Например, посмотрите, сможете ли вы определить, почему вычитание с исключением является лучшим вариантом для решения следующей системы.
\(-5x-3y=30\)
Вы правы, если заметили, что оба уравнения имеют одну и ту же переменную с одинаковым знаком: \(-3y\) и \(-3y\). Это означает, что если одно из уравнений вычесть из другого, член выпадет, оставив только одну переменную (это цель).
| \(\phantom{000}2x-3y=9\) | ||
| \(–\) | \((-5x-3y=30)\) | |
| \(7x=-21\) |
Теперь \(-3\) можно подставить в одно из исходных уравнений, чтобы найти \(y\).
\(2x-3y=9\) становится \(2(-3)-3y=9\), что упрощается до \(y=-5\). \((-3, -5)\) является решением.
Практические вопросы
Вопрос №1:
Методом подстановки решите следующую систему уравнений:
\(y=3x+2\)
\(y=5x+6\)
\ ((-1,-1)\)
\((1,11)\)
\((-2,-4)\)
\((4,-2)\)
Показать ответ
Ответ:
Шаг 1. Чтобы использовать метод подстановки, решите один уравнение для одной из переменных и подставить его в другое уравнение, чтобы найти значение другой переменной. Оба уравнения уже решены для \(y\), поэтому мы подставим \(y=3x+2\) во второе уравнение, чтобы получить:
\(3x+2=5x+6\)
Шаг 2 Теперь решите новое уравнение для \(x\).
| \(3x+2=5x+6\) | Запишите второе уравнение с подставленным значением.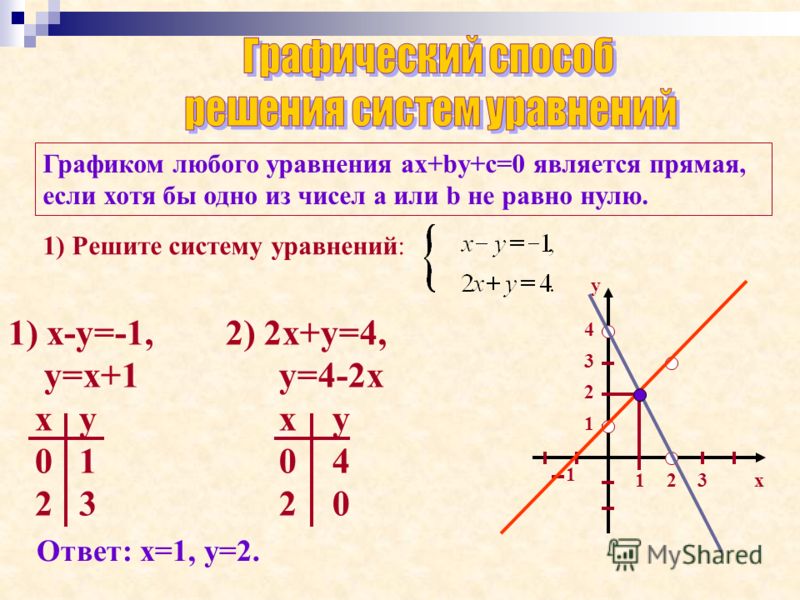 \(5x\) из обеих частей уравнения, чтобы изолировать \(x\). \(5x\) из обеих частей уравнения, чтобы изолировать \(x\). |
| \(-2x+2=6\) | Упростите каждую часть уравнения. | \(-2x+2-2=6-2\) | Вычтите 2 из обеих частей уравнения.. |
| \(-2x=4\) | Упростите каждую часть уравнения. |
| \(\frac{-2x}{-2}=\frac{4}{-2}\) | Разделите обе части уравнения на \(–2\). |
| \(x=-2\) | Упростите каждую часть уравнения. |
Шаг 3. Затем подставьте значение \(x\) в любое из двух исходных уравнений, чтобы найти значение \(y\). Подстановка в первое уравнение дает:
\(y=3-2+2\)
\(y=-6+2\)
\(y=-4\)
Шаг 4. Запишем ответьте как упорядоченную пару \((-2,-4)\).
Скрыть ответ
Вопрос №2:
Методом исключения решите следующую систему уравнений:
\(2x-3y=-9\)
\(x+4y=23\)
\((0,3)\)
\((7,4)\)
\((5,3)\)
\((3,5)\)
Показать ответ
Ответ :
Шаг 1. Измените уравнения так, чтобы одна переменная сокращалась при сложении или вычитании уравнений. Мы можем умножить второе уравнение на \(–2\), чтобы исключить \(x\)-переменные при объединении двух уравнений.
Измените уравнения так, чтобы одна переменная сокращалась при сложении или вычитании уравнений. Мы можем умножить второе уравнение на \(–2\), чтобы исключить \(x\)-переменные при объединении двух уравнений.
\(-2x+4y=23\)
\(-2x-8y=-46\)
Шаг 2. Объедините два уравнения, чтобы исключить \(x\). Затем решите полученное уравнение относительно \(y\).
| \(\phantom{-}2x-3y=-9\) \(-2x-8y=-46\) | Сопоставьте два уравнения, которые будут объединены. |
| \(-11y=-55\) | Объедините два уравнения, чтобы исключить переменную \(x\). |
| \(\frac{-11y}{11}=\frac{-55}{-11}\) | Разделите обе части уравнения на \(–11\). | \(y=5\) | Упростите, чтобы найти \(y\). |
Шаг 3. Теперь мы можем подставить значение \(y\) в любое из исходных уравнений, чтобы найти значение \(x\). Подставив \(y=5\) во второе уравнение, получим:
\(x+4(5)=23\)
\(x+20=23\)
\(x+20-20=23 -20\)
\(x=3\)
Шаг 4. Ответ запишите в виде упорядоченной пары \((3,5)\).
Ответ запишите в виде упорядоченной пары \((3,5)\).
Скрыть ответ
Вопрос №3:
Методом исключения решите следующую систему уравнений:
\(x+\frac{1}{3}y=7\)
\(3x-y=9\)
\((6,5 )\)
\((5,6)\)
\((8,-3)\)
\((1,-6)\)
Показать ответ
Ответ:
Шаг 1. Измените уравнения так, чтобы одна переменная сокращалась при добавлении или вычитании уравнений. Мы можем умножить первое уравнение на \(3\), чтобы \(y\)-переменные были исключены при объединении двух уравнений.
\(3(x+\frac{1}{3}y=7)\)
\(3x+y=21\)
Шаг 2. Объедините два уравнения, чтобы исключить \(y\). Затем решите полученное уравнение относительно \(x\).
| \(3x+y=21\) \(3x-y=9\) | Соедините два уравнения, которые будут объединены. |
| \(6x\phantom{+y}=30\) | Сложите два уравнения, чтобы исключить переменную \(y\). |
| \(\frac{6x}{6}=\frac{30}{6}\) | Разделите обе части уравнения на \(6\). | \(x=5\) | Упростите, чтобы найти \(x\). |
Шаг 3. Теперь мы можем подставить \(x\)-значение в любое из исходных уравнений, чтобы найти \(y\)-значение. Подставляя \(x=5\) в первое уравнение, получаем:
\(5+\frac{1}{3}y=7\)
\(5+\frac{1}{3}y- 5=7-5\)
\(\frac{1}{3}y=2\)
\(3(\frac{1}{3}y)=3∙2\)
\(y=6 \)
Шаг 4. Запишите ответ в виде упорядоченной пары \((5,6)\).
Скрыть ответ
Вопрос №4:
Сумма двух чисел равна 75. Меньшее число, умноженное на четыре, равно большему. Какие два числа?
12 и 48
10 и 10
30 и 45
15 и 60
Показать ответ
Ответ:
Шаг 1: Пусть \ (x \) — меньшее количество и \ ( у\) — большее число. Сумма двух чисел равна 75, поэтому:
Сумма двух чисел равна 75, поэтому:
\(x+y=75\)
Поскольку большее число в четыре раза меньше меньшего числа, мы также имеем:
\(y=4x\)
Чтобы найти каждое число, мы можем решить следующую систему линейных уравнений:
\(x+y=75\)
\(y=4x\)
Шаг 2. Поскольку второе уравнение решается относительно \(y\), воспользуемся методом подстановки, подставив его значение в первое уравнение.
\(x+4x=75\)
Шаг 3. Теперь решите первое уравнение для \(x\).
| \(\фантом{-}х+(4х)=75\) \(-2х-8у=-46\) | Напишите первое уравнение с подставленным значением. |
| \(5x=75\) | Объедините одинаковые члены в левой части уравнения. |
| \(\frac{5x}{5}=\frac{75}{5}\) | Разделите обе стороны на 5. | \(x=15\) | Упростите каждую сторону уравнение. |
Шаг 4. Затем подставьте значение \(x\) в одно из двух исходных уравнений, чтобы найти значение \(y\). Подставляя наше значение для \(x\) в первое уравнение, мы имеем:
Подставляя наше значение для \(x\) в первое уравнение, мы имеем:
| \(15+y=75\) | Подставим \(x=15\) в первое уравнение. |
| \(15+y-15=75-15\) | Вычтите \(15\) из обеих частей уравнения. |
| \(y=60\) | Упростите обе части уравнения. |
Шаг 5. Поскольку \(x=15\) и \(y=60\), два числа равны \(15\) и \(60\).
Скрыть ответ
Вопрос №5:
Местный ресторан быстрого питания продает хот-доги по 2,75 доллара за штуку и гамбургеры по 4,50 доллара за штуку. Во время обеденного ажиотажа ресторан продает в общей сложности 225 хот-догов и гамбургеров, а общий доход составляет 881,25 доллара. Сколько хот-догов и сколько гамбургеров продал ресторан во время обеденного ажиотажа?
100 хот-догов и 125 гамбургеров
75 хот-догов и 150 гамбургеров
150 хот-догов и 75 гамбургеров
85 хот-догов и 140 гамбургеров
Показать ответ
Ответ:
Шаг 1. Пусть \(x\) будет количеством проданных хот-догов, а \(y\) будет количеством проданных гамбургеров, тогда:
Пусть \(x\) будет количеством проданных хот-догов, а \(y\) будет количеством проданных гамбургеров, тогда:
\(x+y=225 \)
Доход от продажи хот-догов составляет \(2,75x\), а доход от продажи гамбургеров составляет \(4,50y\). Так как выручка комбината равна 881,25 долл., то имеем:
\(2,75x+4,50y=881,25\)
Итак, имеем следующую систему уравнений:
\(x+y=225\)
\(2,75 х+4,50у=881,25\)
Мы будем использовать метод исключения, манипулируя уравнениями так, чтобы одна переменная сокращалась при сложении или вычитании уравнений. Мы можем умножить первое уравнение на -2,75, чтобы исключить \(x\)-переменные при объединении двух уравнений.
\(-2,75x+y=225\)
\(-2,75x-2,75y=-618,75\)
Шаг 2. Теперь объедините два уравнения, чтобы исключить \(x\). Затем решите полученное уравнение относительно \(y\).
| \(-2,75x-2,75y=-618,75\) \(\phantom{-}2,75x+4,50y=881,25\) | Соедините два уравнения, которые будут объединены. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(1,75y=262,50\) | Объедините два уравнения, чтобы исключить переменную \(x\). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\frac{1,75y}{1,75}=\frac{262,50}{1,75}\) | Разделите обе части уравнения на 1,75. Шаг 3. найти \(x\)-значение. Подставляя \(y=150\) в первое уравнение, получаем: \(x+150=225\) Итак, ресторан продал 75 хот-догов и 150 гамбургеров. Скрыть ответ
Уравнение — это утверждение, что два математических выражения равны. Выражения представляют количества и могут быть строго числовыми или содержать некоторую комбинацию числовых терминов и терминов, содержащих переменные. Например, \(6 + 3\) — числовое выражение, а \(2x — 7\) — выражение, содержащее переменную. Уравнения подобны предложениям, и их можно оценить как истинные или ложные. Например, \(2 × 5 = 10\) является верным утверждением, потому что количество \(2\умножить на 5\) равно количеству 10. Когда уравнения содержат переменные, задача решения состоит в том, чтобы найти значения переменных, которые делают уравнение верным. Например, \(x = 10\) верно только тогда, когда \(x\) имеет значение 10, а \(2x = 10\) верно только тогда, когда \(x\) имеет значение 5. 92} \), который часто представляет собой расстояние между двумя точками на координатной плоскости. Иногда нам нужно создать собственные уравнения на основе имеющейся информации. Пример: Макс — младший брат Руби. Руби вдвое старше Макса в три раза, а сумма их возрастов составляет 25 лет. Сколько лет каждому брату? Пусть выражение \(a\) представляет возраст Макса. Тогда возраст Руби представлен выражением \(\frac{3a}{2}\), а уравнение, которое нам нужно решить, будет \(a+ \frac{3a}{2} = 25\). Другими словами, возраст Макса плюс возраст Руби составляют 25 лет. Иногда уравнение можно представить несколькими способами. Иногда порядок, который мы используем, зависит от того, как мы видим термины. Например, давайте рассмотрим несколько различных способов визуализации и решения \(\frac{3x}{4} = 30 \): Такая визуализация проблемы приведет вас к двум различным путям ее решения: Наконец, давайте рассмотрим несколько различных способов визуализации и решения \(\frac{3}{4x} = 30:\)
Вернуться к алгебре I Видео 4.2 Решение приложений с помощью систем уравнений — Алгебра среднего уровня 2eЦели обученияК концу этого раздела вы сможете:
Приготовься 4.4Прежде чем приступить к работе, пройдите этот тест на готовность. Сумма удвоенного числа и девяти равна 31. Приготовься 4,5 Близнецы Джон и Рон вместе заработали в прошлом году 96 000 долларов. Рон заработал 8000 долларов, что более чем в три раза превышает заработок Джона. Сколько заработал каждый из близнецов? Приготовься 4.6 Экспресс-поезд и пригородный поезд отправляются из Питтсбурга в Вашингтон, округ Колумбия. Экспресс-поезд может совершить поездку за четыре часа, а местный поезд — за пять часов. Скорость экспресса на 12 миль в час больше, чем скорость пригородного поезда. Найдите скорость обоих поездов. Решение приложений прямого перевода Системы линейных уравнений очень полезны для решения приложений. Некоторым людям проще решать текстовые задачи с двумя переменными, чем с одной переменной. КакРешите приложения с системами уравнений.
Ранее мы решали числовые задачи с одной переменной. Давайте посмотрим, как по-разному это работает, используя две переменные. Пример 4.14Сумма двух чисел равна нулю. Одно число на девять меньше другого. Найдите числа. Решение
Попытайся 4,27Сумма двух чисел равна 10. Одно число на 4 меньше другого. Найдите числа. Попытайся 4,28Сумма двух чисел равна −6,−6. Одно число на 10 меньше другого. Найдите числа. Пример 4.15Хизер предложили два варианта оплаты труда тренера в тренажерном зале. В варианте А ей платили 25 000 долларов плюс 15 долларов за каждую тренировку. Вариант B будет платить ей 10 000 долларов + 40 долларов 10 000 долларов + 40 долларов за каждую тренировку. Сколько учебных занятий уравняло бы варианты заработной платы? Решение
Попытайся 4.29Джеральдин предложили работу две страховые компании. Первая компания платит зарплату в размере 12 000 долларов плюс комиссионные в размере 100 долларов за каждый проданный полис. Второй платит зарплату в размере 20 000 долларов плюс комиссионные в размере 50 долларов за каждый проданный полис. Сколько полисов нужно продать, чтобы общая сумма выплат осталась прежней? Попытайся 4.30В настоящее время Кеннет продает костюмы для компании А, получая зарплату в размере 22 000 долларов плюс комиссионные в размере 10 долларов за каждый проданный костюм. Компания B предлагает ему должность с окладом в размере 28 000 долларов плюс комиссионные в размере 4 долларов за каждый проданный костюм. Сколько костюмов нужно продать Кеннету, чтобы варианты были равны? При решении каждой задачи не забывайте анализировать, какой метод решения системы уравнений будет наиболее удобным. Пример 4.16Переведите в систему уравнений и решите: Когда Дженна провела 10 минут на эллиптическом тренажере, а затем 20 минут занималась круговой тренировкой, ее фитнес-приложение сообщает, что она сожгла 278 калорий. Когда она провела 20 минут на эллиптическом тренажере и 30 минут круговой тренировки, она сожгла 473 калории. Сколько калорий она сжигает за каждую минуту занятий на эллиптическом тренажере? Сколько калорий в минуту круговой тренировки? Решение
Попытайся 4.31Переведите в систему уравнений и затем решите: Марк пошел в спортзал и сделал 40 минут горячей бикрам-йоги и 10 минут прыжков. Он сжег 510 калорий. В следующий раз, когда он пошел в спортзал, он 30 минут занимался бикрам-йогой и 20 минут прыгалками, сжигая 470 калорий. Сколько калорий было сожжено за каждую минуту занятий йогой? Сколько калорий было сожжено за каждую минуту прыжков с места на место? Попытайся 4.32Переведите в систему уравнений и решите: Эрин провела 30 минут на гребном тренажере и 20 минут, поднимая тяжести в тренажерном зале, и сожгла 430 калорий. Во время своего следующего визита в спортзал она потратила 50 минут на гребной тренажер и 10 минут на поднятие тяжестей и сожгла 600 калорий. Решить геометрические задачиТеперь мы будем решать приложения по геометрии, используя системы линейных уравнений. Нам нужно будет добавить дополнительные углы и дополнительные углы в наш список некоторых свойств углов. Сумма двух дополнительных углов равна 90 градусов. Меры двух дополнительных углов в сумме дают 180 градусов. Дополнительные и дополнительные углыДва угла являются дополнительными, если сумма мер их углов равна 90 градусов. Два угла являются дополнительными, если сумма мер их углов равна 180 градусам. Если два угла дополняют друг друга, то говорят, что один угол является дополнением другого. Если два угла являются дополнительными, мы говорим, что один угол является дополнением другого. Пример 4.17Переведите в систему уравнений и затем решите. Разница двух дополнительных углов составляет 26 градусов. Найдите меры углов. Решение
Попытайся 4,33Переведите в систему уравнений и решите: Разница двух дополнительных углов составляет 20 градусов. Найдите меры углов. Попытайся 4,34Переведите в систему уравнений и решите: Разница двух дополнительных углов составляет 80 градусов. Найдите меры углов. В следующем примере мы помним, что дополнительные углы в сумме дают 180. Пример 4. 18 18Переведите в систему уравнений и решите: Два угла являются дополнительными. Мера большего угла на двенадцать градусов меньше, чем в пять раз меньше меры меньшего угла. Найдите меры обоих углов. Решение
Попытайся 4,35Переведите в систему уравнений и решите: Два угла являются дополнительными. Мера большего угла на 12 градусов больше, чем в три раза меньше меньшего угла. Найдите меры углов. Попытайся 4,36Переведите в систему уравнений и решите: Два угла являются дополнительными. Напомним, что сумма углов треугольника составляет 180 градусов. В прямоугольном треугольнике один угол равен 90 градусов. Что это говорит нам о двух других углах? В следующем примере мы будем находить меры двух других углов. Пример 4.19Размер одного из малых углов прямоугольного треугольника в десять раз больше, чем размер другого малого угла. Найдите меры обоих углов. РешениеНарисуем и подпишем фигуру.
Попытайся 4,37Размер одного из малых углов прямоугольного треугольника в 2 и более раза больше, чем размер другого малого угла. Найдите величину обоих углов. Попытайся 4,38Размер одного из малых углов прямоугольного треугольника на 18 меньше, чем удвоенный размер другого малого угла. Найдите величину обоих углов. Часто при решении геометрических задач бывает полезно нарисовать картинку для визуализации ситуации. Пример 4.20Переведите в систему уравнений и решите: У Рэндалла есть забор длиной 125 футов, чтобы оградить часть его заднего двора, примыкающую к его дому. Ему нужно будет только огородить три стороны, потому что четвертая сторона будет стеной дома. Он хочет, чтобы длина огороженного двора (параллельно стене дома) была на 5 футов больше ширины, чем в четыре раза. Решение
Попытайся 4,39Переведите систему уравнений и решите: Марио хочет поставить забор вокруг бассейна на заднем дворе. Так как одна сторона примыкает к дому, ему нужно будет огородить только три стороны. Есть две длинные стороны и одна короткая сторона параллельна дому. Ему нужно 155 футов ограждения, чтобы огородить бассейн. Длина длинной стороны на 10 футов меньше ширины в два раза. Найдите длину и ширину ограждаемой площади бассейна. Попытайся 4.40Переведите в систему уравнений и решите: Алексис хочет построить прямоугольную собачью площадку во дворе рядом с соседским забором. Решение приложений с равномерным движениемМы использовали таблицу для организации информации в задачах равномерного движения, когда мы вводили их ранее. Мы продолжим использовать таблицу здесь. Основное уравнение было D=rtD=rt, где D — пройденное расстояние, r — скорость, t — время. Наш первый пример приложения равномерного движения будет для ситуации, похожей на некоторые, которые мы уже видели, но теперь мы можем использовать две переменные и два уравнения. Пример 4.21Переведите в систему уравнений и решите: Джони выехала из Сент-Луиса по межштатной автомагистрали, двигаясь на запад в сторону Денвера со скоростью 65 миль в час. РешениеДиаграмма помогает нам визуализировать ситуацию. Определите и назовите то, что мы ищем. Диаграмма поможет нам организовать данные. Нам известны ставки и Джони, и Келли, поэтому мы вводим их в таблицу. Мы ищем отрезок времени, в течение которого Келли, k , и Джони, j , будут водить машину. Поскольку D=r·tD=r·t, мы можем заполнить столбец Distance. Переведите в систему уравнений. Чтобы составить систему уравнений, мы должны признать, что Келли и Джони проедут одинаковое расстояние. Итак, 65j=78k65j=78k Кроме того, поскольку Келли ушла позже, ее время будет на 1212 часов меньше, чем время Джони. Итак,
Попытайся 4.41Переведите в систему уравнений и затем решите: Митчелл выехал из Детройта по межштатной автомагистрали, двигаясь на юг в сторону Орландо со скоростью 60 миль в час. Кларк покинул Детройт через 1 час, двигаясь со скоростью 75 миль в час по тому же маршруту, что и Митчелл. Сколько времени потребуется Кларку, чтобы поймать Митчелла? Попытайся 4,42Переведите в систему уравнений и затем решите: Чарли покинул дом своей матери, путешествуя со средней скоростью 36 миль в час. Его сестра Салли уехала через 15 минут (14 часов) (14 часов), путешествуя по тому же маршруту со средней скоростью 42 мили в час. Сколько времени пройдет, прежде чем Салли догонит Чарли? Многие реальные приложения равномерного движения возникают из-за влияния потоков воды или воздуха на фактическую скорость транспортного средства. Давайте посмотрим на лодку, плывущую по реке. В зависимости от того, в каком направлении движется лодка, течение воды либо замедляет ее, либо ускоряет. На изображениях ниже показано, как течение реки влияет на скорость, с которой движется лодка. Обозначим скорость лодки в стоячей воде b , а скорость течения реки c . Лодка плывет по течению в том же направлении, что и течение реки. Течение помогает толкать лодку, поэтому фактическая скорость лодки больше, чем ее скорость в стоячей воде. Фактическая скорость, с которой движется лодка, равна b+c.b+c. Теперь лодка идет вверх по течению, против течения реки. Течение идет против лодки, поэтому фактическая скорость лодки меньше, чем ее скорость в стоячей воде. Действительная скорость лодки равна b−c. В следующем примере мы добавим некоторые числа к этой ситуации. Пример 4.22Переведите в систему уравнений и затем решите. Речной круизный лайнер проплыл 60 миль вниз по течению за 4 часа, а затем 5 часов плыл вверх по течению, чтобы вернуться к пристани. Найдите скорость корабля в стоячей воде и скорость течения реки. Решение
Попытайся 4,43Преобразуйте в систему уравнений и затем решите: Круиз по реке Миссисипи проплыл 120 миль вверх по течению за 12 часов, а затем вернулся к причалу за 10 часов. Попытайся 4,44Переведите в систему уравнений и решите: Джейсон проплыл на своем каноэ 24 мили вверх по течению за 4 часа. Ему потребовалось 3 часа, чтобы плыть обратно. Найдите скорость каноэ в стоячей воде и скорость течения реки. Ветровые течения влияют на скорость самолета так же, как водные течения влияют на скорость лодки. Мы увидим это в следующем примере. Поток ветра в том же направлении, что и самолет, называется попутным ветром 9.0019 . Поток ветра, дующий против направления самолета, называется встречным ветром . Пример 4.23Переведите в систему уравнений и решите: Частный самолет может пролететь 1095 миль за три часа при попутном ветре, но только 987 миль за три часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра. Решение
Попытайся 4,45Переведите в систему уравнений и решите: Небольшой самолет может пролететь 1325 миль за 5 часов при попутном ветре, но только 1035 миль за 5 часов при встречном ветре. Попытайся 4,46Переведите систему уравнений и решите: Коммерческий самолет может пролететь 1728 миль за 4 часа при попутном ветре, но только 1536 миль за 4 часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра. СМИПолучите доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практики с системами уравнений.
Раздел 4.2 УпражненияПрактика ведет к совершенствуПриложения прямого перевода В следующих упражнениях переведите систему уравнений и решите. 72. Сумма двух чисел равна 15. Одно число на 3 меньше другого. Найдите числа. 73. Сумма двух чисел равна 30. 74. Сумма двух чисел равна −16. Одно число на 20 меньше другого. Найдите числа. 75. Сумма двух чисел равна −26.−26. Одно число на 12 меньше другого. Найдите числа. 76. Сумма двух чисел равна 65. Их разница равна 25. Найдите числа. 77. Сумма двух чисел равна 37. Их разница равна 9. Найдите числа. 78. Сумма двух чисел равна −27.−27. Их разница составляет −59,−59. Найдите числа. 79. Сумма двух чисел равна −45.−45. Их разница составляет −89,−89. Найдите числа. 80. Максиму предложили работу две автомобильные компании. Первая компания платит зарплату в размере 10 000 долларов плюс комиссионные в размере 1000 долларов за каждую проданную машину. 81. Джеки предложили работу две кабельные компании. Первая компания платит зарплату в размере 14 000 долларов плюс комиссионные в размере 100 долларов за каждый проданный кабельный пакет. Второй получает зарплату в размере 20 000 долларов плюс комиссионные в размере 25 долларов за каждый проданный пакет кабельного телевидения. Сколько пакетов кабельного телевидения необходимо продать, чтобы общая сумма выплат осталась прежней? 82. В настоящее время Амара продает телевизоры для компании А с зарплатой в 17 000 долларов плюс комиссионные в размере 100 долларов за каждый телевизор, который она продает. Компания B предлагает ей должность с зарплатой 29 долларов.000 плюс комиссия в размере 20 долларов за каждый телевизор, который она продает. 83. В настоящее время Митчелл продает печи для компании А, получая зарплату в размере 12 000 долларов плюс комиссионные в размере 150 долларов за каждую проданную им печь. Компания B предлагает ему должность с окладом в размере 24 000 долларов плюс комиссионные в размере 50 долларов за каждую проданную им печь. Сколько печей нужно продать Митчеллу, чтобы варианты были равными? 84. Две емкости с бензином вмещают пятьдесят галлонов. Большой контейнер может вместить на десять галлонов меньше, чем в два раза меньше, чем маленький контейнер. Сколько галлонов вмещает каждый контейнер? 85. Джун требуется 48 галлонов пунша для вечеринки, и у него есть два разных холодильника для его перевозки. Большой холодильник в пять раз больше меньшего. Сколько галлонов может вместить каждый охладитель? 86. Шелли бегала трусцой 10 минут и ехала на велосипеде 20 минут и сожгла 300 калорий. На следующий день Шелли поменяла время, пробежав 20 минут и покатавшись на велосипеде 10 минут, и сожгла такое же количество калорий. Сколько калорий было сожжено за каждую минуту бега трусцой и сколько за каждую минуту езды на велосипеде? 87. В пятницу Дрю сжег 1800 калорий, играя час в баскетбол и два часа катаясь на каноэ. В субботу он два часа играл в баскетбол и три часа катался на каноэ и сжег 3200 калорий. Сколько калорий он сжигал в час, играя в баскетбол? Сколько калорий он сжигал в час во время гребли на каноэ? 88. Трой и Лиза покупали школьные принадлежности. Каждый приобрел разное количество одного и того же ноутбука и флэш-накопителя. Трой купил четыре ноутбука и пять флэш-накопителей за 116 долларов. Лиза купила два блокнота и три дайвера за 68 долларов. Найдите стоимость каждого ноутбука и каждого флэш-накопителя. 89. Нэнси купила семь фунтов апельсинов и три фунта бананов за 17 долларов. Позже ее муж купил три фунта апельсинов и шесть фунтов бананов за 12 долларов. Сколько стоил фунт апельсинов и бананов? 90. Андреа покупает новые рубашки и свитера. Она может купить 3 рубашки и 2 свитера за 114 долларов или 2 рубашки и 4 свитера за 164 доллара. Сколько стоит рубашка? Сколько стоит свитер? 91. Питер покупает канцтовары. Он может купить 3 упаковки бумаги и 4 степлера за 40 долларов или 5 упаковок бумаги и 6 степлеров за 62 доллара. Сколько стоит пачка бумаги? Сколько стоит степлер? 92. Общее количество натрия в 2 хот-догах и 3 чашках творога составляет 4720 мг. Общее количество натрия в 5 хот-догах и 2 чашках творога составляет 6300 мг. Сколько натрия в хот-доге? Сколько натрия в чашке творога? 93. Общее количество калорий в 2 хот-догах и 3 чашках творога составляет 960 калорий. Общее количество калорий в 5 хот-догах и 2 чашках творога составляет 1190 калорий. Сколько калорий в хот-доге? Сколько калорий в чашке творога? 94. Молли готовит воду с клубникой. На каждую унцию клубничного сока она использует в три раза больше воды, чем сока. Сколько унций клубничного сока и сколько унций воды ей нужно, чтобы приготовить 64 унции воды, настоянной на клубнике? 95. Оуэн делает лимонад из концентрата. Количество литров воды, которое ему нужно, в 4 раза превышает количество литров концентрата. Сколько литров воды и сколько литров концентрата нужно Оуэну для приготовления 100 литров лимонада? Решить геометрические задачи В следующих упражнениях переведите систему уравнений и решите. 96. Разница двух дополнительных углов составляет 55 градусов. 97. Разница двух дополнительных углов составляет 17 градусов. Найдите меры углов. 98. Два угла дополняют друг друга. Мера большего угла на двенадцать меньше, чем удвоенная мера меньшего угла. Найдите меры обоих углов. 99. Два угла дополняют друг друга. Мера большего угла в десять раз больше, чем мера меньшего угла. Найдите меры обоих углов. 100. Разница двух дополнительных углов составляет 8 градусов. Найдите меры углов. 101. Разница двух дополнительных углов составляет 88 градусов. Найдите меры углов. 102. Два дополнительных угла. Мера большего угла в четыре раза больше, чем мера меньшего угла. Найдите меры обоих углов. 103. Два дополнительных угла. Мера большего угла в пять раз меньше, чем мера меньшего угла, умноженная на четыре. Найдите меры обоих углов. 104. Размер одного из малых углов прямоугольного треугольника в 14 раз больше, чем размер другого малого угла. Найдите величину обоих углов. 105. Размер одного из малых углов прямоугольного треугольника в 26 раз больше, чем размер другого малого угла. Найдите величину обоих углов. 106. Размер одного из малых углов прямоугольного треугольника на 15 меньше, чем удвоенный размер другого малого угла. Найдите величину обоих углов. 107. Размер одного из малых углов прямоугольного треугольника на 45 меньше, чем удвоенный размер другого малого угла. Найдите величину обоих углов. 108. Уэйн развешивает гирлянду из ламп длиной 45 футов по трем сторонам своего внутреннего дворика, примыкающего к его дому. 109. Даррин вешает 200-футовую рождественскую гирлянду по трем сторонам забора, ограждающего его передний двор. Длина на пять футов меньше, чем в три раза больше ширины. Найдите длину и ширину забора. 110. Рамка вокруг семейного портрета имеет периметр 90 дюймов. Длина в пятнадцать меньше ширины в два раза. Найдите длину и ширину рамы. 111. Периметр детской игровой площадки составляет 100 футов. Длина в десять раз больше ширины, чем в три раза. Найдите длину и ширину игровой площадки. Решение задач равномерного движения В следующих упражнениях переведите систему уравнений и решите. 112. Сара выехала из Миннеаполиса и направилась на восток по межштатной автомагистрали со скоростью 60 миль в час. 113. Соседи по комнате в колледже Джон и Дэвид ехали домой в один и тот же город на каникулы. Джон ехал со скоростью 55 миль в час, а Дэвид, который уехал через час, ехал со скоростью 60 миль в час. Сколько времени понадобится Давиду, чтобы догнать Джона? 114. В конце весенних каникул Люси покинула пляж и поехала домой со скоростью 40 миль в час. Подруга Люси уехала с пляжа домой через 30 минут (полчаса) и ехала со скоростью 50 миль в час. Сколько времени потребовалось другу Люси, чтобы догнать Люси? 115. Фелесия выехала из дома, чтобы навестить дочь, двигаясь со скоростью 45 миль в час. Ее муж дождался прибытия няни и ушел из дома через двадцать минут (1/3 часа). Он ехал со скоростью 55 миль в час, чтобы догнать Фелесию. 116. Семья Джонсов совершила 12-мильную прогулку на каноэ по реке Индиан за два часа. После обеда обратный путь вверх по реке занял три часа. Найдите скорость каноэ в стоячей воде и скорость течения. 117. Моторная лодка проходит 60 миль вниз по реке за три часа, но возвращается вверх по течению за пять часов. Найдите скорость лодки в стоячей воде и скорость течения. 118. Моторная лодка проплыла 18 миль вниз по реке за два часа, но обратно вверх по течению ей потребовалось 4,54,5 часа из-за течения. Найдите скорость моторной лодки в стоячей воде и скорость течения. 119. Речной круизный катер проплыл 80 миль по реке Миссисипи за четыре часа. Возвращение заняло пять часов. Найдите скорость круизного катера в стоячей воде и скорость течения. 120. Небольшой самолет может пролететь 1072 мили за 4 часа при попутном ветре, но только 848 миль за 4 часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра. 121. Небольшой самолет может пролететь 1435 миль за 5 часов при попутном ветре, но только 1215 миль за 5 часов при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра. 122. Коммерческий самолет может пролететь 868 миль за 2 часа при попутном ветре, но только 792 мили за 2 часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра. 123. Коммерческий самолет может пролететь 1320 миль за 3 часа при попутном ветре, но только 1170 миль за 3 часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра. Письменные упражнения 124. |

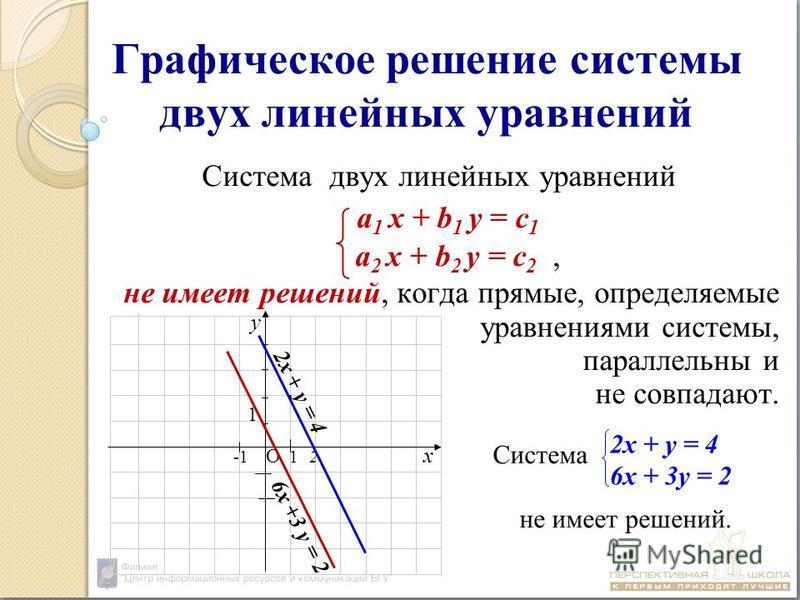 То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями
То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями Если оставить одно уравнений системы и не изменять его, а второе уравнение системы заменять равносильными, то мы получим систему, которая будет равносильна данной. Следствием данной теоремы является то, что, если каждое уравнение заданной системы заменять равносильными, то получим систему, которая будет равносильна данной.
Если оставить одно уравнений системы и не изменять его, а второе уравнение системы заменять равносильными, то мы получим систему, которая будет равносильна данной. Следствием данной теоремы является то, что, если каждое уравнение заданной системы заменять равносильными, то получим систему, которая будет равносильна данной.



 С другой стороны, \(25 = 4\умножить на 5\) равно ложное утверждение, потому что количество 25 не равно количеству \(4\умножить на 5\).
С другой стороны, \(25 = 4\умножить на 5\) равно ложное утверждение, потому что количество 25 не равно количеству \(4\умножить на 5\).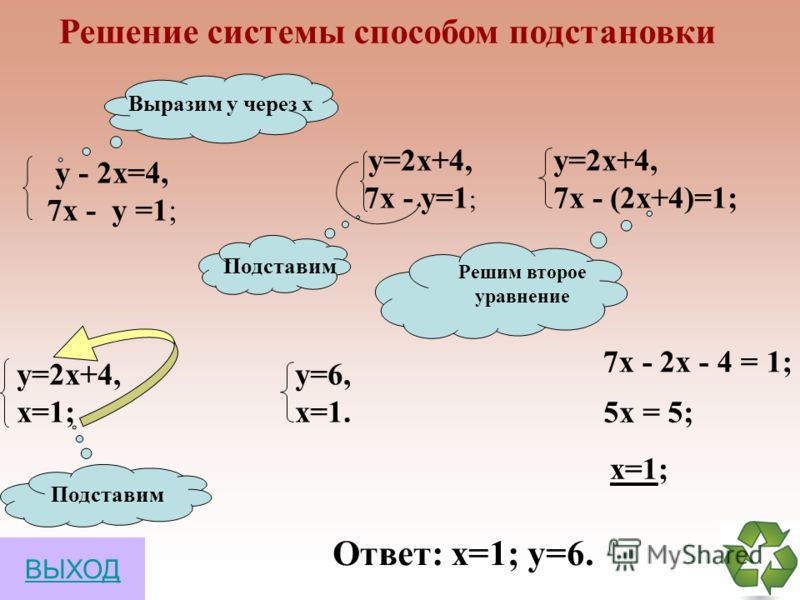 0005
0005 Найдите число.
Найдите число.  Чтобы решить приложение, мы сначала переведем слова в систему линейных уравнений. Затем мы выберем наиболее удобный для использования метод, а затем решим систему.
Чтобы решить приложение, мы сначала переведем слова в систему линейных уравнений. Затем мы выберем наиболее удобный для использования метод, а затем решим систему.


 Проверьте ответ в задаче.
Проверьте ответ в задаче. Прочтите проблему.
Прочтите проблему.
 Ответьте на вопрос.
Ответьте на вопрос.

 Решить систему уравнений.
Решить систему уравнений. Ответьте на вопрос.
Ответьте на вопрос. Сколько калорий она сжигала за каждую минуту занятий на гребном тренажере? Сколько калорий она сжигала за каждую минуту поднятия тяжестей?
Сколько калорий она сжигала за каждую минуту занятий на гребном тренажере? Сколько калорий она сжигала за каждую минуту поднятия тяжестей?
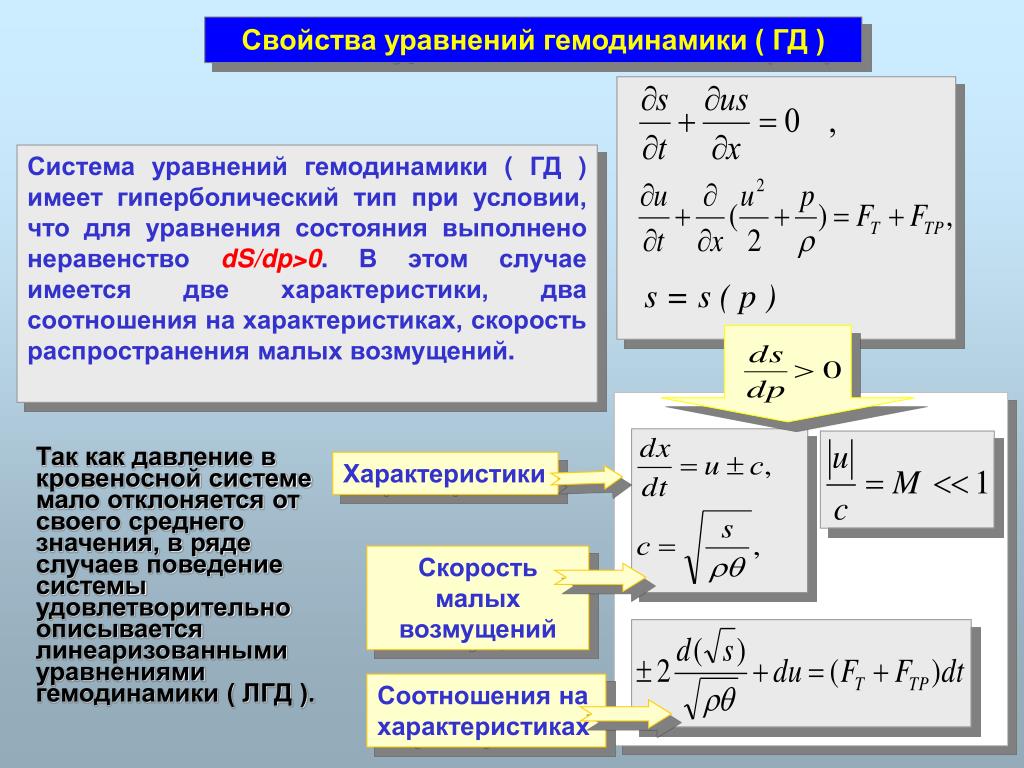 Решить систему уравнений методом исключения.
Решить систему уравнений методом исключения. Переведите в систему уравнений.
Переведите в систему уравнений.
 Мера большего угла на 18 меньше, чем удвоенная мера меньшего угла. Найдите меры углов.
Мера большего угла на 18 меньше, чем удвоенная мера меньшего угла. Найдите меры углов. Назовите то, что мы ищем.
Назовите то, что мы ищем. Решить систему уравнений. Мы будем использовать подстановку, так как первое уравнение решается для a .
Решить систему уравнений. Мы будем использовать подстановку, так как первое уравнение решается для a . Ответьте на вопрос.
Ответьте на вопрос. Найдите длину и ширину.
Найдите длину и ширину.
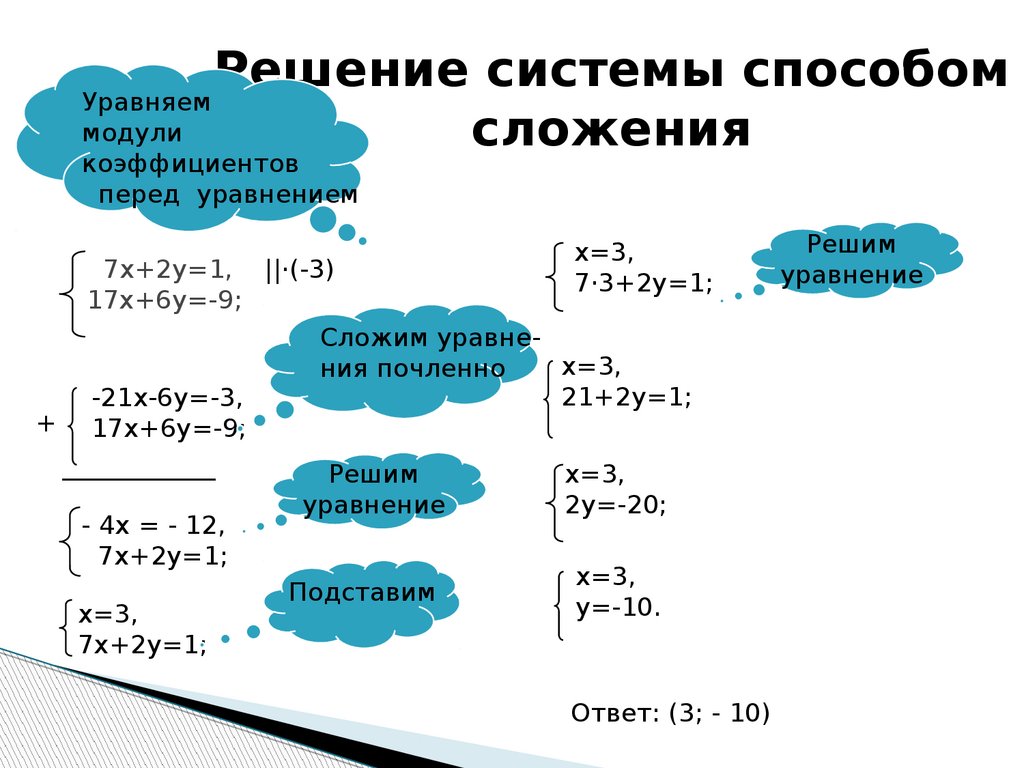
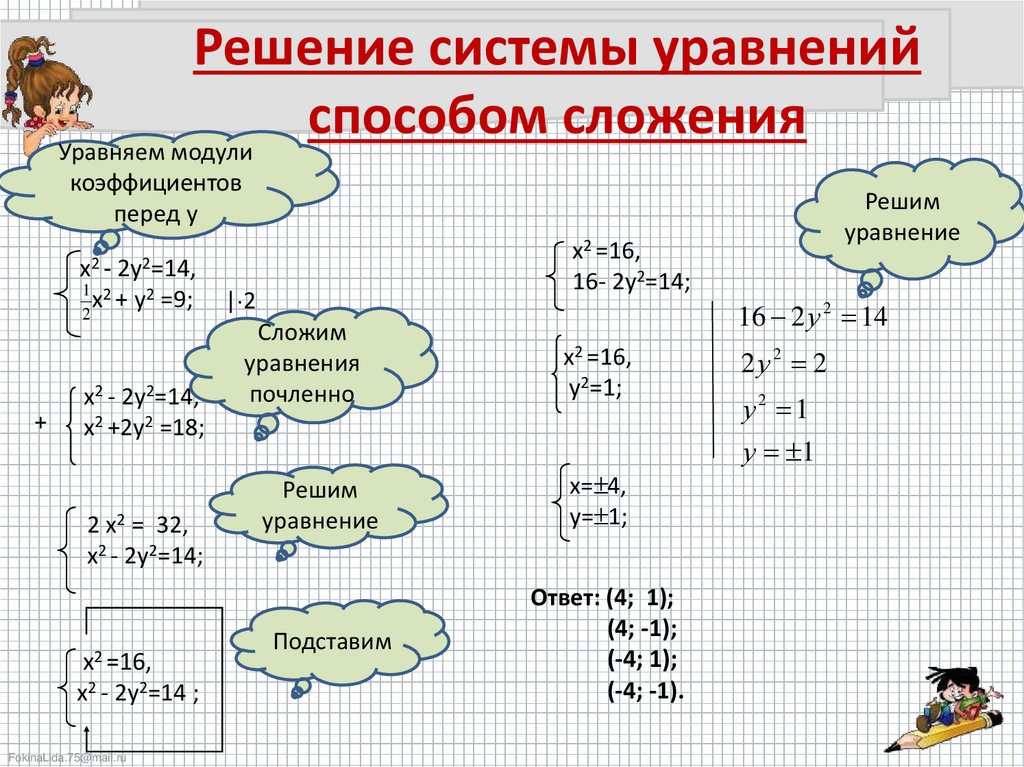 Она будет использовать 136 футов ограждения, чтобы полностью оградить прямоугольную собачью дорожку. Длина собачьей дорожки вдоль забора соседа будет на 16 футов меньше, чем в два раза больше ширины. Найдите длину и ширину собачьей дорожки.
Она будет использовать 136 футов ограждения, чтобы полностью оградить прямоугольную собачью дорожку. Длина собачьей дорожки вдоль забора соседа будет на 16 футов меньше, чем в два раза больше ширины. Найдите длину и ширину собачьей дорожки. Через полчаса Келли выехала из Сент-Луиса по тому же маршруту, что и Джони, со скоростью 78 миль в час. Сколько времени понадобится Келли, чтобы догнать Джони?
Через полчаса Келли выехала из Сент-Луиса по тому же маршруту, что и Джони, со скоростью 78 миль в час. Сколько времени понадобится Келли, чтобы догнать Джони?

 Полеты на самолетах по пересеченной местности в Соединенных Штатах обычно занимают больше времени на запад, чем на восток из-за преобладающих ветров.
Полеты на самолетах по пересеченной местности в Соединенных Штатах обычно занимают больше времени на запад, чем на восток из-за преобладающих ветров. b−c.
b−c.


 Найдите скорость речного катера в стоячей воде и скорость течения реки.
Найдите скорость речного катера в стоячей воде и скорость течения реки.


 Найдите скорость струи в неподвижном воздухе и скорость ветра.
Найдите скорость струи в неподвижном воздухе и скорость ветра. Одно число на 4 меньше другого. Найдите числа.
Одно число на 4 меньше другого. Найдите числа.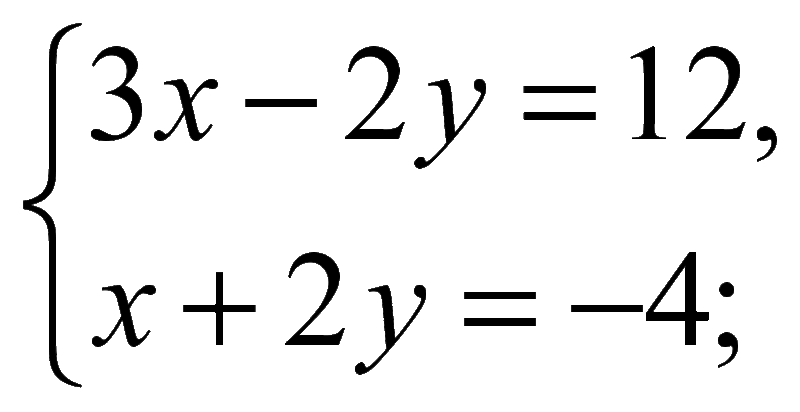 Второй платит зарплату в размере 20 000 долларов плюс комиссионные в размере 500 долларов за каждую проданную машину. Сколько автомобилей нужно продать, чтобы общая сумма выплат осталась прежней?
Второй платит зарплату в размере 20 000 долларов плюс комиссионные в размере 500 долларов за каждую проданную машину. Сколько автомобилей нужно продать, чтобы общая сумма выплат осталась прежней? Сколько телевизоров Амара должна продавать, чтобы варианты были равными?
Сколько телевизоров Амара должна продавать, чтобы варианты были равными?


 Найдите меры углов.
Найдите меры углов.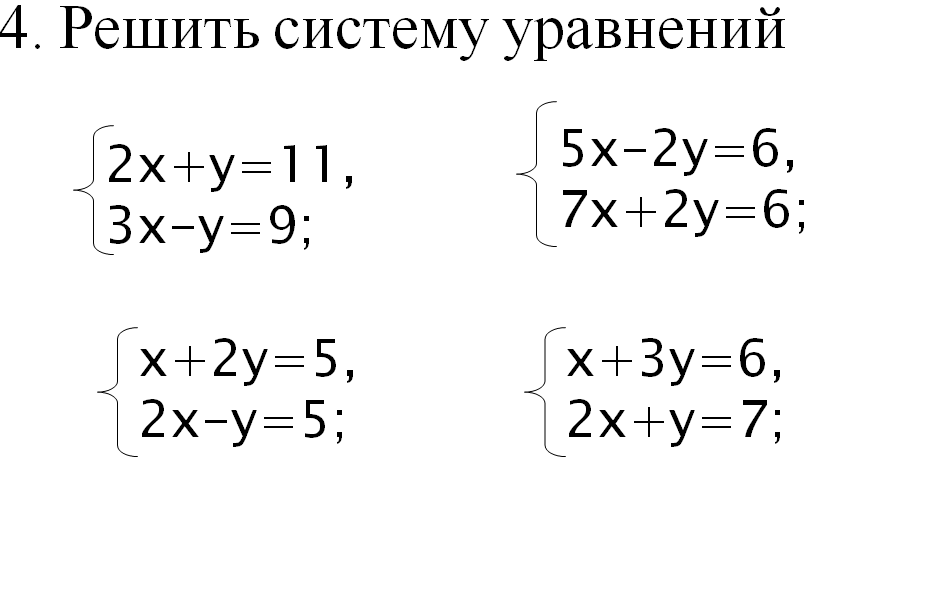
 Длина его внутреннего дворика, сторона вдоль дома, на пять футов длиннее, чем в два раза больше его ширины. Найдите длину и ширину террасы.
Длина его внутреннего дворика, сторона вдоль дома, на пять футов длиннее, чем в два раза больше его ширины. Найдите длину и ширину террасы. Ее сестра последовала за ней по тому же маршруту, уехав через два часа и двигаясь со скоростью 70 миль в час. Сколько времени понадобится сестре Сары, чтобы догнать Сару?
Ее сестра последовала за ней по тому же маршруту, уехав через два часа и двигаясь со скоростью 70 миль в час. Сколько времени понадобится сестре Сары, чтобы догнать Сару? Как скоро он доберется до нее?
Как скоро он доберется до нее?