Точечные оценки: 3.3. Точечные оценки параметров распределения

3.3. Точечные оценки параметров распределения

На практике часто удается предсказать или оценить с помощью гистограммы вид распределения наблюдаемой случайной величины ξ с точностью до неизвестного параметра (или нескольких параметров). Одной из основных задач математической статистики является нахождение оценки (приближенного значения) неизвестного параметра по имеющейся выборке.

Основные понятия

Пусть наблюдается случайная величина ξ с функцией распределения и плотностью распределения . Случайная выборка представлена вектором с реализацией . (3.7)

Параметром распределения случайной величины называется любая числовая характеристика этой случайной величины (математическое ожидание, дисперсия и т. п.) или любая константа, явно входящая в выражение для функции или плотности распределения.

Если параметр неизвестен, то его точечной оценкой называется произвольная функция элементов выборки

. (3.8) Реализацию оценки, т. е. значение оценки для наблюдавшейся в эксперименте реализации выборки, принимают за приближенное значение неизвестного параметра

Из соотношения (3. 8) видно, что как функция случайных величин сама также является случайной величиной. Закон распределения оценки зависит от вида функции , числа наблюдений и значения оцениваемого параметра.

Ясно, что существует много разных способов построения точечной оценки, и не всякая зависимость может давать удовлетворительную оценку неизвестного параметра . Рассмотрим некоторые свойства, которыми должна обладать оценка, чтобы ее можно было считать хорошим приближением к неизвестному параметру.

Оценка параметра называется Несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть

. (3.9)

Если свойство (2.2) не выполняется, то есть

, (3.10)

То оценку называют Смещенной, при этом величину называют систематической ошибкой оценки .

Требование несмещенности означает, что выборочные значения оценок, полученных в результате повторения выборок, группируются около оцениваемого параметра.

Оценка параметра называется Состоятельной, если при она сходится по вероятности к оцениваемому параметру , т. е. для любого ε > 0 выполняется равенство

. (3.11)

Следующая теорема устанавливает достаточные условия состоятельности оценки параметра .

Теорема. Если при и , то оценка параметра является состоятельной.

Состоятельность оценки означает, что, при достаточно большом объеме выборки с вероятностью близкой к единице, отклонение оценки от истинного значения параметра меньше ранее заданной величины.

Обычно в качестве Меры точности оценки используется среднеквадратическая ошибка (среднее значение квадрата ошибки) . Очевидно, чем меньше эта ошибка, тем теснее сгруппированы значения оценки около оцениваемого параметра. Поэтому всегда желательно, чтобы ошибка оценки была по возможности малой. Используя свойства математического ожидания, нетрудно получить

. (3.12)

Для несмещенных оценок

, (3.13)

То есть их мерой точности является дисперсия.

Несмещенная оценка параметра называется его Эффективной Оценкой, если ее дисперсия является наименьшей среди дисперсий всех возможных оценок параметра , вычисленных по одному и тому же объему выборки.

Точечные оценки математического ожидания и дисперсии

Пусть случайная выборка порождена наблюдаемой случайной величиной ξ, математическое ожидание и дисперсия которой неизвестны. В качестве оценок для этих характеристик было предложено использовать выборочное среднее

И выборочную дисперсию

. (3.14)

Рассмотрим некоторые свойства оценок математического ожидания и дисперсии.

1. Вычислим математическое ожидание выборочного среднего:

. (3.15)

Следовательно, выборочное среднее является несмещенной оценкой для .

2. Напомним, что результаты наблюдений – независимые случайные величины, каждая из которых имеет такой же закон распределения, как и величина , а значит, , , . Будем предполагать, что дисперсия конечна. Тогда, согласно теореме Чебышева о законе больших чисел, для любого ε > 0 имеет место равенство ,

Которое можно записать так: . (3.16) Сравнивая (3.16) с определением свойства состоятельности (3.11), видим, что оценка является состоятельной оценкой математического ожидания .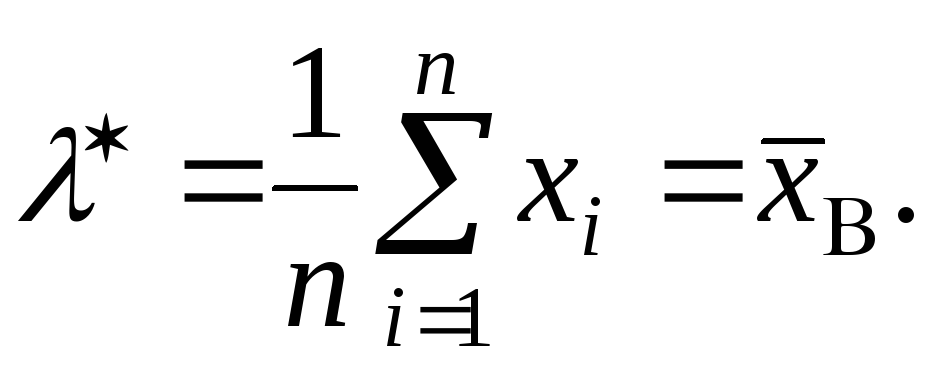

3. Найдем дисперсию выборочного среднего:

. (3.17)

Таким образом, дисперсия оценки математического ожидания уменьшается обратно пропорционально объему выборки.

Можно доказать, что если случайная величина ξ распределена нормально, то выборочное среднее является эффективной оценкой математического ожидания , то есть дисперсия принимает наименьшее значение по сравнению с любой другой оценкой математического ожидания. Для других законов распределения ξ это может быть и не так.

Выборочная дисперсия является смещенной оценкой дисперсии , так как . (3.18)

Действительно, используя свойства математического ожидания и формулу (3.17), найдем

.

Чтобы получить несмещенную оценку дисперсии, оценку (3.14) нужно исправить, то есть домножить на . Тогда получим несмещенную выборочную дисперсию

. (3.19)

Отметим, что формулы (3.14) и (3.19) отличаются лишь знаменателем, и при больших значениях выборочная и несмещенная дисперсии отличаются мало. Однако при малом объеме выборки следует пользоваться соотношением (3.19).

Для оценки среднего квадратического отклонения случайной величины используют так называемое “исправленное” среднее квадратическое отклонение, которое равно квадратному корню из несмещенной дисперсии: .

< Предыдущая		Следующая >

Точечные оценки параметров распределений

Точечная оценка математического ожидания
Пусть выборка из генеральной совокупности, соответствующей случайной величине x с неизвестным математическим ожиданием Mx =q  и известной дисперсией  .
Рассмотрим оценку неизвестного математического ожидания

.

Оценка несмещённая, поскольку её математическое ожидание равно Mx =q  :

,
Оценка состоятельная, поскольку при n®¥, :

.

Итак, для оценки неизвестного математического ожидания случайной величины будем использовать выборочное среднее: .

Точечная оценка дисперсии
Для дисперсии  случайной величины  можно предложить следующую оценку:

, где  — выборочное среднее.

Доказано, что эта оценка состоятельная, но смещенная.
В качестве состоятельной несмещенной оценки дисперсии используют величину

.

Именно несмещенностью оценки  объясняется ее более частое использование в качестве оценки дисперсии.

Пример 1

Пример 1. Задана выборка, содержащая 100 значений случайной величины.

Вычислим точечные оценки математического ожидания и дисперсии случайной величины.

На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.

Получили .

 

Точечная оценка вероятности события

Предположим, что в некотором эксперименте событие A происходит (благоприятный исход испытания) с вероятностью p и не происходит с вероятностью q =1– p и пусть случайная величина  m — количество  благоприятных исходов в серии испытаний. Задача состоит в получении по результатам серии n случайных экспериментов оценки  неизвестного параметра  распределения p.

При заданном числе испытаний n  величина m — случайная величина, имеющая биномиальное распределение. Если событие A в серии из n независимых испытаний произошло m раз, то m — значение случайной величиныm.

Оценку  величины  будем вычислять по формуле .

Эта оценка несмещённая, состоятельная и эффективная.

Доказано, что эта оценка эффективна — обладает при прочих равных условиях минимальной дисперсией.

На рисунке приведен график зависимости точечной оценки вероятности p числа успехов от числа испытаний n в серии испытаний Бернулли. График построен по выборке 1000 значений случайной величины, имеющей биномиальное распределение с параметром p = 0.4. Видно, что с ростом числа испытаний точечная оценка приближается к известному точному значению параметра, которое равно 0. 4.

 

График зависимости точечной оценки вероятности от числа испытаний

Пример 2

Пример 2. Задана выборка, содержащая  20 значений случайной величины (значения m) — количество успехов в эксперименте из 1000 независимых испытаний (проведено 20 одинаковых экспериментов по 1000 независимых испытаний в каждом).

Найдём точечную оценку  вероятности успеха  p и исследуем статистические свойства этой оценки.

На приведенных ниже рисунках изображены фрагменты листа Excel с вычислениями.

 

Вычисленные значения оценки вероятности записаны в столбце B. Видно, что все эти значения близки к 0.3.

 

Значения вероятности  лежат в интервале [0.2672, 0.3525], . Можно достаточно уверенно полагать вероятность успеха равной 0.3.

 

Точечная оценка параметров равномерного распределения

Пусть  выборка из генеральной совокупности, соответствующей случайной величине x, имеющей равномерное распределение на [0, q ] с неизвестным параметром q. Наша задача — оценить этот неизвестный параметр.

Для случайной величины  x , имеющей равномерное распределение на [0, q] математическое ожидание и дисперсия известны:  и .

 

А поскольку оценка  величины Mx  известна, , то за оценку  параметра  q можно взять оценку .

 

Несмещенность оценки очевидна: .

Состоятельность:

 

 ,

 

т.е. при n® ¥ дисперсия оценки  стремится к нулю.

Для получения другой оценки  параметра  обратимся к другой статистике:  

Пусть .

Найдем функцию распределения случайной величины :

,  для .

Тогда математическое ожидание и дисперсия случайной величины  равны соответственно  и , т.е. оценка  состоятельная, но смещенная.

Однако если вместо  рассмотреть , то  и , — состоятельная и несмещенная оценка.

А поскольку , то оценка  существенно эффективнее оценки . Например, при  разброс оценки  в 33 раза меньше разброса оценки .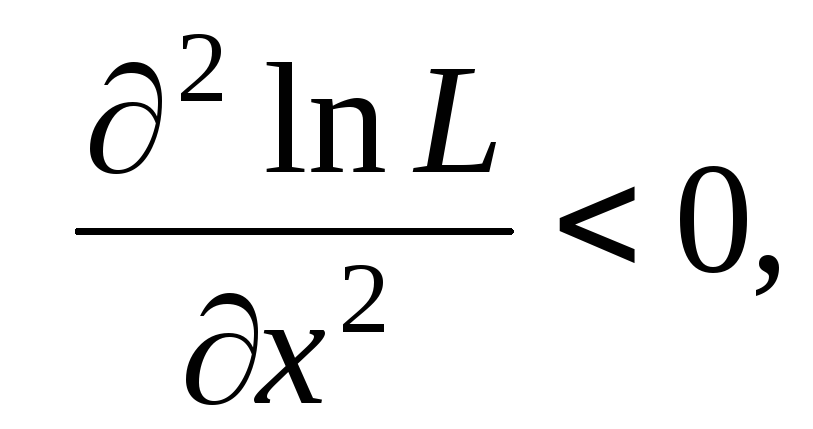

Последний пример еще раз показывает, что выбор статистической оценки неизвестного параметра распределения — важная и нетривиальная задача.

Пример 3

Пример 3. Задана выборка, содержащая 100 значений случайной величины, о которой известно, что она имеет равномерное распределение на промежутке [0, q].

Вычислим и сравним три оценки неизвестного параметра q, котрые вычисляются по формулам:

, , .

На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.

Получили, что оценки  и  близки. Это и понятно, сомножитель  в оценке  при больших  мало отличается от единицы.

Статистическое оценивание

Распределение случайной величины (распределение генеральной совокупности) характеризуется обычно рядом числовых характеристик:

• для нормального распределения N(a, σ) — это математическое ожидание a и среднее квадратическое отклонение σ ;
• для равномерного распределения R(a,b) — это границы интервала [a;b], в котором наблюдаются значения этой случайной величины.

Такие числовые характеристики, как правило, неизвестные, называются параметрами генеральной совокупности.

Оценка параметра — соответствующая числовая характеристика, рассчитанная по выборке. Оценки параметров генеральной совокупности делятся на два класса: точечные и интервальные.

Когда оценка определяется одним числом, она называется точечной оценкой. Точечная оценка, как функция от выборки, является случайной величиной и меняется от выборки к выборке при повторном эксперименте.
К точечным оценкам предъявляют требования, которым они должны удовлетворять, чтобы хоть в каком-то смысле быть «доброкачественными». Это несмещённость, эффективность и состоятельность.

Интервальные оценки определяются двумя числами – концами интервала, который накрывает оцениваемый параметр. В отличие от точечных оценок, которые не дают представления о том, как далеко от них может находиться оцениваемый параметр, интервальные оценки позволяют установить точность и надёжность оценок.

В качестве точечных оценок математического ожидания, дисперсии и среднего квадратического отклонения используют выборочные характеристики соответственно выборочное среднее, выборочная дисперсия и выборочное среднее квадратическое отклонение.

Свойство несмещенности оценки.
Желательным требованием к оценке является отсутствие систематической ошибки, т.е. при многократном использовании вместо параметра θ его оценки среднее значение ошибки приближения равно нулю — это свойство несмещенности оценки.

Определение. Оценка называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра:

Выборочное среднее арифметическое является несмещенной оценкой математического ожидания, а выборочная дисперсия — смещенная оценка генеральной дисперсии

D. Несмещенной оценкой генеральной дисперсии является оценка

Свойство состоятельности оценки.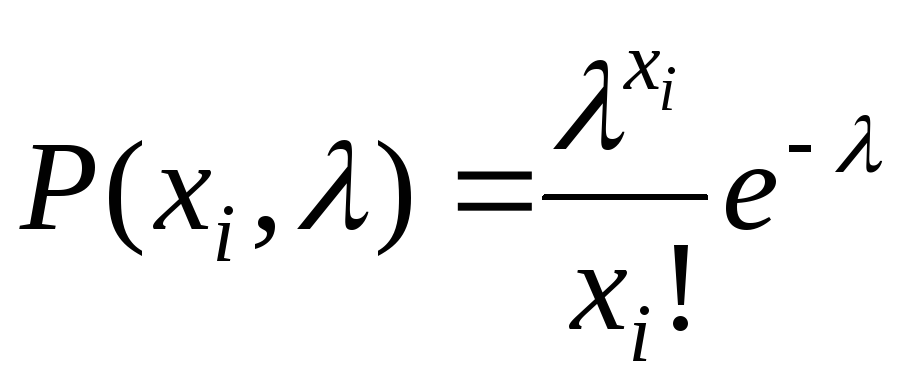
Второе требование к оценке — ее состоятельность — означает улучшение оценки с увеличением объема выборки.

Определение. Оценка называется состоятельной, если она сходится по вероятности к оцениваемому параметру θ при n→∞.

Сходимость по вероятности означает, что при большом объеме выборки вероятность больших отклонений оценки от истинного значения мала.

Свойство эффективной оценки.
Третье требование позволяет выбрать лучшую оценку из нескольких оценок одного и того же параметра.

Определение. Несмещенная оценка является эффективной, если она имеет наименьшую среди всех несмещенных оценок дисперсию.

Это означает, что эффективная оценка обладает минимальным рассеиванием относительно истинного значения параметра. Заметим, что эффективная оценка существует не всегда, но из двух оценок обычно можно выбрать более эффективную, т.е. с меньшей дисперсией. Например, для неизвестного параметра a нормальной генеральной совокупности N(a,σ) в качестве несмещенной оценки можно взять и выборочное среднее арифметическое, и выборочную медиану.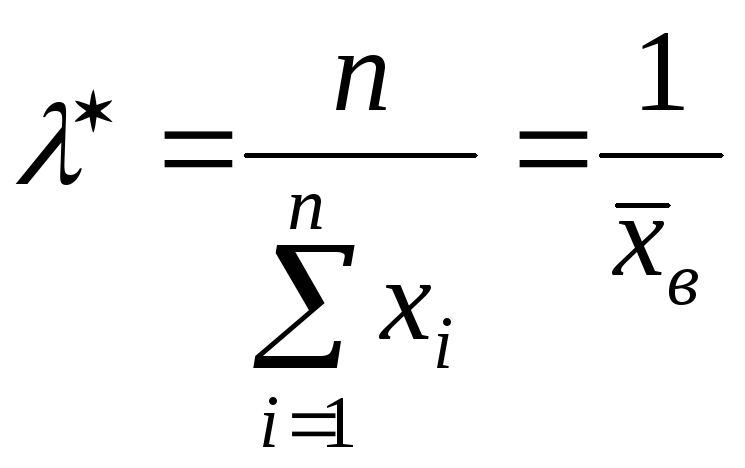

Но дисперсия выборочной медианы примерно в 1.6 раза больше, чем дисперсия среднего арифметического. Поэтому более эффективной оценкой является выборочное среднее арифметическое.

Пример №1. Найдите несмещенную оценку дисперсии измерений некоторой случайной величины одним прибором (без систематических ошибок), результаты измерения которой (в мм): 13,15,17.
Решение. Таблица для расчета показателей.

x	|x — xср|	(x — xср)2
13	2	4
15	0	0
17	2	4
45	4	8

Простая средняя арифметическая (несмещенная оценка математического ожидания)


Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т. е. отклонения от среднего — смещенная оценка).


Несмещенная оценка дисперсии — состоятельная оценка дисперсии (исправленная дисперсия).

Пример №2. Найдите несмещенную оценку математического ожидания измерений некоторой случайной величины одним прибором (без систематических ошибок), результаты измерения которой (в мм): 4,5,8,9,11.
Решение. m = (4+5+8+9+11)/5 = 7.4

Пример №3. Найдите исправленную дисперсию S² для выборки объема n=10, если выборочная диспресия равна D = 180.
Решение. S² = n*D/(n-1) = 10*180/(10-1) = 200

Точечная оценка — Энциклопедия по экономике

С точки зрения статистики использованные нами точечные оценки спроса — лишь выборка из множества возможных значений. То, насколько точно эта выборка представляет реальную действительность, — вопрос не бесспорный. Если допущения, принимаемые для облегчения анализа, будут чрезмерными, ценность результатов анализа для лица, принимающего решения, окажется ограниченной.  [c.422]
Выборочные оценки параметров нормального распределения. Точечная оценка математического ожидания случайной величины с нормальным распределением определяется величиной выборочного среднего значения  [c.60]

Е — оцененная точечная оценка для ошибки совокупности.  [c.68]

В обоих вариантах получены показатели снижения объема продажи и роста цен, но в первом случае объем продажи снизился на 3,58%, цены повысились на 3,7%, а во втором — снижение объема продажи на 3,7% и рост цен на 3,78%. Следуя статистической логике, можно сказать, что точечные оценки в принципе невозможны можно говорить лишь о поле или интервале оценок для объема продажи — снижение от -3,58% до — 3,7% для цен — рост от 3,7% до 3,78%.  [c.383]

Каждый факт хозяйственной жизни описывается тем самым не одной (точечной) оценкой, а их набором. Поскольку каждому методу оценки соответствует свое распределение вероятностей, то поле оценок состоит из доверительных интервалов их точечных значений, исчисленных различными способами.  [c.206]

Экстраполяция дает возможность получить точечное значение прогноза. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, имеет малую вероятность. Поэтому любой статистический прогноз носит приближенный характер. В связи с этим целесообразно определение доверительных интервалов прогноза. Величина доверительного интервала определяется следующим образом  [c.90]

Наряду с точечными оценками параметров (в виде одного числа) рассматривают интервальные оценки.  [c.44]

Чоу 122, 123, 124 Точечная оценка 44 Транспонирование матрицы 260, 261  [c.305]

Следует заметить, что несмотря на чрезвычайную важность (в том числе в маркетинговых исследованиях рынков новых продуктов) рассматриваемой категории полезности, которая, как бы к этому ни относиться, составляет главную цель потребления, до настоящего времени нет надежных методов ее количественного измерения. Еще более сложным является точечная оценка уровней полезности.  [c.232]

Доверительная граница параметра Пн (Пв) всегда может быть выражена через его точечную оценку П и относительную ошибку бд  [c.169]

Прогноз ожидаемого прироста запасов в регионе характеризуется гораздо большей неопределенностью, чем прогноз добычи из открытых месторождений. И это обстоятельство серьезно осложняет общепринятую процедуру планирования. Действительно, нелегко оперировать с неопределенностью в рамках детерминированных плановых показателей. Именно этим объясняется стремление представить прогноз ресурсов нефти и газа и ожидаемых приростов в виде точечной оценки. Однако такой подход совершенно не оправдан, поскольку невозможно сравнивать и анализировать оценки ресурсов, полученные различными методами и для разных объектов. Оценку ресурсов можно производить по шкале времени или по шкале затрат. В первом случае прогнозируется величина ресурсов, выявляемых за рассматриваемый период времени, во втором — приросты запасов на единицу затрат. Результаты таких прогнозов позволяют оценить ресурсный потенциал региона (страны), но не обеспечивают данными для построения  [c. 48]

Ясно, что можно выстроить точечные оценки доходности и риска по  [c.97]

Корреляционная матрица активов, построенная как точечная оценка за два  [c.101]

Точечные оценки — это оценки некоторых неизвестных числовых параметров распределения случайных величин. Они представляют собой числа, полученные путем подстановки выборочных значений х,, х,,…, хп, в формулу для оценивания искомого параметра. Точечные оценки параметров 04 не дают информации о степени близости к соответствующему теоретическому параметру генеральной совокупности 0, Поэтому более информативный способ оцени-  [c.45]

Точечные оценки параметров распределения случайных величин.  [c.46]

Основными методами получения точечных оценок являются метод моментов, метод наименьших квадратов (МНК) и метод максимального правдоподобия (ММП).  [c.46]

Метод моментов является наиболее простым и общим способом точечной оценки. Пусть имеется выборка (хр х2,. .., х случайной величины X. Среднее значение наблюдаемого признака можно определить по формуле  [c. 46]

Метод максимального правдоподобия имеет большое преимущество по сравнению с другими методами точечной оценки. Он дает состоятельные, распределенные асимптотически нормально, эффективные оценки. Хотя эти оценки могут быть несколько смещенными.  [c.48]

Интервальные оценки параметров распределения случайных величин. Точечные оценки параметров не дают информации о степени близости оценки интервальной оценки параметра 0.  [c.52]

При использовании прежних методов моделирования, которые в основном ориентировались на определение «ожидаемых» дисконтированных затрат как единственной точечной оценки, акцент делался на строительство крупных атомных и тепловых электростанций. Поскольку крупные станции относительно более экономичны, энергокомпании отдавали им предпочтение, не учитывая связанного с этим решением потенциального риска, вызванного  [c.432]

Обычно составляется несколько альтернативных вариантов сценария, реализация которых возможна при различных допущениях (о политической, правовой и экономической обстановке, о положении в данной отрасли, о новых возможностях и проблемах данной фирмы и т. п.). Следовательно, сценарий — это характеристика будущего в духе изыскательского прогнозирования, а не определение одного желательного состояния или точечная оценка того, что произойдет в будущем.  [c.186]

Здесь и далее при прогнозировании методом регрессионного анализа принимаем во внимание точечную оценку прогноза результирующего показателя без построения доверительных интервалов.  [c.86]

Анализ риска по показателю ЧДД может быть выполнен одним из следующих трех методов 1) методом точечных оценок 2) методом дискретных вероятностей (дерева вероятных исходов) 3) методом моделирования распределений (Монте-Карло).  [c.233]

МЕТОД ТОЧЕЧНЫХ ОЦЕНОК ПАРАМЕТРОВ  [c.233]

По трем известным значениям показателя находят точечные оценки параметров его распределения. Обычно используется следующая процедура. Обозначим расчетные значения показателя М — базовое, П — пессимистическое (минимальное) и О — оптимистическое (максимальное). Тогда оценкой среднего (математического ожидания) будет  [c. 233]

Метод точечных оценок параметров……………………………………….. 233  [c.255]

Точечные оценки числовых характеристик  [c.97]

Для того чтобы найти 95%-ный доверительный интервал для точечной оценки дисперсии, мы должны определить значение X2, задающее по 2,5% в каждой из граничных площадей под кривой распределения (рис. 5.3). Таким образом, мы должны знать величину х2 Для 97,5% значений, лежащих справа, и другую величину х2 — Для 2,5% значений, лежащих справа. Если обозначить степень доверия через 1-а, тогда нам необходимы величины х в/2 и Ха/2 Если мы работаем с 95%-ным уровнем доверительной вероятности, тогда значение а будет 0,05, a  [c.234]

Например, если вас попросят дать «точечную оценку» доходности акций Gen o в следующем году, то ваш ответ  [c.180]

НЕСМЕЩЕННАЯ ОЦЕНКА [unbiased estimator] — статистическая точечная оценка, математическое ожидание которой совпадает с оцениваемой величиной (у нее нет систематической ошибки).  [c.226]

В основе кригинга лежит представление о пространственных переменных, среднее значение которых для некоторой области может быть вычислено через точечные оценки внутри и вне этой области с учетом пространственной взаимокорреляции значений переменной от расстояния между точечными наблюдениями.  [c.68]

Напомним, что прогноз должен давать несмещенную оценку будущей ситуации. Вместе с тем црогноз должен сопровождаться двусторонними границами, в которых с достаточной степенью уверенности следует ожидать появления прогнозируемого показателя. Точечная оценка в этом смысле представляется малозначащей.  [c.84]

Мы уже узнали, что при известных выборочном распределении различных описательных статистических показателей, объеме выборки и непосредственном значении самих показателей можно построить доверительные интервалы для точечных оценок. Но часто мы располагаем некоторыми предварительными (а priori) догадками или предположениями относительно величины параметров генеральной совокупности.  [c.236]

CFA — Точечные оценки среднего значения совокупности | программа CFA

Статистические выводы традиционно состоят из двух направлений: проверки статистических гипотез и статистической оценки.

Проверка гипотез рассматривает вопрос:

Равен ли данный параметр (например, среднее по совокупности) некоторому определенному значению (например, 0)?.

Здесь мы имеем гипотезу о значении параметра, и пытаемся или доказать или опровергнуть ее на основе выборки из совокупности. Мы подробно обсудим проверку гипотез далее, в чтении о проверке статистических гипотез.

Второе направление статистического вывода, рассматриваемое в данном чтении, — это статистическая оценка.

Статистическая оценка (англ. ‘estimation’) ищет ответ на вопрос:

Каким является значение данного параметра (например, среднего по совокупности)?

При оценке, в отличие от проверки гипотез, мы не начинаем с выдвижения гипотезы о значении параметра и ее проверки. Вместо этого мы стараемся наилучшим образом использовать информацию о выборке, чтобы сформировать один из нескольких типов оценок значения параметра.

При оценке мы заинтересованы в нахождении правила для лучшего расчета одного значения для оценки неизвестного параметра совокупности (при точечной оценке).

Вместе с расчетом точечной оценки, мы также можем быть заинтересованы в расчете диапазона значений, в рамках которого может находится неизвестный параметр совокупности с некоторой заданной степенью вероятности (доверительный интервал).

Ниже мы обсудим точечные оценки параметров, а в следующем разделе — формулировку доверительных интервалов для среднего по совокупности.

Точечные оценки параметров совокупности.

Важная концепция, представленная в этом чтении, заключается в том, что статистики рассматриваемые как формулы, приводящие к случайным результатам, являются случайными величинами.

Формулы, которые мы используем для вычисления выборочного среднего и всех других выборочных статистик являются примерами формулы оценки (или функции оценки или просто оценки, англ. ‘estimator’).

Значение, которое вычисляется на основе наблюдений выборки с использованием функций оценки, называется оценкой (англ. ‘estimate’). Функция оценки имеет распределение выборки; оценка является фиксированным числом, относящимся к данной выборке, и, таким образом, не имеет распределения выборки.

Среднее значение, т.е. вычисленное значение выборочного среднего на основе данной выборки, используется в качестве оценки среднего по совокупности и называется точечной оценкой (англ. ‘point estimate’) среднего по совокупности.

---

В Примере 3 показано, что формула для выборочного среднего, может и будет давать различные результаты в повторных выборках, так как из совокупности берутся различные выборки.

Во многих случаях, у нас есть выбор из нескольких возможных формул оценки для оценки данного параметра.

Как мы делаем наш выбор?

Мы часто выбираем определенные формулы оценки, потому что они имеют одно или более желательных статистических свойств. 2 \).

Если бы мы вычислили дисперсию выборки, используя делитель \( n \), то оценка была бы смещена: его ожидаемое значение было бы меньше, чем дисперсия совокупности. Мы бы сказали, что выборочная дисперсия, рассчитанная с делителем \( n \), является смещенной оценкой дисперсии совокупности.

Всякий раз, когда можно найти одну несмещенную оценку параметра, как правило, можно найти большое количество других несмещенных оценок.

Как мы делаем выбор среди альтернативных несмещенных оценок?

Критерий эффективности дает возможность выбирать несмещенные оценки параметра.

Определение эффективности оценки.

Несмещенная оценка является эффективной (англ. ‘efficient unbiased estimator’), если никакая другая несмещенная оценка того же параметра не имеет распределение выборки с меньшей дисперсией.

Это определение можно объяснить следующим образом: делая повторные выборки, мы ожидаем, что эффективные оценки будут более плотно группироваться вокруг среднего значения, чем другие несмещенные оценки. 2 \).

Напомним, что выборочное распределение статистики определено для выборки заданного размера. Различные размеры выборки определяют различные распределения выборки. Например, дисперсия выборочного распределения выборочного среднего значения будет меньше для выборок больших размеров.

Несмещенность и эффективность является свойствами выборочного распределения функции оценки, которые распространяются на выборки любого размера.

Несмещенная оценка является в равной мере несмещенной для выборки размером 10 и выборки размером 1,000. В некоторых ситуациях мы, однако, мы не можем найти функции оценки, которые обладают такими желанными свойствами. Например, сложно добиться несмещенности в очень малых выборках.

Такие проблемы часто возникают в регрессионном анализе и анализе временных рядов.

В этом случае, аналитики могут обосновать выбор функции оценки на основе свойств выборочного распределения функции оценки при очень больших выборках, — так называемых асимптотических свойствах функции оценки (англ. ‘asymptotic properties’).

Среди таких свойств, наиболее важным является состоятельность.

Определение состоятельности оценки.

Состоятельная оценка (англ. ‘consistent estimator’) — это функция оценки, для которой вероятность того, что оценка близка к значению параметра совокупности, увеличивается по мере увеличения размера выборки.

Несколько более технически, мы можем определить состоятельную оценку в качестве функции оценки, выборочное распределение которой концентрируется на значении оцениваемого параметра, по мере того, как размер выборки стремится к бесконечности.

Выборочное среднее, помимо того, что является эффективной оценкой, также является состоятельной оценкой среднего значения по совокупности:

По мере того, как размер выборки \(n\) стремится к бесконечности, стандартная ошибка выборочного среднего \( \sigma / \sqrt n \) стремится к 0, а выборочное распределение среднего концентрируется вокруг значения среднего по совокупности \( \mu \).

Подводя итог, мы можем воспринимать состоятельную оценку как имеющую тенденцию давать все более и более точные оценки параметров совокупности по мере увеличения размера выборки.

Если оценка состоятельна, мы можем попытаться повысить точность оценок параметра совокупности путем расчета оценок с использованием большей выборки.

Однако, для несостоятельной оценки увеличение размера выборки не поможет увеличить вероятность точных оценок.

Статистики, их выборочные распределения и точечные оценки параметров распределений в EXCEL. Примеры и описание

В статье напомним некоторые понятия математической статистики: выборка, статистика, точечная оценка, выборочное распределение. Продемонстрируем в MS EXCEL сходимость некоторых распределений статистик к нормальному распределению, распределению ХИ-квадрат, распределению Стьюдента и F — распределению.

В математической статистике обычно выделяют 2 основных направления исследований. Первое направление связано с оценкой неизвестных параметров распределения; второе – с проверкой статистических гипотез . В этой статье рассмотрим подходы, используемые для оценки неизвестных параметров распределения.

Сначала напомним основные понятия математической статистики, необходимые для оценки параметров.

О выборке

В математической статистике вероятностная модель явления (распределение) определена с точностью до неизвестных параметров. Например, предполагается известным, что случайная величина распределена по нормальному закону , но неизвестны его параметры ( среднее и дисперсия ). Отсутствие сведений о параметрах компенсируется тем, что нам позволено проводить «пробные» испытания ( выборки , samples) и на их основе восстанавливать недостающую информацию.

Почему необходимо иметь результат более чем одного испытания? Потому, что результаты одного испытания менее точны, чем среднее значение выборки .

Число испытаний в выборке обозначим n. Каждое испытание состоит в том, что мы случайным образом выбираем один объект генеральной совокупности ( population ) и записываем его характеристику X. Полученный таким образом ряд чисел Х ₁ ,…, Х _n будем называть случайной выборкой объема n, а числа X _i — элементами выборки . Элементы выборки являются независимыми случайными величинами и, как все случайные величины, имеет функцию распределения (одинаковую для всех Х _i ).

После того, как выборка была получена, следующим вопросом является то, каким образом получить информацию о неизвестном распределении:

• во-первых, из выборки можно оценить среднее и дисперсию исходного распределения (будем называть их показателями распределения).
• во-вторых, можно оценить параметр(ы) распределения (см. ниже).

Примечание : Для некоторых распределений дисперсия и стандартное отклонение случайной величинымогут быть одновременно показателями и параметрами распределения (например, для нормального распределения ).

О статистиках и точечной оценке параметров распределения

На основании значений выборки можно вычислить различные величины, например, сумму, среднее арифметическое или сумму квадратов значений выборки . Эти или иные другие величины, полученные на основании значений выборки , называются статистиками ( statistics ) .

На основе выборки можно построить, вообще говоря, бесконечное число статистик , но лишь некоторые статистики могут служить оценкой параметров исходного распределения, из которого была взята выборка . Например, среднее значение выборки из нормального распределения служит оценкой параметра μ этого распределения; а стандартное отклонение выборки служит оценкой его параметра σ .

Примечание : Для нормального распределения μ является как параметром распределения, так и его средним значением ( математическим ожиданием ), а также медианой и модой .

Процедура оценки параметров распределения с помощью статистик называется точечной оценкой ( point estimation ), а сама статистика называется точечной оценкой неизвестного параметра ( point estimator ) .

Примечание : Про оценку параметров конкретного распределения можно прочитать в статье, относящейся к этому распределению (см. заглавную статью о распределениях ).

Выборочные распределения статистик

Т.к. статистики получены из случайной выборки , то они сами являются случайными величинами и, соответственно, имеют свое собственное распределение (в общем случае не обязательно совпадающее с исходным распределением, из которого взята выборка ). Это распределение называется выборочным распределением (sampling distribution).

Чтобы определить точность оценки необходимо исследовать ее выборочное распределение , особенно среднее и дисперсию этого распределения . Т.к. на основе выборки можно построить множество различных статистик , то необходимо сформулировать критерии, которые позволят выбрать «лучшие» статистики для оценки параметров распределения. Например, если среднее значение выборочного распределения статистики совпадает с оцениваемым параметром (для всевозможных значений параметра), то такая статистика называется несмещенной оценкой . Также очевидно, что среди двух несмещенных оценок лучше та, чья дисперсия соответствующего выборочного распределения меньше . Такая статистика называется несмещённой оценкой с минимальной дисперсией (MVUE, minimum variance unbiased estimator).

Во многих случаях выборочное распределение статистики , такой как, например, среднее выборки , близко к нормальному даже тогда, когда распределение отдельных элементов выборки отличается от нормального . Этот результат, который называют Центральной предельной теоремой , упрощает статистический вывод , поскольку известно, как вычислять вероятность для нормального распределения , что в свою очередь позволяет получить информацию о генеральной совокупности (об исходном распределении, из которого была взята выборка ).

Некоторые статистики и их распределения играют важную роль в математической статистике. Например, они позволяют вычислить точечную оценку параметра и построить соответствующий доверительный интервал , а также провести процедуру проверки гипотез .

Ниже рассмотрим некоторые важные статистики , вычисленные на основе выборки из нормального распределения.

Выборочное распределение среднего

Пусть выборка извлекается из нормального распределения с параметрами N(μ;σ ² ). Рассмотрим статистику Х _ср ( среднее выборки ):

Из Центральной предельной теоремы известно, что выборочное распределение статистики Х _ср ( выборочное распределение среднего ) при достаточно большом размере выборки n стремится к нормальному распределению с параметрами N(μ;σ ² /n).

Проверим это утверждение в MS EXCEL (см. файл примера Лист Нормальное ). Для этого возьмем 60 значений выборочных средних (Хср), вычисленныхна основе 60 случайных выборок, взятых из нормального распределения с параметрами N(μ;σ ² ). Размер выборки n взят равным 50.

С помощью Графика проверки на нормальность (Normal Probability Plot) покажем, что выборочное распределение среднего соответствует нормальному закону .

Как видно из рисунка выше, средние значения выборок хорошо укладываются на прямой, что позволяет сделать вывод о нормальности распределения. Параметры этого распределения можно, например, с помощью линии регрессии, которые близки к расчетным.

Использование выборочного распределения статистики Х _ср позволяет при ИЗВЕСТНОЙ дисперсии исходного нормального распределения построить доверительный интервал для оценки математического ожидания этого распределения , а также провести проверку гипотез .

Выборочное распределение статистики

Пусть выборка извлекается из нормального распределения с параметрами N(μ;σ ² ). Рассмотрим статистику , где s – стандартное отклонение выборки , n – размер выборки .

Известно, что выборочное распределение статистики при достаточно большом размере выборки стремится к распределению Стьюдента с n-1 степенью свободы.

Аналогично статистике Х _ср , в файле примера на листе СТЬЮДЕНТ построен График вероятности для проверки этого утверждения.

Использование выборочного распределения вышеуказанной статистики позволяет построить доверительный интервал для оценки математического ожидания при НЕИЗВЕСТНОЙ дисперсии исходного нормального распределения , а также провести проверку соответствующих гипотез .

Выборочное распределение статистики (n-1)s

² /σ ²

Пусть выборка извлекается из нормального распределения с параметрами N(μ;σ ² ). Рассмотрим статистику (n-1)s ² /σ ² , где s – стандартное отклонение выборки .

Известно, что Выборочное распределение статистики (n-1)s ² /σ ² при достаточно большом размере выборки стремится к распределению ХИ-квадрат с n-1 степенью свободы.

Аналогично рассмотренной статистике Х _ср , в файле примера на листе ХИ2 построен График вероятности для проверки этого утверждения.

Использование выборочного распределения вышеуказанной статистики позволяет построить доверительный интервал для оценки дисперсии исходного нормального распределения ( из которого берется выборка) , а также провести проверку соответствующих гипотез .

Выборочное распределение статистики

Пусть из двух нормальных распределений с параметрами N(μ ₁ ;σ ₁ ² ) и N(μ ₂ ;σ ₂ ² ) извлекается по одной выборке (в общем случае разного размера n ₁ и n ₂ ) .

Известно, что при достаточно большом размере выборок Выборочное распределение статистики стремится к F-распределению вероятности с n ₁ -1 и n ₂ -1 степенями свободы .

F-распределение используется в F-тесте, который сравнивает степени разброса ( дисперсии ) двух наборов данных и при построении соответствующего доверительного интервала .

В файле примера на листе F-расп построен График вероятности для проверки этого утверждения.

Точечные оценки и доверительные интервалы

Существует три вида лжи: ложь, наглая ложь и статистика. – Бенджамин Дизраэли

Мы собираемся перейти к интересной части статистики – Логической статистике, и я очень взволнован!

Инференциальная статистика представляет собой набор инструментов и методов, которые позволяют нам делать выводы о популяциях на основе информации, полученной из выборочных данных.

Лучшее место для начала в Инференциальная статистика основана на базовой концепции Оценщиков.

Существует два типа оценок: Точечные оценки и Интервальные оценки , и мы обсудим сходства и различия между ними в этой главе.

В самом общем виде эти два инструмента позволяют оценить параметры генеральной совокупности (среднее значение, дисперсию и т. д.), используя данные, взятые из выборки.

Повторю еще раз. . .

Мы используем выборочных данных от до оценки и параметра совокупности .

Эта глава состоит из двух разделов, первый посвящен Point Estimate , а второй Interval Estimate .

В разделе Оценка точек этой главы мы:

• Рассмотрим концепцию совокупности и выборки
• Обсудите точечную оценку среднего значения совокупности, дисперсии совокупности и стандартного отклонения,
• Обсудить концепцию объективных и эффективных оценок &
• Обзор концепции стандартной ошибки

В разделе Оценка интервала мы будем:

• Что такое доверительный интервал
• Доверительные интервалы для среднего значения совокупности
• Доверительные интервалы для дисперсии генеральной совокупности и стандартного отклонения
• Доверительные интервалы для пропорций

Популяции, выборки и статистические выводы

Итак, мы обсудили тот факт, что статистика вывода представляет собой набор методов, которые позволяют нам делать выводы о совокупности на основе информации, полученной из выборки данных.

Итак, давайте перейдем к этому и рассмотрим некоторые из этих ключевых терминов и посмотрим на их определения, чтобы вы поняли, что мы здесь делаем.

В статистике совокупность определяется как общий набор объектов, событий или наблюдений, которые вы хотите изучить.

В инженерии качества нам часто интересно знать среднее значение и стандартное отклонение, связанные с популяциями, с которыми мы имеем дело.

Однако у нас редко есть время или ресурсы для измерения всех значений, связанных с нашей совокупностью, и в этом нам помогает выборка.

Образец — это , определенный как уникальное подмножество генеральной совокупности.

Вы можете видеть это на изображении ниже, где у нас есть группа людей, и мы взяли выборку из этой группы.

Вспомните вторую главу о статистике (сбор и обобщение данных, часть 2), где мы обсуждали разницу между Statistic и Parameter .

Когда мы говорим о выборочных данных и вычисляем среднее значение или стандартное отклонение, мы вычисляем статистику .

Статистика связана с выборками .

Когда мы говорим обо всей популяции — о среднем популяции или стандартном отклонении популяции, мы говорим о Параметр .

В приведенной ниже таблице вы можете увидеть общие параметры населения и связанные с ними примеры статистики.

Параметры, статистика и оценки

В логической статистике мы берем нашу выборку данных и вычисляем нашу выборочную статистику .

Затем мы можем использовать эти выборочные статистические данные для оценки параметра совокупности; что часто бывает тем, что мы действительно хотим понять.

Эти выборочные статистические данные используются в рамках этой концепции оценки , , где есть два типа оценок: Точечные оценки и Интервальные оценки .

Точечная оценка — это тип оценки, в котором используется одно значение, часто выборочная статистика, для вывода информации о параметре генеральной совокупности в виде отдельного значения или точки.

Интервальная оценка — это тип оценки, в котором используется диапазон (или интервал) значений, основанный на информации о выборке, для «захвата» или «охвата» истинного выводимого параметра генеральной совокупности.

Вероятность того, что интервальная оценка содержит истинный параметр генеральной совокупности, определяется уровнем достоверности .

Вы можете увидеть обе эти оценки ниже.

В верхней части изображения показано распределение населения , с показанным истинным средним значением населения , которое является параметром населения, который мы пытаемся оценить .

Это среднее значение генеральной совокупности можно оценить с помощью одноточечной оценки или интервальной оценки.

Хорошо, давайте быстро перейдем к первому типу оценок, Point Estimate .

Точечная оценка — это тип оценки, в которой используется одно значение, часто выборочная статистика , чтобы вывести информацию о параметре совокупности .

Давайте рассмотрим некоторые из основных точечных оценок, которые включают точечные оценки для населения среднего , населения дисперсии и стандартное отклонение населения .

Точечная оценка среднего значения совокупности

Итак, допустим, мы недавно приобрели 5000 изделий для использования в нашем следующем производственном заказе, и нам требуется, чтобы средняя длина изделия из 5000 изделий составляла 2 дюйма.

Вместо того, чтобы измерять все 5000 единиц, что потребовало бы чрезвычайно много времени и денег, а в других случаях, возможно, было бы разрушительным, мы можем взять выборку из этой совокупности и измерить среднюю длину выборки.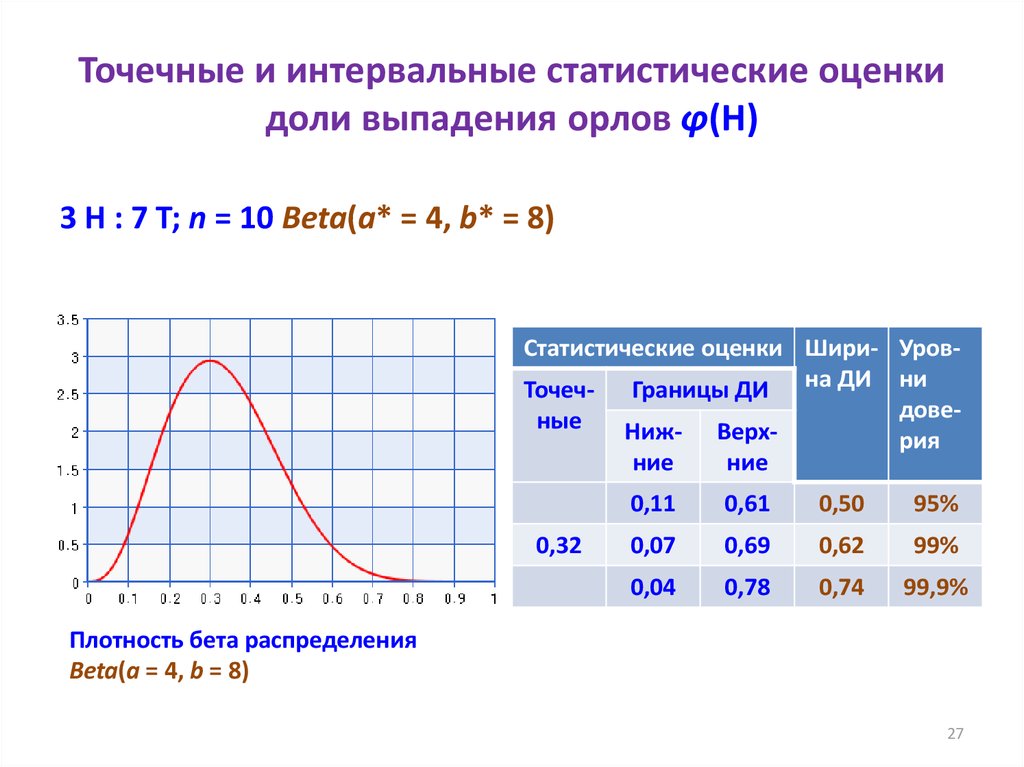

Как вы знаете, выборочное среднее значение можно рассчитать, просто суммировав отдельные значения и разделив их на количество измеренных образцов.

Пример вычисления выборочного среднего

Рассчитайте выборочное среднее значение следующих 5 измерений длины для нашей партии виджетов: 16,5, 17,2, 14,5, 15,3, 16,1

Стандартное отклонение

Как и в этом примере, вы можете оценить дисперсию или стандартное отклонение, связанное с совокупностью продуктов.

Точечная оценка дисперсии и стандартного отклонения генеральной совокупности представляет собой просто дисперсию и стандартное отклонение выборки:

Пример стандартного отклонения выборки

Давайте найдем стандартное отклонение выборки для того же набора данных, который мы использовали выше:  16,5 , 17.2, 14.5, 15.3, 16.1

Разумно? Теперь давайте переключимся на несколько важных тем, прежде чем перейти к разделу доверительных интервалов.

Беспристрастные и эффективные оценщики

В любое время, когда мы используем оценщик для вывода параметра совокупности , вы, естественно, подвергнетесь некоторому риску (или вероятности) того, что сделаете неверный вывод .

Тогда все поле Инференциальная статистика по своей природе включает в себя определенный элемент риска, о котором мы будем много говорить в следующих нескольких главах.

Таким образом, чтобы минимизировать риск , связанный с оценщиками , нам нужны две характеристики высококачественный оценщик , что они беспристрастны и эффективны .

Непредвзятый

Непредвзятый оценщик — это тот, чье ожидаемое значение равно оцениваемому параметру генеральной совокупности.

Рассмотрим ситуацию, когда у нас повторяется выборка (размер выборки = n) из распределения населения.

Каждая выборка будет иметь свое собственное распределение значений, которые все показаны под основным распределением генеральной совокупности.

Допустим, вы выбрали 100 единиц из 1000 населения и вычислили среднее значение выборки.

Исходя из случайного характера выборки, вы ожидаете, что каждая взятая выборка, вероятно, будет иметь другое выборочное среднее.

Предположим, вы повторили эту выборку 30 раз; и вы построили распределение выборочных средних .

Это новое распределение выборочных средних имеет собственную дисперсию и ожидаемое значение (среднее значение).

Точечная оценка (в данном примере среднее значение выборки) считается несмещенной, если ее ожидаемое значение равно оцениваемому параметру.

Смещение и дисперсия

То же самое можно сказать и о выборочной дисперсии (S ² ), поскольку можно показать, что ожидаемое значение выборочной дисперсии равно дисперсии генеральной совокупности (σ ² ) .

Небольшое предостережение об этом здесь, если вы сравните уравнение для Дисперсия населения против Sample Variance , вы заметите, что они имеют различных знаменателей .

Дисперсия генеральной совокупности делится на N , а дисперсия выборки делится на n-1 , то есть приходится на погрешность .

Если бы вы рассчитали выборочную дисперсию, используя только N, вы бы обнаружили, что оценка имеет тенденцию быть слишком низкой и, следовательно, необъективной.

Вот почему мы делим на n-1, так как было показано, что это несмещенная оценка дисперсии генеральной совокупности.

Эффективность

Второй характеристикой высококачественного оценщика является эффективность и отражение выборочной изменчивости статистики .

Когда дело доходит до оценки такого параметра совокупности, как среднее значение совокупности, часто может быть много способов оценить это среднее значение совокупности.

Более эффективное средство оценки имеет наименьшую дисперсию (изменчивость выборки), связанную с ним.

Например, чтобы оценить среднее значение генеральной совокупности, можно использовать два разных оценщика.

Первой оценкой может быть выборочное среднее , а второй выборкой может быть просто одно наблюдение из совокупности в качестве оценки.

Чтобы выбрать более эффективную оценку из этих двух вариантов (выборочное среднее по сравнению с одним наблюдением), мы должны понять дисперсию, связанную с каждой оценкой.

Дисперсия одиночного наблюдения простая, равна дисперсии генеральной совокупности σ ² .

Дисперсия выборочного среднего распределения составляет:

Если мы сравним их вместе, мы увидим, что дисперсия выборочного среднего меньше, чем дисперсия отдельного наблюдения.

Следовательно, мы можем заключить, что выборочное среднее является более эффективной оценкой среднего значения генеральной совокупности, чем единичное наблюдение, поскольку его дисперсия ниже.

Для средней совокупности мы измеряем эффективность (изменчивость выборки) нашего образца с использованием стандартной ошибки .

Стандартная ошибка

Как обсуждалось выше, всякий раз, когда мы создаем распределение выборочных средних, это распределение выборочных средних также будет иметь определенную степень изменчивости.

Это отражение эффективности (изменчивости выборки) , связанной с нашей выборкой (размером n). Чем меньше стандартная ошибка, тем меньше вариабельность выборки.

В контексте этой главы мы собираемся обсудить только стандартную ошибку, связанную с выборочным средним распределением.

С помощью некоторой статистической работы, которая выходит за рамки этого текста, мы можем доказать, что дисперсия выборочного среднего распределения:

является отражением дисперсии или разброса средних значений выборки вокруг среднего значения генеральной совокупности.

Подобно стандартному распределению, стандартная ошибка представляет собой квадратный корень из дисперсии выборочного среднего распределения.

Стандартная ошибка равна стандартному отклонению генеральной совокупности, деленному на квадратный корень из n.

Мы будем использовать эту концепцию стандартной ошибки в следующем разделе, когда будем обсуждать доверительный интервал . Эта стандартная ошибка также называется погрешностью .

Доверительный интервал (интервальная оценка)

Интервальная оценка — это тип оценки, в котором используется диапазон (или интервал) значений, основанный на выборочной информации, для «захвата» или «охвата» истинной совокупности предполагаемый/оцениваемый параметр.

Интервальные оценки создаются с использованием уровня достоверности , который является вероятностью того, что ваш интервал действительно отражает оцениваемый параметр генеральной совокупности.

Поскольку мы используем доверительный интервал, мы часто называем эти интервальные оценки доверительным интервалом .

Вы можете увидеть пример доверительного интервала ниже.

Изображение начинается с распределения населения оранжевым цветом, и это распределение имеет неизвестное среднее значение населения, которое мы пытаемся оценить.

Затем мы берем выборку (размером n) из этой совокупности, и распределение этой выборки показано фиолетовым цветом.

Затем мы можем создать наш доверительный интервал на основе данных выборки.

Давайте поговорим подробнее об этом доверительном уровне, прежде чем переходить к расчетам интервалов.

Что означает уровень достоверности?

Уровень достоверности — понятие, которое часто не понимают.

Когда мы говорим, что имеем 95-процентную уверенность в нашей интервальной оценке, мы не имеем в виду, что 95% всего населения попадает в доверительный интервал.

Доверительный уровень — это вероятность того, что ваш доверительный интервал действительно отражает оцениваемый параметр генеральной совокупности.

Таким образом, если у нас есть уровень достоверности 95%, мы можем быть уверены, что в 95% случаев (19 из 20) наша интервальная оценка будет точно отражать истинный оцениваемый параметр.

Если вы посмотрите на график ниже, истинный параметр населения (в данном случае μ) показан сплошной синей линией посередине.

В 19 из 20 созданных интервалов истинное среднее значение совокупности фиксируется в пределах этих 19 интервалов. Существует только 1 интервал, который не отражает истинное среднее значение генеральной совокупности, и он показан красным цветом .

До этого момента я использовал только уровень достоверности 95%, но ваш уровень достоверности может варьироваться.

Вы можете быть уверены на 80%, 90%, 99% и т.д.

Уровень достоверности, который вы выбираете, основан на риске, в частности на вашем альфа-риске (α).

Альфа-риск также называется вашим уровнем значимости , и это риск того, что вы не сможете точно отразить истинный параметр популяции.

Ваш уровень достоверности равен 100% минус ваш уровень значимости ( α).

Уровень достоверности = 100% – Уровень значимости (α)

Таким образом, если ваш уровень значимости равен 0,05 (5%), то ваш уровень достоверности равен 95%.

Уравнение доверительного интервала

Хорошо, аналогично уровню достоверности, я хотел начать с общего обсуждения уравнения доверительного интервала, чтобы вы понимали различные компоненты.

Как только вы получите эту часть, различные ситуации (среднее значение, дисперсия, пропорция) будут просто адаптацией этого уравнения.

Уравнение доверительного интервала состоит из 3 частей: точечная оценка (также иногда называемая выборочной статистикой) , доверительный уровень и предел погрешности .

Точечная оценка или статистика является наиболее вероятным значением параметра генеральной совокупности, а уровень достоверности и предел погрешности представляют величину неопределенности, связанную с взятой выборкой.

Доверительный интервал = Оценка в баллах + Уровень достоверности * Погрешность

При работе со средним значением генеральной совокупности доверительный интервал выглядит следующим образом:Предел погрешности 0009 для среднего значения генеральной совокупности равен стандартной ошибке , рассмотренной выше.

На стандартную ошибку может влиять размер выборки (n), связанный с вашей выборкой, где большая выборка означает меньшую погрешность. На погрешность также влияет стандартное отклонение.

Уровень достоверности и Z-показатель

Вы заметите, что в приведенном выше примере уровень достоверности выражается в виде Z-показателя, который также ссылается на альфа-риск ( уровень значимости ).

В этой ситуации мы используем Z-оценку, потому что распределение выборочных средних нормально.

По сути, этот уровень достоверности фиксирует определенную долю (например, 95%) выборочного среднего распределения при создании интервальной оценки.

В различных других ситуациях, когда мы создаем доверительный интервал для дисперсии и стандартного отклонения, эти данные следуют распределению хи-квадрат.

Таким образом, эти доверительные интервалы используют значение хи-квадрат вместо Z-показателя.

На этом графике видно, что область, заштрихованная серым цветом посередине, охватывает определенную часть распределения, например, если ваш уровень достоверности равен 95 %, он будет охватывать 95 % распределения.

Область красного цвета часто называют областью отторжения , но я показал ее таким образом, чтобы продемонстрировать альфа-риск .

Альфа-риск, 5% в этом примере, равен делится пополам между левым и правым концами выборочного распределения, поэтому уравнение и изображение показывают его как α/2 .

В этом примере выборочное распределение является нормальным распределением, но в других интервальных оценках мы можем использовать t-распределение или распределение хи-квадрат.

Доверительный интервал для среднего значения совокупности

Хорошо, пора перейти к сути обсуждения доверительного интервала и показать вам фактические уравнения.

Итак, когда дело доходит до создания интервальной оценки для среднего значения совокупности, есть два возможных уравнения.

Эти два возможных уравнения основаны на том, известна или неизвестна дисперсия генеральной совокупности.

Когда дисперсия генеральной совокупности известна, вы используете нормальное распределение (z-показатель) и дисперсию генеральной совокупности для создания интервальной оценки с помощью следующего уравнения:

распределение (t-оценка) и выборочная дисперсия для создания интервальной оценки с использованием следующего уравнения:

Я выделил разницу между z-показателем и t-показателем выше в красный , и я выделил разницу между выборочной дисперсией и дисперсией генеральной совокупности в синий .

Другой способ выбора между приведенными выше уравнениями основан на размере выборки n .

Как правило, если размер выборки меньше 30, следует использовать t-распределение. Если размер выборки больше 30, можно использовать нормальное распределение.

Давайте рассмотрим каждый пример.

Пример интервальной оценки среднего значения генеральной совокупности с известной дисперсией

Вы отобрали 40 единиц из последней производственной партии для измерения веса продукта, и среднее значение выборки составляет 10,40 фунтов. Если известно, что стандартное отклонение генеральной совокупности составляет 0,60 фунта, рассчитайте 95% доверительный интервал.

Хорошо, давайте посмотрим, что мы знаем после прочтения вопроса:

n = 40, σ = 0,60 фунта, α = 0,05, x-bar = 10,4 фунта.

Прежде чем мы сможем подставить это в наше уравнение, нам нужно найти Z-оценку, связанную с доверительным интервалом 95%.

Если мы посмотрим на Z-таблицу NIST, мы найдем Z = 1,96.

Z-показатель 1,96 связан с площадью под кривой 0,475.

Это связано с тем, что нормальное распределение является двусторонним, а альфа-риск, связанный с одной стороной распределения, составляет 0,500 – 0,025 = 0,475.

Пример интервальной оценки среднего значения генеральной совокупности с неизвестной дисперсией

Вы измерили 10 единиц из последней производственной партии, чтобы измерить длину изделия.

Вы вычисляете среднее значение выборки, равное 17,55 дюйма, и стандартное отклонение выборки равное 1,0 дюйма.

Вычислите 95% доверительный интервал для среднего значения генеральной совокупности.

Хорошо, давайте посмотрим, что мы знаем после прочтения условия задачи:

n = 10, x-bar = 17,55 дюйма, s = 1,0 дюйма, α = 0,05.

Прежде чем мы сможем подставить это в наше уравнение, нам нужно найти t-показатель, связанный с 95% доверительный интервал.

При n = 10 мы можем рассчитать наши степени свободы (n – 1) равными 9.

Поскольку этот доверительный интервал является двусторонним, мы разделим наш альфа-риск (5%) пополам (2,5% или 0,025), чтобы найти критическое t-значение 0,975 (1 – α/2) в таблице t-распределения NIST на уровне 2,262.

Давайте теперь переключим передачу и перейдем к доверительным интервалам для дисперсии населения и стандартного отклонения.

Доверительный интервал для дисперсии генеральной совокупности и стандартного отклонения

Как и в случае со средним значением, в логической статистике часто бывает так, что мы хотим использовать выборочные данные для оценки параметра генеральной совокупности дисперсии или стандартного отклонения.

Ниже приведены те уравнения, которые идентичны, за исключением квадратного корня, взятого за стандартное отклонение.

Одно ключевое отличие этого уравнения от приведенных выше для среднего значения генеральной совокупности заключается в том, что эти доверительных интервалов не являются симметричными.

Это отсутствие симметрии вызвано основным распределением, распределением хи-квадрат.

Этот доверительный интервал также основан на альфа-риске (уровень значимости), и этот альфа-риск используется в сочетании с распределением хи-квадрат .

Пример доверительного интервала для стандартного отклонения генеральной совокупности

Вы взяли образец из 10 единиц из последней производственной партии и измерили общую длину детали.

Вы вычисляете среднее значение выборки, равное 17,55 дюйма, и стандартное отклонение выборки, равное 1,0 дюйма.

Вычислите 95% доверительный интервал для стандартного отклонения генеральной совокупности.

n = 10, s = 1,0 дюйма, α = 0,05, x-bar = 17,55

Сначала мы должны найти наши критические значения хи-квадрат, связанные с нашим альфа-риском и размером выборки, давайте сделаем это в первую очередь.

Я выделил два значения хи-квадрат, связанные с доверительным интервалом:

Теперь мы можем перейти к таблице хи-квадрат NIST и найти критические значения для степеней свободы 9 (n-1):

   Теперь мы можем завершить уравнение, используя эти значения хи-квадрат вдоль с размером выборки и стандартным отклонением выборки для расчета нашего интервала.

Доверительный интервал для пропорций населения

Хорошо, перейдем к теме доверительных интервалов, и это доверительные интервалы для пропорций.

Уравнение доверительного интервала для доли населения очень похоже на уравнение среднего значения населения.

В этом интервале используются 3 разные переменные:

• Критическая Z-оценка, связанная с альфа-риском
  
• p = доля выборки
• n = объем выборки

В других учебниках вы увидите примерную пропорцию под названием .р-шляпа ; это сделано для того, чтобы отличить его от p , который также часто используется для представления доли населения .

Пример доверительного интервала для пропорций населения

Вы опросили 1000 человек из вашего района, чтобы определить, сколько из них были бы готовы платить более высокую плату Ассоциации владельцев домов, чтобы создать районный пул. 612 сказал да.

Найдите 95-процентный доверительный интервал для истинной доли населения в вашем районе.

В этом интервале используются 3 разные переменные:

• Критическая Z-оценка, связанная с альфа-риском
• p = доля выборки
• n = объем выборки

Сначала мы можем рассчитать долю выборки , p , используя n = 1000 и 612 голосов «за» :

Инференциальная статистика на информации, полученной из выборочных данных.

Мы начали с Выводная статистика с базовой концепции Оценщиков, и двух типов оценок: Точечные оценки и Интервальные оценки .

Эта глава состоит из двух разделов, первый посвящен Point Estimate , а второй Interval Estimate .

Точечная оценка — это тип оценки, в котором используется одно значение, часто выборочная статистика, для вывода информации о параметре генеральной совокупности в виде отдельного значения или точки.

Среднее значение выборки, дисперсия выборки, стандартное отклонение выборки и пропорция выборки — все это точечные оценки параметра сопутствующей совокупности (среднее значение совокупности, дисперсия совокупности и т. д.)

оценщик, то есть оценщик, который является беспристрастным и эффективным .

Непредвзятый оценщик — это тот, чье ожидаемое значение равно оцениваемому параметру совокупности.

Эффективный оценщик имеет наименьшую связанную с ним дисперсию по сравнению с другими потенциальными оценками.

Затем мы перешли ко второй половине главы, чтобы обсудить интервальных оценок .

Интервальная оценка — это тип оценки, в котором используется диапазон (или интервал) значений, основанный на информации о выборке, для «захвата» или «охвата» истинного выводимого параметра генеральной совокупности.

Интервальные оценки создаются с использованием уровень достоверности , то есть вероятность того, что ваш интервал действительно отражает оцениваемый параметр генеральной совокупности.

Затем мы рассмотрели доверительный интервал для среднего значения генеральной совокупности, как для случаев, когда дисперсия была известна, так и для неизвестной: доверительное интервью для населения пропорция.

Точечные оценки и параметры совокупности

Пропустить навигацию

• МЕТОДЫ ИССЛЕДОВАНИЯ И СТАТИСТИКА
• ВВЕДЕНИЕ
  • 0 Об этих материалах
  • 1 Введение и обзор
• ФУНДАМЕНТ
  • 2 Понимание, описание и изучение данных
    • Определение данных
    • Проверь себя
    • Числовые сводки и дисплей
    • Проверь себя
    • Категориальные сводки и отображение
    • Проверь себя
    • Две числовые переменные
    • Проверь себя
    • Трансформации: Z-счета
    • Проверь себя
    • Преобразования: регистрируемые переменные
    • Проверь себя
    • Описание бинарных переменных (распространенность и заболеваемость)
    • Проверь себя
  • 3 Основные принципы дизайна исследования
    • От популяции к выборке
    • Введение в наблюдательный и экспериментальный дизайн
    • Проверь себя
  • 4 Идеи статистического вывода
    • Точечные оценки и параметры генеральной совокупности
    • Варианты выборки и распределения выборки
    • Проверь себя
    • Смещение и точность
    • Проверь себя
    • Что такое доверительный интервал?
    • Проверь себя
    • Что такое проверка гипотез?
    • Проверь себя
  • 5 Базовая вероятность
    • Понимание вероятности и связи с выводом
    • Проверь себя
• СТАТИСТИЧЕСКИЙ ВЫВОД
  • 6 Оценка и проверка гипотез
    • Центральная предельная теорема и нормальное распределение
    • Проверь себя
    • Центральная предельная теорема на практике: единичные средние и пропорции
    • Проверь себя
    • Связь между проверкой гипотезы и CI
    • Проверь себя
• ПРОСТЫЕ СРАВНЕНИЯ
  • 7 простых сравнений
    • Средства сравнения
    • Проверь себя
    • Сравнение пропорций
    • Критерий независимости хи-квадрат
    • Проверь себя
    • Отчет о результатах и ​​выводы
  • 8 Непараметрические тесты
    • Ранговые непараметрические тесты
  • Какой тест?
• ДИЗАЙН И ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
  • 9 Клинические испытания
    • Лекция
    • Проверь себя
  • 10 Наблюдательные исследования
    • Введение в обсервационные исследования
    • Построение доказательств — пример
    • Поперечные исследования
    • Когортные исследования
    • Исследования случай-контроль
    • Проверь себя
    • Интерпретация обсервационных исследований
  • 11 Лабораторные навыки
    • Лекция
  • 12 Размер образца и мощность
    • Расчет мощности и размера выборки
    • Проверь себя
  • 13 Этика
    • Лекция
• СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
  • 14 Введение в регрессионные модели
    • Модели и статистические модели
    • Электронная лекция: Введение в статистическое моделирование
• СИНТЕЗ ДОКАЗАТЕЛЬСТВ
  • 15 систематических обзоров
  • 16 Метаанализ
• ГЛОССАРИЙ
• КРЕДИТЫ

При просмотре этого видео учащиеся должны уметь:

1. Объяснять, что понимается под статистическим выводом.
2. Определите точечную оценку и параметр генеральной совокупности и перечислите распространенные типы точечных оценок и параметров
3. Определение точечных оценок и параметров при чтении научной литературы.

Некоторый жаргон, пожалуйста, убедитесь, что вы понимаете это полностью:

Выборочные статистические данные или статистические данные доступны для наблюдения, поскольку мы рассчитываем их на основе данных (или выборки), которые мы собираем. Мы используем «статистику», рассчитанную по выборке, для оценки значения интереса к совокупности. Мы называем эту выборочную статистику «точечными оценками», а это значение, представляющее интерес для генеральной совокупности, параметром генеральной совокупности. Например, можно использовать среднее значение выборки в качестве точечной оценки среднего значения генеральной совокупности, здесь среднее значение генеральной совокупности — это параметр генеральной совокупности, который нас интересует.

Параметр совокупности считается фиксированным или принимает только одно значение. Параметры популяции неизвестны и почти всегда непознаваемы, потому что они «принадлежат» популяциям, а мы почти никогда не наблюдаем целые популяции. Общие параметры населения в исследовании – это те, которые используются для описания распределений переменных, например, среднего значения; но мы можем оценить любой интересующий нас параметр, например разницу между двумя средними значениями или разницу в риске между двумя группами.

В двух словах, точечная оценка – это выборочная статистика, полученная из наблюдаемой выборки, которая используется в качестве нашего наилучшего предположения ненаблюдаемого параметра совокупности.

Точечная и интервальная оценка — учебное пособие «Шесть сигм»

Точечная оценка и интервальная оценка — это две формы оценки параметров генеральной совокупности на основе выборочных данных. Балльную оценку очень легко вычислить. Однако интервальная оценка является гораздо более надежным и практичным подходом, чем точечная оценка.

Что такое оценка?

Оценка — это процесс, в котором мы получаем значения неизвестных параметров совокупности с помощью выборочных данных. Другими словами, это структура анализа данных, которая использует комбинацию размеров эффекта, доверительных интервалов для планирования эксперимента, анализа данных и интерпретации результатов.

Кроме того, основной целью методов оценки является оценка размера эффекта и отчет о размере эффекта вместе с его доверительным интервалом.

Оценщик — это метод, формула или функция, которые конкретно указывают, как вычислить оценку. Другими словами, для оценки значения параметра совокупности можно использовать информацию из выборки в виде оценщика.

Свойства оценщиков

Выборочные показатели используются для оценки показателей генеральной совокупности; эти статистические данные являются оценочными. Ниже приведены свойства хороших оценок.

• Оценка должна быть последовательной. Например, если оно согласовано, значение оценщика приближается к значению параметра, оцениваемому по мере увеличения размера выборки.
• Оценщики должны быть беспристрастными. Другими словами, ожидаемое значение, полученное по выборке, равно оцениваемому параметру. В противном случае оценщик необъективен.
• Оценщик должен быть эффективным. Другими словами, она должна иметь минимальную дисперсию фактической дисперсии оценщика.

Переменные

• x: Индивидуальное значение
• x̅: Оценка точечной оценки для среднего значения
• σ: Фактическое стандартное отклонение / символ для измерения.
• n:  Статистика количества данных в выборке
• N  приведена для популяций
• X̿ : (двойная полоса): общее среднее средних значений подгруппы. AKA X-bar bar или X-double bar
• s (или sd):  Стандартное отклонение выборки — это точечная оценка стандартного отклонения генеральной совокупности / статистика дисперсии для выборок
• µ:  статистика центральной тенденции для популяций

См. также типы статистики

Типы оценок

Оценки двух разных типов

• Точечные оценки
• Интервальные оценки

Точечные оценки

неизвестный параметр населения. Другими словами, точечная оценка представляет собой отдельное значение, полученное из выборки и используемое для оценки значения генеральной совокупности.

Например, если мы используем значение x̅ для оценки среднего значения µ населения.

x̅ = Σx/n

Например, 62 — это средняя (x̅) оценка, полученная выборкой из 15 учащихся, случайно отобранных из класса из 150 учащихся, и считается средней оценкой всего класса. Поскольку он представлен в единственной числовой форме, он является точечным оценщиком.

Основным недостатком точечной оценки является отсутствие информации о надежности. На самом деле вероятность того, что статистика отдельной выборки равна параметру генеральной совокупности, очень мала.

Возьмите образец, найдите x̅. x̅ является близким приближением µ. Но, в зависимости от размера вашей выборки, это может быть не очень хорошей точечной оценкой. s является хорошим приближением σ. Таким образом, если мы хотим получить более надежную уверенность в том, в каком диапазоне лежит наша оценка, нам нужно задать доверительный интервал.

Оценки интервалов

Оценка доверительного интервала представляет собой диапазон значений, построенный на основе выборочных данных, так что параметр генеральной совокупности может находиться в пределах диапазона при заданной вероятности. Указанная вероятность является уровнем достоверности.

• Более широкая и, вероятно, более точная, чем точечная оценка
• Используется с выводной статистикой для построения доверительного интервала, когда мы считаем с определенной степенью уверенности, что параметр генеральной совокупности находится.
• Любая оценка параметра, основанная на статистической выборке, имеет некоторую ошибку выборки.

В статистике интервальная оценка — это использование выборочных данных для расчета интервала возможных значений неизвестного параметра совокупности.

Ниже приведены факторы, определяющие ширину доверительного уровня

• Размер выборки
• Изменчивость генеральной совокупности
• Желаемый уровень достоверности

Доверительный интервал

Доверительный интервал, связанный с неоднозначностью метод. Кроме того, уравнение доверительного интервала состоит из 3 частей.

Доверительный интервал  – это диапазон значений, которые, вероятно, содержат среднее значение генеральной совокупности.

Достоверность уровень  является процентом уверенности в том, что в любой данной выборке этот доверительный интервал будет содержать среднее значение генеральной совокупности.

Точечная оценка — это статистика (значение из выборки), предназначенная для оценки параметра (значение из совокупности).

Погрешность — это максимальная ожидаемая разница между фактическим параметром генеральной совокупности и выборочной оценкой параметра. Другими словами, это диапазон значений выше и ниже выборочной статистики.

Interval Estimates Examples

Пример 1:

Крупная компания провела серию тестов, чтобы определить, сколько данных отдельные пользователи хранят на файловом сервере. Итак, случайная выборка из 15 пользователей выявила в среднем 15,32 ГБ при стандартном отклонении 0,18 ГБ. Какой интервал содержит фактическое среднее значение пользователя компании?

Пример 2:

Компания по литью пластмасс под давлением испытывает новую матрицу. Итак, на основе выборки из 25 испытаний среднее время цикла составило 7,49.секунд со стандартным отклонением 0,22 секунды. Однако для этой машины известная дисперсия процесса составляет 0,0576. Найдите доверительные пределы µ. Протестируйте с доверительной вероятностью 99%.

Пример 3:

Средняя длина процесса литья пластмасс под давлением из 25 деталей составляет 4,32 см со стандартным отклонением 0,17 см. Каков 95% доверительный интервал для фактического среднего значения этого процесса?

Видео по точечной и интервальной оценке

Авторы

6.1 Точечная оценка и выборочное распределение – важные статистические данные

К концу этой главы учащийся должен уметь:

• Понимать балльную оценку
• Применение и интерпретация центральной предельной теоремы
• Построение и интерпретация доверительных интервалов для средних значений, когда известно стандартное отклонение генеральной совокупности
• Понимание поведения доверительных интервалов
• Проведение проверки гипотез для средних значений, когда известно стандартное отклонение генеральной совокупности
• Понимание вероятностей ошибок при проверке гипотез

 

Рисунок 6.1: Мелкая сдача. Если вы хотите выяснить распределение сдачи, которую люди носят в карманах, и ваша выборка достаточно велика, вы обнаружите, что распределение следует определенным закономерностям.

использует то, что мы знаем о вероятности, чтобы сделать наши лучшие «догадки» или оценки на основе того, откуда они пришли. Основные формы Инференса:

Предположим, вы пытаетесь определить среднюю арендную плату за квартиру с двумя спальнями в вашем городе. Вы можете заглянуть в специальный раздел газеты, записать несколько перечисленных арендных плат и усреднить их вместе. Вы бы получили истинное среднее значение. Если вы пытаетесь определить процент попаданий в корзину при броске баскетбольного мяча, вы можете подсчитать количество сделанных вами бросков и разделить его на количество выполненных бросков. В этом случае вы бы получили точечную оценку истинной пропорции.

Наиболее естественным способом оценки характеристик генеральной совокупности () является использование соответствующей сводки, рассчитанной по выборке. Некоторые общие точечные оценки и соответствующие им параметры приведены в следующей таблице:

Рисунок 6. 2: Параметры и оценки точек

Параметр	Мера	Статистика
μ	Среднее значение одной совокупности	x̅
р	Доля отдельного населения	ˆp
μ D	Средняя разница двух зависимых совокупностей (MP)	x̅  D
мк 1 — мк 2	Разница в средствах двух независимых совокупностей	x̅ 1 -x̅ 2
стр 1 – р 2	Разница в пропорциях двух популяций	ˆp 1 -ˆp 2
σ 2	Дисперсия одной совокупности	С 2
о	Стандартное отклонение отдельной совокупности	С

 

Предположим, что средний вес выборки из 60 взрослых составляет 173,3 фунта; это выборочное среднее является точечной оценкой среднего веса совокупности, µ. Помните, что это одна из многих выборок, которые мы могли бы взять у населения. Если бы из той же популяции была взята другая случайная выборка из 60 человек, новое среднее значение выборки, вероятно, было бы другим в результате . Хотя оценки обычно варьируются от одной выборки к другой, среднее значение генеральной совокупности является фиксированным значением.

Предположим, опрос показал, что рейтинг одобрения президента США составляет 45%. Мы бы считали 45% точечной оценкой рейтинга одобрения, который мы могли бы увидеть, если бы собирали ответы от всего населения. Эта доля ответов всего населения обычно называется интересующим параметром. Когда параметр представляет собой пропорцию, ее часто обозначают буквой p, и мы часто называем пропорцию выборки ˆp (произносится как «p-hat»). Если мы не соберем ответы от каждого человека в популяции, p останется неизвестным, и мы используем ˆp в качестве нашей оценки p.

Как можно оценить разницу в среднем весе мужчин и женщин? Предположим, что выборка мужчин дает средний вес 185,1 фунта, а выборка женщин-мужчин дает средний вес 162,3 фунта. Что является хорошей точечной оценкой разницы в этих двух средних совокупностях? Мы расширим это в следующих главах.

Мы установили, что разные выборки дают разные статистические данные из-за изменчивости выборки. Эти статистические данные имеют свои собственные распределения, называемые выборочными распределениями, которые отражают это как случайную величину. Статистика выборки — это распределение точечных оценок на основе выборок фиксированного размера n из определенной совокупности. Полезно думать о конкретной точечной оценке как о взятой из выборочного распределения.

Вызов среднего веса образца, рассчитанного по предыдущему образцу в 173,3 фунта. Предположим, что другая случайная выборка из 60 участников может дать другое значение x, например 169,5 фунтов. Повторная случайная выборка может привести к дополнительным различным значениям, возможно, 172,1 фунта, 168,5 фунта и так далее. Каждое среднее значение выборки можно рассматривать как одно наблюдение случайной величины X. Распределение X называется распределением выборки среднего значения выборки и имеет свое собственное среднее значение и стандартное отклонение, как и случайные величины, обсуждавшиеся ранее. Мы смоделируем концепцию выборочного распределения, используя технологию повторной выборки, расчета статистики и ее графического отображения. Однако фактическое распределение выборки было бы достижимо только в том случае, если бы мы теоретически могли взять бесконечное количество выборок.

Каждая из точечных оценок в приведенной выше таблице имеет собственное уникальное распределение выборки, которое мы рассмотрим в будущем

Несмотря на то, что в выборках присутствует изменчивость, остается фиксированное значение для любого параметра совокупности. Что делает статистическую оценку этого интересующего параметра «хорошей»? Он должен быть точным и точным.

Точность оценки означает, насколько хорошо она оценивает фактическое значение этого параметра. Математически это верно, когда ожидаемое значение вашей статистики равно значению этого параметра. Это можно представить себе как центр выборочного распределения, находящийся при значении этого параметра.

Согласно , вероятности с течением времени сходятся к тому, что мы ожидаем. Точечные оценки следуют этому правилу, становясь более точными с увеличением размера выборки. На рисунке ниже показан средний вес выборки, рассчитанный для случайных выборок, где размер выборки увеличивается на 1 для каждой выборки, пока размер выборки не станет равным 500. Горизонтальная пунктирная линия темно-бордового цвета соответствует среднему весу всех взрослых 169,7 фунта, который представляет население. средний вес по данным CDC.

Рисунок 6.3: Закон больших чисел

Обратите внимание, как размер выборки около 50 может дать среднее значение выборки, которое на 10 фунтов выше или ниже среднего значения генеральной совокупности. По мере увеличения размера выборки колебания среднего значения совокупности уменьшаются; другими словами, по мере увеличения размера выборки среднее значение выборки становится менее изменчивым и обеспечивает более надежную оценку среднего значения генеральной совокупности.

Помимо точности, точная оценка также более полезна. Это означает, что при повторной выборке значения статистики кажутся довольно близкими друг к другу. Точность оценки можно визуализировать как разброс выборочного распределения, обычно измеряемый стандартным отклонением. Фразу «стандартное отклонение выборочного распределения» часто сокращают до 9.0009 . Меньшая стандартная ошибка означает более точную оценку и также зависит от размера выборки.

Рисунок 6.1: Майкл Лонгмайр (2019 г.). «Монеты высыпаются из банки». Всеобщее достояние. Получено с https://unsplash.com/photos/lhltMGdohc8

Рисунок 6.3: Киндред Грей (2020 г.). «Рисунок 6.3». СС BY-SA 4.0. Получено с https://commons.wikimedia.org/wiki/File:Figure_6.3.png

 

Оценка

баллов и доверительный интервал

В этой статье вы узнаете о различиях между точечные оценки и доверительные интервалы . Если у вас мало статистического опыта, вы будете склоняться к наблюдениям, основанным на точечных оценках (даже не подозревая об этом). С другой стороны, если у вас есть опыт или вы просто хотите стать лучше в статистике, вы предпочтете более широкую картину. Именно тогда вы поймете, что доверительных интервалов на самом деле имеют преимущество над точечными оценками .

Так что это точка оценка против оценка доверительного интервала различие о?

Во-первых, давайте представим концепцию оценщика . оценщик параметра генеральной совокупности приближение, зависящее исключительно от выборочной информации.

Конкретное значение называется оценкой .

Два типа оценок: точечная оценка и оценка доверительного интервала

Существует два типа оценок – точечные оценки и оценки доверительного интервала .

Точечная оценка — это одно число. Тогда как доверительный интервал , естественно, является интервалом.

Они тесно связаны. На самом деле -точечная оценка расположена точно в середине -го доверительного интервала . Однако доверительных интервалов предоставляют гораздо больше информации и являются предпочтительными при выводе.

Есть несколько оценок , которые вы, возможно, уже видели.

. Кроме того, выборка дисперсия   S ² является оценкой совокупности дисперсия : сигма

2

90.

Два свойства разных оценщиков: смещение и эффективность

Может быть много оценок для одной и той же переменной. Однако все они имеют два свойства: смещение и эффективность .

Мы не будем их доказывать, так как связанная с ними математика выходит за рамки наших руководств. Тем не менее, вы должны иметь представление о понятиях.

Оценщики как судьи — мы всегда ищем самых эффективные несмещенные оценщики .

Смещенные и несмещенные оценщики

Несмещенный оценщик имеет ожидаемое значение, равное параметру совокупности.

Пример

Давайте подумаем о смещенной оценке , чтобы объяснить это. Что, если бы кто-то сказал вам, что вы найдете средний рост американцев по:

?

1. Отбор проб
2. В поисках означает
3. А затем добавить к этому результату 1 фут.

Итак, формула х бар + 1 фут .

Что ж, надеюсь, ты им не поверишь. Они дали вам оценку , но со смещением . Гораздо логичнее то, что средний рост американцев аппроксимируется только средним значением выборки . Мы говорим, что погрешность этого оценщика составляет 1 фут.

Эффективные оценщики

Давайте перейдем к эффективности!

Самые эффективные оценщики имеют наименьшую изменчивость результатов. Достаточно знать, что наиболее эффективных означает : несмещенная оценка с наименьшей дисперсией .

В чем разница между оценщиками и статистикой?

Последнее замечание, которое стоит сделать, касается разницы между оценки и статистика . Слово «статистика » является более широким термином. точечная оценка является статистикой .

Примечание автора: Причудливая статистика? Вы можете узнать больше в наших учебных пособиях «Изучение допущений МНК», «Измерение объяснительной силы с помощью R-квадрата», «Центральная предельная теорема» и «Меры изменчивости».

В чем недостаток оценщика баллов?

Оценщики баллов , как вы можете догадаться, не очень надежны. Представьте себе, что вы посещаете 5% ресторанов Лондона и говорите, что средний обед стоит 22,50 фунта стерлингов.

Возможно, вы близки, но есть вероятность, что истинное значение на самом деле не 22,50, а где-то около него. Когда вы думаете об этом, гораздо безопаснее сказать, что средняя еда в Лондоне составляет где-то между 20 и 25 фунтами. Таким образом, вы создали доверительный интервал вокруг вашей точечной оценки в 22,50!

В чем преимущество доверительного интервала?

Доверительный интервал является гораздо более точным представлением реальности. Однако все еще остается некоторая неопределенность, которую мы измеряем в уровнях достоверности . Итак, возвращаясь к нашему примеру, вы можете сказать, что на 95% уверены, что параметр населения находится между 20 и 25 фунтами стерлингов.

Примечание: Имейте в виду, что вы никогда не сможете быть на 100% уверены, если не проверите все население!

И, конечно же, существует 5% вероятность того, что фактический параметр популяции находится за пределами диапазона от 20 до 25 фунтов.

Мы увидим, что если рассматриваемая нами выборка значительно отклоняется от всего населения.

Уровень уверенности

Необходим еще один ингредиент: уровень уверенности . Обозначается: 1 — альфа , и называется доверительным уровнем интервала .

Alpha — значение от 0 до 1.

Например, если мы хотим быть на 95% уверены, что параметр находится внутри интервала, альфа составляет 5%.

Если нам нужен более высокий уровень достоверности, скажем, 99%, альфа будет 1%.

Точечная оценка и формула доверительного интервала

Формула для всех доверительных интервалов это: ОТ точечная оценка — коэффициент надежности * стандартная ошибка К точечная оценка + коэффициент надежности * стандартная ошибка .

Мы знаем, что такое точечная оценка – такие значения, как x бар и s бар . Мы также рассмотрели, что такое стандартная ошибка .

Связь между доверительным интервалом и точечной оценкой

Теперь мы пройдемся по точечным оценкам и доверительным интервалам в последний раз.

Представьте, что вам дан набор данных с выборочным средним из 10. В этом случае 10 является точечной оценкой или оценкой ? Конечно, это баллов, оценка . Это единственное число, данное оценщиком . Здесь оценщик является оценщиком баллов , и это формула для означает .

Теперь об отношении между доверительным интервалом и точечной оценкой . точечная оценка является просто средней точкой доверительного интервала .

Подробнее о среднем , медиане и моде читайте в нашем руководстве Введение в показатели центральной тенденции.

Точечная оценка и доверительный интервал

В заключение, есть один главный фактор, который вы должны иметь в виду, решая, какой из них использовать. И это независимо от того, хотите ли вы быть максимально точным. А доверительный интервал будет давать достоверный результат в большинстве случаев. Принимая во внимание, что оценка баллов почти всегда будет неточной, но ее проще понять и представить.

Теперь, если вы хотите узнать что-то новое, связанное со статистикой, но вы устали от всех цифр и вычислений, у нас есть то, что вам нужно. Ознакомьтесь с разделом «Введение в нормальное распределение и примеры различных распределений». Затем выясните, каково t-распределение Стьюдента — это все, что нужно для погружения в наш учебник.

***

Хотите узнать больше? Вы можете улучшить свои навыки с помощью нашего курса статистики!

Попробовать курс статистики бесплатно

Следующее руководство:  Что такое Т-распределение Стьюдента?

Что такое стори поинты и как вы их оцениваете?

Оценка сложна. Для разработчиков программного обеспечения это один из самых сложных — если не самый сложный — аспект работы. Он должен учитывать множество факторов, которые помогают владельцам продуктов принимать решения, влияющие на всю команду и бизнес. Учитывая все, что поставлено на карту, неудивительно, что все, от разработчиков до высшего руководства, склонны ссориться из-за этого. Но это ошибка. Agile-оценка — это всего лишь оценка. Не клятва крови.

Нет необходимости работать по выходным, чтобы компенсировать недооценку работы. Тем не менее, давайте рассмотрим некоторые способы сделать agile-оценки максимально точными.

Сотрудничество с владельцем продукта

В гибкой разработке владелец продукта должен расставить приоритеты в невыполненной работе — упорядоченном списке работ, который содержит краткие описания всех необходимых функций и исправлений для продукта. Владельцы продукта улавливают требования бизнеса, но не всегда понимают детали реализации. Таким образом, хорошая оценка может дать владельцу продукта новое представление об уровне усилий для каждого рабочего элемента, что затем отразится на его оценке относительного приоритета каждого элемента.

Когда команда инженеров начинает процесс оценки, обычно возникают вопросы о требованиях и историях пользователей. И это хорошо: эти вопросы помогают всей команде лучше понять работу. В частности, для владельцев продуктов разбивка рабочих элементов на детализированные части и оценки с помощью баллов помогают им расставить приоритеты во всех (и потенциально скрытых!) областях работы. И как только у них есть оценки от команды разработчиков, владелец продукта нередко переупорядочивает элементы в невыполненной работе.

Agile-оценка — это командный вид спорта

Вовлечение всех (разработчиков, дизайнеров, тестировщиков, развертывателей… всех) в команду является ключевым. Каждый член команды привносит свой взгляд на продукт и работу, необходимую для создания пользовательской истории. Например, если менеджеры по продукту хотят сделать что-то, что кажется простым, например, поддержку нового веб-браузера, разработчики и отдел контроля качества должны принять участие, потому что их опыт научил их тому, какие драконы могут скрываться под поверхностью.

Подобным образом, изменения дизайна требуют участия не только команды дизайнеров, но и разработчиков и QA. Исключение части более широкой группы разработчиков продукта из процесса оценки приводит к более низким оценкам качества, снижению морального духа, поскольку ключевые участники не чувствуют себя включенными, и ставит под угрозу качество программного обеспечения.

Так что не позволяйте вашей команде стать жертвой оценок, сделанных в вакууме. Это быстрый путь к провалу!

Хотите попробовать очки истории?  Сначала зарегистрируйтесь или войдите в Jira Software >>

• Воспользуйтесь этим интерактивным учебным пособием, чтобы настроить свой первый scrum-проект 
• Узнайте, как настроить оценку в баллах и отслеживать истории пользователей 

Баллы в сравнении с часами

Традиционные команды разработчиков программного обеспечения дают оценки в формате времени: дни, недели, месяцы. Однако многие agile-команды перешли на Story Points. Story Points — это единицы измерения для выражения оценки общих усилий, необходимых для полной реализации элемента невыполненной работы по продукту или любой другой части работы. Команды присваивают баллы в зависимости от сложности работы, объема работы и риска или неопределенности. Ценности назначаются для более эффективного разбиения работы на более мелкие части, чтобы они могли устранить неопределенность. Со временем это помогает командам понять, чего они могут достичь за определенный период времени, и формирует консенсус и приверженность решению. Это может показаться нелогичным, но эта абстракция на самом деле полезна, потому что заставляет команду принимать более жесткие решения в отношении сложности работы. Вот несколько причин использовать стори-пойнты:

• Свидания не учитывают работу, не связанную с проектом, которая неизбежно проникает в наши дни: электронные письма, встречи и интервью, в которых может участвовать член команды.
• Свидания имеют эмоциональную привязанность к ним. Относительная оценка устраняет эмоциональную привязанность.
• Каждая команда будет оценивать работу по несколько разной шкале, что означает, что их скорость (измеряемая в баллах), естественно, будет разной. Это, в свою очередь, делает невозможным играть в политику, используя скорость как оружие.
• Как только вы согласуете относительную трудоемкость каждой ценности в баллах, вы сможете быстро распределять баллы без особых споров.
• Очки истории вознаграждают членов команды за решение проблем в зависимости от сложности, а не затраченного времени. Это заставляет членов команды сосредоточиться на стоимости доставки, а не тратить время.

К сожалению, сюжетные очки часто используются не по назначению. Story Points не работают, когда их используют для оценки людей, назначения подробных сроков и ресурсов, а также когда их ошибочно принимают за меру производительности. Вместо этого командам следует использовать стори-пойнты, чтобы понять объем работы и ее приоритетность. Для подробного обсуждения сюжетных баллов и методов оценки посетите этот круглый стол с отраслевыми экспертами и прочтите дополнительные советы по гибкой оценке.

Очки истории и покер планирования

Команды, начинающие с очков истории, используют упражнение, называемое покером планирования. В Atlassian планирование покера — обычная практика для всей компании. Команда возьмет элемент из бэклога, кратко обсудит его, и каждый участник мысленно сформулирует оценку. Затем каждый держит карточку с числом, отражающим их оценку. Если все согласны, отлично! Если нет, потратьте некоторое время (но не слишком много времени — всего пару минут), чтобы понять причину разных оценок. Помните, однако, оценка должна быть деятельностью высокого уровня. Если команда зашла слишком далеко, сделайте передышку и поднимите обсуждение на более высокий уровень.

Готовы попробовать?

• Установите это приложение Planning Poker
• Узнайте больше о Planning Poker

Оценивайте умнее, а не сложнее

Ни одна отдельная задача не должна занимать более 16 часов работы. (Если вы используете баллы, вы можете решить, что, скажем, 20 баллов — это верхний предел.) Просто слишком сложно оценить отдельные рабочие элементы с высокой степенью достоверности. И эта уверенность особенно важна для элементов, находящихся на вершине невыполненной работы. Когда что-то оценивается выше 16-часового (или 20-балльного) порога вашей команды, это сигнал к тому, чтобы разбить это на более мелкие части и переоценить.

Для элементов, находящихся глубже в списке невыполненных работ, дайте приблизительную оценку. К тому времени, когда команда действительно начнет работать над этими элементами, требования могут измениться, и ваше приложение, безусловно, изменится. Поэтому предварительные оценки не будут такими точными. Не тратьте время на оценку работы, которая может сместиться. Просто дайте владельцу продукта ориентировочную цифру, которую он может использовать, чтобы правильно расставить приоритеты в дорожной карте продукта.

Учитесь на прошлых оценках

Ретроспективы — это время, когда команда может использовать информацию из прошлых итераций, включая точность своих оценок. Многие agile-инструменты (например, Jira Software) отслеживают точки обзора, что значительно упрощает анализ и повторную калибровку оценок. Попробуйте, например, найти последние 5 пользовательских историй, которые команда представила со значением 8 баллов. Обсудите, требовалось ли для каждого из этих рабочих элементов одинаковый уровень усилий.

No related posts.