| Алгоритм Луна Вычисляет контрольную сумму последовательности цифр при помощи алгоритма Луна, вычисляет проверочную цифру (цифру, которую можно добавить к исходной последовательности, чтобы получить последовательность с контрольной суммой оканчивающейся на 0). |
| Антилогарифм Калькулятор для вычисления антилогарифма. |
| Аппроксимация функции одной переменной Калькулятор использует методы регрессии для аппроксимации функции одной переменной. |
| Быстрое возведение в степень по модулю Калькулятор возводит большие числа в степень по модулю |
| Вероятность возникновения некоторого числа событий при проведении нескольких испытаний. Испытания Бернулли. Используя формулу Бернулли, вычисляет вероятность возникновения нескольких событий. Таблица и график функции биноминального распределения показывает вероятность всех возможных случаев. |
| Взаимно простые числа и попарно взаимно простые числа Этот калькулятор проверяет, являются ли введенные числа взаимно простыми и попарно взаимно простыми. |
| Выражение длины разными единицами Калькулятор выражает заданную длину через разные единицы. |
| Вычисление выражений с несколькими переменными Калькулятор вычисляет значение математического выражения с несколькими переменными. |
| Вычисление производной по ее определению Этот онлайн калькулятор выполняет численное дифференцирование — приближенное вычисление производной функции в заданной точке. Используется метод перехода к пределу последовательными приближениями до достижения заданной точности. |
| Вычисление частной производной по ее определению Этот онлайн калькулятор выполняет численное дифференцирование функции нескольких переменных — приближенное вычисление всех частных производных функции в заданной точке — по всем переменным. |
| Генератор нормально распределенных случайных чисел Калькулятор генерирует заданное количество нормально распределенных случайных чисел, используя преобразование Бокса-Мюллера над равномерно распределенными случайными числами, полученными из встроенного в Javascript генератора случайных чисел. |
| Генератор последовательности выпадания чисел Калькулятор генерирует последовательность выпадания чисел из заданного диапазона. Например, порядок вытаскивания бочонков в лото — числа от 1 до 90 будут перечислены в случайном порядке, или лотерея «5 из 36». |
| Генератор случайной матрицы Этот онлайн калькулятор генерирует случайную матрицу с заданными параметрами. |
| Двоично-десятичное кодирование Калькулятор преобразует число из десятичное в двоичное, но записанное упакованным двоично-десятичным кодом, и наоборот. |
| Дополнение числа Этот онлайн калькулятор вычисляет дополнение числа и дополнение числа с уменьшенным основанием для заданной системы счисления |
| Дроби с факториалом Этот онлайн калькулятор вычисляет результат деления, когда и в числителе и в знаменателе находится факториал числа |
| Египетские дроби Калькулятор преобразует дробь в Египетскую дробь. |
| Египетские числа Калькулятор отображает числа в виде набора древнеегипетских иероглифов. |
| Задача про бочку и ведра Как набрать из бочки определенный объем воды, используя ведра разного размера? |
| Запись математических выражений Содержит калькулятор с примерами записи математических выражений. |
| Золотое сечение Расчет длин отрезков в золотом сечении. |
| Из египетской дроби в рациональное число Калькулятор преобразует египетскую дробь в простую дробь |
| Интерполяционный многочлен Лагранжа (полином Лагранжа) Этот онлайн калькулятор строит интерполяционный многочлен Лагранжа для заданного набора точек. Калькулятор также строит график, на который выводит как полином Лагранжа, так и базисные полиномы, интерполирует заданные точки и показывает пошаговое решение. |
| Интерполяционный многочлен Ньютона (полином Ньютона) Этот онлайн калькулятор строит интерполяционный многочлен Ньютона для заданного набора точек. Калькулятор показывает пошаговое решение, интерполирует заданные точки, а также строит график. |
| Ковариация Этот онлайн калькулятор рассчитывает значение ковариации, или корреляционного момента для двух дискретных случайных величин |
| Корень и степень Возведение в произвольную степень, извлечение корня произвольной степени. |
| Линейная рекуррентная последовательность Этот онлайн калькулятор выполняет расчет заданного числа членов линейной рекуррентной последовательности (возвратной последовательности), а также выводит их сумму нарастающим итогом. |
| Линейные диофантовы уравнения с двумя переменными Калькулятор решает линейные диофантовы уравнения с двумя переменными. |
| Мальтузианская модель роста Этот онлайн калькулятор по заданным начальным параметрам строит график мальтузианской модели роста также известной как экспоненциальный закон. |
| Метод Крамера с подробным решением Калькулятор для решения систем линейных уравнений методом Крамера. Приведено подробное решение — калькулятор выводит все промежуточные матрицы и значения определителей. |
| Метод Рунге — Кутты Этот онлайн калькулятор реализует классический метод Рунге — Кутты (встречается также название метод Рунге — Кутта) четвертого порядка точности. Метод используется для решения дифференциальных уравнений первой степени с заданным начальным значением |
| Метод Эйлера Этот онлайн калькулятор реализует метод Эйлера, числовой метод решения дифференциальных уравнений первой степени первого порядка точности. |
| Метод итераций (метод последовательных приближений) Отыскание корней функциональных уравнений методом итераций (последовательных приближений). |
| Модель Ферхюльста Этот онлайн калькулятор по заданным начальным параметрам строит график уравнения Ферхюльста — Пирла, или логистическую кривую. |
| Наибольший общий делитель (НОД) двух целых чисел Этот калькулятор находит наибольший общий делитель (НОД) двух целых чисел алгоритмом Евклида. |
| Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) нескольких чисел Этот калькулятор находит наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) двух и более целых чисел, выполняя разложение чисел на простые множители. |
| Наименьшее общее кратное и наибольший общий делитель двух целых чисел Нахождение наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух целых чисел. |
| Наименьший общий знаменатель для двух или нескольких дробей Нахождение наименьшего общего знаменателя для двух или нескольких дробей. |
| Непрерывная дробь Калькулятор представляет обычную дробь в виде непрерывной (цепной) дроби. |
| Нормальное распределение Строит график плотности вероятности и функции плотности распределения для нормального распределения. |
| Обратная матрица Нахождение обратной матрицы с помощью союзной матрицы. |
| Обратная матрица по модулю Нахождение обратной матрицы по модулю с помощью союзной матрицы и обратного элемента в кольце по модулю. |
| Олимпиадные задания Калькуляторы, решающие несколько олимпиадных задач по математике. |
| Определение ранга матрицы Калькулятор, определяющий ранг матрицы |
| Определитель (детерминант) матрицы Расчет определителя (детерминанта) матрицы по определению. |
| Определитель матрицы методом Гаусса Нахождение определителя матрицы путем преобразования матрицы к треугольному виду. Работает в рациональных и комплексных числах |
| Остаток от деления Калькулятор выдает остаток от деления двух целых (или дробных) чисел. |
| Перевод меры угла из часовой системы в градусную и из градусной системы в часовую Статья содержит два калькулятора, первый предназначен для перевода угла из часовой меры в градусную, второй — из градусной меры в часовую |
| Подсчет суммы и произведения чисел, соответствующих буквам в слове Нумерологический калькулятор по запросу пользователя. |
| Поиск пропущенных номеров При помощи этого калькулятора можно искать пропуски в последовательности номеров. |
| Поиск простых чисел. Решето Эратосфена. Калькулятор находит простые числа используя алгоритм, известный как «Решето Эратосфена» |
| Приведение матрицы к треугольному виду Приведение матрицы к треугольному виду методом Гаусса и методом Барейса. |
| Производная показательно-степенной функции Функция возводится в степень самой себя заданное количество раз и затем берется производная. |
| Пропорция Расчет неизвестного члена пропорции. Создано по запросу пользователя. |
| Разложение квадратной матрицы на симметричную и кососимметричную матрицы Этот онлайн калькулятор представляет квадратную матрицу как сумму симметричной и кососимметричной матрицы |
| Распределение Стьюдента Вычисляет значение функции распределения и плотности вероятности для распределения Стьюдента. Вычисляет квантили Стьюдента для заданного количества степеней свободы и заданной вероятности. |
| Расстояние Левенштейна Калькулятор для расчета расстояния Левенштейна между двумя словами. |
| Расчет спирали Расчет неизвестных размеров спирали по известным размерам. Параметры спирали: внешний диаметр, внутренний диаметр, толщина (шаг спирали), длина спирали, число витков. |
| Расширенный алгоритм Евклида Калькулятор, реализующий расширенный алгоритм Евклида. |
| Результант Калькулятор вычисляет результант для двух многочленов. Также отображается матрица Сильвестра. |
| Решение задач Калькулятор выводит и вычисляет значения недостающих переменных из заданных формул и входных параметров. |
| Решение задач на арифметическую прогрессию Этот онлайн калькулятор помогает решить некоторые типы задач на арифметическую прогрессию |
| Решение задач на геометрическую прогрессию Этотонлайн калькулятор помогает решить некоторые типы задач на геометрическую прогрессию |
| Решение канонической задачи линейного программирования симплекс-методом Решение канонической задачи линейного программирования однофазным симплекс-методом. |
| Решение квадратных уравнений Квадратные уравнения — это уравнения вида axx+bx+c=0. Например, 4xx+2x+1=0. Такие уравнения решаются через дискриминант. Данный калькулятор поможет вам быстрее высчитать значение квадратного уравнения. Только прежде его приведите к вышеуказанному виду. Например, из 5xx-2x-0=0 в 5xx+(-2x)+0=0, из 3xx=0 в 3xx+0x+0=0. |
| Решение неоднородной системы линейных алгебраических уравнений матричным методом Решение неоднородной системы линейных алгебраических уравнений (СЛАУ) матричным методом (методом решения через обратную матрицу). |
| Решение системы линейных алгебраических уравнений методом Гаусса Калькулятор решает систему линейных алгебраических уравнений, заданных в виде матрицы методом Гаусса. Выдается пошаговое решение. |
| Решение системы линейных алгебраических уравнений методом Гаусса с сохранением дробей Калькулятор решает систему линейных алгебраических уравнений, заданных в виде матрицы, методом Гаусса, сохраняя дроби на всем протяжении процесса. |
| Решение системы линейных уравнений методом Гаусса с нахождением общего решения Решает систему линейных алгебраических уравнений методом Гаусса. Умеет выводить решение для совместных неопределенных систем линейных уравнений. Кроме того, выводит результат в формате с плавающей точкой и в формате дроби. |
| Решение системы нелинейных уравнений Этот онлайн калькулятор пытается найти решение системы нелинейных уравнений методом покоординатного поиска. |
| Решение сравнений по модулю Этот калькулятор находит решения линейных сравнений, или сравнений первой степени по модулю m |
| Сложение / вычитание многочленов Калькулятор вычисляет сумму или разность двух многочленов |
| Соотношения между двумя числами Всевозможные соотношения между двумя числами. Создано по запросу пользователя. |
| Стандартный вид числа Преобразует число в стандартный вид — произведение мантиссы от 1 до 10 и порядка числа 10. |
| Сумма сумм арифметической прогрессии Калькулятор вычисляет ряд сумм арифметической прогрессии до указанного номера, а также ряд, представляющий суммы сумм прогрессии. |
| Сумма чисел Этот онлайн калькулятор поможет вычислить сумму чисел записанных друг за другом. |
| Таблица независимых испытаний по формуле Бернулли Этот онлайн калькулятор рассчитывает вероятность k успехов при выполнении n повторных независимых испытаний с заданной вероятностью успеха p (схема Бернулли), для k меняющегося от нуля до n. |
| Теорема Байеса Этот онлайн калькулятор рассчитывает апостериорные вероятности событий в соответствии с теоремой Байеса |
| Тест простоты Миллера-Рабина Калькулятор проверяет является ли число составным, используя тест Миллера-Рабина. |
| Тест простоты Ферма Выполняет тест простоты числа, основанный на малой теореме Ферма по заданным основаниям. |
| Транспонирование матрицы Транспонирование матрицы, что тут еще сказать. |
| Умножение матриц Калькулятор умножает две матрицы. |
| Уравнение Мальтуса Этот онлайн калькулятор рассчитывает неизвестный параметр мальтузианского уравнения по известным параметрам. |
| Уравнение прямой по двум точкам Данный онлайн калькулятор находит формулы параметрического уравнения прямой и уравнения прямой с угловым коэффициентом по координатам двух точек, принадлежащих прямой. |
| Факториал Этот онлайн калькулятор рассчитывает факториал положительного целого числа. Практически любого положительного целого числа — он ограничен только временем, которое вы готовы потратить, чтобы дождаться окончания расчета. Я, например, дождался результата расчета факториала 100000! |
| Факторизация целых чисел. Перебор делителей Факторизация целых чисел методом перебора делителей. |
| Функция распределения дискретной случайной величины Этот онлайн калькулятор для заданных значений случайной величины строит распределение вероятностей и функцию распределения дискретной случайной величины. |
| Центрированное скользящее среднее Этот калькулятор рассчитывает центрированное скользящее среднее для заданного периода усреднения |
| Числа Ацтеков Калькулятор преобразует целые положительные числа в форму записи числа Ацтеков. |
| Числительные Майя Калькулятор переводит число в систему счисления Майя |
| Числовые ребусы — замена цифр буквами Решатель числовых ребусов. Числовые или математические ребусы — математические выражения, в котором все или часть цифр заменены на некоторые символы, например, буквы. Требуется вместо каждого символа подставить нужную цифру, чтобы выражение было верным. |
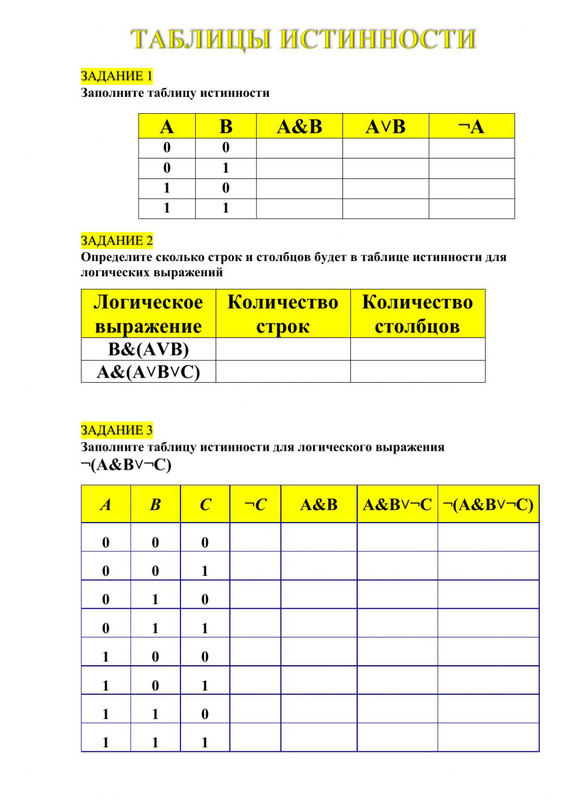
Таблицы истинности логических операций ✔️ алгоритм построения и решение задач
Определения и понятия
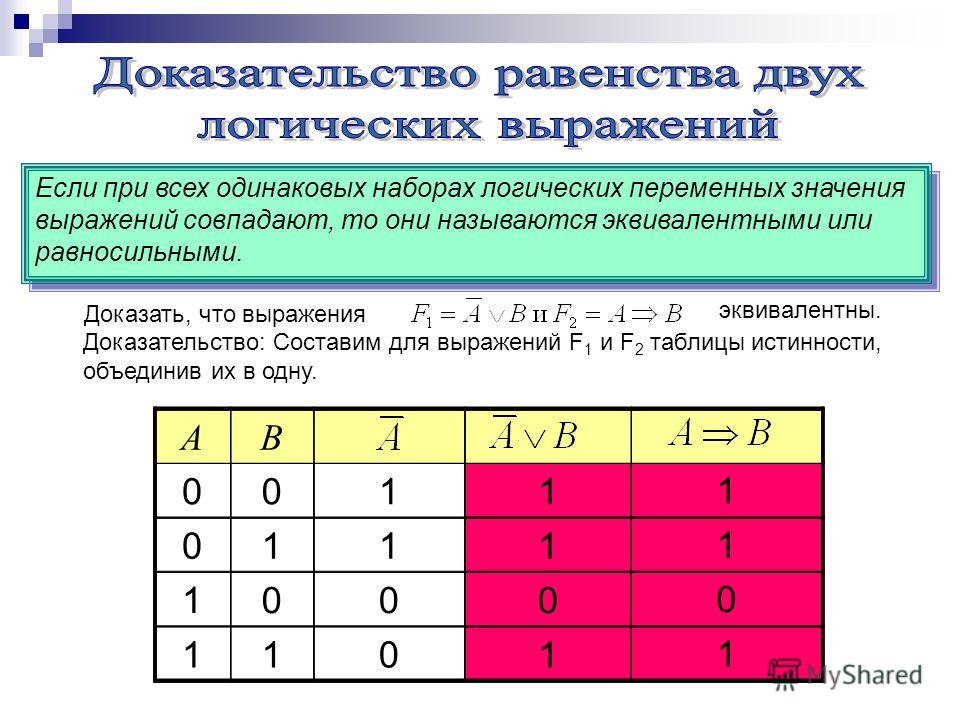
Под таблицей истинности понимают свод значений, которые может принять высказывание при сочетании различных входящих комбинаций.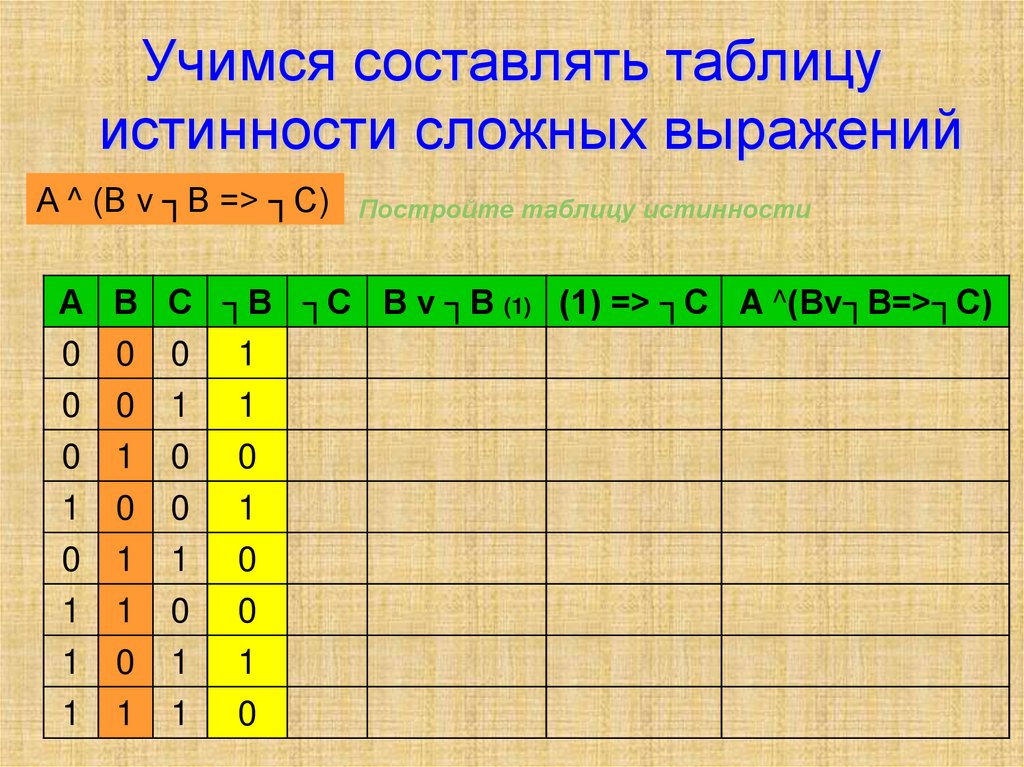 Другими словами, каждому набору функций или сигналам, присутствующим на входе чего-либо, соответствует строго определённые показатели на выходе. Все значения, являющиеся всевозможными высказываниями, называют логическими выражениями. Если в таблице последние столбцы логичных выражений идентичны, то рассматриваемый объект считается равносильным.
Другими словами, каждому набору функций или сигналам, присутствующим на входе чего-либо, соответствует строго определённые показатели на выходе. Все значения, являющиеся всевозможными высказываниями, называют логическими выражениями. Если в таблице последние столбцы логичных выражений идентичны, то рассматриваемый объект считается равносильным.
Любое выражение можно описать формулой, в которую будут включаться переменные, характеризующие состояния, и обозначающие функции знаки логических операций. Поэтому используя язык математики, в частности, алгебры, любое сложное высказывание можно разделить на несколько простых, а затем объединить логической связью.
Обычно значениями истинности описывают логическую функцию, у которой показатели параметров определяют верность. Раздел математики рассматривающий их на правдивость или ложность называется булевым. В 1854 году английский учёный Джордж Буль предложил метод, позволяющий проводить анализ классов и высказываний. Согласно ему, любое значение может принимать одно из двух состояний — истина или ложь.
Эти состояния принято обозначать арабскими цифрами один либо ноль или словами true и false. Это возможно из-за того, что для математики важна только истинность высказываний, а конкретное содержание второстепенно. Простые высказывания принято считать логическими переменными, а сложные — функциями логики. Выражения для упрощения записи обозначают латинскими буквами A, B, C.
Применение двух цифр подчёркивает соответствие между двоичной системой счисления и математической логикой. В итоге с помощью последней стало удобным описывать работу цифровых схем радиоэлектронной аппаратуры, алгоритмы в программировании, проводить синтез и анализ результата выполнения операций.
Суждение о правильности построения таблиц истинности для логических выражений основано на учёте всех переменных и операций, последовательно выполняющихся в рассматриваемой функции. Обычно для начертания используют 2n+1 строк, где n обозначает количество входных переменных, и n+m столбцов, m — число значений на выходе.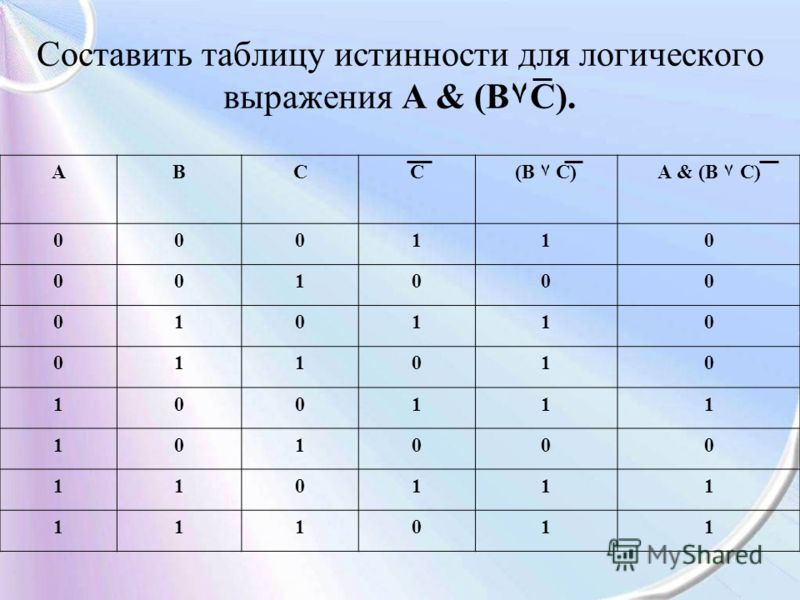
Виды логических операций
В качестве наименьшей единицы измерения объёма данных принято считать бит. В него заносится одно из двух значений — ложь (0) или правда (1). Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний.
- AND (И) — применяется для сравнения двух бит. Результатом действия будет единица, но лишь в том случае, если значения двух ячеек одинаковое. При остальных вариантах итог будет иметь устойчивое нулевое состояние.
- OR (ИЛИ) — по сути, операция обратная AND. Результат становится нулевым, если содержимое двух сравниваемых бит одинаковое. В остальных случаях он равный единице.
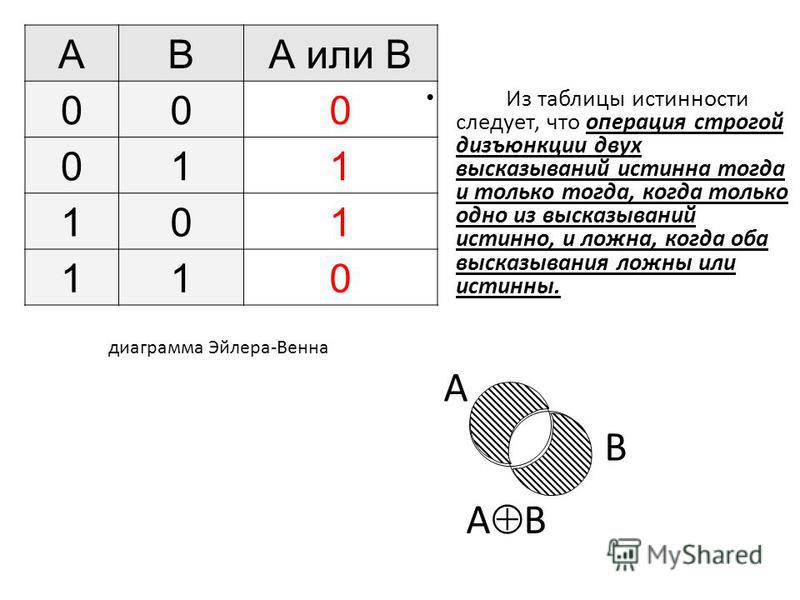
- XOR (ИЛИ) — если значения, содержащиеся в двух сравниваемых битах противоположны, при выполнении логического действия результат будет равный единице.
 Во всех остальных случаях он будет равняться нулю.
Во всех остальных случаях он будет равняться нулю. - NOT (НЕ) — действие, используемое для одного бита. Если первоначально ячейка находилась в нулевом состоянии, то после выполнения над ней операции она станет равной единице и наоборот. Фактические это логическая инверсия.
Эти операции являются основными элементами при составлении таблиц истинности и получения возможного результата. На основании их построена алгебра Буля. Некоторые элементы получаются путём объединения нескольких операций. Так, существует состояние: NAND (И-НЕ) и NOR (ИЛИ-НЕ). Первый элемент является инверсией операции «И», а второй — «ИЛИ». На основании рассмотренных операторов строится работа всех цифровых интегральных схем.
В информатике существует своя терминология, обозначающая то или иное логическое действие. Так, AND называют операцией конъюнкции, OR — дизъюнкции, XOR — сложение по модулю 2, NOT — отрицание. Задача инженера при анализе схем или алгоритма сводится к выполнению булевой арифметики и упрощению выражений.
Для этого используют различные правила и положения не требующих доказательства.
Аксиомы и законы
Построение таблиц в удобной форме позволяет определить, когда определённое действие или высказывание принимает верное значение, а в каком случае нет. В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:
- Торжества. Записывается в виде утверждения: А = А. В этом случае таблица будет состоять из двух комбинаций: ложной и правдивой. Бинарная логическая связка «Если А, то А» является материальной импликацией. Для такого варианта всегда можно сказать, что А есть А. Этот закон обозначает то, что нельзя подменять одно понятие другим, иначе возникнут логические ошибки.

- Противоречия. Согласно ему, утверждение, что А и НЕ-А, неверно: A & A = 0. Другими словами, если А истинное значение, то его отрицание не может быть ложным. То есть их перемножение будет всегда фальшивой операцией. Этот закон довольно часто применяется для упрощения сложных логических суждений.
- Третьего исключённого. Закон записывается в виде A v A = 1 и обозначает, что в один и тот же момент высказывание может быть только правдивым или ложным. То есть третьего не дано.
Эти три закона фундаментальны. Без их соблюдения сделать любое правильное утверждение невозможно.
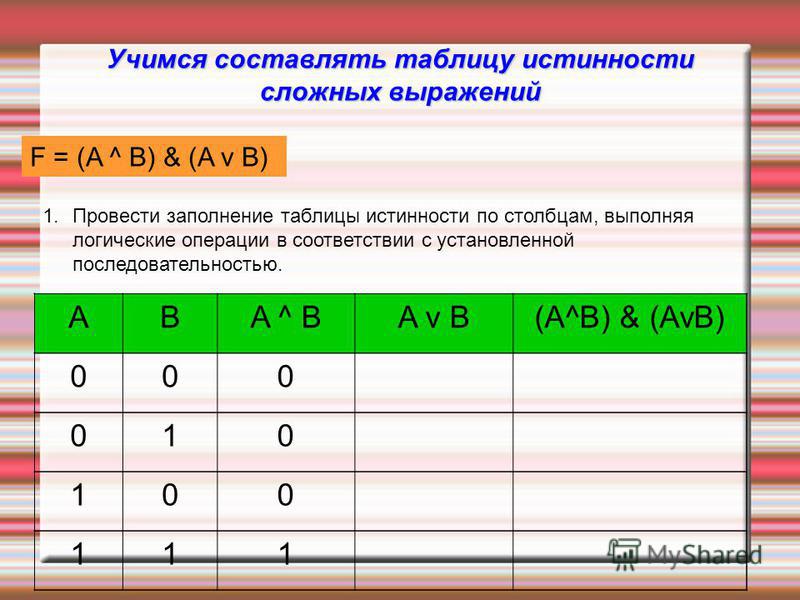
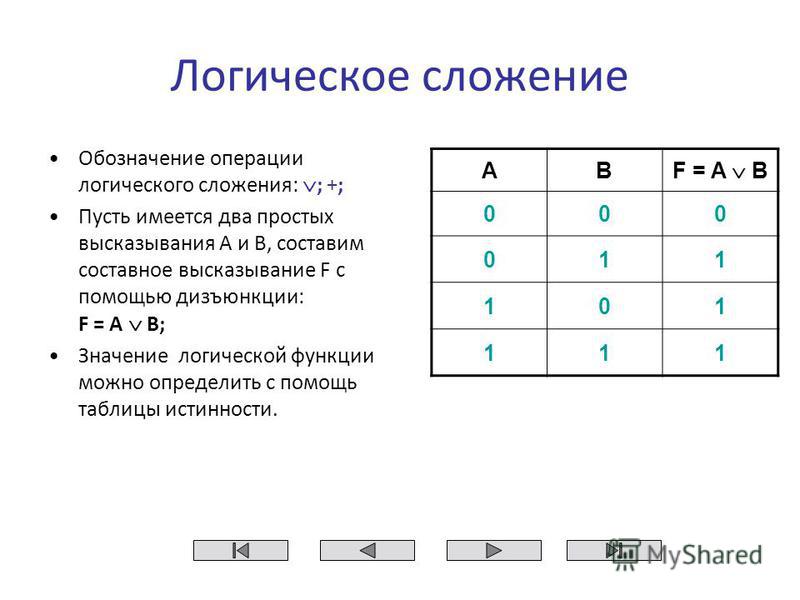
Для решения логических задач с помощью таблиц истинности используют различные формулы, соответствующие разного вида операциям. Одно из них логическое умножение (конъюнкция). В этом случае считается, что функция истинная лишь тогда, когда оба выражения являются верными: F = A & B. Другое логическое сложение (дизъюнкция). Оно гласит, что если оба выражения ложны, то и логическая функция будет неверной.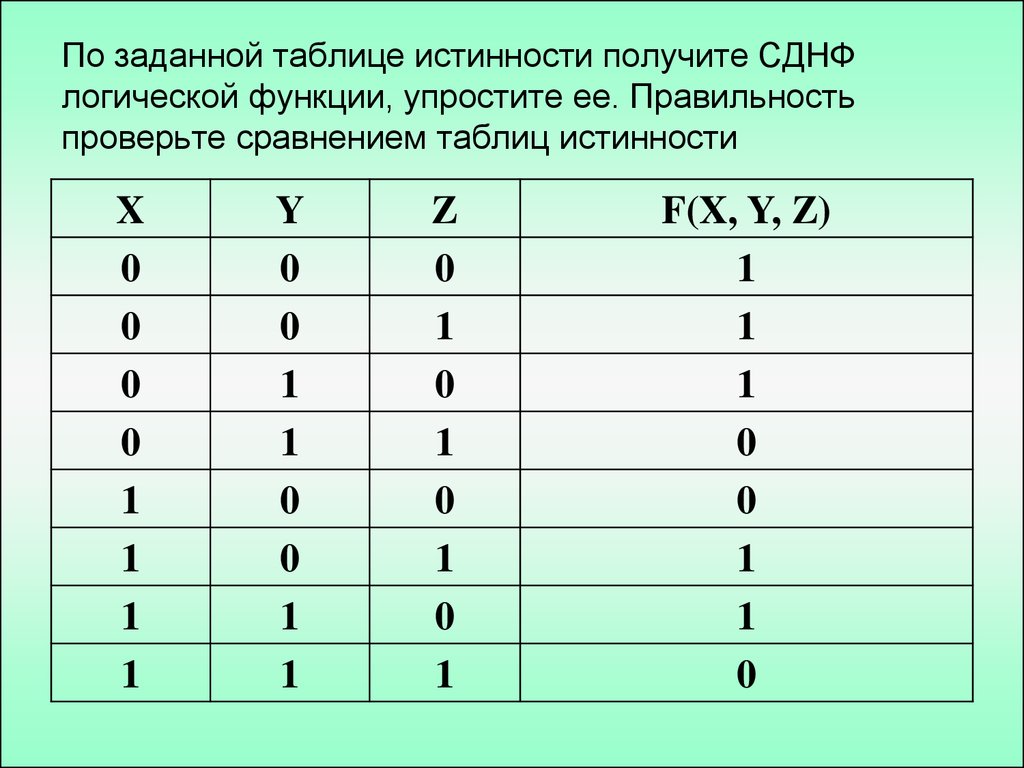
Кроме того, используется закон:
- инверсии (отрицания) — если логическое высказывание истинно, то отрицание его будет ложным выражением;
- импликации (следования) — для всегда истинного сложного логического выражения ложь будет тогда, когда из верности следует отрицание;
- эквивалентности (равнозначности) — выражение будет истинным лишь тогда, когда оба высказывания имеют одинаковое значение.
При построении таблиц нужно придерживаться установленного порядка выполнения упрощения операций. Вначале считают инверсию и конъюнкцию, а затем дизъюнкцию, импликацию и эквиваленцию. При изменении же порядка выполнения действий в описании логических операций используют скобки.
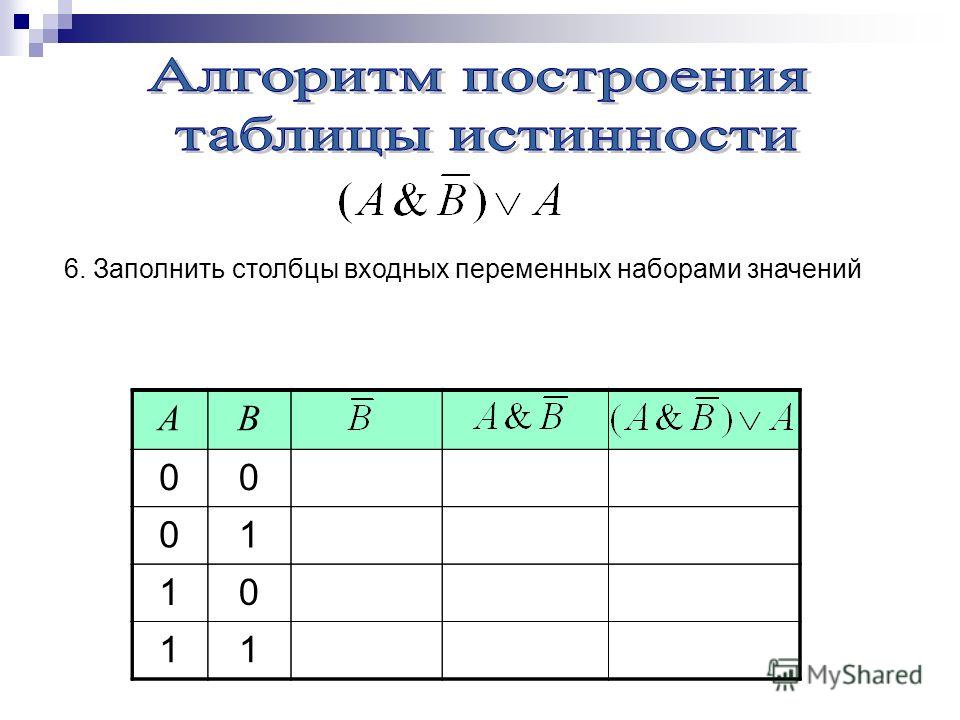
Алгоритм построения
Таблицы истинности показывают, какой вид может принять выражение при различных входящих в него значениях переменных.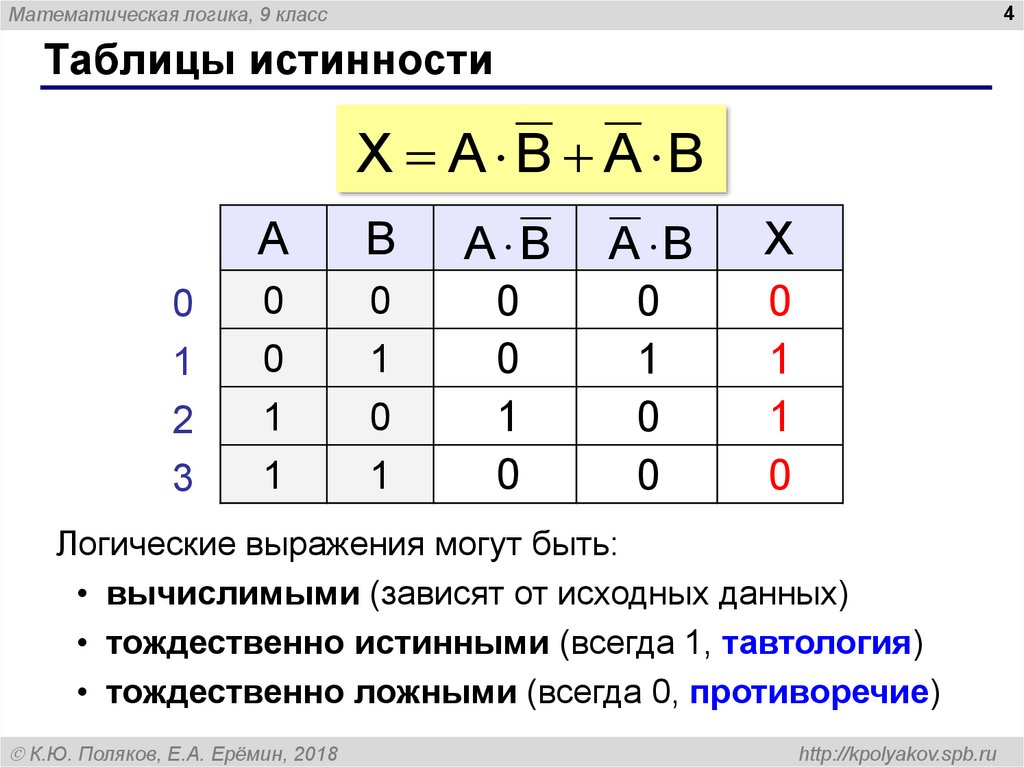 Для того чтобы их правильно построить и выполнить вычисление логического выражения нужно придерживаться установленного алгоритма. Построение таблиц выполняют в следующей последовательности:
Для того чтобы их правильно построить и выполнить вычисление логического выражения нужно придерживаться установленного алгоритма. Построение таблиц выполняют в следующей последовательности:
- подсчитывают количество переменных n;
- вычисляют число строк для будущей таблицы используя формулу m = 2n+1;
- определяют число логических операций;
- устанавливают порядок выполнения операций в соответствии со скобками и приоритетами;
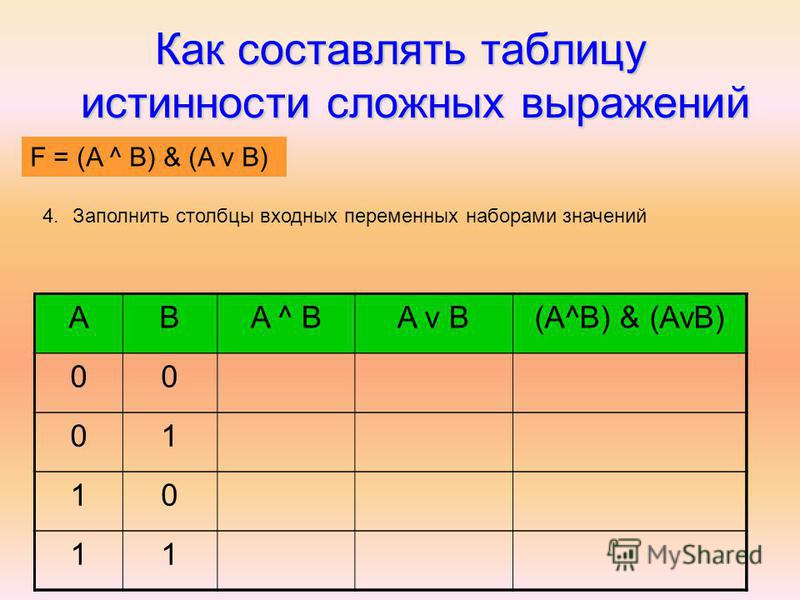
- строят таблицу с указанием столбцов и наборов значений, заданных логических операций;
Для заполнения таблиц нужно упрощать выражения с учётом последовательности выполнения операций. При этом учитывать, что если значение какого-то из аргументов функции в соответствующей строке таблицы будет равное нулю, то записывать его нужно в виде отрицания.
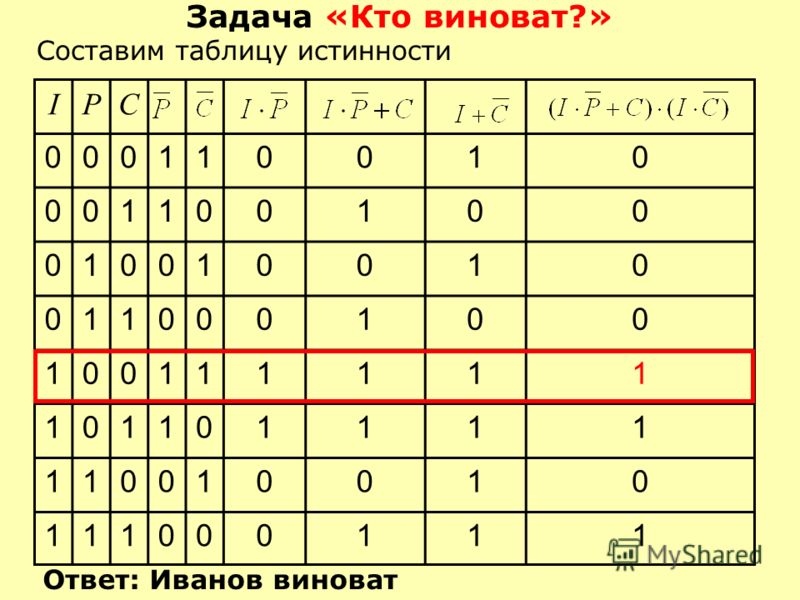
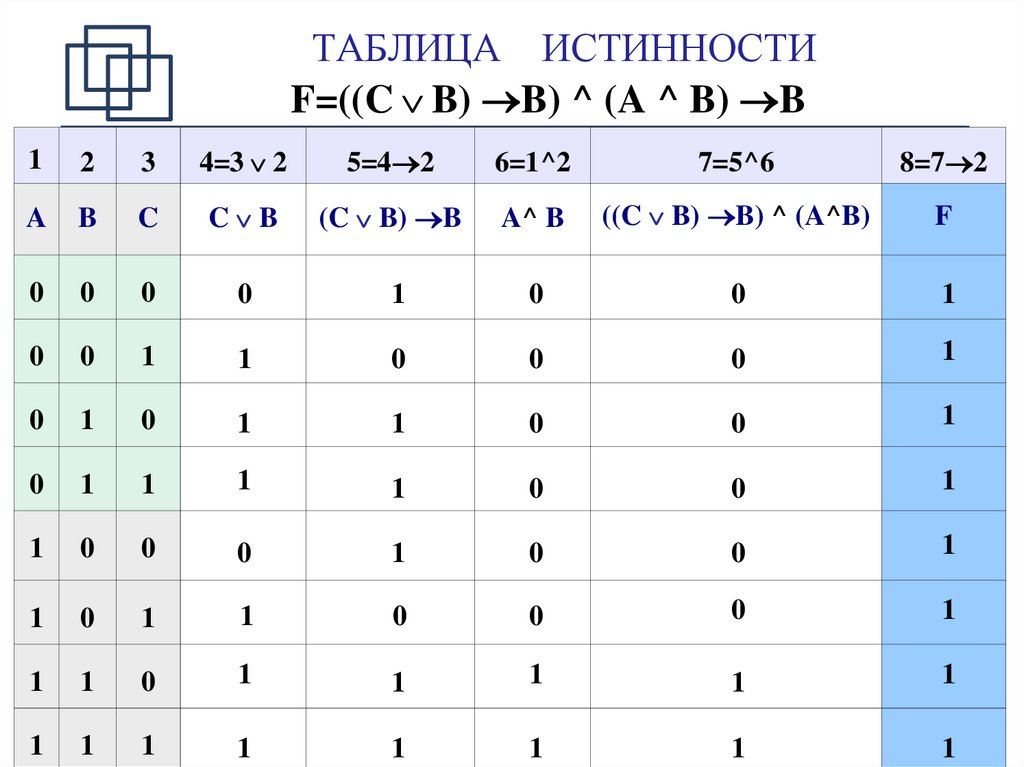
Пример задания
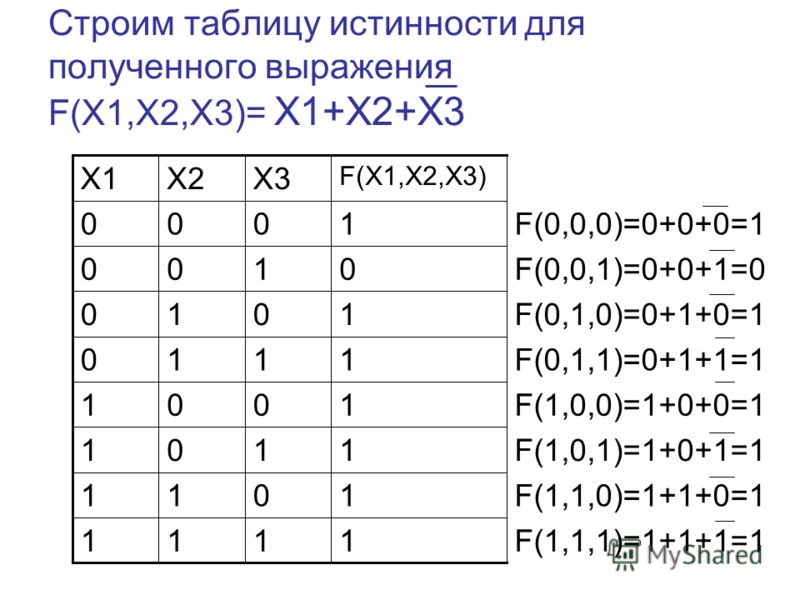
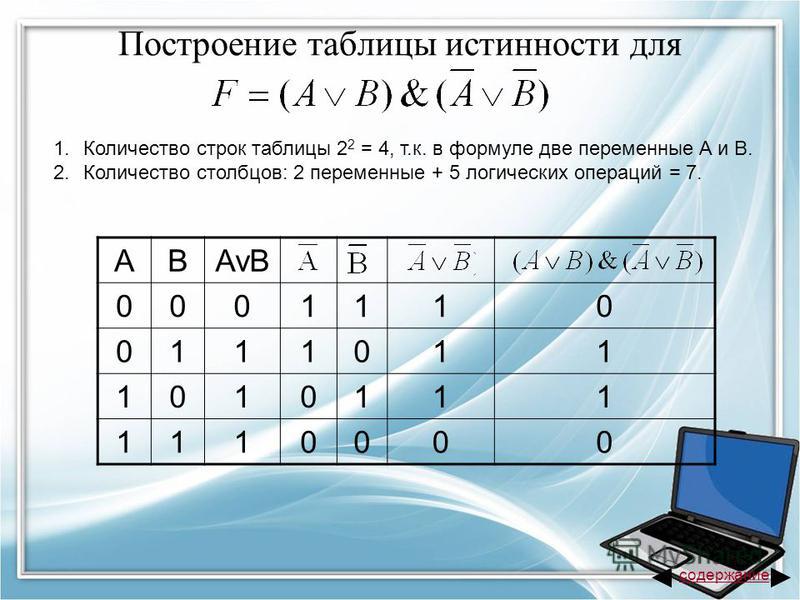
Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A + B).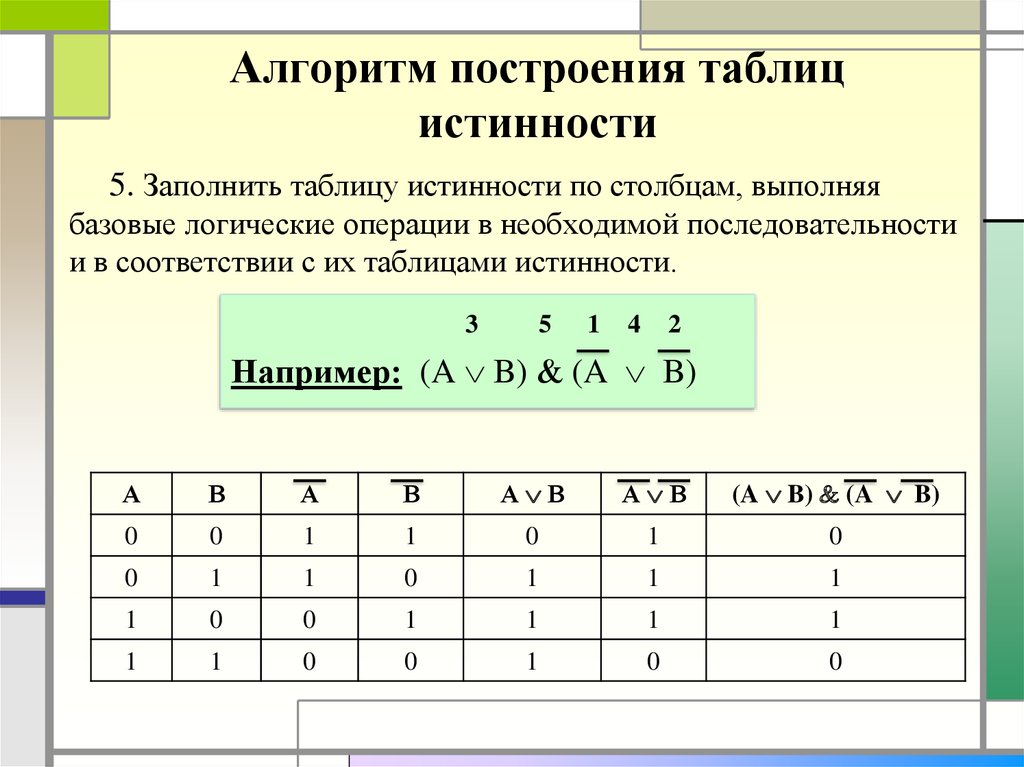 Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.
Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.
Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:
- Импликация в первой скобке.
- Инверсия во второй скобке переменной A.
- Отрицание во второй скобке неизвестной B.
- Сложение во втором члене.
- Конъюнкция.
В итоге получится, что столбцов будет: Y = 2 + 5 = 7. Теперь нужно построить таблицу 7Х5. В шапку первого и второго столбца вписывают переменные, а затем операции над ними. Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.
Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.
Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой — ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.
Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше. Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Например, заданно выражение (x + y + z) * (x + y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z.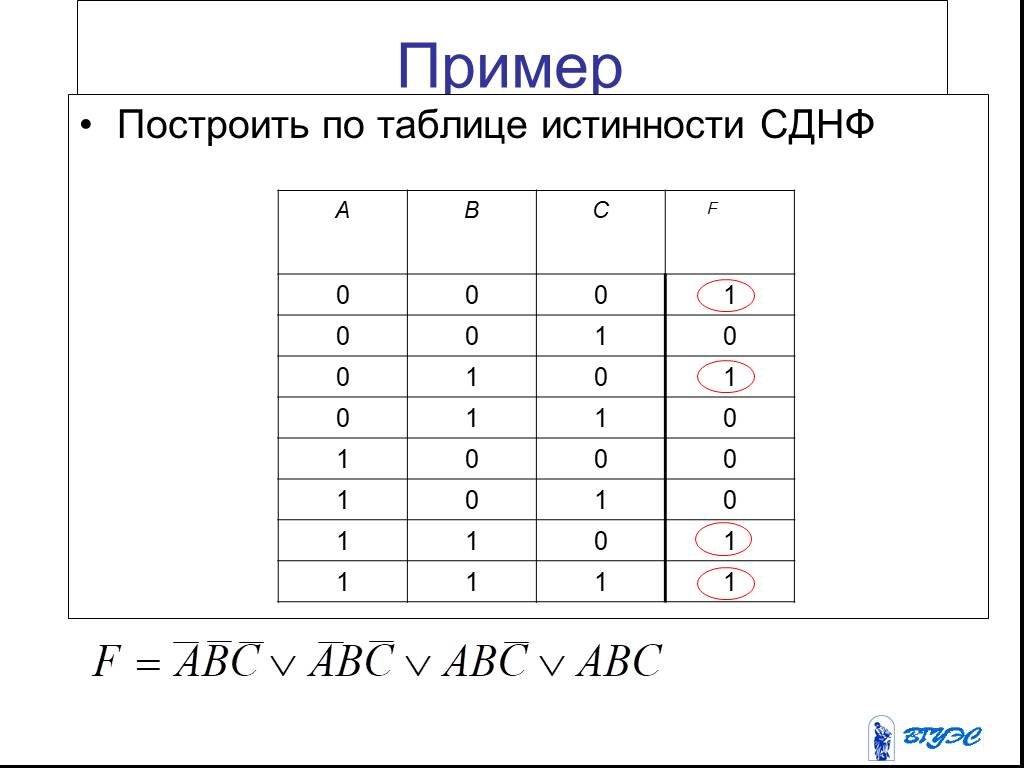 Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится. Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.
Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится. Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.
Вычисления онлайн
В интернете есть сервисы, автоматически строящие таблицы истинности. Такие сайты предлагают свои услуги бесплатно и доступны даже тем, кто слабо ориентируется в теме. С их помощью можно находить таблицы для довольно сложных выражений, решение которых требует скрупулёзности в расчёте. В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.
Для того чтобы воспользоваться сайтами-калькуляторами пользователю необходимо знать обозначение операций, иметь подключение к интернету и установленный веб-обозреватель, поддерживающий Flash-технологию. Регистрацию, указание личных данных сервисы, предлагающие такого рода услуги, не требуют.
Регистрацию, указание личных данных сервисы, предлагающие такого рода услуги, не требуют.
Из различных порталов можно отметить три наиболее популярных калькулятора:
- Allcalc.
- Programforyou.
- Uchim.
Эти сайты имеют интуитивно понятный интерфейс и что довольно полезно, на своих страницах содержат краткую теорию, используемую для составления таблиц истинности и даже примеры решений.
Генератор таблиц истинности — онлайн-калькулятор логической алгебры для таблиц
Генератор таблиц истинности
Логическое/логическое выражениеОтображение
Полная таблица истинности (входные переменные + выходные значения)
Таблица истинности с этими переменными
Только выходные значения (список 0 и 1)
Соответствующие minterms $ Σm(…) $ (0-индексированные)
Соответствующие Maxterms $ ΣM(…) $ (0-индексированные)
См. также: Калькулятор логических выражений — Boolean Minterms и Maxterms
также: Калькулятор логических выражений — Boolean Minterms и Maxterms
Найти уравнение по таблице истинности
Указывать только выходные значения функции (последний столбец из булевой таблицы истинности)
Выходные значения (список 0 и 1)| Таблица упорядочена (входные значения) | От 0,…,0 до 1,…,1 От 1,…,1 до 0,…,0 |
| Булева запись | Литеральная (И, ИЛИ, НЕ) Логическая (∧, ∨, ¬) Программирование (&&, ||, ~) Алгебраическая (*, +, !) |
См. также: Калькулятор логических выражений
Ответы на вопросы (FAQ)
Что такое таблица истинности? (Определение)
Таблица истинности представляет собой таблицу, представляющую выходные логические значения логического выражения на основе их записей. Таким образом, таблица отображает все возможные комбинации $n$ входных логических переменных (обычно 0/FALSE и 1/TRUE по $n$ столбцам) и результат уравнения в качестве вывода (последний столбец).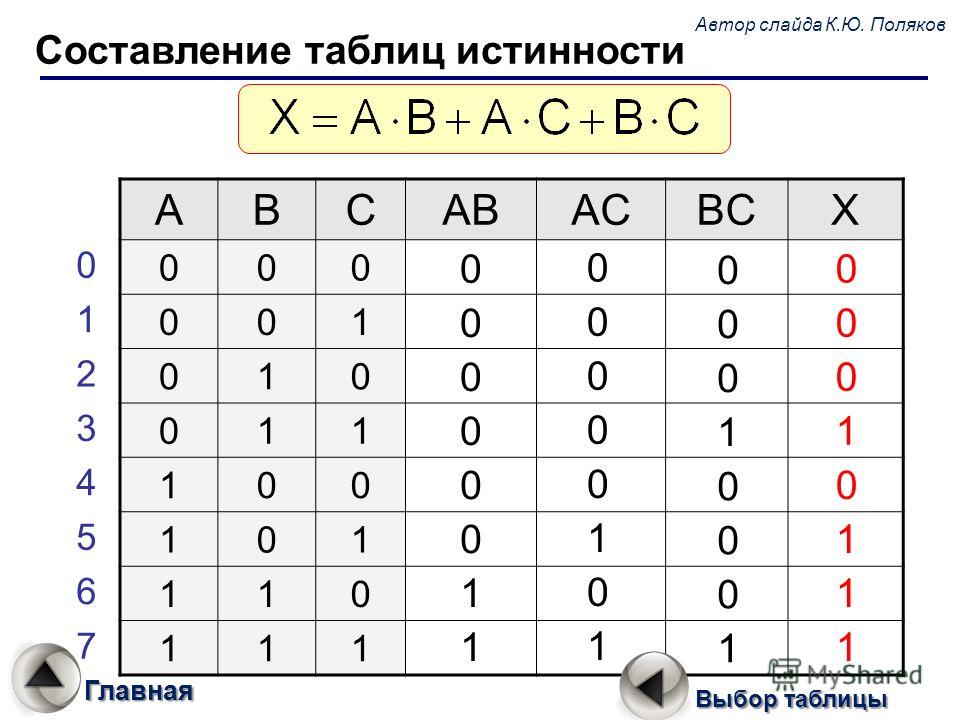
Пример: Таблица функции логического НЕ с 1 входом А (1-й столбец) и выходным значением НЕ А (последний столбец):
| А | НЕ А | 01 |
|---|---|
| 1 | 0 |
Каждая электронная схема связана с таблицей истинности , которая описывает ее.
Обычно массив начинается с входных значений в $ 0 $ и заканчивается входными значениями в $ 1 $, но иногда это наоборот.
Как работает калькулятор таблицы истинности?
dCode Генератор таблицы истинности интерпретирует логическое логическое выражение и вычисляет (используя алгебру логики) все возможные комбинации 0 и 1 для каждой переменной (среди запрошенных логических переменных), чтобы составить таблицу истинности .
dCode также позволяет найти булеву логическую функцию/выражение из таблицы истинности .
Как найти уравнение из таблицы истинности?
Единственным важным столбцом таблицы истинности является последний, который описывает выходные значения (первые столбцы всегда идентичны для заданного количества входных данных) и который позволяет преобразовать в логическое выражение.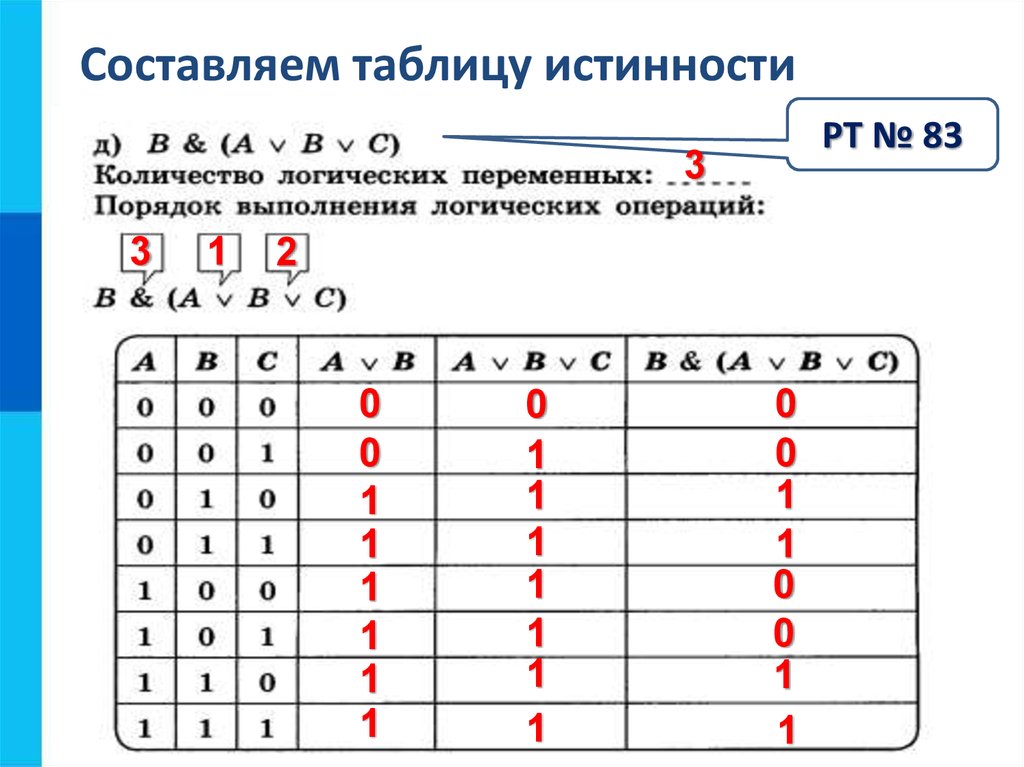
Существует 2 метода нахождения логического уравнения из таблицы истинности : либо с использованием выходных значений 0 (расчет Maxterms), либо с использованием выходных значений 1 (расчет Minterms).
Пример: Выходные значения: 0,1,1,0 , (и таблица упорядочена от 00 до 11), поэтому таблица истинности :
X
Вот различные вычисления (которые дают одинаковый результат для данного примера) 1 , запишите соответствующие входные значения, разделенные логическими И , затем сгруппируйте эти результаты с помощью логических ИЛИ .
Пример: Строки 2 и 3 равны 1 , строка 2 записывается как A AND NOT(B) (поскольку A равно 1 , а B равно 0 ), строка 3 записывается как NOT(A) AND B , поэтому уравнение равно (A AND NOT (B)) OR (NOT(A) AND B) , что, возможно, упрощается до A XOR B
Вычисление на основе выходных значений 0 таблицы истинности (Maxterms): для каждого 0 напишите соответствующие входные значения, разделенные логическим ИЛИ , затем сгруппируйте эти результаты с помощью логического И .
Пример: Строки 1 и 4 равны 0 , строка 1 записывается как A OR B , строка 4 записывается как НЕ(А) ИЛИ НЕ(В) и поэтому уравнение равно (A OR B) AND (NOT(A) OR NOT(B)) , что, возможно, упрощается до A XOR B
Какая таблица истинности для логического И?
Таблица истинности для функции И:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
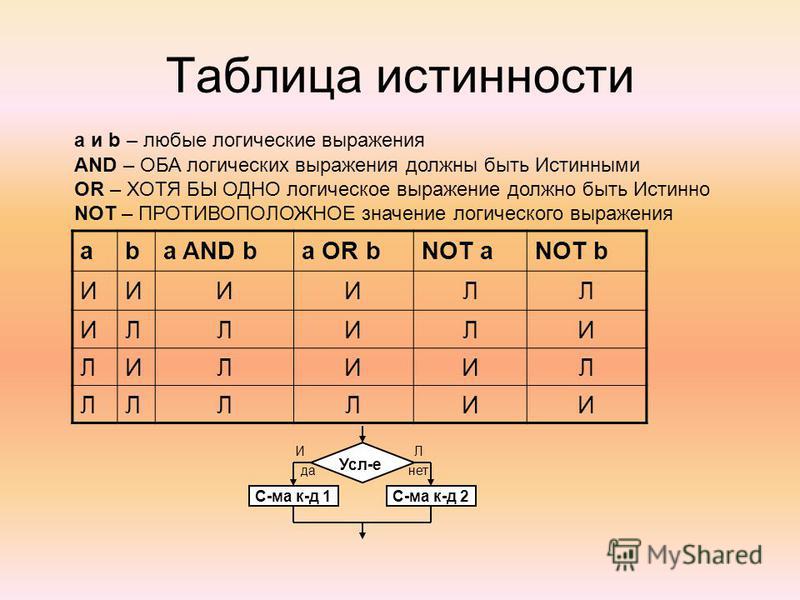
Что такое таблица истинности для логического ИЛИ?
Таблица истинности для функции ИЛИ:
| A | B | A OR B |
|---|---|---|
| 0 | 0032 0||
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
What is the truth table for logical XOR?
The truth table for the XOR function is:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
What The Prame Table Table Tabil Talecil?
The truth table for the NAND function is:
| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Какая таблица истинности для логического НЕ-ИЛИ?
The truth table for the NOR function is:
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Какая таблица истинности для логического ИСТИНА?
The truth table for the TRUE (=1) function is:
| A | TRUE |
|---|---|
| 0 | 1 |
| 1 | 1 |
What is the таблица истинности для логического FALSE?
Таблица истинности для функции ЛОЖЬ (=0):
| A | ЛОЖЬ |
|---|---|
| 0 | 0 |
| 1 | 0 |

 Правило проверки описано под калькулятором.
Правило проверки описано под калькулятором.

 Описание алгоритма можно найти под калькулятором.
Описание алгоритма можно найти под калькулятором.
 В конце результат выдается как в виде действительного числа, так и в виде дроби с числителем и знаменателем.
В конце результат выдается как в виде действительного числа, так и в виде дроби с числителем и знаменателем.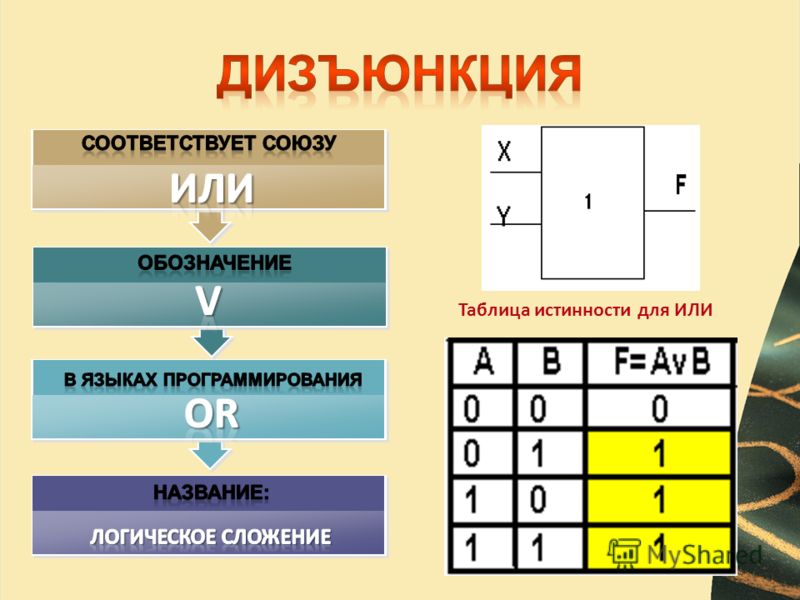
 Данные представляются в виде графика и в табличном виде
Данные представляются в виде графика и в табличном виде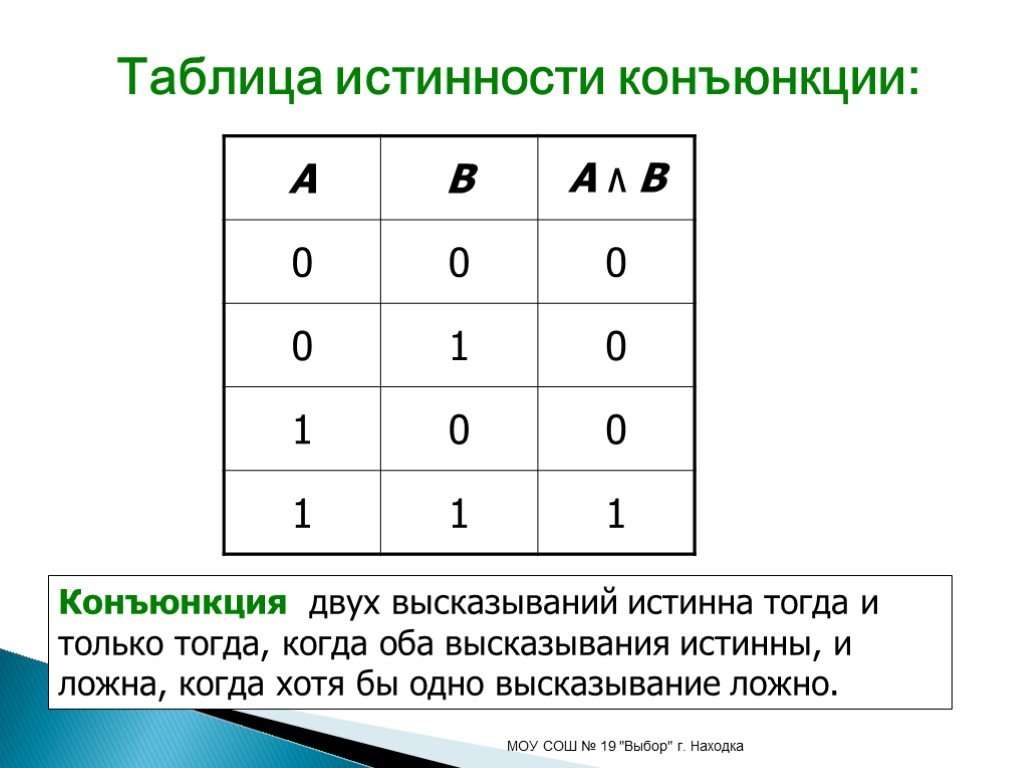 Во всех остальных случаях он будет равняться нулю.
Во всех остальных случаях он будет равняться нулю. Для этого используют различные правила и положения не требующих доказательства.
Для этого используют различные правила и положения не требующих доказательства.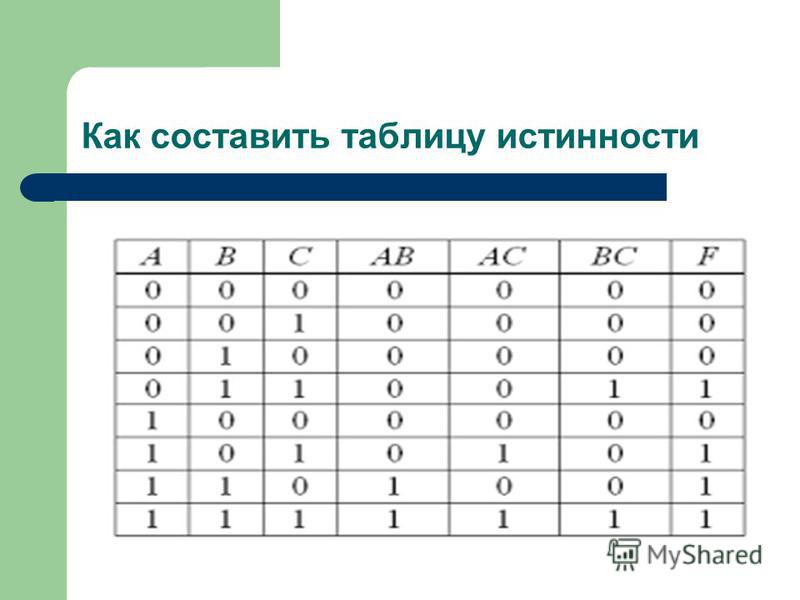
 д.) и загрузка всех данных, скрипт, или API-доступ к «Таблице правды» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
д.) и загрузка всех данных, скрипт, или API-доступ к «Таблице правды» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!  Если вы также хотите создавать таблицы истинности, используя действительные уравнения, ознакомьтесь с этими приложениями для создания таблиц истинности.
Если вы также хотите создавать таблицы истинности, используя действительные уравнения, ознакомьтесь с этими приложениями для создания таблиц истинности. Некоторые приложения даже позволяют пользователям редактировать некоторые элементы выходной таблицы истинности. Эти приложения также поставляются с дополнительными инструментами, с помощью которых пользователи могут решать логические выражения, просматривать историю уравнений, моделировать логические схемы, и т. д. Просмотрите список, чтобы узнать больше об этих приложениях.
Некоторые приложения даже позволяют пользователям редактировать некоторые элементы выходной таблицы истинности. Эти приложения также поставляются с дополнительными инструментами, с помощью которых пользователи могут решать логические выражения, просматривать историю уравнений, моделировать логические схемы, и т. д. Просмотрите список, чтобы узнать больше об этих приложениях. д.), а также истинных и ложных функций . Кроме того, в нем присутствуют стандартные символы логических операторов. Хотя основным преимуществом этого приложения является его способность отображать шаги для составления таблицы истинности. Теперь выполните следующие шаги, чтобы составить таблицу истинности с помощью этого приложения для Android.
д.), а также истинных и ложных функций . Кроме того, в нем присутствуют стандартные символы логических операторов. Хотя основным преимуществом этого приложения является его способность отображать шаги для составления таблицы истинности. Теперь выполните следующие шаги, чтобы составить таблицу истинности с помощью этого приложения для Android.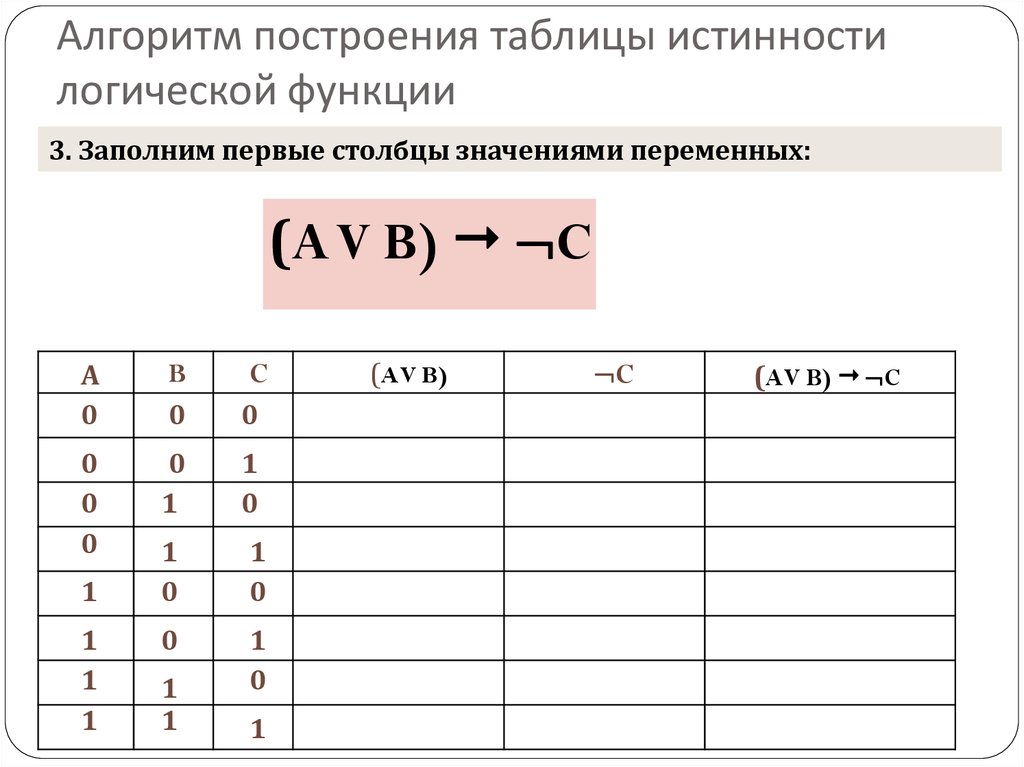

 С помощью этого приложения пользователи могут легко создать таблицу истинности, введя уравнение. Для ввода уравнения это приложение предлагает экранную клавиатуру, содержащую все основные 9, (, ), так далее.). После ввода действительного уравнения пользователи могут создать его таблицу истинности. Теперь выполните следующие шаги.
С помощью этого приложения пользователи могут легко создать таблицу истинности, введя уравнение. Для ввода уравнения это приложение предлагает экранную клавиатуру, содержащую все основные 9, (, ), так далее.). После ввода действительного уравнения пользователи могут создать его таблицу истинности. Теперь выполните следующие шаги.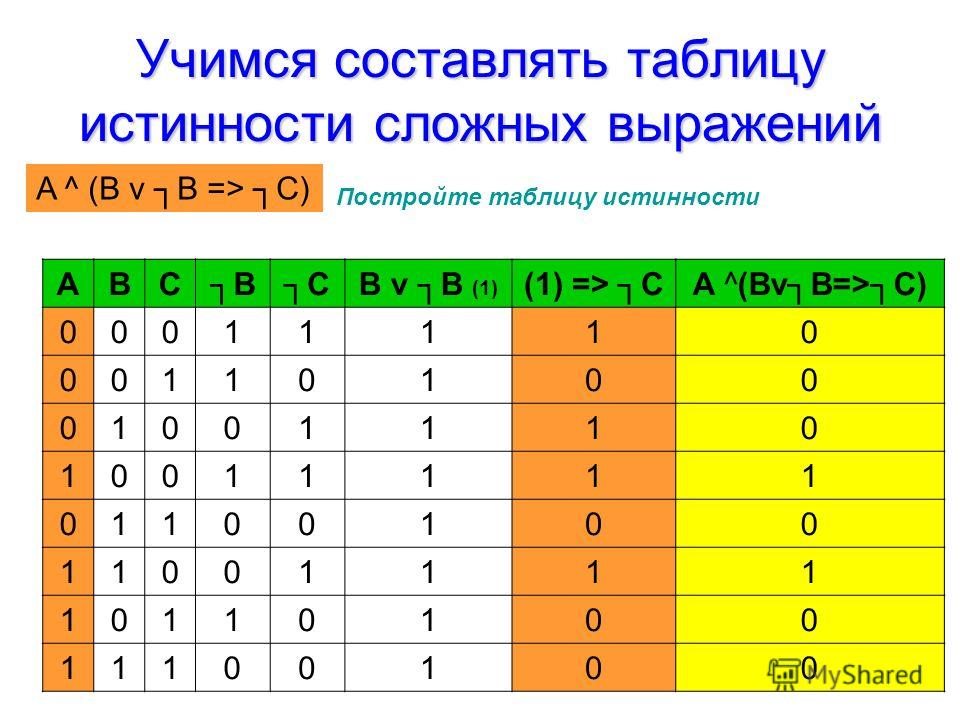

 Плюс 0 и 1 для ввода false и true в нем тоже присутствует. Теперь проверьте следующие шаги.
Плюс 0 и 1 для ввода false и true в нем тоже присутствует. Теперь проверьте следующие шаги. С помощью этого приложения пользователи могут создавать все типы таблиц истинности, а также просматривать упрощенные сгенерированные таблицы истинности. Как и в других приложениях, оно также имеет экранная клавиатура с предложными константами и логическими выражениями. Хотя он предлагает только очень ограниченные логические выражения, такие как AND
С помощью этого приложения пользователи могут создавать все типы таблиц истинности, а также просматривать упрощенные сгенерированные таблицы истинности. Как и в других приложениях, оно также имеет экранная клавиатура с предложными константами и логическими выражениями. Хотя он предлагает только очень ограниченные логические выражения, такие как AND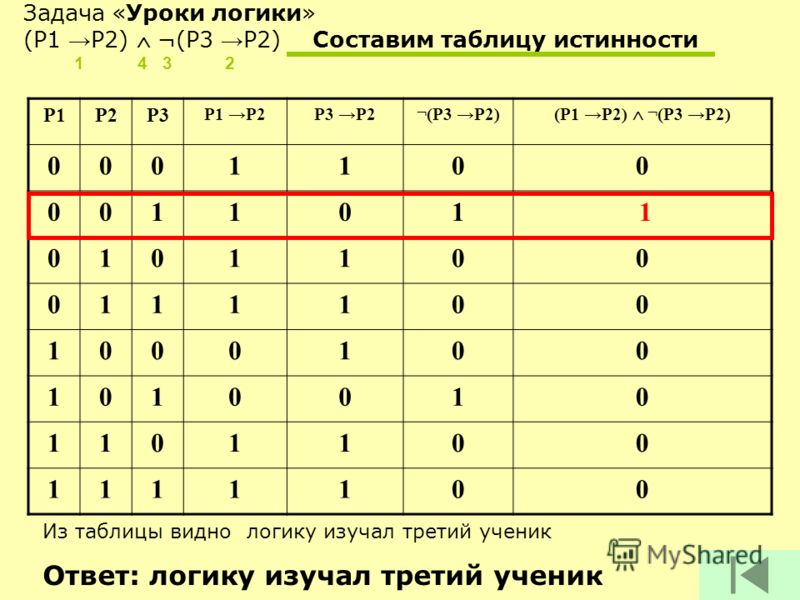

 Для создания таблицы истинности он предлагает раздел генератора таблицы истинности. Помимо этого, другие разделы, такие как калькулятор , логическая схема, решатель карт Карно, и др., в нем также присутствуют разделы. В разделе «Генератор таблиц истинности » пользователи получают экранную клавиатуру для ввода нужных выражений. Теперь проверьте следующие шаги.
Для создания таблицы истинности он предлагает раздел генератора таблицы истинности. Помимо этого, другие разделы, такие как калькулятор , логическая схема, решатель карт Карно, и др., в нем также присутствуют разделы. В разделе «Генератор таблиц истинности » пользователи получают экранную клавиатуру для ввода нужных выражений. Теперь проверьте следующие шаги.
