Написать уравнение параболы, если известно, что… Упр. 614, Алгебра, 8 класс, Алимов Ш.А. – Рамблер/класс
Написать уравнение параболы, если известно, что… Упр. 614, Алгебра, 8 класс, Алимов Ш.А. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Как написать уравнение параболы, если известно, что парабола проходит через точку (-1; 6), а ее вершиной является точка (1; 2).
Лучший ответ
Очень просто
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
ЕГЭ
10 класс
9 класс
похожие вопросы 5
Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.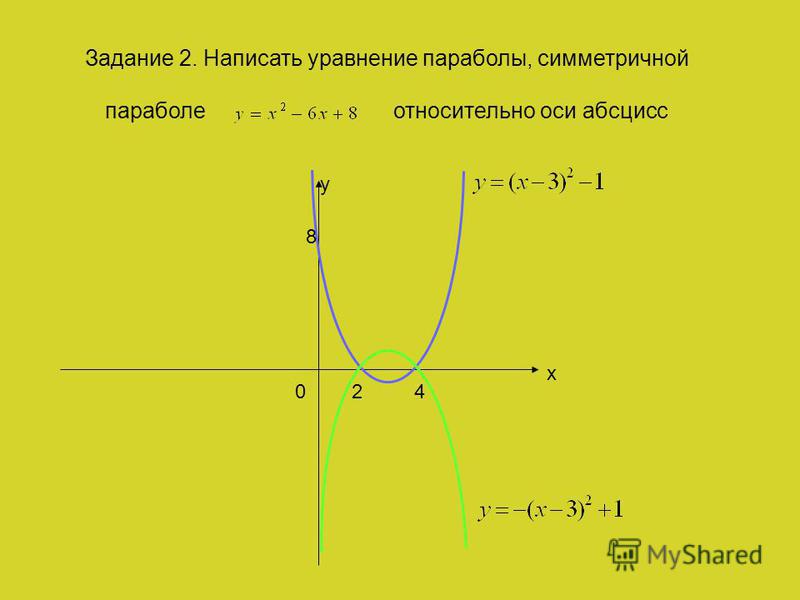
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Еще одно уравнение параболы : Геометрия
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| dmitryf |
| ||
11/10/10 |
| ||
| |||
| paha |
| |||
|
| |||
| ||||
| dmitryf |
| ||
11/10/10 |
| ||
| |||
| ||||
03/02/10 |
| |||
| ||||
| dmitryf |
| ||
11/10/10 |
| ||
| |||
Алексей К.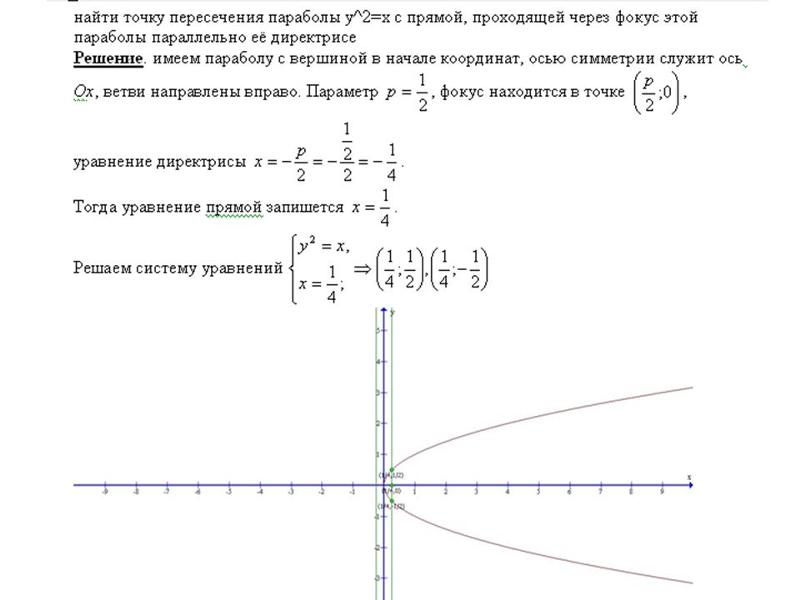 |
| ||
29/09/06 |
| ||
| |||
| dmitryf |
| ||
11/10/10 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 7 ] |
Модераторы: Модераторы Математики, Супермодераторы
Калькулятор гиперболы — eMathHelp
Этот калькулятор найдет либо уравнение гиперболы по заданным параметрам, либо центр, фокусы, вершины, ко-вершины, (полу)длину большой оси, (полу)длину малой оси, латеральную прямую, длина латерального отдела прямой кишки (ширина фокуса), параметр фокуса, эксцентриситет, линейный эксцентриситет (фокусное расстояние), директрисы, асимптоты, точки пересечения x, точки пересечения y, домен и диапазон введенной гиперболы. Кроме того, он будет отображать гиперболу. Шаги доступны.
Кроме того, он будет отображать гиперболу. Шаги доступны.
Связанные калькуляторы: Калькулятор параболы, Калькулятор окружности, Калькулятор эллипса, Калькулятор конического сечения
Тип:
из уравненияиз данных
Уравнение:
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже. 9{2}} = 3 \sqrt{5}$$$.
Эксцентриситет равен $$$e = \frac{c}{a} = \frac{\sqrt{5}}{2}$$$.
Первый фокус $$$\left(h — c, k\right) = \left(- 3 \sqrt{5}, 0\right)$$$.
Второй фокус $$$\left(h + c, k\right) = \left(3 \sqrt{5}, 0\right)$$$.
Первая вершина $$$\left(h — a, k\right) = \left(-6, 0\right)$$$.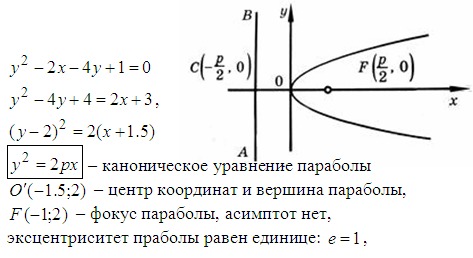
Вторая вершина $$$\left(h + a, k\right) = \left(6, 0\right)$$$.
Первая ковершина $$$\left(h, k — b\right) = \left(0, -3\right)$$$. 9{2}}{c} = \frac{12 \sqrt{5}}{5}$$$.
Первая асимптота: $$$y = — \frac{b}{a} \left(x — h\right) + k = — \frac{x}{2}$$$.
Вторая асимптота: $$$y = \frac{b}{a} \left(x — h\right) + k = \frac{x}{2}$$$.
Х-пересечения можно найти, установив $$$y = 0$$$ в уравнении и решив $$$x$$$ (шаги см. в калькуляторе перехватов).
x-отрезки: $$$\left(-6, 0\right)$$$, $$$\left(6, 0\right)$$$
y-отрезки можно найти, установив $ $$x = 0$$$ в уравнении и решение для $$$y$$$: (шаги см. в калькуляторе перехватов). 9{2}}{4}$$$А.
График: см. графический калькулятор.
Центр: $$$\влево(0, 0\вправо)$$$A.
Первый фокус: $$$\влево(- 3 \sqrt{5}, 0\вправо)\приблизительно \влево(-6,708203932499369, 0\вправо)$$$A.
Второй фокус: $$$\влево(3\sqrt{5}, 0\вправо)\приблизительно \влево(6,708203932499369, 0\вправо)$$$A.
Первая вершина: $$$\left(-6, 0\right)$$$A.
Вторая вершина: $$$\left(6, 0\right)$$$A.
Первая ковершина: $$$\left(0, -3\right)$$$A.
Вторая ковершина: $$$\left(0, 3\right)$$$A.
Длина по главной (поперечной) оси: $$$12$$$A.
Длина большой полуоси: $$$6$$$A.
Длина малой (сопряженной) оси: $$$6$$$A.
Длина малой полуоси: $$$3$$$A.
Первая широкая прямая кишка: $$$x = — 3 \sqrt{5}\приблизительно -6,708203932499369$$$A.
Вторая широкая прямая кишка: $$$x = 3 \sqrt{5}\приблизительно 6,708203932499369$$$A.
Концы первой широкой прямой кишки: $$$\left(- 3 \sqrt{5}, — \frac{3}{2}\right)\приблизительно \left(-6,708203932499369, -1,5\right) $$$, $$$\left(- 3 \sqrt{5}, \frac{3}{2}\right)\приблизительно \left(-6,708203932499369, 1,5\right)$$$A.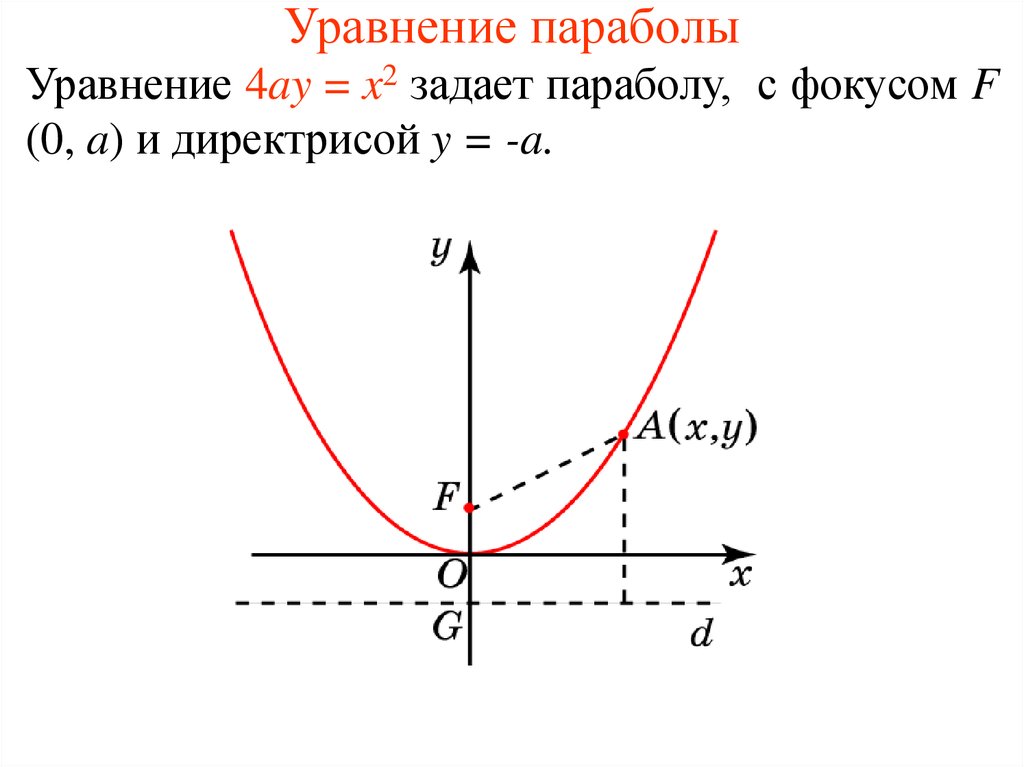
Концы второй широкой прямой кишки: $$$\left(3 \sqrt{5}, — \frac{3}{2}\right)\приблизительно \left(6.708203932499369, -1.5\right)$$ $, $$$\left(3\sqrt{5}, \frac{3}{2}\right)\приблизительно \left(6.708203932499369, 1,5\справа)$$$А.
Длина латерального отдела прямой кишки (ширина фокуса): $$$3$$$A.
Параметр фокуса: $$$\frac{3 \sqrt{5}}{5}\приблизительно 1,341640786499874$$$A.
Эксцентриситет: $$$\frac{\sqrt{5}}{2}\приблизительно 1,118033988749895$$$A.
Линейный эксцентриситет (фокусное расстояние): $$$3 \sqrt{5}\приблизительно 6,708203932499369$$$A.
Первая направляющая: $$$x = — \frac{12 \sqrt{5}}{5}\приблизительно -5,366563145999495$$$А.
Вторая направляющая: $$$x = \frac{12 \sqrt{5}}{5}\примерно 5,366563145999495$$$A.
Первая асимптота: $$$y = — \frac{x}{2} = — 0,5 x$$$A.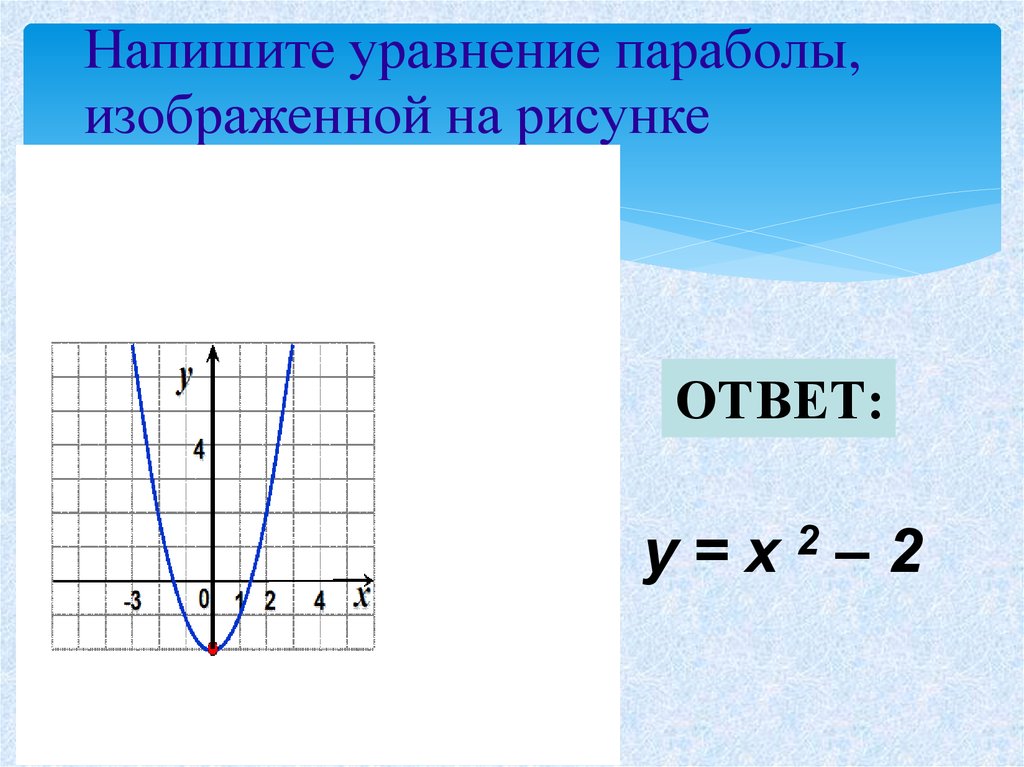
Вторая асимптота: $$$y = \frac{x}{2} = 0,5 x$$$A.
x-отрезки: $$$\left(-6, 0\right)$$$, $$$\left(6, 0\right)$$$A.
y-пересечения: нет y-пересечений.
Домен: $$$\left(-\infty, -6\right] \cup \left[6, \infty\right)$$$A.
Диапазон: $$$\left(-\infty, \infty\right)$$$A.
запишите уравнение параболы в вершинной форме. вершина (0,3), точка (-4, -45)
Форма вершины
Эми Т.
спросил 05.04.13Запишите уравнение параболы в вершинной форме.
вершина (0,3), точка (-4, -45)
Подписаться І 2
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Тамара Дж.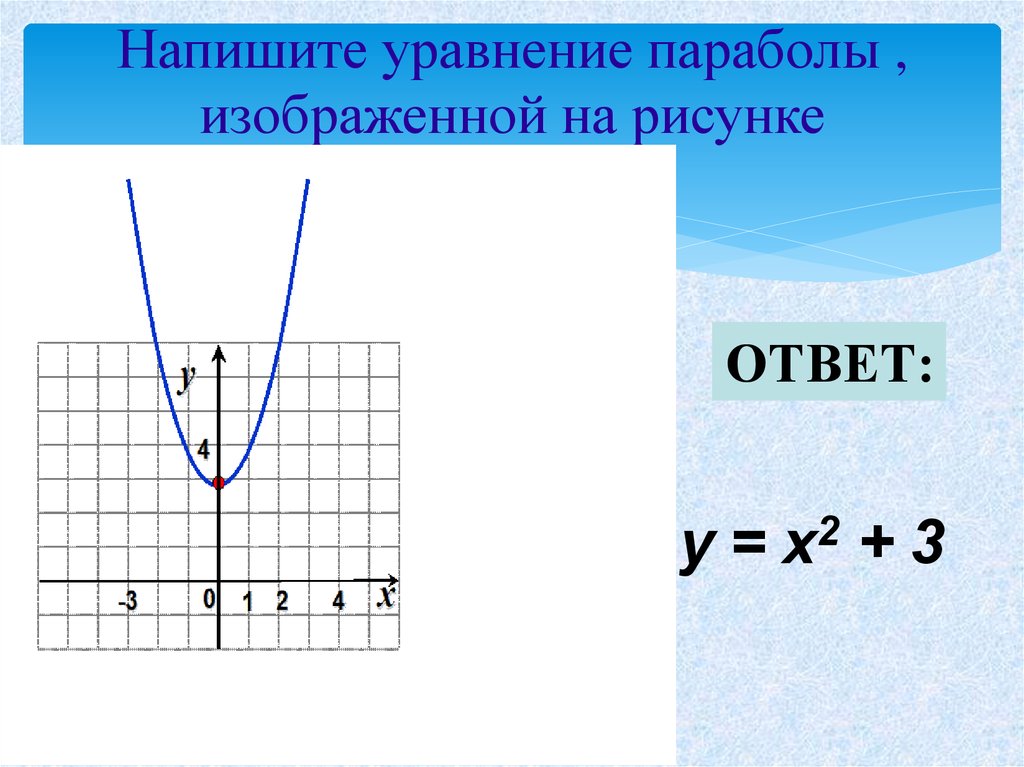 ответил 06.04.13
ответил 06.04.13
Репетитор
4.9 (51)
Репетиторство по математике – алгебра и исчисление (все уровни)
См. таких репетиторов
Смотрите таких репетиторов
Напомним, что парабола представляет собой график, представляющий квадратное уравнение, стандартная форма которого имеет следующий вид:
y = ax 2 + bx + c
(т. е. парабола открывается вверх, если a>0, и открывается вниз, если a<0), а ось симметрии задается линией x = -b/(2a).
Вершинная форма уравнения параболы (или квадратного уравнения) определяется следующей формулой:
y = a(x — h) 2 + k , где (h, k) — вершина, а ось симметрии задается линией x = h.
Учитывая, что вершина находится в (0, 3), тогда ….. h = 0 и k = 3 ….. таким образом,
y = a(x — 0) 2 + 3
y = a(x) 2 + 3
С точкой в (-4, -45), тогда .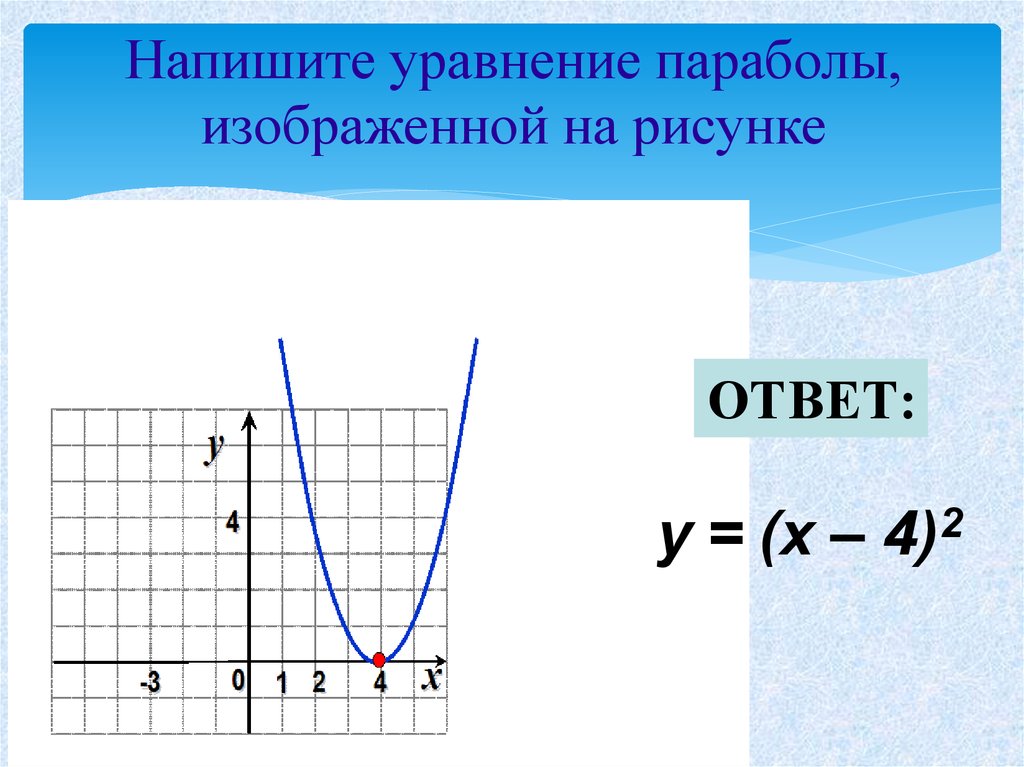 …. x = -4 и y = -45 ….. следовательно,
…. x = -4 и y = -45 ….. следовательно,
-45 = а(-4) 2 + 3
-45 = а(16) + 3
Найдите a, сначала вычитая 3 из обеих частей уравнения, а затем разделив обе части уравнения на 16:
-45 — 3 = a(16) + 3 — 3
-48 = a(16)
-48/16 = 16a/16
-3 = a
С вершиной (h, k) в точке (0, 3) и при условии, что a = -3, уравнение этой параболы в вершинной форме выглядит следующим образом :
y = a(x — h) 2 + k
y = -3(x — 0) 2 + 3
y = -3x 2 + 3
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.

 01.2011, 10:45
01.2011, 10:45  Вычислили коэффициенты:
Вычислили коэффициенты: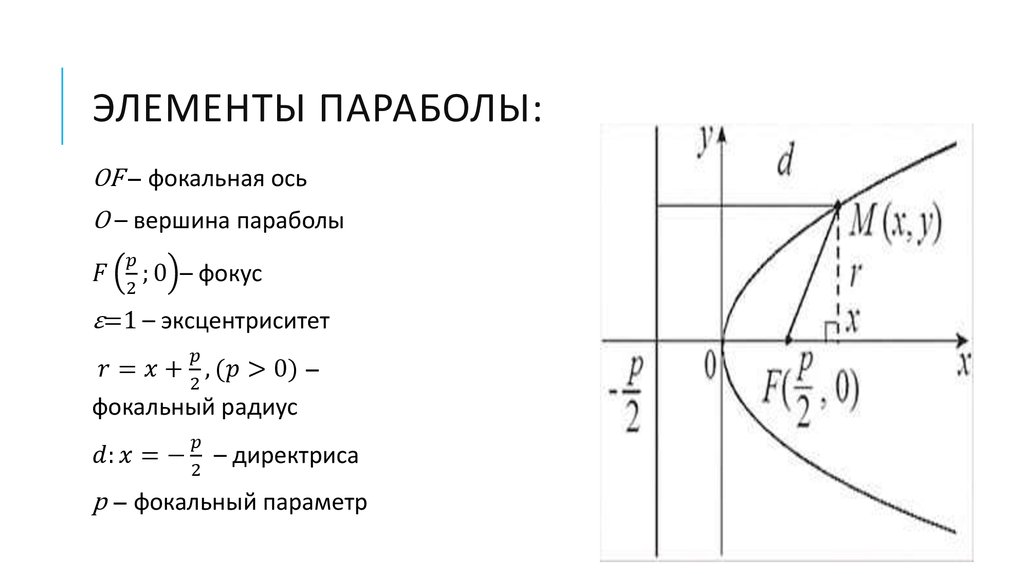
 01.2011, 11:46
01.2011, 11:46  01.2011, 13:27
01.2011, 13:27 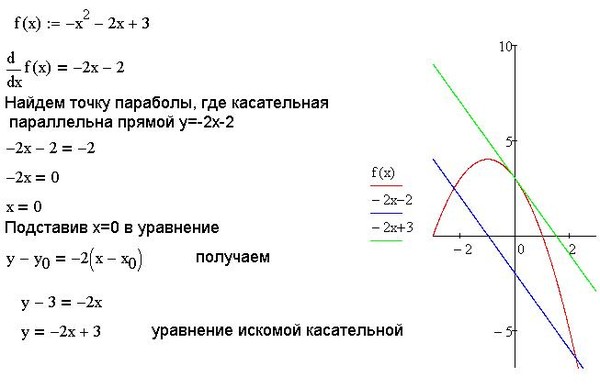 Точнее, в формуле, написанной paha
Точнее, в формуле, написанной paha Спасибо.
Спасибо.