Меридиана треугольника: Что такое медиана треугольника? Ответ на webmath.ru

{3} \)

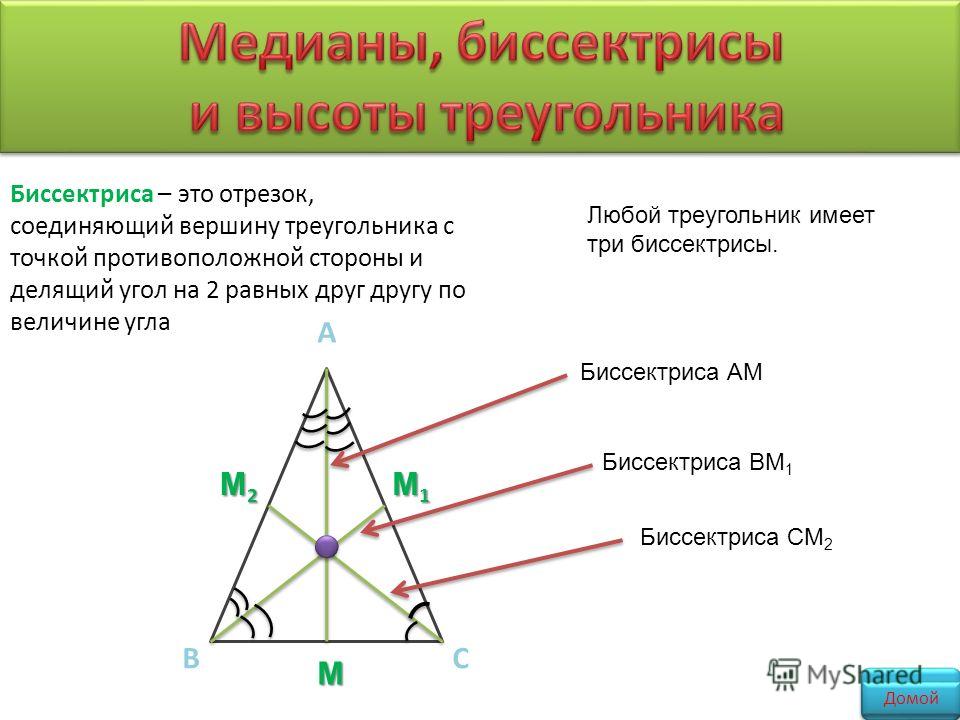
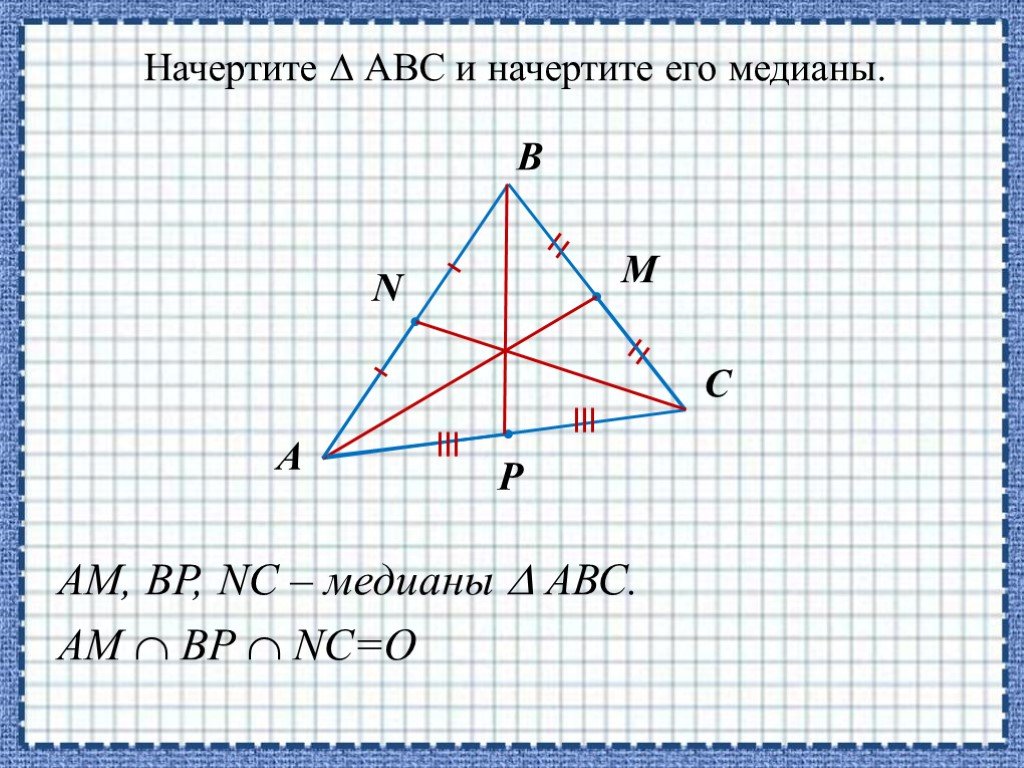
Медиана \(\ \mathrm{BL} \) делит треугольник \(\ \mathrm{ABC} \) на два треугольника равного размера, т. е. \(\ S_{A B L}=S_{B C L} \) см2, откуда следует, что

\(\ S_{A B C}=2 S_{A B L}=12 \)см2

Ответ

\(\ S_{A B C}=12 \) см.

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Высота треугольника Окружность, описанная около треугольника Окружность, вписанная в треугольник Равнобедренный треугольник

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

что это такое в геометрии, ее свойства, как построить и найти

Определение медианы в треугольнике

Определение 1

Медиана — важное понятие в геометрии. Это отрезок, проведенный из вершины треугольника, и делящий противоположную сторону пополам. Это «говорящее» название, оно произошло от латинского слова mediāna, что значит «середина».

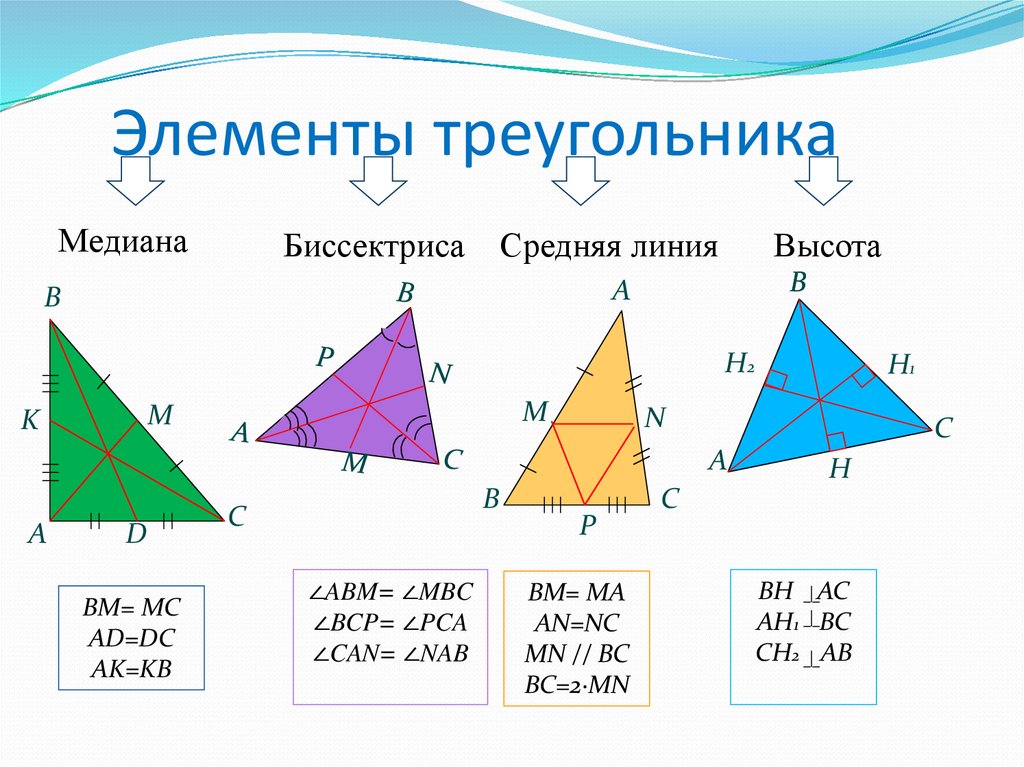
На чертеже медиана выглядит так:

Красная линия — медиана. Для ΔABС отрезок АD — медиана к стороне BС, при этом BD=DC. Для ΔMNK NO — медиана из ∠MNK к NK, MO=OK. Равенство отрезков на рисунке обозначают одинаковым количеством черточек. Сколько медиан у треугольника? Их столько же, сколько и сторон, то есть три.

 Характерные особенности медианы

Медиана обладает многими свойствами, ниже их краткое перечисление. Некоторые из них будут рассмотрены подробнее.

1. Медиана треугольника делит его на два равновеликих треугольника: S▵ACD=S▵BDC  , S▵MNO=S▵ONK
2. Все медианы треугольника пересекаются в одной точке и разбивают его на 6 треугольников одной площади.
3. Медиана, проведенная из прямого угла прямоугольного треугольника, равна половине гипотенузы: CD=½AB=AD=BD.
4. У правильного или равностороннего треугольника медиана является одновременно биссектрисой и высотой, проведенными из того же угла.
5. У равнобедренного треугольника совпадают медиана, биссектриса и высота, которые проводятся к основанию.
6. Для нахождения длины медианы треугольника используется следующая формула: BD=12a2+12c2-14b2, где BD — медиана, а a, b и c — стороны треугольника.

Формулы и соотношения связанные с медианой

Пересечение медиан треугольника

Теорема 1

Медианы треугольника пересекаются в одной точке, которая делит их в отношении 2:1 от вершины.

Доказательство:

Строим медианы AD и CM треугольника ABC, пересекающиеся в точке О.

Найдем середины L и H отрезков ОA и ОC, и рассмотрим четырехугольник DHLM.

Его стороны MD и HL параллельны и равны как средние линии ΔABC и ΔAOC с общей стороной AC.

Из этого делаем вывод, что DHLM — параллелограмм.

Поскольку точка пересечения делит диагонали параллелограмма пополам, то OD = ОL.

L — середина отрезка ОA ⇒ AL = LO = ОD. Значит, AО:ОD = 2:1. Также CО:ОM = 2:1.

Остается доказать, что третья медиана BK проходит через точку О.

Пусть медианы BK и AD пересекаются в точке O1. Тогда по доказанному AO1:O1D=2:1.

Учитывая, что и AO:OD=2:1, заключаем, что точки O1 и О делят отрезок AD в одном и том же отношении.

А это значит, что точка O1 совпадает с точкой О.

Из этого сделаем окончательный вывод: медиана BK проходит через точку О пересечения медиан AD и CM.

Теорема о трех медианах и шести равновеликих треугольниках

 Теорема 2

Три медианы треугольника пересекаются в одной точке и делят его на 6 треугольников с равной площадью.

Доказательство:

Докажем, что S▵AOM=S▵MOB=S▵BOD=S▵DOC=S▵COK=S▵KOA

1. Построим медианы ΔABС.
2. Из вершины B опустим перпендикуляр BP на медиану AD и рассмотрим ΔBDO. S▵BOD=½OD·BP,OD=13AD по свойству медиан треугольника ⇒ S▵BOD=12·13AD·BP.
3. Следующим шагом рассмотрим ΔABD. S▵ABD=½AD·BP.
4. Из пунктов 2 и 3 следует, что S▵BOD=13S▵ABD.
5. AD — медиана ΔABC, ⇒ S▵ABD=S▵ADC,а S▵ABC=S▵ABD+S▵ADC=2S▵ABD,а S▵ABD=½S▵ABC.
6. Из двух предыдущих пунктов следует, что S▵BOD=16S▵ABC.
7. Аналогично доказываем, что S▵COD=16S▵ABC, S▵COK=16S▵ABC, S▵KOA=16S▵ABC, S▵AOM=16S▵ABC, S▵MOB=16S▵ABC.

Пример нахождения и построения медианы

Для того чтобы узнать длину медианы, нужно знать:

• длины всех сторон треугольника;
• либо периметр и две стороны.

Задача

Дан ΔABC с известными сторонами АВ=9 см, СВ=8 см, АС=13 см. Необходимо вычислить длину медианы, построенной к наибольшей стороне.

Решение: чтобы найти длину медианы, используют дополнительные построения. Продлим медиану BO ΔABC и построим параллелограмм. Отрезок BO равен ½ диагонали получившегося параллелограмма. Согласно теореме о диагоналях параллелограмма, сумма квадратов его диагоналей равна удвоенной сумме квадратов его сторон.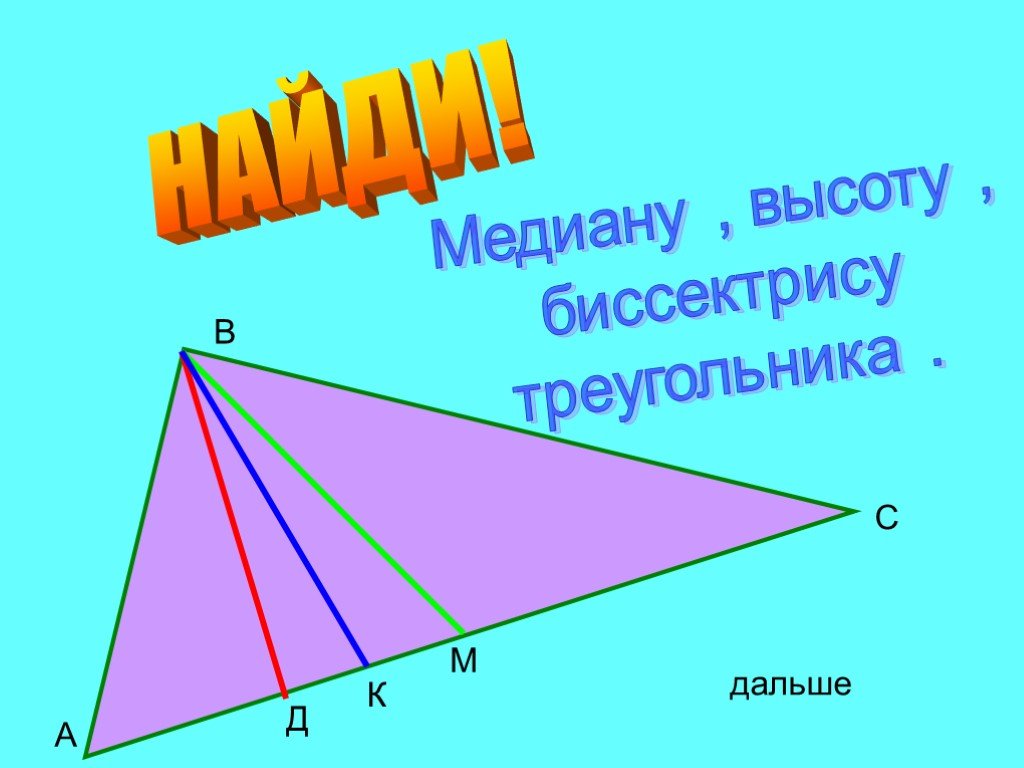

2(a2+b2)=d12+d22;

2(82+92)+132+x2;

290=169+x2;

x2=121;

x=11.

Медиана равна половине найденной диагонали, 11:2=5,5 (см).

Ответ: 5,5 см.

Меридиан в Маунт -Вернон Треугольник — Квартиры для аренды

Новые 20 часов назад

Сделка

3D Прохождение

View

См. 47 Фотографии

Направления

— мин.

Планы

— мин.

Планы

— мин.

.

• Все (25)
• Студия (3)
• 1 спальня (14)
• 2 спальни (8)

Дома Меридиана в Маунт-Вернон Треугольник
задают новый взгляд на дизайн квартир. Экспансивный
окна и частные балконы растворяют границу
между внутренним и внешним. Четкие архитектурные линии
пересекаются с современными отделками
, такими как нержавеющая сталь, гранит и твердая древесина,
, а открытые планы этажей позволяют рассредоточиться во всех
направлениях. В Meridian at Mount Vernon Triangle,
, гибкость аренды приходит по адресу, который занимает рынок стиля. ТЕПЕРЬ В ЛИЗИНГ!

Узнайте больше об этом объекте

Часы работы

Понедельник

10:00 утра — 18:00

Во вторник

10:00 — 18:00

Среда

10:00 — 18:00

Четверг

10:00 AM — 18:00

Пятница

10:00 — 18:00

Суббота

10:00 утра — 17:00

Добро пожало

• Кондиционер
• Балкон
• Кабель готов
• Ceiling Fan(s)
• Deck
• Dishwasher
• Elevator
• Garbage Disposal
• Hardwood Flooring
• Island Kitchens
• Microwave
• New/Renovated Interior
• Oversized Closets
• Patio
• Refrigerator
• Smoke Бесплатно
• Бытовая техника из нержавеющей стали
• Сводчатые потолки
• Вид
• Соединения для стиральной и сушильной машин
• Стиральная и сушильная машины в блоке

Этот дом находится на территории государственных школ округа Колумбия.

Показаны близлежащие школы. Пожалуйста, посетите веб-сайт школьного округа, чтобы увидеть все школы, обслуживающие этот дом.

Сводный рейтинг GreatSchools

Данные о школах предоставлены некоммерческой организацией GreatSchools. Redfin рекомендует покупателям и арендаторам использовать информацию и рейтинги GreatSchools в качестве первого шага, а также провести собственное расследование, чтобы определить желаемые школы или школьные округа, в том числе связавшись с самими школами и посетив их. Redfin не подтверждает и не гарантирует эту информацию. Границы школьных услуг предназначены только для справки; они могут измениться, и их точность не гарантируется. Чтобы проверить право на зачисление в школу, свяжитесь напрямую со школьным округом.

96 /100

Paradise Walker’s

Оценка Walk®

96 /100

Райдер Райдер

Транзит. Меридиан в треугольнике Маунт -Вернон возле Вашингтона

• 1 /43

  3D Прохождение

• 1 /48

  Новый 1 день назад

  3D Прохождение

• 002 1 /32

  3D & Video Tour

• 1 /19

• 1 /10

• 1 /14

См.

Что -то неправильно?

Мы очень серьезно относимся к мошенничеству. Если что-то выглядит подозрительно, сообщите нам.

Меридиан в Маунт-Вернон Треугольник состоит из 52 единиц. Meridian at Mount Vernon Triangle в настоящее время сдает в аренду от 1880 до 3625 долларов в месяц и предлагает условия аренды на 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 месяцев. Меридиан в треугольнике Маунт-Вернон расположен в Вашингтоне, почтовый индекс 20001 и государственные школы округа Колумбия. Полный адрес этого здания: 425 L St NW Washington, DC 20001.

ГдеiPark Home — Найдите и забронируйте парковку на месяц

Ищете более 10 мест для ваших сотрудников, команды или команды?

Свяжитесь с одним из наших преданных сотрудников сегодня.

Узнать больше

Популярные города

Торонто

Сан-Франциско

Сиэтл

Вашингтон

Чикаго

Лос-Анджелес

Нью-Йорк

Бостон

Посмотреть больше

Найдите и забронируйте безопасную парковку на месяц для себя или своей команды

Как это работает

Что наши парковщики говорят о нас

«WhereiPark был для нас отличным партнером в поиске и аренде парковочных мест для наших сотрудников в районе Догпэтч в Сан-Франциско.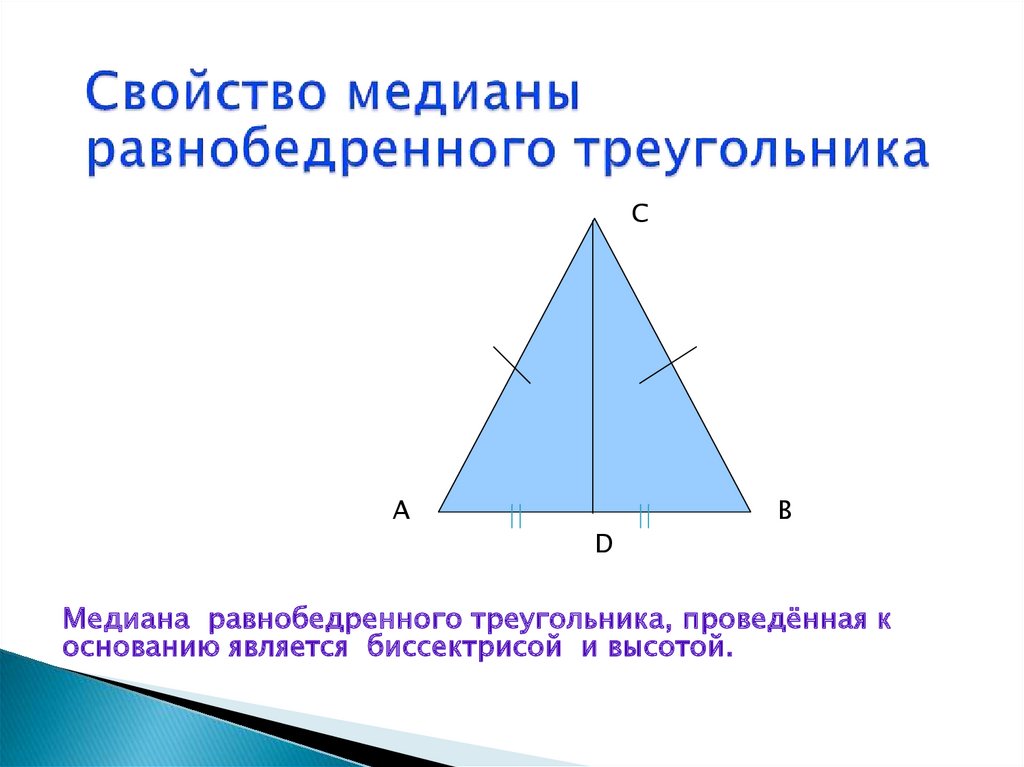 Мы рассмотрели другие варианты, в том числе платные участки поблизости; все эти варианты имели существенные недостатки и несли риски для имущества наших сотрудников и даже для личной безопасности. WhereiPark разместил нас на частных подземных участках в местных зданиях, и ни разу за почти два года ни у кого не было проблем. Большое спасибо команде WhereiPark!»

Даниэль Де Руле, соучредитель Mitokinin

Сан-Франциско

«Я использовал WhereiPark в двух городах, Сиэтле и Лос-Анджелесе. В обоих случаях я бы потерялся без них. на дополнительную парковку для моего офиса. Когда я переехал в Лос-Анджелес, и новый офис нуждался в дополнительной парковке, моей первой мыслью было найти их. Они были настоящим спасением для дополнительной парковки».

Даррен Браунелл

Лос-Анджелес и Сиэтл

«Я живу в Марина-дель-Рей, штат Калифорния, где трудно и дорого найти безопасную крытую парковку. Где iPark смог предоставить мне удивительно удобные, безопасные, чистые, крытые парковочные места с круглосуточным доступом 7 дней в неделю — неслыханно в пляж, в котором я живу. Соотношение цены и качества не имеет себе равных, и всегда приятно иметь дело с их офисом! У меня есть 7 классических автомобилей, и я очень хорошо отдыхаю ночью, зная, что они чистые и безопасные — все благодаря WhereiPark — я очень рекомендую их использовать»

Джо Ловинг, коллекционер классических автомобилей. объясняя нам процедуры, терпя некоторые проблемы с размером и пространством, которые у нас были, и сразу же предлагал решения. Я надеюсь снова работать с WhereiPark, как только мы вернемся к скорости. У WhereiPark есть яркий пример образцового обслуживания клиентов. WhereiPark также показал сострадание и отличное обслуживание клиентов, когда они приостановили наш контракт из-за проблем с вирусом».

Джинни Гатри из благотворительного фонда Millionair Club

Сиэтл

Что наши партнеры говорят о нас

«Я работаю с WIP более 4 лет и не добился ничего, кроме успеха в компании, их способности беспрепятственно работать с командой на месте, минимизировать операционное воздействие и помогать в областях возможность, связанная с доходом от парковки. Это одна из самых гибких и простых в навигации программ, с которыми я когда-либо работал, это не проблема, если у вас есть пустые парковочные места, с которых вы могли бы получать доход, и вы’ в настоящее время этого не делаем — это беспроигрышный вариант!»

Арин Томас, старший региональный менеджер по недвижимости, Greystar Owned Assets

«Где iPark значительно изменил правила игры, увеличив другие доходы на нескольких объектах в моем портфолио. Прелесть партнерства с ними заключается в том, насколько легко получить настроены, и это очень мало работы для выездных команд. Процесс гладкий, и на сегодняшний день у нас не возникло никаких проблем с людьми, арендующими помещения. Я рекомендую использовать WhereiPark в любом объекте с избыточной парковкой, даже если она всего несколько мест».

Сара Вака, региональный менеджер по недвижимости

«Сначала я немного опасалась нашего партнерства с WhereiPark, так как опасалась, что у нас будет меньше парковочных мест для наших жильцов и будущих жильцов. адресовано с решениями или альтернативными вариантами, чтобы обеспечить удовлетворение потребностей наших жителей.Помимо невероятного профессионализма, который я испытал с WhereiPark, я обнаружил, что все, с кем я разговаривал, были очень полезны и готовы ответить на все мои вопросы.Наше решение участвовать в партнерство с WhereiPark оказалось одним из наших самых разумных, так как я обнаружил, что общий процесс работы с WhereiPark был очень простым».

Бриттани Уэллс — помощник менеджера сообщества — Белль Фонтейн/Марина 41

Лос-Анджелес

«Партнерство Met с платформой и командой WhereiPark было восхитительным деловым предприятием. Команда WhereiPark продемонстрировала свою профессиональную работу и доказала свою группа, которая предоставила своим клиентам быструю и эффективную помощь с их платформой и любыми проблемами с парковкой на месте, которые у них возникали. Наличие дополнительной парковки в центре Лос-Анджелеса дало The Met возможность получать дополнительный ежемесячный доход от неиспользуемых парковочных мест».

Оскар Падилья — старший директор службы безопасности — 950 S Flower (The Met)

Лос-Анджелес

Где вам нужна парковка?

О нас

WhereiPark упрощает ежемесячную парковку. Мы связываем компании и группы, нуждающиеся в парковке, и связываем их с владельцами недвижимости, у которых есть избыточные парковочные места.

Мы помогаем компаниям, пассажирам и командам находить и обеспечивать ежемесячные парковочные места, которые просто недоступны больше нигде. WhereiPark упрощает поиск ежемесячной парковки, сравнение цен и бронирование безопасного и доступного ежемесячного парковочного места в удобном месте.

Для владельцев недвижимости WhereiPark предлагает простое решение, позволяющее разблокировать свободные парковочные места и превратить их в новый источник дохода. Где iPark управляет всей администрацией от имени владельца, включая обработку платежей, управление залоговыми депозитами и решение всех вопросов обслуживания клиентов.