Простые и составные числа / Обыкновенные дроби / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Простые и составные числа
Любое натуральное число, за исключением 1, имеет как минимум два делителя (единица имеет единственный делитель — единицу) — это единица и само это число. Пусть — данное натуральное число, действительно, для него мы можем записать, что : 1 = и : = 1.
Некоторые числа имеют только два делителя — единицу и само это число, примером такого число является 11, это число делится только на 1 и на 11. Также только два делителя имеют, например, числа 2, 3, 5, 7, 13, 17. Все такие числа называют простыми числами.
Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число. |
Наименьшим простым числом является 2, при этом оно единственное чётное простое число, так как все остальные чётные числа делятся не только на себя и единицу, но и на 2, то есть имеют минимум 3 делителя.
Число простых чисел бесконечно, и хотя не известен алгоритм их нахождения.
| Натуральное число называют составным, если оно имеет больше двух натуральных делителей. |
Наименьшим составным числом является 4, оно имеет три делителя: 1, 2, 4.
Число составных чисел бесконечно. При этом любое составное число можно разложить на два множителя, каждый из которых больше 1. Например, рассмотрим число 186:
186 : 6 = 31, значит, 186 = 631.
Говорят, что число 186 на разложено на множители 6 и 31.
Обратите внимание, что 1 не относят ни к составным числам, ни к простым, так как оно имеет только один делитель.
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 8, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 164, Мерзляк, Полонский, Якир, Учебник
Номер 171, Мерзляк, Полонский, Якир, Учебник
Номер 779, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Задание 155, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 201, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 229, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 7, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 8, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 131, Мерзляк, Полонский, Якир, Учебник
Номер 349, Мерзляк, Полонский, Якир, Учебник
Номер 555, Мерзляк, Полонский, Якир, Учебник
Номер 674, Мерзляк, Полонский, Якир, Учебник
Номер 741, Мерзляк, Полонский, Якир, Учебник
Номер 788, Мерзляк, Полонский, Якир, Учебник
Номер 848, Мерзляк, Полонский, Якир, Учебник
Номер 998, Мерзляк, Полонский, Якир, Учебник
Номер 1138, Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 376, Мерзляк, Полонский, Якир, Учебник
дроби
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы.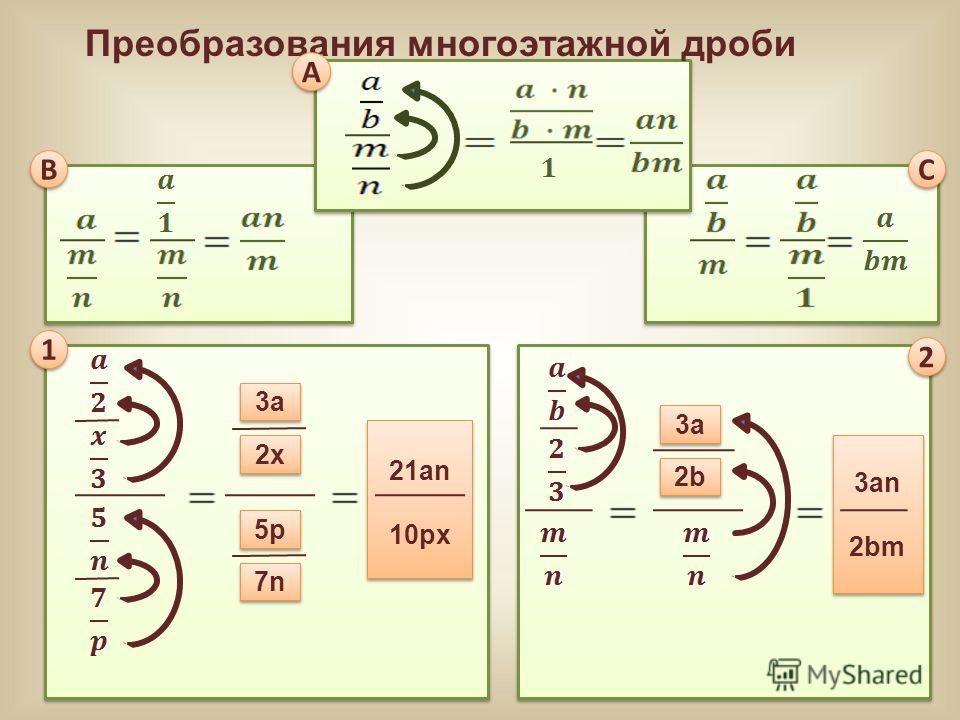 Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата:обыкновенные вида и десятичные.
Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата:обыкновенные вида и десятичные.
Обыкновенные дроби
Обыкновенная (или простая) дробь — запись рационального числа в виде или где Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимоеназывается числителем дроби, а делитель — знаменателем.
Обозначения обыкновенных дробей
Есть несколько видов записи обыкновенных дробей в печатном виде:
- ½
- 1/2 или (наклонная черта называется «солидус»)
- выключная формула: (горизонтальная черта называется Винкулум (англ.))
- строчная формула:
Правильные и неправильные дроби
Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.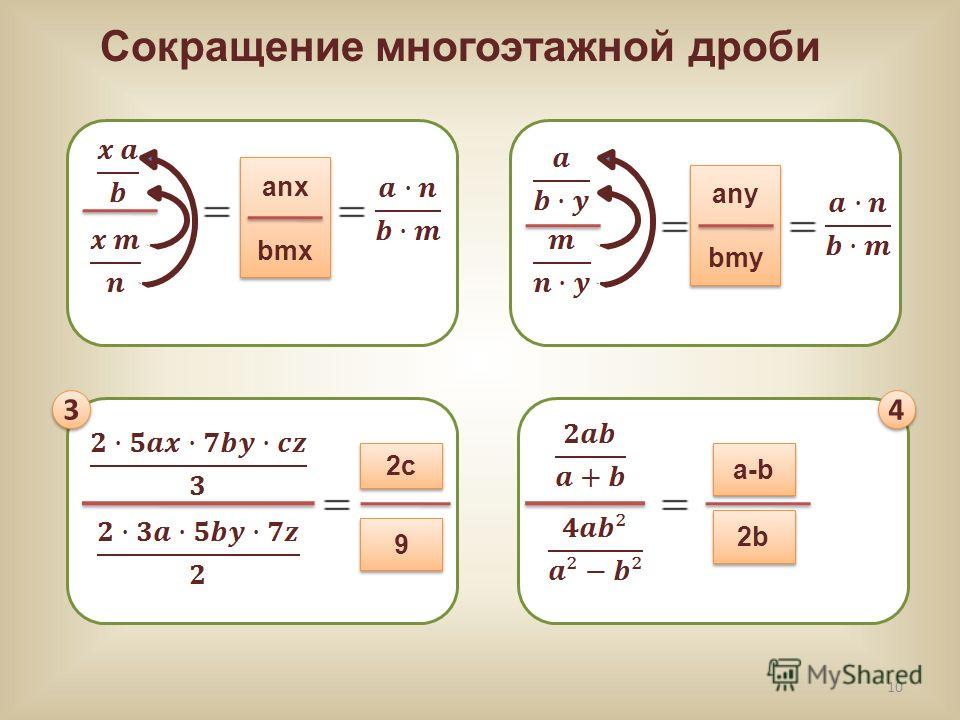
Например, дроби , и — правильные дроби, в то время как , , и — неправильные дроби. Всякое отличное от нуля целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.
Смешанные дроби
Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.
Например, . В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь, а также из-за более громоздкой записи и менее удобных вычислений.
Высота дроби
Высота обыкновенной дроби — модуль суммы числителя и знаменателя этой дроби. Высота рационального числа — модуль суммы числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу.
Например, высота дроби равна . Высота же соответствующего рационального числа равна , так как дробь сокращается на .
Составные дроби
Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт:
- или или
Десятичные дроби
Основная статья: Десятичная дробь
Десятичной дробью называют позиционную запись дроби. Она выглядит следующим образом:
Пример: .
Часть записи, которая стоит до позиционной запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Всякую обыкновенную дробь можно преобразовать в десятичную, которая в этом случае либо имеет конечное число знаков после запятой, либо является периодической дробью.
Вообще говоря, для позиционной записи числа́ можно использовать не только десятичную систему счисления, но и другие (в том числе и специфические, такие, как фибоначчиева).
Значение дроби и основное свойство дроби
Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные.
Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные.
Если умножить числитель и знаменатель дроби на одинаковую величину:
то значение дроби останется прежним, хотя дроби — разные. Например:
И обратно, если числитель и знаменатель заданной дроби имеют общий делитель, то обе части можно разделить на него; такая операция называется сокращением дроби. Пример:
- — здесь числитель и знаменатель дроби сократили на общий делитель 4.
Несократимой называется дробь, числитель и знаменатель которой взаимно просты, т. е. не имеют общих делителей, кроме
Для десятичной дроби запись почти всегда однозначна, однако имеются исключения. Пример:
- — две разные дроби соответствуют одному числу.
Действия с дробями
В этом разделе рассматриваются действия над обыкновенными дробями. О действиях над десятичными дробями см. Десятичная дробь.
Приведение к общему знаменателю
Для сравнения, сложения и вычитания дробей их следует преобразовать (привести) к виду с одним и тем же знаменателем. Пусть даны две дроби: и . Порядок действий:
Пусть даны две дроби: и . Порядок действий:
- Находим наименьшее общее кратное знаменателей: .
- Умножаем числитель и знаменатель первой дроби на .
- Умножаем числитель и знаменатель второй дроби на .
После этого знаменатели обеих дробей совпадают (равны M). Вместо наименьшего общего кратного можно в простых случаях взять в качестве M любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.
Сравнение
Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.
Пример. Сравниваем и . НОК(4, 5) = 20. Приводим дроби к знаменателю 20.
Следовательно,
Сложение и вычитание
Чтобы сложить две обыкновенные дроби, следует привести их к общему знаменателю. Затем сложить числители, а знаменатель оставить без изменений:
- + = + =
НОК знаменателей (здесь 2 и 3) равно 6.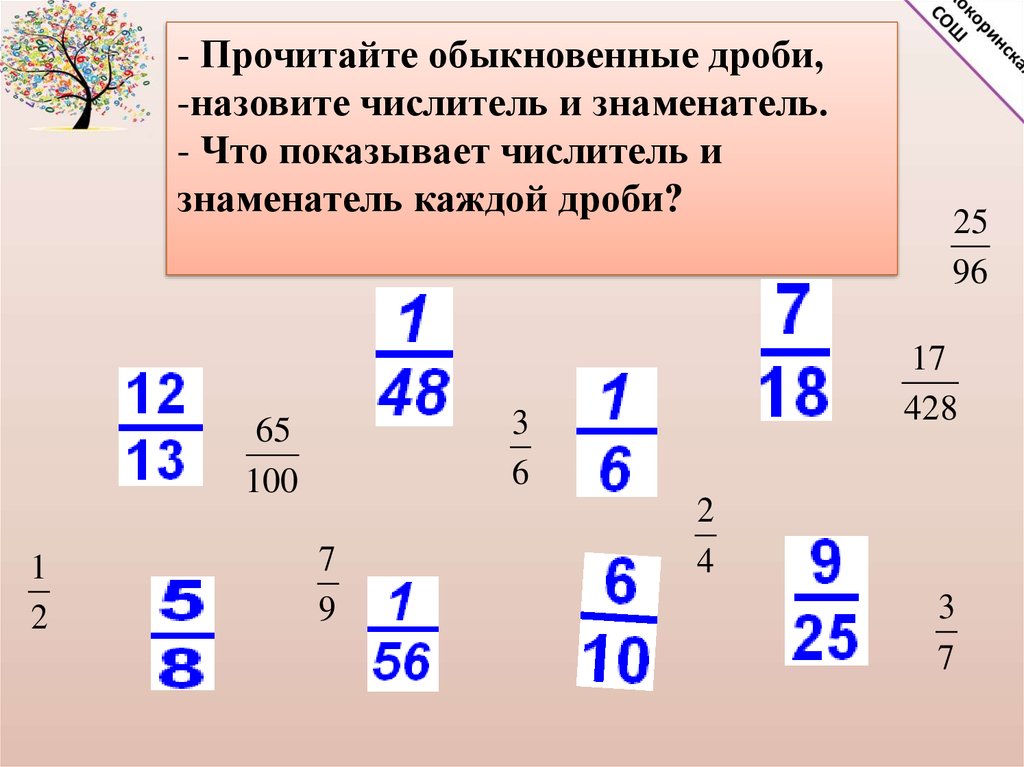 Приводим дробь к знаменателю 6, для этого числитель и знаменатель надо умножить на 3.
Приводим дробь к знаменателю 6, для этого числитель и знаменатель надо умножить на 3.
Получилось . Приводим дробь к тому же знаменателю, для этого числитель и знаменатель надо умножить на 2. Получилось .
Чтобы получить разность дробей, их также надо привести к общему знаменателю, а затем вычесть числители, знаменатель при этом оставить без изменений:
- — = — =
НОК знаменателей (здесь 2 и 4) равно 4. Приводим дробь к знаменателю 4, для этого надо числитель и знаменатель умножить на 2. Получаем .
Умножение и деление
Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:
В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:
В общем случае, числитель и знаменатель результирующей дроби могут не быть взаимно простыми, и может потребоваться сокращение дроби, например:
Чтобы поделить одну обыкновенную дробь на другую, нужно умножить первую на дробь, обратную второй:
Например,
Преобразование между разными форматами записи
Чтобы преобразовать обыкновенную дробь в дробь десятичную, следует разделить числитель на знаменатель.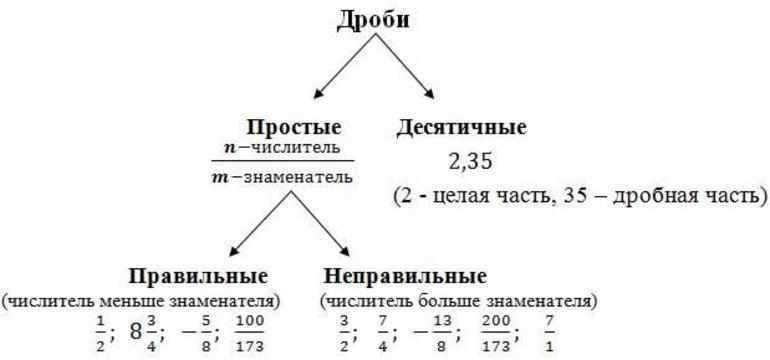 Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:
Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:
- — бесконечно повторяющийся период принято записывать в круглых скобках.
Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на соответствующую степень 10. Затем к результату приписывается целая часть со знаком, формируя смешанную дробь. Пример:
Составные дроби
Составная дробь — это дробь, в которой числитель, знаменатель или оба являются дробными выражениями.
Примеры:
(1/a) / (b/2), (x + 1/y) / (y + 1/x)
Упрощение составной дроби: метод I
Шаг 1 :
Упростите числитель и знаменатель сложной дроби, чтобы что каждый из них представляет собой одну дробь.
Шаг 2 :
Чтобы разделить дробь в числителе на дробь в знаменателе, инвертируйте делитель и умножьте.
Шаг 3 :
Если возможно, упростите.
Пример 1:
(2x /27y 2 ) / (6x 2 /
Решение:
= (2x /27Y 2 ) / (2x /27Y 2 ) / (2x /27Y 2 ) 6x 2 /9)
Числитель сложной дроби — это уже одна дробь, как и знаменатель.
Переверните дробь в знаменателе и умножьте.
= (2x/27 лет 2 ) ⋅ (9/6x 2 )
= (2x ⋅ 9) / (6x 2 ⋅ 27y 2 )
Отменить общие делители.
= 1/ (3x ⋅ 3y 2 )
= 1/ 9xy 2
Пример 2:
(x/ y + 1) / (1- Y/ y/ y/ y/ y/ y/ y/ y/ y////// c x)
Решение:
= (x/y + 1) / (1 — y/x)
Объединим члены в числителе в одну дробь и проделаем то же самое в знаменателе. Затем инвертируем и умножаем.
= [(x + y)/y] / [(x — y)/x]

= [(x + y)/y)] ⋅ [x/(x – y)]
= [x(x + y)] / [y(x – y)]
Упрощение сложной дроби : Метод II
Шаг 1 :
Найдите наименьший общий знаменатель дробей как в числителе, так и в знаменателе сложной дроби.
Шаг 2 :
Умножьте числитель и знаменатель составной дроби на ЖК-дисплей, найденный на шаге 1.
Шаг 3 :
Если возможно, упростите.
Пример 3:
[5x/(x + 2)] / [10/(x — 2)]
Решение: +
/ [10/(x — 2)]Наименьший общий знаменатель дробей как в числителе, так и в знаменателе равен (x + 2)(x — 2).
Умножить числитель и знаменатель на ЖК.
= [5x/(x + 2)](x + 2)(x — 2) / [10/(x — 2)](x + 2)(x — 2)
Упрощение.
= [5x(x — 2)]/[10(x + 2)]
= x(x — 2)/2(x + 2)
2 + 1/y] / [y/x 2 + 1/x]
Решение:
= [x/y 2 7/0 9y [00/0 1/x] + 9 + 1/1 x 2 + 1/x]
Наименьший общий знаменатель дробей как в числителе, так и в знаменателе равен x 2 y 2 .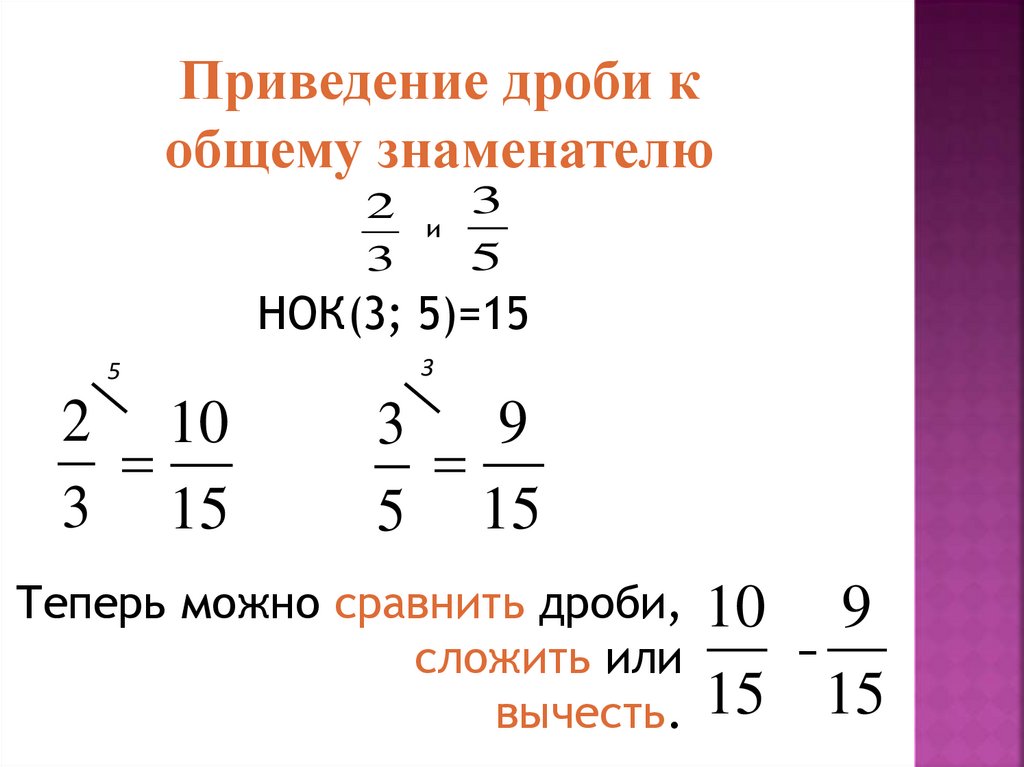
Умножение числителя и знаменателя на ЖК-дисплее.
= [x/y 2 + 1/y](x 2 y 2 ) / [y/x 2 + 1/x](x 90 3 2 2 )
Использовать свойство дистрибутива.
= [x/y 2 ⋅ x 2 Y 2 + 1/Y ⋅ x 2 Y 2 ] / [Y/x 2 ⋅ x 2 Y 131 2 ⋅ x 2 Y 3131. 2 + 1/x ⋅ x 2 y 2 ]
Упростить.
= [x 3 + x 2 y]/[y
Коэффициент.
= [x 2 (x + y)]/[y 2 (y + x)]
= x 2 /y 2
Кроме материалов, указанных выше, любой другой материал по математике, пожалуйста, используйте наш пользовательский поиск Google здесь.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Как найти решение сложной дроби
Все математические ресурсы верхнего уровня SSAT
6 Диагностические тесты 311 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике верхнего уровня SSAT » Понятия и операции с числами » Рациональное число » Фракции » Сложные дроби » Как найти решение сложной дроби
Упростить:
Возможные ответы:
Правильный ответ:
Пояснение:
Упростите до сложной дроби для числителя и знаменателя.
В числителе нам нужно умножить тогда вверху должно читаться .
Для основания нам нужно умножить , чтобы добавить компоненты. Таким образом, внизу должно быть указано .
Деление дробей аналогично умножению числителя на обратную величину знаменателя.
Следовательно, умножьте верхнюю и нижнюю часть на и тогда вы должны увидеть, что если вы умножите на нижнюю часть, отменится вместе с .
Тогда ответ должен быть .
Сообщить об ошибке
Преобразовать в дробь.
Возможные ответы:
Правильный ответ:
Объяснение:
Целое число умножается на знаменатель. Затем добавляем числитель . Это значение делится на знаменатель. Окончательный ответ .
Сообщить об ошибке
Преобразовать в неправильную дробь.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы преобразовать в неправильную дробь, возьмите целое число и умножьте его на знаменатель .
Затем мы добавляем это к числителю, который равен .
Затем мы берем эту сумму и помещаем ее в знаменатель, что дает нам ответ:
.
Сообщить об ошибке
Упростить.
Возможные ответы:
Правильный ответ:
Объяснение:
Давайте сосредоточимся на левой дроби. Давайте попробуем умножить три дроби. Чтобы добиться этого, мы можем умножить числитель левой дроби на обратную величину знаменателя.
Таким образом, умножьте числитель и знаменатель на .
Теперь у нас есть . Мы можем упростить это, вычеркнув на и на а .
Затем зачеркните в и в . Это должно выглядеть так:
.
Умножьте это, и вы получите ответ.
Сообщить об ошибке
Решить и упростить.
Возможные ответы:
Правильный ответ:
Объяснение:
Преобразуйте числитель и знаменатель в дроби. Сначала преобразуйте целые числа в дроби.
Сначала преобразуйте целые числа в дроби.
Теперь, когда наши дроби имеют общий знаменатель и числитель, мы можем их вычесть.
Затем умножьте верх и низ на , поскольку это величина, обратная знаменателю, и при делении дробей это то же самое, что умножить числитель на величину, обратную знаменателю.
Затем уменьшите, зачеркнув на а , а на а .
Затем умножьте, чтобы получить ответ.
Сообщить об ошибке
Решите и упростите.
Возможные ответы:
Правильный ответ:
Объяснение:
Помните PEMDAS, порядок операций для работы с выражениями, который является аббревиатурой (круглые скобки, экспоненты, умножение, деление, сложение, вычитание).
Умножение имеет приоритет перед сложением. Глядя на дроби, которые перемножаются вместе, мы видим, что сводится к , а к .
