48. Теорема о числе решений совместной системы линейных уравнений.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений
Правило
решения произвольной системы уравнений.
Найти ранг основной и расширенной
матриц,если они не равны,то система
несовместна(нет решений). Найти какой-либо
базисный минор порядка r.
Взять r
уравнений из коэффициентов которых
составлен базисный минор(остальные
отбросить). Коэффициенты которые входят
в базисный минор-главные,записываются
слева, остальные переносятся в правые
части уравнений(свободные). Далее найти
выражения главных неизвестных через
свободные. Получается общее решение
системы. Затем придавая свободным
неизвестным произвольные значения
получим соответствующие значения
главных неизвестных(частные решения
исходной системы).
Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность.
Исследовать систему линейных алгебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой A, а расширенную матрицу системы – буквой A˜.
Теорема Кронекера-Капелли
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. rangA=rangA˜.
Напомню,
что система называется совместной,
если она имеет хоть одно решение. Теорема
Кронекера-Капелли говорит вот о чём:
если rangA=rangA˜, то решение есть;
если rangA≠rangA˜, то данная СЛАУ не имеет
решений (несовместна).
Следствие из теоремы Кронекера-Капелли
Если rangA≠rangA˜, то СЛАУ несовместна (не имеет решений).
Если rangA=rangA˜<n, то СЛАУ является неопределённой (имеет бесконечное количество решений).
Если rangA=rangA˜=n, то СЛАУ является определённой (имеет ровно одно решение).
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения нет, а если существуют – то сколько.
Пусть имеется квадратная матрица n-го порядка
Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная
матрица может
существовать только
для квадратных матриц т.
е.
для тех матриц, у которых число строк
и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…Аn
) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы r. Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.Алгоритм нахождения обратной матрицы
1)Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
2)Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
3)Если
необходимо, то переставить строки
(уравнения) последней таблицы так, чтобы
под матрицей А исходной таблицы
получилась единичная матрица Е.
4)Записать
обратную матрицу А
50. Лекция 13. Системы линейных уравнений
Основные понятия:
Система линейных уравнений; решение системы линейных уравнений; совместная система линейных уравнений; определенная система линейных уравнений; эквивалентные системы линейных уравнений; матрица системы; расширенная матрица системы линейных уравнений; теорема Кронекера-Капелли; правило Крамера; метод Гаусса; однородная система линейных уравнений; разрешенная переменная; набор разрешенных переменных; свободные переменные.
Для исследования процессов функционирования экономики, при построении математических моделей конкретных задач, возникающих перед менеджером в процессе его деятельности, в ряде случаев используются системы линейных уравнений. Так, например, при межотраслевом анализе – изменение объема выпуска отрасли при фиксированном коэффициенте прямых затрат в случае изменения спроса необходимо искать путем решения системы линейных уравнений, которая является моделью изучаемого процесса.
Нахождение решений системы линейных уравнений может быть осуществлено различными методами. Выбор метода зависит от рассматриваемой задачи и соответствующей математической модели.
В ряде случаев необходимо лишь знать – существует ли решение рассматриваемой системы.
Цель данного раздела – исследовать совместность системы линейных уравнений и дать некоторые методы их решения. Эти методы позволяют найти точное решение системы. Кроме этого, существуют методы, позволяющие находить приближенные решения, например, метод Якоби, метод Гаусса-Зейделя, метод пошагового агрегирования. В этом разделе они не рассматриваются.
Рассмотрим совокупность уравнений:
, | (13.1) |
Где ‑ действительные числа, а ‑ неизвестные. Эту совокупность называют системой линейных уравнений с неизвестными, числа ‑ коэффициенты системы (1), ‑ свободные члены. Упорядоченный набор действительных чисел называется решением системы (13.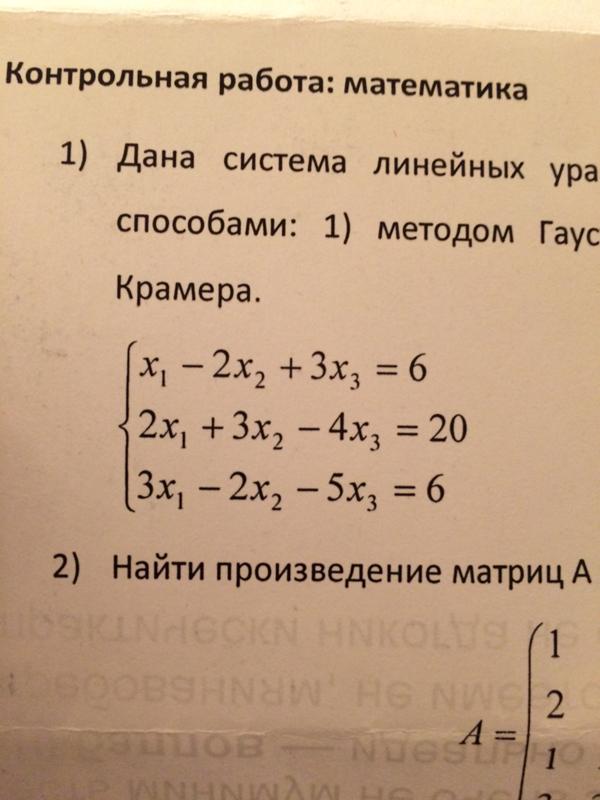
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения.
Система называется определенной, если она имеет единственное решение, и неопределенной, если у нее есть, по крайней мере, два различных решения.
Две системы с неизвестными называются эквивалентными, если множества их решений совпадают.
Матрица , составленная из коэффициентов системы (13.1), называется матрицей системы.
Обозначив через , систему (13.1) можно записать в виде матричного уравнения:
(13.2) |
Матрица , полученная приписыванием к матрице справа столбца свободных членов системы (13.1), называется Расширенной матрицей системы (13.1).
При исследовании системы (13.1) ищут ответ на следующие три вопроса:
1.
когда система совместна;
2. если система совместна, то определена ли она;
3. как отыскать ее решения.
Ответ на первый вопрос дает теорема Кронекера-Капелли – критерий совместности системы линейных уравнений.
Теорема. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.
| < Предыдущая | Следующая > |
|---|
матриц — при каком условии уравнения несовместны в системе линейных уравнений?
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация занимает всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Любой может задать вопрос
Любой может ответить
Лучшие ответы голосуются и поднимаются на вершину
Задавать вопрос
спросил
Изменено 6 лет, 6 месяцев назад
Просмотрено 3к раз
$\begingroup$
даны три уравнения
1,5х — 0,5у = 2; 4x + 2y + 3z= 9; 7x+y+5z=10;
Я решаю эти уравнения, используя матрицы как AX=B, где A=
$$
\begin{bматрица}
15&-5&0\
4 и 2 и 3 \\
7 и 1 и 5 \\
\end{bmatrix}
$$
В= $$
\begin{bmatrix}
20\\
9\\
10\
\end{bmatrix}
$$
Х= $$
\begin{bматрица}
Икс \\
у \\
з\
\end{bmatrix}
$$
Обратное к A существует, поскольку определитель равен 100, поэтому это означает, что решение существует.
{-1} = \begin{bmatrix}
\frac{7}{100} & \frac{1}{4} & \frac{-3}{20} \\
\frac{1}{100} & \frac{3}{4} & \frac{-9{-1}Б
$$
А теперь вычислив умножение матриц, вы получите:
$$
Х = \begin{bmatrix}
\frac{7}{100} & \frac{1}{4} & \frac{-3}{20} \\
\frac{1}{100} & \frac{3}{4} & \frac{-9}{20} \\
\frac{-1}{10} & \frac{-1}{2} & \frac{1}{2} \\
\end{bmatrix}
\begin{bmatrix}
20\\
9\\
10\
\end{bmatrix} =
\begin{bmatrix}
\ гидроразрыв {43} {20} \\
\ гидроразрыв {49} {20} \\
\фракция{-3}{2} \\
\end{bmatrix}
$$
Так что это совместимо и имеет решение!
$\endgroup$
функциональный анализ — Хан-Банах Из систем линейных уравнений
В этой статье 1 по истории функционального анализа автор упоминает следующий пример бесконечной системы линейных уравнений с бесконечным числом переменных $c_i = A_ {ij} x_j$:
\begin{align*} \begin{массив}{ccccccccc} 1 & = & x_1 & + & x_2 & + & x_3 & + & \dots \\ 1 & = & & & x_2 & + & x_3 & + & \dots \\ 1 & = & & & & & x_3 & + & \точки\\ & \vdots & & & & & & & & \ddots \end{массив} \to \begin{bmatrix} 1 \\ 1 \\ 1 \\ \vdots \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & \ точки \\ & 1 & 1 & \ точки \\ & & 1 & \ точки \\ & & & \ddots \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \end{bmatrix} \end{выравнивание*}
в качестве примера системы, у которой любое конечное усечение системы до $n \times n$ системы имеет единственное решение $x_1 = \dots = x_{n=1} = 0, x_n = 1$, но для которых полная система не имеет решения.
В этой книге 2 есть следующий отрывок о системах, подобных этой:
Теорема Хана-Банаха возникла из попыток решить бесконечные системы линейных уравнений… Ключом к разрешимости является определение «совместности» системы уравнений. Например, система $x + y = 2$ и $x + y = 4$ не может быть решена, потому что она требует противоречивых вещей и поэтому «несовместима». Первые попытки определить совместность для бесконечных систем линейных уравнений расширили известные методы определения определителя и сокращения строк. Это был классический анализ — почти решить задачу в конечной ситуации, затем взять предел. Фатальным недостатком этих подходов была необходимость (очень редкой) сходимости бесконечных произведений».0003
, а затем упоминает теорему об этих системах, которая мотивирует Гана-Банаха:
Теорема 7.10.1 показывает, что для решения некоторой системы линейных уравнений необходимо и достаточно выполнения условия типа непрерывности.
Теорема 7.10.1 (Функциональная задача): Пусть $X$ — нормированное пространство над $\mathbb{F} = \mathbb{R}$ или $\mathbb{C}$, пусть $\{x_s \ : \ s \in S \}$ и $\{ c_s \ : \ s \in S \}$ — наборы векторов и скаляров соответственно. Тогда существует непрерывный линейный функционал $f$ на $X$ такой что $f(x_s) = c_s$ для каждого $s \in S$ тогда и только тогда, когда существует $K > 0$ такое, что \begin{уравнение} \left|\sum_{s \in S} a_s c_s \right| \leq K \влево\| \sum_{s \in S} a_s x_S \right\| \тег{1}, \end{уравнение} для любого выбора скаляров $\{a_s \ : \ s \in S \}$, для которых $a_s = 0$ для всех, кроме конечного числа $s \in S$ («почти все» $a_s = 0$).
Банах использовал теорему Хана-Банаха для доказательства теоремы 7.10.1, но из теоремы 7.10.1 вытекает теорема Хана-Банаха: Предполагая, что теорема 7.10.1 верна, пусть $\{x_s \}$ — векторы подпространства $M $, пусть $f$ — непрерывный линейный функционал на $M$; для каждого $s \in S$ пусть $c_s = f(x_s)$.
