Способы вычисления определителей: Способы вычисления определителей:

ИССЛЕДОВАНИЯ СПОСОБОВ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ

• Главная
• Список секций
• Математика
• ИССЛЕДОВАНИЯ СПОСОБОВ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Тимиркаева А.В. 1Нигматуллина А.М. 1

---

1

Миронова Ю.Н. 1

---

1

Автор работы награжден дипломом победителя II степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение.  

Матрицы и определители используются во многих областях знаний. Эти понятия изучаются на 1-ом курсе высших учебных заведений.

С их помощью решаются системы линейных уравнений, задачи классификации, геометрические задачи и пр.

Именно поэтому свою научно-исследовательскую работу мы решили посвятить понятию определителя и изучению его свойств.

§1. Понятие определителя.

Рассмотрим понятие определителя.

Определение 1. ОПРЕДЕЛИТЕЛЬ – в математике запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число («значение» определителя). Очень часто под понятием «определитель» имеют в виду как значение определителя, так и форму его записи. Определители позволяют удобно записывать сложные выражения, возникающие, например, при решении линейных уравнений в аналитической геометрии и в математическом анализе.

Определение 2. Матрица- это математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.

) между ним и другими подобными объектами.

§2. Способы вычисления определителей.

Символ вида

, где — некоторые действительные числа, называется определителем второго порядка, который вычисляется следующим образом:

.

Определителем третьего порядка называется число, которое вычисляется следующим образом:

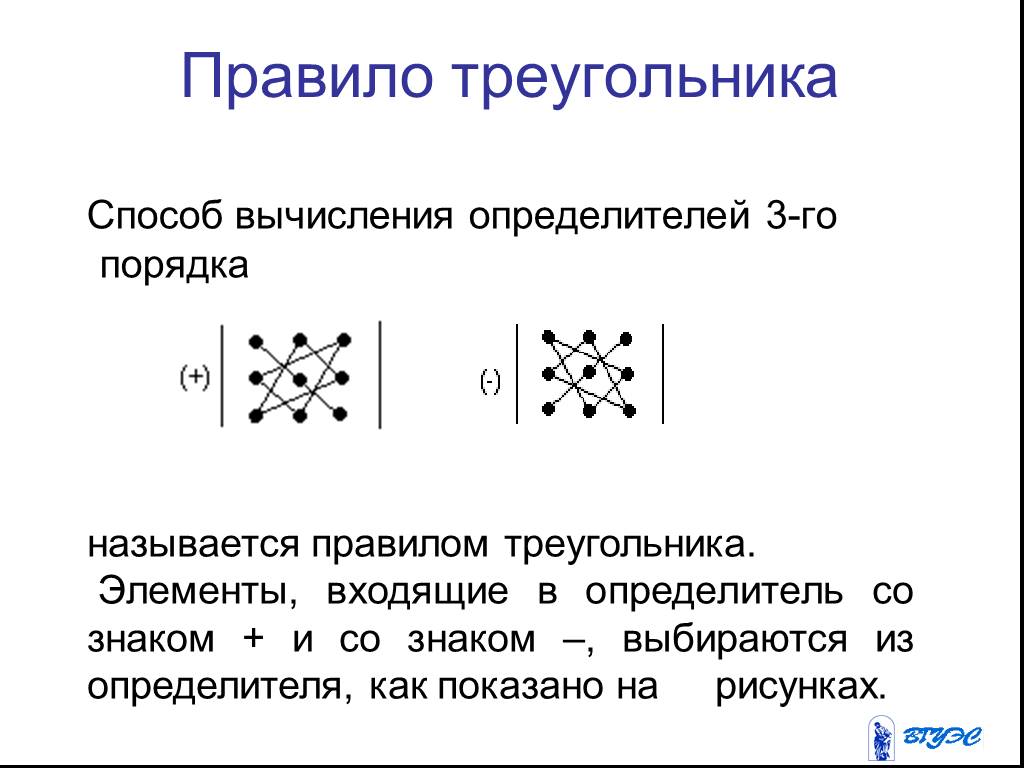
При вычислении определителей третьего порядка пользуются правилом Саррюса (правило треугольников).

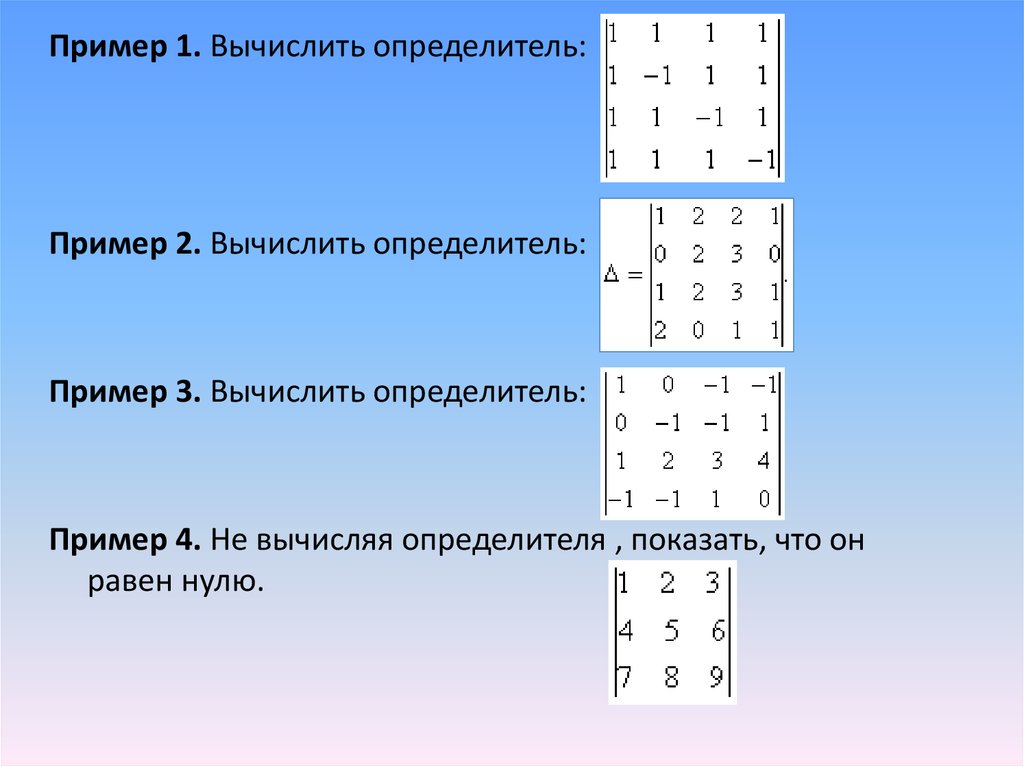
Пример 1.1. Вычислить определитель второго порядка:

=27.

Ответ: 27.

Пример 1.2. Вычислить определитель второго порядка:

Ответ: -27.

Пример 1.3. Вычислить определитель третьего порядка:

.

Ответ: 9.

Пример 1.4.Вычислить определитель третьего порядка:

§3 Понятие минора.

Определение 1.

Определитель, полученный из определителя вычеркиванием-ой строки и-го столбца, на пересечении которых стоит элемент называется минором элемента определителя

Пример 1:

Ответ: -6

Пример 2.

Ответ: -18.

Определение 2. Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком «+» , если сумма (i+j) чётное число, и со знаком «-», если (i+j) нечётное число.

С их помощью понижается порядок определителей.

Пример 3.1.

Ответ: 98.

Пример 3.2.

Ответ: 0.

§4.Свойства определителей.

Свойства определителей.

1. Определитель не изменится, если его строки заменить столбцами или наоборот.

2. При перестановке двух параллельных строк или столбцов определитель меняет свой знак.

3. Определитель, имеющий две одинаковые строки или два одинаковых столбца равен нулю

4. Общий множитель элементов какой-либо строки или столбца определителя можно вынести знак определителя.

5. Если элементы какого-либо столбца(строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей.

6. Определитель не изменится, если к элементам одной строки или столбца прибавить соответствующие элементы параллельной строки или столбца умноженное на любое число

7. Определитель равен сумме произведений элементов некоторой строки или столбца на соответствующие или алгебраические дополнения.

Свойство 7 содержит в себе способ вычисления определителя высоких порядков.

1. Сумма произведений элементов какого-либо столбца или строки определителя на алгебраические дополнения соответствующих элементов параллельных рядов равна нулю.

Заключение

Таким образом, мы исследовали понятие определителя, иизучили его свойства, с помощью которых мы можем рассмотреть и вычислить примеры задач и их решения.

Список источников и литературы:

1. StudFiles. URL: http://www.studfiles.ru/preview/4404558/ (Дата обращения 15.10.2016)

2. Т.И. Анисимова. Лекции по высшей математике. (Линейная алгебра и аналитическая геометрия): Учебное пособие. – Елабуга: Изд-во ЕГПУ, 2007 г. – 48 с.

3. В.П. Минорский. Сборник задач по высшей математике. — Москва, 1987 г.

Просмотров работы: 339

Определители и методы их вычисления.

Лекция 2

Похожие презентации:

Определители. Свойства определителей и методы их вычисления

Матрицы и определители

Определители второго порядка

Матрицы и определители

Линейная алгебра. Определители. (Лекция 2)

Определители. Свойства определителей

Матрицы и определители. (Лекция 1)

Определители. Свойства определителей

Определители, системы

Матрицы. Действия над матрицами. Определители и их свойства

Линейная алгебра
Определители второго и третьего порядка.
Определители n – ого порядка.
Свойства определителей.
Методы вычисления определителей.
Определители широко применяются во многих
разделах высшей математики, в теоретической
механике, физике и т.д. для сокращения записей и
удобства вычислений.
Любой квадратной матрице порядка n можно
сопоставить число, которое называется
определителем.

Обозначается det A или
A или .
Определитель матрицы также называется её
детерминантом.
Определители 2 порядка
Определитель 2 — го порядка — это число, записанное в
виде: a11 a22 a12 a21
a11 a12
a11a22 a12 a21
a21 a22
ai j
Номер строки
Элементы определителя,
Индексы
Номер столбца
из произведения элементов главной диагонали вычитается
Главная
диагональ
произведение элементов
побочной
диагонали.
определителя
Побочная диагональ
определителя
Определители 3 порядка
Определитель 3 — го порядка — это число, записанное в
a11a22 a33 a12 a23 a31 a13 a21a32
a13 a22 a31 a12 a21a33 a11a23 a32
Метод треугольников
или схема Саррюса
_
виде:
+
1
3
0
2 1 4
5
6
1
1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
2 3 1 1 6 4 29
Метод треугольника применим только для определителей 3 порядка
Определители n – ого порядка
Определителем n – ого порядка называется число:
a11
a12
a1n
a 21
a 22
a 2n
an1 an 2 ann
Методы вычисления определителей n – ого порядка
рассмотрим на примере вычисления определителей
третьего порядка.
Методы вычисления определителей
1
Метод разложения определителя по элементам строки
(столбца)
Определитель (n-1)-ого порядка, который получается из
определителя n — ого порядка путем вычеркивания i — ой строки и
j — ого столбца, т.е. строки и столбца, на пересечении которых стоит
элемент
ai j называется минором элемента и обозначается Mi j
Алгебраическим дополнением элемента
Ai j ( 1)i j M i j
aa1111 aa1212 aa1313
aa2121 aa2222 aa2323
aa3131 aa3232 aa3333
ai j
называется
aa2211 aa2312
MM1123
aa3231 aa3332
2 3 1 1
( 1) M
23
M M 23
AA23 M
( 1)
11
11
11
Методы вычисления определителей
Величина определителя равна сумме произведений элементов
какой – либо строки (столбца) определителя на их
алгебраические дополнения:
n
ai j A i j
Разложение определителя по элементам
i – ой строки
ai j A i j
Разложение определителя по элементам
j – ого столбца
j 1
n
i 1
2 1 0
3 1
0 1
0 3 1 2
( 1)
( 1) 1
2 1
5
1
2 5 1
1 1
2 (3 1 5 1) 1 (0 1 2 1) 2
1 2
0
0 3
2 5
( 1)1 3
Методы вычисления определителей
2
Использование свойств определителя
Свойства определителя:
Величина определителя:
равна нулю, если элементы какого — либо столбца или строки
равны нулю:
0 0
a21 a22
0 a22 0 a21 0
равна нулю, если соответствующие элементы двух строк
(столбцов) равны
a11 a12
a11 a12
a11 a12 a11 a12 0
меняет знак, если поменять местами строки (столбцы):
a11 a12
a21 a22
a11 a22 a12 a21 a12 a21 a11a22
a12 a11
a22 a21
увеличивается в k раз, если элементы какого — либо столбца
(строки) увеличить в k раз:
k a11 k a12
a21
a22
k a11 a22 k a12 a21 k
a11 a12
a21 a22
не меняется при замене строк соответствующими столбцами:
a11 a12
a21 a22
a11 a21
a12 a22
Методы вычисления определителей
не меняется, если к элементам какой-либо строки (столбца)
прибавить соответствующие элементы другой строки (столбца),
умноженные на произвольный множитель
a11
a12
a 21 ka11 a 22 ka12
a11a 22 a 21a12
a11a 22 a11ka12 a 21a12 ka11a12
a11 a12
a 21 a 22
Если определитель имеет так называемый треугольный вид,
то он вычисляется как произведение чисел, стоящих на
главной диагонали: a a a
11
12
13
0 a 22 a 23 a11a 22 a 33
0 0 a 33
Методы вычисления определителей
1
3 1
1
3
1
1
3
1
5 1
1 3 0 5 1 0 5 1 1
7
1 4 1
1 4 1 0 7 2
2
5 2 7 1 17
2
( 1)1 1
Выберем 1
К элементам
2
Разложим
столбец
и
К элементам
3
строки
прибавим
определитель
по
превратим
второй
строки
прибавим
элементы 11строки,
элементам
столбца
и третий
элементы
1
строки
умноженные на (-2)
элементы в нули
Также, используя свойства, можно привести определитель к
треугольному виду и вычислить по последнему свойству.
Методы вычисления определителей
1. Определители 3-го порядка вычисляются с
помощью правила треугольников или путем
приписывания справа первых двух столбцов и
тогда определитель равен произведению
элементов главной диагонали минус произведение
элементов побочной диагонали.
1
2
3 1 2
1 0 0 2 1 2 3 ( 8) 3
8 0 1 8 0 2 0 3 1 1 ( 3) 2 ( 8) 0
79
2 3 0 2 3
2. Метод разложения определителя по
элементам строки (столбца) или метод
понижения порядка определителя.
3. Метод использования элементарных
преобразований или метод приведения
к треугольному виду.
4. Метод рекуррентных соотношений.

English     Русский Правила

линейная алгебра — Альтернативные методы вычисления определителя матрицы

спросил 5 лет, 8 месяцев назад

Изменено 5 лет, 8 месяцев назад

Просмотрено 5к раз

$\begingroup$

Я нашел литературу, в которой вычислялась матрица, но не указывалось, как это делается. При традиционном подходе мой метод не совпадает с литературным. В литературе для следующей матрицы:

$M = \begin{bmatrix} a & b & 0 & d \\ b & c & e & 0 \\ 0 & g & i & h \\ f & 0 & h & j\end{bmatrix}$

Определитель M равен

$ ( aj — df)(ci-eg) — X$

и X — другие термины. Я знаю, что приведенные выше результаты можно рассчитать обычным способом и, вероятно, экстраполировать, чтобы получить вышеуказанное. Есть ли другой способ сделать определитель, который дает вышеизложенное вместо обычного способа, такого как:

$M = a\begin{bmatrix} c & e & 0 \\ g & i & h \\ 0 & h & j\end{bmatrix} — b \begin{bmatrix} b & e & 0 \\ 0 & i & h \\ f & h & j\end{bmatrix}- d\begin{bmatrix} b & c & e \\ 0 & g & i \\ f & 0 & h\end{bmatrix}$

• линейная алгебра
• определитель

$\endgroup$

0

$\begingroup$ 9{-1}B)дет(D) $$

Если дополнительно $CD=DC$, то можно заключить, что:

$det(X)=det(DA-CB)$

$\endgroup$

$\begingroup$

В общем, существует множество способов вычисления определителей. Специальные матрицы позволяют использовать специальные методы. Для матрицы размером $n$ на $n$ рассмотрим индексы элементов по модулю $n$. Таким образом, главная диагональ — это элементы, разность индексов которых равна нулю. Другие диагонали имеют постоянную разницу индексов, отличную от нуля. Определитель матрицы только с одной диагональю равен произведению элементов этой диагонали со знаком плюс или минус. Матрица $M$ у вас трехдиагональная. Главная диагональ — это $(a, c, i, j)$, а следующие верхние и нижние диагонали — это $(b, e, h, f)$ и $(b, g, h, d)$. Определитель $M$ представляет собой сумму двух произведений двух подматриц $2$ на $2$ за вычетом трех диагональных произведений: $$ (a j-d f)(c i-e g) + (a c-b b)(i j-h h) — (a c i j) — (b e h f) — (b g h d). $$ Это можно обобщить, но результаты, возможно, не заслуживают внимания.

$\endgroup$

2

линейная алгебра — Существуют ли простые методы вычисления определителя симметричных матриц?

У вас была хорошая симметричная матрица, в которой все диагональные элементы равны. Это особенно простая форма, как, конечно, уже отмечали другие. Возможно, стоит увидеть, что ваше уравнение аналитически не такое безумное, как все это, и его можно решить до некоторой степени, чтобы выкашлять кое-что полезное.

Проверка определителя нуля

Посмотрите, что всегда происходит, когда c=a. Катастрофа для обратимости. Определитель для такой матрицы всегда должен быть равен нулю . Когда вы получите такое уравнение для определителя, приравняйте его к нулю и посмотрите, что произойдет! Это по определению описание всех ваших сингулярных матриц.

Это, пожалуй, самый полезный тест, о котором следует сразу подумать, потому что вам нужно беспокоиться о вычислении значения определителя только в том случае, если он это не ноль. Другой способ сказать, что если в вашей симметричной матрице все диагональные элементы такие же, как в исходном сообщении, вы можете использовать свое уравнение, чтобы проверить, равен ли этот определитель нулю, без фактического вычисления определителя.

2b ² (c−a)+a(a ² −c ² )= f (a,b,c)

Эта функция может выглядеть ужасно, но в других местах она содержит нули. чем тривиальный случай, когда a=c. Это также ноль, где

2b ² (a−c)=a(a ² −c ² )

Обратите внимание, что: (a ² −c ² )=(a+c)(a-c) означает

2b ² =a(a+c)

или,

2b ² =a ² +ac

= 705 (52 c, 9009 900) 2 -a ² )/a

Или, если вы предпочитаете b,

b = sqrt(a ² +ac)

Если либо c=a, либо c = (2b ² -a ² )/ahold, тогда вам абсолютно гарантировано нулевой определитель, и вам не нужно на самом деле вычислять определитель, вычисляя что-либо, кроме (2b ² -a ² )/a и сравнивая это со значением c. Конечно, это справедливо только для матриц той формы, которую вы опубликовали, со всеми одинаковыми элементами главной диагонали.

Определение определителей методом расширенной матрицы/диагоналей

Если вам нужен аккуратный метод грубой силы для определения определителей таким образом, чтобы было почти невозможно ошибиться только потому, что он так организован, есть такой- называется американским методом. Это трудно превзойти по простоте, но это требует некоторой избыточности.

Предположим, у вас есть, $$ \влево[ \begin{массив}{ccc} 1&2&3\\ 4&5&6\\ 7&8&9 \конец{массив} \right] $$

Теперь переключитесь на расширенную матричную нотацию… возьмите первые два столбца и сделайте что-то, что выглядит совершенно избыточным, но в конечном итоге действительно упростит. Перепишите первые два столбца снова справа от исходной матрицы, чтобы получить что-то вроде

$$ \left[ \begin{массив}{ccc|cc} 1&2&3&1&2\\ 4&5&6&4&5\\ 7&8&9&7&8 \конец{массив} \right] $$

Если вы посмотрите на диагонали, которые находятся справа от главной диагонали и параллельны ей, если вы возьмете произведение любых трех членов на этих трех соседних диагоналях, просто посмотрите на них, это все положительные члены, входящие в определитель, теперь перегруппированные в диагонали .