Средняя линия треугольника | Геометрия 8 класс
Средняя линия треугольника
План урока
- Средняя линия треугольника
- Свойство медиан треугольника
- Применение определения и свойства средней линии треугольника для решения задач
Цели урока
- Знать определение и свойство средней линии треугольника, свойство медиан треугольника
- Уметь применять определение и свойство средней линии треугольника при решении задач
Разминка
- Какие треугольники называются подобными?
- Что называют коэффициентом подобия?
- Как доказать подобие треугольников?
- Чему равно отношение площадей подобных треугольников?
Средняя линия треугольника
Определение
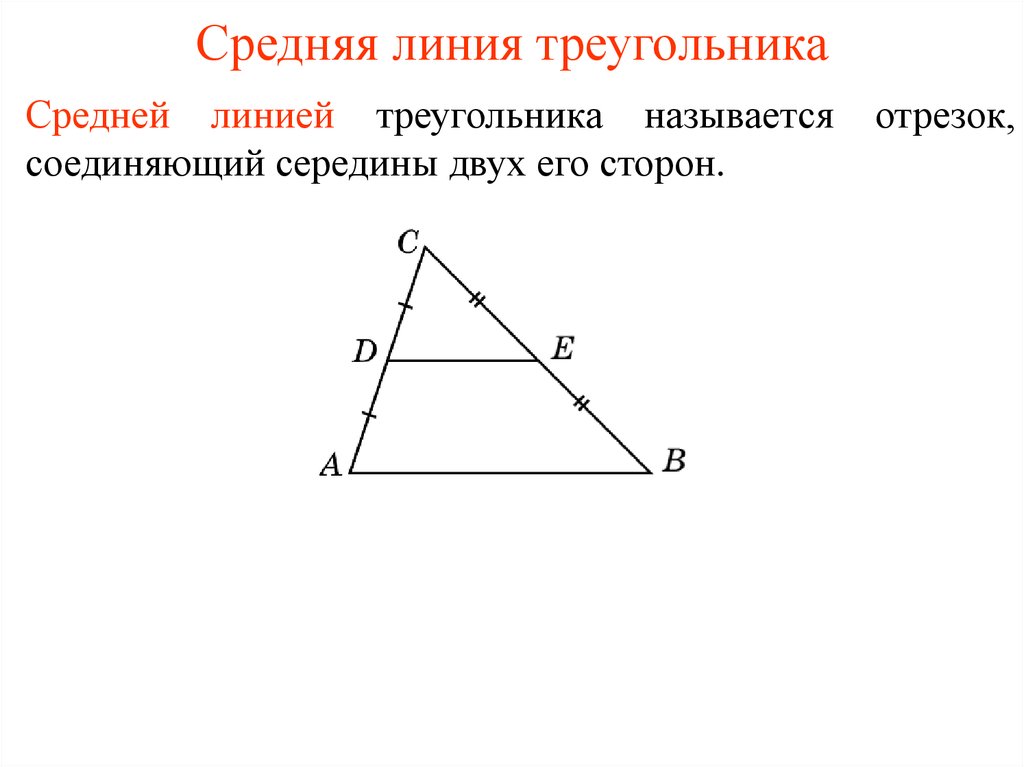
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Теорема ( свойство средней линии треугольника )
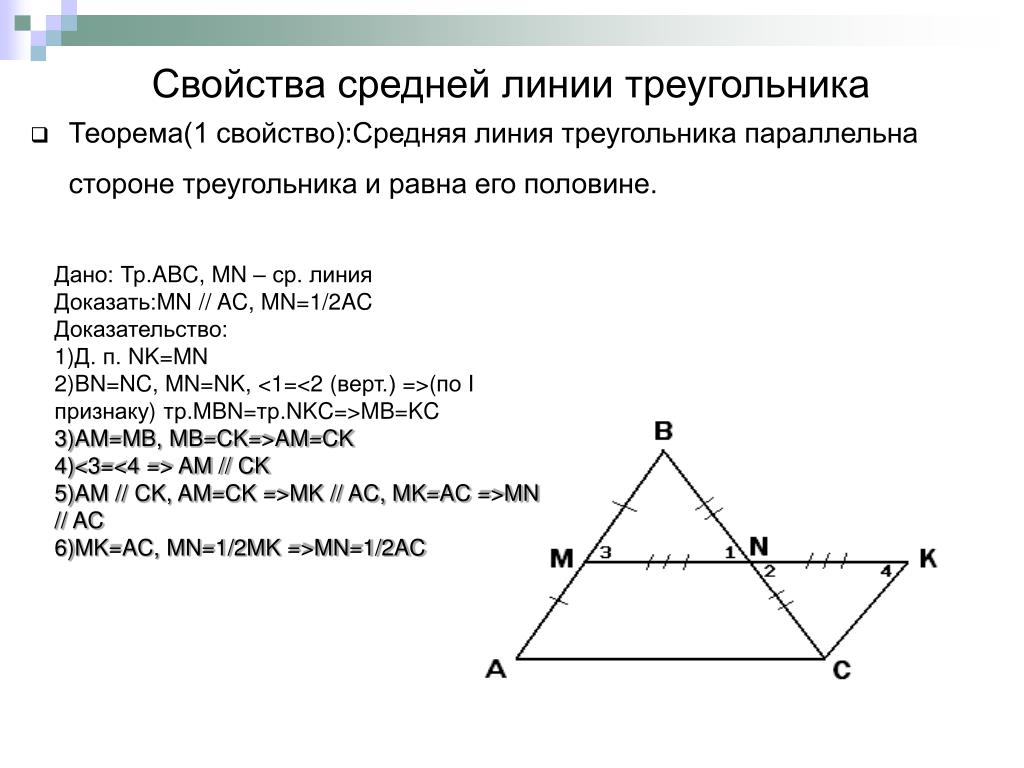
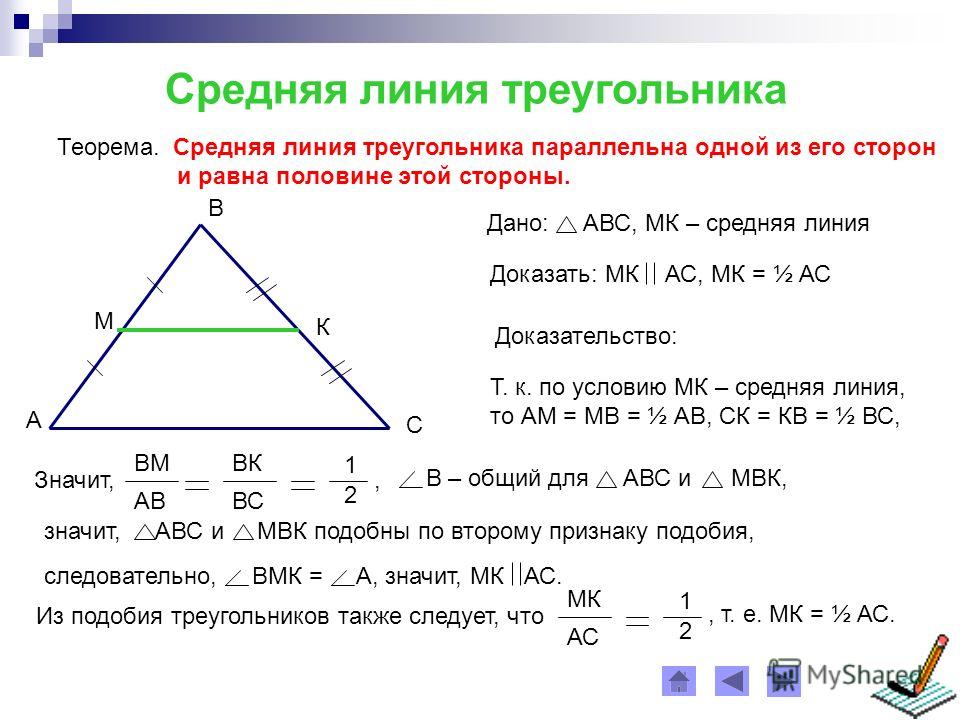
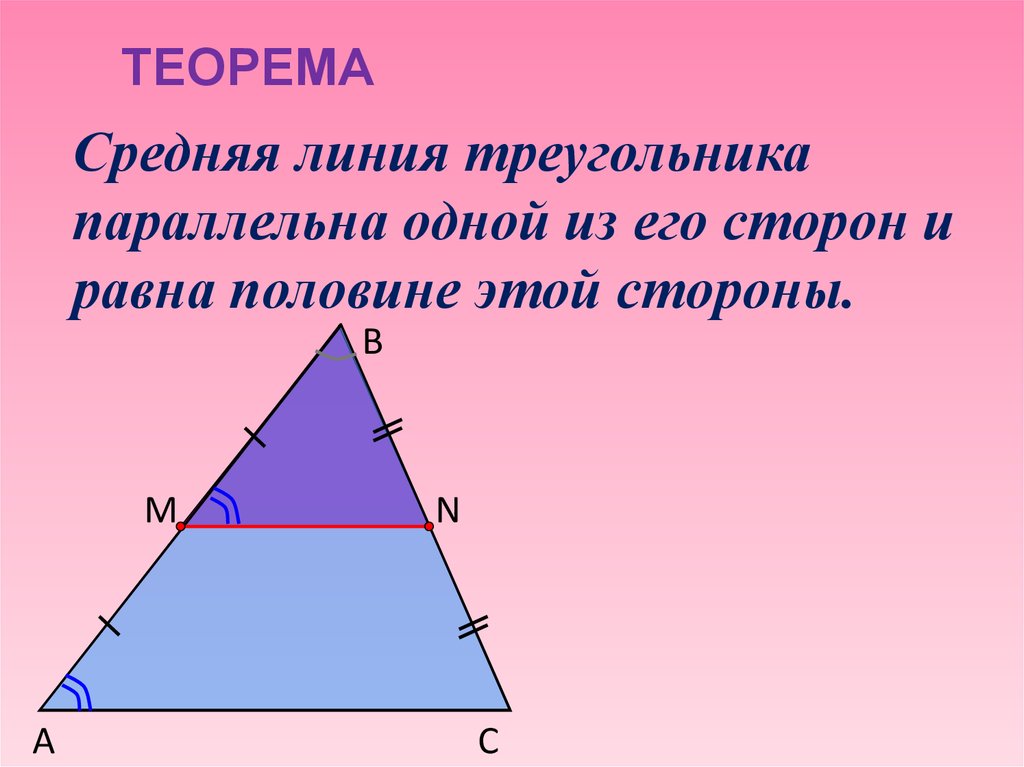
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство
Рис. 1. DE — средняя линия ∆ABC
Рассмотрим треугольник ABC, DE — его средняя линия (рис. 1).
По определению средней линии треугольника DB=12AB, EB=12CB, тогда треугольники ABC и DBE подобны по двум пропорциональным сторонам и углу между ними (∠B — общий, ABDB=CBEB=2).
Тогда ∠BAC=∠BDE, а они соответственные при пересечении прямых AC и DE секущей AB, следовательно AC∥DE.
Поскольку коэффициент подобия треугольников равен 2, то AC=2DE или DE=12AC.
Теорема доказана.
В любом треугольнике можно провести три средних линии, которые делят треугольник на четыре равных треугольника, подобных исходному (докажите самостоятельно).
Пример 1
Периметр треугольника равен 76 см. Стороны треугольника, образованного средними линиями данного треугольника, относятся как 4 : 7 : 8. Найдите стороны данного треугольника.
Решение
Рис. 2. К решению примера 1
Рассмотрим ∆ABC, PABC=76 см, DE, EF, DF — средние линии треугольника, EF : DF : DE = 4 : 7 : 8 (рис. 2).
Треугольники ABC и DEF подобны по трем пропорциональным сторонам, т. к. DE=12AC, EF=12AB, DF=12BC по свойству средней линии треугольника. Следовательно отношение сторон треугольника ABC такое же, как в треугольнике DEF, т.е. AB : BC : AC = 4 : 7 : 8.
Пусть x — одна часть, тогда AB=4x, BC=7x, AC=8x. Периметр треугольника равен сумме длин сторон, тогда:
4x+7x+8x=76,
19x = 76,
x=4.
4·4=16 (см) — AB,
7·4 = 28 (см) — BC,
8·4 = 32 (см) — AC.
Ответ: 16 см, 28 см, 32 см.
Упражнение 1
- Стороны треугольника равны 12 см, 16 см и 20 см. Найдите стороны треугольника, вершинами которого являются середины сторон данного треугольника.
- Средняя линия треугольника отсекает от него трапецию с боковыми сторонами 3 м и 4 м и меньшим основанием 5 м. Найдите периметр треугольника.
- Прямая, параллельная основанию равнобедренного треугольника и проходящая через середину боковой стороны, отсекает от данного треугольника трапецию. Найдите ее периметр, если периметр данного треугольника равен 26 см, а основание относится к боковой стороне как 5 : 4.
Пример 2
Докажите, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма ( теорема Вариньона ).
Решение
Рис. 3. Теорема Вариньона
Рассмотрим четырехугольник ABCD, E, F, G, H — середины сторон данного четырехугольника. Докажем, что EFGH — параллелограмм (рис. 3).
В треугольнике ABC: EF— средняя линия, значит, EF∥AC, EF=12AC. В треугольнике ADC: GH — средняя линия, значит, GH∥AC, GH=12AC.
Получили, что в четырехугольнике EFGH противоположные стороны EF=GH и EF∥GH, следовательно EFGH — параллелограмм, что и требовалось доказать.
Докажите теорему Вариньона для невыпуклого четырехугольника самостоятельно.
Теорема ( свойство медиан треугольника )
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Доказательство
Рис. 4. К доказательству свойства медиан
Рассмотрим треугольник ABC, AE, BF, CD — медианы треугольника, медианы AE и CD пересекаются в точке O (рис. 4).
Так как D — середина AB, E — середина BC,
то DE — средняя линия треугольника ABC, по свойству средней линии треугольника DE=12AC, DE∥AC, тогда накрест лежащие углы при параллельных прямых равны: ∠OAC=∠OED, ∠OCA=∠ODE.
Треугольники AOC и EOD подобны по двум углам, следовательно:
ACDE=AOOE=COOD=21.
Таким образом, точка пересечения медиан AE и CD делит их в отношении 2 : 1 считая от вершины.
Аналогично доказываем, что точка пересечения медиан BF и CD делит каждую из них в отношении 2 : 1, считая от вершины, значит совпадает с точкой O.
Все три медианы пересекаются в одной точке и точкой пересечения делятся в отношении 2 : 1, считая от вершины, что и требовалось доказать.
Контрольные вопросы
- Отрезок DE — средняя линия треугольника ABC (см. рис. 1).
а) определите вид четырехугольника ADEC.
б) назовите медиану треугольника, проведенную из вершины A. - Может ли средняя линия треугольника быть перпендикулярной его стороне; двум его сторонам?
- Могут ли средние линии треугольника быть равными 3 см, 4 см и
10 см? Почему? - В треугольнике ABC проведена средняя линия DE, параллельная стороне AC. В каком отношении прямая DE делит медиану BM; высоту BH?
Ответы
Упражнение 1
1. 6 см, 8 см, 10 см
2. 24 м
3. 23 см.
Средняя линия треугольника — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.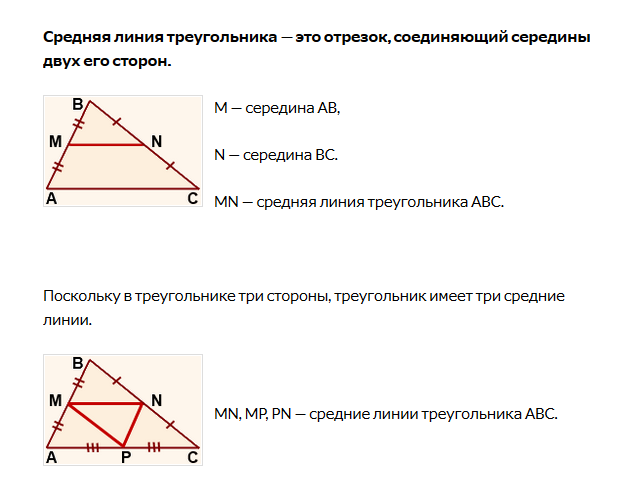
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Мой университет – www.moi-mummi.ru
Урок геометрии в8 классе
Учитель: Бижова Т.В.
г. Снежинск
2011 г.
2. Муниципальное общеобразовательное учреждение “Средняя общеобразовательная школа № 135 имени академика Б.В. Литвинова”
Тема урока:Средняя линия
треугольника
Тип урока:
Урок усвоения новых знаний
3. Муниципальное общеобразовательное учреждение “Средняя общеобразовательная школа № 135 имени академика Б.В. Литвинова”
Цели урока :Рассмотреть понятие средней
линии треугольника.
Доказать теорему о средней
линии треугольника.
Показать применение
теоремы к решению задач.
Развитие графических
навыков при построении
средних линий.
4. Муниципальное общеобразовательное учреждение “Средняя общеобразовательная школа № 135 имени академика Б.В. Литвинова”
План урока:1. Актуализация опорных знаний;
2. Подготовка к восприятию
нового материала;
3. Изучение нового материала;
4. Закрепление изученного
материала, решение задач;
5. Итоги урока;
6. Домашнее задание
1. Актуализация опорных знаний
C
B
A
D
K
F
Дано: KBDF – прямоугольник
Доказать: ∆BCD ~∆ACE
E
M
C
400
Доказать: ∆KMN ~ ∆CNM
400
K
N
C
Дано: BD ║ AF
Найти: AC, AB
2
B
A
3
12
D
F
2. Подготовка к восприятию нового материала
AB = 2MP
A
B
M
P
O
3. Изучение нового материала
3.1. Построение средней линии треугольника (1-й способ)
• Начертите произвольный треугольник ABC
B
• С помощью циркуля и линейки разделите
боковую сторону на две равные части
N
M
• Через точку N проведите прямую,
параллельную стороне AC
C
A
• Измерьте длины отрезков BM и MC и
сделайте вывод
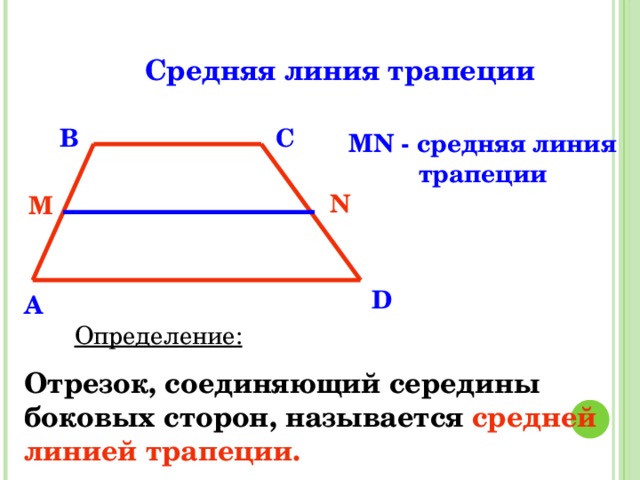
NM — средняя линия треугольника ABC
Определение:
Средней линией треугольника называют отрезок,
соединяющий середины двух сторон треугольника.
3. Изучение нового материала
3.2. Построение средней линии треугольника (2-й способ)
B
N
• Начертите произвольный треугольник ABC
• Отметьте середины сторон AB и BC и
соедините их отрезком;
M
Ответьте на вопросы:
A
C
1. Сколько средних линий можно провести в
треугольнике?
2. Как они будут расположены по отношению
к третьей стороне?
3. Измерьте среднюю линию треугольника и
его основание. Что Вы заметили?
NM — средняя линия треугольника ABC
3. Изучение нового материала
3.3. Доказательство теоремы о средней линии треугольника
Средняя линия треугольника параллельна одной из
его сторон и равна половине этой стороны.
Теорема:
B
1
N
2
A
Дано:
M
∆ABC, M Є BC, N Є AB.
NM-средняя линия.
Доказать: NM ║ AC, NM = ½ AC
Доказательство:
C
1. ∆BNM ~ ∆ABC (∠B–общий, BM:BC = BN:BA = ½ ),
значит ∠1 = ∠2 и NM:AC = ½;
2. Т.к. ∠1 =∠2 (как соответственные), то NM ║ AC и т.
к.NM:AC = ½, то 2NM = AC, значит NM=1/2AC, ч.т.д.
4. Закрепление изученного материала,
решение задач (Часть 1)
B
B
2
3
N
L
2
A
3
3
M
3
C
A
C
B
4
32°
2
K
G
F
3
2
C
32 °
A
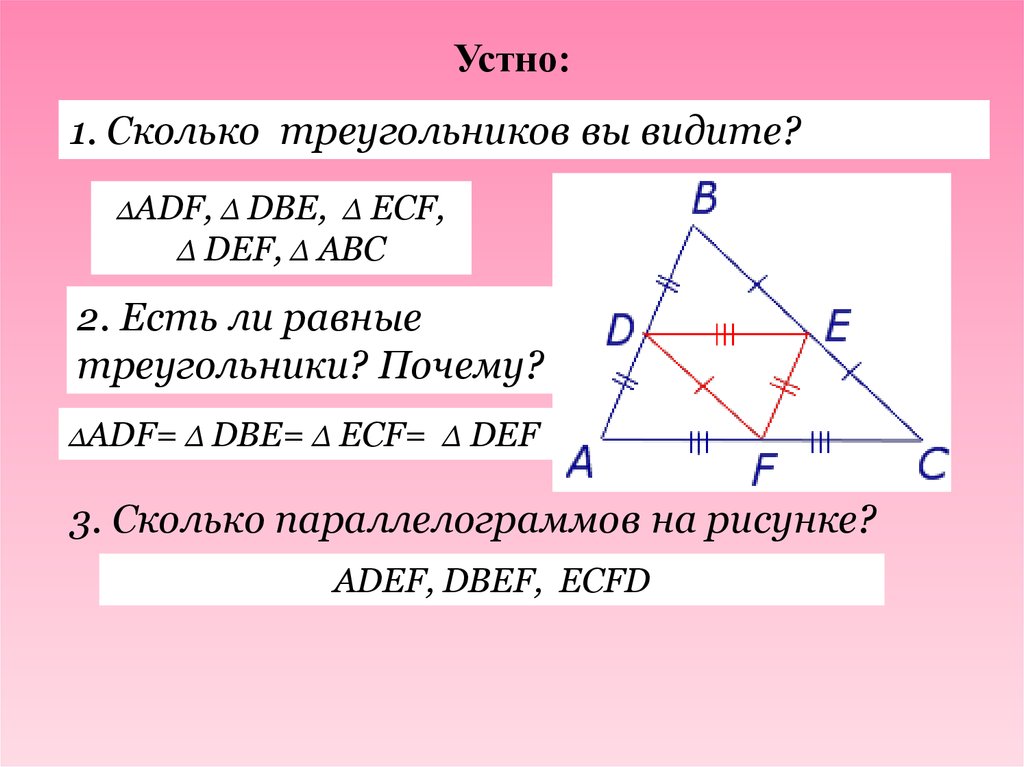
По данным рисунков установить, являются ли отрезки
средними линиями?
11. Решить задачу:
4. Закрепление изученного материала,решение задач (Часть 2)
Решить задачу:
B
F
C
Диагональ прямоугольника равна 17 см.
Найти периметр четырехугольника,
E
O
G
вершинами сторон которого являются
середины сторон прямоугольника.
A
H
D
4. Закрепление изученного материала,
решение задач (Часть 3)
Задача с практическим применением
Найти длину поля, если в ней
оказалось сто «шагов»
полевого циркуля при условии,
что DE = 1 м
B
D
A
E
C
13. Итоги урока
5. Итоги урокаОтветить на вопросы:
Какой отрезок называют средней
линией треугольника?
Какими способами можно построить
среднюю линию треугольника?
Каким свойством обладает средняя
линия треугольника?
Где на практике применяется свойство
средней линии треугольника?
14.
Домашнее задание6. Домашнее заданиеОтветить на вопросы учебника, стр.
154, № 564, 566, 567, доказать
теорему о средней линии
треугольника. Найти другие
способы доказательства свойства в
дополнительной литературе.
15. Мой университет — www.moi-mummi.ru
Список использованной литературыУстные упражнения по геометрии для 7-11 классов. Кн. для учителя /И.М. Смирнова,
В.А. Смирнов – М.: Просвещение, 2003
Упражнения по планиметрии на готовых чертежах: Пособие для учителя. Авторы: С.М.
Саврасова, Г.А. Ястребинецкий – М.: Просвещение, 1987
Задачи по геометрии. Пособие для учащихся 7 -11 кл. общеобразовательных
учреждений /Б.Г.Зив, В.М. Мейлер, А.Г. Баханский – 3-е изд. – М.: Просвещение, 2000
Геометрия, 7-9: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф.
Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И.Юдина – 15 изд. – М.: Просвещение, 2005
Геометрия 7-9: учебник для 7-9 классов общеобразовательных учреждений.
Под ред.А.Я. Цукаря. / В.Н. Руденко, Г.А. Бахурин — 2-е изд. – М.: Просвещение, 1994
Геометрия. Пособие для классов вечерних (сменных) школ с ускоренным
прохождением курса восьмилетней школы. Под ред. З.А. Скопец, М., «Просвещение»,
1971
English Русский Правила
Срединная линия Определение и значение — Merriam-Webster
средняя · линия ˈmid-ˌlīn
-ˈlīn
: срединная линия
специально : срединная линия или срединная плоскость тела или части тела
Примеры предложений
Недавние примеры в Интернете
Поверните бутылку или кастрюлю по направлению к средней линии , верните ее в центр, затем поверните в противоположном направлении.
— Мэллори Кревелинг, 9 лет.0017 Женское здоровье , 23 февраля 2023 г.
Он состоит в основном из двух мышц (большой и малой грудных), и его основная задача заключается в выполнении очень специфического действия: подтягивании плеч к средней линии тела (т. е. приведении).
— Мужское здоровье , 6 июня 2022 г.
Одной из основных функций грудной клетки является приведение или приведение рук к средней линии туловища, чтобы сжать грудные мышцы.
— Бретт Уильямс, Men’s Health , 2 июня 2022 г.
Оттуда потяните локти назад к средней линии тела, держите их плотно прижатыми к бокам.
— Бен Уокер, Outside Online , 28 августа 2020 г.
Ее мать, Хизер Крингс, сообщила на сайте Делани CaringBridge, что у Делейни был диффузный рак.
0017 срединная глиома , известная как DMG.
— Кэти Козлович, 
— Элиэзер Дж. Штернберг, Discover Magazine , 15 ноября 2018 г.
Узнать больше
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «средняя линия». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Первое известное использование
14 век, в значении, определенном выше
Путешественник во времени
Первое известное использование средняя линия была в 14 веке
Посмотреть другие слова из того же века кризис среднего возраста
средняя линия
Мидлотиан
Посмотреть другие записи рядом
Процитировать эту запись
Стиль
MLAЧикагоAPAMМерриам-Вебстер
«Средняя линия».
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/midline. По состоянию на 23 марта 2023 г.
Копия цитирования
Детское определение
средняя линия
существительное
средняя · линия ˈmid-ˌlīn
: линия, проходящая через середину чего-либо
особенно : линия, проходящая через тело или одну из его частей, которая лежит в плоскости, делящей его на половины, являющиеся зеркальным отражением друг друга
Медицинское определение
срединная линия
существительное
средняя · линия ˈmid-ˌlīn, ˌmid-ˈlīn
: срединная линия
особенно : срединная линия или срединная плоскость тела или части тела
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
определение средней линии в The Free Dictionary
Также найдено в: Thesaurus, Medical, Encyclopedia, Wikipedia.
Относится к средней линии: MEDLINE, срединный разрез
средняя·линия
(средняя линия)n.
Средняя линия, особенно средняя линия или плоскость тела.
Словарь английского языка American Heritage®, пятое издание. Авторские права © 2016, издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
средняя линия
(ˈmɪdˌlaɪn)n
линия, расположенная посередине чего-либо, особенно воображаемая линия, которая делит организм или орган на симметричные части Издательства 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014
средняя строка
(ˈmɪdˌlaɪn) сущ.
средняя плоскость, особ. тела или части тела.
Рэндом Хаус Словарь колледжа Кернермана Вебстера, © 2010 K Dictionaries Ltd. Авторские права Random House, Inc., 2005, 1997, 1991. Все права защищены.
TheSaurusantonynomysReleted WordsSynonyms Легенда:
Переключение на новый тезаурус
| О существительный | 1. | 1. | 1. | . 7. . . . . . 7. 7. 7. 7. 7. 7. 7. плоскость, лист — (математика) неограниченная двумерная форма; «мы будем называть плоскость графика плоскостью X-Y»; «любая линия, соединяющая две точки на плоскости, целиком лежит на этой плоскости» |
На основе WordNet 3.0, коллекции клипартов Farlex. © 2003-2012 Принстонский университет, Farlex Inc. линия СМИ дель Куэрпо.
Медицинский словарь англояна Медицинский словарь Copyright © 2006 McGraw-Hill Companies, Inc.
Все права защищены.
Упоминается в ?
- abducent
- abduct
- abductee
- abducting
- abduction
- abductor
- adducent
- adducting
- adduction
- adductive
- alveolar point
- anatomy
- breadbasket
- cerebral vein
- cleft palate
- краниометрическая точка
- деформация
- дистальная
- эпигастральная ямка
Ссылки в архиве периодических изданий ?
рынок межтеловых устройств, объем которого оценивается более чем в 1,2 миллиарда долларов США, и расширяет весь портфель AMS на глобальную аудиторию пациентов со значительной долей рынка имплантатов TLIF, устанавливаемых спереди.1 Кроме того, система предназначена для бесперебойной работы с Системы доступа MAS(R) TLIF и MAS Midline, позволяющие настраивать параметры для конкретных хирургических методов.
NuVasive объявляет о коммерческом запуске Modulus TLIF-A
Среди результатов КТ чувствительность и специфичность составили 85,9 и 61,0%, 80,9 и 42,7% и 20,7 и 89,2% соответственно для компрессии базальных цистерн, любого смещения средней линии, и смещение средней линии не менее 10 мм.
В обзоре рассматриваются методы диагностики повышенного внутричерепного давления у больных в критическом состоянии; Признаки физикального обследования недостаточно чувствительны для диагностики повышенного ВЧД у пациентов в критическом состоянии
(2) Несмотря на то, что периферические венозные катетеры широко используются для внутривенного (IV) введения лекарств, факторы, отмеченные ранее, иногда диктуют использование альтернативных устройств сосудистого доступа, таких как срединный периферический катетер (средняя линия), периферически вводимый центральный катетер (PICC ), или центральный венозный катетер (ЦВК), введенный через яремную или подключичную вену.
Алгоритм принятия решения не превосходит суждения клинициста для определения необходимости катетеризации периферических и центральных вен
Полное или неполное нарушение спондилодеза по срединной линии на этой стадии приводит к нарушениям, варьирующим от изолированного ЭК до полного вентрального потрошения.
Чем может быть эта грудная масса?
В Индии был проведен ряд исследований, которые предполагают, что новая прерывистая Х-техника закрытия брюшной полости после срединной лапаротомии значительно снижает риск разрыва брюшной полости7,8.
СРАВНЕНИЕ ТЕХНИКИ НЕПРЕРЫВНОГО И НЕПРЕРЫВНОГО Х-ОБРАЗНОГО ШВА ДЛЯ ЗАШИВАНИЯ БРЮШНОЙ СТЕНКИ ПРИ СРОЧНОЙ СРЕДНЕЙ ЛАПАРОТОМИЧЕСКОЙ РАНЕ
###Протез до средней линии челюсти (мм)###-0,30###0,84###-2,00###1,30
ЗАДНЯЯ ПЕРЕДНЯЯ (PA) ЦЕФАЛОМЕТРИЧЕСКАЯ ОЦЕНКА ДЛЯ ВЗРОСЛОГО МУЖСКОГО НАСЕЛЕНИЯ САУДОВ
Наиболее широко распространенный Теория заключается в том, что кисты возникают из-за захвата эктодермальной ткани по средней линии на третьей или четвертой неделе эмбрионального развития из первой или второй жаберной дуги, поэтому был принят термин врожденная киста.
ДЕРМОИДНАЯ КИСТА ПОЛОСТИ РТА — Клинический случай/DERMOIDNA CISTA USNE DUPLJE — PRIKAZ SLUCAJA
За последние несколько десятилетий хирургическое лечение рака вульвы стало более консервативным, поскольку границы опухоли более важны, чем фактическое удаление органа.1 Van der Zee et al в исследовании 403 пациентов сообщили, что в пациенты с раком вульвы на ранней стадии с отрицательным сигнальным узлом имели 3-летнюю выживаемость 97% с минимальной заболеваемостью после процедуры локализации сигнального узла..2 Способность идентифицировать двусторонние паховые СЛУ, по-видимому, связана с близостью к средней линии.
Картирование сторожевого узла при карциноме вульвы
Цель: Сравнить технику парамедианного и срединного доступов субарахноидальной блокады с точки зрения количества попыток и частоты успеха у пожилых пациентов, перенесших плановые операции на нижней части тела.
СРАВНЕНИЕ ПАРАМЕДИАНСКОЙ И СРЕДНЕЙ ТЕХНИКИ СПИНАЛЬНОЙ АНЕСТЕЗИИ У ПОЖИЛЫХ
Отмеченные радиологические параметры: смещение средней линии, типы внутричерепных кровоизлияний, такие как эпидуральная гематома, субдуральная гематома, внутримозговая гематома, перелом и диффузное повреждение головного мозга, пораженная область головного мозга, состояние всего 9цистерны (межножковые, две голени, две окружающие, квадригеминальные, селлярные и две сильвиевы цистерны), открытые или закрытые.