Геометрия 7-9 класс. Средняя линия трапеции — math200.ru
Skip to contentГеометрия 7-9 класс. Средняя линия трапецииadmin2022-12-26T19:13:05+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Средняя линия трапеции
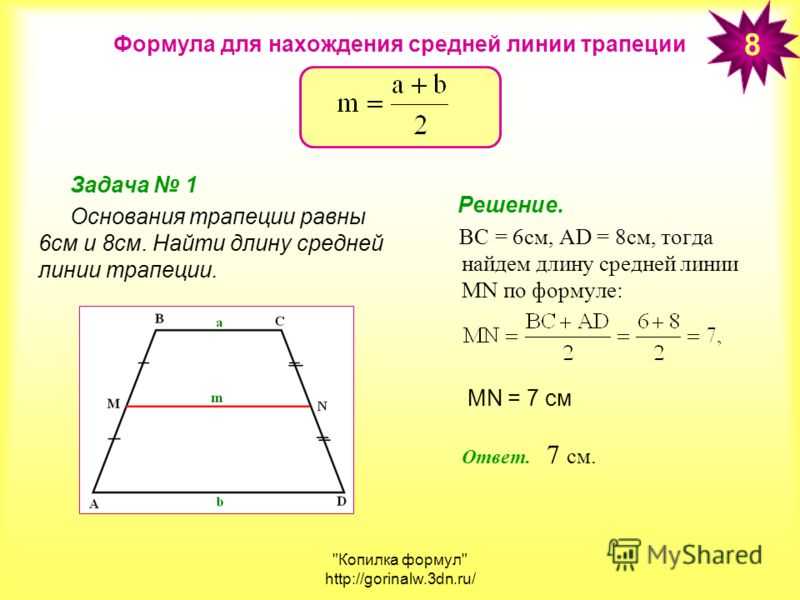
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон). Трапеция, у которой боковые стороны равны, но не параллельны, называется равнобедренной или равнобокой.
Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
| Задача 1. Найдите периметр равнобедренной трапеции с боковыми сторонами равными 7 и средней линией равной 8. Ответ ОТВЕТ: 30. | |
Задача 2. \circ }.\) \circ }.\)Ответ ОТВЕТ: 13,5. | |
Ответ ОТВЕТ: 10,5. | |
| Задача 10. По данным на рисунке найдите \({\rm{tg}}\,\angle \,FCK,\) если средняя линия трапеции MN = 5, а площадь трапеции CEFK равна 10. Ответ ОТВЕТ: 0,4. | |
| Задача 11. В равнобедренной трапеции ABCD с основаниями AD = 12 и ВС диагональ АС – биссектриса \(\angle \,BAD.\) Найдите среднюю линии трапеции, если периметр трапеции равен 33. Ответ ОТВЕТ: 9,5. | |
Задача 12. В равнобедренную трапецию с основаниями AD и ВС можно вписать окружность. Найдите радиус этой окружности, если средняя линия трапеции равна 10, а AD – BC =12.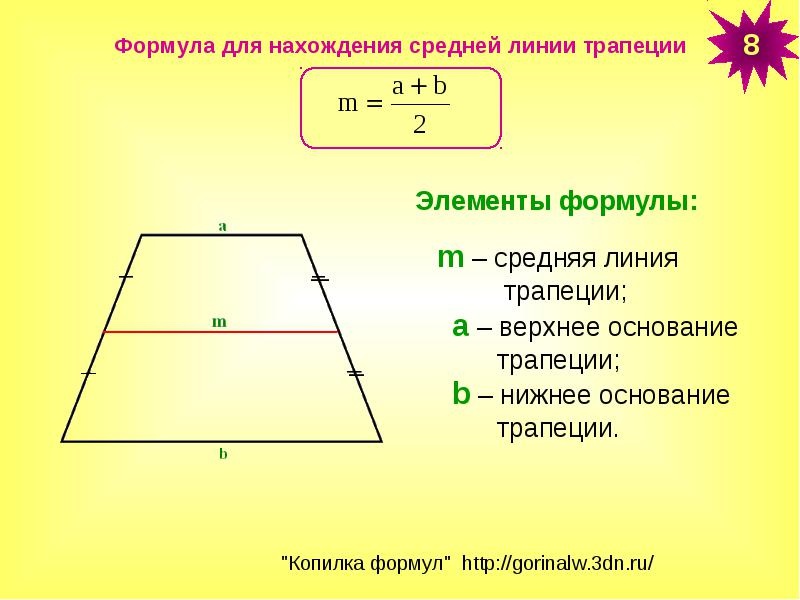 Ответ ОТВЕТ: 4. | |
| Задача 13. По данным на рисунке найдите среднюю линии прямоугольной трапеции KLMN, если ОМ = 6 и ON = 8. Ответ ОТВЕТ: 9,8. | |
| Задача 14. В равнобедренную трапецию можно вписать окружность, радиус которой равен 2. Найдите среднюю линию трапеции, если одно основание в 2 раза больше другого. Ответ ОТВЕТ: \(3\sqrt 2 .\) | |
| Задача 15. В равнобедренную трапецию, площадь которой равна 20, можно вписать окружность. Найдите среднюю линию трапеции, если синус острого угла трапеции равен 0,8. Ответ ОТВЕТ: 5. | |
| Задача 16. По данным на рисунке найдите основание ВС трапеции ABCD Ответ ОТВЕТ: 8. | |
Задача 17. \circ },\) а средняя линия трапеции равна 4. \circ },\) а средняя линия трапеции равна 4.Ответ ОТВЕТ: 6. | |
Реклама
Поддержать нас
Формула площади трапеции
- Главная
- Справочник
- Геометрия
- Формулы площади
- Формула площади трапеции
- Площадь трапеции через основания и высоту
- Площадь трапеции через высоту и среднюю линию
- Площадь трапеции через четыре стороны
- Площадь трапеции через диагонали и угол между ними
- Площадь трапеции через основания и два угла
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами. Площадь трапеции S равна произведению полусуммы ее оснований (a, b) на высоту (h)
Площадь трапеции через основания и высоту
Площадь трапеции равна произведению полусуммы оснований a и b на высоту h
\[ S = \frac{ a + b }{2} \cdot h \]
Площадь трапеции через высоту и среднюю линию
\[ S = m \cdot h \]
Площадь трапеции через четыре стороны
\[ S = \frac{ a + b }{2} \cdot \sqrt{ c^{2} — \left( \frac{ (b-a)^{2} + c^{2} -d^{2}}{2(a-b)} \right) ^{2} } \]
Площадь трапеции через диагонали и угол между ними
Если \(d_{1}\), \(d_{2}\) – диагонали трапеции, а \( \angle \alpha \) – угол между ними , то площадь трапеции можно вычислить по формуле
\[ S = \frac{1}{2} d_{1} \cdot d_{2} \cdot \sin (\alpha) \]
Площадь трапеции через основания и два угла
\[ S = \frac{1}{2} \left( b^{2} — a^{2} \right) \frac{ sin(\alpha) \cdot sin(\beta) }{sin(\alpha + \beta)} \]
- Параллельные стороны называются основаниями трапеции.

- Две другие стороны называются боковыми сторонами.
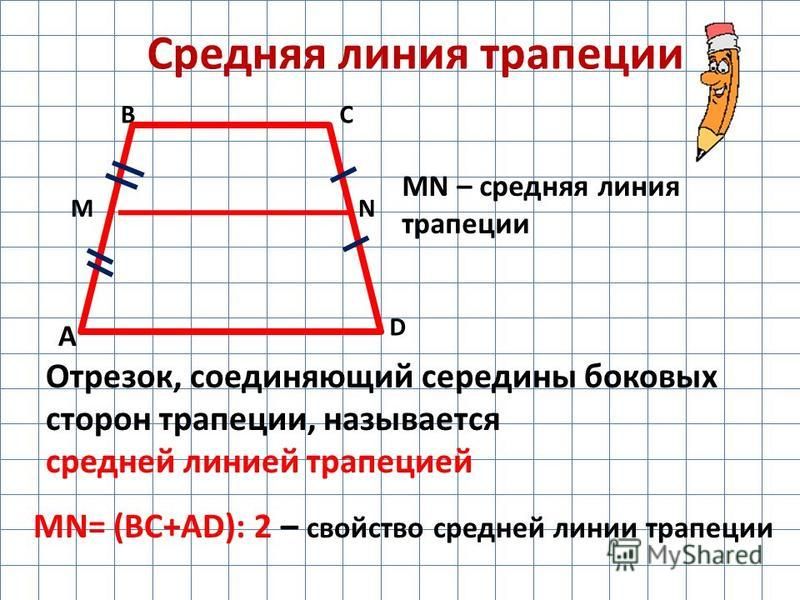
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
- Трапеция, у которой боковые стороны равны, называется равнобокой (или равнобедренной)
- Трапеция, один из углов которой прямой, называется прямоугольной.
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
- У равнобокой трапеции углы при основании равны.
- У равнобокой трапеции диагонали равны.
- Если трапеция равнобокая, то около нее можно описать окружность.

- Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.
- В трапеции середины оснований, точка пересечения диагоналей и продолжения боковых сторон находятся на одной прямой.
Площадь геометрической фигуры, или площадь фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади фигуры выражается числом заключающихся в него квадратных единиц.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Формулы площади Площадь Формулы Геометрия 20465
Источник
Пример 1
Площадь • Формулы • Геометрия
Основания равнобедренной (равнобокой) трапеции равны 8 и 20 сантиметров. Боковая сторона равна 10 см. Найдите площадь трапеции, подобной данной, которая имеет высоту 12 см.
Из вершины B трапеции ABCD опустим высоту BM на основание AD. Из вершины C на основание AD опустим высоту CN. Поскольку MBCN является прямоугольником, то
Из вершины C на основание AD опустим высоту CN. Поскольку MBCN является прямоугольником, то
AD = BC + AM + ND
Треугольники, получившиеся в результате того, что мы опустили из меньшего основания равнобокой трапеции на большее две высоты — равны. Таким образом,
AD = BC + AM * 2
AM = (AD — BC) / 2
AM = ( 20 — 8 ) / 2 = 6 см
Таким образом, в треугольнике ABM, образованном высотой, опущенной из меньшего основания трапеции на большее нам известны катет и гипотенуза. Оставшийся катет, который одновременно является высотой трапеции, найдем по теореме Пифагора:
BM2 = AB2 — AM2
BM2 = 102 — 62
BM = 8 см
Поскольку высота трапеции ABCD равна 8 см, а высота подобной трапеции — 12 см, то коэффициент подобия будет равен
k = 12 / 8 = 1,5
Поскольку в подобных фигурах все геометрические размеры пропорциональны друг другу с коэффициентом подобия, найдем площадь подобной трапеции. Произведение полусуммы оснований подобной трапеции на высоту выразим через известные геометрические размеры исходной трапеции и коэффициент подобия:
Sпод = (AD * k + BC * k ) / 2 * ( BM * k )
Sпод = ( 20 * 1,5 + 8 * 1,5 ) / 2 * (8 * 1,5) = ( 30 + 12 ) / 2 * 12 = 252 см2
252 см2
Уровень8 класс ПредметМатематика СложностьПростая
Пример 2
Площадь • Формулы • Геометрия
Диагональ равнобокой трапеции является биссектрисой ее острого угла и делит среднюю линию трапеции на отрезки длиной 15 см и 33 см.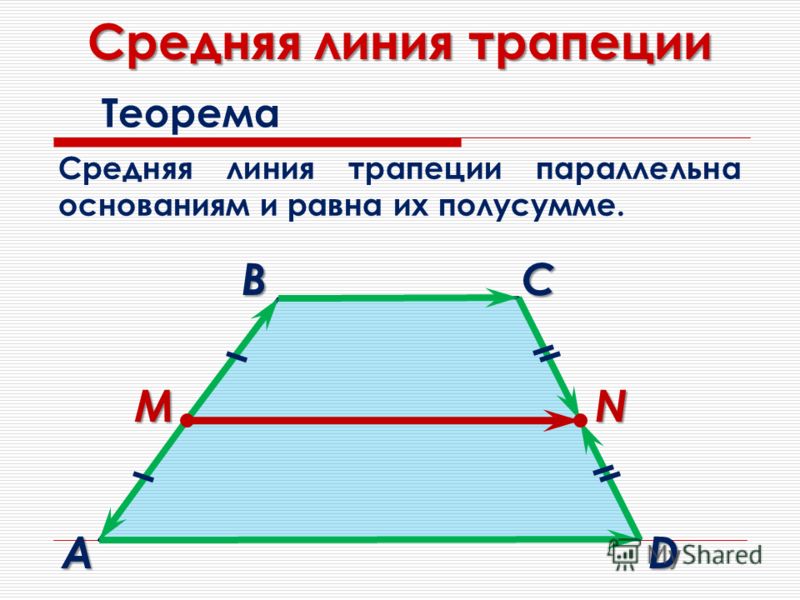 Вычислить (в см2) площадь трапеции.
Вычислить (в см2) площадь трапеции.
Пусть \( ABCD \) — трапеция, \( AC \) — диагональ трапеции и биссектриса острого угла \( \angle A \), т.е. \( \angle BAC=\angle CAD \). \( EF \) — средняя линия трапеции. \( EO=15 \) см, \( OF=33 \) см (\( AC \) пересекает \( EF \) в точке \( O \)). Опустим высоты на \( AD \) из \( B \) и \( C \) (\( BM\perp AD \), \( CK\perp AD \)).
\( S_{ABCD}=\frac{AD+BC}{2}\cdot BM=EF\cdot BM \)
\( EF=EO+OF=15+33=48 \) см
Рассмотрим треугольники \( \triangle ABC \) и \( \triangle ACD \) для которых \( EO \) и \( OF \) являются соответственно средними линиями. Значит \( BC=2\cdot EO=30 \) см, \( AD=2\cdot OF=66 \) см.
\( \angle CAD=\angle BCA \) как внутренние накрест лежащие при параллельных прямых \( BC\parallel AD \) и секущей \( AC \), но по условию \( \angle CAD = \angle BAC \), следовательно \( \angle BCA = \angle BAC \) и треугольник \( \triangle ABC \) равнобедренный, т.е. \( AB=BC=30 \) см.
Тогда площадь трапеции равна \( S_{ABCD}=48\cdot24=1152 \) см2.
1152 см2.
Уровень8 класс ПредметМатематика СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Формула площади прямоугольного треугольника
Площадь прямоугольного треугольника равна половине произведения катетов треугольника
Формулы площади Площадь Формулы Геометрия
Формула площади равнобедренного треугольника
Площадь равнобедренного треугольника равна произведению половины основания треугольника на его высоту
Формулы площади Площадь Формулы Геометрия
Формула площади равностороннего треугольника
Площадь равностороннего треугольника — половина произведения его основания на высоту
Формулы площади Площадь Формулы Геометрия
Формула площади круга
Площадь круга равна произведению квадрата радиуса на число пи, или половине произведения длины ограничивающей его окружности на радиус.

Формулы площади Площадь Формулы Геометрия
Формула площади параллелограмма
Площадь параллелограмма равна произведению его основания (a) на высоту (h)
Формулы площади Площадь Формулы Геометрия
Формула площади прямоугольника
Площадь прямоугольника равна произведению его сторон
Формулы площади Площадь Формулы Геометрия
Формула площади ромба
Площадь ромба равна произведению длины его стороны на высоту (a, h), или половине произведения его диагоналей.
Формулы площади Расчёт Площадь Формулы Геометрия Фигуры
Формула площади квадрата
Площадь квадрата равна квадрату его стороны.
Формулы площади Площадь Формулы Геометрия
Что такое дюйм? Чему равен 1 дюйм?
Дюйм — это длина, которая соответствует 2,54 сантиметра (приблизительно 25 миллиметров)
Размеры и расстояния Длина Формулы
Сколько метров в километре?
В одном километре содержится тысяча метров.
 1 км = 1000 м
1 км = 1000 мРазмеры и расстояния Длина Формулы
Сколько весит ребенок?
Согласно нормам Всемирной Организацией Здравоохранения (ВОЗ)
Масса и вес Масса Теория Единицы измерения
Что такое Ватт
1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль.
Электротехника Формулы Физика Теория Электричество
Бесплатный генератор паролей онлайн
Создать бесплатно пароль любой длины и уровня сложности для ваших приложений, аккаунтов, соц. сетей, паролей к Windows, зашифрованным архивам и т.д.
Работа с текстом Генератор Инструмент Текст Пароли
Закон Авогадро
В равных объемах газов (V) при одинаковых условиях (температуре Т и давлении Р) содержится одинаковое число молекул.
Законы термодинамики Формулы Физика Теория 10 класс Закон Термодинамика Динамика
Закон Гука
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.

Законы Формулы Физика Теория Закон
Что такое масса, вес нетто и вес брутто: в чем разница? Что больше: вес, масса нетто или брутто?
Вес — это физическая величина, а именно сила, воздействующая на горизонтальную поверхность или вертикальную подвеску.
Масса и вес Масса Физика Теория Единицы измерения
математических слов: медиана трапеции
математических слов: медиана трапеции
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Математическая задача: трапеция — центральная медиана
Центральная медиана делит трапецию на две меньшие трапеции.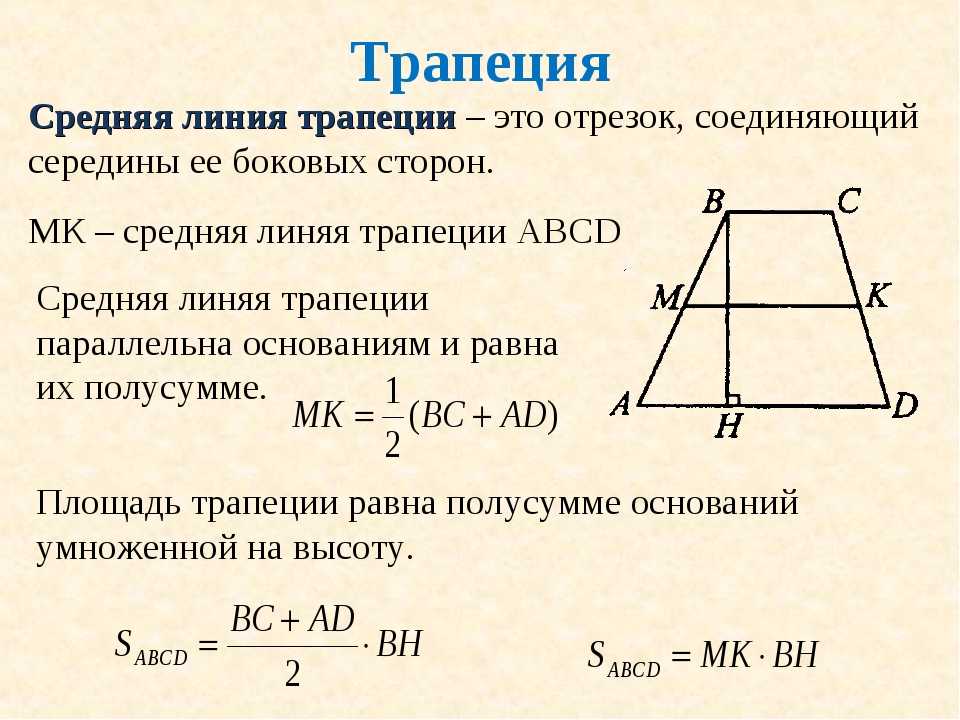 Найдите отношение его площадей.
Найдите отношение его площадей.
Правильный ответ:
p = (3a+c)/(a+3c)Пошаговое объяснение:
S1=((a+c)/2+c)h/2 S2=((a+c)/2+a)h/2 p=S2:S1 =((а+в)/2+а)/((а+в)/2+в) р=(1,5а+0,5в)/(0,5а+1,5в) р=(3а+в)/ (a+3c)
Вы нашли ошибку или неточность? Не стесняйтесь
написать нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Воспользуйтесь нашим калькулятором коэффициентов.
Чтобы решить эту математическую задачу, вам необходимо знать следующие знания:
- алгебра
- Экспрессия переменной из формулы
- Planimetrics
- Площадь формы
- Trapezoid
- Основные функции
- .
- средняя школа
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: видео1
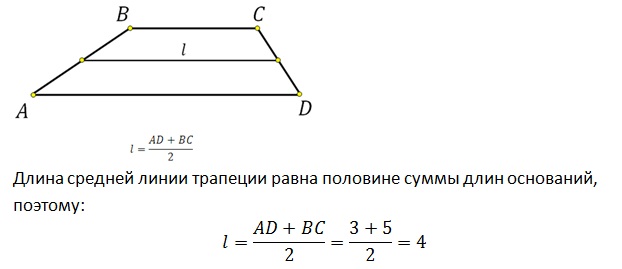
- Длина 26
Длина медианы трапеции составляет 10 дюймов. Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина более короткого основания:
Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина более короткого основания: - Внутренние углы
Величина внутреннего угла при центральной вершине C равнобедренного треугольника ABC равна 72°. Прямая p, параллельная основанию этого треугольника, делит треугольник на трапецию и меньший треугольник. Насколько велики внутренние углы трапеций - Стороны 2
Стороны трапеции относятся как 2:5:8:5. Площадь трапеции равна 245. Найдите высоту и периметр трапеции. - Герб
Класс создал свой герб, который имел форму равнобедренной трапеции ABCD (короткое основание а = 4,5 см, более длинное 2а = 9 см).см, высота трапеции 6 см) и полукруг с центром S и диаметром АВ. Три одинаковых равнобедренных треугольника fo - Трети трапеции
Трапеция ABCD имеет параллельные стороны AB и CD. Точка Е лежит на стороне АВ. Отрезок DE делит трапецию на две части одинаковой площади. Найдите длину отрезка AE. - Концентрический 6751
Дана окружность K с радиусом r = 8 см. Какого радиуса должна быть меньшая концентрическая окружность, которая делит окружность K на две части одинаковой площади?
Какого радиуса должна быть меньшая концентрическая окружность, которая делит окружность K на две части одинаковой площади? - МО Z9–I–2 — 2017
VO является более длинным основанием в трапеции VODY, а диагональное пересечение K делит линию VD в отношении 3:2. Площадь треугольника КОВ равна 13,5 см². Найдите площадь всей трапеции. - MO Z8–I–6 2018
В трапеции KLMN KL имеет основание 40 см и MN 16 см. Точка P лежит на прямой KL так, что отрезок NP делит трапецию на две части одинаковой площади. Найдите длину линии КП. - Трапеции
В равнобедренной трапеции ABCD мы знаем: AB||CD, |CD| = c = 8 см, высота h = 7 см, |∠CAB| = 35°. Найдите площадь трапеции. - Концентрические окружности
Дана окружность K радиусом r = 8 см. Насколько большим должен быть радиус меньшей концентрической окружности, которая делит окружность К на две части одинаковой площади? - Круги
Площади двух кругов находятся в соотношении 2:20. Диаметр большего круга равен 20. Вычислите радиус меньшего круга.
Вычислите радиус меньшего круга. - Разделение равнобедренного треугольника
Как разделить равнобедренный треугольник на две части с равными площадями, перпендикулярными оси симметрии (на трапецию и треугольник)? - Трапеция KLMN
Трапеция KLMN имеет основания KL 40см и MN 16см. В основании KL находится точка P. Отрезок NP делит трапецию на звенья одинаковой площади. На каком расстоянии точка P от точки K? - См. гармоники
Верно ли, что размер центрального сегмента любой трапеции равен среднему гармоническому размеру ее оснований? Докажите это. Центральный отрезок пересекает пересечение диагоналей и параллелен основаниям. - Две земли
Общая площадь двух соседних земель равна 964 м². Второй участок меньше на 77 м 2 , вдвое больше первого участка. Найдите площади каждой земли. - Отношение площадей треугольников
В равностороннем треугольнике ABC точка T является его центром тяжести, точка R является образом точки T в осевой симметрии вдоль линии AB, а точка N является образом точки T в осевой симметрии вдоль линии BC.



 1 км = 1000 м
1 км = 1000 м
 Медиана параллельна основаниям.
Примечание. Его длина равна арифметической
среднее значение длин
базы.
Медиана параллельна основаниям.
Примечание. Его длина равна арифметической
среднее значение длин
базы.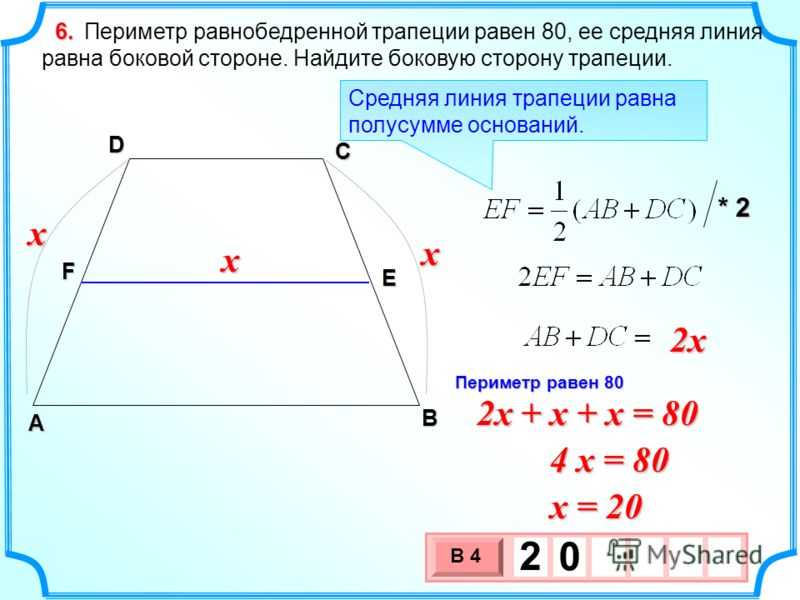 Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина более короткого основания:
Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина более короткого основания: Какого радиуса должна быть меньшая концентрическая окружность, которая делит окружность K на две части одинаковой площади?
Какого радиуса должна быть меньшая концентрическая окружность, которая делит окружность K на две части одинаковой площади?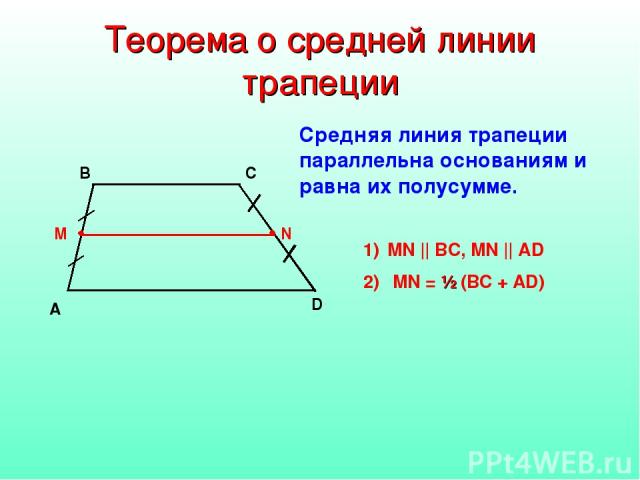 Вычислите радиус меньшего круга.
Вычислите радиус меньшего круга.