Обратная матрица и ее вычисление. Матричные уравнения
Определение 25. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае она называется вырожденной.
Определение 26. Обратной к квадратной матрице называется матрица , которая удовлетворяет условию
. (16)
Теорема 3. Матрица A тогда и только тогда имеет обратную матрицу, когда она невырожденная.
Доказательство.
Достаточность. Для матрицы ;, составим матрицу из алгебраических дополнений и затем транспонируем ее. Получившуюся в результате матрицу обозначим и назовем присоединенной (или союзной) к A. Иными словами,
где – алгебраическое дополнение
Вычисляя произведения и матриц, с учетом теоремы 1 получим
.
Разделив последнее соотношение на величину, имеем:
откуда c учетом равенств (16), (10), найдем: . Мы получили формулу нахождения обратной матрицы и, следовательно, доказали ее существование.
Таким образом, формула для вычисления обратной матрицы имеет вид:
(17)
Замечание. Для каждой невырожденной матрицы А существует единственная обратная матрица .
Существует еще
один способ нахождения обратной матрицы
при помощи элементарных преобразований.
Этот способ состоит в следующем:
составляется матрица размера
,
при помощи приписывания к матрице A справа единичной матрицы. Элементарными
преобразованиями строк преобразуют
полученную матрицу так, чтобы обратить
ее левую половину в единичную матрицу.
Свойства обратных матриц:
1. .
Непосредственно следует из равенства 16.
2. .
Доказательство.
. Следовательно, матрицы и обратные по отношению друг к другу, т. е. .
3. .
Доказательство.
Из соотношения 16: . По свойству 4 операции транспонирования . Следовательно, матрицы и взаимообратные, т. е. .
Определение 27. Простейшими матричными уравнениями будем называть уравнения следующих трех типов:
, , , (18)
где , , – некоторые числовые матрицы, а – неизвестная матрица, которую нужно найти.
Под решением
матричного уравнения будем понимать
матрицу X, которая обращает матричное
уравнение в тождество.
Искать решение матричных уравнений будем с помощью обратных матриц в зависимости от типа уравнения следующими тремя способами:
1) Если, то домножая обе части уравнения на слева, получим .
2) Если, то домножая обе части уравнения на справа, получим .
3) Если и , то домножая уравнение на слева и на справа, получим
.
Использование алгебры матриц в экономике
Понятие матрицы часто используется в практической деятельности. Например, данные о выпуске продукции нескольких видов в каждом квартале года или нормы затрат нескольких видов ресурсов на производство продукции нескольких типов и т. д. удобно записать в виде матриц.
Пример.
Предприятие выпускает продукцию трех
видов P1, P2, P3 и для их производства использует сырье
двух видов. Нормы расхода сырья, стоимость
единицы сырья и план выпуска продукции
приведены в таблице.
Вид сырья | Виды продукции | Стоимость сырья | |||
Р1 | P2 | P3 | |||
1 | 1 | 4 | 2 | 10 | |
2 | 2 | 5 | 3 | 20 | |
План выпуска продукции | 50 | 30 | 40 | ||
Определить
расход сырья, необходимый для выполнения
плана выпуска продукции, а также общую
стоимость сырья.
Решение. Введем матрицы:
где А – технологическая матрица, элементы которой выражают норму расхода сырья для производства каждой единицы продукции, В – матрица-план выпуска продукции, С – матрица-стоимость единицы каждого типа сырья. Тогда общий расход сырья S можно выразить матричным произведением:
что в денежном выражении составит
обратная матрица и матричные уравнения
Похожие презентации:
Электронный курс «Линейная алгебра»
Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 1 семестр
Линейная алгебра и аналитическая геометрия. Дифференциальное исчисление
Определители и их свойства. Лекции 9,10
Линейная алгебра
Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения
Определители
Матрицы.
Элементы линейной алгебры
Линейная алгебра. Матрицы
«Обратная матрица. Матричные уравнения.»
1. Определение обратной матрицы
Квадратная матрица называется невырожденной, если ее
определитель не равен нулю.
A 1 называется обратной по отношению к
матрице А, если A A 1 A 1 A E
Матрица
Теорема. Для невырожденной матрицы А существует
единственная обратная матрица A 1
2. Способы нахождения обратной матрицы
,
1)
С помощью алгебраических дополнений
Алгоритм нахождения обратной матрицы:
1)
Вычисление определителя матрицы А,
2)
Построение и транспонирование матрицы
A11
A
*Т
A 12
…
A1п
алгебраических дополнений
(союзная матрица)
3)
Нахождение обратной матрицы
А 1
1
A*Т
det A
A22
A22
…
A2 n
… Aп1
… …
… Ann
Рассмотрим примеры.
2 3
A
4 5
1.
Найти матрицу, обратную данной2 3
2 5 ( 3) 4 22
1) det A
4 5
2)
5 4
A
3 2
*
3) A*T 5 3
4 2
1 5 3
4) A 22 4 2
1
5. Нахождение обратной матрицы
2. Найти матрицу, обратную данной1) Находим определитель матрицы
2
4 5 18 0 1
3
4
1 2 1
1 1 4
4 5
2
A 3 1 2
4 1 1
0 3 1 ( 1)
1 1
3 2
18 1
(18 3 1) 55 0
1 3
2) Составляем союзную матрицу
3 2
1 2
3
2
A12 ( 1)
(3 8) 11
A11 ( 1)
1 2 3
4
1
1 1
Т.о. обратная матрица существует.
A13 ( 1) 4
3 1
3 4 1
4 1
2 4
2 5
4 5
5
4
(2 16) 18
2 20 22 A23 ( 1)
A21 ( 1)
(4 5) 1 A22 ( 1)
4
1
4
1
1 1
3
A31 ( 1) 4
4 5
2 5
2 4
8 5 13 A32 ( 1)5
(4 15) 11 A33 ( 1) 6
2 12 14
1 2
3 2
3 1
3 11 1
*
A 1 22 18
13 11 14
3) Полученную матрицу транспонируем 4) Обратная матрица
1
13
1
13
3
3
1
A*T 11 22
11
A 1 11 22 11
55
1 18 14
1 18 14
2) С помощью элементарных преобразований (Метод Гаусса)
Алгоритм нахождения обратной матрицы :
1)
К матрице А справа приписывается Е,
2)
Проделывая преобразования над строками расширенной
матрицей (А|Е), матрицу А приводят к Е,
3)
Справа на месте приписанной матрицы Е будет
получена обратная матрица.
7. Элементарные преобразования матриц
• 1 строки матрицы можно менятьместами
• 2 строку можно умножать на любое
число, не равное нулю
• 3 к элементам любой строки можно
прибавлять соответствующие
элементы другой строки,
умноженные на одно и то же число
13. Матричные уравнения
Матричные уравнения – это уравнения, в которых участвуюткак известные матрицы, так и неизвестная матрица, которую
и нужно найти. Существуют два основных типа матричных уравнений.
1 тип (левое умножение)
A X B
A 1 A X A 1 B
E X A 1 B
X A 1 B
2 тип (правое умножение)
X A B
X A A 1 B A 1
X E B A 1
X B A 1
В виде матричного уравнения A X B может быть
записана система линейных уравнений, решение которой
существует, если определитель основной
X A 1 B
матрицы отличен от нуля.
2 5
4 6
Х
1 3
2 1
detA=
2 5
=1≠0, следовательно, А – невырожденная матрица.
1 3
Находим А-1:
А11=(-1)1+1∙3=3,
3
А12=(-1)1+2∙1=-1, А21=(-1)2+1∙5= -5, А22=(-1)2+2∙2=2, А*=
.
А-1=
1 3 5 3 5
1 1 2 1 2
5
1 2
Так как дано матричное уравнение первого типа, то Х=А-1∙В=
3 5 4 6 3 4 ( 5) 2 3 ( 6) ( 5) ( 1) 2 13
4
1 2 2 1 1 4 2 2 1 ( 6) 2 ( 1) 0
15. Матричный метод решения систем линейных уравнений
Если в системе количество уравнений и неизвестных разное,то нельзя говорить об определителе основной матрицы и решать
систему матричным методом нельзя.
English Русский Правила
Представление систем линейных уравнений с использованием матриц
Горячая математикаА система линейных уравнений может быть представлено в матричной форме, используя матрицу коэффициентов, переменную матрицу и постоянную матрицу.
Рассмотрим систему,
2
Икс
+
3
у
знак равно
8
5
Икс
−
у
знак равно
−
2
.
Матрица коэффициентов может быть сформирована путем выравнивания коэффициентов переменных каждого уравнения в строке. Убедитесь, что каждое уравнение записано в стандартная форма с постоянным членом справа.
Тогда матрица коэффициентов для вышеуказанной системы равна
[ 2 3 5 − 1 ] .
Переменные у нас есть Икс и у . Таким образом, мы можем записать переменную матрицу как [ Икс у ] .
В правой части равенства имеем постоянные члены уравнений,
8
и
−
2
. Два числа в таком порядке соответствуют первому и второму уравнениям и, следовательно, занимают места в первой и второй строках постоянной матрицы. Таким образом, матрица становится
[
8
−
2
]
.
Теперь систему можно представить в виде [ 2 3 5 − 1 ] [ Икс у ] знак равно [ 8 − 2 ] .
С использованием умножение матриц вы можете видеть, что матричное представление эквивалентно системе уравнений.
[ 2 3 5 − 1 ] [ Икс у ] знак равно [ 2 ( Икс ) + 3 ( у ) 5 ( Икс ) + ( − 1 ) у ] знак равно [ 2 Икс + 3 у 5 Икс − у ]
Это,
[
2
Икс
+
3
у
5
Икс
−
у
]
знак равно
[
8
−
2
]
.
Приравнивая соответствующие элементы двух матриц, получаем:
2 Икс + 3 у знак равно 8 5 Икс − у знак равно − 2
Теперь давайте разберемся, что означает это представление.
Если рассматривать это как функцию вектора [ Икс у ] , его можно определить как
ф ( [ Икс у ] ) знак равно [ 2 3 5 − 1 ] [ Икс у ]
Тогда, решая систему, мы находим вектор
[
Икс
у
]
для которого
ф
(
[
Икс
у
]
)
знак равно
[
8
−
2
]
.
Это представление может упростить вычисления, потому что, если мы сможем найти обратную матрицу коэффициентов, входной вектор [ Икс у ] можно вычислить, умножив обе части на обратную матрицу.
Аналогично, для системы трех уравнений с тремя переменными
а 1 Икс + б 1 у + с 1 г знак равно д 1 а 2 Икс + б 2 у + с 2 г знак равно д 2 а 3 Икс + б 3 у + с 3 г знак равно д 3
Матричное представление будет
[
а
1
б
1
с
1
а
2
б
2
с
2
а
3
б
3
с
3
]
[
Икс
у
г
]
знак равно
[
д
1
д
2
д
3
]
.
Мы можем обобщить результат на н переменные.
Решение линейных систем с помощью матричной алгебры — концепция
Одним из наиболее часто используемых приложений квадратных матриц является решение систем линейных уравнений. Методы решения систем линейных уравнений с использованием матричной алгебры намного эффективнее, чем ручное вычисление систем с помощью подстановки. Это особенно верно при работе с системами с тремя и более переменными. Два метода матричной алгебры включают сокращение строк и поиск обратного.
матрицы квадратные матрицы матричное уравнение матрица коэффициентов обратная матрица единичная матрица умножение матриц
Матричные алгебры можно использовать для решения линейных систем уравнений, мы покажем вам, как это сделать, но прежде всего позвольте мне взглянуть на 3 матрицы a, x и b.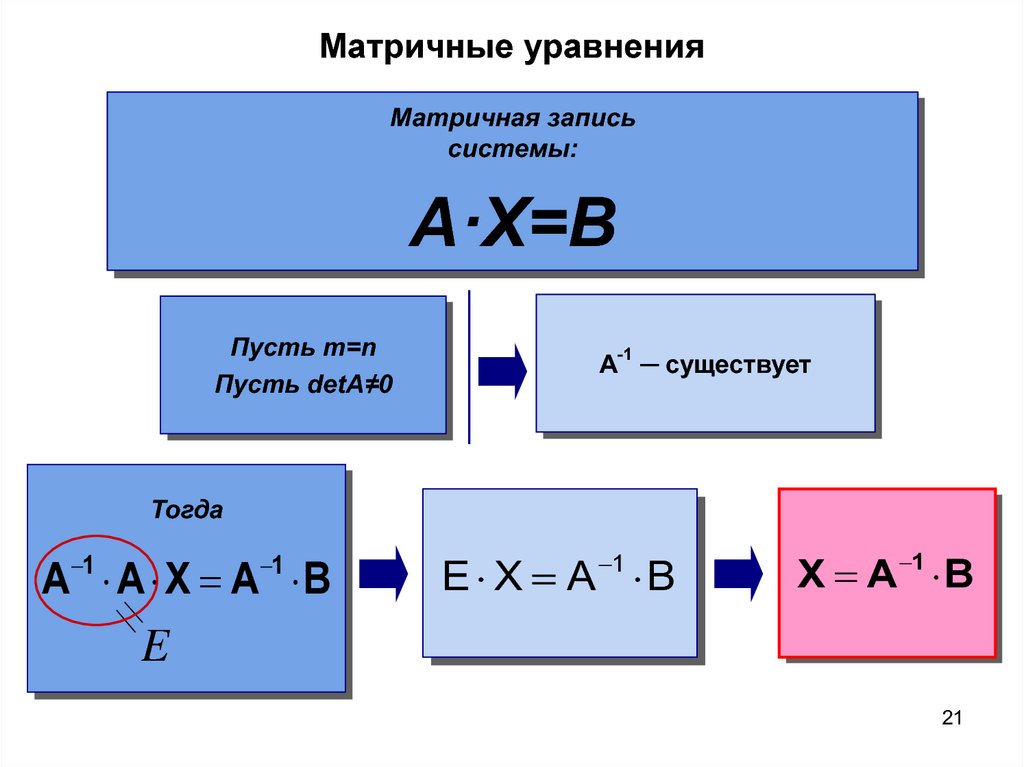
И давайте заметим, что означает уравнение, матричное уравнение ax=b, умножив это, теперь ax равно 5, -3, 7, -4, правильно x равно xy, это 2 на 1. И если я умножу это, я получу 5x -3y, и я получаю 7x-4y правильно. Я получаю эту матрицу 2 на 1, и эта матрица равна b 5,6. Теперь вы знаете, что две матрицы равны, только если они имеют одинаковые размеры, они обе 2 на 1, и они обе имеют одинаковые в точности одинаковые элементы, поэтому 5x-3y должно равняться 5, а 7x-4y должно равняться 6, так что позвольте мне просто запишите это 5x-3y=5, 7x-4y=6 теперь эта система представляет собой систему линейных уравнений эта линейная система полностью эквивалентна матричному уравнению ax=b и это предлагает способ, которым мы можем использовать матричные уравнения для решения линейные системы, поэтому давайте сосредоточимся на решении этой линейной системы.
Теперь, сначала, когда вы превращаете линейную систему в матричное уравнение, давайте сделаем наблюдение, что в левой части вам нужны члены x и y, и вы хотите в этом порядке, так что вот эти числа здесь называются коэффициентами и что вы хотите сделать, это вы хотите придумать матрицу коэффициентов для системы, и это может быть 5, -3, 7, -4, это матрица a, а затем переменная матрица xy, это и затем постоянная матрица 5,6 является матрицей б.
Как теперь решить матричное уравнение ax=b? Что ж, получается, что это в основном похоже на линейное уравнение с действительными числами, единственная разница в том, что мы не можем делить на матрицы, нет способа разделить на матрицы, но вы можете умножить на обратное, поэтому, если матрица а имеет обратную, вы можно умножать на обратное и помните, когда вы умножаете обе стороны на матрицу, вы должны умножать либо обе стороны слева, либо обе стороны справа, потому что умножение матриц не является коммутативным, что вы собираетесь получить здесь обратное время а — это единичная матрица, умноженная на х, а единичная матрица, умноженная на х, будет равна х, так что это х равно инверсии, б это на самом деле ваше решение, у вас будет ху равно, а затем несколько чисел, так что все, что вам нужно сделать, это выяснить, что обратная матрица a. Теперь предположим, что мы знаем, что обратная матрица равна -4, 3 -7, 5. Хорошо, скажем, мы нашли обратную матрицу и нашли это, тогда x будет равняться обратному b, то есть -4, 3, -7, 5 умножить на б, что равно 5,6.