Треугольник. Виды треугольников презентация, доклад
Треугольник и все что его касается.
Выполнили: Терехова Анна
Якушева Наталья
Треугольник
простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны;
часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки;
замкнутая ломаная линия с тремя звеньями.
Виды треугольников по сторонам
Равносторонний
Равнобедренный
Разносторонний
Углы при основании равны;
Медиана является биссектрисой и высотой.
Все углы равны 60°.
Виды треугольников по углам
Прямоугольный
Тупоугольный
Н
О
Т
Остроугольный
катет
катет
гипотенуза
∠PMK=90°-прямой
Свойства медиан треугольника:
1. Медианы треугольника делятся точкой пересечения в отношении 2:1(считая от вершины треугольника).
Медианы треугольника делятся точкой пересечения в отношении 2:1(считая от вершины треугольника).
2. Медиана делит треугольник, равных по площади на два треугольника.
Высота треугольника.
Биссектриса треугольника.
Свойства биссектрис треугольника:
1. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам.
2.Биссектриса треугольника делит площадь треугольника в отношении, пропорциональном прилежащим сторонам.
3. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
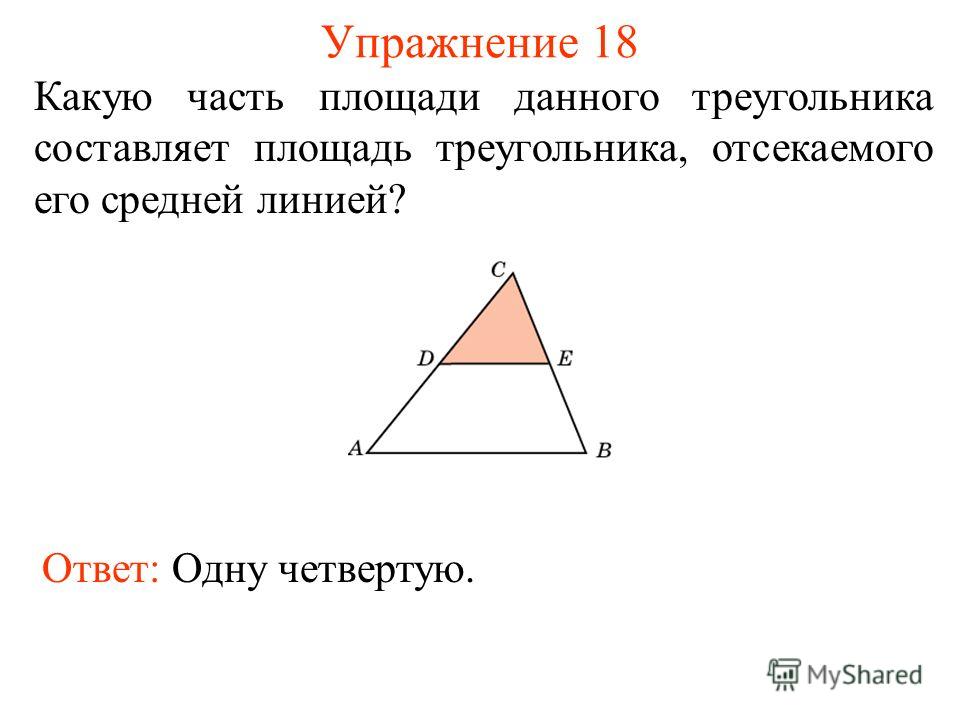
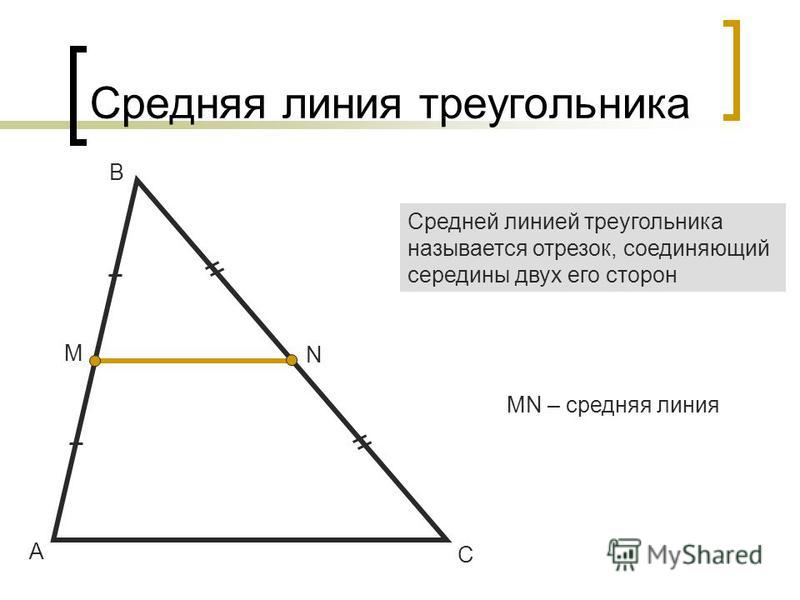
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.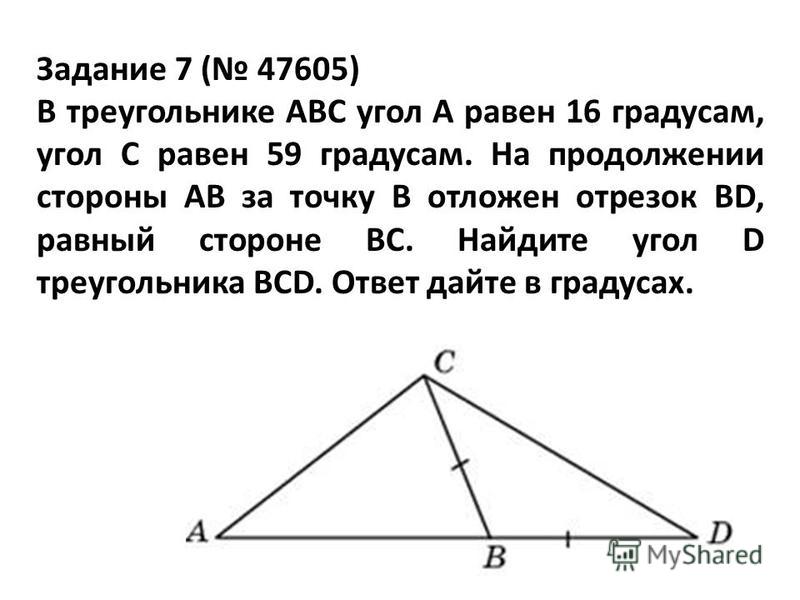
2. Средняя линия треугольника отсекает от треугольника подобный треугольник. Площадь отсекаемого треугольника относится к площади основного треугольника в отношении 1:4.
Длина любой стороны треугольника не превосходит сумму длин двух других.
Площадь треугольника.
Площадь треугольника
Равенство треугольников
Признаки равенства треугольников:
2. По стороне и двум прилежащим к ней углам.
3. По трём сторонам.
1. По двум сторонам и углу между ними.
Подобие треугольников
Признаки подобия треугольников:
1. По двум углам.
По двум углам.
2. По двум сторонам и углу между ними.
3. По трём сторонам.
Равнобедренный треугольник.
Равносторонний треугольник.
Теорема Пифагора
c²= а²+b²
Прямоугольный треугольник.
Доказательство теоремы Пифагора
Дано: а,b- катеты, с-гипотенуза.
Доказать: a2+b2=c2.
Доказательство:
Достроим до квадрата со стороной (a+b).
S1=(a+b)2
S2=4(1/2ab)+c2
Приравняем площади:S1=S2.
(a+b)2=4(1/2ab)+c2
а2+2ab+b2=2ab+c2
а2+b2=c2
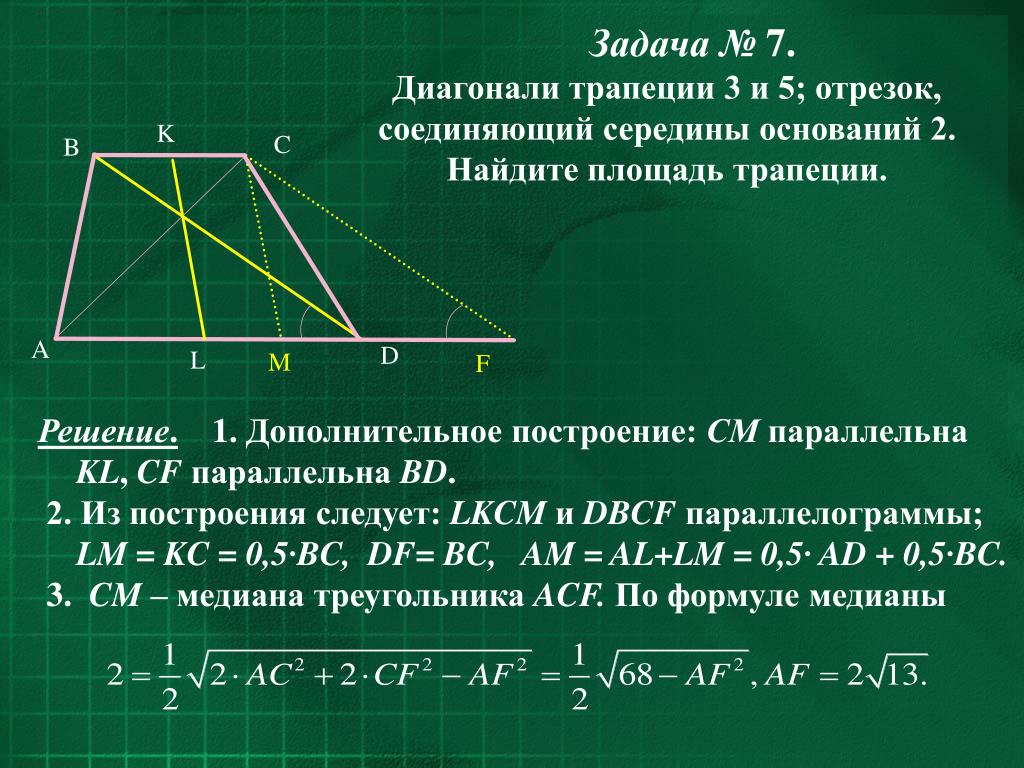
Задача
Вот задача индийского математика 12в. Бхаскары
На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал.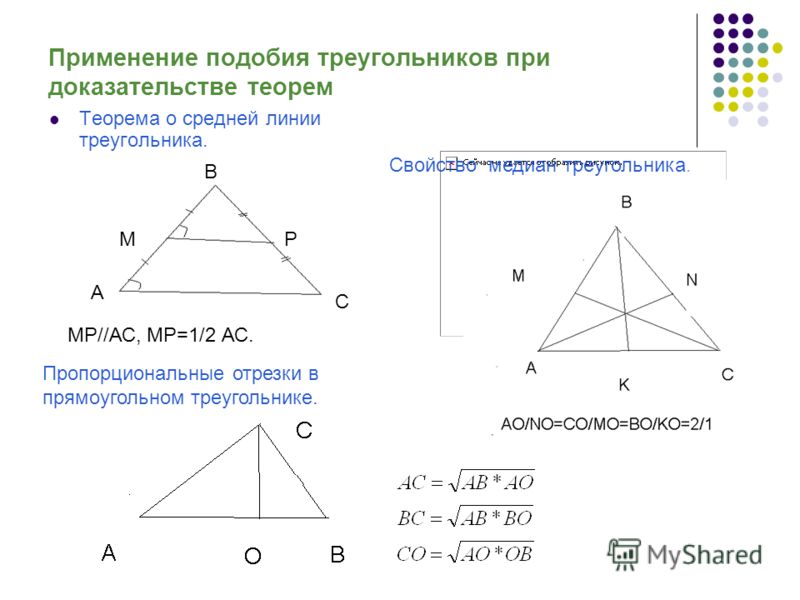 Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола, прошу тебя, скоро теперь мне скажи: у тополя как велика высота?
Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола, прошу тебя, скоро теперь мне скажи: у тополя как велика высота?
Решение:
По теореме Пифагора находим СD:
CD = 3 + 4 = 9 + 16 =25 => CD= 5.
Высота тополя равна: CB+CA. Т.к. CD=CB =>
AB=AC+CD= 3 + 5 = 8.
Ответ: высота тополя 8 футов.
2
2
2
Признаки равенства прямоугольных треугольников.
Признак равенства прямоугольных треугольников по двум катетам
Признак равенства прямоугольных треугольников по катету и гипотенузе
Признак равенства по гипотенузе и острому углу
Признак равенства прямоугольных треугольников по катету и острому углу
Свойства прямоугольного треугольника
1.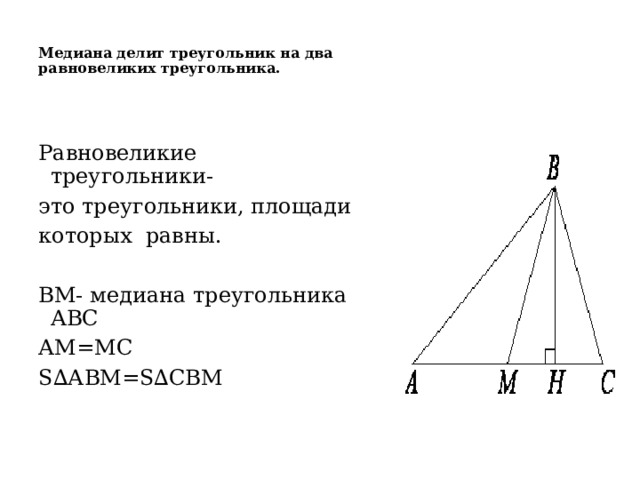 Сумма острых углов прямоугольного треугольника равна 90˚.
Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
3. И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
Теорема синусов.
Теорема косинусов.
Задача
Задача 2.
Спасибо за внимание!
Скачать презентацию
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит… Интересное: Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 5Следующая ⇒
Треугольники Четырехугольники Окружности Комбинации
Треугольники Задание 26 № 78 1. Решение. Проведём отрезок MT, параллельный AP. Тогда MT — средняя линия треугольника APC и CT = TP, а KP — средняя линия треугольника 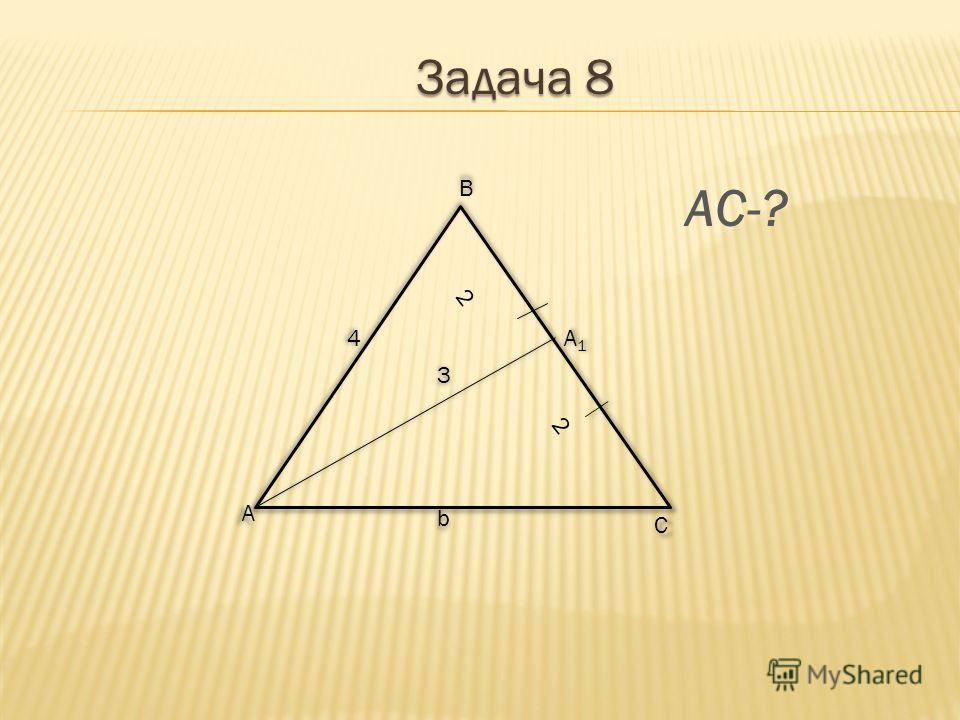 Итак, Значит, Итак, Значит,
Ответ: 0,6. Критерии проверки: Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1301. Задание 26 № 311242 2.Площадь треугольника ABC равна 80. Биссектриса AD пересекает медиану BK в точке E, при этом BD:CD=1:3. Найдите площадь четырехугольника EDCK. Решение.
Пусть AK=KC=3x, тогда AB=2x, так как по свойству биссектрисы. Значит, Пусть S — площадь треугольника ABC, тогда
Таким образом,
Ответ: 36. Критерии проверки: Задание 26 № 340325 3.В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 4 : 1. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM. Решение. Пусть площадь треугольника равна Медиана делит треугольник на два равновеликих треугольника, значит, У треугольников и высота, проведенная к стороне общая, поэтому площади этих треугольников относятся как их основания и откуда:
Проведём прямую параллельную Точка — середина следовательно, — средняя линия треугольника значит, По теореме Фалеса для угла находим: а так как получаем, что Стороны треугольников и сонаправлены, их площади относятся как произведение отношений сонаправленных сторон, поэтому
то есть откуда Тем самым, для искомого отношения площадей имеем:
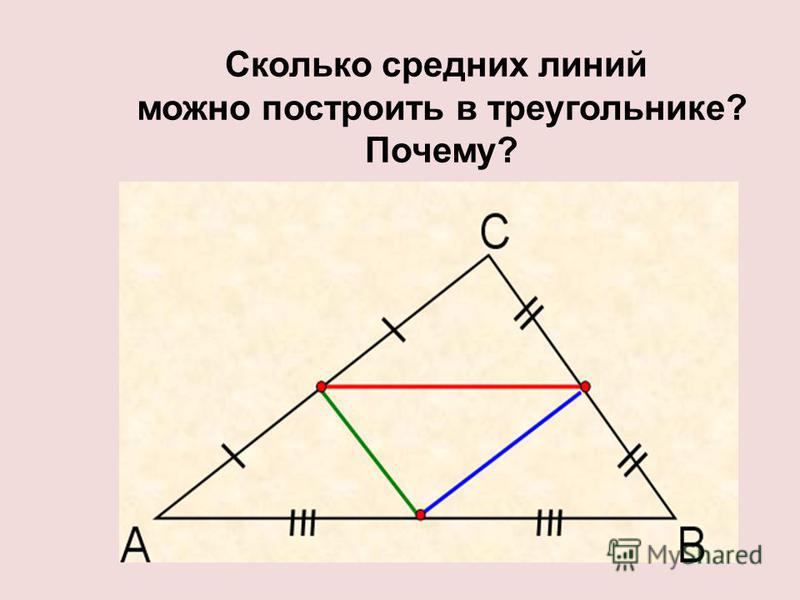
Ответ: Критерии проверки: Задание 26 № 314829 4. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м? Решение. Введём обозначения как показано на рисунке. Здесь AC — положение «журавля» до опускания, BD — положение после опускания, AH — высота, на которую поднялся конец короткого плеча, CK — высота, на которую опустился конец длинного. В равнобедренных треугольниках AOB и COD углы AOB и COD, противолежащие основаниям, равны как вертикальные, поэтому равны и углы при их основаниях. Тем самым, эти треугольники подобны по двум углам, и
Накрест лежащие углы 1 и 2, образованные при пересечении секущей BD прямых AB и CD, равны, поэтому прямые AB и CD параллельны. Тогда стороны углов 3 и 4 попарно параллельны, а значит, эти углы равны. Следовательно, прямоугольные треугольники AHB и CDK подобны, поскольку имеют равные острые углы. Имеем:
 Критерии проверки: Источник: Банк заданий ФИПИ Задание 26 № 314841 5.Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK. Решение. Проведём отрезок параллельный вспомним, что точка — середина следовательно, — средняя линия треугольника значит Аналогично — средняя линия треугольника то есть Пусть площадь треугольника равна Рассмотрим треугольник он имеет общую высоту с треугольником и вдвое большее основание, следовательно его площадь равна Площадь треугольника равна и такую же площадь имеет треугольник поскольку они имеют одну высоту, проведённую из вершины и равные основания. Аналогично площадь треугольника равна площади треугольника а площадь треугольника равна площади треугольника Подведём итог:
Отношение площади четырёхугольника к площади четырёхугольника
Ответ: Критерии проверки: Источник: Банк заданий ФИПИ Задание 26 № 315070 6. Решение. Пусть площадь треугольника равна Медиана делит треугольник на два равновеликих треугольника, поэтому Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Откуда Рассмотрим треугольник — биссектриса, следовательно:
Откуда Выразим площадь треугольника
Найдём отношение площади четрёхугольника к площади треугольника
Ответ: Критерии проверки: Источник: Банк заданий ФИПИ Задание 26 № 314866 7. Решение. Пусть площадь треугольника равна Медиана делит треугольник на два равновеликих треугольника, поэтому Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Откуда Рассмотрим треугольник — биссектриса, следовательно:
Откуда Выразим площадь треугольника
Найдём отношение площади треугольника к площади четырёхугольника
Ответ: Критерии проверки: Источник: Банк заданий ФИПИ Задание 26 № 316361 8. Решение. Из вершины прямого угла прямоугольного треугольника проведём медиану и высоту Тогда
В прямоугольном треугольнике катет равен половине гипотенузы поэтому
Следовательно,
Ответ: 15°, 75° . Критерии проверки: Источник: МИОО: Тренировочная работа по математике 19.02.2014 вариант МА90501. Задание 26 № 333323 9.В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC . Решение. Пусть — точка пересечения отрезков и (см. рис.). Треугольник — равнобедренный, так как его биссектриса является высотой.
; .
По свойству биссектрисы треугольника
Проведём через вершину прямую, параллельную . Пусть — точка пересечения этой прямой с продолжением медианы . Тогда Из подобия треугольников и следует, что Поэтому и Следовательно
; ; Ответ: ; ; Критерии проверки: Источник: МИОО: Тренировочная работа по математике 06.05.2014 вариант МА90701. Задание 26 № 339514 10.Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM. Решение. Пусть площадь треугольника равна Медиана делит треугольник на два равновеликих треугольника, поэтому Биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Откуда Рассмотрим треугольник — биссектриса, следовательно:
Откуда Выразим площадь треугольника
Найдём отношение площади треугольника к площади четырёхугольника
Ответ: Критерии проверки: Задание 26 № 311252 11. Решение. Рассмотрим подобные треугольники и и установим соответствие между их углами. —наибольшая сторона треугольника а значит, — наибольший угол треугольника Так как в треугольнике есть тупой угол то в треугольнике это угол Следовательно, угол треугольника не равен углу треугольника Он также не равен углу т. к. больше его (луч проходит между лучами и ). Следовательно, . По теореме косинусов в треугольнике имеем: Ответ: Критерии проверки: Задание 26 № 340065 12.Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Решение. Проведем построения и введём обозначения как показано на рисунке. Рассмотрим треугольник — биссектриса, по свойству биссектрисы:
Рассмотрим треугольник — биссектриса, по свойству биссектрисы:
Складывая два получившихся равенства, получаем:
Таким образом, периметр треугольника равен 1230.
Ответ: 1230. Критерии проверки: Задание 26 № 351296 13.Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 28, а площадь равна 98. Решение. Из вершины прямого угла прямоугольного треугольника проведём медиану и высоту Тогда
В прямоугольном треугольнике катет равен половине гипотенузы поэтому Следовательно,
Ответ: 15°, 75° . Задание 26 № 352418 14.В треугольнике на его медиане отмечена точка так, что . Найдите отношение площади треугольника к площади треугольника Решение. По свойству медианы, медиана делит треугольник на два равновеликих, т.е. . Из условия известно, что . Следовательно,
Ответ: 0,15 Задание 26 № 353377 15.Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:2, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 16. Решение. Проведем построения и введём обозначения как показано на рисунке. Рассмотрим треугольник — биссектриса, по свойству биссектрисы:
Рассмотрим треугольник — биссектриса, по свойству биссектрисы:
Складывая два получившихся равенства, получаем:
Таким образом, периметр треугольника равен 72.
Ответ: 72. Ответ: 72 Задание 26 № 353380 16.В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 84. Найдите стороны треугольника ABC.
Четырёхугольники Задание 26 № 339388 1.Высота AH ромба ABCD делит сторону CD на отрезки DH = 21 и CH = 8. Найдите высоту ромба. Решение. Введём обозначения как показано на рисунке. Угол и равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники и они прямоугольные, углы и равны, следовательно, эти треугольники подобны, откуда Диагонали ромба делятся точкой пересечения пополам: Получаем:
Из прямоугольного треугольника используя теорему Пифагора найдём
Ответ: 20.
———— Приведем другое решение:
Критерии проверки: Задание 26 № 339373 2.Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28. Решение. Введём обозначения как показано на рисунке. Поскольку и получаем, что — параллелолограмм, следовательно, углы и равны. Рассмотрим треугольники и угол — общий, углы и равны как соответственные при параллельных прямых, углы и — аналогично, следовательно, треугольники и подобны по двум углам. Откуда Аналогично подобны треугольники и откуда Пусть сторона ромба равна а длина короткой диагонали равна Сложим два полученных уравнения:
Площадь ромба можно найти как произведение сторон на синус угла между ними: Площадь параллелограмма можно найти как половину произведения диагоналей на синус угла между ними: Найдём отношение площадей ромба и параллелограмма:
Ответ: Критерии проверки: Задание 26 № 339398 3. Решение. Введём обозначения как показано на рисунке. Продолжим биссектрису до пересечения с прямой в точке Углы и равны как накрест лежащие при параллельных прямых. Значит, следовательно, треугольник — равнобедренный: Найдём Углы и равны как вертикальные. Рассмотрим треугольники и стороны и равны, углы и равны как вертикальные, углы и равны как накрест лежащие при параллельных прямых, следовательно, эти треугольники равны, откуда Проведём прямую параллельную Прямая параллельна прямая параллельна следовательно, четырёхугольник — параллелограмм, откуда Найдём Рассмотрим треугольник заметим, что
Следовательно, по теореме, обратной теореме Пифагора, получаем, что треугольник — прямоугольный, следовательно, — высота трапеции.
Ответ: 250. Критерии проверки: Задание 26 № 340359 4.Основания трапеции относятся как 1:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции? Решение. Введём обозначения как показано на рисунке. Отрезок, проходящий через точку пересечения диагоналей трапеции, равен среднему гармоническому её оснований. Пусть тогда и Поскольку треугольники и подобны, их высоты и , проведенные соответственно к сторонам и относятся как 3:1. Тем самым, для отношения искомого отношения площадей трапеций и имеем:
Ответ: 5:27. Критерии проверки: Задание 26 № 341292 5.Основания трапеции относятся как 2:3. Решение. Пусть диагонали AC и BD трапеции ABCD с основаниями BC = 2a, AD = 3a пересекаются в точке O, а прямая, параллельная основаниям и проходящая через точку O, пересекает боковые стороны AB и CD в точках M и N соответственно (см. рис.). Треугольник BOC подобен треугольнику DOA с коэффициентом поэтому треугольник AMO подобен треугольнику ABC с коэффициентом Значит, Аналогично, Следовательно, Пусть h1 и h2 — высоты подобных треугольников BOC и DOA, проведённые из общей вершины O. Тогда Следовательно,
Ответ: 44:81. Критерии проверки: Задание 26 № 311926 6. Решение. По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции ⇐ Предыдущая12345Следующая ⇒ Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции. Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… |
геометрия — Почему центр тяжести треугольника совпадает с его треугольником средней точки
Задавать вопрос
спросил
Изменено 5 лет назад
Просмотрено 804 раза
$\begingroup$
Вопрос следующий:
Пусть $A’$, $B’$ и $C’$ — треугольник с серединами треугольника $ABC$. Другими словами, $A’$, $B’$ и $C’$ являются серединами отрезков $BC$, $CA$ и $AB$ соответственно.
Докажите, что треугольники $A’B’C’$ и $ABC$ имеют один и тот же центр тяжести.
Мои рассуждения основывались на теореме о средней линии. Нарисовав диаграмму, мы видим, например, что $C’A’$ является средней линией $\треугольника ABC$, а это означает, что $C’A’$ параллелен основанию $AC$ и составляет половину длины треугольника. это также. Следовательно, медиана $B’B$ проходит через середину $C’A’$, включая середину $AC$.
Верны ли мои рассуждения или, по крайней мере, они на правильном пути? Будем очень признательны за любые советы по решению этой проблемы.
- геометрия
- евклидова геометрия
- треугольники
- центроид
- геометрическое преобразование
$\endgroup$
6
$\begingroup$
Пусть $A(a)$, $B(b)$ и $C(c)$ лежат в плоскости Гаусса.
Таким образом, $M\left(\frac{a+b+c}{3}\right)$ является центром тяжести $\Delta ABC$ или
$$M\left(\frac{\frac{b+c}{2}+\frac{a+c}{2}+\frac{a+b}{2}}{3}\right),$ $
который является центром тяжести $\Delta A’B’C’$.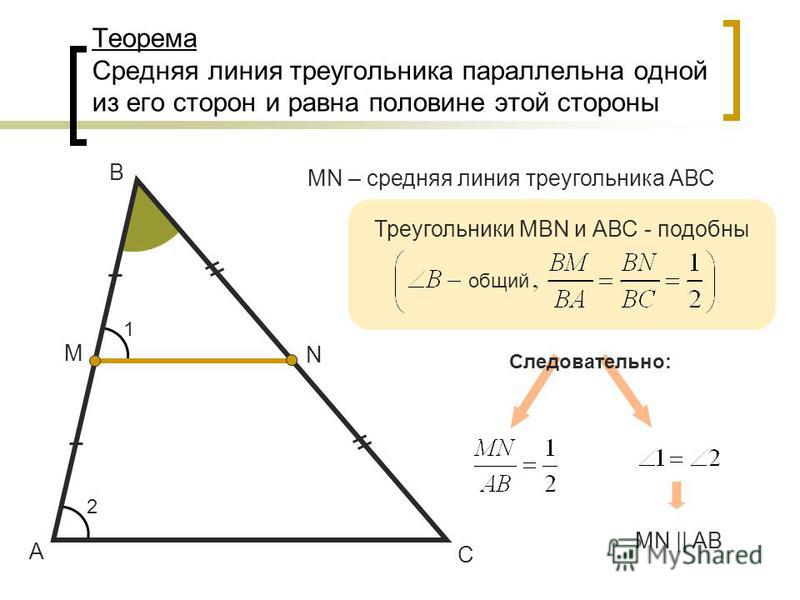
Готово!
$\endgroup$
6
$\begingroup$
Соблюдается гомотетия с центром в центроиде $T$ треугольника $ABC$ и $k=-{1\over 2}$. Эта гомотетия переводит $A$ в $A’$ и так далее. Таким образом, он переводит центроид $T$ в центроид $T’$ $A’B’C’$ (поскольку гомотетия — это преобразование подобия). Но центр гомотетии является фиксированной точкой для гомотетии, поэтому $T’=T$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Середины треугольников и теорема о средней линии треугольника — Криста Кинг Математика
Средние отрезки делят стороны треугольника ровно пополам
В этом уроке мы определим средний отрезок треугольника и используем его для нахождения недостающих длин.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Середина треугольника Подобно сегментам, разделяющим стороны, о которых мы говорили в предыдущем разделе, a средний сегмент в треугольнике – это линия, проведенная поперек треугольника от одной стороны к другой параллельно стороне, с которой она не соприкасается. Разница между любым другим сегментом, разделяющим стороны, и средним сегментом заключается в том, что средний сегмент специально делит стороны, которых он касается, ровно пополам.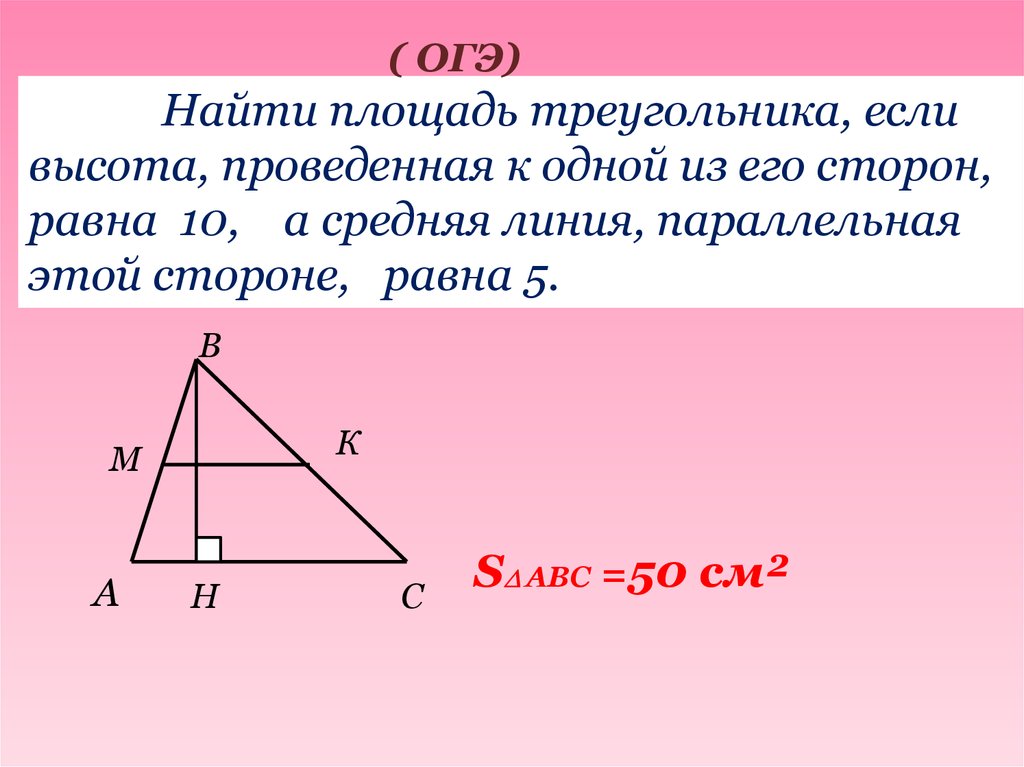 Итак, на рисунке ниже ???\overline{DE}??? режет ???\overline{AB}??? и ???\overline{AC}??? ровно пополам.
Итак, на рисунке ниже ???\overline{DE}??? режет ???\overline{AB}??? и ???\overline{AC}??? ровно пополам.
Помните, что середина имеет особое свойство: она делит стороны треугольника на две равные части, а это означает, что ???\overline{AD}=\overline{DB}??? и ???\overline{AE}=\overline{EB}???.
Треугольники имеют три возможных серединыЕсли ???D??? является серединой ???\overline{AB}???, ???E??? является серединой ???\overline{AC}???, а ???F??? является средней точкой ???\overline{BC}???, затем ???\overline{DE}???, ???\overline{DF}??? и ???\overline{EF} ??? являются средними сегментами треугольника ???ABC???.
Есть два особых свойства средней линии треугольника, которые являются частью средней линии теоремы треугольника.
Средняя линия теоремы треугольника Средняя линия треугольника параллельна третьей стороне треугольника и всегда равна ???1/2??? длины третьей стороны.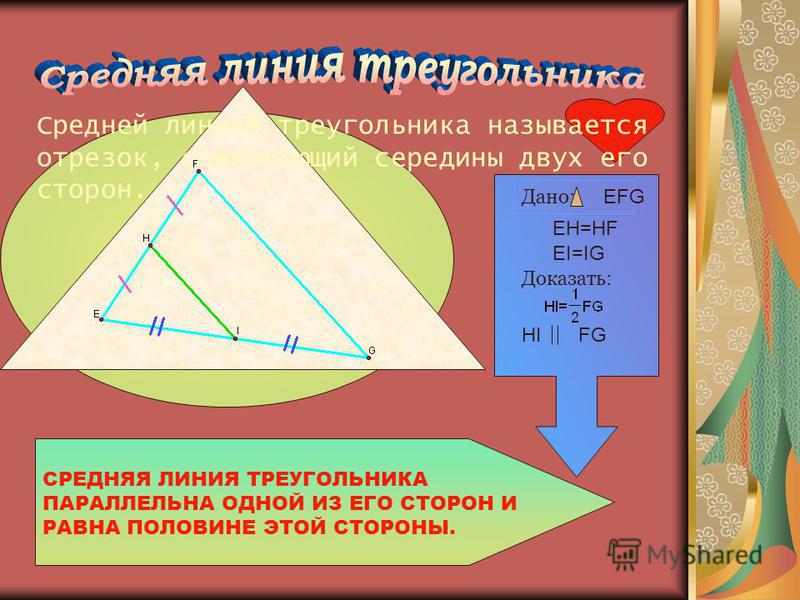 Это означает, что если вы знаете, что ???\overline{DE}??? является средней линией этого треугольника,
Это означает, что если вы знаете, что ???\overline{DE}??? является средней линией этого треугольника,
затем
???\overline{DE}\parallel\overline{BC}??? и ???DE=(1/2)BC???
Тогда также логично сказать, что если вы знаете ???F??? является серединой ???\overline{BC}???, тогда ???DE=BF=FC???.
Работа со средними сегментами для определения других значений в треугольнике
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Учить больше
Решение для x, когда вам известна длина среднего отрезка
Пример
Если ???8??? это середина треугольника, каково значение ???x????
Потому что средняя линия треугольника имеет длину ???8??? мы можем сказать
???8=\frac{1}{2}(2x+4)???
???8=x+2???
???6=х???
a средний сегмент в треугольнике — это линия, проведенная через треугольник от одной стороны к другой параллельно стороне, которой она не касается.
Как найти периметр треугольника, зная длину середины сегмента и длину одной стороны
Пример
Если ???D??? является серединой ???\overline{AB}???, ???E??? является серединой ???\overline{AC}???, а ???F??? является серединой треугольника ???\overline{BC}???, найдите периметр треугольника ???ABC???.
???\overline{DE}???, ???\overline{DF}??? и ???\overline{EF}??? все являются средними сегментами треугольника ???ABC???, что означает, что мы можем использовать тот факт, что средний сегмент треугольника составляет половину длины третьей стороны, чтобы заполнить треугольник.
Обозначим цветом, какой средний сегмент соответствует каждой стороне.
Теперь мы можем заполнить то, что знаем.
Чтобы найти периметр, мы просто сложим все внешние длины вместе.

 ..
..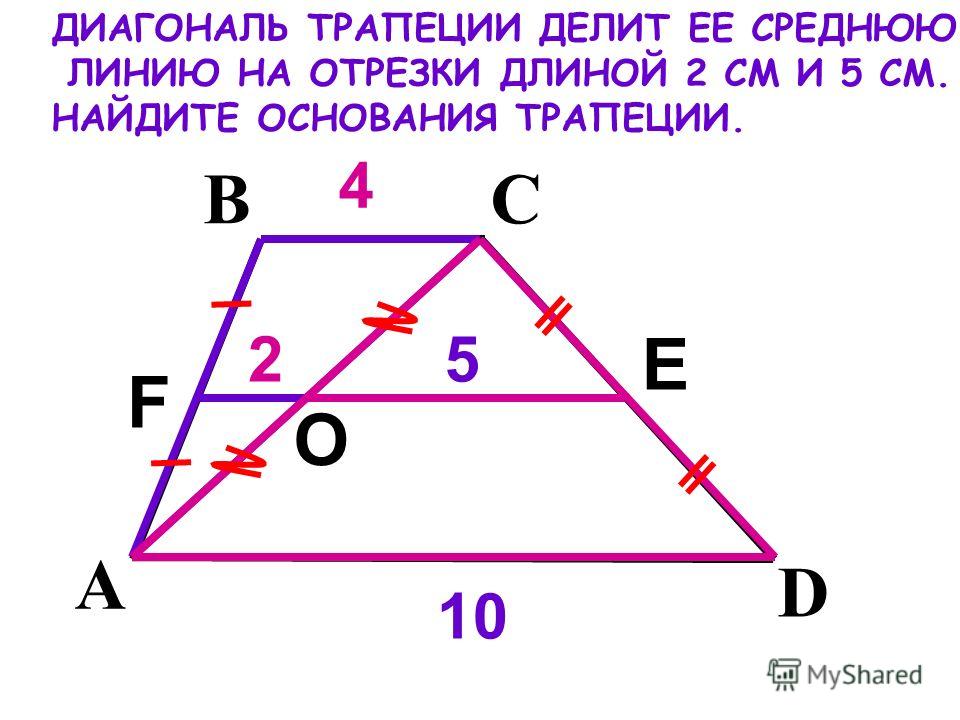 Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.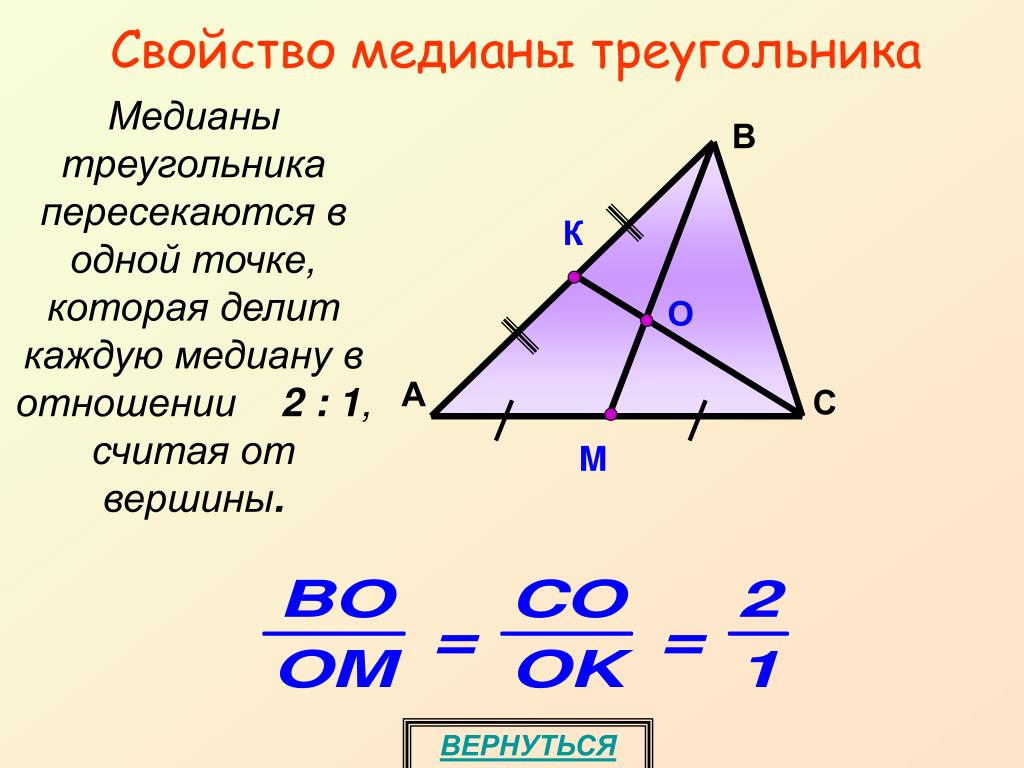

 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC. Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.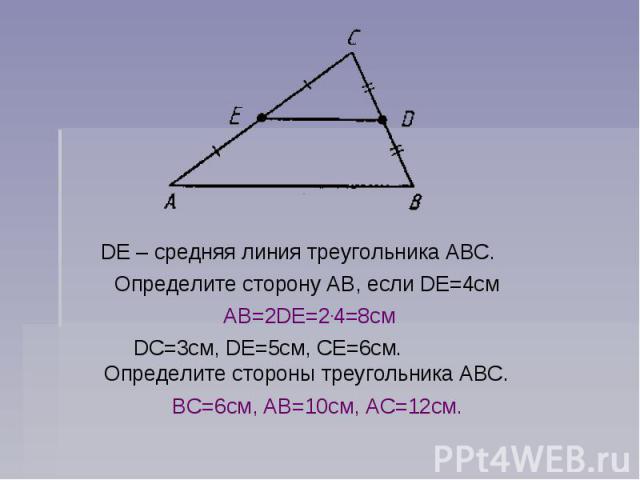 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18. Поэтому
Поэтому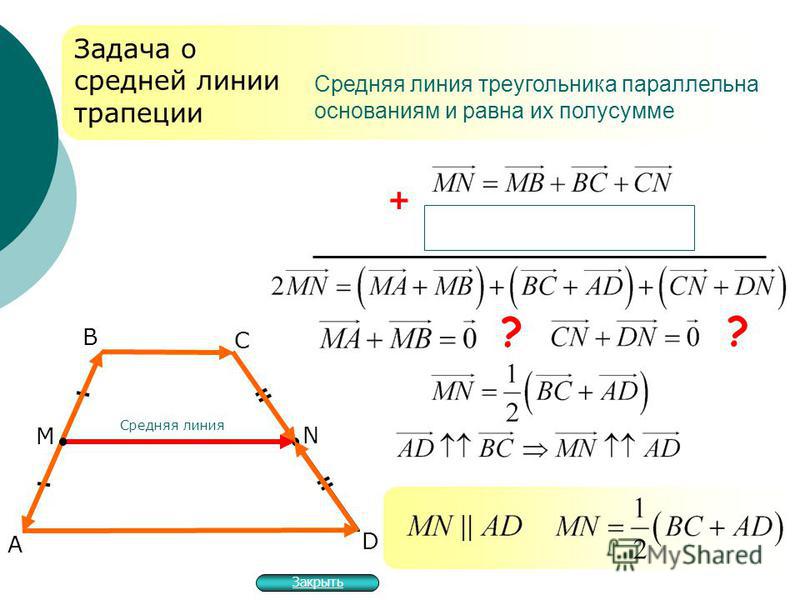 Стороны треугольника равны соответственно. Точка расположена вне треугольника причем отрезок пересекает отрезок в точке, отличной от Известно, что треугольник с вершинами и подобен исходному. Найдите косинус угла если
Стороны треугольника равны соответственно. Точка расположена вне треугольника причем отрезок пересекает отрезок в точке, отличной от Известно, что треугольник с вершинами и подобен исходному. Найдите косинус угла если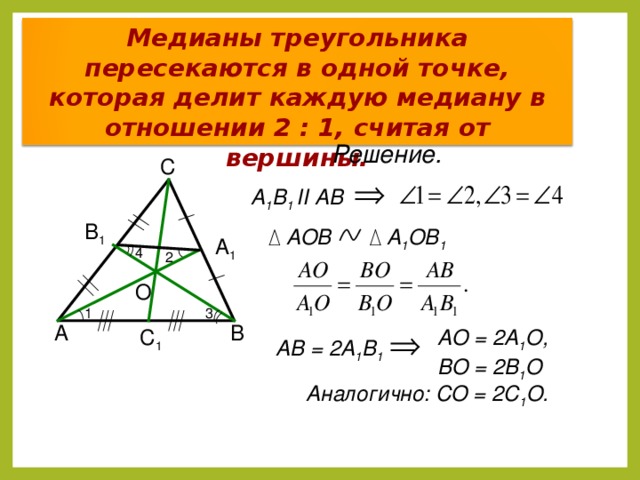 Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
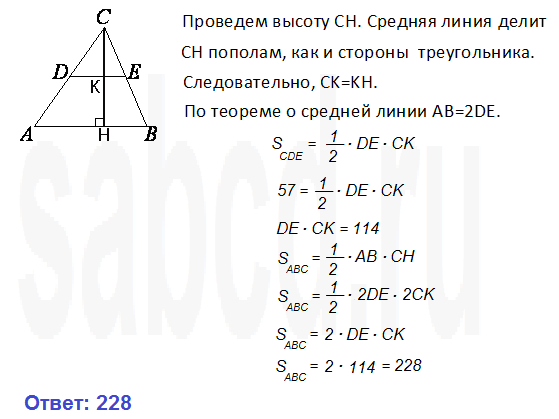
 Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции. Найдём площадь трапеции:
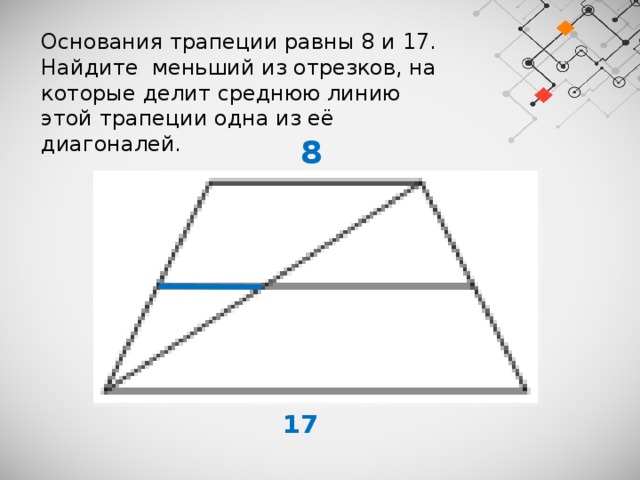
Найдём площадь трапеции: Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?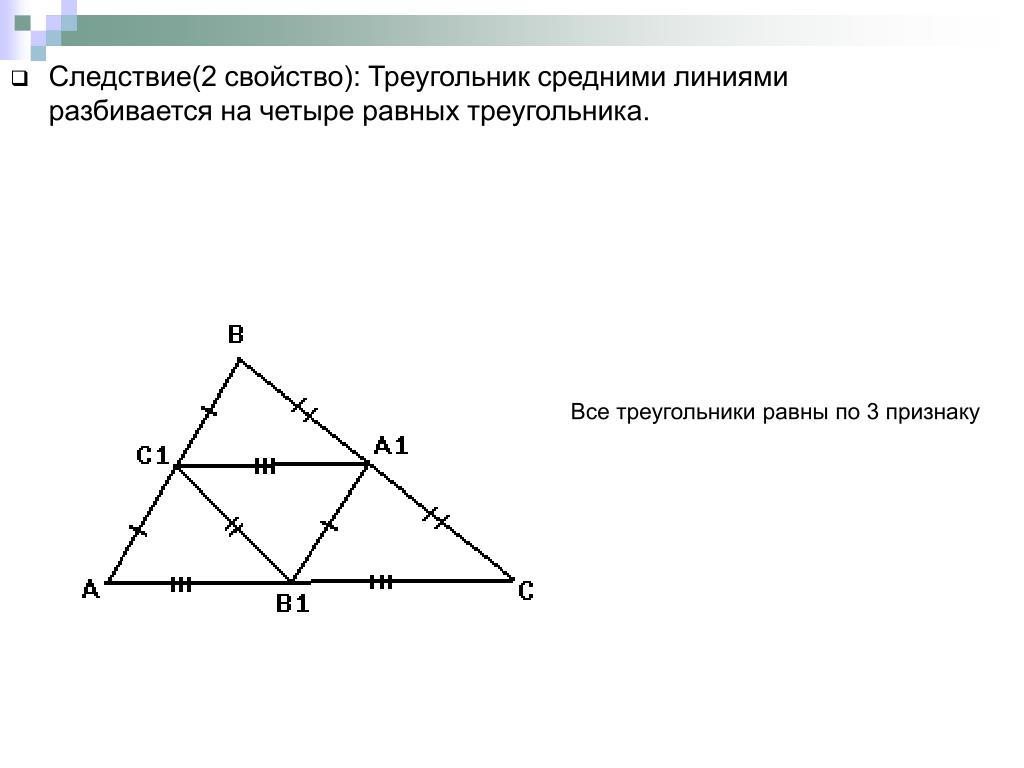 В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .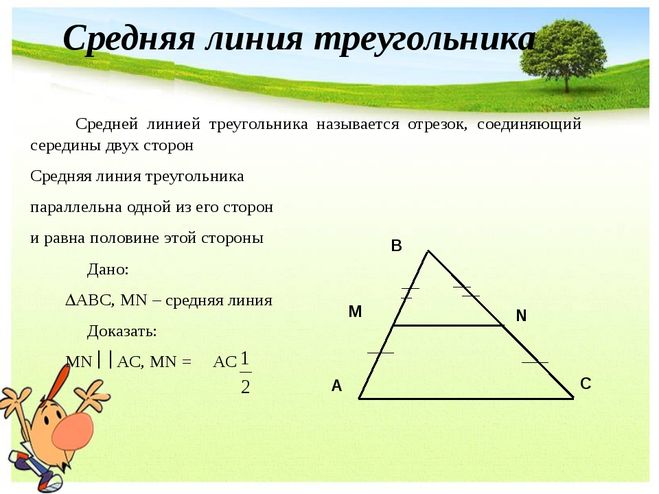 ..
.. Докажите, что треугольники $A’B’C’$ и $ABC$ имеют один и тот же центр тяжести.
Докажите, что треугольники $A’B’C’$ и $ABC$ имеют один и тот же центр тяжести.