Средняя линия треугольника и трапеции: Средняя линия — урок. Геометрия, 8 класс.

Средняя линия прямоугольного треугольника – формула

4.4

Средняя оценка: 4.4

Всего получено оценок: 181.

Обновлено 11 Января, 2021

4.4

Средняя оценка: 4.4

Всего получено оценок: 181.

Обновлено 11 Января, 2021

Средняя линия прямоугольного треугольника – это прекрасная возможность для составителей задач. Большая часть обучающихся знают, что такое средняя линия и умело используют ее свойства в решении. Но как только этот отрезок появляется на чертеже прямоугольного треугольника, то сразу впадают в ступор из-за некоторой необычности рисунка, поэтому разберемся в теме подробнее.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Что такое прямоугольный треугольник?

В общем случае, треугольник это фигура, состоящая из трех сторон и трех углов. В зависимости от величин углов, входящих в состав треугольника выделяют:

• Остроугольные треугольники, все углы которых меньше 90 градусов.
• Тупоугольные треугольники, один из углов которых больше 90 градусов.
• Прямоугольные треугольники, один из углов которых равен 90 градусам.

Прямоугольные треугольники интересны специальными формулами, которые значительно упрощают решение. Но средняя линия прямоугольного треугольника ни чем не отличается от средней линии произвольного. Почему задачи с этим отрезком вызывают затруднения?

Только из-за необычности чертежа Рис. 1. Средние линии прямоугольного треугольника.

Средняя линия

Что такое средняя линия? Это один из характеризующих отрезков любого треугольника. Средняя линия соединяет середины смежных сторон многоугольника.

Средняя линия есть не только у треугольника. Она существует у каждой выпуклой фигуры. При этом свойства средних линий треугольников не всегда совпадают с свойствами средних линий трапеций. Поэтому будьте аккуратны, у каждой фигуры есть свои свойства и признаки.

Рис. 2. Средняя линия трапеции.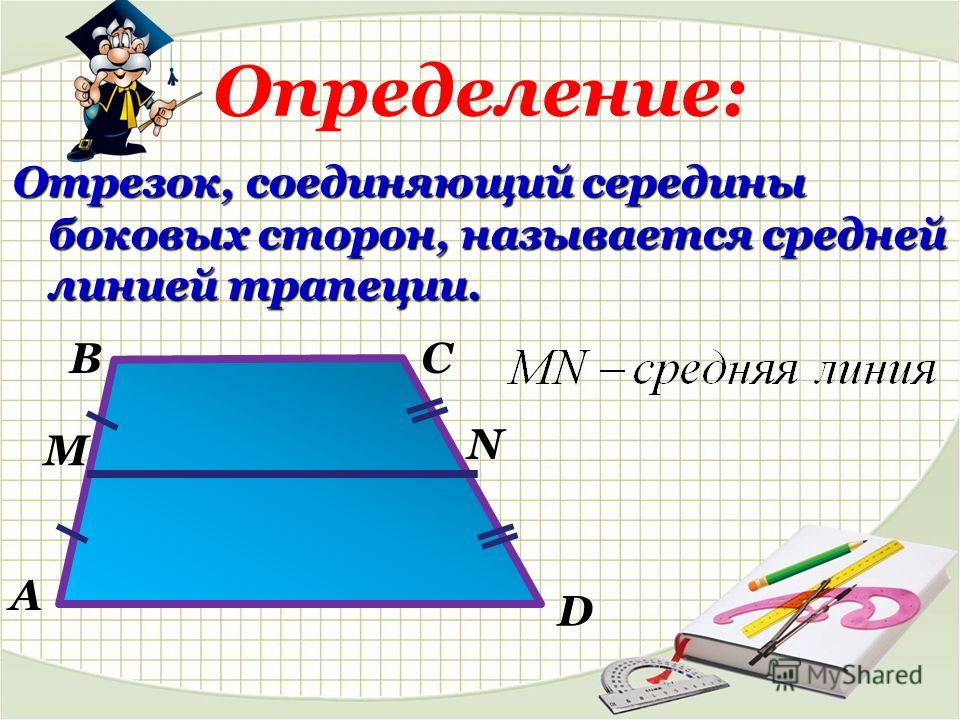

Свойства средней линии

Свойств у средней линии не так много, но все они более чем интересны.

• Средняя линия всегда параллельна стороне, через которую она не проходит. Иначе говорят, что средняя линия параллельна основанию. Так проще запомнить это свойство, но немного страдает формулировка. Дело в том, что в любом треугольнике можно провести 3 средних линии, а основание только одно, поэтому будьте аккуратнее в формулировках.
• Средняя линия равна половине основания. А вернее не основания, а стороны, которую средняя линия не пересекает. Это и есть формула средней линии любого треугольника, в том числе и прямоугольного.
• Средняя линия отсекает треугольник подобный изначальному с коэффициентом подобия 1:2

Если формулировка «Средняя линия параллельна основанию» не совсем правильная, то почему же ее применяют в учебнике? Дело в том, что любое свойство должно быть коротким и ясным для простоты запоминания. Поэтому и сокращают некоторые высказывания.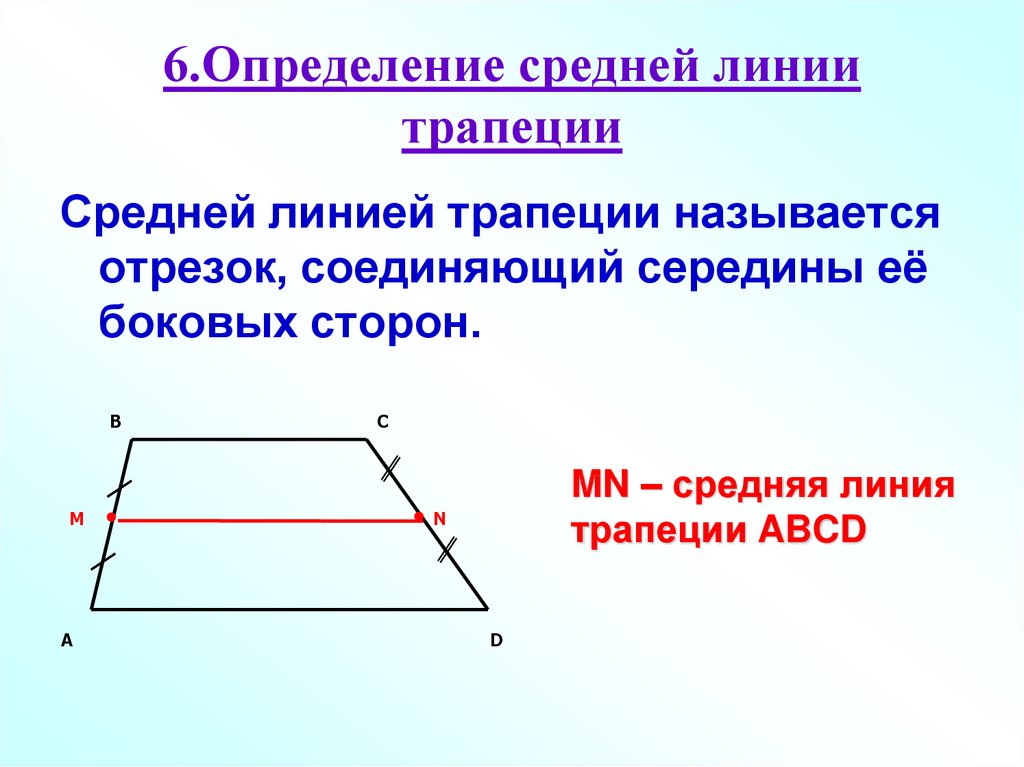

2}=\sqrt{9+16}=\sqrt{25}=5$$

Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.

$$S=5*5*0,5=12,5$$

В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольнику, нужно умножить площадь прямоугольника на 2.

$S=12,5*2=25$ – ответ получен.

Что мы узнали?

Мы узнали, что такое средняя линия прямоугольного треугольника. Поговорили о свойствах средней линии и решили небольшую задачу для закрепления материала.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Милана Швецова

  5/10

• Виктория Белоносова

  10/10

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 181.

---

А какая ваша оценка?

ГДЗ по геометрии 8 класс Атанасян.

Гл.VIII №797. Докажите, что средняя линия трапеции … – Рамблер/класс ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №797. Докажите, что средняя линия трапеции … – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Не могу додуматься, как решить задачу Гл.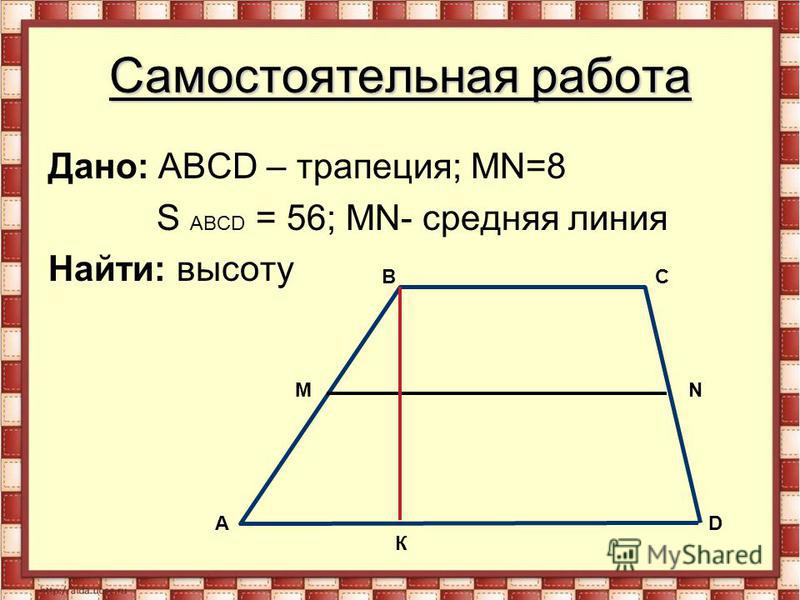 VIII №797.
Докажите, что средняя линия трапеции проходит через середины диагоналей.
 

ответы

Надеюсь помогу, задание Гл.VIII №797 решается вот так:
Средняя линия трапеции параллельна основаниям, следовательно она проходит и через средины сторон треугольников образованных из диагоналей трапеции (по теореме Фалеса).
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №704. Докажите, что точка О — середина гипотенузы…

 Не могу додуматься, как решить задачу Гл.VIII №704, необходима помощь.
Окружность с центром О описана около прямоугольного (Подробнее. ..)

ГДЗАтанасян Л.С.Геометрия

Стороны параллелограмма

Стороны параллелограмма находятся в отношении 4:5. Найти стороны параллелограмма если периметр равен 10.8 см   (Подробнее…)

ГДЗ

Задание 38 Однородные члены предложения. Что такое однородные члены предложения? Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ

Всем привет, поделитесь ответом на задание
Прочитайте.
Рассмотрите условные обозначения однородных членов. (Подробнее…)

ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс

ГДЗ по геометрии 8 класс Атанасян. Гл.IX №780. Докажите, что для любого вектора…

Если не затруднит, объясните задачу  Гл.IX №780.
Докажите, что для любого вектора а справедливы равенства: а)1∙͞а = ͞͞͞а; б) (-1) (Подробнее…)

ГДЗАтанасян Л.С.Геометрия8 класс

ГДЗ, русский язык, 8 класс, Ладыженская, упр. 28. Заполните таблицу своими примерами.

Слова данных частей речи (см. таблицу на с. 22) употребляются только с отрицательной частицей не. Они не образуются с приставкой не-. (Подробнее…)

ГДЗРусский язык8 классЛадыженская Т.А.

средний сегмент треугольника | Облегчение синдрома спешки

 

Теоремы подобия

Докажите теоремы о подобиях

G-СТО 4. Докажите теоремы о треугольниках. Теоремы включают: линия, параллельная одной стороне треугольника, делит две другие пропорционально и наоборот; теорема Пифагора доказана с помощью подобия треугольников.

G-SRT 5. Использовать критерии конгруэнтности и подобия треугольников для решения задач и доказательства взаимосвязей в геометрических фигурах.

Я изо всех сил пытался понять, какие дополнительные теоремы мы должны включить при обучении G-SRT 4. Так что, по крайней мере, на данный момент, мой лучший источник для того, чтобы учить тому, что мы традиционно включаем, — это спросить моих младших и старших, кто недавно прошли стандартизированный тест с высокими ставками для поступления в колледж и получения стипендий. Я понимаю, что моя единственная причина учить чему-то не должна состоять в том, находится ли это «на тесте» или нет, но я не хочу, чтобы мои ученики были в невыгодном положении, когда они идут сдавать тест.

Мы начали модуль «Расширения», показав, что два треугольника подобны, когда есть расширение и, если необходимо, набор жестких движений для отображения одной фигуры на другую. В нашем уроке по теоремам подобия мы обсуждаем критерии подобия треугольников в терминах традиционных теорем подобия: AA~, SAS~, SSS~. Мы формирующе оцениваем, что учащиеся могут использовать теоремы подобия.

      

Цифры похожи? Если да, то почему?

      

Если фигуры подобны, то каково значение x?

Студенты всегда хорошо справляются с первым треугольником, но не со вторым. Вопрос о втором раскрывает неправильные представления учащихся.

Мы кратко изучили еще 3 теоремы, касающиеся подобных фигур.

 

1. Средняя линия треугольника — это отрезок, соединяющий середины двух сторон треугольника.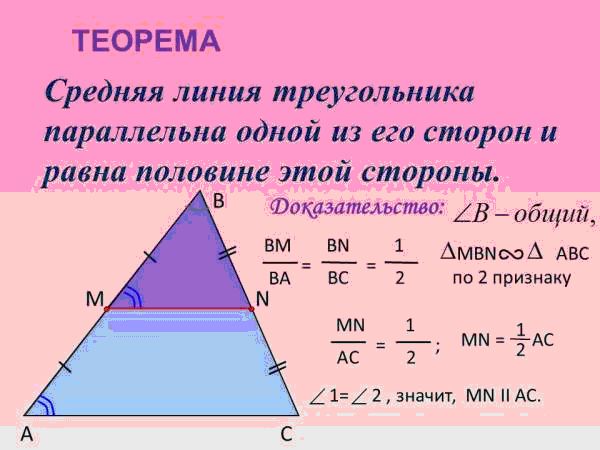 Какая связь между средней линией и третьей стороной треугольника? Для этого исследования мы использовали часть активности Geometry Nspired под названием Triangle Midsegments.

Это пример того, как технология заставляет меня замедляться. Для меня было бы намного быстрее сказать студентам, что середина сегмента параллельна третьей стороне треугольника и что она составляет половину длины третьей стороны треугольника. Но я обнаружил, что учащиеся дольше запоминают информацию, когда они ее понимают: от построения среднего сегмента до наблюдения за тем, что происходит при изменении треугольника.

Мы проводим формирующую оценку, чтобы убедиться, что учащиеся могут использовать то, что они наблюдали.

А потом докажем теорему.

С чего бы вы начали?

Какой стандарт для математической практики был бы полезен?

 

2. Теорема о боковых делителях.

Смотри, что происходит.

Формально оценивайте, чтобы убедиться, что учащиеся могут использовать то, что они наблюдали.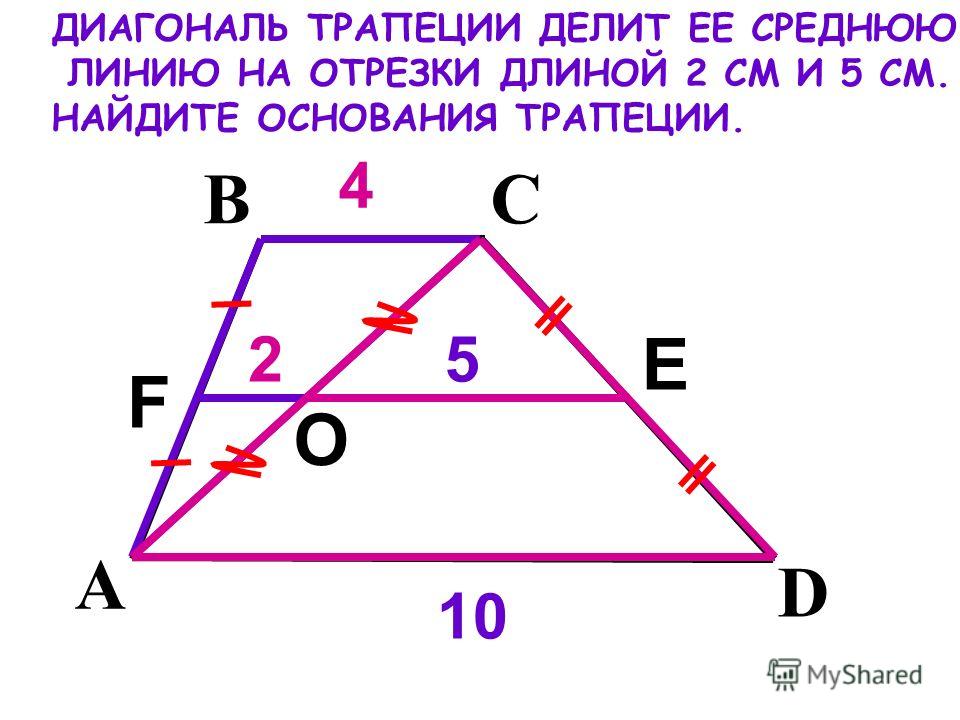

А потом докажи теорему.

С чего бы вы начали?

Какой стандарт для математической практики был бы полезен?

Мы использовали для поиска и использования структуры . Вспомогательная линия дает нам два случая, когда «прямая, параллельная одной стороне треугольника, делит две другие пропорционально», а затем мы можем использовать параллельные прямые и поперечную, чтобы показать, что два треугольника подобны друг другу на AA~ .

 

3. Теорема о биссектрисе угла.

Смотри, что происходит.

Формально оценивайте, чтобы убедиться, что учащиеся могут использовать то, что они наблюдали.

А потом докажи теорему.

С чего бы вы начали?

Какой стандарт для математической практики был бы полезен?

Какие вспомогательные линии были бы полезны?

На самом деле нам не удалось полностью доказать теорему о биссектрисах угла… наше время истекло. Но я думаю, что это нормально. Мы рассмотрели теорему о биссектрисе угла, потому что мои бывшие студенты предположили, что она полезна. И поскольку мы весь год старались наблюдать за тем, что происходит, и доказывать большую часть того, что происходит, мои ученики понимают, что результат не волшебный.

Сегодня утром я начал читать «Радость X». Мне нравится цитата Стивена Строгаца внизу страницы 5: «Логика не оставляет нам выбора. В этом смысле математика всегда включает в себя как изобретение , так и открытие : мы изобретаем концепции, но обнаруживаем их следствия. …в математике наша свобода заключается в вопросах, которые мы задаем, и в том, как мы их преследуем, а не в ожидающих нас ответах».

Итак, путешествие, чтобы задать больше вопросов, продолжается …

 

Теги: теорема о биссектрисе угла, CCSS-M G-SRT.4, CCSS-M G-SRT.5, Geometry Nspired, ищите и используйте структуру , теорема о делителях сторон, TI-Nspire, середина треугольника

Теорема о средней линии – Математический удар по иглобрюху

Добро пожаловать в третью часть второго урока «Теорема о средней линии!» После прочтения этого урока вы должны использовать свойства треугольника для решения задач по геометрии и применять определение треугольника и теоремы о свойствах.

треугольника. Прежде чем мы приступим к собственно уроку, мы должны сначала ответить на предварительный тест.

ПРЕДВАРИТЕЛЬНЫЙ ТЕСТ

Найдите четырех друзей и потребуйте от каждого участника необходимые материалы. Подписаться
данная процедура.
Материалы: 4 куска короткой высокосортной бумаги, карандаш, линейка, клейкая лента, транспортир и ножницы
Процедура:
1. Каждый член группы должен нарисовать и вырезать из облигационная бумага.
(равносторонний треугольник, прямоугольный треугольник, тупоугольный треугольник и остроугольный неравноугольный треугольник)
2. Выберите третью сторону треугольника. Отметьте каждую середину двух других сторон, затем соедините 90 120 средних точек, чтобы сформировать сегмент.
• Нарисованный отрезок выглядит параллельным третьей стороне выбранного вами треугольника?
3. Измерьте нарисованный сегмент и третью выбранную сторону.
• Сравните длины нарисованных отрезков и длины выбранной вами третьей стороны. Что вы
наблюдали?
4. Разрежьте треугольник по нарисованному отрезку.
• Какие две фигуры образуются после разрезания треугольника по проведенному отрезку?
5. С помощью клейкой ленты снова соедините треугольник с другой фигурой таким образом, чтобы их
общая вершина была средней точкой, и что конгруэнтные сегменты, образованные средней точкой, совпадают.
• Какая новая фигура образуется после повторного соединения вырезов? Почему?
• Что вы можете сказать о своих выводах по сравнению с выводами ваших одноклассников?
• Считаете ли вы, что выводы применимы ко всем видам треугольников? Почему?

Предварительный тест помог вам открыть теорему о средней линии. Ниже приведены теоремы или свойства, связанные с треугольниками. Необходимо запомнить эти теоремы, потому что они понадобятся, когда вы будете писать доказательство в два столбца, или теоремы понадобятся при решении вычислений на уроке.

Теорема о средней линии

Теорема 5

• Отрезок, соединяющий середины двух сторон треугольника, параллелен
  третьей стороне и вдвое короче третьей стороны треугольника.

  No related posts.