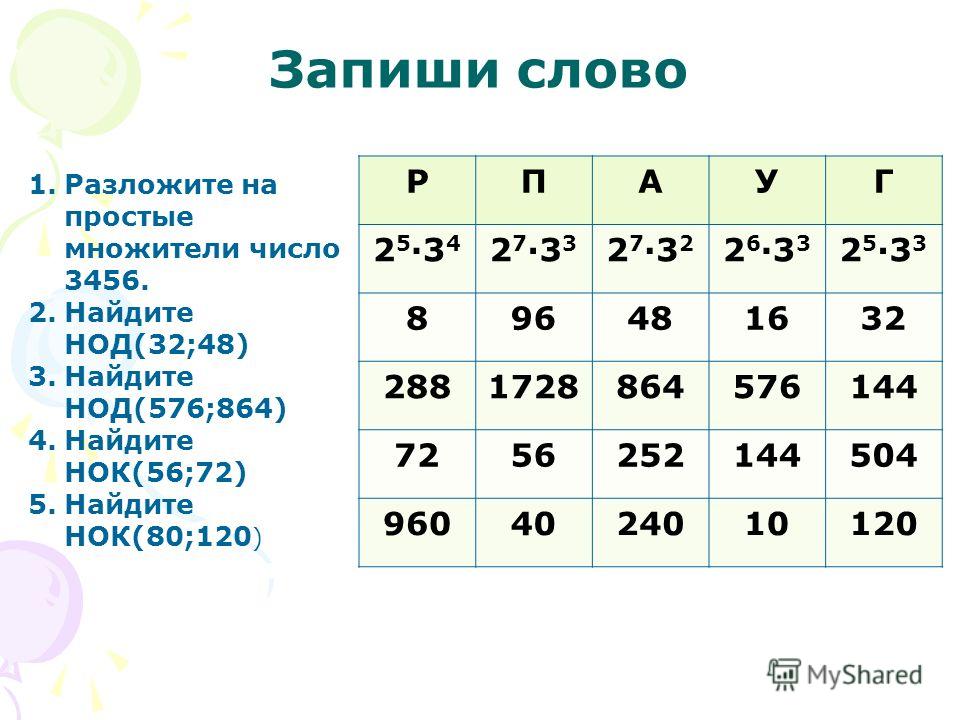
675 разложить на простые множители: Разложить число 675 на простые множители

alexxlab / / Разное

Простые множители числа 673 — Calculatio

Калькулятор «Разложение чисел на простые множители»

Какие простые множители у числа 673?

Ответ: Простые множители числа 673: 673

Объяснение разложения числа 673 на простые множители

Разложение 673 на простые множители (факторизация) — это представление числа 673 как произведения простых чисел. Другими словами, необходимо выяснить, какие простые числа нужно перемножить, чтобы получилось число 673.

Так как число 673 является простым — его невозможно разложить на простые множители. 673 — это единственный простой множитель.

Минимальное простое число на которое можно разделить 673 без остатка — это 673. Следовательно, первый этап расчета будет выглядеть следующим образом:

673 ÷ 673 = 1

В итоге мы получили список всех простых множителей числа 673. Это: 673

Поделитесь текущим расчетом

Печать

https://calculat. io/ru/number/prime-factors-of/673

<a href=»https://calculat.io/ru/number/prime-factors-of/673″>Простые множители числа 673 — Calculatio</a>

О калькуляторе «Разложение чисел на простые множители»

Данный калькулятор поможет разложить заданное число на простые множители. Например, Какие простые множители у числа 673? Выберите начальное число (например ‘673’). После чего нажмите кнопку ‘Посчитать’.

Простые множители - это положительные целые числа, имеющие только два делителя - 1 и само себя.

Калькулятор «Разложение чисел на простые множители»

Таблица разложения чисел на простые множители

ЧислоПростые множители
6582, 7, 47
659659
66022 × 3 × 5 × 11
661661
6622, 331
6633, 13, 17
66423 × 83
6655, 7, 19
6662 × 32 × 37
66723, 29
66822 × 167
6693, 223
6702, 5, 67
67111, 61
67225 × 3 × 7
673673
6742, 337
67533 × 52
67622 × 132
677677
6782, 3, 113
6797, 97
68023 × 5 × 17
6813, 227
6822, 11, 31
683683
68422 × 32 × 19
6855, 137
6862 × 73
6873, 229

Решить x^2-60x+675=0 | Microsoft Math Solver

x=15

x=45

Викторина

Quadratic Equation

5 задач, подобных этой:

{ x }^{ 2 } -60x+675=0

Подобные задачи из результатов поиска в Интернете

Поделиться

Скопировано в буфер обмена

a+b=-60 ab=675

Чтобы решить уравнение, разложите x^{2}-60x+675 на множители по формуле x^{2}+\left(a+b\right)x+ab=\left(x+a\right)\left(x+b\right). {2}+2 x-3}

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32
20 Оценить квадратный корень из 18 92-20x-675=0 Tiger Algebra Solver

Пошаговое решение:

Шаг 1 :

Уравнение в конце шага 1 : 
 (3x  2  - 20x) - 675 = 0

Шаг 2 :

Попытка разложения путем разделения среднего члена

Средний член равен -20x, его коэффициент равен -20.
Последний член, «константа», равен  -675 

Шаг-1: Умножьте коэффициент первого члена на константу   3 • -675 = -2025 

Шаг-2: Найдите два множителя -2025 , сумма которых равна коэффициенту среднего члена, который равен -20 .

      -2025    +    1    =    -2024
      -675    +    3    =    -672
      -405    +    5    =    -400
      -225    +    9    =    -216
      -135+ 15 = -120
-81+ 25 = -56
      -75    +    27    =    -48
      -45    +    45    =    0
-27+ 75 = 48
-25+ 81 -250005    =    56
      -15    +    135    =    120
      -9    +    225    =    216
-5+ 405 = 400
-3+ 675 = 672
-1+ 2025 = 2024


77955


7777


777777


77777.
Заключение: Трехчлен нельзя разложить на множители

Уравнение в конце шага 2 : 
 3x  2  - 20x - 675 = 0

Шаг 3 :

Парабола, нахождение вершины :

 3.1      Найдите вершину   y = 3x 2 -20x-675

Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 3 , положителен (больше нуля).

 Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.

 Параболы могут моделировать многие реальные жизненные ситуации, например, высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам такую ​​информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.

 Для любой параболы, Ax 2 +Bx+C, x координата вершины определяется как -B/(2A) . В нашем случае координата x равна  3,3333  

Подключение в формулу параболы 3.3333 Для x Мы можем рассчитать y -координату:
y = 3,0 * 3,33 * 3,33 -20,0 * 3,33 -675,0
или y = -708.333

Parbola, графики вершины и X -intterceptts:

, графики и x -intterceptts:

, графики и x -intterceptts:

, графики и x -intterceptts:

, графики и x -inttercec.

Корневой график для:  y = 3x 2 -20x-675
Ось симметрии (штриховая)  {x}={ 3,33} 
Вершина в  {x,y} = {3,33,-708,33} 
 x -Перехваты (корни ) :
Корень 1 в точке {x, y} = {-12,03, 0,00}
Корень 2 в точке {x, y} = {18,70, 0,00}

Решить квадратное уравнение, заполнив квадрат

 3. 2     Решение   3x 2 -20x-675 = 0, заполнив квадрат.

 Поделите обе части уравнения на 3, чтобы получить 1 в качестве коэффициента при первом члене:
   x 2 -(20/3)x-225 = 0

Добавьте  225  к обеим частям уравнения:
   x 2 -(20/3)x = 225

Теперь немного хитрости: возьмите коэффициент при x, равный 20/3, разделите на два, что даст 10/3, и, наконец, возведите его в квадрат, чтобы получить 100/9.

Прибавьте 100/9 к обеим частям уравнения:
 В правой части имеем:
   225  +  100/9    или (225/1)+(100/9)
  Общий знаменатель двух дробей равен 9   Добавление (2025/9)+(100/9) дает 2125/9
 Таким образом, прибавив к обеим частям, мы окончательно получим:
   x 2 -(20/3)x+(100/9) = 2125/9

Добавление  100/9 завершило левую часть в полный квадрат:
   x 2 -(20/3)x+(100/9)  =
   (x-(10/3)) • (x-(10/ 3))  =
  (x-(10/3)) 2
Вещи, равные одной и той же вещи, также равны друг другу. Поскольку
   x 2 -(20/3)x+(100/9) = 2125/9 и
   x 2 -(20/3)x+(100/9) = (x-(10/3)) 2
, тогда, согласно закону транзитивности,
   (x-(10/3)) 2 = 2125/9

Мы будем называть это уравнение уравнением #3.2.1  

Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.

Обратите внимание, что квадратный корень из
   (x-(10/3)) 2   равен
   (x-(10/3)) 2/2  =
  (x-(10/3)) 1  =
   x-(10/3)

Теперь, применяя принцип квадратного корня к уравнению #3.2.1  получаем:
   x-(10/3) = √ 2125/9

Прибавляя 10/3 к обеим частям, получаем:
   x = 10/3 + √ 2125/9

Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное
   x 2 — (20/3)x — 225 = 0
   имеет два решения:
x = 10/3 + √ 2125/9
или
x = 10/3 — √ 2125/9

Обратите внимание, что √ 2125/9 можно записать как
√ 2125/√ 9, что является √ 2125/3

Решение квадратного уравнения с помощью квадратной формулы

 3. 3     Решение    3x 2 -20x-675 = 0 по квадратной формуле .

 Согласно квадратичной формуле,  x  , решение для   Ax 2 +Bx+C = 0  , где A, B и C – числа, часто называемые коэффициентами, определяется следующим образом:

-B ± √ B 2 -4AC
x = ————————
2A

В нашем случае A = 3
B = -20
C = -675

2020, Actorly, Actorly, Actorly, Actorly, ACRODILY, ACRODINY, ACRODILY, ACRODINY, ACRODILY, ACRODINY, ACRODINY, ACRODILY, A -20

C = -675

202020. B 2 -4AC =
400-(-8100) =
8500

Применение квадратичной формулы:

20 ± √ 8500
   x  =    ——————
                     6

Можно ли упростить √ 8500?

Да! Первичная факторизация 8500   это
   2•2•5•5•5•17
Чтобы иметь возможность удалить что-то из-под корня, должно быть  2 экземпляра этого (потому что мы берем квадрат, то есть второй корень).

√ 8500 = √ 2 • 2 • 5 • 5 • 5 • 17 = 2 • 5 • √ 85 =
± 10 • √ 85

√ 85, округлые до 4 десятичных цифров, 9,2195
Итак, теперь мы ищем.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *