Степень 2 это: Таблица степеней от 2 до 16. Возведение в степень, правила, примеры

Игра 2048: как легко и быстро выучить степени числа 2 / Newtonew: новости сетевого образования

Мы в соц.сетях:

• Статьи
• ·
• Авторские колонки
• ·
• Коллекции
• ·
• Новости
• ·
• События

Написать статью

12+

  вернуться Время чтения: 2 минуты   |   Комментариев: 1

Сохранить

На просторах интернета обнаружилась простая, но очень забавная математическая игра — 2048.

Помимо простого удовольствия она может дать и более полезный результат: помочь легко и просто выучить степени числа 2. То, до какой степени вы их выучите, зависит от ваших успехов в игре. Знание степеней двойки — вещь нужная и в хозяйстве полезная. Но просто так их заучивать может быть очень скучно и непродуктивно. Поиграть же в игру и самому не заметить, что ты что-то выучил, — это гораздо более приятный подход.

Игра 2048 — очень простая, но от этого не менее увлекательная. Всё, что от вас требуется, — это передвигать по игровому полю фишки, на которых написаны различные степени числа 2 (начиная с 2). Когда 2 одинаковые фишки оказываются рядом, их можно сложить друг с другом, получив, таким образом, следующую степень. Цель игры — получить число 2048 (что равно 2 в 11 степени). 

Сыграть в игру можно онлайн. Кроме того, есть версии для iOs и Android. Изучать математику играя — что может быть лучше. 

Посмотрите также наш обзор игры DragonBox Algebra — игры, которая позволяет легко и просто изучать алгебру даже самым маленьким детям.

 

20 мая 2014, 10:17

лайфхаки

вечный студент

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

статьи по теме

лайфхаки

Как легко учить лексику иностранного языка

лайфхаки

Одеваем Надежду в одежду, или кое-что о паронимах

культура лайфхаки

Почему вам нужно научиться скучать

Выделенный текст:

Сообщение:

Сообщение об ошибке успешно отправлено, благодарим вас за помощь!

– Oбразование как Стиль Жизни

Присылайте свои колонки

и предложения

У вас есть интересная новость или материал из сферы образования или популярной науки?
Расскажите нам!

[email protected]

© 2014-2023 Newtonew. 12+

Просветительский медиа-проект об образовании, посвящённый самым актуальным и полезным концепциям, теориям и методикам, технологиям и исследованиям, продуктам и сервисам.

Мы говорим о том, как развиваются и изменяются образование и наука.
Копирование материалов возможно только с разрешения редакции Newtonew.

ЕГЭ спецпроект ProTeachers

MOOC 2016 Большая переменная

Физика: игра света

Маршрут в будущее

Считаные годы

Образование XXI века

Мы используем файлы cookie для улучшения пользовательского опыта. Подробнее вы можете посмотреть в нашем пользовательском соглашении.

App Store Google Play

Подписаться на рассылку

Подписаться на рассылку

Авторизация на сайте

Вход через соц.сети:

ВКонтакте Facebook Google

---

Новый пользователь

Введите ваш email:

Введите пароль:

Повторите пароль:

---

  назад

Напомнить пароль

Введите email, на который вы зарегистрированы:

---

  назад

Пароль выслан

Мы выслали ваш пароль для входа в систему на указанный email.

---

Не забывайте о том, что вы можете авторизоваться в системе через социальные сети. Если при регистрации в соц.сетях вы указывали тот же email что и на нашем сайте, то после авторизации вы попадете в свой профиль.

Вход через соц.сети:

ВКонтакте Facebook Google

Подтвердите регистрацию

На указанный e-mail было отправлено письмо со ссылкой. Пожалуйста, перейдите по ссылке для подтверждения.

Вход через соц.сети:

ВКонтакте Facebook Google

Регистрация подтверждена

Вы успешно зарегистрировались

Сила двух

Степень двойки — это число вида 2 ⁿ , где n — целое число , то есть результат возведения в степень с числом два в качестве основания и целым числом  n в качестве показателя степени .

В контексте, где рассматриваются только целые числа, n ограничен неотрицательными значениями, ^[1] поэтому 1, 2 и 2 умножаются сами на себя определенное количество раз.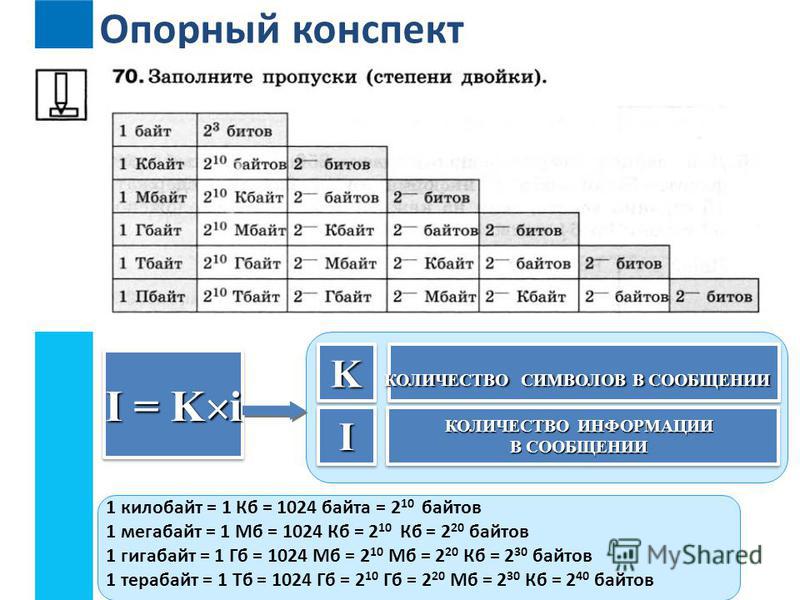 ^[2]

Поскольку двойка является основанием двоичной системы счисления , степени двойки широко распространены в компьютерных науках . Записанная в двоичном формате, степень двойки всегда имеет вид 100…000 или 0,00…001, точно так же, как степень 10 в десятичной системе.

Два в степени n , записанное как 2 ⁿ , — это количество способов расположения битов в двоичном слове длины n . Слово, интерпретируемое как целое число без знака , может представлять значения от 0 ( 000…000

2 ) до 2 ⁿ − 1  ( 111…111 ₂ ) включительно. Соответствующие целые числа со знаком могут быть положительными, отрицательными и нулевыми; см. числовые представления со знаком. В любом случае, единица меньше степени двойки часто является верхней границей целого числа в двоичных компьютерах. Как следствие, числа в этой форме часто появляются в компьютерном программном обеспечении. Например, видеоигра, работающая на 8-битной системе, может ограничить количество очков или количество предметов, которые может удержать игрок, до 255 — результат использования байта длиной 8 бит для хранения числа, что дает максимальное значение 2 ⁸ − 1 = 255 .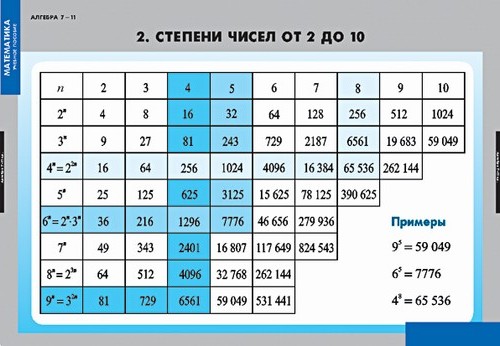 Например, в оригинальной

Legend of Zelda главный герой был ограничен ношением 255 рупий (валюта игры) в любой момент времени, а видеоигра Pac-Man, как известно, имеет экран убийства на уровне 256.

Степени двойки часто используются для измерения памяти компьютера. Байт теперь считается восемью битами (октетом ) , что дает возможность иметь 256 значений (2 ⁸ ). (Термин байт когда-то означал (а в некоторых случаях все еще означает) набор битов , обычно от 5 до 32 бит, а не только 8-битный блок.) Префикс kilo в сочетании с байтом может быть и традиционно используется для обозначения 1024 (2 ¹⁰ ). Однако, как правило, термин « килограмм» используется в Международной системе единиц для обозначения 1000 (10 ³ ). Двоичные префиксы были стандартизированы, напримеркиби  (Ки), что означает 1024. Почти все регистры процессора имеют размеры, равные степеням двойки, 32 или 64, которые встречаются очень часто.

Степени двойки встречаются и в ряде других мест.

Для многих дисководов по крайней мере один из следующих параметров: размер сектора, количество секторов на дорожку и количество дорожек на поверхность является степенью двойки. Размер логического блока почти всегда равен степени двойки.

---

Визуализация степеней двойки от 1 до 1024 (от 2 ⁰ до 2 ¹⁰ )

Поскольку каждое увеличение размерности удваивает количество форм, сумма коэффициентов в каждой строке треугольника Паскаля равна степени двойки.

Сумма степеней двойки от нуля до данной степени включительно на 1 меньше следующей степени двойки, тогда как сумма степеней двойки от минус бесконечности до данной степени включительно равна следующей степени двойки

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Что такое многочлен, степень, типы и примеры

Введение

В математике многочлен — это понятие, которое изучается в разделе алгебры.

Прежде чем перейти к определению многочлена и его различных типов, давайте пройдемся по основным терминам, из которых состоят многочлены.

Переменная

Переменные определяются и используются в алгебре. Его определение гласит, что символ, который можно использовать для присвоения различных числовых значений, известен как переменная.

Пример

\(x,y,z,p,q,r,s\) и т. д.

Константа

В математике символ, имеющий фиксированное значение, называется константой.

Пример

\(8, 5, 9, \pi\) и т. д.

Что такое алгебраическое выражение?

Комбинация констант и переменных, связанных некоторыми или всеми основными операциями \(+\), \(-\), \(\times\), \(\div\), называется алгебраическим выражением.

Пример

\(7+8x\)
Итак, здесь мы составили алгебраическое выражение, связанное операцией \(+\) путем объединения константы 7 и константы 8 с переменной \(x\). 92+8\)

Этот многочлен является многочленом от одной переменной, т. е. x.
Степени переменной x равны 4, 3 и 2
\(\следовательно\) наивысшая степень равна 4.
Следовательно, степень многочлена равна 4.

Какие бывают многочлены?

Полиномы бывают разных типов в зависимости от степени полинома и количества членов, входящих в полином.

Типы многочленов на основе количества членов

Многочлены классифицируются и называются на основе количества членов, которые они имеют. 92+0x\) и т. д.

Примечание

Степень нулевого многочлена не определена.

Часто задаваемые вопросы

В) Что такое многочлен?

Алгебраическое выражение, в котором переменные имеют в качестве показателей только целые числа, называется полиномиальным.

В) Что такое степень многочлена?

В полиноме наивысшая степень переменной называется степенью полинома.

В) Что такое степень постоянного многочлена?

Степень постоянного многочлена всегда равна нулю.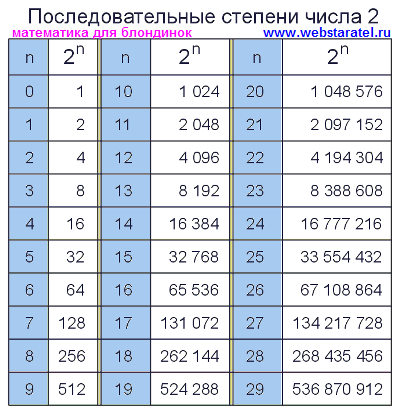

В) Является ли 100 постоянным полиномом?

Да, потому что мы можем записать 100 как 100x ⁰ , поэтому высшая степень равна нулю, что называется постоянным многочленом.

В) Что такое стандартная форма многочлена?

Полином, в котором все переменные расположены либо в порядке возрастания, либо в порядке убывания, называется стандартной формой полинома. то есть многочлены 8x ⁴ + 3x ³ + 7x ² + 3x + 5 и 5 + 3x + 7x ² + 3x ³ + 8x ⁴ имеют стандартную полиномиальную форму. В общем, стандартная форма многочлена: , где a ₀ , a ₁ , a ₂ , a ₃ _ _ _ _ _ _ _ _ _ _ , a _n — все действительные числа, а n — любое целое число.

В) Что такое старший коэффициент и его пример?

Коэффициент старшей степени члена называется его старшим коэффициентом. Пример ведущего коэффициента: 8×9.1124 4 + 6x ³ + 8x ² — 4x + 2 и его старший коэффициент равен 8, так как старший коэффициент x равен 4.

В) Что такое старший член в многочлене и его пример?

В полиноме член с более высоким показателем степени называется ведущим членом. Пример ведущего члена: 8x ⁴ + 3x ³ + 2x ² — 7x + 6. Здесь 8x ⁴ — начальный член.

Вопросы с несколькими вариантами ответов

1) 7x

⁵ + 3x ² — 5x + 2 — многочлен.

1. Да
2. Нет
3. Возможно
4. Ничего из перечисленного

Отвечать

2) x

⁵ + 7 — многочлен.

1. Да
2. Нет
3. Возможно
4. Ничего из перечисленного

Отвечать

3) 4x + 3 — многочлен.