Метод наименьших квадратов | это… Что такое Метод наименьших квадратов?
Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения.
Запрос «МНК» перенаправляется сюда; см. также другие значения.
Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.
Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т.
Содержание
|
Сущность МНК
Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x
где — вектор неизвестных параметров модели
- — случайная ошибка модели.
Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть — номер наблюдения ().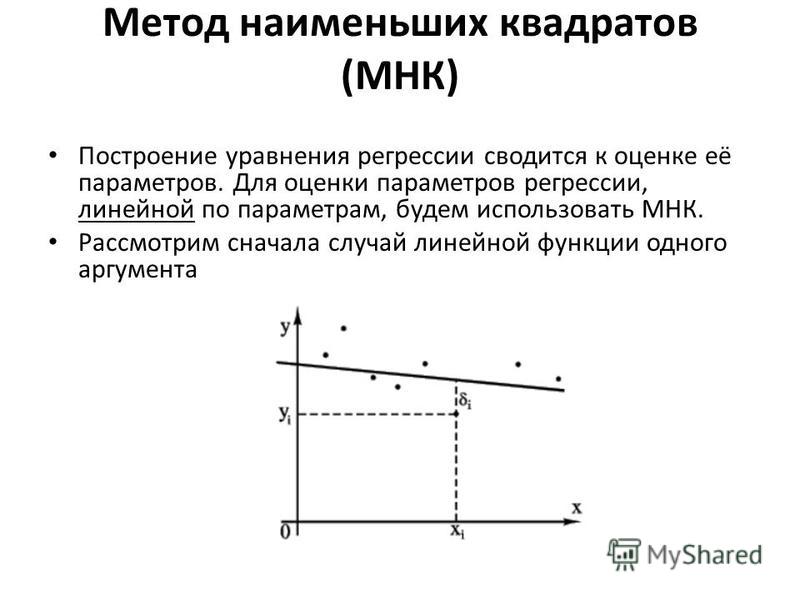
Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):
Величина остатков зависит от значений параметров b.
Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков (англ. Residual Sum of Squares) будет минимальной:
где:
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ.
Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценками метода максимального правдоподобия (ММП).
МНК в случае линейной модели
Пусть регрессионная зависимость является линейной:
Пусть y — вектор-столбец наблюдений объясняемой переменной, а — матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:
Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны
соответственно сумма квадратов остатков регрессии будет равна
Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):
- .
Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:
Для аналитических целей оказывается полезным последнее представление этой формулы. Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге
Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге
Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.
Пример: простейшая (парная) регрессия
В случае парной линейной регрессии формулы расчета упрощаются (можно обойтись без матричной алгебры):
Свойства МНК-оценок
В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы.
- математическое ожидание случайных ошибок равно нулю, и
- факторы и случайные ошибки — независимые случайные величины.
Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).
Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности.
Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:
- Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности):
- Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой
Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок
Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbaised Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:
Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.
Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясь несмещёнными и состоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщённого МНК.
Обобщенный МНК
Основная статья: Обобщенный метод наименьших квадратов
Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную форму от вектора остатков , где — некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение . Следовательно, указанный функционал можно представить следующим образом , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение . Следовательно, указанный функционал можно представить следующим образом , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т. н. обобщенного МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: .
Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид
Ковариационная матрица этих оценок соответственно будет равна
Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
Взвешенный МНК
В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS — Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.
Некоторые частные случаи применения МНК на практике
Аппроксимация линейной зависимости
Рассмотрим случай, когда в результате изучения зависимости некоторой скалярной величины от некоторой скалярной величины (Это может быть, например, зависимость напряжения от силы тока : , где — постоянная величина, сопротивление проводника) было проведено измерений этих величин, в результате которых были получены значения и соответствующие им значения .
Таблица. Результаты измерений.
| № измерения | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Вопрос звучит так: какое значение коэффициента можно подобрать, чтобы наилучшим образом описать зависимость ? Согласно МНК это значение должно быть таким, чтобы сумма квадратов отклонений величин от величин
была минимальной
Сумма квадратов отклонений имеет один экстремум — минимум, что позволяет нам использовать эту формулу. Найдём из этой формулы значение коэффициента . Для этого преобразуем её левую часть следующим образом:
Далее идёт ряд математических преобразований:
Последняя формула позволяет нам найти значение коэффициента , что и требовалось в задаче.
История
До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés)[2]. Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения[3]. Метод распространён и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других.
Альтернативное использование МНК
Идея метода наименьших квадратов может быть использована также в других случаях, не связанных напрямую с регрессионным анализом. Дело в том, что сумма квадратов является одной из наиболее распространенных мер близости для векторов (евклидова метрика в конечномерных пространствах).
Одно из применений — «решение» систем линейных уравнений, в которых число уравнений больше числа переменных
,
где матрица не квадратная, а прямоугольная размера .
Такая система уравнений, в общем случае не имеет решения (если ранг на самом деле больше числа переменных). Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений
Используя оператор псевдоинверсии, решение можно переписать так:
- ,
где — псевдообратная матрица для .
Данную задачу также можно «решить» используя взвешенный МНК, когда разные уравнения системы получают разный вес из теоретических соображений.
Естественно, данный подход может быть использован и в случае нелинейных систем уравнений.
Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.
См. также
- Регрессионный анализ
- Метод наименьших модулей
- Обобщенный метод наименьших квадратов
- Рекурсивный МНК
- Метод инструментальных переменных
- Двухшаговый метод наименьших квадратов
Примечания
- ↑ Legendre, On Least Squares. Translated from the French by Professor Henry A. Ruger and Professor Helen M. Walker, Teachers College, Columbia University, New York City. (англ.)
- ↑ Александрова, 2008, с. 102
Литература
- Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд. — М., 1962. (математическая теория)
- Айвазян С. А. Прикладная статистика. Основы эконометрики. Том 2. — М.: Юнити-Дана, 2001. — 432 с. — ISBN 5-238-00305-6
- Доугерти К. Введение в эконометрику: Пер.
 с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7
с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7 - Кремер Н. Ш., Путко Б. А. Эконометрика. — М.: Юнити-Дана, 2003-2004. — 311 с. — ISBN 8-86225-458-7
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с. — ISBN 978-5-7749-0473-0
- Эконометрика. Учебник / Под ред. Елисеевой И. И. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с. — ISBN 5-279-02786-3
- Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. — 3-е изд.. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4
Ссылки
- Теория и пример использования
- Метод наименьших квадратов. Аппроксимация зависимостей, отличных от линейных.
- Метод наименьших квадратов для зависимости y = a + bx на JavaScript.
- Метод наименьших квадратов онлайн для зависимости y = a + bx с вычислением погрешностей коэффициентов и оцениванием автокорреляции.
При написании этой статьи использовался материал из Энциклопедического словаря Брокгауза и Ефрона (1890—1907).
Метод наименьших квадратов | это… Что такое Метод наименьших квадратов?
Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения.
Запрос «МНК» перенаправляется сюда; см. также другие значения.
Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.
Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т. д.
д.
Содержание
|
Сущность МНК
Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x
где — вектор неизвестных параметров модели
- — случайная ошибка модели.
Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть — номер наблюдения ().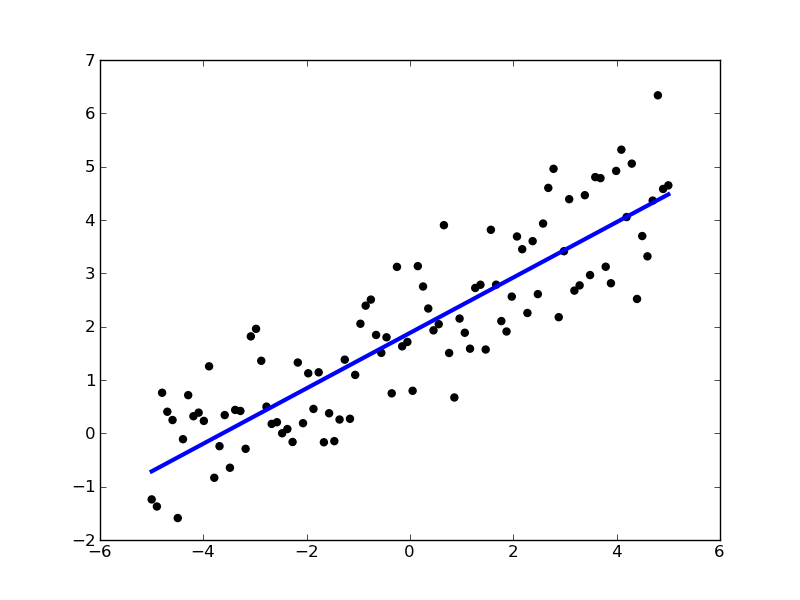 Тогда — значения переменных в -м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y:
Тогда — значения переменных в -м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y:
Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):
Величина остатков зависит от значений параметров b.
Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков (англ. Residual Sum of Squares) будет минимальной:
где:
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции , продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений:
Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценками метода максимального правдоподобия (ММП).
МНК в случае линейной модели
Пусть регрессионная зависимость является линейной:
Пусть y — вектор-столбец наблюдений объясняемой переменной, а — матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:
Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны
соответственно сумма квадратов остатков регрессии будет равна
Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):
- .
Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:
Для аналитических целей оказывается полезным последнее представление этой формулы. Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.
Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.
Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.
Пример: простейшая (парная) регрессия
В случае парной линейной регрессии формулы расчета упрощаются (можно обойтись без матричной алгебры):
Свойства МНК-оценок
В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если
Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если
- математическое ожидание случайных ошибок равно нулю, и
- факторы и случайные ошибки — независимые случайные величины.
Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).
Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.
В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.
Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:
- Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности):
- Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой
Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок
Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbaised Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:
Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.
Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясь несмещёнными и состоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщённого МНК.
Обобщенный МНК
Основная статья: Обобщенный метод наименьших квадратов
Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную форму от вектора остатков , где — некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение . Следовательно, указанный функционал можно представить следующим образом , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение . Следовательно, указанный функционал можно представить следующим образом , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т. н. обобщенного МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: .
Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид
Ковариационная матрица этих оценок соответственно будет равна
Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
Взвешенный МНК
В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS — Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.
Некоторые частные случаи применения МНК на практике
Аппроксимация линейной зависимости
Рассмотрим случай, когда в результате изучения зависимости некоторой скалярной величины от некоторой скалярной величины (Это может быть, например, зависимость напряжения от силы тока : , где — постоянная величина, сопротивление проводника) было проведено измерений этих величин, в результате которых были получены значения и соответствующие им значения . Данные измерений должны быть записаны в таблице.
Данные измерений должны быть записаны в таблице.
Таблица. Результаты измерений.
| № измерения | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Вопрос звучит так: какое значение коэффициента можно подобрать, чтобы наилучшим образом описать зависимость ? Согласно МНК это значение должно быть таким, чтобы сумма квадратов отклонений величин от величин
была минимальной
Сумма квадратов отклонений имеет один экстремум — минимум, что позволяет нам использовать эту формулу. Найдём из этой формулы значение коэффициента . Для этого преобразуем её левую часть следующим образом:
Далее идёт ряд математических преобразований:
Последняя формула позволяет нам найти значение коэффициента , что и требовалось в задаче.
История
До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés)[2]. Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения[3]. Метод распространён и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других.
Альтернативное использование МНК
Идея метода наименьших квадратов может быть использована также в других случаях, не связанных напрямую с регрессионным анализом. Дело в том, что сумма квадратов является одной из наиболее распространенных мер близости для векторов (евклидова метрика в конечномерных пространствах).
Одно из применений — «решение» систем линейных уравнений, в которых число уравнений больше числа переменных
,
где матрица не квадратная, а прямоугольная размера .
Такая система уравнений, в общем случае не имеет решения (если ранг на самом деле больше числа переменных). Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений
Используя оператор псевдоинверсии, решение можно переписать так:
- ,
где — псевдообратная матрица для .
Данную задачу также можно «решить» используя взвешенный МНК, когда разные уравнения системы получают разный вес из теоретических соображений.
Естественно, данный подход может быть использован и в случае нелинейных систем уравнений.
Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.
См. также
- Регрессионный анализ
- Метод наименьших модулей
- Обобщенный метод наименьших квадратов
- Рекурсивный МНК
- Метод инструментальных переменных
- Двухшаговый метод наименьших квадратов
Примечания
- ↑ Legendre, On Least Squares. Translated from the French by Professor Henry A. Ruger and Professor Helen M. Walker, Teachers College, Columbia University, New York City. (англ.)
- ↑ Александрова, 2008, с. 102
Литература
- Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд. — М., 1962. (математическая теория)
- Айвазян С. А. Прикладная статистика. Основы эконометрики. Том 2. — М.: Юнити-Дана, 2001. — 432 с. — ISBN 5-238-00305-6
- Доугерти К. Введение в эконометрику: Пер.
 с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7
с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7 - Кремер Н. Ш., Путко Б. А. Эконометрика. — М.: Юнити-Дана, 2003-2004. — 311 с. — ISBN 8-86225-458-7
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с. — ISBN 978-5-7749-0473-0
- Эконометрика. Учебник / Под ред. Елисеевой И. И. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с. — ISBN 5-279-02786-3
- Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. — 3-е изд.. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4
Ссылки
- Теория и пример использования
- Метод наименьших квадратов. Аппроксимация зависимостей, отличных от линейных.
- Метод наименьших квадратов для зависимости y = a + bx на JavaScript.
- Метод наименьших квадратов онлайн для зависимости y = a + bx с вычислением погрешностей коэффициентов и оцениванием автокорреляции.
При написании этой статьи использовался материал из Энциклопедического словаря Брокгауза и Ефрона (1890—1907).
Метод наименьших квадратов в финансах, трейдинге и инвестировании
Что такое метод наименьших квадратов?
Метод наименьших квадратов — это статистическая процедура, используемая для оценки отношений между определенными переменными. Этот метод также известен как метод обычных наименьших квадратов (OLS) или линейный метод наименьших квадратов.
Метод наименьших квадратов находит линию наилучшего соответствия для заданного набора точек данных путем минимизации суммы квадратов невязок.
Термин «остаток» относится к разнице между фактическим значением и прогнозируемым значением.
Таким образом, по сути, метод наименьших квадратов находит линию, минимизирующую сумму этих расхождений.
Этот метод используется в различных приложениях, таких как регрессионный анализ, аппроксимация кривых и аппроксимация поверхности.
Он также используется в машинном обучении, где его можно использовать для нахождения коэффициентов линейной модели.
Основные выводы – метод наименьших квадратов
1. Метод наименьших квадратов – это метод математической оптимизации, используемый для нахождения наилучшего соответствия набору точек данных путем минимизации суммы квадратов разностей между прогнозируемыми значениями и фактические значения.
2. Метод наименьших квадратов можно использовать для поиска линии наилучшего соответствия набору точек данных, а также для оценки неизвестных параметров в модели линейной регрессии.
3. Метод наименьших квадратов не всегда является лучшим выбором для нахождения линии наилучшего соответствия, особенно когда в наборе данных есть выбросы.
4. Метод наименьших квадратов прост в вычислительном отношении и эффективен, что делает его популярным среди статистиков и специалистов по данным.
5. Существуют варианты метода наименьших квадратов, которые можно использовать, когда набор данных не распределен линейно, например взвешенный метод наименьших квадратов и обобщенный метод наименьших квадратов.
6. Преимущества использования метода наименьших квадратов включают его простоту, эффективность и гибкость. Однако важно иметь в виду, что этот метод не всегда является лучшим выбором для поиска линии наилучшего соответствия, особенно когда в наборе данных есть выбросы.
Как использовать метод наименьших квадратов
Существует несколько различных способов использования метода наименьших квадратов.
Один из способов — использовать его для поиска линии, наиболее подходящей для набора точек данных. Для этого вам нужно будет рассчитать наклон и точку пересечения линии.
Вы также можете использовать метод наименьших квадратов, чтобы найти коэффициенты линейной модели. Для этого вам нужно будет создать матрицу ваших точек данных, а затем взять инверсию этой матрицы.
После этого вы можете умножить обратную матрицу на ваш вектор зависимых переменных. Это даст вам вектор коэффициентов, который вы ищете.
Метод наименьших квадратов — это мощный инструмент, который можно использовать для извлечения информации из данных. Однако важно отметить, что этот метод имеет некоторые ограничения.
Однако важно отметить, что этот метод имеет некоторые ограничения.
Например, метод наименьших квадратов предполагает, что данные являются линейными. Это означает, что если в данных присутствуют нелинейные отношения, результаты анализа методом наименьших квадратов могут быть неточными.
Также важно отметить, что метод наименьших квадратов может быть чувствителен к выбросам. Это означает, что если есть несколько точек данных, которые находятся далеко от остальных данных, они могут оказать большое влияние на результаты анализа.
Преимущества метода наименьших квадратов
Метод наименьших квадратов имеет несколько преимуществ.
Во-первых, это относительно простой для понимания и реализации метод.
Во-вторых, он эффективен в вычислительном отношении и не требует большого объема данных для получения точных результатов.
Наконец, метод наименьших квадратов является гибким и может использоваться для различных типов данных.
Одним из преимуществ метода наименьших квадратов является то, что его относительно легко понять и реализовать. Концепция метода проста, и в вычислениях задействовано всего несколько шагов.
Концепция метода проста, и в вычислениях задействовано всего несколько шагов.
Это делает его привлекательным вариантом для исследователей, которым нужен быстрый и простой способ анализа данных.
Еще одним преимуществом метода наименьших квадратов является его вычислительная эффективность. Расчеты, необходимые для реализации метода, относительно просты и могут быть выполнены с использованием стандартных пакетов программ. Кроме того, метод не требует большого количества данных для получения точных результатов.
Это важно для исследователей, у которых может не быть доступа к большим наборам данных или которые хотят быстро анализировать данные.
Наконец, метод наименьших квадратов является гибким и может использоваться для различных типов данных. Метод может применяться как к линейным, так и к нелинейным наборам данных. Кроме того, метод наименьших квадратов можно использовать с множественным регрессионным анализом.
Это делает его ценным инструментом для исследователей, которым необходимо анализировать данные, которые не вписываются ни в одну категорию.
Некоторые специалисты в области финансов могут возразить, что существуют и другие методы, столь же надежные, как и метод наименьших квадратов. Но факт остается фактом: метод наименьших квадратов по-прежнему остается самым популярным методом регрессии, используемым сегодня в финансах.
Ограничения метода наименьших квадратов
Метод наименьших квадратов — это мощный инструмент, который можно использовать для извлечения информации из данных. Однако важно отметить, что этот метод имеет некоторые ограничения.
Например, метод наименьших квадратов предполагает, что данные являются линейными. Это означает, что если в данных присутствуют нелинейные отношения, результаты анализа методом наименьших квадратов могут быть неточными.
Также важно отметить, что метод наименьших квадратов может быть чувствителен к выбросам. Это означает, что если есть несколько точек данных, которые находятся далеко от остальных данных, они могут оказать большое влияние на результаты анализа.
Несмотря на эти ограничения, метод наименьших квадратов по-прежнему является широко используемым и мощным инструментом для анализа данных.
Линейная регрессия с использованием метода наименьших квадратов – уравнение наилучшего соответствия
Пример метода наименьших квадратов в трейдинге и инвестировании
Метод наименьших квадратов — это статистический метод, который можно использовать для оценки будущего значения зависимой переменной на основе прошлых значений независимой переменной.
В контексте торговли и инвестирования метод наименьших квадратов может использоваться для прогнозирования будущей цены ценной бумаги на основе движения индекса.
Чтобы проиллюстрировать, как можно использовать метод наименьших квадратов в торговле и инвестировании, рассмотрим следующий пример.
Предположим, вы хотите предсказать будущую цену акций компании XYZ. Вы заметили, что за последний год цена акций увеличивалась на 1 процент каждый раз, когда индекс поднимался на 1,5 процента.
Основываясь на этом соотношении, вы можете использовать метод наименьших квадратов, чтобы оценить, что если индекс увеличится на 3 процента, то цена акций компании XYZ увеличится примерно на 2 процента, если соотношение верно.
Конечно, это всего лишь прогноз, основанный на конкретном методе, и нет никаких гарантий, что он будет точным.
Однако метод наименьших квадратов может оказаться полезным для оценки будущих цен на основе прошлых движений индекса.
Часто задаваемые вопросы – метод наименьших квадратов
Как метод наименьших квадратов используется в финансах?
Метод наименьших квадратов используется при анализе связи между двумя переменными.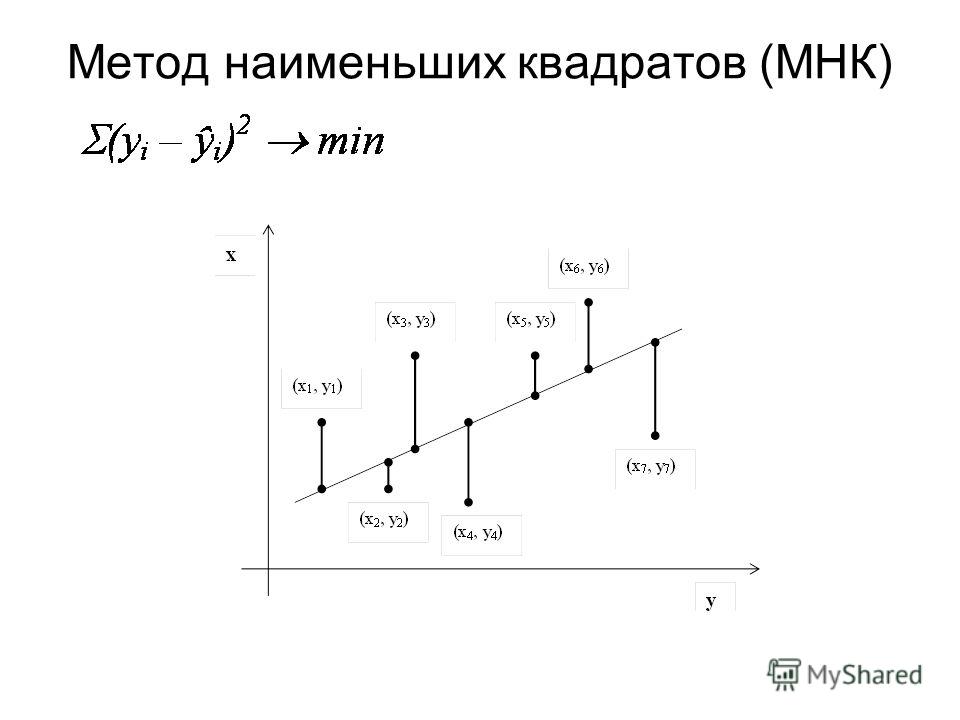
Например, прибыль на акцию и цена акции логически связаны друг с другом. Таким образом, метод наименьших квадратов используется для нахождения линии наилучшего соответствия между этими двумя переменными.
Для любого анализа важно установить причину и следствие. Многие переменные могут проявлять взаимосвязь, но не обязательно из-за причинно-следственной связи.
Например, потребление мороженого положительно коррелирует с повышением температуры, но мороженое не вызывает жару.
Метод наименьших квадратов — мощный инструмент, но, как и все инструменты, он имеет ограничения. Важно понимать эти ограничения при использовании метода наименьших квадратов для финансового анализа.
Каковы ограничения метода наименьших квадратов?
1. Предположение о линейной зависимости является слишком ограничительным. В реальном мире многие отношения нелинейны.
2. Предположение о равной дисперсии также является слишком ограничительным. Во многих ситуациях зависимая переменная будет иметь разную дисперсию при разных значениях независимой переменной. Это нарушает предположение о гомоскедастичности, лежащее в основе метода наименьших квадратов.
Это нарушает предположение о гомоскедастичности, лежащее в основе метода наименьших квадратов.
3. Остатки должны быть нормально распределены. Однако в реальном мире это предположение часто нарушается.
4. Метод наименьших квадратов чувствителен к выбросам. Один выброс может оказать существенное влияние на результаты анализа.
5. Метод наименьших квадратов также чувствителен к мультиколлинеарности. Это происходит, когда существует высокая корреляция между независимыми переменными. Это может привести к неточным оценкам коэффициентов регрессии.
6. Метод наименьших квадратов предполагает отсутствие автокорреляции остатков. Это предположение часто нарушается в данных временных рядов.
7. Наконец, метод наименьших квадратов дает только точечные оценки коэффициентов регрессии. Он не предоставляет никакой информации о точности этих оценок.
Почему метод наименьших квадратов используется в финансах?
Метод наименьших квадратов используется в финансах по ряду причин.
Во-первых, это относительно простой метод, не требующий большого количества данных.
Во-вторых, его можно использовать с неравномерно распределенными данными.
В-третьих, что наиболее важно, метод наименьших квадратов дает надежные результаты. Этот метод использовался в течение десятилетий, и его точность была доказана как надежная форма анализа.
Заключение. Метод наименьших квадратов
Метод наименьших квадратов — это мощный инструмент, который широко используется в финансах. Его популярность обусловлена простотой и точностью.
Однако метод наименьших квадратов имеет некоторые ограничения, которые следует учитывать при его использовании для финансового анализа.
Связанные
- Автокорреляция
- Ковариация
Представление линейной алгебры регрессии методом наименьших квадратов | Эндрю Чемберлен, доктор философии.
Линейная регрессия — самый важный статистический инструмент, который когда-либо изучало большинство людей. Однако из-за того, как его обычно преподают, трудно увидеть суть того, что на самом деле делает регрессия.
Однако из-за того, как его обычно преподают, трудно увидеть суть того, что на самом деле делает регрессия.
Большинство курсов сосредоточены на представлении «вычисления». С этой точки зрения регрессия начинается с большого алгебраического выражения суммы квадратов расстояний между каждой наблюдаемой точкой и гипотетической линией. Затем выражение минимизируется, беря первую производную, устанавливая ее равной нулю и выполняя массу алгебры, пока мы не получим наши коэффициенты регрессии.
Большинство учебников проводят учащихся через один болезненный расчет этого, а затем полагаются на статистические пакеты, такие как R или Stata, что практически побуждает учащихся становиться зависимыми от программного обеспечения и никогда не развивать глубокую интуицию о том, что происходит. Именно так люди, которые на самом деле не понимают математику, учат регрессии.
В этом посте я проиллюстрирую более элегантный взгляд на регрессию методом наименьших квадратов — так называемый взгляд «линейной алгебры».
Проблема
Цель регрессии — подогнать математическую модель к набору наблюдаемых точек. Допустим, мы собираем данные о количестве отказов оборудования в день на каком-то заводе. Представьте, что у нас есть три точки данных: (день, количество отказов) (1,1) (2,2) (3,2)
Цель состоит в том, чтобы найти линейное уравнение, соответствующее этим точкам. Мы полагаем, что существует базовое математическое соотношение, которое однозначно связывает «дни» с «количеством отказов оборудования», или
в форме
, где b — количество отказов в день, x — день, а C и D — количество отказов. коэффициенты регрессии, которые мы ищем.
Мы можем записать эти три точки данных в виде простой линейной системы, например:
Для первых двух точек модель представляет собой идеальную линейную систему. Когда х = 1, b = 1; и когда x = 2, b = 2. Но что-то идет не так, когда мы достигаем третьей точки. Когда x = 3, снова b = 2, так что мы уже знаем, что три точки не лежат на прямой, и наша модель будет в лучшем случае приближенной.
Теперь, когда у нас есть линейная система, мы находимся в мире линейной алгебры. Это хорошая новость, поскольку она помогает нам сделать шаг назад и увидеть общую картину. Вместо сотен чисел и алгебраических терминов нам нужно иметь дело только с несколькими векторами и матрицами.
Вот наша линейная система в матричной форме Ax = b:
Это говорит о том, что мы надеемся, что вектор b лежит в пространстве столбцов A, C(A). То есть мы надеемся, что существует некоторая линейная комбинация столбцов A, которая даст нам наш вектор наблюдаемых значений b.
К сожалению, мы уже знаем, что b не совсем соответствует нашей модели. Это означает, что 90 207 вне 90 208 пространства столбца A. Поэтому мы не можем просто решить это уравнение для вектора x.
Давайте посмотрим на картину того, что происходит.
На рисунке ниже пространство столбца A отмечено C(A). Он образует плоскую плоскость в трехмерном пространстве. Если представить столбцы матрицы A как векторы a1 и a2, плоскость представляет собой все возможные линейные комбинации a1 и a2. Они отмечены на картинке.
Они отмечены на картинке.
Напротив, вектор наблюдаемых значений b не лежит в плоскости. Он торчит в каком-то направлении, отмеченном буквой «b» на рисунке.
Плоскость C(A) на самом деле всего лишь наша долгожданная математическая модель. А ошибочный вектор b — это наши наблюдаемые данные, которые, к сожалению, не соответствуют модели. так что нам делать?
Ответ линейной регрессии заключается в том, что мы должны забыть о поиске модели, которая идеально соответствует b, и вместо этого заменить b на другой вектор, который довольно близок к нему, но соответствует нашей модели. В частности, мы хотим выбрать вектор p, который находится в пространстве столбцов A, но при этом максимально близок к b.
На рисунке ниже показан процесс. Подумайте о том, чтобы посветить фонариком на b сверху. Это отбрасывает тень на C(A). Это проекция вектора b на пространство столбцов A. Эта проекция обозначена на рисунке буквой p.
Линия, отмеченная e, представляет собой «ошибку» между нашим наблюдаемым вектором b и спроецированным вектором p, который мы планируем использовать вместо этого. Цель состоит в том, чтобы выбрать вектор p так, чтобы e было как можно меньше. То есть мы хотим минимизировать ошибку между вектором p, используемым в модели, и наблюдаемым вектором b.
Цель состоит в том, чтобы выбрать вектор p так, чтобы e было как можно меньше. То есть мы хотим минимизировать ошибку между вектором p, используемым в модели, и наблюдаемым вектором b.
На рисунке e — это просто наблюдаемый вектор b минус проекция p, или b — p. А сама проекция — это просто комбинация столбцов A — вот почему она в конце концов находится в пространстве столбцов — так что она равна A, умноженному на некоторый вектор x-hat.
Чтобы минимизировать e, мы хотим выбрать p, который перпендикулярен вектору ошибки e, но указывает в том же направлении, что и b. На рисунке точка пересечения e и p отмечена углом 90 градусов.
Геометрия делает довольно очевидным то, что происходит. Мы начали с b, который не соответствует модели, а затем переключились на p, который является довольно хорошим приближением и имеет то преимущество, что находится в пространстве столбца A.
Решение для коэффициентов регрессии
Поскольку вектор e перпендикулярен плоскости пространства столбца A, это означает, что скалярное произведение между ними должно быть равно нулю. То есть
То есть
. Но поскольку e = b — p и p = A, умноженное на x-hat, мы получаем
Решая x-hat, мы получаем
Элементы вектора x-hat представляют собой оценочные коэффициенты регрессии. C и D мы ищем. Они минимизируют расстояние e между моделью и наблюдаемыми данными элегантным способом, не использующим вычисления или явные алгебраические суммы.
Вот простой способ запомнить, как это работает: линейная регрессия — это просто попытка решить Ax = b. Но если какая-либо из наблюдаемых точек в b отклоняется от модели, A не будет обратимой матрицей. Поэтому вместо этого мы заставляем его стать обратимым, умножая обе части на транспонирование А. Транспонирование А на А всегда будет квадратным и симметричным, поэтому оно всегда обратимо. Тогда мы просто решаем для x-шляпы.
В этом представлении есть и другие положительные стороны. Во-первых, гораздо проще интерпретировать коэффициент корреляции r. Если наши точки данных x и y нормализованы относительно их средних значений, то есть если мы вычтем их среднее значение из каждого наблюдаемого значения, r будет просто косинусом угла между b и плоскостью на чертеже.

 с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7
с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7 с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7
с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7