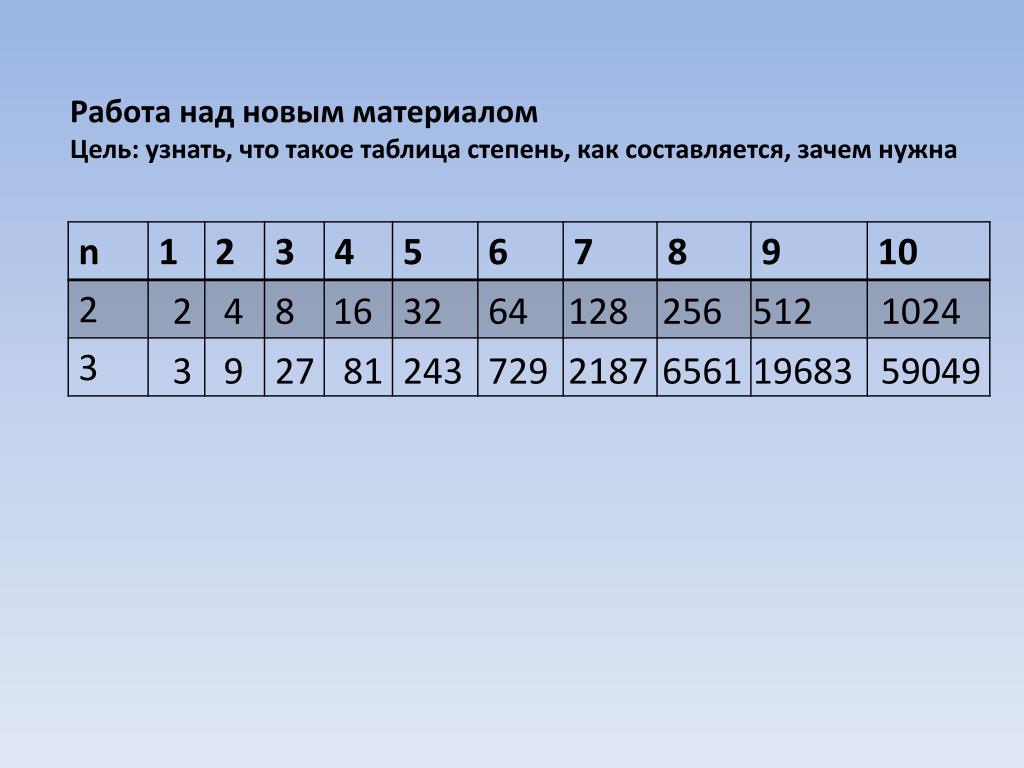
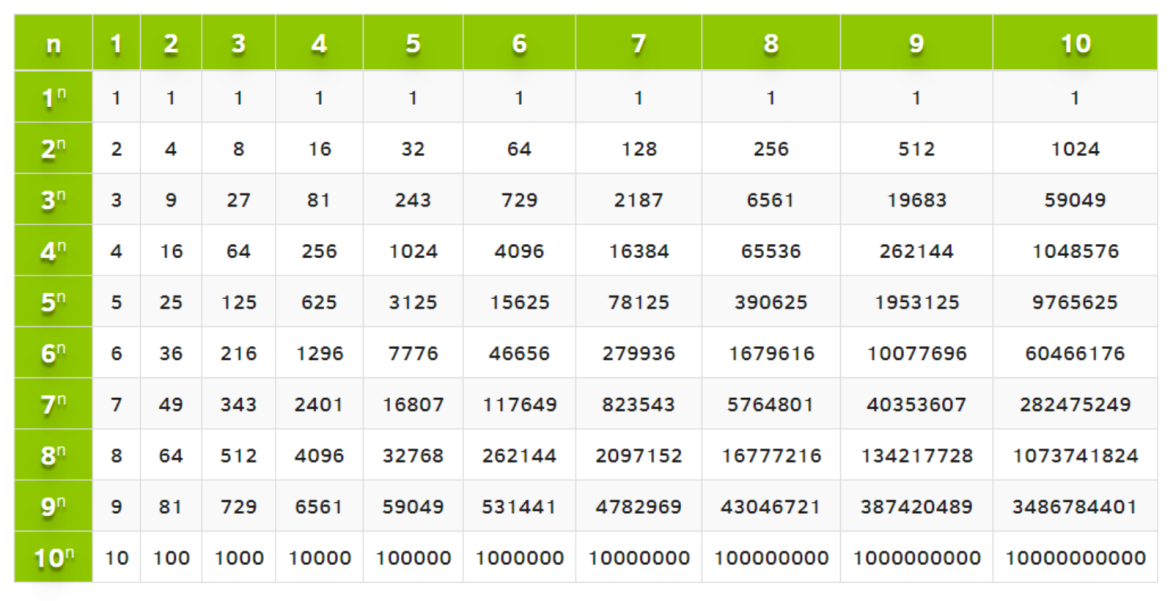
Таблица степеней — Таълим / Образование
Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет 6 в 4-ой степени! Вся таблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть другие темы в разделе «Единицы измерения» !
Также на сайте работает интерактивный чат (на левой стороне сайта), на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
Таблица степеней 1 — 10
11 = 1
12 = 1
13 = 1
14 = 1
15 = 1
16 = 1
17 = 1
18 = 1
1
110 = 1
2 в степени:
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
210 = 1024
3 в степени:
31 = 3
32 = 9
33 = 27
34 = 81
35 = 243
36 = 729
37 = 2187
38 = 6561
39 = 19683
310 = 59049
4 в степени:
41 = 4
4 2 = 16
43 = 64
44 = 256
45 = 1024
46 = 4096
47 = 16384
48 = 65536
49 = 262144
410 = 1048576
5 в степени:
51 = 5
52 = 25
53 = 125
54 = 625
55 = 3125
56 = 15625
57 = 78125
58 = 390625
59 = 1953125
510 = 9765625
6 в степени:
61 = 6
62 = 36
63 = 216
64 = 1296
65
66 = 46656
67 = 279936
68 = 1679616
69 = 10077696
610 = 60466176
7 в степени:
71 = 7
72 = 49
73 = 343
74 = 2401
75 = 16807
76 = 117649
77 = 823543
78 = 5764801
79 = 40353607
710 = 282475249
8 в степени:
81 = 8
82 = 64
83 = 512
84 = 4096
85 = 32768
86 = 262144
87 = 2097152
89 = 134217728
810 = 1073741824
9 в степени:
91 = 9
92 = 81
93 = 729
94 = 6561
95 = 59049
96 = 531441
97 = 4782969
98 = 43046721
99 = 387420489
910 = 3486784401
10 в степени:
101 = 10
102 = 100
103 = 1000
104 = 10000
105 = 100000
106 = 1000000
107 = 10000000
108 = 100000000
109 = 1000000000
Таблица степенейСкачать
источник
Похожие темы
🔥12. 8 K раз просмотрено
8 K раз просмотрено
daraja,darajalar jadvali,даража,даражалар жадвали,единицы измерения,жадвал,сонлар,сонларнинг даражаси,степень,таблица,таблица степеней,таблица степень,ўлчов бирликлари
- ← Русско-узбекский разговорник (первые слова)
- Дошкольное образование за рубежом →
Таблица степеней.
| Twitt | Нравится |
Возведение в степень — операция, происходящая из сокращения для множественного умножения числа на самого себя.
| 11 = 1 12 = 1 13 = 1 14 = 1 15 = 1 16 = 1 17 = 1 18 = 1 19 = 1 110 = 1 111 = 1 112 = 1 | 21 = 2 22 = 4 23 = 8 24 = 16 25 = 32 26 = 64 27 = 128 28 = 256 29 = 512 210 = 1024 211 = 2048 212 = 4096 | 31 = 3 32 = 9 33 = 27 34 = 81 35 = 243 36 = 729 37 = 2187 38 39 = 19683 310 = 59049 311 = 177147 312 = 531441 |
| 41 = 4 42 = 16 43 = 64 44 = 256 45 = 1024 46 = 4096 47 = 16384 48 = 65536 49 = 262144 410 = 1048576 411 = 4194304 412 = 16777216 | 51 = 5 52 = 25 53 = 125 54 = 625 55 = 3125 56 = 15625 57 = 78125 58 = 390625 59 = 1953125 510 = 9765625 511 = 48828125 512 = 244140625 | 61 = 6 62 = 36 63 = 216 64 = 1296 65 = 7776 66 = 46656 67 = 279936 68 = 1679616 69 = 10077696 610 = 60466176 611 = 362797056 612 = 2176782336 |
| 71 = 7 72 = 49 73 = 343 74 = 2401 75 = 16807 76 = 117649 77 = 823543 78 = 5764801 79 = 40353607 710 = 282475249 711 = 1977326743 712 = 13841287201 | 81 = 8 82 = 64 83 = 512 84 = 4096 85 = 32768 86 = 262144 87 = 2097152 88 = 16777216 89 = 134217728 810 = 1073741824 811 = 8589934592 812 = 68719476736 | 91 = 9 92 = 81 94 = 6561 95 = 59049 96 = 531441 97 = 4782969 98 = 43046721 99 = 387420489 910 = 3486784401 911 = 31381059609 912 = 282429536481 |
| 101 = 10 102 = 100 103 = 1000 104 = 10000 105 = 100000 106 = 1000000 107 = 10000000 108 = 100000000 109 = 1000000000 1010 = 10000000000 1011 = 100000000000 1012 = 1000000000000 | 111 = 11 112 = 121 113 = 1331 114 = 14641 115 = 161051 116 = 1771561 117 = 19487171 118 = 214358881 119 = 2357947691 11 10 = 25937424601 1111 = 285311670611 1112 = 3138428376721 | 121 = 12 122 = 144 123 = 1728 124 = 20736 125 = 248832 126 = 2985984 127 = 35831808 128 = 429981696 129 = 5159780352 1210 = 61917364224 1211 = 743008370688 1212 = 8916100448256 |
| Twitt | Нравится |
Добавить комментарий
Таблицахи-квадрат (Χ²) | Примеры и загружаемая таблица
Опубликован в
31 мая 2022 г.
Таблица распределения хи-квадрат (Χ 2 ) представляет собой справочную таблицу, в которой перечислены критические значения хи-квадрата . Критическое значение хи-квадрат представляет собой порог статистической значимости для определенных проверок гипотез и определяет доверительные интервалы для определенных параметров.
Критические значения хи-квадрата рассчитываются из распределений хи-квадрат. Их трудно рассчитать вручную, поэтому большинство людей вместо этого используют справочную таблицу или статистическое программное обеспечение.
Скачать таблицу хи-квадрат (PDF)
Содержание
- Когда использовать таблицу распределения хи-квадрат
- Таблица распределения хи-квадрат (правосторонние вероятности)
- Как пользоваться таблицей
- Левосторонние и двусторонние вероятности
- Практические вопросы
- Часто задаваемые вопросы о таблицах хи-квадрат
Когда использовать таблицу распределения хи-квадрат
Вам понадобится критическое значение хи-квадрат, если вы хотите:
- Расчет доверительного интервала для дисперсии генеральной совокупности или стандартного отклонения
- Проверить, равна ли дисперсия или стандартное отклонение совокупности определенному значению (проверка одной дисперсии)
- Проверить, отличается ли частотное распределение категориальной переменной от ваших ожиданий (критерий согласия хи-квадрат)
- Проверить, связаны ли две категориальные переменные друг с другом (критерий независимости хи-квадрат)
- Проверка равенства пропорций двух тесно связанных переменных (критерий Макнемара)
Таблица распределения хи-квадрат (правосторонние вероятности)
Используйте приведенную ниже таблицу, чтобы найти критическое значение хи-квадрат для теста хи-квадрат или доверительного интервала, или загрузите таблицу распределения хи-квадрат (PDF).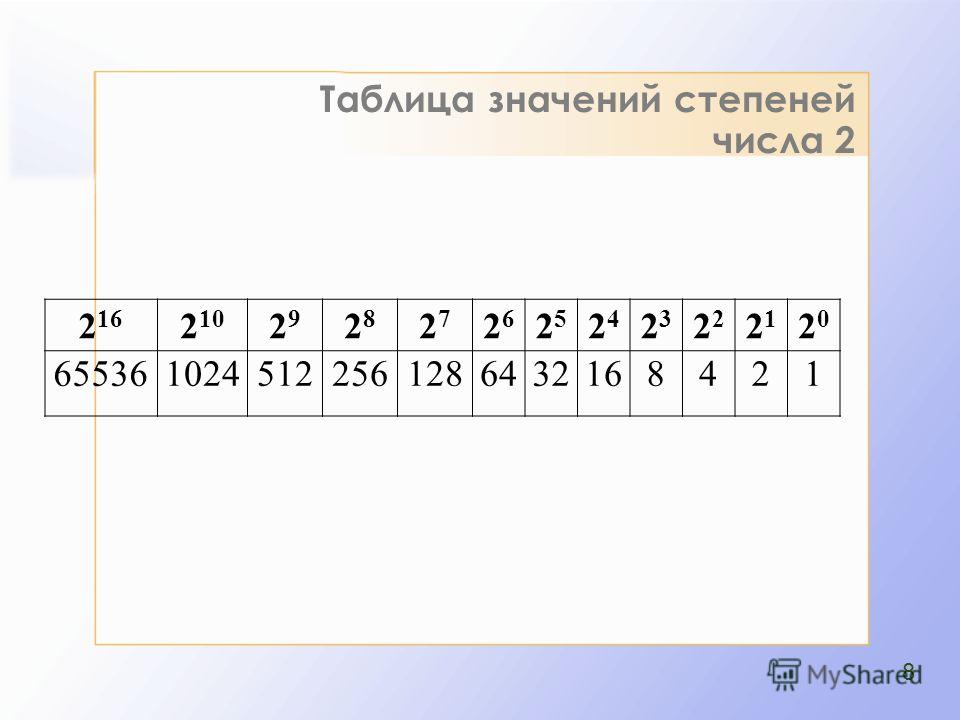
В таблице представлены вероятности правого хвоста. Если вам нужны вероятности левого хвоста, вам нужно будет сделать небольшой дополнительный расчет.
Предотвращение плагиата. Запустите бесплатную проверку.
Попробуй бесплатноКак пользоваться столом
Чтобы найти критическое значение хи-квадрат для проверки гипотезы или доверительного интервала, выполните следующие три шага.
Пример: исследование хи-квадрата. Представьте, что служба безопасности большого офисного здания устанавливает камеры видеонаблюдения на четырех входах в здание. Чтобы помочь им решить, где установить камеры, они хотят знать, как часто используется каждый вход. Они случайным образом выбирают 500 человек внутри здания и спрашивают их, через какой вход они вошли в здание. Команда хочет использовать критерий согласия хи-квадрат для проверки нулевой гипотезы ( H 0 ) о том, что четыре входа одинаково часто используются населением.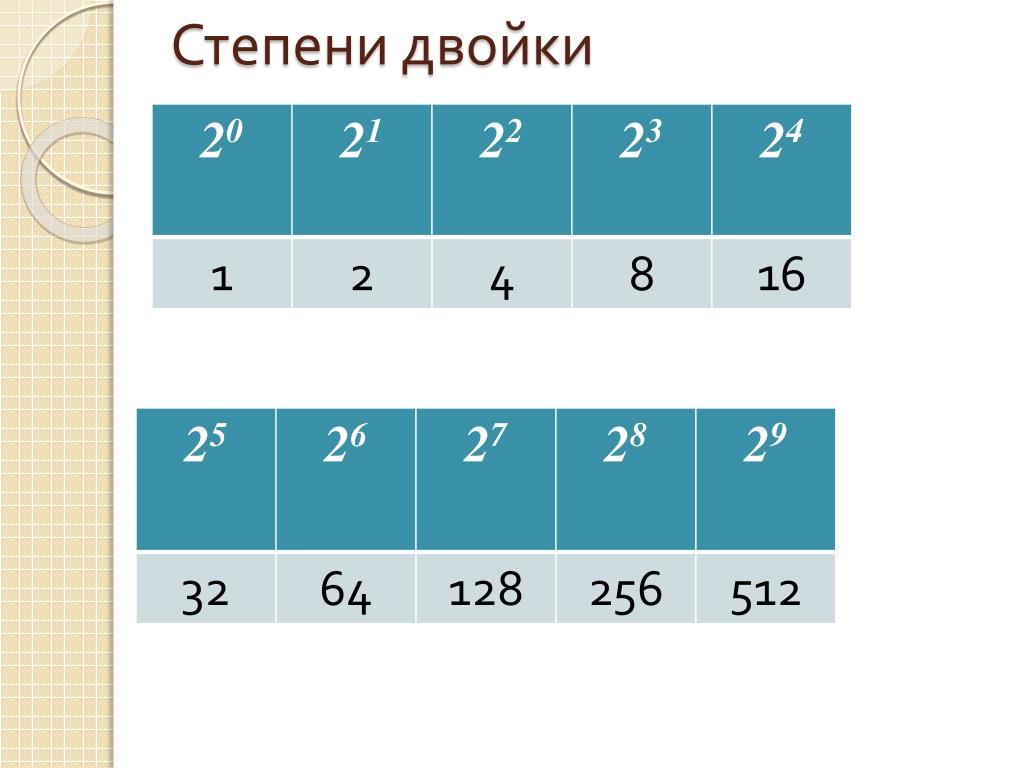
Чтобы узнать, следует ли отклонить нулевую гипотезу, им необходимо сравнить хи-квадрат Пирсона выборки с соответствующим критическим значением хи-квадрат.
Шаг 1. Расчет степеней свободы
Существует не одно распределение хи-квадрат — их много, и их формы различаются в зависимости от параметра, называемого «степенями свободы» (также называемого 9).0065 df или к ). Каждая строка таблицы распределения хи-квадрат представляет собой распределение хи-квадрат с различным df.
Вам необходимо использовать распределение с правильным df для вашего теста или доверительного интервала. В таблице ниже приведены уравнения для расчета df для нескольких распространенных процедур:
| Тест или процедура | Степени свободы ( df ) уравнение |
|---|---|
| Проверка одной дисперсии Доверительный интервал для дисперсии или стандартного отклонения | df = объем выборки − 1 |
| Хи-квадрат критерия согласия | df = количество групп − 1 |
| Критерий независимости хи-квадрат | df = (количество групп переменных 1 — 1) * (количество групп переменных 2 — 1) |
| Тест Макнемара | дф = 1 |
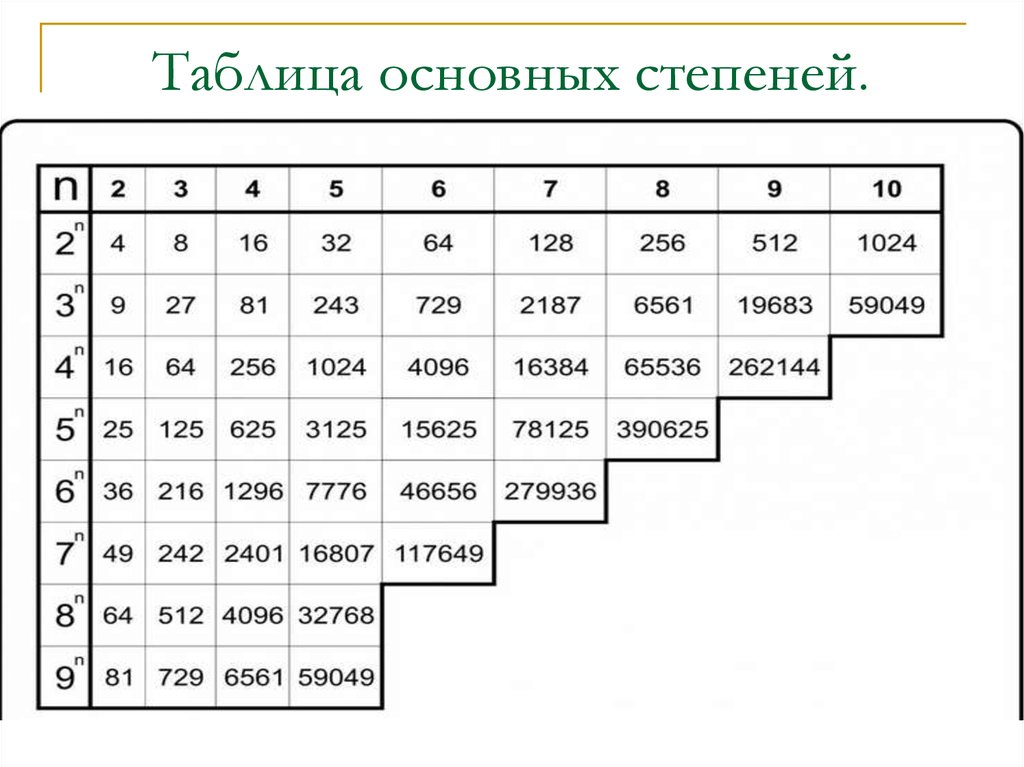 Формула критерия согласия хи-квадрат выглядит следующим образом:
Формула критерия согласия хи-квадрат выглядит следующим образом:df = количество групп − 1
дф = 4 — 1
df = 3
Шаг 2: Выберите уровень значимости
В столбцах таблицы распределения хи-квадрат указан уровень значимости критического значения. По соглашению уровень значимости (α) почти всегда равен 0,05, поэтому столбец для 0,05 выделен в таблице.
В редких случаях вы можете увеличить α, чтобы уменьшить частоту ошибок типа II, или уменьшить α, чтобы уменьшить частоту ошибок типа I.
Чтобы рассчитать доверительный интервал, выберите уровень значимости на основе желаемого уровня достоверности:
α = 1 − уровень достоверности
Наиболее распространенный доверительный уровень составляет 95% (0,95), что соответствует α = 0,05.
Пример: выбор уровня значимости Группа безопасности следует соглашению, выбирая уровень значимости 0,05.Шаг 3: Найдите критическое значение в таблице
Теперь у вас есть два числа, необходимые для нахождения критического значения в таблице распределения хи-квадрат:
- Степени свободы ( df ) перечислены в левой части таблицы.
 Найдите строку таблицы, соответствующую вычисленным вами степеням свободы.
Найдите строку таблицы, соответствующую вычисленным вами степеням свободы. - Уровни значимости (α) перечислены вверху таблицы. Найдите столбец, соответствующий выбранному вами уровню значимости.
- Ячейка таблицы, где встречаются строка и столбец, является вашим критическим значением.
Команда безопасности теперь может сравнить это критическое значение хи-квадрата с хи-квадратом Пирсона, рассчитанным для их выборки. Если критическое значение больше, чем хи-квадрат выборки, они могут отклонить нулевую гипотезу.
Левосторонние и двусторонние вероятности
В приведенной здесь таблице указаны вероятности правого хвоста. Вы должны использовать эту таблицу для большинства тестов хи-квадрат, включая критерий согласия хи-квадрат соответствия и критерий независимости хи-квадрат, а также критерий Макнемара.
Если вы хотите выполнить двусторонний или левосторонний тест, вам нужно будет сделать небольшой дополнительный расчет.
Левосторонние тесты
Наиболее распространенный левосторонний тест — это тест одной дисперсии при определении того, равна ли дисперсия совокупности или стандартное отклонение меньше определенного значения.
Чтобы найти критическое значение левосторонней вероятности в приведенной выше таблице, просто используйте столбец таблицы для 1 − α.
Пример: левосторонний тестПредставьте, что вы подрабатываете печеньем в пекарне. Владелец пекарни говорит вам, что их печенье обычно различается по размеру со стандартным отклонением всего в 0,2 дюйма в диаметре.Вы гордитесь тем, что делаете все файлы cookie одинакового размера, поэтому решаете случайным образом выбрать 25 файлов cookie, чтобы проверить, не превышает ли их стандартное отклонение 0,2 дюйма.
Это левосторонний тест, потому что вы хотите знать, меньше ли стандартное отклонение определенного значения. Вы ищете левостороннюю вероятность в правосторонней таблице, вычитая единицу из вашего уровня значимости: 1 — α = 1 — 0,05 = 0,95.
Вы ищете левостороннюю вероятность в правосторонней таблице, вычитая единицу из вашего уровня значимости: 1 — α = 1 — 0,05 = 0,95.
Критическое значение для df = 25 − 1 = 24 и α = 0,95 равно 13,848.
Если хи-квадрат вашей выборки больше этого критического значения, вы можете отклонить нулевую гипотезу о том, что ваши файлы cookie имеют стандартное отклонение в 0,2 дюйма в диаметре.
Двусторонние тесты
Наиболее распространенный левосторонний тест — это тест одной дисперсии при определении того, равна ли дисперсия или стандартное отклонение совокупности определенному значению.
Двусторонний тест имеет два критических значения. Чтобы найти критические значения, используйте столбцы таблицы для
и . Пример: двусторонний тест. Производитель детской одежды хочет спроектировать свои детские шапочки таким образом, чтобы они подходили любому шестимесячному ребенку с точностью до двух стандартных отклонений от среднего диаметра головы.
Они находят в медицинском учебнике, что стандартное отклонение диаметра головы шестимесячных младенцев составляет 1 дюйм, но хотят сами подтвердить это число. Они случайным образом выбирают 20 шестимесячных младенцев и измеряют их головы.
Это двусторонний тест, потому что они хотят знать, равно ли стандартное отклонение определенному значению. Они должны искать два критических значения в столбцах для:
- и
Критическое значение для df = 20 — 1 = 19 и α = 0,025 равно 32,852. Критическое значение для df = 19 и α = 0,975 равно 8,907.
Если хи-квадрат их выборки не находится между этими двумя критическими значениями, компания по производству одежды может отвергнуть нулевую гипотезу о том, что стандартное отклонение диаметра головы составляет 1 дюйм.
Практические вопросы
на базе Typeform
Часто задаваемые вопросы о таблицах хи-квадрат
Вы можете использовать функцию qchisq() , чтобы найти критическое значение хи-квадрат в R.
Например, чтобы вычислить критическое значение хи-квадрат для теста с df = 22 и α = 0,05:
qchisq(p = 0,05, df = 22, нижний.хвост = ЛОЖЬ)
Вы можете использовать функцию CHISQ.INV.RT() , чтобы найти критическое значение хи-квадрат в Excel.
Например, чтобы вычислить критическое значение хи-квадрат для теста с df = 22 и α = 0,05, щелкните любую пустую ячейку и введите:
Процитировать эту статью Scribbr
Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.
Терни, С. (2022, 10 ноября). Таблица хи-квадрат (Χ²) | Примеры и загружаемая таблица. Скриббр. Проверено 10 февраля 2023 г., с https://www.scribbr.com/statistics/chi-square-distribution-table/
Процитировать эту статью
Полезна ли эта статья?
Вы уже проголосовали. Спасибо 🙂 Ваш голос сохранен 🙂 Обработка вашего голоса…
Во время учебы в магистратуре и докторантуре Шон научился применять научные и статистические методы в своих исследованиях в области экологии. Теперь он любит учить студентов, как собирать и анализировать данные для собственных диссертаций и исследовательских проектов.
Таблица ANOVA (SS, df, MS, F) в двухфакторном ANOVA — FAQ 1909
Вы можете интерпретировать результаты двухфакторного дисперсионного анализа, взглянув на значения P и особенно на множественные сравнения. Многие ученые игнорируют таблицу ANOVA. Но если вам интересны подробности, на этой странице объясняется, как рассчитывается таблица ANOVA.
Интерпретация результатов двухфакторного дисперсионного анализа
Я ввел данные с двумя строками, тремя столбцами и тремя параллельными повторениями на ячейку. Нет пропущенных значений. Итак, всего введено 18 значений. Призматический файл.
Я проанализировал данные четырьмя способами: предполагая отсутствие повторных измерений, предполагая повторные измерения с наложенными друг на друга совпавшими значениями, предполагая повторные измерения с разбросанными по строке совпавшими значениями и повторяя измерения в обоих направлениях. Таблицы ниже имеют цветовую кодировку, чтобы объяснить эти конструкции. Каждый цвет в таблице представляет один предмет. Цвета повторяются между столами, но это ничего не значит.
Каждый цвет в таблице представляет один предмет. Цвета повторяются между столами, но это ничего не значит.
Файл Powerpoint
Таблица двухфакторного дисперсионного анализа
Вот таблицы дисперсионного анализа для четырех условий. Все эти значения сообщает Prism. Я немного переставил и переименовал, чтобы все четыре можно было отобразить в одной таблице (файл Excel).
Как представить результаты двухфакторного дисперсионного анализа в виде таблицы
Сумма квадратов
Сначала сосредоточить внимание на столбце суммы квадратов (СС) без повторных измерений:
В первой строке показано взаимодействие строк и столбцов. Он количественно определяет, насколько вариативна из-за того, что различия между строками неодинаковы для всех столбцов. Эквивалентно, он количественно определяет степень вариации из-за того, что различия между столбцами неодинаковы для обеих строк.
- Во второй строке показана величина вариации, вызванная систематическими различиями между двумя строками.

- В третьей строке показана величина вариации, вызванная систематическими различиями между столбцами.
- В предпоследней строке показан вариант, не объясняемый ни одной из других строк. Это называется остатком или ошибкой.
- В последней строке показана общая величина вариации среди всех 18 значений.
Теперь посмотрите на столбцы SS для анализа тех же данных, но с различными предположениями о повторных измерениях.
- Общий SS остается прежним. Это имеет смысл. Это измеряет общую вариацию среди 18 значений.
- Значения SS для взаимодействия и для систематических эффектов строк и столбцов (три верхних строки) одинаковы во всех четырех анализах.
- SS для остатка меньше, если вы предполагаете повторные измерения, поскольку некоторые из этих вариаций могут быть связаны с вариациями между субъектами. В последних столбцах некоторые из этих вариаций также можно отнести к взаимодействию между субъектами и строками или столбцами.

Степени свободы
Теперь посмотрим на значения DF.
Подробности о том, как вычисляются SS и DF, можно найти у Максвелла и Делани (ссылка ниже). Таблица 12.2 на стр. 576 поясняет таблицу ANOVA для повторных измерений обоих факторов. Но обратите внимание, что они используют термин «A x B x S», где мы говорим «Остаток». Таблица 12.16 на стр. 595 поясняет таблицу ANOVA для повторных измерений одного фактора. Они говорят «B x S/A», где Prism говорит «остаток», и говорят «S/A», где Prism говорит «субъект».
Средние квадраты
Каждое среднеквадратичное значение вычисляется путем деления значения суммы квадратов на соответствующие степени свободы. Другими словами, для каждой строки в таблице ANOVA разделите значение SS на значение df, чтобы вычислить значение MS.
Отношение F
Каждое отношение F вычисляется путем деления значения MS на другое значение MS. Значение MS для знаменателя зависит от плана эксперимента.
- Для двустороннего дисперсионного анализа без повторных измерений: Значение MS в знаменателе всегда равно MSresidual.

- Для двустороннего дисперсионного анализа с повторными измерениями в одном факторе (стр. 596 Максвелла и Делани):
- Для взаимодействия знаменатель MS равен MSresidual
- Для фактора, который не является повторным измерением, знаменатель MS равен MSsubjects
- Для коэффициента, который измеряется повторно, знаменатель MS равен MSостаток
- Для двустороннего дисперсионного анализа с повторными измерениями обоих факторов (стр. 577 Максвелла и Делани): MS для знаменателя — это MS для взаимодействия тестируемого фактора с субъектами.
- Для Row Factor знаменатель MS соответствует взаимодействию Row factor x Subjects
- Для коэффициента столбца знаменатель MS соответствует взаимодействию коэффициента столбца x предметов
- Для взаимодействия:Коэффициент строки x Коэффициент столбца, знаменатель MS предназначен для остатков (также называемых взаимодействием Строка x Столбец x Субъекты)
Значения P
Каждое отношение F вычисляется как отношение двух значений MS.

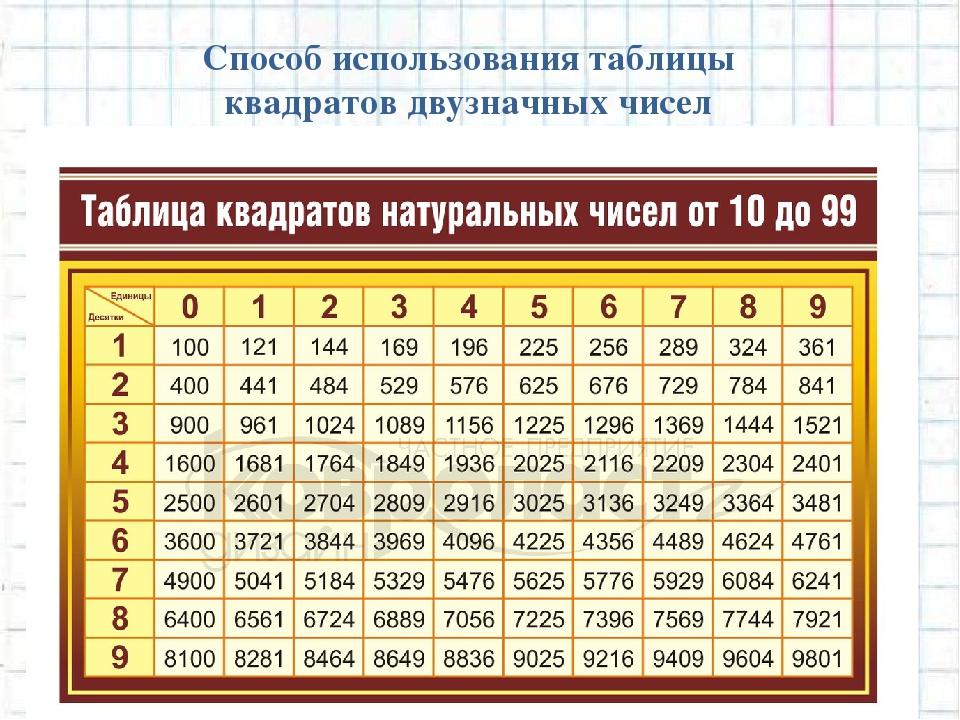 Найдите строку таблицы, соответствующую вычисленным вами степеням свободы.
Найдите строку таблицы, соответствующую вычисленным вами степеням свободы.