Степень корень квадратный: Квадратный корень из степени: правила и примеры

2

Корень n-й степени и его свойства

Корень n-й степени и его свойства

Что такое корень n-й степени? Как извлечь корень?

                В восьмом классе вы уже успели познакомиться с квадратным корнем. Решали типовые примеры с корнями, применяя те или иные свойства корней. Также решали квадратные уравнения, где без извлечения квадратного корня — никак. Но квадратный корень — это лишь частный случай более широкого понятия — корня n-й степени. Помимо квадратного, бывает, например, кубический корень, корень четвёртой, пятой и более высоких степеней. И для успешной работы с такими корнями неплохо бы всё-таки для начала быть на «ты» с корнями квадратными.) Поэтому у кого проблемы с ними — настоятельно рекомендую повторить.

            Извлечение корня — это одна из операций, обратных возведению в степень.) Почему «одна из»? Потому, что, извлекая корень, мы ищем основание по известным степени и показателю. А есть ещё одна обратная операция — нахождение показателя по известным степени и основанию. Такая операция называется нахождением логарифма. Она более сложная, чем извлечение корня и изучается в старших классах.)

            Итак, знакомимся!

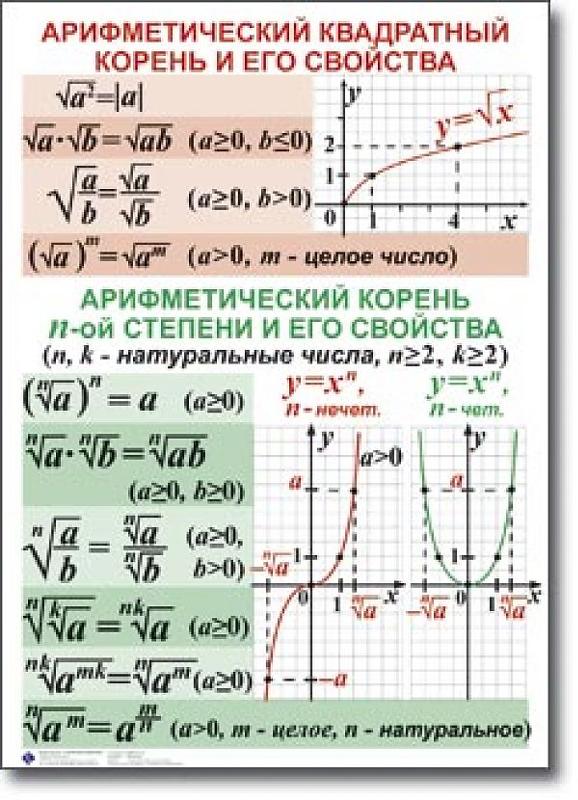
            Во-первых, обозначение. Квадратный корень, как мы уже знаем, обозначается вот так: . Называется этот значок очень красиво и научно — радикал. А как обозначают корни других степеней? Очень просто: над «хвостиком» радикала дополнительно пишут показатель той степени, корень которой ищется. Если ищется кубический корень, то пишут тройку: . Если корень четвёртой степени, то, соответственно, . И так далее.) В общем виде корень n-й степени обозначается вот так:

, где .

            Число a, как и в квадратных корнях, называется подкоренным выражением, а вот число n для нас здесь новое. И называется показателем корня.

            Как извлекать корни любых степеней? Так же, как и квадратные — сообразить, какое число в n-й степени даёт нам число a.)

            Как, например, извлечь кубический корень из 8? То есть ? А какое число в кубе даст нам 8? Двойка, естественно.) Вот и пишут:

            Или . Какое число в четвёртой степени даёт 81? Тройка.) Значит,

            А корень десятой степени из 1? Ну, ежу понятно, что единица в любой степени (в том числе и в десятой) равна единице. ) То есть:

 и вообще .

   С нулём та же история: ноль в любой натуральной степени равен нулю. Стало быть, .

           Как видим, по сравнению с квадратными корнями, здесь уже посложнее соображать, какое число в той или иной степени даёт нам подкоренное число a. Сложнее подбирать ответ и проверять его на правильность возведением в степень n. Ситуация существенно облегчается, если знать в лицо степени популярных чисел. Поэтому сейчас — тренируемся. 🙂 Распознаём степени!)

Ответы (в беспорядке):

          Да-да! Ответов побольше, чем заданий.) Потому, что, к примеру, 2⁸, 4⁴ и 16² – это всё одно и то же число 256.

          Потренировались? Тогда считаем примерчики:

                                                           

          Ответы (тоже в беспорядке): 6; 2; 3; 2; 3; 5.

          Получилось? Великолепно! Движемся дальше.)

Ограничения в корнях. Арифметический корень n-й степени.

          В корнях n-й степени, как и в квадратных, тоже есть свои ограничения и свои фишки. По своей сути, они ничем не отличаются от таковых ограничений для квадратных корней.

          Например, попробуем посчитать вот такой корень:

          Не подбирается ведь, да? Что 3, что -3 в четвёртой степени будет +81. 🙂 И с любым корнем чётной степени из отрицательного числа будет та же песня. А это значит, что извлекать корни чётной степени из отрицательных чисел нельзя. Это запретное действие в математике. Такое же запретное, как и деление на ноль. Поэтому такие выражения, как ,  и тому подобные — не имеют смысла.

          Зато корни нечётной степени из отрицательных чисел — пожалуйста!

          Например, ; , и так далее.)

          А из положительных чисел можно со спокойной душой извлекать любые корни, любых степеней:

          В общем, понятно, думаю. ) И, кстати, корень совершенно не обязан извлекаться ровно. Это просто примеры такие, чисто для понимания.) Бывает, что в процессе решения (например, уравнений) выплывают и довольно скверные корни. Что-нибудь типа . Из восьмёрки кубический корень извлекается отлично, а тут под корнем семёрка. Что делать? Ничего страшного. Всё точно так же.  – это число, которое при возведении в куб даст нам 7. Только число это очень некрасивое и лохматое. Вот оно:

          Причём, это число никогда не кончается и не имеет периода: цифры следуют совершенно беспорядочно. Иррациональное оно… В таких случаях ответ так и оставляют в виде корня.) А вот если корень извлекается чисто (к примеру, ), то, естественно, надо корень посчитать и записать:

          Идём дальше.

          Снова берём наше подопытное число 81 и извлекаем из него корень четвёртой степени:

          Потому, что три в четвёртой будет 81. Ну, хорошо! Но ведь и минус три в четвёртой тоже будет 81!

          Получается неоднозначность:

          И, чтобы её устранить, так же, как и в квадратных корнях, ввели специальный термин: арифметический корень n-й степени из числа a – это такое неотрицательное число, n-я степень которого равна a.

          А ответ с плюсом-минусом называется по-другому — алгебраический корень n-й степени. У любой чётной степени алгебраическим корнем будет два противоположных числа. В школе же работают только с арифметическими корнями. Поэтому отрицательные числа в арифметических корнях попросту отбрасываются. Например, пишут: . Сам плюс, конечно же, не пишут: его подразумевают.

          Всё, казалось бы, просто, но… А как же быть с корнями нечётной степени из отрицательных чисел? Ведь там-то всегда при извлечении получается отрицательное число! Так как любое отрицательное число в нечётной степени также даёт отрицательное число. А арифметический корень работает только с неотрицательными числами! На то он и арифметический.)

          В таких корнях делают вот что: выносят минус из-под корня и ставят перед корнем. Вот так:

          В таких случаях говорят, что  выражен через арифметический (т.е. уже неотрицательный) корень .

          Но есть один пунктик, который может вносить путаницу, — это решение простеньких уравнений со степенями. Например, вот такое уравнение:

          Пишем ответ: . На самом деле, этот ответ — всего-навсего сокращённая запись двух ответов:

          Непонятка здесь заключается в том, что чуть выше я уже написал, что в школе рассматриваются только неотрицательные (т.е. арифметические) корни. А тут один из ответов с минусом… Как быть? Да никак! Знаки здесь — это результат решения уравнения. А сам корень — величина всё равно неотрицательная! Смотрите сами:

          Ну как, теперь понятнее? Со скобочками?)

          С нечётной степенью всё гораздо проще — там всегда получается один корень. С плюсом или с минусом. Например:

          Итак, если мы просто извлекаем корень (чётной степени) из числа, то мы всегда получаем один неотрицательный результат. Потому что это — арифметический корень. А вот, если мы решаем уравнение с чётной степенью, то мы получаем два противоположных корня, поскольку это — решение уравнения.

          С корнями нечётных степеней (кубическими, пятой степени и т.д.) проблем никаких. Извлекаем себе и не паримся со знаками. Плюс под корнем — значит, и результат извлечения с плюсом. Минус — значит, минус.)

          А теперь настал черёд познакомиться со свойствами корней. Некоторые уже будут нам знакомы по квадратным корням, но добавится и несколько новых. Поехали!

Свойства корней. Корень из произведения.

           Это свойство уже знакомо нам из квадратных корней. Для корней других степеней всё аналогично:

       То есть, корень из произведения равен произведению корней из каждого множителя отдельно.

        Если показатель n чётный, то оба подкоренных числа a и b должны быть, естественно, неотрицательными, иначе формула смысла не имеет. В случае нечётного показателя ограничений никаких нет: выносим минусы из-под корней вперёд и дальше работаем с арифметическими корнями.)

        Как и в квадратных корнях, здесь эта формула одинаково полезна как слева направо, так и справа налево. Применение формулы слева направо позволяет извлекать корни из произведения. Например:

        Эта формула, кстати говоря, справедлива не только для двух, а для любого числа множителей. Например:

        Также по этой формуле можно извлекать корни из больших чисел: для этого число под корнем раскладывается на множители поменьше, а дальше извлекаются корни отдельно из каждого множителя.    

        Например, такое задание:

       Число достаточно большое. Извлекается ли из него корень ровно — тоже без калькулятора непонятно. Хорошо бы его разложить на множители. На что точно делится число 3375? На 5, похоже: последняя цифра — пятёрка.) Делим:

        Ой, снова на 5 делится! 675:5 = 135. И 135 опять на пятёрку делится. Да когда ж это кончится!)

   135:5 = 27. С числом 27 всё уже ясно — это тройка в кубе. Значит,  

        Тогда:

        Извлекли корень по кусочкам, ну и ладно.)

        Или такой пример:

         Снова раскладываем на множители по признакам делимости. Каким? На 4, т.к. последняя парочка цифр 40 — делится на 4. И на 10, т.к. последняя цифра — ноль. Значит, можно поделить одним махом сразу на 40:

         Про число 216 мы уже знаем, что это шестёрка в кубе. Стало быть,

         А 40, в свою очередь, можно разложить как . Тогда

         И тогда окончательно получим:

         Чисто извлечь корень не вышло, ну и ничего страшного. Всё равно мы упростили выражение: мы же знаем, что под корнем (хоть квадратным, хоть кубическим — любым) принято оставлять самое маленькое число из возможных. ) В этом примере мы проделали одну весьма полезную операцию, тоже уже знакомую нам из квадратных корней. Узнаёте? Да! Мы вынесли множители из-под корня. В данном примере мы вынесли двойку и шестёрку, т.е. число 12.

Как вынести множитель за знак корня?

             Вынести множитель (или множители) за знак корня очень просто. Раскладываем подкоренное выражение на множители и извлекаем то, что извлекается.) А что не извлекается — так и оставляем под корнем. Смотрите:

          Раскладываем число 9072 на множители. Так как у нас корень четвёртой степени, в первую очередь пробуем разложить на множители, являющиеся четвёртыми степенями натуральных чисел — 16, 81 и т.д.

          Попробуем поделить 9072 на 16:

 Поделилось!

           А вот 567, похоже, делится на 81:

           Значит, .

           Тогда

Свойства корней. Умножение корней.

                Рассмотрим теперь обратное применение формулы — справа налево:

           На первый взгляд, ничего нового, но внешность обманчива. ) Обратное применение формулы значительно расширяет наши возможности. Например:

           Хм, ну и что тут такого? Умножили и всё. Здесь и впрямь ничего особенного. Обычное умножение корней. А вот такой пример!

           Отдельно из множителей корни чисто не извлекаются. Зато из результата — отлично. )

           Опять же формула справедлива для любого числа множителей. Например, надо посчитать вот такое выражение:

           Здесь главное — внимание. В примере присутствуют разные корни — кубические и четвёртой степени. И ни один из них точно не извлекается…

           А формула произведения корней применима только к корням с одинаковыми показателями. Поэтому сгруппируем в отдельную кучку кубические корни и в отдельную — четвёртой степени. А там, глядишь, всё и срастётся.))

            И калькулятора не понадобилось.)

Как внести множитель под знак корня?

                Следующая полезная вещь — внесение числа под корень. Например:

           Можно ли убрать тройку внутрь корня? Элементарно! Если тройку превратить в корень, то сработает формула произведения корней. Итак, превращаем тройку в корень. Раз у нас корень четвёртой степени, то и превращать будем тоже в корень четвёртой степени.) Вот так:

           Тогда

           Корень, между прочим, можно сделать из любого неотрицательного числа. Причём той степени, какой хотим (всё от конкретного примера зависит). Это будет корень из n-й степени этого самого числа:

           А теперь — внимание! Источник очень грубых ошибок! Я не зря здесь сказал про неотрицательные числа. Арифметический корень работает только с такими. Если у нас в задании где-то затесалось отрицательное число, то либо минус так и оставляем, перед корнем (если он снаружи), либо избавляемся от минуса под корнем, если он внутри. Напоминаю, если под корнем чётной степени получается отрицательное число, то выражение не имеет смысла.

           Например, такое задание. Внести множитель под знак корня:

           Если мы сейчас внесём под корень минус два, то жестоко ошибёмся:

           В чём здесь ошибка? А в том, что четвёртая степень, в силу своей чётности, благополучно «съела» этот минус, в результате чего заведомо отрицательное число  превратилось в положительное . А верное решение выглядит так:

           В корнях нечётных степеней минус хоть и не «съедается», но его тоже лучше оставлять снаружи:

           Здесь корень нечётной степени — кубический, и мы имеем полное право минус тоже загнать под корень. Но предпочтительнее в таких примерах минус также оставлять снаружи и писать ответ выраженным через арифметический (неотрицательный) корень , поскольку корень  хоть и имеет право на жизнь, но арифметическим не является.

           Итак, с внесением числа под корень тоже всё ясно, я надеюсь.) Переходим к следующему свойству.

Свойства корней. Корень из дроби. Деление корней.

               Это свойство также полностью повторяет таковое для квадратных корней. Только теперь мы его распространяем на корни любой степени:

       Корень из дроби равен корню из числителя, делённому на корень из знаменателя.

        Если n чётно, то число a должно быть неотрицательным, а число b – строго положительным (на ноль делить нельзя). В случае нечётного показателя единственным ограничением будет .

        Это свойство позволяет легко и быстро извлекать корни из дробей:

       Идея понятна, думаю. Вместо работы с дробью целиком мы переходим к работе отдельно с числителем и отдельно со знаменателем.) Если дробь десятичная или, о ужас, смешанное число, то предварительно переходим к обыкновенным дробям:

       А теперь посмотрим, как эта формула работает справа налево. Здесь тоже выявляются очень полезные возможности. Например, такой примерчик:

       Из числителя и знаменателя корни ровно не извлекаются, зато из всей дроби — прекрасно.) Можно решить этот пример и по-другому — вынести в числителе множитель из-под корня с последующим сокращением:

       Как вам будет угодно. Ответ всегда получится один — правильный. Если ошибок не наляпать по дороге.)

       Итак, с умножением/делением корней разобрались. Поднимаемся на следующую ступеньку и рассматриваем третье свойство — корень в степени и корень из степени.

Корень в степени. Корень из степени.

        Как возвести корень в степень? Например, пусть у нас есть число . Можно это число возвести в степень? В куб, например? Конечно! Помножить корень сам на себя три раза, и — по формуле произведения корней:

       Здесь корень и степень как бы взаимоуничтожились или скомпенсировались. Действительно, если мы число, которое при возведении в куб даст нам тройку, возведём в этот самый куб, то что получим? Тройку и получим, разумеется! И так будет для любого неотрицательного числа. В общем виде:

       Если показатели степени и корня разные, то тоже никаких проблем. Если знать свойства степеней.)

       Если показатель степени меньше показателя корня, то просто загоняем степень под корень:

       В общем виде будет:

        Идея понятна: возводим в степень подкоренное выражение, а дальше упрощаем, вынося множители из-под корня, если это возможно. Если n чётно, то a должно быть неотрицательным. Почему — понятно, думаю.) А если n нечётно, то никаких ограничений на a уже нету:

        Разберёмся теперь с корнем из степени. То есть, в степень будет возводиться уже не сам корень, а подкоренное выражение. Здесь тоже ничего сложного, но простора для ошибок значительно больше. Почему? Потому, что в игру вступают отрицательные числа, которые могут вносить путаницу в знаках. Пока начнём с корней нечётных степеней — они гораздо проще.

        Пусть у нас есть число 2. Можно его возвести в куб? Конечно!

        А теперь — обратно извлечём из восьмёрки кубический корень:

        С двойки начали, к двойке же и вернулись.) Ничего удивительного: возведение в куб скомпенсировалось обратной операцией — извлечением кубического корня.

        Другой пример:

        Здесь тоже всё путём. Степень и корень друг друга скомпенсировали. В общем виде для корней нечётных степеней можно записать такую формулку:

        Эта формула справедлива для любого действительного числа a. Хоть положительного, хоть отрицательного.

        То есть, нечётная степень и корень этой же степени  всегда друг друга компенсируют и получается подкоренное выражение. 🙂

        А вот с чётной степенью этот фокус может уже не пройти. Смотрите сами:

        Здесь пока ничего особенного. Четвёртая степень и корень четвёртой же степени тоже друг друга уравновесили и получилась просто двойка, т. е. подкоренное выражение. И для любого неотрицательного числа будет то же самое. А теперь всего лишь заменим в этом корне два на минус два. То есть, посчитаем вот такой корень:

        Минус у двойки благополучно «сгорел» из-за четвёртой степени. И в результате извлечения корня (арифметического!) мы получили положительное число. Было минус два, стало плюс два.) А вот если бы мы просто бездумно «сократили» степень и корень (одинаковые же!), то получили бы

        Что является грубейшей ошибкой, да.

        Поэтому для чётного показателя формула корня из степени выглядит вот так:

        Здесь добавился нелюбимый многими знак модуля, но в нём страшного ничего нет: благодаря ему, формула также работает для любого действительного числа a. И модуль просто отсекает минусы:

        И так далее.) Эта формула — аналог формулы корня квадратного из квадрата:

        Только в корнях n-й степени появилось дополнительное разграничение на чётные и нечётные степени. Чётные степени, как мы видим, более капризные, да.)

        А теперь рассмотрим новое полезное и весьма интересное свойство, уже характерное именно для корней n-й степени: если показатель корня и показатель степени подкоренного выражения умножить (разделить) на одно и то же натуральное число, то значение корня не изменится.

        Чем-то напоминает основное свойство дроби, не правда ли? В дробях мы тоже числитель и знаменатель можем умножать (делить) на одно и то же число (кроме нуля). На самом деле, это свойство корней — тоже следствие основного свойства дроби. Когда мы познакомимся со степенью с рациональным показателем, то всё станет ясно. Что, как и откуда. )

        Прямое применение этой формулы позволяет нам упрощать уже совершенно любые корни из любых степеней. В том числе, если показатели степени подкоренного выражения и самого корня разные. Например, надо упростить вот такое выражение:

        Поступаем просто. Выделяем для начала под корнем четвёртую степень из десятой и — вперёд! Как? По свойствам степеней, разумеется! Выносим множитель из-под корня или работаем по формуле корня из степени.

        А вот  упростим, используя как раз это свойство. Для этого четвёрку под корнем представим как :

        И теперь — самое интересное — сокращаем мысленно показатель под корнем (двойку) с показателем корня (четвёркой)! И получаем:

        Вся цепочка преобразований выглядит так:

        Или такой пример:

        Это было прямое применение формулы. А вот обратное применение ещё сильнее повышает наш математический уровень. Сомневаетесь? Напрасно! Дело в том, что обратное применение этой формулы справа налево  позволяет нам сравнивать различные корни. Очень мощная штука!

Как сравнивать корни?

       Допустим, надо (без калькулятора!) сравнить два числа:

 и

       Корень квадратный из пяти — это двойка с хвостиком. Корень кубический из десяти — это тоже двойка с хвостиком. А вот какой из двух хвостиков длиннее, а какой короче — вопрос. С ходу так и не скажешь. Пока показатели корней — разные.) А вот, если их как-то преобразовать к одинаковым, то всё, глядишь, и наладится! Для этого ищем наименьшее общее кратное показателей корней. В данном случае показатели корней равны 2 и 3, т.е. оба корня будем приводить к шестёрке. Как? По вышеупомянутому свойству:

            Берём . Как корень из квадратного превратить в корень шестой степени, но так, чтобы суть выражения не изменилась? Чтобы получить шестёрку в показателе корня, надо исходный показатель корня 2 домножить на 3. Это нам надо. Но тогда и пятёрку под корнем придётся дополнительно возвести в степень 3 (т.е. в куб): это уже математике надо. Значит,

.

        С числом  всё аналогично. Только десятку под корнем будем дополнительно возводить в квадрат:

        Теперь дело за малым — сравнить два числа  и .

        Ясно, что , а значит, и  и, стало быть,

        Если перед корнями тусуются какие-то множители, то убираем их внутрь корней и — по накатанной колее. Например, такое задание:

        Сравнить  и .

        Первым делом вносим множители под корни:

        А теперь — приводим оба корня к одному показателю. К четвёрке.)

        Ну, число  уже и так приведено и уже готово для сравнения. А вот  преобразуем:

.

        Вот теперь всё и прояснилось: , поэтому .

        А это значит, что

        Этот принцип сравнения одинаковых корней по подкоренным выражениям, строго говоря, основывается на монотонном возрастании функции . То есть, большему числу соответствует и больший корень. И наоборот.) В разделе по функциям и графикам мы этому факту уделим отдельное внимание, а здесь мы просто им пользуемся. Себе во благо. 🙂

        Что ж, осталось последнее усилие. Собираем волю в кулак и знакомимся с последним (и тоже новым для нас) свойством корней — корень под корнем.

Как извлечь корень из корня?

        Это свойство на самом деле очень простое и по своей сути очень похоже на возведение степени в степень. Так как является обратным к этой операции.) Вот как оно выглядит:

        Чтобы извлечь корень из корня, надо перемножить показатели корней.

        Это свойство позволяет несколько вложенных корней заменить одним корнем. Например:

        Или такой пример:

        Причём вложений может быть сколько угодно — формула всё равно сработает:

        Как видим, никаких хитростей. Просто перемножаем показатели и считаем (если считается).

        Вот, собственно, всё что я пока хотел рассказать.)) Следующим этапом нашей работы с корнями будет преобразование иррациональных выражений. Но это — в следующий раз.

        А теперь, как всегда, делаем задания.

Задание 1

        Вычислить:

Задание 2

        Вычислить:

Задание 3

        Найти значение выражения:

Задание 4

        Вынести множитель из-под знака корня:

        Внести множитель под знака корня:

Задание 5

        Решите уравнение: 

Задание 6

        Вычислите:

        Ответы в беспорядке: 1,2; ; 2; ; 3; 6; ; 20; ; 72; 2,1; 5; 0,4; -2; ; 12; 6; 14; 4; 20/3; ; -8; ; ; 20; 42.

        Всё решилось? Одной левой? Великолепно! Корни — не ваш камень преткновения.) Не всё получилось? Не беда! Не ошибается тот, кто ничего не делает.)

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Степени и корни

Степень с целочисленным показателем

Арифметический корень

Избавление от иррациональностей в знаменателе дроби

Степень с целочисленным показателем

      Понятие степени с целочисленным показателем включает в себя три определения.

      Определение. Пусть   n   – произвольное натуральное число, а   a   – произвольное действительное число. Тогда   n – ой степенью числа   a   называют произведение   n   сомножителей, равных   a :

      Число   a   называют основанием степени, а число   n   – показателем степени.

      Определение. Пусть   a   – произвольное действительное число, отличное от   0 . Тогда, по определению:

a⁰ = 1 .

      Число a называют основанием степени, а число   0   – показателем степени.

      Определение. Пусть   n   – произвольное натуральное число, а   a   – произвольное действительное число, отличное от   0 . Тогда, по определению:

      Число   a   называют основанием степени, а число   (– n)   – показателем степени.

      Таким образом, степень с целочисленным показателем определена.

      Пример 1.

      Замечание 1. Число нуль нельзя возвести в нулевую степень и нельзя возвести в отрицательную степень.

Арифметический корень

      Пусть   n   – произвольное натуральное число, а   a   – произвольное положительное число.

      Определение. Число   x   называют арифметическим корнем   n – ой степени из числа   a ,   если, во-первых, число   x   положительное, а, во-вторых, является решением уравнения

xⁿ = a .

      В этом случае при     для арифметического корня используется обозначение:

или эквивалентное обозначение:

      Если же   n = 2,   то для арифметического квадратного корня используется обозначение:

или эквивалентное обозначение:

      Замечание 2. В курсах математики, выходящих за рамки средней школы, доказывается, что арифметический корень всегда существует, причем только один.

      Замечание 3. Очень важно помнить о том, что в формуле

содержится ошибка, за которую мгновенно следует безжалостная кара на экзаменах.

      Пример 2. Решить уравнение

x² = 25 .

      Решение. Это уравнение имеет два корня:

x₁ = 5       и       x₂ = – 5 .

      Корень уравнения   x₁ = 5   является арифметическим квадратным корнем из числа 25, а корень уравнения     x₂ = – 5     является числом, противоположным к арифметическому квадратному корню из числа 25.

      Пример 3. Решить уравнение

x³ = – 27 .

      Решение. Это уравнение имеет единственный вещественный корень   x = – 3,   но это число не является арифметическим кубическим корнем из числа   (– 27), так как у отрицательных чисел не бывает арифметических корней. Число   x = – 3   является числом, противоположным к арифметическому кубическому корню из числа   27.   Поэтому

      Замечание 4. Желающие могут ознакомиться с нашей презентацией «Степень с рациональным показателем», содержание которой связано с данным разделом.

Избавление от иррациональностей в знаменателе дроби

      В некоторых задачах требуется перейти от дроби к равной ей дроби, но такой, у которой в знаменателе нет корней (иррациональностей). Эта операция носит название «избавление от иррациональностей в знаменателе дроби» и осуществляется при помощи умножения числителя и знаменателя дроби на подходящее число. Часто это число находится с помощью формул сокращенного умножения. Покажем это на примере.

      Пример 4. Преобразовать дробь

к такому виду, чтобы в знаменателе не было иррациональностей.

      Решение. Воспользовавшись формулой сокращенного умножения «Разность квадратов», совершим следующие эквивалентные преобразования:

      Мы получили дробь, у которой в знаменателе иррациональностей нет, что и требовалось.

      С понятием степени с рациональным показателем и свойствами степеней можно ознакомиться в разделе «Степень с рациональным показателем» нашего справочника.

      Графики степенных и показательных функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.

      На сайте можно также ознакомиться с нашимиучебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Корень из 2 в 3 степени. Кубический корень (извлечение без калькулятора)

Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.

Шаги

Часть 1

Извлечение кубического корня на простом примере

Запишите задачу. Извлечение кубического корня вручную похоже на деление в столбик, но с некоторыми нюансами. Сначала запишите задачу в определенной форме.

• Запишите число, из которого нужно извлечь кубический корень. Число разбейте на группы по три цифры, причем отсчет начните с десятичной запятой. Например, нужно извлечь кубический корень из 10. Напишите это число так: 10, 000 000. Дополнительные нули призваны повысить точность результата.
• Возле и над числом нарисуйте знак корня. Представьте, что это горизонтальная и вертикальная линии, которые вы рисуете при делении в столбик. 2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.

Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток).

Подумайте, является ли полученный ответ достаточно точным.

Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1.

• Чтобы проверить точность ответа, возведите его в куб: 2,1*2,1*2,1 = 9,261.
• Если вы считаете, что ответ достаточно точный, вычисления можно не продолжать; в противном случае проделайте еще одно вычитание.

Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше. {3}=729} , то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.

Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа.

• В нашем примере число 600 находится между числами 512 и 729. Например, к первому найденному числу (8) припишите цифру 5. Получится число 8,5.

• В нашем примере: 8 , 5 ∗ 8 , 5 ∗ 8 , 5 = 614 , 1. {\displaystyle 8,5*8,5*8,5=614,1.}

Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число. {3}=614,1} . Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.

Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа.

• В нашем примере 8 , 44 ∗ 8 , 44 ∗ 8 , 44 = 601 , 2 {\displaystyle 8,44*8,44*8,44=601,2} . Это чуть больше исходного числа, поэтому оцените другое (меньшее) число, например, 8,43: 8 , 43 ∗ 8 , 43 ∗ 8 , 43 = 599 , 07 {\displaystyle 8,43*8,43*8,43=599,07} . Таким образом, значение кубического корня из 600 лежит между 8,43 и 8,44.

Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее.

{3}=599,93} , то есть результат меньше исходного числа менее чем на 0,1.

Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.

Математическое обозначение

«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.

Квадратный корень

Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.

Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.

Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…

Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.

Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.

Кубический корень

Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:

1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…

Для остальных чисел кубические корни являются иррациональными числами. В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.

Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.

Корень n-ной степени

Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.

Рассмотрим пример

Диагональ квадрата

Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из и в конечном итоге принимает вид:

d = a × sqrt(2).

Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.

Заключение

Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.

При решении некоторых технических задач бывает нужно посчитать корень третьей степени

. Иногда это число еще называют кубическим корнем. Корнем третьей степени из данного числа называют такое число, куб (третья степень) которого равняется данному. То есть если y – корень третьей степени числа x, то должно выполняться условие: y?=x (икс равно игрек куб).

Вам понадобится

• калькулятор или компьютер

Инструкция

• Чтобы посчитать корень третьей степени , воспользуйтесь калькулятором. Желательно, чтобы это был не обычный калькулятор, а калькулятор, используемый для инженерных расчетов. Однако даже на таком калькуляторе вы не найдете специальную кнопку для извлечения корня третьей степени . Поэтому используйте функцию для возведения числа в степень. Извлечению корня третьей степени соответствует возведение в степень 1/3 (одна треть).
• Для возведения числа в степень 1/3 наберите на клавиатуре калькулятора само число.
  y.
• Если корень третьей степени приходится считать систематически, то воспользуйтесь программой MS Excel. Чтобы посчитать корень третьей степени в «Екселе», введите в любую клетку знак «=», а затем, выберите значок «fx» — вставка функции. В появившемся окошке в списке «Выберите функцию» выберите строку «СТЕПЕНЬ». Нажмите кнопку «Ок». Во вновь появившемся окошке введите в строку «Число» значение числа, из которого нужно извлечь корень. В строку «Степень» введите число «1/3» и нажмите «Ок». В клетке таблицы появится искомое значение кубического корня из исходного числа.

Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.

Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.

Что нужно знать о корне произвольной степени?

Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».

Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.

Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.

Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.

Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.

Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».

В-третьих, для них справедливы все действия со степенями.

• Их можно перемножать. Тогда показатели степеней складываются.
• Корни можно разделить. Степени нужно будет вычесть.
• И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.

В чем сходства и различия квадратного и кубического корней?

Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.

А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.

Извлечение кубического корня на калькуляторе

Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?

На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.

А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».

Извлечение кубического корня вручную

Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.

Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?

1. Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
2. Определить число, куб которого меньше целой части подкоренного выражения.
   Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
3. Выполнить вычитание.
4. К остатку приписать первую группу цифр после запятой.
5. В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
6. Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
7. Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.

Наглядный пример вычисления кубического корня

Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.

Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.

1. 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
2. После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
3. а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3
4. Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
5. Вычитание дает 1176, а над корнем появилось число 4.
6. Приписать к остатку три нуля.
7. а = 24. Тогда 172800 х + 720 х 2 + х 3
8. х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
9. Снова приписать нули.
10. а = 246. Неравенство получается таким: 18154800х + 7380х 2 + х 3
11. х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.

Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.

Необычный способ извлечения кубического корня

Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.

К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.

Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.

Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.

Из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:

Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.

*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.

Мы знаем, что:

Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):

Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?

1. Это кубы чисел кратных десяти:

Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.

2. Это свойство чисел при произведении.

Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?

Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.

1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …

То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.

При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.

Покажем соответствие в табличке для всех чисел:

Знания представленных двух моментов вполне достаточно.

Рассмотрим примеры:

Извлечь кубический корень из 21952.

Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.

Извлечь кубический корень из 54852.

Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.

Извлечь кубический корень из 571787.

Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.

Извлечь кубический корень из 614125.

Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.

Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.

Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.

После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉

На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.

Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Корень из числа: определения, примеры

В этой статье мы введем понятие корня из числа. Будем действовать последовательно: начнем с квадратного корня, от него перейдем к описанию кубического корня, после этого обобщим понятие корня, определив корень n-ой степени. При этом будем вводить определения, обозначения, приводить примеры корней и давать необходимые пояснения и комментарии.

Квадратный корень, арифметический квадратный корень

Чтобы понять определение корня из числа, и квадратного корня в частности, нужно иметь представление о степени с натуральным показателем. В этом пункте мы часто будем сталкиваться со второй степенью числа — квадратом числа.

Начнем с определения квадратного корня.

Определение

Квадратный корень из числа a — это число, квадрат которого равен a.

Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (5²=5·5=25, (−0,3)²=(−0,3)·(−0,3)=0,09, (0,3)²=0,3·0,3=0,09 и 0²=0·0=0). Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.

Следует отметить, что не для любого числа a существует действительное число, квадрат которого равен a. А именно, для любого отрицательного числа a не существует ни одного действительного числа b, квадрат которого равнялся бы a. В самом деле, равенство a=b² невозможно для любого отрицательного a, так как b² – неотрицательное число при любом b. Таким образом, на множестве действительных чисел не существует квадратного корня из отрицательного числа. Иными словами, на множестве действительных чисел квадратный корень из отрицательного числа не определяется и не имеет смысла.

Отсюда вытекает логичный вопрос: «А для любого ли неотрицательного a существует квадратный корень из a»? Ответ – да. Обоснованием этого факта можно считать конструктивный способ, используемый для нахождения значения квадратного корня.

Тогда встает следующий логичный вопрос: «Каково число всех квадратных корней из данного неотрицательного числа a – один, два, три, или еще больше»? Вот ответ на него: если a равно нулю, то единственным квадратным корнем из нуля является нуль; если же a – некоторое положительное число, то количество квадратных корней из числа a равно двум, причем корни являются противоположными числами. Обоснуем это.

Начнем со случая a=0. Сначала покажем, что нуль действительно является квадратным корнем из нуля. Это следует из очевидного равенства 0²=0·0=0 и определения квадратного корня.

Теперь докажем, что 0 – единственный квадратный корень из нуля. Воспользуемся методом от противного. Предположим, что существует некоторое число b, отличное от нуля, которое является квадратным корнем из нуля. Тогда должно выполняться условие b²=0, что невозможно, так как при любом отличном от нуля b значение выражения b² является положительным. Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.

Переходим к случаям, когда a – положительное число. Выше мы сказали, что всегда существует квадратный корень из любого неотрицательного числа, пусть квадратным корнем из a является число b. Допустим, что существует число c, которое тоже является квадратным корнем из a. Тогда по определению квадратного корня справедливы равенства b²=a и c²=a, из них следует, что b²−c²=a−a=0, но так как b²−c²=(b−c)·(b+c), то (b−c)·(b+c)=0. Полученное равенство в силу свойств действий с действительными числами возможно лишь тогда, когда b−c=0 или b+c=0. Таким образом, числа b и c равны или противоположны.

Если же предположить, что существует число d, являющееся еще одним квадратным корнем из числа a, то рассуждениями, аналогичными уже приведенным, доказывается, что d равно числу b или числу c. Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.

Для удобства работы с квадратными корнями отрицательный корень «отделяется» от положительного. С этой целью вводится определение арифметического квадратного корня.

Определение

Арифметический квадратный корень из неотрицательного числа a – это неотрицательное число, квадрат которого равен a.

Для арифметического квадратного корня из числа a принято обозначение . Знак называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.

Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня – подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.

При чтении слово «арифметический» часто опускается, например, запись читают как «квадратный корень из семи целых двадцати девяти сотых». Слово «арифметический» произносят лишь тогда, когда хотят особо подчеркнуть, что речь идет именно о положительном квадратном корне из числа.

В свете введенного обозначения из определения арифметического квадратного корня следует, что и для любого неотрицательного числа a.

Квадратные корни из положительного числа a с помощью знака арифметического квадратного корня записываются как и . Например, квадратные корни из числа 13 есть и . Арифметический квадратный корень из нуля равен нулю, то есть, . Для отрицательных чисел a записи мы не будем придавать смысла вплоть до изучения комплексных чисел. Например, лишены смысла выражения и .

На базе определения квадратного корня доказываются свойства квадратных корней, которые часто применяются на практике.

Нахождение квадратных корней заслуживает детального изучения, этой теме посвящена отдельная статья извлечение квадратных корней.

В заключение этого пункта заметим, что квадратные корни из числа a являются решениями квадратного уравнения вида x²=a относительно переменной x.

К началу страницы

Кубический корень из числа

Определение кубического корня из числа a дается аналогично определению квадратного корня. Только оно базируется на понятии куба числа, а не квадрата.

Определение

Кубическим корнем из числа a называется число, куб которого равен a.

Приведем примеры кубических корней. Для этого возьмем несколько чисел, например, 7, 0, −2/3, и возведем их в куб: 7³=7·7·7=343, 0³=0·0·0=0, . Тогда, основываясь на определении кубического корня, можно утверждать, что число 7 – это кубический корень из 343, 0 есть кубический корень из нуля, а −2/3 является кубическим корнем из −8/27.

Можно показать, что кубический корень из числа a, в отличие от квадратного корня, всегда существует, причем не только для неотрицательных a, но и для любого действительного числа a. Для этого можно использовать тот же способ, о котором мы упоминали при изучении квадратного корня.

Более того, существует только единственный кубический корень из данного числа a. Докажем последнее утверждение. Для этого отдельно рассмотрим три случая: a – положительное число, a=0 и a – отрицательное число.

Легко показать, что при положительном a кубический корень из a не может быть ни отрицательным числом, ни нулем. Действительно, пусть b является кубическим корнем из a, тогда по определению мы можем записать равенство b³=a. Понятно, что это равенство не может быть верным при отрицательных b и при b=0, так как в этих случаях b³=b·b·b будет отрицательным числом либо нулем соответственно. Итак, кубический корень из положительного числа a является положительным числом.

Теперь предположим, что помимо числа b существует еще один кубический корень из числа a, обозначим его c. Тогда c³=a. Следовательно, b³−c³=a−a=0, но b³−c³=(b−c)·(b²+b·c+c²) (это формула сокращенного умножения разность кубов), откуда (b−c)·(b²+b·c+c²)=0. Полученное равенство возможно только когда b−c=0 или b²+b·c+c²=0. Из первого равенства имеем b=c, а второе равенство не имеет решений, так как левая его часть является положительным числом для любых положительных чисел b и c как сумма трех положительных слагаемых b², b·c и c². Этим доказана единственность кубического корня из положительного числа a.

При a=0 кубическим корнем из числа a является только число нуль. Действительно, если предположить, что существует число b, которое является отличным от нуля кубическим корнем из нуля, то должно выполняться равенство b³=0, которое возможно лишь при b=0.

Для отрицательных a можно привести рассуждения, аналогичные случаю для положительных a. Во-первых, показываем, что кубический корень из отрицательного числа не может быть равен ни положительному числу, ни нулю. Во-вторых, предполагаем, что существует второй кубический корень из отрицательного числа и показываем, что он обязательно будет совпадать с первым.

Итак, всегда существует кубический корень из любого данного действительного числа a, причем единственный.

Дадим определение арифметического кубического корня.

Определение

Арифметическим кубическим корнем из неотрицательного числа a называется неотрицательное число, куб которого равен a.

Арифметический кубический корень из неотрицательного числа a обозначается как , знак называется знаком арифметического кубического корня, число 3 в этой записи называется показателем корня. Число под знаком корня – это подкоренное число, выражение под знаком корня – это подкоренное выражение.

Хотя арифметический кубический корень определяется лишь для неотрицательных чисел a, но удобно также использовать записи, в которых под знаком арифметического кубического корня находятся отрицательные числа. Понимать их будем так: , где a – положительное число. Например, .

О свойствах кубических корней мы поговорим в общей статье свойства корней.

Вычисление значения кубического корня называется извлечением кубического корня, это действие разобрано в статье извлечение корней: способы, примеры, решения.

В заключение этого пункта скажем, что кубический корень из числа a является решением кубического уравнения вида x³=a.

К началу страницы

Корень n-ой степени, арифметический корень степени n

Обобщим понятие корня из числа – введем определение корня n-ой степени для натуральных чисел n.

Определение

Корень n-ой степени из числа a – это число, n-я степень которого равна a.

Из данного определения понятно, что корень первой степени из числа a есть само число a, так как при изучении степени с натуральным показателем мы приняли a¹=a.

Выше мы рассмотрели частные случаи корня n-ой степени при n=2 и n=3 – квадратный корень и кубический корень. То есть, квадратный корень – это корень второй степени, а кубический корень – корень третьей степени. Для изучения корней n-ой степени при n=4, 5, 6, … их удобно разделить на две группы: первая группа – корни четных степеней (то есть, при n=4, 6, 8, …), вторая группа – корни нечетных степеней (то есть, при n=5, 7, 9, …). Это связано с тем, что корни четных степеней аналогичны квадратному корню, а корни нечетных степеней – кубическому. Разберемся с ними по очереди.

Начнем с корней, степенями которых являются четные числа 4, 6, 8, … Как мы уже сказали, они аналогичны квадратному корню из числа a. То есть, корень любой четной степени из числа a существует лишь для неотрицательного a. Причем, если a=0, то корень из a единственный и равен нулю, а если a>0, то существует два корня четной степени из числа a, причем они являются противоположными числами.

Обоснуем последнее утверждение. Пусть b – корень четной степени (обозначим ее как 2·m, где m – некоторое натуральное число) из числа a. Предположим, что существует число c – еще один корень степени 2·m из числа a. Тогда b^2·m−c^2·m=a−a=0. Но мы знаем формулу сокращенного умножения вида b^2·m−c^2·m=(b−c)·(b+c)·(b^2·m−2+b^2·m−4·c²+b^2·m−6·c⁴+…+c^2·m−2), тогда (b−c)·(b+c)·(b^2·m−2+b^2·m−4·c²+b^2·m−6·c⁴+…+c^2·m−2)=0. Из этого равенства следует, что b−c=0, или b+c=0, или b^2·m−2+b^2·m−4·c²+b^2·m−6·c⁴+…+c^2·m−2=0. Первые два равенства означают, что числа b и c равны или b и c – противоположны. А последнее равенство справедливо лишь при b=c=0, так как в его левой части находится выражение, которое неотрицательно при любых b и c как сумма неотрицательных чисел.

Что касается корней n-ой степени при нечетных n, то они аналогичны кубическому корню. То есть, корень любой нечетной степени из числа a существует для любого действительного числа a, причем для данного числа a он является единственным.

Единственность корня нечетной степени 2·m+1 из числа a доказывается по аналогии с доказательством единственности кубического корня из a. Только здесь вместо равенства a³−b³=(a−b)·(a²+a·b+c²) используется равенство вида b^2·m+1−c^2·m+1=(b−c)·(b^2·m+b^2·m−1·c+b^2·m−2·c²+… +c^2·m). Выражение в последней скобке можно переписать как b^2·m+c^2·m+b·c·(b^2·m−2+c^2·m−2+b·c·(b^2·m−4+c^2·m−4+b·c·(…+(b²+c²+b·c)))). Например, при m=2 имеем b⁵−c⁵=(b−c)·(b⁴+b³·c+b²·c²+b·c³+c⁴)=(b−c)·(b⁴+c⁴+b·c·(b²+c²+b·c)). Когда a и b оба положительны или оба отрицательны их произведение является положительным числом, тогда выражение b²+c²+b·c, находящееся в скобках самой высокой степени вложенности, является положительным как сумма положительных чисел. Теперь, продвигаясь последовательно к выражениям в скобках предыдущих степеней вложенности, убеждаемся, что они также положительны как суммы положительных чисел. В итоге получаем, что равенство b^2·m+1−c^2·m+1=(b−c)·(b^2·m+b^2·m−1·c+b^2·m−2·c²+… +c^2·m)=0 возможно только тогда, когда b−c=0, то есть, когда число b равно числу c.

Пришло время разобраться с обозначениями корней n-ой степени. Для этого дается определение арифметического корня n-ой степени.

Определение

Арифметическим корнем n-ой степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.

Арифметический корень n-ой степени из неотрицательного числа a обозначается как . Число a называют подкоренным числом, а число n – показателем корня. Для примера рассмотрим запись , здесь подкоренным числом является 125,36, а показатель корня равен 5.

Заметим, что при n=2 мы имеем дело с квадратным корнем из числа, в этом случае показатель корня принято не записывать, то есть, записи и означают одно и то же число.

Несмотря на то, что определение арифметического корня n-ой степени, а также его обозначение введены для неотрицательных подкоренных чисел, мы в целях удобства для нечетных показателей корня и отрицательных подкоренных чисел будем использовать записи вида , которые будем понимать как . Например, и .

Корням же четной степени с отрицательными подкоренными числами мы не будем придавать никакого смысла (до начала изучения комплексных чисел). К примеру, выражения и не имеют смысла.

Вычисление корней n-ой степени подробно разобрано в статье извлечение корней.

На основании данного выше определения обосновываются свойства корней n-ой степени, которые имеют широкое практическое применение.

В заключение стоит сказать, что корни n-ой степени являются корнями уравнений вида xⁿ=a.

К началу страницы

Практически важные результаты

Первый практически важный результат: .

Этот результат по сути отражает определение корня четной степени. Знак ⇔ означает равносильность. То есть, приведенную запись стоит понимать так: если , то , и если , то . А теперь то же самое, но словами: если b есть корень четной степени 2·k из числа a, то b – это неотрицательное число, удовлетворяющее равенству b^2·k=a, и обратно, если b – неотрицательное число, удовлетворяющее равенству b^2·k=a, то b есть корень четной степени 2·k из числа a.

Из первого равенства системы понятно, что число a – неотрицательное, так как оно равно неотрицательному числу b, возведенному в четную степень 2·k.

Таким образом, в школе рассматривают корни четных степеней только из неотрицательных чисел, понимают их как , а корням четных степеней из отрицательных чисел не придают никакого смысла.

Второй практически важный результат: .

Он по сути объединяет определение арифметического корня нечетной степени и определение корня нечетной степени из отрицательного числа. Поясним это.

Из определений, данных в предыдущих пунктах, понятно, что придают смысл корням нечетных степеней из любых действительных чисел, не только неотрицательных, но и отрицательных. Для неотрицательных чисел b считают, что . Из последней системы вытекает условие a≥0. Для отрицательных чисел −a (при этом a – положительное число) принимают . Понятно, что при таком определении — отрицательное число, так как оно равно , а есть положительное число. Также понятно, что возведение в степень 2·k+1 корня дает подкоренное число –a. Действительно, учитывая такое определение и свойства степеней, имеем

Из этого заключаем, что корень нечетной степени 2·k+1 из отрицательного числа −a есть такое отрицательное число b, степень 2·k+1 которого равна −a, в буквенном виде . Объединяя результаты для a≥0 и для –a<0, приходим к следующему выводу: корень нечетной степени 2·k+1 из произвольного действительного числа a есть число b (оно может быть как неотрицательным, так и отрицательным), которое при возведении в степень 2·k+1 равно a, то есть .

Таким образом, в школе рассматривают корни нечетных степеней из любых действительных чисел и понимают их так: .

В заключение еще раз запишем два интересующих нас результата: и .

04.

Счет, степени, корни — MAPHY.COM

Некоторые рекомендации к проведению алгебраических вычислений, преобразований и упрощений

При выполнении численных вычислений с большим количеством операций и дробей желательно выполнять следующие рекомендации:

• Переводите десятичные дроби в обыкновенные, т.е. такие у которых есть числитель и знаменатель.
• Не старайтесь посчитать сразу все выражение. Выполняйте вычисления по одному действию, пошагово. При этом учтите, что:
  • сначала выполняют операции в скобках;
  • затем считают произведения и/или деления;
  • потом суммируют или вычитают;
  • и в последнюю очередь, если это была многоэтажная дробь, делят уже полностью упрощенный числитель на тоже полностью упрощенный знаменатель;
  • причем выполняя в первую очередь операции в скобках также соблюдают ту же последовательность, сначала произведения или деления внутри скобок, потом суммирование или вычитание в скобках, а если внутри скобки есть другая скобка то действия в ней выполняются прежде всего.
• Не спешите умножать и делить «страшные числа». Скорее всего, в одном из следующих действий что-то сократится. Чтобы проще было сократить можно числа раскладывать на простые множители.
• При сложении и вычитании выделяйте в дробях целую часть (если это возможно). При умножении и делении, наоборот, приводите дробь к виду без целой части.

От корней в знаменателе принято избавляться. Для избавления от корня над всем знаменателем умножают числитель и знаменатель на выражение, равное знаменателю. Для избавления от корня над частью знаменателя умножают числитель и знаменатель на сопряженное знаменателю выражение. В этом случае образуется разность квадратов (сопряжённым для (a — b) является выражение (a + b) и наоборот).

При преобразовании или упрощении алгебраических выражений последовательность действий такова:

• Разложить на множители все, что можно разложить на множители.
• Сократить все, что можно сократить.
• И только потом приводить к общему знаменателю. Ни в коем случае не пытайтесь сразу сломя голову приводить к общему знаменателю. Пример будет становиться чем дальше, тем страшнее.
• Снова разложить на множители и сократить.

Для того чтобы перевести десятичную периодическую дробь в обыкновенную (с числителем и знаменателем) необходимо:

• Из числа, стоящего до второго периода в исходной периодической дроби вычесть число, стоящее до первого периода в этой же дроби и записать полученную разность в числитель будущей обыкновенной дроби.
• В знаменателе же записать столько девяток, сколько цифр в периоде исходной дроби, и столько нулей, сколько цифр между запятой и первым периодом.
• Не забыть про целую часть, если она есть.

При решении задач из данной темы также необходимо помнить много сведений из предыдущих тем. Приведём далее основные из них.

 

Формулы сокращенного умножения

При выполнении различных алгебраических преобразований часто удобно пользоваться формулами сокращенного умножения. Зачастую эти формулы применяются не столько для того чтобы сократить процесс умножения, а наоборот скорее для того, чтобы по результату понять, что его можно представить как произведение некоторых множителей. Таким образом, данные формулы нужно уметь применять не только слева направо, но и справа налево. Перечислим основные формулы сокращенного умножения:

Последние две формулы также часто удобно использовать в виде:

 

Квадратный трехчлен и теорема Виета

В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения согласно теореме Виета может быть вычислено по формуле:

Итак, еще раз о теореме Виета:

• Если D < 0 (дискриминант отрицателен), то уравнение корней не имеет и теорему Виета применять нельзя.
• Если D > 0 (дискриминант положителен), то уравнение имеет два корня и теорема Виета прекрасно работает.
• Если D = 0, то уравнение имеет единственный корень, для которого бессмысленно вводить понятие суммы или произведения корней, поэтому теорему Виета тоже не применяем.

 

Основные свойства степеней

У математических степеней есть несколько важных свойств, перечислим их:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:

 

Основные свойства математических корней

Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:

Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:

Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):

Так как значение корня четной степени может быть только неотрицательным, то для таких корней имеется следующее важное свойство:

Итак всегда нужно помнить, что под корнем четной степени может стоять только неотрицательное выражение, и сам корень тоже есть неотрицательное выражение.  Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум:

 

Основные свойства квадратного корня

Квадратным корнем называется математический корень второй степени:

Квадратный корень можно извлечь только из неотрицательного числа. При этом значение квадратного корня также всегда неотрицательно:

Для квадратного корня существует два важных свойства, которые важно очень хорошо запомнить и не путать:

Если под корнем стоит несколько множителей, то корень можно извлекать из каждого из них по-отдельности. При этом важно понимать, что каждый из этих множителей по-отдельности (а не только их произведение) должны быть неотрицательными:

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Нахождение квадратного корня из многочлена

Нахождение квадратного корня из многочлена

В этом разделе вы узнаете, как находить квадратный корень из многочлена с помощью деления в большую сторону.

Перед тем, как научиться находить квадратный корень из многочлена, советуем посмотреть, как найти квадратный корень из числа с помощью деления в длину шаг за шагом.

Чтобы иметь возможность находить квадратный корень из числа с помощью деления в большую сторону,

Пожалуйста, нажмите здесь

Примечание: 

Прежде чем приступить к нахождению квадратного корня многочлена, необходимо убедиться, что степени переменных находятся в порядке убывания или возрастания.

Examples

Example 1 :

Find the square root of the following polynomial :

x ⁴  — 4x ³  + 10x ²  — 12x + 9

Solution :

Следовательно, квадратный корень из данного многочлена равен

|x ² — 2x + 3|

Example 2 :

Find the square root of the following polynomial :

4x ⁴  + 8x ³  + 8x ²  + 4x + 1

Solution :

Therefore the square root данного многочлена равно

|2x ²  + 2x + 1|

Пример 3:

Найдите квадратный корень из следующего многочлена:

9x ⁴ — 6x ³ + 7x ² — 2x + 1

Решение:

Следовательно, квадратный корень данного полинома-

| 3x

937.

Example 4 :

Find the square root of the following polynomial :

4 + 25x ²  — 12x — 24x ³  + 16x ⁴

Solution :

First arrange the член многочлена от старшего показателя до наименьшего показателя и найти квадратный корень.

Затем,

16x ⁴ — 24x ³ + 25x ² — 12x + 4

Поэтому квадратный корень данного полинома-

. Поэтому квадратный корень данного полинома-

. Поэтому квадратный корень данного полинома-

. Поэтому квадратный корень данного полинома-

.

Example 5 :

Find the values ​​of a and b if the following polynomial is a perfect square

4x ⁴  — 12x ³  + 37x ²  + ax + b

Решение:

Поскольку данный многочлен является полным квадратом,

a + 42  = 0 и b — 49 = 0

Example 6 :

Find the values ​​of a and b if the following polynomial is a perfect square

x ⁴  — 4x ³  + 10x ²  — ax + b

Решение:

Поскольку данный многочлен является полным квадратом,

-a + 12  = 0 и b — 9 = 0

Решая вышеприведенные уравнения для a и b, мы получаем Example 7 :

Find the values ​​of a and b if the following polynomial is a perfect square

ax ⁴  + bx ³  + 109x ²  — 60x + 36

Solution :

Здесь a и b являются коэффициентами x ⁴ и х ³ соответственно.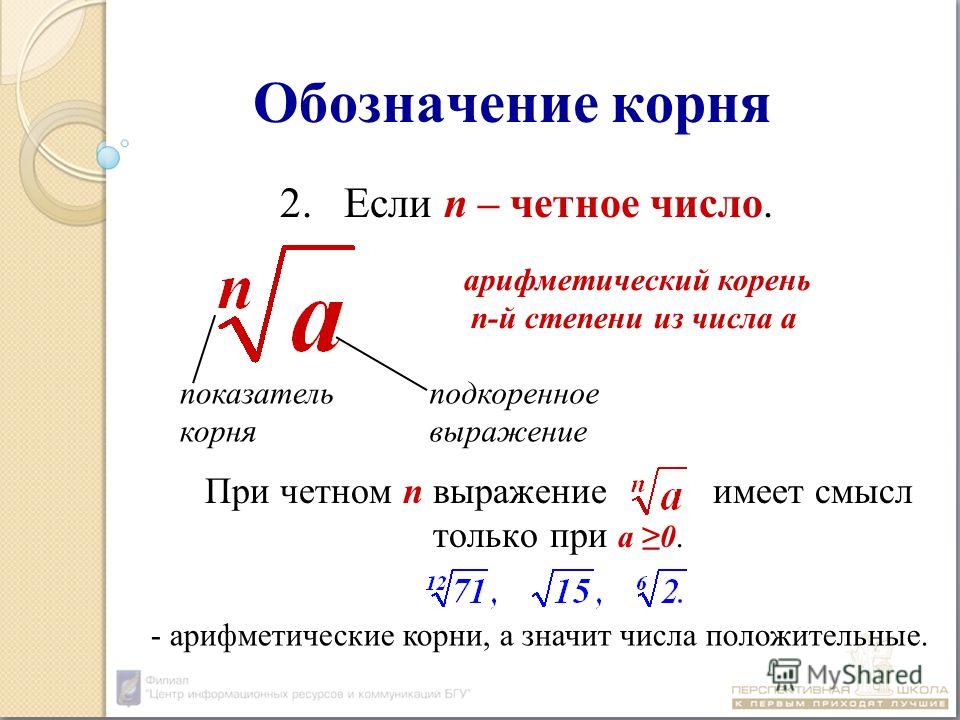

Чтобы решить для a и b, они всегда должны прийти наконец.

Итак, запишите данный многочлен от младшего показателя к старшему показателю.

36 — 60x+ 109x ² + BX ³ + AX ⁴

Потому что заданный полиномиаль — 49x ⁴   =  0

Решите приведенные выше уравнения для a и b.

bx 3  + 70x 3   =  0 (b + 70)x 3   =  0 Разделите каждую сторону на x 3 . б + 70 = 0 б = -70

x 4  — 49x 4   =  0 (a — 49)x 4   =  0 Разделите каждую сторону на x 4 . а — 49  =  0  а  =  49

Следовательно,

а = 49

B = -70

Пример 8:

Найдите значения A и B, если следующий полиномиаль + 36

Решение:

Здесь a и b являются коэффициентами x ⁴ и x ³ соответственно.

Чтобы решить для a и b, они всегда должны прийти наконец.

Итак, запишите данный многочлен от младшего показателя к старшему показателю.

36 + 24x + 40x ²  — bx ³  + ax ⁴

Because the given polynomial is a perfect square,

-bx ³  — 12x ³   =  0  and  ax ⁴ — 9x ⁴   =  0

Решите приведенные выше уравнения для a и b.

-bx 3  — 12x 3   =  0 (b + 12)(-x 3 )  =  0 Разделите каждую сторону на (-x 3 ). б + 12  =  0 б  = -12

x 4  — 9x 4   =  0 (a — 9)x 4   =  0 Разделите каждую сторону на x 4 . а — 9 = 0 а = 9

Следовательно, 

a  =  9

b  =  -12

Помимо приведенного выше материала, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Пожалуйста, отправьте свой отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Квадратный корень из 45 — Как найти квадратный корень из 45?

LearnPracticeDownload

Прежде чем мы начнем, давайте поймем значение квадратного корня. Символ квадратного корня записывается как √ и является неотъемлемой частью математики. Как только вы поймете основы нахождения квадратного корня из числа, вы сможете решить любую задачу, связанную с квадратным корнем. В этом коротком уроке мы узнаем о квадратном корне из 45. Мы сделаем это, используя такие методы, как разложение на простые множители и деление, а также найдем квадратный корень из 45.

• Квадратный корень из 45 : √ 45 = 6,708
• Квадрат 45: 45 ² = 2025

1.	Чему равен квадратный корень из 45?
2.	Является ли квадратный корень из 45 рациональным или иррациональным?
3.	Как найти квадратный корень из 45?
4.	Важные замечания по квадратному корню из 45
5.	Нестандартное мышление!
6.	Часто задаваемые вопросы о квадратном корне из 45

Чему равен квадратный корень из 45?

Мы знаем, что операция сложения обратна вычитанию, а операция умножения обратна делению. Точно так же нахождение квадратного корня является операцией, обратной возведению в квадрат. Квадратный корень из 45 — это число, которое умножается на себя, чтобы получить число 45. Итак, нам нужно придумать число, квадрат которого равен 45. Мы видим, что не существует целого числа, квадрат которого равен 45. квадратный корень из числа — это число, которое умножается на себя, чтобы получить исходное число. Квадратный корень из 45 равен 6,7082039. 325.

Является ли квадратный корень из 45 рациональным или иррациональным?

Невозможно разбить 45 на два таких множителя, которые при возведении в квадрат дают 45. Его можно приблизительно записать в виде квадрата 6,708, который является неповторяющимся и неконечным десятичным числом. Это показывает, что это не идеальный квадрат, что также доказывает, что квадратный корень из 45 является иррациональным числом. Как вы думаете, есть ли что-то общее между квадратным корнем из 45 и квадратным корнем из 5? Да, оба не являются идеальными квадратами. Итак, √ 45 – иррациональное число.

Как найти квадратный корень из 45?

Мы можем найти квадратный корень из 45, выполнив следующие шаги:

• Шаг 1. Проверьте, является ли число полным квадратом или нет. В этом случае 45 не является идеальным квадратом, поскольку его нельзя разбить на произведение двух одинаковых чисел.
• Шаг 2. После проверки номера необходимо выполнить следующий процесс:

1. Если число представляет собой полный квадрат, его можно записать в следующем формате  √ х ²  = х
2. Если это не полный квадрат, квадратный корень находится методом деления в длинную сторону. Его также можно записать в упрощенной радикальной форме.

Поскольку 45 не является полным квадратом, мы найдем его квадратный корень, используя метод деления в длинную сторону. Упрощенная радикальная форма квадратного корня из 45 приведена ниже.

Упрощенная радикальная форма квадратного корня из 45

45 может быть записана как произведение 9 и 5. Следовательно, квадратный корень из 45 может быть выражен как √ 45  = √ (9 × 5) = 3√5. 45 не является полным квадратом, следовательно, оно остается в пределах корней. Упрощенная радикальная форма квадратного корня из 45 – 3√5.

Квадратный корень из 45 путем деления в длину

Давайте разберемся с процессом нахождения квадратного корня из 45 путем деления в длину.

• Шаг 1:  Соедините цифры числа, начиная с правого конца, поместив над ними черту.
• Шаг 2:  Теперь мы найдем число, квадрат которого дает произведение, меньшее или равное этой паре. Квадрат 6 равен 36, что меньше 45. Если из 45 вычесть 36, получится 9..
• Шаг 3: Теперь мы удваиваем частное и помещаем его в качестве следующего делителя с пробелом справа. Двойное число 6 дает 12 и рядом с ним ставится пробел. Этот пробел необходимо заполнить числом, которое также станет следующей цифрой в частном. Он должен быть заполнен максимально возможной цифрой, чтобы при умножении нового делителя на новое частное произведение было меньше или равно делимому.
• Шаг 4:  Повторяя описанные выше шаги, частное 67 удваивается, что дает 134, и к делимому добавляется пара нулей.
• Шаг 5: Повторяются те же шаги, и цифра, записанная в пустом месте, равна 8. Произведение 13408 и 8 дает 1072. После вычитания 107264 из 110000 мы получаем 2736. Наконец, квадратный корень из 45 рассчитывается как 6,708, как показано:

Изучение квадратных корней с помощью иллюстраций и интерактивных примеров

• Квадратный корень из 64
• Квадратный корень из 35
• Квадратный корень из 28
• Квадратный корень из 25
• Квадратный корень из 169

Важные примечания:

• 45 не является полным квадратом, поэтому его квадратный корень является иррациональным числом. Отсюда следует, что квадратный корень любого числа «n», которое не является полным квадратом, всегда будет иррациональным числом.

Аналитический центр:

• Может ли значение квадратного корня быть отрицательным? Подсказка: подумайте, чему равен квадрат отрицательного числа.
• =√-45 действительное число? Подсказка: подумайте, существует ли действительное число, квадрат которого отрицателен.

 

1. Пример 1 : Гарри купил картину для своей комнаты. Стена комнаты имеет квадратную форму и имеет площадь 45 квадратных футов. Какова длина стены?

   Решение

   Предположим, что длина стены равна x футов. Тогда площадь пола стены равна x ² квадратных футов.
   По предоставленным данным:
   х ² = 45
   х = √ 45 = 6,70 фута
   Здесь вычисляется квадратный корень из 45 . Следовательно, длина стены составляет 6,70 фута.

2. Пример 2 : Питер заказал пиццу площадью 45π квадратных дюймов. Найдите его радиус. Округлите ответ до ближайшего целого числа.

   Решение

   Предположим, что радиус пиццы равен r дюймов. Тогда его площадь по формуле площади круга равна πr ² квадратных дюймов. По данной информации πr ²  = 45π
   г ² = 45
   Извлекая квадратный корень с обеих сторон, √ r ² = √ 45. Мы знаем, что квадратный корень из r ² равен r. Вычисляя квадратный корень из 45 и округляя результат до ближайшего целого числа. Следовательно, радиус пиццы = 6,70 дюйма 90 912

перейти к слайдуперейти к слайду

 

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами

Закажите бесплатный пробный урок

перейти к слайдуперейти к слайдуперейти к слайду

 

Часто задаваемые вопросы о квадратном корне из 45

Что такое квадратный корень из 45?

Квадратный корень из 45 равен 6,7082039325.

Чему равен квадрат 45?

Квадрат 45 равен 2025.

Как найти квадратный корень из 45?

909:10 Мы можем найти квадратный корень из 45, используя разложение на простые множители и деление в длинную сторону.

Является ли квадратный корень из 45 иррациональным числом?

Да, квадратный корень из 45 — иррациональное число.

Чему равен квадратный корень из 45 в упрощенной форме?

Квадратный корень из 45 в упрощенной форме равен 3√5.

Рабочие листы по математике и
наглядный учебный план

Кокомбинаторика — Нижняя граница суммы квадратного корня из степеней связного графа 9n d_i =2mn$, с равенством тогда и только тогда, когда граф регулярен (постоянной степени). Здесь $d_i$ — степень вершины $i$, $m$ — количество ребер, а $n$ — количество вершин.

Существует ли хорошая нижняя граница для простого связного графа? Интересно, может ли нижняя граница быть половиной верхней границы?

• кокомбинаторика
• теория графов
• н. численный анализ

$\endgroup$

$\begingroup$

При фиксированном числе ребер и вершин Линиал и Розенман предположили, что графы, минимизирующие $\sum_i \sqrt{d_i}$, получаются путем взятия максимально возможного полного графа вместе с дополнительной вершиной оставшейся степени и остальные как изолированные вершины. Их гипотеза была доказана в «Минимизирующих графах для класса экстремальных задач» Дэна Исмаилеску и Дэна Стефаники, Journal of Graph Theory (39).2.$$

$\endgroup$

1

$\begingroup$

Поскольку я не проверял детали, обратите внимание, что этот ответ предоставляется без гарантии; используйте его на свой страх и риск.

Если вы исследуете функционал $F(d_1,\dots,d_n)$ над областью, заданной $\sum d_i=2m$ и $d_i\geq 1$, вы обнаружите, что единственная критическая точка – это это дает вашу верхнюю границу (которая, кстати, является родственной арифметико-геометрическому неравенству и следствием вогнутости $\sqrt{\cdot}$ : среднее арифметическое сравнивается с его $\sqrt{\cdot }$-сопряженный). n \sqrt{d_i} \geq \sqrt{2m-n+1}+n-1$$ и это должно быть достигнуто любым звездным графиком. 9n \sqrt{d_i} \geq \sqrt{n-1}+n-1$$ (опять же достигается с помощью стартового графика).

$\endgroup$

$\begingroup$

Бенуа:

• не является ли многогранник, который вы оптимизируете, немного сложнее, а как насчет ограничения $d_i \leq n-1$, которое подразумевает граничные ограничения с $d_i = n-1$?

• не каждая точка, удовлетворяющая вашим ограничениям неравенства, будет последовательностью степеней (связного, простого) графа.

• ваша первая конструкция сломается, если $2m-n+1 > n-1$, т.е. если $m > n-1$. Поскольку граф считается связным, это означает, что ваша первая конструкция не работает для всех графов, не являющихся деревьями.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Градусное разделение среднеквадратичных графиков

Прикладная математика Vol. 06 No.06(2015), ID статьи:56857,12 страниц
10.4236/am.2015.66086

Степень расщепления графиков среднего уровня корневой площади

S. S. Sandhya ¹ , S. Somasundaram ² , S. Anusa ³

¹ Отделение Mathematics, Smare Ayyyy -Seally, Sharey -Ayyy, Sharey -Ayyy, Sharey -Ayyy, Sharey -Ayyy.0912

² Математический факультет Университета Манонманиам Сундаранар, Тирунелвели, Индия

³ Математический факультет Женского инженерного колледжа Аруначала, Велличантай, Индия

Электронная почта: [email protected] авторов и Scientific Research Publishing Inc.

Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Поступила в редакцию 15 апреля 2015 г.; принято 30 мая 2015 г.; опубликовано 2 июня 2015 г.

АННОТАЦИЯ

Пусть — инъективная функция. Для вершины с меткой f индуцированная маркировка ребер определяется или тогда метки ребер различны и исходят из. Тогда f называется среднеквадратичной разметкой графа G. В этой статье мы доказываем среднеквадратичную разметку графов расщепления некоторых степеней.

Ключевые слова:

Граф, Путь, Цикл, Графы с разбиением на степени, Графы среднеквадратичного значения, Объединение графов

1. Введение

Рассматриваемые здесь графы простые, конечные и неориентированные. Пусть обозначает множество вершин и обозначает множество ребер графа G. Подробный обзор разметки графов мы отсылаем к Галлиану [1] . Для всех других стандартных терминов и обозначений мы следуем Harary [2] . Понятие средней маркировки на графе разложения степеней было введено в [3] . По инициативе авторов мы изучаем маркировку среднеквадратичного значения на графах разложения степеней. Метка среднеквадратичного значения была введена в [4], а нумерация среднеквадратичного значения некоторых стандартных графов была доказана в [5] — [11]. Определения и теоремы полезны для нашего настоящего исследования.

Определение 1.1. Граф с p вершинами и q ребрами называется среднеквадратичным графом, если можно пометить вершины разными метками таким образом, что при

каждое ребро помечено знаком или, тогда ребро

этикетки различны и взяты из. В этом случае f называется разметкой среднего квадратного корня G.

Определение 1.2: Маршрут, в котором различны, называется путем. Путь на n вершинах обозначается .

Определение 1.3: Замкнутый путь называется циклом. Цикл на n вершинах обозначается .

Определение 1.4: Позвольте быть графиком с, где каждый представляет собой набор вершин, имеющих по крайней мере две вершины и имеющих одинаковую степень и. Граф расщепления степеней графа G обозначается и получается из G путем добавления вершин и соединения с каждой вершиной графа G и его графа расщепления степеней показаны на рисунке 1.

Определение 1.5: Объединение двух графов и граф с набором вершин и набором ребер.

Теорема 1.6: Любой путь является графом среднеквадратичного корня.

Теорема 1.7: Любой цикл является графом среднеквадратичного корня.

2. Основные результаты

Теорема 2.1: является графом среднеквадратичного значения.

Доказательство: график показан на рисунке 2.

Пусть. Пусть множество вершин G находится где. Задайте функцию с помощью

Рис. 1. Граф G и его граф расщепления степеней.

Рис. 2. График.

Тогда ребра помечены как

Тогда метки ребер различны и от. Следовательно, по определению 1.1 G является графом среднеквадратичного корня.

Пример 2.2: Обозначение среднеквадратичного значения показано на рисунке 3.

Теорема 2.3: является графом среднеквадратического значения.

Доказательство: график показан на рисунке 4.

Пусть. Пусть множество вершин G находится где. Определите функцию с помощью

Рисунок 3. Обозначение среднеквадратичного значения.

Рисунок 4. График.

Then the edges are labeled as

Then the edge labels are distinct and are from. Следовательно, по определению 1.1 G является графом среднеквадратичного корня.

Пример 2.4: Маркировка среднеквадратичного значения показана на рисунке 5.

Теорема 2.5: является графом среднеквадратического значения.

Доказательство: график показан на рисунке 6.

Пусть. Пусть набор вершин G будет где

. Определите функцию с помощью

Рисунок 5. Обозначение среднеквадратичного значения.

Рис. 6. График.

Then the edges are labeled as

Then the edge labels are distinct and are from. Следовательно, по определению 1.1 G является графом среднеквадратичного корня.

Пример 2.6: Схема маркировки показана на рисунке 7.

Теорема 2.7: граф среднеквадратичного значения.

Доказательство: график показан на рисунке 8.

Пусть. Пусть набор вершин G будет где

. Определите функцию с помощью

Рисунок 7. Шаблон маркировки.

Рисунок 8. График.

Then the edges are labeled as

Then the edge labels are distinct and are from. Следовательно, по определению 1.1 G является графом среднеквадратичного корня.

Пример 2.8: Схема маркировки показана на рисунке 9.

Теорема 2.9: граф среднеквадратичного значения.

Доказательство: график показан на рисунке 10.

Пусть. Пусть множество вершин G находится там, где

.

Define a function by

Then the edges are labeled as

Figure 9. The labeling pattern из.

Рисунок 10. График.

Тогда метки ребер различны и от. Следовательно, по определению 1.1 G является графом среднеквадратичного корня.

Пример 2.10: Обозначение среднеквадратичного значения показано на рисунке 11.

Теорема 2.11: является графом среднеквадратичного значения.

Доказательство: график показан на рисунке 12.

Пусть. Пусть его набор вершин равен

, где.

Определение функции с помощью

Рисунок 12. График.

Тогда ребра помечены как

Тогда метки отличны от ребер. Следовательно, по определению 1.1 G является графом среднеквадратичного корня.

Пример 2.12: Схема маркировки показана на рис. 13.

Теорема 2.13: является графом среднеквадратичного корня.

Доказательство: график показан на рисунке 14.

Рисунок 13. Шаблон маркировки.

Рисунок 14. График.

Лет. Пусть его набор вершин равен

, где.

Define a function by

Then the edges are labeled as

Тогда метки ребер различны и исходят из. Следовательно, по определению 1.1 G является графом среднеквадратичного корня.

Пример 2.14: Схема маркировки показана на рисунке 15.

Теорема 2.15: граф среднеквадратичного значения.

Доказательство: график показан на рисунке 16.

Пусть. Пусть его набор вершин равен

Рис. 15. Шаблон маркировки.

Рисунок 16. График.

где.

Определить функцию с помощью

Then the edges are labeled as

Then the edge labels are distinct and are из. Следовательно, по определению 1.1 G является графом среднеквадратичного корня.

Рис. 17. Обозначение среднего квадратного корня.

Пример 2.16: Обозначение среднеквадратичного значения приведено на рисунке 17.

Ссылки

1. Галлиан, Дж.А. (2012) Динамический обзор разметки графиков. Электронный журнал комбинаторики.
2. Харари, Ф. (1988) Теория графов. Издательство Нароса Рединг, Нью-Дели.
3. Сандхья, С.С., Джаясекаран, К. и Радж, К.Д. (2013) Гармоническая средняя маркировка графов разделения степеней. Бюллетень чистых и прикладных наук, 32E, 99-112.
4. Сандхья, С.С., Сомасундарам, С. и Ануса, С. (2014) Квадратичная маркировка графиков. Международный журнал современных математических наук, 9, 667-676.
5. Сандхья, С.С., Сомасундарам, С. и Ануса, С. (2015) Еще несколько результатов на графиках среднеквадратичного значения. Journal of Mathematics Research, 7.
6. Сандхья, С.С., Сомасундарам, С. и Ануса, С. (2014) Маркировка среднеквадратичного значения некоторых новых несвязанных графов. Международный журнал математических тенденций и технологий, 15, 85–92. http://dx.doi.org/10.14445/22315373/IJMTT-V15P511
7. Сандхья, С.С., Сомасундарам, С. и Ануса, С. (2014) Разметка среднеквадратичного значения подразделения некоторых других графиков. Международный журнал математических исследований, 6, 253-266.
8. Сандхья, С.С., Сомасундарам, С. и Ануса, С. (2014) Некоторые новые результаты по маркировке среднеквадратичного значения. Международный журнал математического архива, 5, 130-135.
9. Сандхья, С.С., Сомасундарам, С. и Ануса, С. (2015) Маркировка среднеквадратичного значения подразделения некоторых графиков. Глобальный журнал теоретических и прикладных математических наук, 5, 1-11.
10. Сандхья, С.С., Сомасундарам, С. и Ануса, С. (2015) Маркировка среднеквадратичного значения некоторых несвязанных графов. Международный математический форум, 10, 25-34.
11. Сандхья, С.С., Сомасундарам, С. и Ануса, С. (2015) Некоторые результаты на графиках среднеквадратичного значения. Сообщено в Journal of Scientific Research.

h3g2 — Как вычислить квадратный корень из любого числа вручную

Вычисление квадратного корня вручную — это даже не то, что практикующий математик назвал бы неторопливым времяпрепровождением. Едва ли эта процедура преподается в школе в наш век компьютеров. Однако вполне возможно определить квадратный корень из числа с любой степенью точности, ради которой человек готов растянуть работу, и математика, связанная с этой процедурой, не сложна. Краткий обзор задачи на вычисление квадратного корня, вычисленной вручную, очень похож на задачу на деление в длину, и некоторые аспекты процедуры аналогичны.

Шаг первый — установка

Чтобы проиллюстрировать эти шаги, мы найдем квадратный корень из 1234,56.

Запишите число, для которого нужно вычислить квадратный корень, под знаком квадратного корня (√), удлинив его, если это необходимо, чтобы имитировать вид деления в большую сторону. Найдите и отметьте десятичную точку этого числа. Над подкоренным знаком ¹ поместите еще одну десятичную точку непосредственно над десятичной точкой исходного числа. Эта вторая точка станет десятичной запятой в квадратном корне исходного числа. Обратите внимание, что, поскольку рукописная работа будет очень похожа на задачу деления на длинные числа, следует позаботиться о том, чтобы оставить место для написания произведений, учета различий и переноса цифр, как и при делении на полные числа.

По обе стороны от десятичной точки в исходном номере используйте какую-либо систему маркировки, чтобы спарить соседние цифры номера. Со стороны целого числа (слева от десятичной точки) прекратите спаривание цифр, когда перед числом не останется цифр или останется одна цифра. В дробной части (справа от запятой) разделите цифры на пары, используя нули в качестве заполнителей, если это необходимо. Цифры в нашем примере парные, с апострофами в качестве разделителей.

Каждая пара цифр в дробной (правой) части будет составлять одну цифру точности для окончательного вычисления квадратного корня, поэтому, если требуется исключительная точность, оставьте достаточно места в правой части листа для дополнительной работы. В представленном выше примере можно было бы вычислить квадратный корень из 1234,56 с точностью до четырех знаков после запятой ² . В конец числа можно было добавить столько дополнительных пар нулей, сколько нужно было вычислить.

Шаг второй — первый расчет

Начинается расчет. Посмотрите на самую первую пару в начале числа, в каком-то смысле это похоже на то, как смотрят на число при начале деления в длинном столбце. Эта первая пара будет состоять либо из одной, либо из двух цифр — для процедурных целей это не имеет значения. В нашем примере первая пара — «12». Определите наибольшее число в форме идеального квадрата (1, 4, 9, 16, 25, 36, 49, 64 и 81 будут вашими единственными вариантами для этого первого вычисления), которое меньше или равно значению первой пары. В этом случае самый большой совершенный квадрат меньше 12 равен 9.. Напишите это квадратное число под первой парой, готовясь к вычитанию, и напишите квадратный корень из этого полного квадрата над знаком радикала, прямо над первой парой.

Вычтите правильный квадрат из значения первой пары и запишите разницу ниже (12 — 9 = 3). Перенесите следующую пару цифр в исходном числе (34) к разности, которая только что была написана, и пусть число, содержащее все эти цифры (334), будет называться D для более позднего обращения.

На данный момент задача должна выглядеть очень похожей на задачу деления в длину, как и было обещано. Это помогает соответствовать этому стилю презентации, поскольку отслеживание различий и продуктов будет здесь так же важно, как и при разделении.

Шаг третий — повторение шага методом проб и ошибок

Используемая до сих пор математика была относительно простой. Первая хорошая новость заключается в том, что на третьем этапе становится немного сложнее. Вторая хорошая новость заключается в том, что с этим несколько более длительным шагом процедура начнет повторяться бесконечно, пока, наконец, не будет достигнута желаемая степень точности.

Умножьте число над знаком квадратного корня на 2, рассматривая его как целое число. (Не обращайте внимания на то, где может находиться десятичная дробь.) В нашем примере у нас есть 3 над радикалом, поэтому мы умножаем его на 2, чтобы получить 6. Неважно, что десятичная дробь еще не достигнута. Поместите этот продукт слева от числа D. Оставьте место в конце этого продукта для одной дополнительной цифры — наше число 6, поэтому мы пишем «6_».

Цифра от 0 до 9 должна быть выбрана случайным образом, если хотите. Назовем его X. Эта цифра будет записана в 2-х местах: один раз над знаком квадратного корня, непосредственно над только что снесенной парой (выше 34) и один раз в пустом месте в конце произведения, которое было только что рассчитано (после 6). Пусть буква Y обозначает созданное таким образом число. В нашем примере, если для X выбрано «7», то Y будет равно 67.

Умножьте X и Y. Ищется максимально возможное значение X, при котором произведение X и Y будет меньше, чем D. Выбор максимально возможного значения X является исключительно методом проб и ошибок. Проблеск надежды: для X есть только 10 вариантов, так что держитесь! Мы видим, что 7 слишком велико, потому что 7 * 67 = 469, что больше, чем D (334). Небольшой эксперимент покажет, что наибольший X, который мы можем выбрать, равен 5, что делает Y = 65. (5 * 65 = 325 < 334)

Как только найдено правильное значение X и вычислено произведение X и Y, это произведение записывается под буквой D и вычитается для получения новой разницы. Затем следующая пара цифр исходного числа переносится вниз для получения нового D.

Теперь шаг 3 повторяется до тех пор, пока не будет достигнута желаемая степень точности. Чтобы продолжить наш пример, число, которое мы записываем слева от нового D, равно 35 * 2, что равно 70.