Формула площа прямокутника: Периметр и площадь прямоугольника

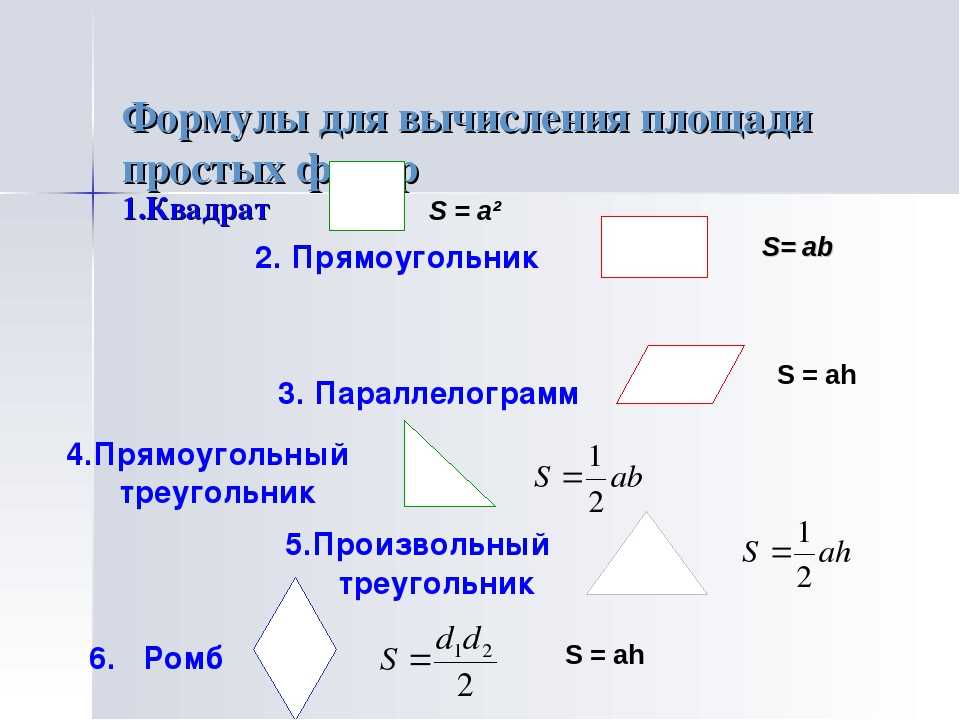
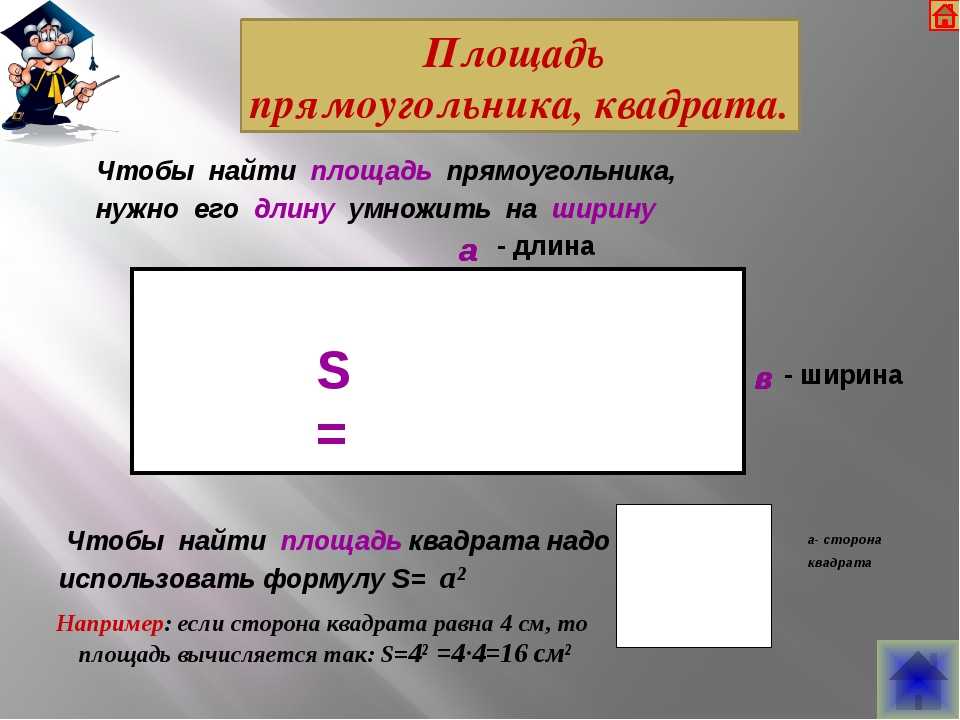
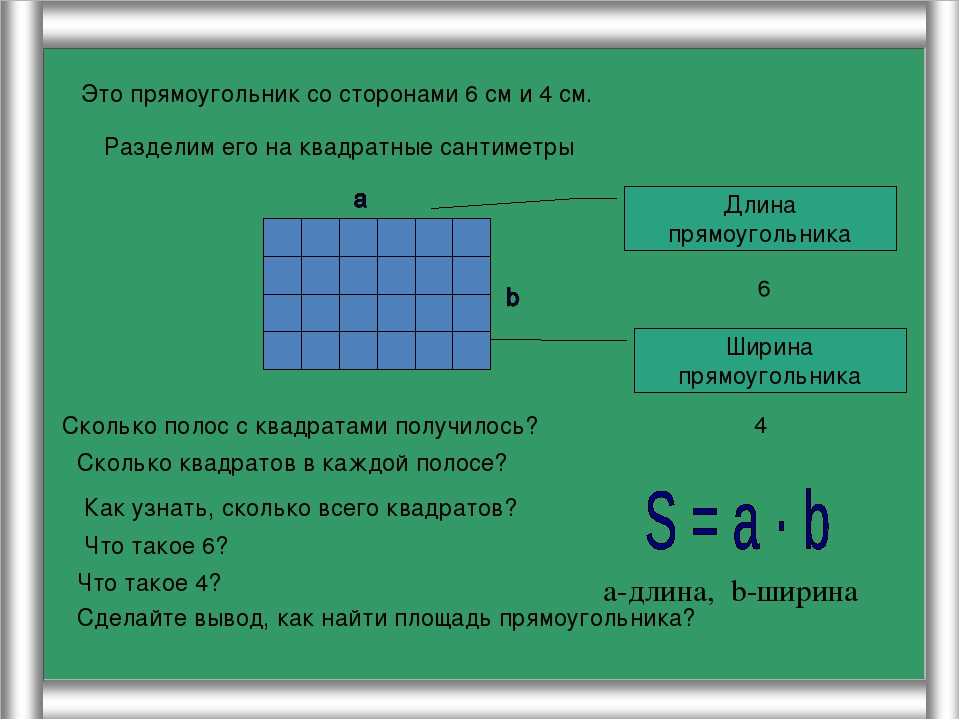
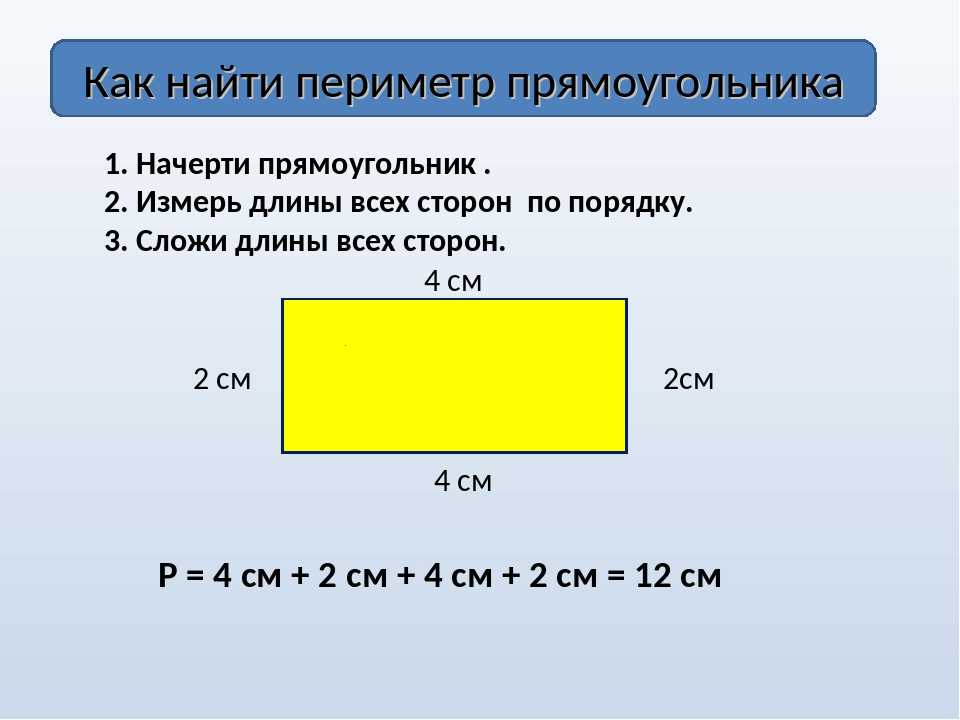
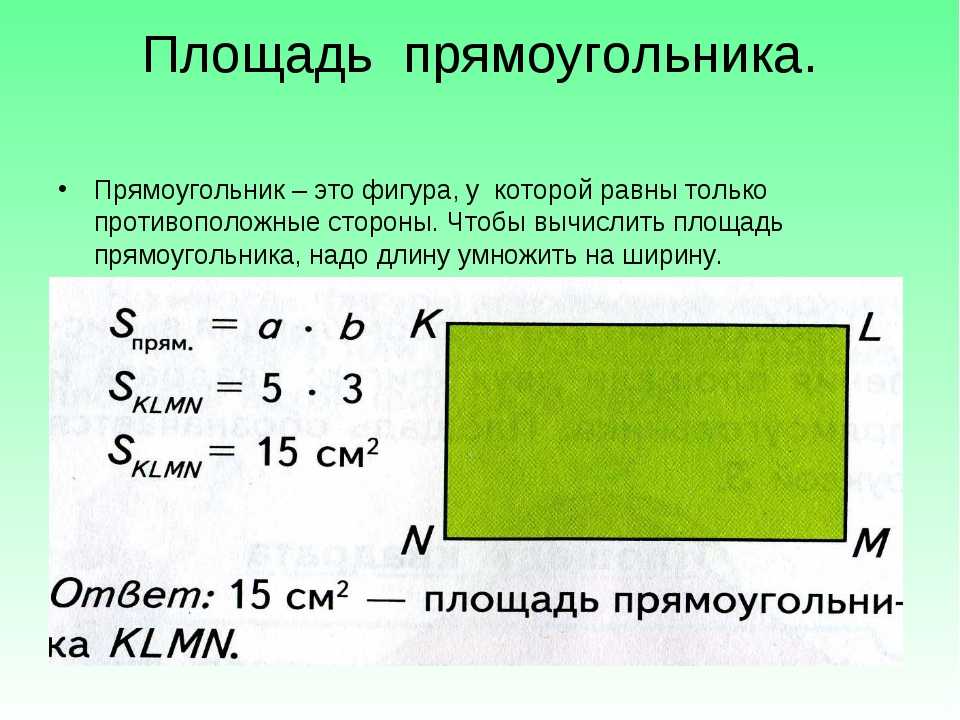
Площа прямокутника. Як знайти площу прямокутника

Прямокутник – це двовимірна фігура з чотирма сторонами, чотирма вершинами і чотирма прямими кутами. Однією з головних характеристик прямокутника є те, що дві його протилежні сторони рівні й паралельні одна одній.

Площа прямокутника визначається як простір, охоплений двовимірною фігурою. Крім того, ми також можемо розглядати площу як простір всередині периметра прямокутника.

В даній публікації ми побачимо, чому площа прямокутника дорівнює добутку двох його сторін. Крім того, розглянемо кілька вправ щодо площ прямокутника, щоб освоїти використання формули.

Навігація по сторінці.

1. За якою формулою обчислюється площа прямокутника?
2. Площа прямокутника – приклади з відповідями.
3. Блок-схема алгоритму знаходження площі прямокутника.

За якою формулою обчислюється площа прямокутника?

Площа прямокутника дорівнює добутку його суміжних сторін (довжини на ширину) і визначається за формулою: , де  – площа прямокутника.

Для доведення даного твердження добудуємо прямокутник  до квадрата зі стороною .

Як нам відомо, площа отриманого квадрата дорівнює .

З іншого боку, цей квадрат складений з прямокутника  з площею , рівного йому прямокутника, також з площею  (так як, по властивості площ, рівні багатокутники мають рівні площі) і двох квадратів з площами  та  відповідно.

Але, виходячи з того, що площа многокутника складеного з кількох многокутників дорівнює сумі площ цих многокутників, отримаємо:

Таким чином твердження доведено, тобто площа прямокутника дорівнює добутку суміжних сторін.

Зауваження: якщо позначити довжини суміжних сторін прямокутника буквами  та  відповідно, то формула площі перепишеться у більш звичній буквенній формі: .

Площа прямокутника через діагоналі.

Також доволі часто трапляються ситуації, коли доводиться шукати площу прямокутника, значення довжини чи ширини якого являються невідомими.

Що робити тоді? В такому випадку доцільно скористатися загальною для всіх чотирьокутників формулою і знайти площу прямокутника через діагоналі.

Площа будь-якого опуклого чотирикутника дорівнює добутку діагоналей на синус кута між ними. Діагоналі прямокутника рівні між собою, тому значення кута та однієї діагоналі вистачить для знаходження площі:

Зауваження: якщо довжини діагоналей прямокутника позначити  буквю , то формула  площі через діагоналі перепишеться у більш звичній буквенній формі:

Площа прямокутника – приклади з відповідями.

У наступних прикладах для отримання відповіді використовується формула для вимірювання площі прямокутника. Кожен приклад має відповідне рішення, але рекомендуємо спробувати розв’язати вправи самостійно, перш ніж дивитися відповідь.

Приклад 1: знайти площу прямокутника, основа якого дорівнює , а висота .

Отже, за умовою маємо, що довжина та ширина прямокутника дорівнює  і  відповідно. Використавши формулу площі із заданими значенням матимемо:

Таким чином, площа прямокутника дорівнює .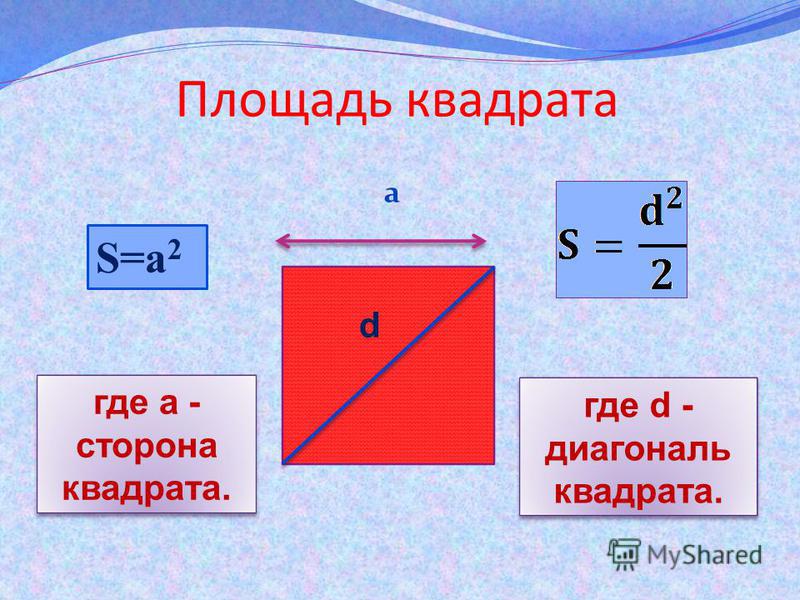

Зауваження: при розв’язуванні задач потрібно пам’ятати, що площа вимірюється в одиницях квадратних, тому якщо розміри задані в міліметрах, то площа буде в міліметрах квадратних, сантиметрах – площа в сантиметрах квадратних, метрах – площа в метрах квадратних і так далі.

Приклад 2: основа прямокутника дорівнює , а його площа . Яка довжина його висоти?

Зазначимо, що у цьому випадку ми повинні знайти вистоту квадрата, знаючи його площу та основу. Отже, використовуючи ту ж формулу, підставляємо задані значення і знаходимо висоту :

Звідси, довжина висоти прямокутника дорівнює .

Приклад 3: периметр прямокутника  дорівнює . Знайти його площу, якщо одна сторона прямокутника в одинадцять разів менша від іншої.

Отже, припустимо, що . Тоді, за умовою, . Далі, за формулою периметра прямокутника будемо мати:

Звідси,  і .

Використавши далі формулу площі із отриманими значенням матимемо:

Таким чином, площа прямокутника  дорівнює .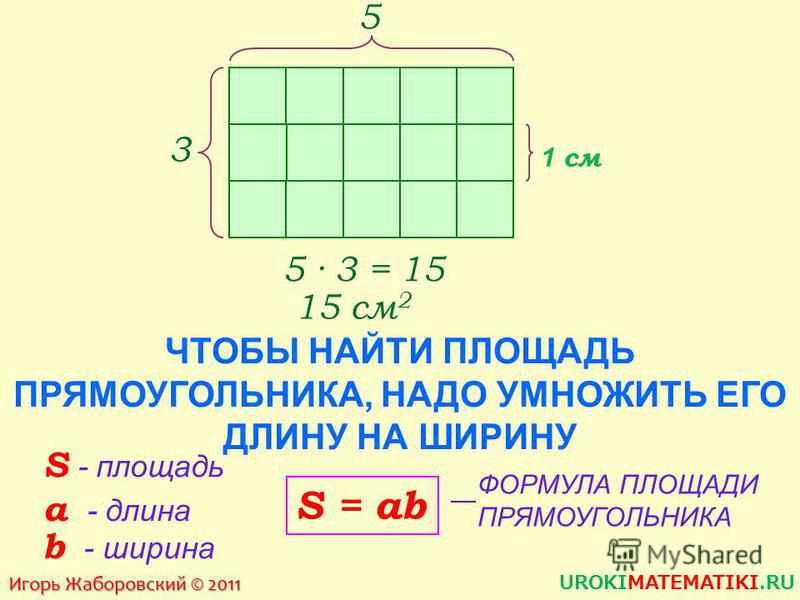

Приклад 4: знайти площу прямокутника  якщо відомо, що діагональ  і сторона .

Отже, для початку, розглянемо прямокутний трикутник , з якого, за теоремою Піфагора, знайдемо невідому сторону заданого прямокутника:

Далі, використавши формулу площі із значенням ширини та довжини прямокутника матимемо:

Звідси, площа прямокутника  дорівнює .

Приклад 5: діагоналі прямокутника перетинаються під кутом 30 градусів і дорівнюють . Чому дорівнює площа прямокутника?

Підставляючи дані у формулу площі прямокутника через діагоналі отримаємо:

Таким чином, площа прямокутника дорівнює .

Дивіться також:

Хочете дізнатися більше про прямокутник? Перегляньте ці сторінки:

1. Прямокутник і його властивості.
2. Діагональ прямокутника – формули та приклади
3. Периметр прямокутника – формули та приклади.

Блок-схема алгоритму знаходження площі прямокутника

Ми в соціальних мережах

Виміряти площу прямокутника з різними сторонами.

Формули площі трапеції

Прямокутник — це окремий випадок чотирикутника. Це означає, що у прямокутника чотири сторони. Його супротивники рівні: так наприклад, якщо одна з його сторін дорівнює 10 см, то протилежна їй буде так само рівні 10 см. Окремим випадком прямокутника є квадрат. Квадрат — це прямокутник, у якого всі сторони рівні. Для обчислення площі квадрата можна користуватися тим же алгоритмом, що і для обчислення площі прямокутника.

Як дізнатися площа прямокутника по двом сторонам

Для того щоб знайти площу прямокутника, треба помножити його довжину на ширину: Площа \u003d Довжина × Ширина. У випадку, зазначеному нижче: Площа \u003d AB × BC.

Як дізнатися площа прямокутника по боці і довжині діагоналі

У деяких завданнях необхідно знайти площу прямокутника, використовуючи довжину діагоналі і одну зі сторін. Діагональ прямокутника ділить його на два рівних прямокутних трикутника. Отже, можна визначити другу сторону прямокутника, скориставшись теоремою Піфагора.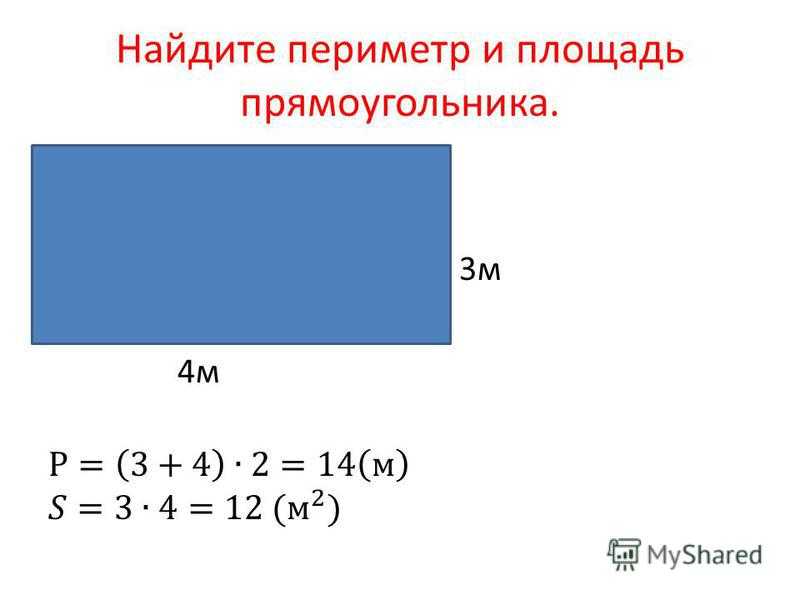 2 × sin (гострого кута між діагоналями) / 2.

Що таке площа і що таке прямокутник

Площа — це така геометрична величина, за допомогою якої можна визначити розмір будь-якої поверхні геометричної фігури.

Протягом багатьох століть так повелося, що обчислення площі називали квадратурою. Тобто, щоб дізнатися площа нескладних геометричних фігур, досить було підрахувати кількість одиничних квадратів, якими умовно були покриті фігури. А постать, яка мала площа, називали квадрованою.

Тому, можна підвести підсумок, що площа — це така величина, яка показує нам розмір частини площині, з’єднаної між собою відрізками.

Прямокутник — це такий чотирикутник, у якого всі кути прямі. Тобто, чотиристоронню фігуру, яка має чотири прямих кута і її супротивники рівні, називають прямокутником.

Як знайти площу прямокутника

Найпростіший спосіб знаходження площі прямокутника — взяти прозору папір, наприклад кальку, або клейонку і розкреслити її на рівні квадратики по 1 см, а потім прикласти до зображення прямокутника. Кількість заповнених квадратиків і буде площею в сантиметрах квадратних. Наприклад, на малюнку видно, що прямокутник потрапляє в 12 квадратів, значить, його площа дорівнює — 12 кв. см.

Але для знаходження площі великих об’єктів, наприклад квартири, необхідний більш універсальний спосіб, тому була доведена формула, щоб знайди площа прямокутника необхідно помножити його довжину на ширину.

А тепер давайте спробуємо записати правило знаходження площі прямокутника у вигляді формули. Позначимо площу нашої фігури буквою S, буква а — означатиме його довжину, а буква b — ширину.

У підсумку отримуємо ось таку формулу:

S \u003d а * b.

Якщо накласти цю формулу на малюнок прямокутника вище, то ми отримаємо ті ж 12 кв.см, тому що а \u003d 4 см, b \u003d 3 см, а S \u003d 4 * 3 \u003d 12 кв.см.

Якщо взяти дві ідентичні фігури, і накласти їх одну на іншу, то вони співпадуть, а будуть називатися рівними. У таких рівних фігур будуть також рівні їх площі і периметри.

Навіщо вміти знаходити площа

По-перше, якщо ви знаєте, як знайти площу будь-якої фігури, то за допомогою її формули ви без проблем зможете вирішувати будь-які завдання з геометрії і тригонометрії.
По-друге, навчившись знаходити площа прямокутника, ви спочатку зможете вирішувати прості завдання, а згодом перейдете до вирішення складніших, і навчитеся знаходити площі фігур, які вписані в прямокутник або біля нього.
По-третє, знаючи таку просту формулу, як S \u003d а * b, ви отримуєте можливість без проблем вирішувати будь-які прості побутові завдання (наприклад, знаходити S квартири або будинку), а згодом і зможете застосувати їх до вирішення складних архітектурних проектів.

Тобто, якщо зовсім спростити формулу знаходження площі, то вона буде виглядати так:

П \u003d Д х Ш,

Що означає П — це шукана площа, Д — це її довжина, Ш — позначає її ширину, а х — є знаком множення.

А чи відомо вам, що площа будь-якого багатокутника можна умовно розбити на певну кількість квадратних блоків, які знаходяться всередині цього багатокутника? Яка різниця між площею і периметром

Давайте на прикладі спробуємо зрозуміти різницю між периметром і площею. Наприклад, наша школа знаходиться на ділянці, який огороджений парканом — сумарна довжина цього паркану буде периметром, а той простір, який знаходиться всередині огорожі і є площею.

Одиниці виміру площі

Якщо периметр одновимірний вимірюється в лінійних одиницях, якими є дюйми, фути і метри, то S відноситься до двовимірним исчислениям і має свою довжину і ширину.

І вимірюється S в квадратних одиницях, таких, як:

Один квадратний міліметр, де S квадрата має сторону, рівну одному міліметру;
Квадратний сантиметр, має S такого квадрата, у якого сторона дорівнює одному сантиметру;
Квадратний дециметр дорівнює S цього квадрата зі стороною в один дециметр;
Квадратний метр має S квадрата, сторона якого дорівнює одному метру;
І нарешті, квадратний кілометр має S квадрата, сторона якого дорівнює одному кілометру.

Для вимірювання площ великих ділянок на поверхні Землі використовують такі одиниці, як:

Один ар або сотка — якщо S квадрата має сторону десять метрів;
Один гектар дорівнює S квадрата, у якого сторона має сто метрів.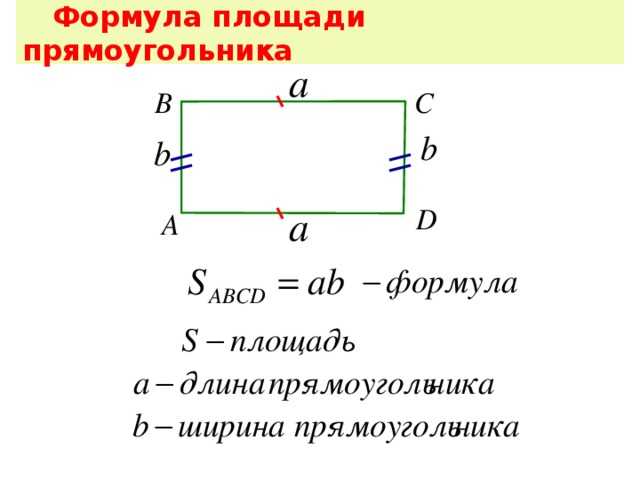

Завдання і вправи

А тепер давайте розглянемо кілька прикладів.

На малюнку 62 намальована фігура, яка має вісім квадратів і кожна сторона цих квадратів дорівнює одному сантиметру. Тому S такого квадрата буде квадратний сантиметр.

Якщо записати, то це буде виглядати так:

1 см2. А S все цієї фігури, що складається з восьми квадратів, буде дорівнювати 8 кв.см.

Якщо взяти якусь фігуру і розбити її на «р» квадратів зі стороною, що дорівнює одному сантиметру, то її площа буде дорівнює:

Р см2.

Давайте розглянемо прямокутник, зображень на малюнку 63. Цей прямокутник складається з трьох смуг, а кожна така смужка розбита на п’ять рівних квадратів, що мають сторону в 1 см.

Спробуємо знайти його площу. І так беремо п’ять квадратів, і множимо на три смужки і отримуємо площу рівну 15 кв.см .:

Розглянемо наступний приклад. На малюнку 64 зображено прямокутник ABCD, ламаною лінією KLMN він розбитий на дві частини. Перша його частина дорівнює площі 12 см2, а друга має площу 9 см2. Тепер давайте знайдемо площу всього прямокутника:

Отже, беремо три і множимо на сім і отримуємо 21 кв.см:

3 +7 \u003d 21 кв.см. При цьому 21 \u003d 12 + 9.

І приходимо до висновку, що площа всієї нашої фігури дорівнює сумі площ її окремих частин.

Розглянемо ще один приклад. І так на малюнку 65 зображено прямокутник, який за допомогою відрізка АС розбитий на два рівних трикутника ABC і ADC

А так, як нам уже відомо, що квадрат — це такий же прямокутник, тільки має рівні сторони, то площа кожного трикутника буде дорівнювати половині площі всього прямокутника.

Уявімо, що сторона квадрата дорівнює а, то:

S \u003d a a \u003d a2.

Робимо висновок, що формула площі квадрата матиме такий вигляд:

А запис a2 називається квадратом числа а.

І так, якщо сторона нашого квадрата дорівнює чотирьом сантиметрам, то його площа буде:

4 4, тобто 4 * 2 \u003d 16 кв.см.

Запитання і завдання

Знайдіть площу фігури, яка розбита на шістнадцять квадратів, сторона яких дорівнює одному сантиметру.
Згадайте формулу прямокутника і запишіть її.
Які вимірювання потрібно зробити, щоб дізнатися площа прямокутника?
Дайте визначення рівним фігурам.
Чи можуть мати рівні фігури різні площі? А периметри?
Якщо вам відомі площі окремих частин фігури, як дізнатися її загальну площу?
Сформулюйте і запишіть, чому дорівнює площа квадрата.

Історична довідка

А чи відомо вам, що стародавні люди в Вавилоні вміли розрахувати площа прямокутника. Так само древні єгиптяни робили розрахунки різних фігур, але так як точних формул вони не знали, то обчислення мали невеликі похибки.

У своїй книзі «Начала» знаменитий давньогрецький математик Евклід, описує різні способи обчислення площ різних геометричних фігур.

Урок на тему: «Формули визначення площі трикутника, прямокутника, квадрата»

Додаткові матеріали

Шановні користувачі, не забувайте залишати свої коментарі, відгуки, побажання. Всі матеріали перевірені антивірусною програмою.

Навчальні посібники та тренажери в інтернет-магазині «Інтеграл» для 5 класу
Тренажер до підручника І.І.Зубаревой і А.Г.Мордковіча
Тренажер до підручника Г.В.Дорофеева і Л.Г.Петерсон

Визначення і поняття площі фігури

Щоб краще зрозуміти, що таке площа фігури, розглянемо малюнок.
Ця довільна фігура розбита на 12 маленьких квадратика. Сторона кожного квадратика дорівнює 1 см. А площа кожного квадратика дорівнює 1 квадратного сантиметра, що записується так: 1 см 2.

Тоді площа фігури дорівнює 12 квадратних сантиметрах. В математиці площа позначається латинською буквою S.
Значить, площа нашої фігури дорівнює: S фігури \u003d 12 см 2.

Площа фігури дорівнює площі всіх маленьких квадратиків, з яких вона складається!

Хлопці, запам’ятайте!
Площа вимірюється квадратними одиницями довжини. Одиниці виміру площі:
1. Квадратний кілометр — км 2 (коли площі дуже великі, наприклад, країна або море).
2. Квадратний метр — м 2 (цілком підходить для того, щоб вимірювати площу ділянки або квартири).
3. Квадратний сантиметр — см 2 (зазвичай використовується на уроках математики, коли малюють фігури в зошиті).
4. Квадратний міліметр — мм 2.

Площа трикутника

Розглянемо два види трикутників: прямокутний і довільний.

Щоб знайти площу прямокутного трикутника необхідно знати довжину підстави і висоту. У прямокутному трикутнику висоту замінює одна зі сторін. Тому в формулу площі трикутника замість висоти підставляємо одну зі сторін.
У нашому прикладі сторони рівні 7 см і 4 см. Формула для розрахунку площі трикутника записується так:

S прямокутного трикутника АВС \u003d ВС * СА: 2

S прямокутного трикутника АВС \u003d 7 см * 4 см: 2 \u003d 14 см 2

Тепер розглянемо довільний трикутник.

Для такого трикутника необхідно провести висоту до основи.
У нашому прикладі висота дорівнює 6 см, а основа дорівнює 8 см. Як і в попередньому прикладі, розраховуємо площу за формулою:
S довільного трикутника АВС \u003d ВС * h: 2.

Підставами в формулу наші дані і отримаємо:
S довільного трикутника АВС \u003d 8 см * 6 см: 2 \u003d 24 см 2.

Площа прямокутника і квадрата

Візьмемо прямокутник АВСD зі сторонами 5 см і 8 см.
Формула розрахунку площі прямокутника записується так:
S прямокутника АВСD \u003d АВ * ВС.

S прямокутника АВСD \u003d 8 см * 5 см \u003d 40 см 2.

Тепер розрахуємо площу квадрата. На відміну від прямокутника і трикутника, для знаходження площі квадрата необхідно знати тільки одну сторону. У нашому прикладі сторона квадрата ABCD дорівнює 9 см. S квадрата АВСD \u003d АВ * НД \u003d АВ 2.

Підставами в формулу наші дані і отримаємо:
S квадрата АВСD \u003d 9 см * 9 см \u003d 81 см 2.

Ми вже познайомилися з поняттям площа фігури, Дізналися одну з одиниць вимірювання площі — квадратний сантиметр. На уроці ми виведемо правило, як обчислити площу прямокутника.

Ми вже вміємо знаходити площа фігур, які розділені на квадратні сантиметри.

наприклад:

Ми можемо визначити, що площа першої фігури 8 см 2, площа другої фігури 7 см 2.

Як знайти площу прямокутника, довжини сторін якого 3 см і 4 см?

Для вирішення завдання розіб’ємо прямокутник на 4 смужки по 3 см 2 кожна.

Тоді площа прямокутника буде дорівнює 3 * 4 \u003d 12 см 2.

Цей же прямокутник можна розбити на 3 смужки по 4 см 2.

Тоді площа прямокутника буде дорівнює 4 * 3 \u003d 12 см 2.

В обох випадках для знаходження площі прямокутника перемножуються числа, що виражають довжини сторін прямокутника.

Знайдемо площу кожного прямокутника.

Розглянемо прямокутник АКМО.

В одній смужці 6 см 2, а таких смужок в цьому прямокутнику 2. Значить, ми можемо виконати наступну дію:

Число 6 позначає довжину прямокутника, а 2 — ширину прямокутника. Таким чином, ми перемножили боку прямокутника для того, щоб знайти площу прямокутника.

Розглянемо прямокутник KDCO.

В прямокутнику KDCO в одній смужці 2см 2, а таких смужок 3. Отже, ми можемо виконати дію

Число 3 означає довжину прямокутника, а 2 — ширину прямокутника. Ми їх перемножили і дізналися площа прямокутника.

Можна зробити висновок: щоб знайти площу прямокутника, не треба кожен раз розбивати фігуру на квадратні сантиметри.

Щоб обчислити площу прямокутника, потрібно знайти його довжину і ширину (довжини сторін прямокутника повинні бути виражені в одних і тих же одиницях виміру), а потім обчислити добуток отриманих чисел (площа буде виражена в одиницях площі)

узагальнимо: площа прямокутника дорівнює добутку його довжини і ширини.

Вирішіть задачу.

Обчислювальні площа прямокутника, якщо довжина прямокутника 9см, а ширина — 2 см.

Міркуємо так. У цьому завданню відомі і довжина і ширина прямокутника.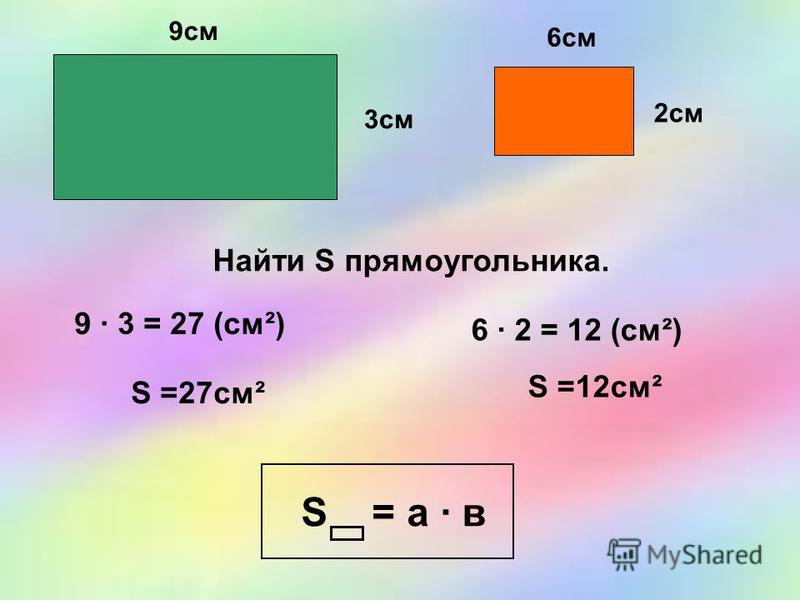 Тому діємо за правилом: площа прямокутника дорівнює добутку його довжини і ширини.

Запишемо рішення.

відповідь: площа прямокутника 18см 2

Як ви думаєте, якими ще можуть бути довжини сторін прямокутника з такою площею?

Можна міркувати так. Оскільки площа — це твір довжин сторін прямокутника, тому треба згадати таблицю множення. При множенні яких чисел виходить відповідь 18?

Правильно, при множенні 6 і 3 теж вийде 18. Значить, у прямокутника можуть бути сторони 6см і 3 см і його площа теж буде дорівнює 18см 2.

Вирішіть задачу.

Довжина прямокутника 8см, а ширина 2см. Знайди його площу і периметр.

Нам відомі довжина і ширина прямокутника. Необхідно згадати, що для знаходження площі необхідно знайти твір його довжини і ширини, а для знаходження периметра потрібно суму довжини і ширини помножити на два.

Запишемо рішення.

відповідь: площа прямокутника 16 см 2, а периметр прямокутника 20 см.

Вирішіть задачу.

Довжина прямокутника 4 см, а ширина — 3 см. Чому дорівнює площа трикутника? (Дивись малюнок)

Щоб відповісти на питання завдання, спочатку треба знайти площу прямокутника. Ми знаємо, що для цього необхідно довжину помножити на ширину.

Подивіться на креслення. Ви помітили, діагональ розділила прямокутник на два рівних трикутника? Отже, площа одного трикутника в 2 рази менше площі прямокутника. Значить, треба 12 зменшити в 2 рази.

відповідь: площа трикутника 6 см 2.

Сьогодні на уроці ми познайомилися з правилом, як обчислити площу прямокутника і вчилися застосовувати це правило при вирішенні задач на знаходження площі прямокутника.

1. М.І.Моро, М.А.Бантова і ін. Математика: Підручник. 3 клас: в 2-х частинах, частина 1. М., «Просвещение», 2012 рік.

2. М.І.Моро, М.А.Бантова і ін. Математика: Підручник. 3 клас: в 2-х частинах, частина 2. М., «Просвещение», 2012 рік.

3. М.І.Моро. Уроки математики: Методичні рекомендації для вчителя.

3 клас. — М .: Просвещение, 2012.

4. Нормативно-правовий документ. Контроль і оцінка результатів навчання. М., «Просвещение», 2011 рік.

5. «Школа Росії»: Програми для початкової школи. — М .: «Просвещение», 2011.

6. С.І.Волкова. Математика: Перевірочні роботи. 3 клас. — М .: Просвещение, 2012.

7. В.Н.Рудніцкая. Тести. М., «Іспит», 2012 (127с.)

2. Видавництво «Просвещение» ()

1. Довжина прямокутника 7 см, ширина 4 см. Знайдіть площу прямокутника.

2. Сторона квадрата 5 см. Знайдіть площу квадрата.

3. Накресліть можливі варіанти прямокутників, площа яких 18 см 2.

4. Складіть завдання по темі уроку для своїх товаришів.

Площа геометричної фігури — чисельна характеристика геометричної фігури показує розмір цієї фігури (частини поверхні, обмеженої замкнутим контуром даної фігури). Величина площі виражається числом полягають в неї квадратних одиниць.

Формули площі трикутника

1. Формула площі трикутника по стороні і висоті
   Площа трикутника дорівнює половині твори довжини сторони трикутника на довжину проведеної до цієї сторони висоти
   
2. Формула площі трикутника за трьома сторонами і радіусу описаного кола
   
3. Формула площі трикутника за трьома сторонами і радіусу вписаного кола
   Площа трикутника дорівнює добутку напівпериметр трикутника на радіус вписаного кола.
   
де S — площа трикутника,
— довжини сторін трикутника,
— висота трикутника,
— кут між сторонами і,
— радіус вписаного кола,
R — радіус описаного кола,

Формули площі квадрата

1. Формула площі квадрата по довжині боку
   Площа квадрата дорівнює квадрату довжини його сторони.
2. Формула площі квадрата по довжині діагоналі
   Площа квадрата дорівнює половині квадрата довжини його діагоналі.
   

   S \u003d	1	2
   	2

де S — Площа квадрата,
— довжина сторони квадрата,
— довжина діагоналі квадрата.

Формула площі прямокутника

Площа прямокутника дорівнює добутку довжин двох його суміжних сторін

де S — Площа прямокутника,
— довжини сторін прямокутника.

Формули площі паралелограма

1. Формула площі паралелограма по довжині боку і висоті
   Площа паралелограма
2. Формула площі паралелограма за двома сторонами і кутом між ними
   Площа паралелограма дорівнює добутку довжин його сторін помноженому на синус кута між ними.

   a · b · sin α

де S — Площа паралелограма,
— довжини сторін паралелограма,
— довжина висоти паралелограма,
— кут між сторонами паралелограма.

Формули площі ромба

1. Формула площі ромба по довжині боку і висоті
   Площа ромба дорівнює добутку довжини його сторони і довжини опущеною на цю сторону висоти.
2. Формула площі ромба по довжині боку і розі
   Площа ромба дорівнює добутку квадрата довжини його сторони і синуса кута між сторонами ромба.
3. Формула площі ромба по довжинах його діагоналей
   Площа ромба дорівнює половині добутку довжин його діагоналей.
де S — Площа ромба,
— довжина сторони ромба,
— довжина висоти ромба,
— кут між сторонами ромба,
1, 2 — довжини діагоналей.

Формули площі трапеції

1. Формула Герона для трапеції

   Де S — Площа трапеції,
   — довжини основ трапеції,
   — довжини бічних сторін трапеції,
   

Формула площі прямокутника

Площа прямокутника дорівнює добутку довжин двох його суміжних сторін

S =  a · b де S — площа прямокутника,

a, b — довжини сторін прямокутника.

У процесі подальшого вимірювання й обчислення площі прямокутники

і розв’язування задач на обчислення площі слід мати на увазі такі моменти:

1. Діти повинні достатньо практикуватися у вимірюванні площ прямокутників на моделях та малюнках.

2. Кожен учень має виконати 2—3 завдання на вимірювання площі класної дошки, вікна, поверхні кришки стола, підлоги, стіни класної кімнати, земельної ділянки тощо.

3. Треба розв’язати достатню кількість задач на обчислення площі прямокутника, сторони якого виражені складеними іменованими числами. Саме тоді стане зрозумілою вимога правила про те, що довжину і ширину прямокутника необхідно вимірювати однією і тією самою мірою. Розв’язування задач на обчислення площі потрібно поєднувати з розв’язуван­ням задач на обчислення периметра.

4. Слід практикувати обчислення площі прямокутних ділянок за їх планом.

Для ознайомлення учнів з палеткою як інструментом для вимірювання площі фігур можна скористатися прийомом аналогії (масштабна лінійка призначена для вимірювання довжини відрізка, палетка — для вимірювання площі фігури). Розкриваючи мету уроку, вчитель повідомляє дітям, що раніше нони знаходили площу фігури тільки прямокутної форми і робили це за правилом. Тепер потрібно навчитись з допомогою особливого пристрою знаходити площу фігур, що мають форму круга, будь-якого многокутника або фігури будь-якої форми. На фігуру накладають палетку — прозору плівку або пластинку, поділену на квадрати, — і лічать, скільки квадратів цієї палетки накладається на дану фігуру. На дошці вчитель креслить довільну криволінійну фігуру, накладає на неї палетку, показує спосіб підрахунку повних і неповних квадратів. (Палетка вчителя поділена на квадратні дециметри). Використовуючи зображення геометричних фігур, учні за допо­могою палетки визначають їх площу.

61.Методика формування в учнів поняття швидкості та залежності між трійкою величин: швидкістю, часом та відстанню (шляхом) при рівномірному прямолінійному русі. Одиниці швидкості. Формули знаходження швидкості, часу і відстані.

Діти вже знайомі з величинами: час та відстань. Чули вони й слово „швидкість”. Але, перед тим, як перейти до розгляду залежності між відстанню, швидкістю та часом при рівномірному русі, поняття про швидкість руху треба ввести.

Спостерігаючи за рухом кількох тіл, учні помітили, що:

Чому так відбувається? Учні можуть відповісти: „Тому що у цих тіл різні швидкості!”. Що таке швидкість? На це запитання навряд можна отримати свідому відповідь. ..

Швидкість — нова величина, з якою ознайомлюють учнів 4 класу. Це векторна величина. У початковій школі поняття напрямленої величини не розглядають, але на малюнках напрям руху тіл вказують. Поняття швидкості пояснюють на основі поданої нижче задачі.

Задача. За 2 год автобус проїхав 120 км. Скільки кілометрів він проїде за І год, коли щогодини проїжджатиме однакову кількість кілометрів?

Розв’язання

120:2 = 60(км).

Відповідь. За 1 год автобус проїде 60 км.

Пояснення. Якщо за кожну годину автобус проїжджає 60 км, то кажуть, що він рухається зі швидкістю 60 км/год. Це записують так: 60 км/год.

Відразу можна подати таке правило: щоб знайти швидкість, треба відстань поділити на час.

З поняттям «швидкість» ми маємо справу часто: «трамвай рухався повільно»; «літак рухався з надзвуковою швидкістю»; «перша космічна швидкість»; «друга комічна швидкість»; «швидкість променя світла» та ін.

Швидкості вимірюються в різних одиницях. Наприклад: 3 м/с; 10 м/хв; 120 км/год. Ці одиниці швидкості можна перетворювати. Так, 5 м/с — це те саме, що 5 • 60 м/хв, тобто 300 м/хв.

Безпосередньо з поняттям швидкості уточнюється поняття відстані і часу, встановлюється залежність між цими величинами.

Одиниці вимірювання швидкості: й тощо

1. Формули для знаходження відстані, якщо відомі час і швидкість мають вигляд: S = v * t, де S — відстань, v — швидкість, t — час; 2.Формули для обчислення швидкості, якщо відомі час і відстань: v = S / t, де S — відстань, v — швидкість, t — час; 3. Формули для визначення часу, якщо відомі швидкість і відстань мають вигляд: t = S / v, де S — відстань, v — швидкість, t — час;

62.Методика вивчення тем „Частини” і „Дроби” в початковому курсі математики. Ознайомлення учнів з частинами. Утворення частин. Задачі на знаходження частини від числа і числа за його частиною. Поняття „дріб”. Утворення та запис дробів. Чисельник і знаменник дробу. Порівняння дробів.

У молодших школярів необхідно створити конкретні уявлення про процес утворення частин від цілого предмета чи сукупності предметів. З цією метою вже в 3 класі дітей ознайомлюють з частинами, їх записом, вчать знаходити частину числа та число за відомою його частиною. У 4 класі продовжують працювати над засвоєнням частини числа, учнів ознайомлюють з дробами та їх записом, вчать порівнювати частини, знаходити кілька частин від числа, дріб від числа, розв’язувати складені задачі, що передбачають знаходження дробу від числа.

Розглядають ці питання з допомогою наочності, виконуючи практичні вправи, пов’язані з кресленням, вимірюванням, перегинанням, практичним поділом круга, прямокутника, смужки на рівні частини.

Ознайомлення з частинами

Діти часто чують від старших слова «півкілограма яблук», «третя частина, кавуна», «чверть години» тощо. Цей життєвий досвід учнів треба впорядкувати і систематизувати. Правильні уявлення про частини, а пізніше про дроби будуть сформовані тоді, коли діти своїми руками зроблять, наприклад, половину круга, знайдуть четверту частину смужки та ін.

Покажемо, як ознайомлювати учнів з частинами. Учитель запитує, хто бачив половину хлібини (кавуна, яблука тощо), ставить завдання показати половину кружечка, розділити навпіл смужку паперу. Перегинаючи круг, смужку паперу навпіл, діти роблять висновок, що половини одного й того самого круга чи тієї самої смужки паперу рівні між собою.

Діти повинні усвідомити, що для знаходження половини числа його треба поділити на 2, для знаходження третини — поділити на 3, для знаходження чверті — поділити на 4.

Наприкінці навчання у 2 класі і впродовж 3 класу учні знаходять довжини вказаних частин смужки, частини чисел (без позначення частин числа циф­рами

У 3 класі дітей вчать позначати частини цифрами. їм потрібно спочатку показати поділ першого круга на дві рівні частини, другого — на чотири рівні частини. Тоді необхідно з’ясувати з ними, на скільки рівних частин поділені дані круги.

Учитель показує, що взяли одну таку частину. Терміни «чисельник», «знаменник» не вводять. Просто кажуть, що число під рискою показує, на скільки рівних частин поділили круг (смужку), а число над рискою показує, що взяли одну таку частину.

Під час виконання вправ на знаходження частини смужки (круга, квадрата тощо) доцільно звертати увагу учнів, що в цілій смужці (крузі, квадраті) є дві половини, три третіх частини, чотири четвертих частини і т. ін.

Задачі на обчислення частин числа діти розв’язують, спираючись на розуміння процесу знаходження частини числа. Щоб знайти, наприклад, четверту частину числа, треба це число поділити на чотири; щоб обчислити довжину 1/3 смужки, потрібно довжину смужки поділити на 3.

Задача. У шкільному саду росте 60 дерев. 1/3 дерев становлять яблуні і 1/4 — груші. Скільки яблунь і груш у саду разом?

Учитель пояснює, що частини записують за допомогою двох цифр. Наприклад, третю частину круга, смужки позначають так: 1/3. Число 3 показує, що круг, смужку або іншу фігуру поділили на три рівні частини, а число 1

Ознайомлення з дробами

У 4 класі актуалізують знання школярів про частини: їх утворення, позначення, знаходження частини числа та числа за його відомою частиною, вчать порівнювати частини.

Порівнюють частини тільки з опорою на унаочнення .

Користуючись малюнком, учні з’ясовують, наприклад, скільки четвертих частин у половині, скільки восьмих частин у цілому і т. ін. Наочно бачать, що 1/4 < 1/2; 1/2 > 1/8; 1/8 > 1/10 і т. ін.

Учні мають зрозуміти, що коли ціле поділити на рівні частини, то кожна частина буде менша від цього цілого; чим на більшу кількість частин поділено ціле, тим меншою буде кожна його частина.

Із дробами учні ознайомлюються, виконуючи під керівництвом учителя такі вправи:

1. На скільки рівних частин поділено кожний квадрат ?

Як називається незаштрихована частина у квадраті? Скільки таких частин у квадраті заштриховано?

2. Полічіть, на скільки рівних частин поділено кожний круг. Скільки таких частин заштриховано?

Ми вже вміємо позначати цифрами одну частину числа. Яка частина першого круга заштрихована? (1/6). (Учитель записує це число на дошці). Скільки таких шостих частин заштриховано у другому крузі? (2). Тобто заштриховано 2/6 частини. (Вчитель записує на дошці). Скільки таких шос­тих частин заштриховано у третьому крузі? І т. д.

Числа виду 1/2, 2/3, 3/4, 1/6, 2/3, 5/6 називаються дробовими числами. Число 5/6 — дріб, 5 — чисельник дробу, а 6 — знаменник дробу. Число під рискою дробу — знаменник дробу — показує, на скільки рівних частин поділено ціле. Число над рискою дробу — чисельник дробу — показує, скільки взято рівних частин цілого.

Здобуті знання про дроби та їх зображення використовують під час розв’язування задач на знаходження дробу від числа. Пояснення знаходження дробу від числа подають на основі готового розв’язання.

Емпіричні формули обчислення площ простих постатей. Як знайти площу геометричних фігур

Щоб розв’язати задачі з геометрії, треба знати формули — такі, як площа трикутника або площа паралелограма — а також прості прийоми, Про які ми розповімо.

Для початку вивчимо формули площ фігур. Ми спеціально зібрали їх у зручну таблицю.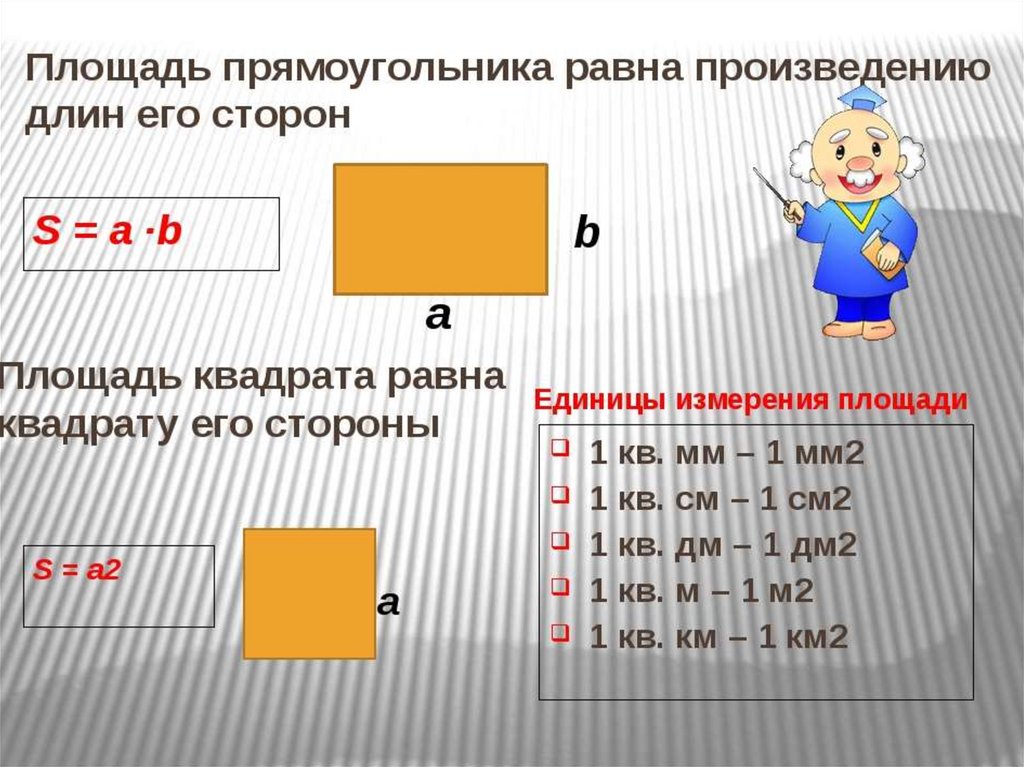 Роздрукуйте, вивчіть та застосовуйте!

Звичайно, не всі формули геометрії є в нашій таблиці. Наприклад, для вирішення задач з геометрії та стереометрії у другій частині профільного ЄДІз математики застосовуються інші формули площі трикутника. Про них ми обов’язково розповімо.

А що робити, якщо треба знайти не площу трапеції чи трикутника, а площу якої-небудь складної фігури? Є універсальні методи! Покажемо їх на прикладах із банку завдань ФІПД.

1. Як знайти площу нестандартної фігури? Наприклад, довільного чотирикутника? Простий прийом – розіб’ємо цю фігуру на такі, про які ми все знаємо, і знайдемо її площу – як суму площ цих фігур.

Поділимо цей чотирикутник горизонтальною лінією на два трикутники з загальною основою, рівним. Висоти цих трикутників рівні і . Тоді площа чотирикутника дорівнює сумі площ двох трикутників: .

Відповідь: .

2. У деяких випадках площу фігури можна представити як різницю будь-яких площ.

Не так просто порахувати, чому рівні основа і висота в цьому трикутнику! Зате можемо сказати, що його площа дорівнює різниці площ квадрата зі стороною і трьох прямокутних трикутників. Бачите їх на малюнку? Отримуємо: .

Відповідь: .

3. Іноді у завданні треба знайти площу не всієї фігури, а її частини. Зазвичай мова йде про площу сектора — частини кола . Знайдіть площу сектора кола радіуса , довжина дуги якого дорівнює .

На цьому малюнку ми бачимо частину кола. Площа всього кола дорівнює, тому що. Залишається дізнатися, яку частину кола зображено. Оскільки довжина всього кола дорівнює (оскільки ), а довжина дуги даного сектора дорівнює , отже, довжина дуги в раз менше, ніж довжина всього кола. Кут, на який спирається ця дуга, також у раз менше, ніж повне коло (тобто градусів). Значить, і площа сектора буде в раз менше, ніж площа всього кола.

Площа геометричної фігури — чисельна характеристикагеометричної фігури, що показує розмір цієї фігури (частини поверхні, обмеженої замкнутим контуромцієї фігури). Величина площі виражається числом квадратних одиниць, що укладаються в неї.

Формули площі трикутника

1. Формула площі трикутника по стороні та висоті
   Площа трикутникадорівнює половині добутку довжини сторони трикутника на довжину проведеної до цієї сторони висоти
   
2. Формула площі трикутника по трьох сторонах та радіусу описаного кола
   
3. Формула площі трикутника по трьох сторонах і радіусу вписаного кола
   Площа трикутникадорівнює добутку півпериметра трикутника на радіус вписаного кола.
   
де S — площа трикутника,
— Довжини сторін трикутника,
— Висота трикутника,
— кут між сторонами та,
— радіус вписаного кола,
R — радіус описаного кола,

Формули площі квадрата

1. Формула площі квадрата по довжині сторони
   Площа квадратадорівнює квадрату довжини його боку.
2. Формула площі квадрата за довжиною діагоналі
   Площа квадратадорівнює половині квадрата довжини його діагоналі.
   

   S =	1	2
   	2

де S — площа квадрата,
— Довжина сторони квадрата,
— Довжина діагоналі квадрата.

Формула площі прямокутника

Площа прямокутникадорівнює добутку довжин двох його суміжних сторін

де S — Площа прямокутника,
— Довжини сторін прямокутника.

Формули площі паралелограма

1. Формула площі паралелограма по довжині сторони та висоті
   Площа паралелограма
2. Формула площі паралелограма з обох боків та кутку між ними
   Площа паралелограмадорівнює добутку довжин його сторін, помноженому на синус кута між ними.

   a · b · sin α

де S — Площа паралелограма,
— Довжини сторін паралелограма,
— Довжина висоти паралелограма,
— Кут між сторонами паралелограма.

Формули площі ромба

1. Формула площі ромба по довжині сторони та висоті
   Площа ромбудорівнює добутку довжини його сторони та довжини опущеної на цей бік висоти.
2. Формула площі ромба по довжині сторони та куту
   Площа ромбудорівнює добутку квадрата довжини його сторони та синуса кута між сторонами ромба.
3. Формула площі ромба за довжинами його діагоналей
   Площа ромбудорівнює половині добутку довжин його діагоналей.
де S — площа ромба,
— Довжина сторони ромба,
— Довжина висоти ромба,
— Кут між сторонами ромба,
1 2 — довжини діагоналей.

Формули площі трапеції

1. Формула Герону для трапеції

   Де S — Площа трапеції,
   — Довжини основ трапеції,
   — Довжини бічних сторін трапеції,
   

Що таке майдан?

Площа — характеристика замкнутої геометричної фігури (коло, квадрат, трикутник і т.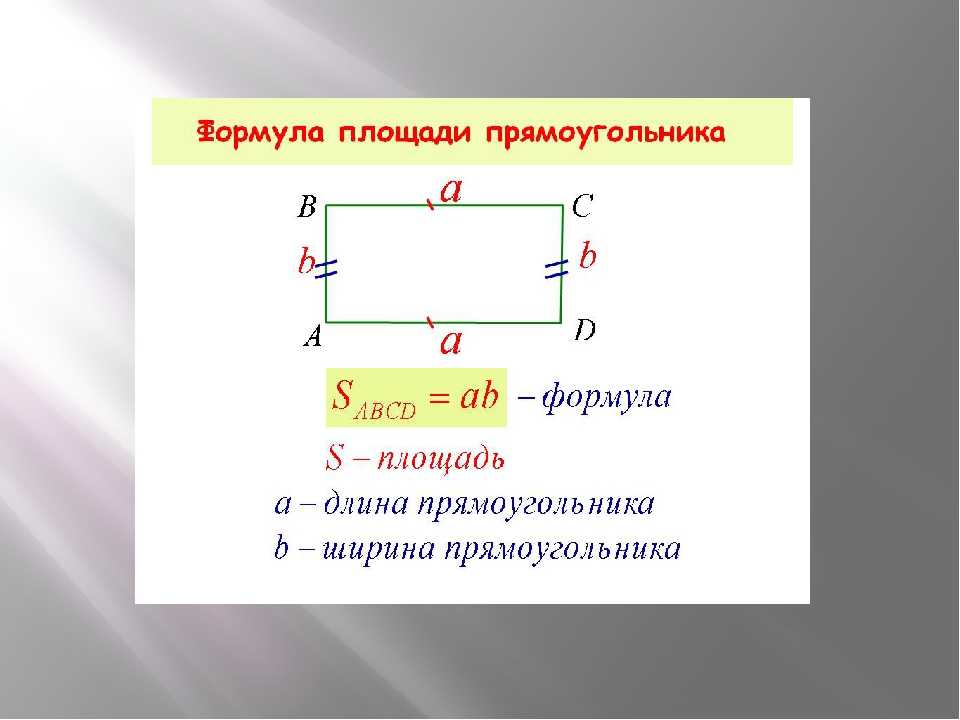 д.), що вказує її розмір. Площа вимірюється у квадратних сантиметрах, метрах тощо. Позначається буквою S(Square).

Як знайти площу трикутника?

S = a · h

де a— Довжина основи, h— Висота трикутника, проведена до основи.

Причому підстава не обов’язково має бути знизу. То теж зійде.

Якщо трикутник тупокутний, то висота опускається на продовження основи:

Якщо трикутник прямокутний, то основою та висотою є його катети:

2. Інша формула, яка є не менш корисною, але яку чомусь завжди забувають:

S = a · b · sinα

де aі b– дві сторони трикутника, sinα– синус кута між цими сторонами.

Головна умова – кут береться між двома відомими сторонами.

3.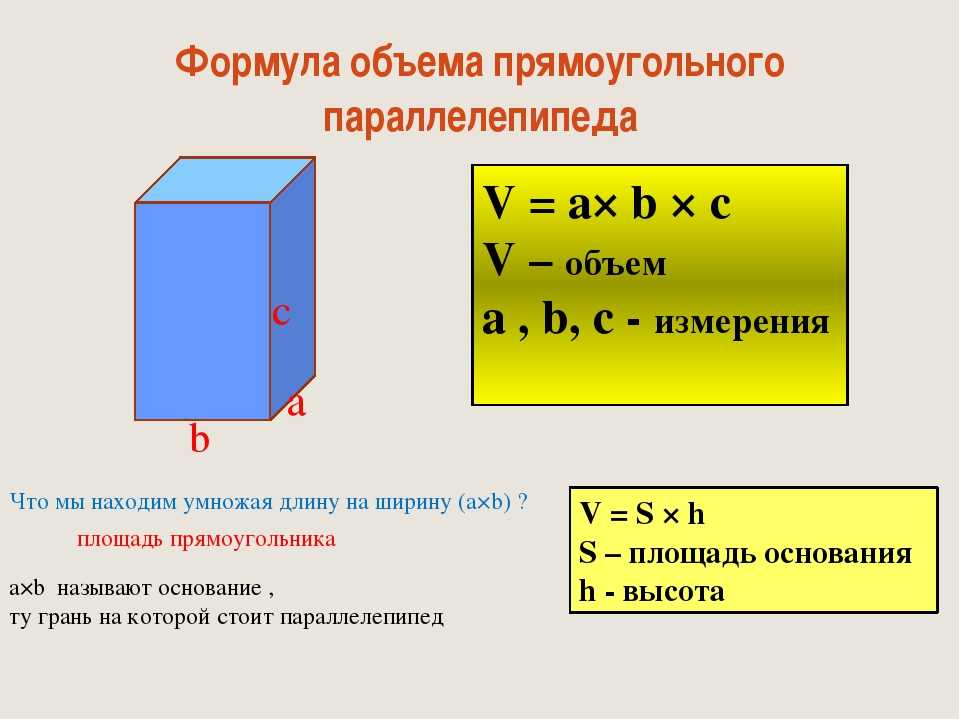 Формула площі з трьох сторін (формула Герона):

S =

де a, bі з— Сторони трикутника, а р —напівпериметр. p = (a + b + c)/2.

4. Формула площі трикутника через радіус описаного кола:

S =

де a, bі з— Сторони трикутника, а R –радіус описаного кола.

5. Формула площі трикутника через радіус вписаного кола:

S = p · r

де р —півпериметр трикутника, а r –радіус вписаного кола.

Як знайти площу прямокутника?

1. Площа прямокутника знаходиться досить просто:

S =a · b

Ніяких каверз.

Як знайти площу квадрата?

1. Оскільки квадрат є прямокутником, у якого всі сторони рівні, то до нього застосовується така сама формула:

S =a · a = a 2

2.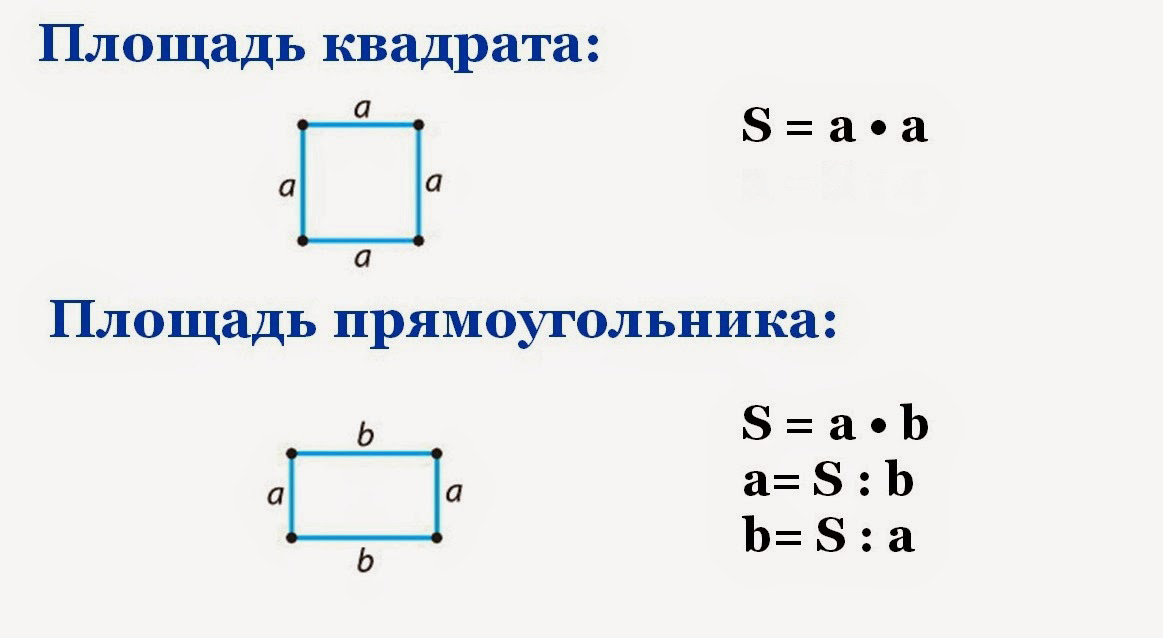 Також площа квадрата можна знайти через його діагональ:

S = d 2

Як знайти площу паралелограма?

1. Площа паралелограма знаходиться за формулою:

S =a · h

Це пов’язано з тим, що якщо від нього відрізати прямокутний трикутникправоруч і приставити його зліва, вийде прямокутник:

2. Також площу паралелограма можна знайти через кут між двома сторонами:

S =a · b · sinα

Як знайти площу ромба?

Ромб за своєю сутністю є паралелограмом, у якого усі сторони рівні. Тому для нього застосовуються самі формули площі.

1. Площа ромба через висоту:

S =a · h

Усі формули площі плоских фігур

Площа рівнобедреної трапеції

1. Формула площі рівнобедреної трапеції через сторони та кут

а — нижня основа

b — верхня основа

с — рівні бічні сторони

α — кут при нижній підставі

Формула площі рівнобедреної трапеції через сторони (S):

Формула площі рівнобедреної трапеції через сторони та кут, (S):

2.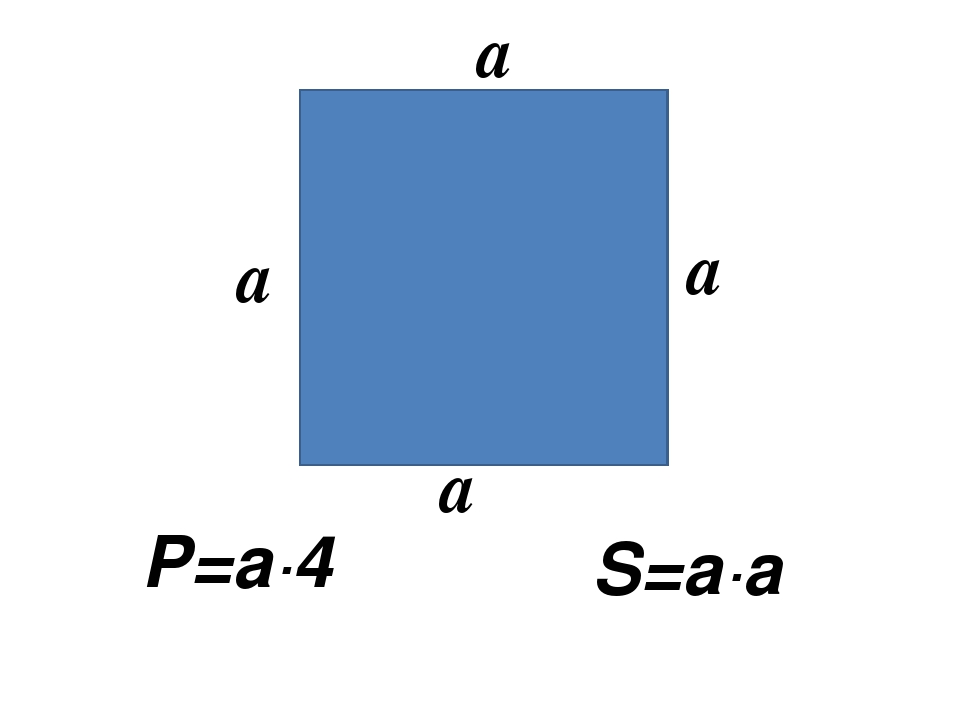 Формула площі рівнобедреної трапеції через радіус вписаного кола

R-радіус вписаного кола

D-діаметр вписаного кола

O-центр вписаного кола

H- висота трапеції

α, β — кути трапеції

Формула площі рівнобедреної трапеції через радіус вписаного кола, (S):

СПРАВЕДЛИВО, для вписаного кола в рівнобедрену трапецію:

3. Формула площі рівнобедреної трапеції через діагоналі та кут між ними

d-діагональ трапеції

α,β- кути між діагоналями

Формула площі рівнобедреної трапеції через діагоналі та кут між ними, (S):

4. Формула площі рівнобедреної трапеції через середню лінію, бічну сторону та кут при підставі

c-бокова сторона

m-середня лінія трапеції

α, β — кути при основі

Формула площі рівнобедреної трапеції через середню лінію, бічну сторону та кут при підставі,

(S):

5. Формула площі рівнобедреної трапеції через основи та висоту

a — нижня основа

b — верхня основа

h — висота трапеції

Формула площі рівнобедреної трапеції через основи та висоту, (S):

Площа трикутника на стороні та двох кутах, формула.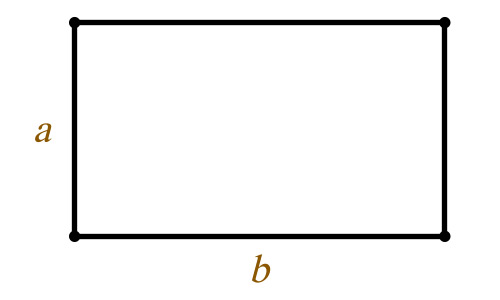

a, b, c-сторони трикутника

α, β, γ- протилежні кути

Площа трикутника через бік та два кути (S):

Формула площі правильного багатокутника

a — сторона багатокутника

n – кількість сторін

Площа правильного багатокутника, (S):

Формула (Герона) площі трикутника через півпериметр (S):

Площа рівностороннього трикутника дорівнює:

Формули розрахунку площі рівностороннього трикутника.

a — сторона трикутника

h – висота

Як обчислити площу рівнобедреного трикутника?

b — основа трикутника

a — рівні сторони

h – висота

3. Формула площі трапеції через чотири сторони

a — нижня основа

b — верхня основа

c, d — бічні сторони

Радіус описаного кола трапеції з боків та діагоналі

a — бічні сторони трапеції

c — нижня основа

b — верхня основа

d — діагональ

h — висота

Формула радіусу описаного кола трапеції, (R)

знайти радіус описаного кола рівнобедреного трикутника по сторонах

Знаючи сторони рівнобедреного трикутника, можна за формулою знайти, радіус описаного кола біля цього трикутника.

a, b — сторони трикутника

Радіус описаного кола рівнобедреного трикутника (R):

Радіус вписаного кола в шестикутник

a — сторона шестикутника

Радіус вписаного кола в шестикутник, (r):

Радіус вписаного кола в ромб

r — радіус вписаного кола

a — сторона ромба

D, d – діагоналі

h — висота ромба

Радіус вписаного кола в рівнобічну трапецію

с — нижня основа

b — верхня основа

a — бічні сторони

h — висота

Радіус вписаного кола в прямокутний трикутник

a, b — катети трикутника

с — гіпотенуза

Радіус вписаного кола в рівнобедрений трикутник

a, b — сторони трикутника

Довести, що площа вписаного чотирикутника дорівнює

\/(р-а)(р-b) (р-с) (р-d),

де р – напівпериметр і а, b, с і d – сторони чотирикутника.

Довести, що площа вписаного в коло чотирикутника дорівнює

1/2 (ab + cb) · sin α де а, b, с і d — сторони чотирикутника і α — кут між сторонами а і b.

S = √[ a c d] sin ½ (α + β). — Читайте на FB.ru:

Площа довільного чотирикутника (рис. 1.13) можна виразити через його сторони а, b, c та суму пари протилежних кутів:

де р — Півпериметр чотирикутника.

Площа вписаного в коло чотирикутника () (рис. 1.14, а) обчислюється за формулою Брахмагупт

а описаного (рис. 1.14, б) () – за формулою

Якщо ж чотирикутник вписаний і описаний одночасно (рис. 1.14, в), то формула стає простою:

Формула Піка

Щоб оцінити площу багатокутника на папері, достатньо підрахувати, скільки клітин покриває цей багатокутник (площу клітини ми приймаємо за одиницю). Точніше, якщо S – площа багатокутника, — число клітин, які повністю лежать усередині багатокутника, та — число клітин, які мають із начинкою багатокутника хоч одну загальну точку.

Розглянемо нижче такі багатокутники, всі вершини яких лежать у вузлах картатого паперу – в таких, де перетинаються лінії сітки. Виявляється, що для таких багатокутників можна вказати таку формулу:

де — площа, r — число вузлів, що лежать строго всередині багатокутника.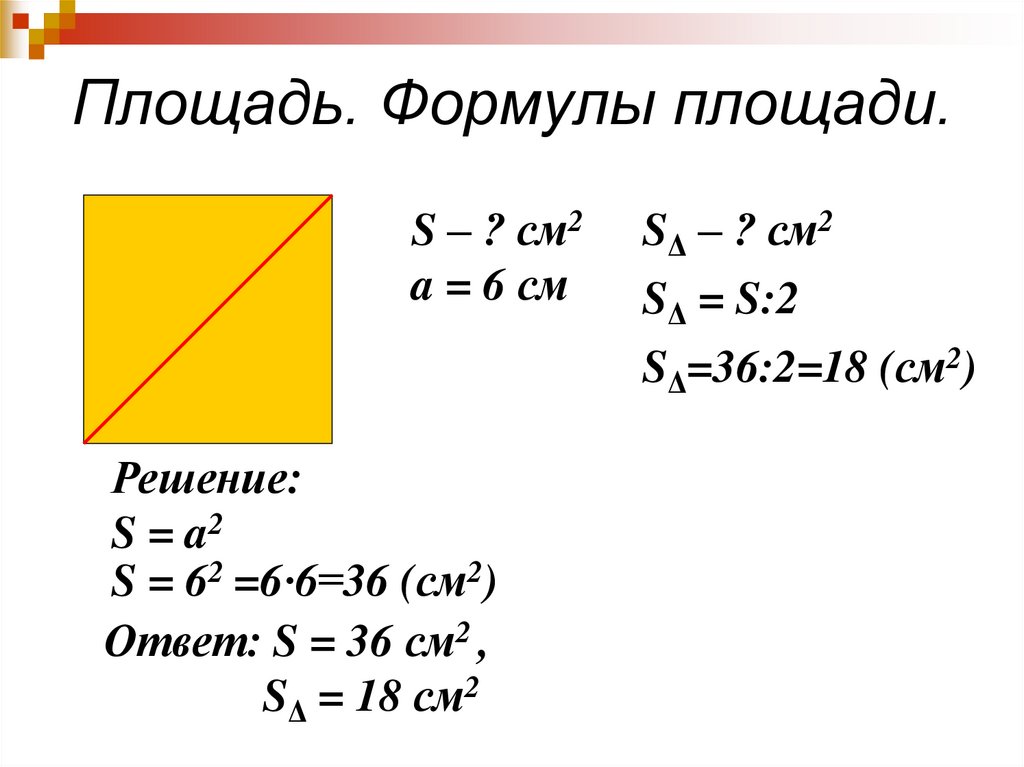

Цю формулу називають «формула Піка» — на ім’я математика, що відкрив її в 1899 році.

Що значить знайти площу прямокутника. Як обчислити і позначити площа

Площа прямокутника, що не буде зухвало звучати, але це важливе поняття. У повсякденному житті ми постійно стикаємося з ним. Дізнатися розмір полів, городів, розрахувати кількість фарби, необхідної для побілки стелі, скільки знадобиться шпалер для обклеювання до

мНАТ і інше.

Геометрична фігура

Для початку поговоримо про прямокутнику. Це фігура на площині, яка має чотири прямих кута, а її супротивники рівні. Сторони його звикли називати довжиною і шириною. Вимірюють їх в міліметрах, сантиметрах, дециметрах, метрах і т. Д. Тепер відповімо на запитання: «Як знайти площу прямокутника?» Для цього необхідно довжину помножити на ширину.

Площа \u003d довжина * ширина

Але ще одне застереження: довжина і ширина повинні бути виражені в однакових одиницях виміру, тобто метр і метр, а не метр і сантиметр. Записується площа латинською буквою S. Для зручності позначимо довжину латинською буквою b, а ширину латинською буквою a, як показано на малюнку. Звідси ми робимо висновок, що одиницею виміру площі є мм 2, см 2, м 2 і т. Д.

Розглянемо на конкретному прикладі, як знайти площу прямокутника. Довжина b \u003d 10 од. Ширина a \u003d 6 од. Рішення: S \u003d a * b, S \u003d 10 од. * 6 од., S \u003d 60 од 2. Завдання. Як дізнатися площа прямокутника, якщо довжина в 2 рази більше ширини і становить 18 м? Рішення: якщо b \u003d 18 м, тоді а \u003d b / 2, a \u003d 9 м. Як знайти площу прямокутника, якщо відомі обидві сторони? Правильно, підставити в формулу. S \u003d a * b, S \u003d 18 * 9, S \u003d 162 м 2. Відповідь: 162 м 2. Завдання. Скільки необхідно купити рулонів шпалер для кімнати, якщо її розміри складають: довжина 5,5 м ширина 3,5, а висота 3 м? Розміри рулону шпалер: довжина 10 м, ширина 50 см. Рішення: зробимо малюнок кімнати.

Площі протилежних сторін рівні. Обчислимо площу стіни з розмірами 5,5 м і 3 м.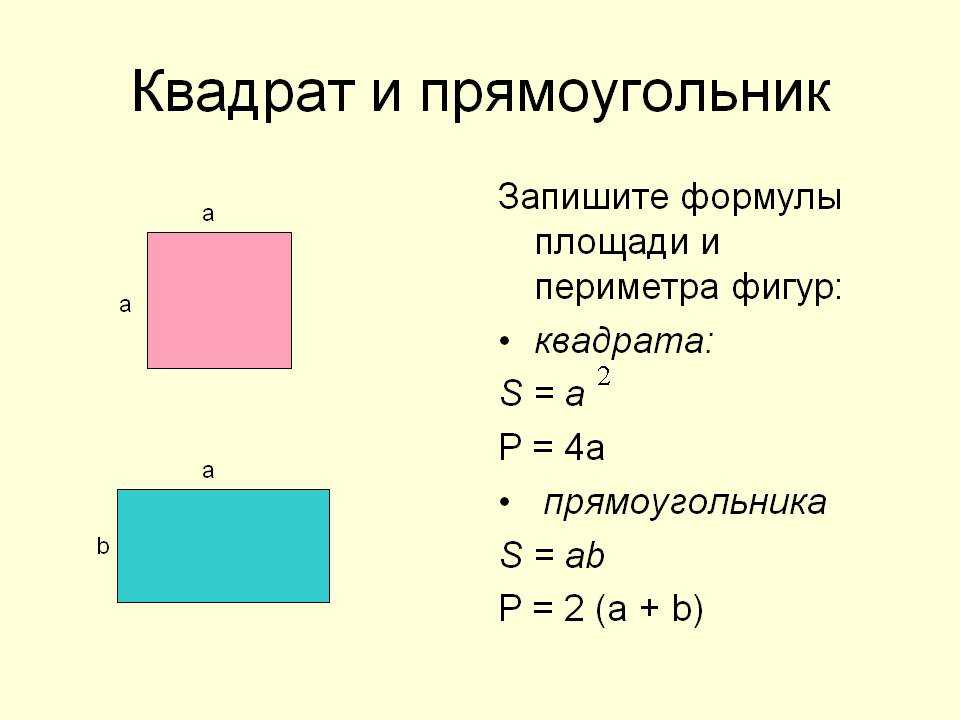 S стіни 1 \u003d 5,5 * 3,

S стіни 1 \u003d 16,5 м 2. Отже, протилежна стіна має площу рівну 16,5 м 2. Знайдемо площі наступних двох стін. Сторони їх, відповідно, рівні 3,5 м і 3 м. S стіни 2 \u003d 3,5 * 3, S стіни 2 \u003d 10,5 м 2. Значить, і протилежна сторона дорівнює 10,5 м 2. Складемо всі результати. 16,5 + 16,5 + 10,5 + 10,5 \u003d 54 м 2. Як обчислити площу прямокутника, якщо сторони виражені в різних одиницях виміру. Раніше ми обчислювали площі в м 2, то і в цьому випадку будемо використовувати метри. Тоді ширина рулону шпалер буде дорівнює 0,5 м. S рулону \u003d 10 * 0,5, S рулону \u003d 5 м 2. Тепер дізнаємося, скільки рулонів необхідно для обклеювання кімнати. 54: 5 \u003d 10,8 (рулонів). Так як вони вимірюються цілими числами, то потрібно купити 11 рулонів шпалер. Відповідь: 11 рулонів шпалер. Завдання. Як обчислити площу прямокутника, якщо відомо, що ширина на 3 см коротше довжини, а сума сторін прямокутника становить 14 см? Рішення: нехай довжина х см, тоді ширина (х-3) см. Х + (х-3) + х + (х-3) \u003d 14, 4х-6 \u003d 14, 4х \u003d 20, х \u003d 5 см — довжина прямокутника, 5-3 \u003d 2 см — ширина прямокутника, S \u003d 5 * 2, S \u003d 10 см 2 Відповідь: 10 см 2.

резюме

Розглянувши приклади, сподіваюся, стало зрозуміло, як знайти площу прямокутника. Нагадаю, що одиниці вимірювання довжини і ширини повинні збігатися, інакше вийде неправильний результат, щоб не допустити помилок, читайте завдання уважно. Іноді сторона може бути виражена через іншу сторону, не варто боятися. Зверніться до наших рішенням завданням, цілком можливо, вони можуть допомогти. Але хоч раз в житті ми стикаємося з перебуванням площі прямокутника.

Що таке площа і що таке прямокутник

Площа — це така геометрична величина, за допомогою якої можна визначити розмір будь-якої поверхні геометричної фігури.

Протягом багатьох століть так повелося, що обчислення площі називали квадратурою. Тобто, щоб дізнатися площа нескладних геометричних фігур, досить було підрахувати кількість одиничних квадратів, якими умовно були покриті фігури.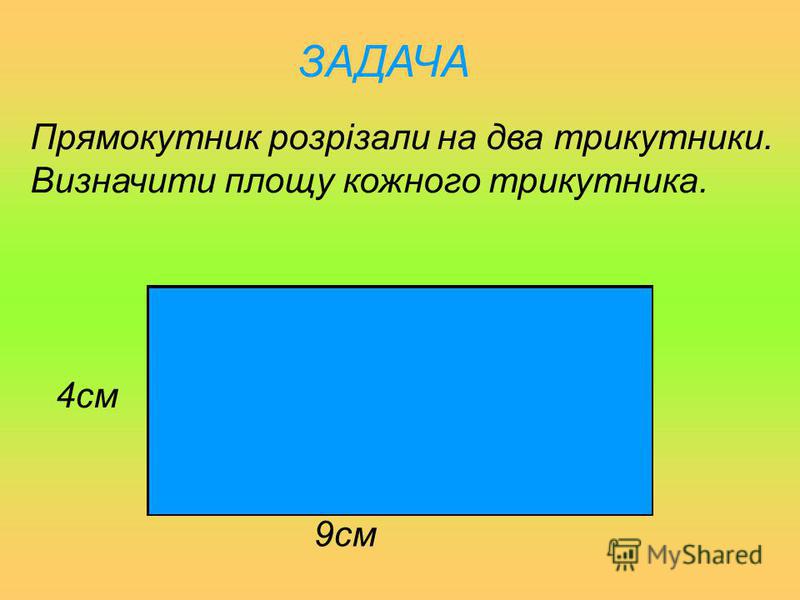 А постать, яка мала площа, називали квадрованою.

Тому, можна підвести підсумок, що площа — це така величина, яка показує нам розмір частини площині, з’єднаної між собою відрізками.

Прямокутник — це такий чотирикутник, у якого всі кути прямі. Тобто, чотиристоронню фігуру, яка має чотири прямих кута і її супротивники рівні, називають прямокутником.

Як знайти площу прямокутника

Найпростіший спосіб знаходження площі прямокутника — взяти прозору папір, наприклад кальку, або клейонку і розкреслити її на рівні квадратики по 1 см, а потім прикласти до зображення прямокутника. Кількість заповнених квадратиків і буде площею в сантиметрах квадратних. Наприклад, на малюнку видно, що прямокутник потрапляє в 12 квадратів, значить, його площа дорівнює — 12 кв. см.

Але для знаходження площі великих об’єктів, наприклад квартири, необхідний більш універсальний спосіб, тому була доведена формула, щоб знайди площа прямокутника необхідно помножити його довжину на ширину.

А тепер давайте спробуємо записати правило знаходження площі прямокутника у вигляді формули. Позначимо площу нашої фігури буквою S, буква а — означатиме його довжину, а буква b — ширину.

У підсумку отримуємо ось таку формулу:

S \u003d а * b.

Якщо накласти цю формулу на малюнок прямокутника вище, то ми отримаємо ті ж 12 кв.см, тому що а \u003d 4 см, b \u003d 3 см, а S \u003d 4 * 3 \u003d 12 кв.см.

Якщо взяти дві ідентичні фігури, і накласти їх одну на іншу, то вони співпадуть, а будуть називатися рівними. У таких рівних фігур будуть також рівні їх площі і периметри.

Навіщо вміти знаходити площа

По-перше, якщо ви знаєте, як знайти площу будь-якої фігури, то за допомогою її формули ви без проблем зможете вирішувати будь-які завдання з геометрії і тригонометрії.
По-друге, навчившись знаходити площа прямокутника, ви спочатку зможете вирішувати прості завдання, а згодом перейдете до вирішення складніших, і навчитеся знаходити площі фігур, які вписані в прямокутник або біля нього.
По-третє, знаючи таку просту формулу, як S \u003d а * b, ви отримуєте можливість без проблем вирішувати будь-які прості побутові завдання (наприклад, знаходити S квартири або будинку), а згодом і зможете застосувати їх до вирішення складних архітектурних проектів.

Тобто, якщо зовсім спростити формулу знаходження площі, то вона буде виглядати так:

П \u003d Д х Ш,

Що означає П — це шукана площа, Д — це її довжина, Ш — позначає її ширину, а х — є знаком множення.

А чи відомо вам, що площа будь-якого багатокутника можна умовно розбити на певну кількість квадратних блоків, які знаходяться всередині цього багатокутника? Яка різниця між площею і периметром

Давайте на прикладі спробуємо зрозуміти різницю між периметром і площею. Наприклад, наша школа знаходиться на ділянці, який огороджений парканом — сумарна довжина цього паркану буде периметром, а той простір, який знаходиться всередині огорожі і є площею.

Одиниці виміру площі

Якщо периметр одновимірний вимірюється в лінійних одиницях, якими є дюйми, фути і метри, то S відноситься до двовимірним исчислениям і має свою довжину і ширину.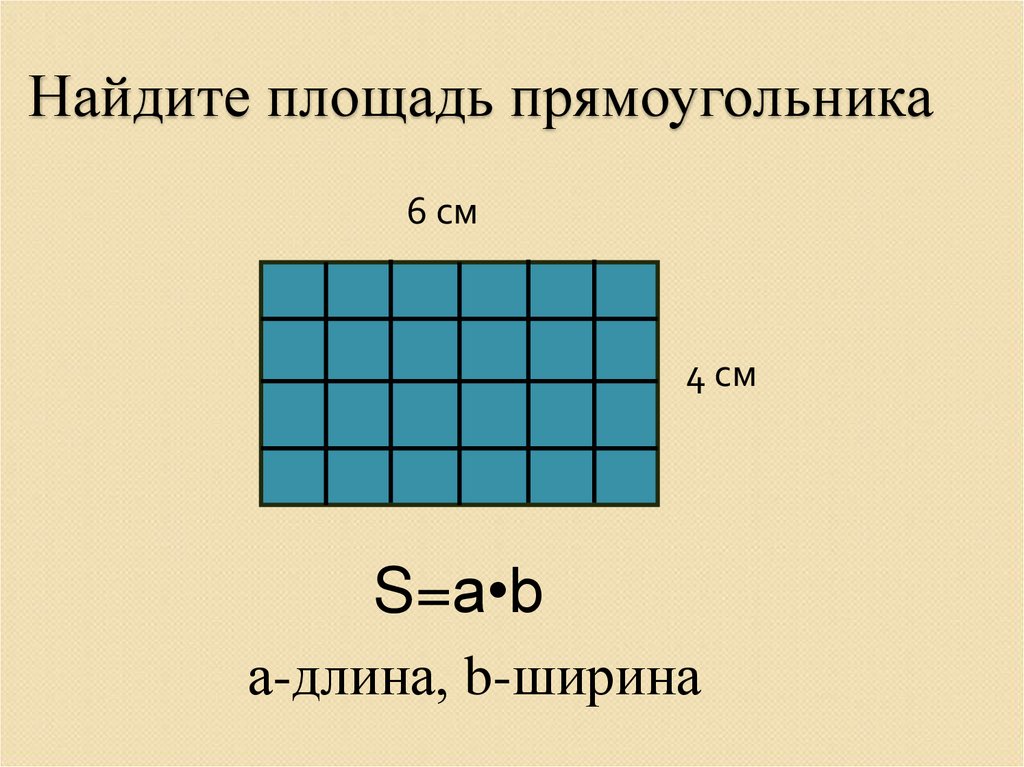

І вимірюється S в квадратних одиницях, таких, як:

Один квадратний міліметр, де S квадрата має сторону, рівну одному міліметру;
Квадратний сантиметр, має S такого квадрата, у якого сторона дорівнює одному сантиметру;
Квадратний дециметр дорівнює S цього квадрата зі стороною в один дециметр;
Квадратний метр має S квадрата, сторона якого дорівнює одному метру;
І нарешті, квадратний кілометр має S квадрата, сторона якого дорівнює одному кілометру.

Для вимірювання площ великих ділянок на поверхні Землі використовують такі одиниці, як:

Один ар або сотка — якщо S квадрата має сторону десять метрів;
Один гектар дорівнює S квадрата, у якого сторона має сто метрів.

Завдання і вправи

А тепер давайте розглянемо кілька прикладів.

На малюнку 62 намальована фігура, яка має вісім квадратів і кожна сторона цих квадратів дорівнює одному сантиметру. Тому S такого квадрата буде квадратний сантиметр.

Якщо записати, то це буде виглядати так:

1 см2. А S все цієї фігури, що складається з восьми квадратів, буде дорівнювати 8 кв.см.

Якщо взяти якусь фігуру і розбити її на «р» квадратів зі стороною, що дорівнює одному сантиметру, то її площа буде дорівнює:

Р см2.

Давайте розглянемо прямокутник, зображень на малюнку 63. Цей прямокутник складається з трьох смуг, а кожна така смужка розбита на п’ять рівних квадратів, що мають сторону в 1 см.

Спробуємо знайти його площу. І так беремо п’ять квадратів, і множимо на три смужки і отримуємо площу рівну 15 кв.см .:

Розглянемо наступний приклад. На малюнку 64 зображено прямокутник ABCD, ламаною лінією KLMN він розбитий на дві частини. Перша його частина дорівнює площі 12 см2, а друга має площу 9 см2. Тепер давайте знайдемо площу всього прямокутника:

Отже, беремо три і множимо на сім і отримуємо 21 кв.см:

3 +7 \u003d 21 кв.см. При цьому 21 \u003d 12 + 9.

І приходимо до висновку, що площа всієї нашої фігури дорівнює сумі площ її окремих частин.

Розглянемо ще один приклад. І так на малюнку 65 зображено прямокутник, який за допомогою відрізка АС розбитий на два рівних трикутника ABC і ADC

А так, як нам уже відомо, що квадрат — це такий же прямокутник, тільки має рівні сторони, то площа кожного трикутника буде дорівнювати половині площі всього прямокутника.

Уявімо, що сторона квадрата дорівнює а, то:

S \u003d a a \u003d a2.

Робимо висновок, що формула площі квадрата матиме такий вигляд:

А запис a2 називається квадратом числа а.

І так, якщо сторона нашого квадрата дорівнює чотирьом сантиметрам, то його площа буде:

4 4, тобто 4 * 2 \u003d 16 кв.см.

Запитання і завдання

Знайдіть площу фігури, яка розбита на шістнадцять квадратів, сторона яких дорівнює одному сантиметру.
Згадайте формулу прямокутника і запишіть її.
Які вимірювання потрібно зробити, щоб дізнатися площа прямокутника?
Дайте визначення рівним фігурам.
Чи можуть мати рівні фігури різні площі? А периметри?
Якщо вам відомі площі окремих частин фігури, як дізнатися її загальну площу?
Сформулюйте і запишіть, чому дорівнює площа квадрата.

Історична довідка

А чи відомо вам, що стародавні люди в Вавилоні вміли розрахувати площа прямокутника. Так само древні єгиптяни робили розрахунки різних фігур, але так як точних формул вони не знали, то обчислення мали невеликі похибки.

У своїй книзі «Начала» знаменитий давньогрецький математик Евклід, описує різні способи обчислення площ різних геометричних фігур.

Урок на тему: «Формули визначення площі трикутника, прямокутника, квадрата»

Додаткові матеріали
Шановні користувачі, не забувайте залишати свої коментарі, відгуки, побажання. Всі матеріали перевірені антивірусною програмою.

Навчальні посібники та тренажери в інтернет-магазині «Інтеграл» для 5 класу
Тренажер до підручника І.І.Зубаревой і А.Г.Мордковіча
Тренажер до підручника Г.В.Дорофеева і Л.Г.Петерсон

Визначення і поняття площі фігури

Щоб краще зрозуміти, що таке площа фігури, розглянемо малюнок.
Ця довільна фігура розбита на 12 маленьких квадратика. Сторона кожного квадратика дорівнює 1 см. А площа кожного квадратика дорівнює 1 квадратного сантиметра, що записується так: 1 см 2.

Тоді площа фігури дорівнює 12 квадратних сантиметрах. В математиці площа позначається латинською буквою S.
Значить, площа нашої фігури дорівнює: S фігури \u003d 12 см 2.

Площа фігури дорівнює площі всіх маленьких квадратиків, з яких вона складається!

Хлопці, запам’ятайте!
Площа вимірюється квадратними одиницями довжини. Одиниці виміру площі:
1. Квадратний кілометр — км 2 (коли площі дуже великі, наприклад, країна або море).
2. Квадратний метр — м 2 (цілком підходить для того, щоб вимірювати площу ділянки або квартири).
3. Квадратний сантиметр — см 2 (зазвичай використовується на уроках математики, коли малюють фігури в зошиті).
4. Квадратний міліметр — мм 2.

Площа трикутника

Розглянемо два види трикутників: прямокутний і довільний.

Щоб знайти площу прямокутного трикутника необхідно знати довжину підстави і висоту. У прямокутному трикутнику висоту замінює одна зі сторін. Тому в формулу площі трикутника замість висоти підставляємо одну зі сторін.
У нашому прикладі сторони рівні 7 см і 4 см. Формула для розрахунку площі трикутника записується так:
S прямокутного трикутника АВС \u003d ВС * СА: 2

S прямокутного трикутника АВС \u003d 7 см * 4 см: 2 \u003d 14 см 2

Тепер розглянемо довільний трикутник.

Для такого трикутника необхідно провести висоту до основи.
У нашому прикладі висота дорівнює 6 см, а основа дорівнює 8 см. Як і в попередньому прикладі, розраховуємо площу за формулою:
S довільного трикутника АВС \u003d ВС * h: 2.

Підставами в формулу наші дані і отримаємо:
S довільного трикутника АВС \u003d 8 см * 6 см: 2 \u003d 24 см 2.

Площа прямокутника і квадрата

Візьмемо прямокутник АВСD зі сторонами 5 см і 8 см.
Формула розрахунку площі прямокутника записується так:
S прямокутника АВСD \u003d АВ * ВС.

S прямокутника АВСD \u003d 8 см * 5 см \u003d 40 см 2.

Тепер розрахуємо площу квадрата. На відміну від прямокутника і трикутника, для знаходження площі квадрата необхідно знати тільки одну сторону. У нашому прикладі сторона квадрата ABCD дорівнює 9 см. S квадрата АВСD \u003d АВ * НД \u003d АВ 2.

Підставами в формулу наші дані і отримаємо:
S квадрата АВСD \u003d 9 см * 9 см \u003d 81 см 2.

Площа геометричної фігури — чисельна характеристика геометричної фігури показує розмір цієї фігури (частини поверхні, обмеженої замкнутим контуром даної фігури). Величина площі виражається числом полягають в неї квадратних одиниць.

Формули площі трикутника

1. Формула площі трикутника по стороні і висоті
   Площа трикутника дорівнює половині твори довжини сторони трикутника на довжину проведеної до цієї сторони висоти
   
2. Формула площі трикутника за трьома сторонами і радіусу описаного кола
   
3. Формула площі трикутника за трьома сторонами і радіусу вписаного кола
   Площа трикутника дорівнює добутку напівпериметр трикутника на радіус вписаного кола.
   
де S — площа трикутника,
— довжини сторін трикутника,
— висота трикутника,
— кут між сторонами і,
— радіус вписаного кола,
R — радіус описаного кола,

Формули площі квадрата

1. Формула площі квадрата по довжині боку
   Площа квадрата дорівнює квадрату довжини його сторони.
2. Формула площі квадрата по довжині діагоналі
   Площа квадрата дорівнює половині квадрата довжини його діагоналі.
   

   S \u003d	1	2
   	2

де S — Площа квадрата,
— довжина сторони квадрата,
— довжина діагоналі квадрата.

Формула площі прямокутника

Площа прямокутника дорівнює добутку довжин двох його суміжних сторін

де S — Площа прямокутника,
— довжини сторін прямокутника.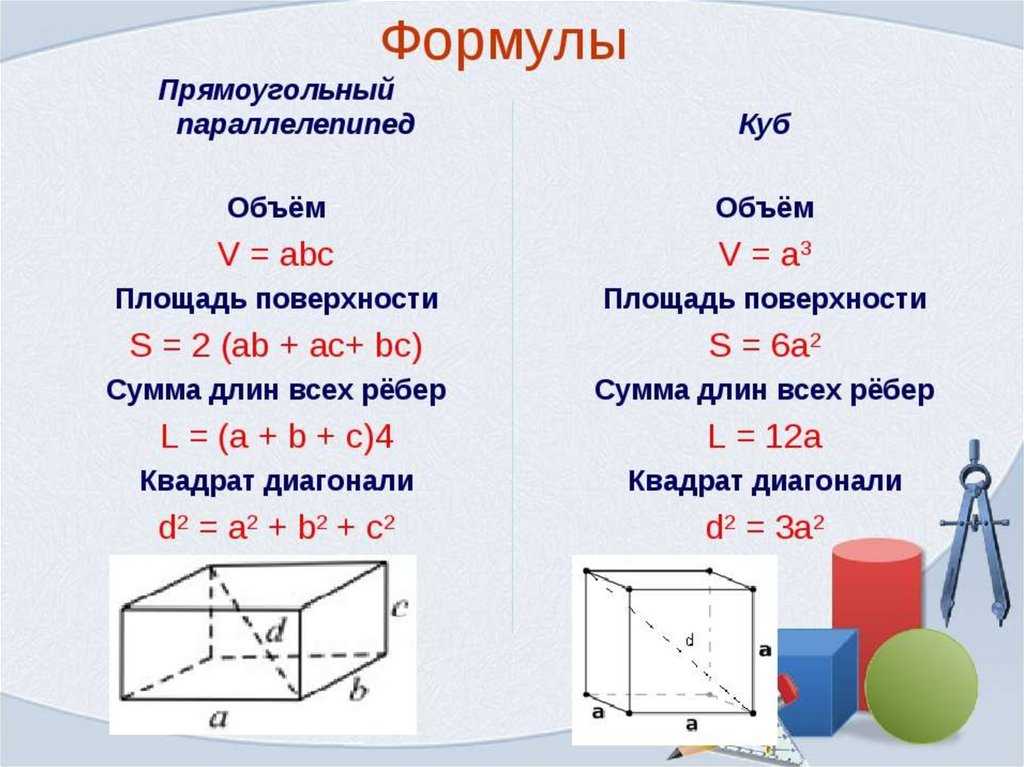

Формули площі паралелограма

1. Формула площі паралелограма по довжині боку і висоті
   Площа паралелограма
2. Формула площі паралелограма за двома сторонами і кутом між ними
   Площа паралелограма дорівнює добутку довжин його сторін помноженому на синус кута між ними.

   a · b · sin α

де S — Площа паралелограма,
— довжини сторін паралелограма,
— довжина висоти паралелограма,
— кут між сторонами паралелограма.

Формули площі ромба

1. Формула площі ромба по довжині боку і висоті
   Площа ромба дорівнює добутку довжини його сторони і довжини опущеною на цю сторону висоти.
2. Формула площі ромба по довжині боку і розі
   Площа ромба дорівнює добутку квадрата довжини його сторони і синуса кута між сторонами ромба.
3. Формула площі ромба по довжинах його діагоналей
   Площа ромба дорівнює половині добутку довжин його діагоналей.
де S — Площа ромба,
— довжина сторони ромба,
— довжина висоти ромба,
— кут між сторонами ромба,
1, 2 — довжини діагоналей.

Формули площі трапеції

1. Формула Герона для трапеції

   Де S — Площа трапеції,
   — довжини основ трапеції,
   — довжини бічних сторін трапеції,
   

Площа основи прямокутного трикутника. Як знайти площу прямокутного трикутника незвичайним способом

Трикутник – плоска геометрична фігура з одним кутом, рівним 90°. При цьому в геометрії дуже часто потрібно обчислити площу такої фігури. Як це зробити, ми розповімо далі.

Найпростіша формула визначення площі прямокутного трикутника

Вихідні дані, де: a та b – сторони трикутника, що виходять із прямого кута.

Тобто площа дорівнює половині твору двох сторін, які виходять із прямого кута. Звичайно, існує формула Герона, яка використовується для обчислення площі звичайного трикутника, але для визначення величини необхідно знати довжину трьох сторін. Відповідно, вам доведеться розрахувати гіпотенузу, а це зайвий час.

Знайти площу прямокутного трикутника через формулу Герона

Це всім відома та вихідна формула, але для цього вам доведеться порахувати гіпотенузу за двома катетами, використовуючи Теорему Піфагора.

У цій формулі: a, b, c – сторони трикутника, а p – напівпериметр.

Знайти площу прямокутного трикутника з гіпотенузи та кута

Якщо у вашому завданні не відомий жоден з катетів, то скористатися самим простим способомви не зможете. Для визначення величини потрібно розрахувати довжину катетів. Це зробити просто з гіпотенузи та косінусу прилеглого кута.

b=c×cos(α)

Дізнавшись довжину одного з катетів, за теоремою Піфагора ви зможете розрахувати другий бік, що виходить із прямого кута.

b 2 =c 2 -a 2

У цій формулі c і a – гіпотенуза та катет відповідно. Тепер можете розрахувати площу за першою формулою. Так само можна обчислити один з катетів, маючи другий і кут. У такому разі одна з шуканих сторін дорівнюватиме добутку катета на тангенс кута. Існують і інші способи обчислення площі, але знаючи основні теореми та правила, ви зможете легко знайти потрібну величину.

Якщо у вас немає жодної зі сторін трикутника, а є лише медіана та один із кутів, то ви зможете обчислити довжину сторін. Для цього використовуйте властивості медіани ділити прямокутний трикутник на два. Відповідно, вона може бути гіпотенузою, якщо виходить з гострого кута. Скористайтеся теоремою Піфагора та визначте довжину сторін трикутника, що виходять із прямого кута.

Як бачите, знаючи основні формули та Теорему Піфагора, ви зможете розрахувати площу прямокутного трикутникамаючи лише один з кутів та довжину однієї зі сторін.

На уроках геометрії в середній школіусім нам говорили про те, що трикутник. Однак у рамках шкільної програмими отримуємо тільки найнеобхідніші знання та вчимося найпоширенішим та стандартним способамобчислень. Чи існують незвичайні засоби знаходження цієї величини?

Як запровадження згадаємо, який трикутник вважається прямокутним, і навіть позначимо поняття площі.

Прямокутним трикутником називають замкнуту геометричну фігуру, один із кутів якої дорівнює 90 0 . Невід’ємними поняттями у визначенні є катети та гіпотенуза. Під катетами мають на увазі дві сторони, які у точці з’єднання утворюють прямий кут. Гіпотенуза – сторона, протилежна прямому куту. Прямий трикутник може бути рівнобедреним (дві його сторони матимуть однакову величину), але ніколи не буде рівностороннім (всі сторони однієї довжини). Визначення висоти, медіани, векторів та інших математичних термінів докладно не розбиратимемо. Їх легко знайти у довідниках.

Площа прямого трикутника. На відміну від прямокутників, правило про

творі сторін у визначенні діє. Якщо говорити сухою мовою термінів, то під площею трикутника розуміють властивість цієї фігури займати частину площини, виражену числом. Досить складно до сприйняття, погодьтеся. Не намагатимемося глибоко вникнути у визначення, наша мета не в цьому. Перейдемо до головного – як знайти площу прямокутного трикутника? Самі обчислення робити не будемо, зазначимо лише формули. Для цього визначимося з позначеннями: A, B, C – сторони трикутника, катети – AB, BC. Кут ACB – прямий. S – площа трикутника, h n n – висота трикутника, де nn – сторона, на яку вона опущена.

Спосіб 1. Як знайти площу прямокутного трикутника, якщо відома величина його катетів

Спосіб 2. Знаходимо площу рівнобедреного прямокутного трикутника

Спосіб 3. Обчислення площі через прямокутник

Добудовуємо прямокутний трикутник до квадрата (якщо трикутник

рівнобедрений) або прямокутника. Отримаємо простий чотирикутник, що складається з 2-х ідентичних прямокутних трикутників. У цьому випадку значення площі одного з них дорівнює половині площі отриманої фігури. S прямокутника обчислюємо добутком сторін. Позначимо цю величину M. Шукане значення площі дорівнює половині M.

Спосіб 4. «Піфагорові штани». Знаменита теорема Піфагора

Ми всі пам’ятаємо її формулювання: «Сума квадратів катетів …». Але не всі можуть

сказати, причому тут деякі «штани». Справа в тому, що спочатку Піфагор вивчав взаємозв’язок побудованих на сторонах прямого трикутника. Виявивши закономірності у співвідношенні сторін квадратів, він зміг вивести і відому нам формулу. Її можна застосовувати у разі, коли невідома величина однієї із сторін.

Спосіб 5. Як знайти площу прямокутного трикутника за формулою Герона

Також досить простий спосіб розрахунку. Формула передбачає вираження площі трикутника через числові значенняйого сторін. Для розрахунків потрібно знати величини всіх сторін трикутника.

S = (p-AC) * (p-BC), де p = (AB + BC + AC) * 0.5

Крім наведених, існує безліч інших способів знайти величину такої загадкової фігури, як трикутник. Серед них: обчислення методом вписаного або описаного кола, обчислення за допомогою координат вершин, використання векторів абсолютної величини, синусів, тангенсів.

Прямокутним трикутником називається трикутник, у якого один із кутів дорівнює 90°. Його площу можна знайти, якщо відомі два катети. Можна, звичайно, піти і довгим шляхом — знайти гіпотенузу і прорахувати площу, але в більшості випадків це тільки займе зайвий час. Саме тому формула площі прямокутного трикутника має такий вигляд:

Площа прямокутного трикутника дорівнює половині добутку катетів.

Приклад розрахунку площі прямокутного трикутника.
Даний прямокутний трикутник із катетами a= 8 см, b= 6 див.
Обчислюємо площу:
Площа дорівнює: 24 см 2

Також у прямокутному трикутнику застосовується теорема Піфагора. — Сума квадратів двох катетів дорівнює квадрату гіпотенузи.
Формула площі рівнобедреного прямокутного трикутника обчислюється як і звичайного прямокутного трикутника.

Приклад розрахунку площі рівнобедреного прямокутного трикутника:
Даний трикутник із катетами a= 4 см, b= 4 см. Обчислюємо площу:
Обчислюємо площу:=8 см 2

Формула площі прямокутного трикутника з гіпотенузи може використовуватися, якщо за умови дано один катет. З теореми Піфагора знаходимо довжину невідомого катета. Наприклад, дана гіпотенуза cта катет a, катет bбуде дорівнює:
Далі обчислюємо площу за звичайною формулою. Приклад розрахунку формули площі прямокутного трикутника з гіпотенузи ідентичний описаному вище.

Розглянемо цікаве завдання, яке допоможе закріпити знання формул на вирішення трикутника.
Завдання: площа прямокутного трикутника дорівнює 180 кв. див. знайдіть менший катет трикутника, якщо він менший за другий на 31 см.
Рішення: позначимо катети aі b. Тепер підставимо дані у формулу площі:, ще ми знаємо, що один катет менший за інший a – b= 31 см
З першої умови отримуємо, що
Підставляємо цю умову в друге рівняння:

Оскільки ми знаходили сторони, то знак мінус прибираємо.
Виходить, що катет a= 40 см, а b= 9 див.

Площадь прямоугольника – формула, определение, примеры

Площадь любой фигуры – это количество единичных квадратов, которые могут в нее поместиться. Здесь «единица» относится к единице (1), а единичный квадрат — это квадрат со стороной, равной 1 единице. Итак, площади прямоугольника — это количество единичных квадратов в пределах границы прямоугольника. В качестве альтернативы пространство, занимаемое внутри периметра этой фигуры, называется площадью прямоугольника. Хорошим примером прямоугольной формы являются плитки единичной длины в вашем доме. Вы можете легко определить, сколько места занимает пол, посчитав количество плитки. Это также поможет вам определить площадь прямоугольного пола.

1.	Что такое площадь прямоугольника?
2.	Площадь прямоугольника Формула
3.	Как рассчитать площадь прямоугольника?
4.	Площадь прямоугольника по диагонали
5.	Почему площадь прямоугольника равна длине × ширине?
6.	Часто задаваемые вопросы о площади прямоугольника

Что такое площадь прямоугольника?

Площадь можно определить как площадь, занимаемую плоской поверхностью определенной формы. Она измеряется с точки зрения «количества» квадратных единиц (квадратные сантиметры, квадратные дюймы, квадратные футы и т. д.). Площадь прямоугольника — это количество единичных квадратов, которые могут вписаться в прямоугольник. Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов ноутбуков, школьных досок, холста для рисования и т. д. Вы можете использовать формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами. Например, давайте рассмотрим прямоугольник длиной 4 дюйма и шириной 3 дюйма.

Площадь прямоугольника Определение

Площадь, занимаемая прямоугольником внутри его границ, называется площадью прямоугольника.

Нарисуем единичные квадраты внутри прямоугольника. Каждый единичный квадрат представляет собой квадрат длиной 1 дюйм.

Теперь подсчитайте количество единичных квадратов на приведенном выше рисунке. Сколько квадратов вы можете наблюдать? Всего 12 квадратов. Мы уже знаем, что площадь измеряется в квадратных единицах. Поскольку единицей измерения этого прямоугольника являются «дюймы», площадь измеряется и записывается в квадратных дюймах. Таким образом, площадь вышеуказанного прямоугольника = 12 квадратных дюймов.

Площадь прямоугольника Формула

Формула площади прямоугольника используется для нахождения площади, занимаемой прямоугольником внутри его границ. В приведенном выше примере площадь прямоугольника, длина которого составляет 4 дюйма, а ширина — 3 дюйма, составляет 12 квадратных дюймов. У нас есть 4 × 3 = 12. Площадь прямоугольника получается путем умножения его длины и ширины. Таким образом, формула площади «A» прямоугольника, длина и ширина которого равны «l» и «w» соответственно, представляет собой произведение » Д × Ш «.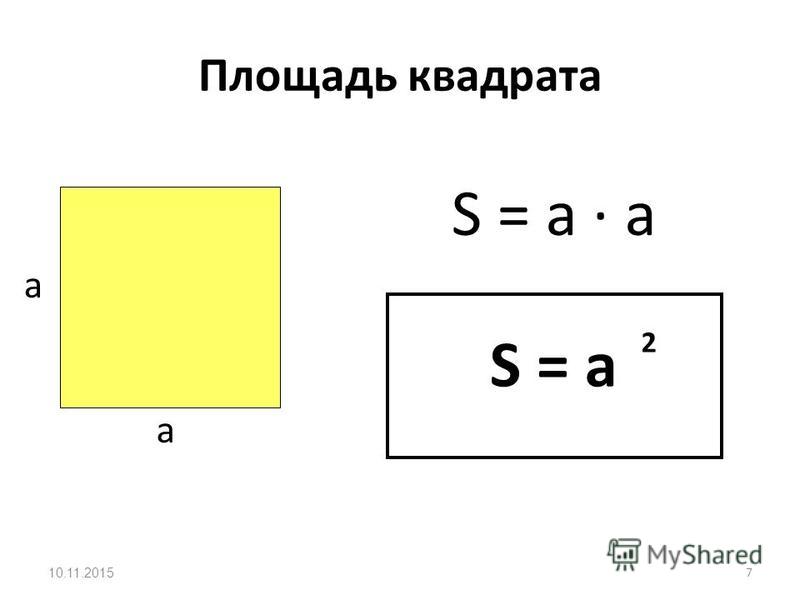

Площадь прямоугольника = (длина × ширина) квадратных единиц

Как рассчитать площадь прямоугольника?

Площадь прямоугольника равна произведению его длины на ширину. Выполните шаги, указанные ниже, чтобы найти площадь прямоугольника:

• Шаг 1: Обратите внимание на размеры длины и ширины из заданных данных.
• Шаг 2: Найдите произведение значений длины и ширины.
• Шаг 3: Дайте ответ в квадратных единицах.

Давайте рассмотрим пример, чтобы понять вычисление площади прямоугольника. Найдем площадь прямоугольника, длина которого 15 единиц, а ширина 4 единицы. Чтобы найти площадь, сначала найдите длину и ширину.

Дано, длина = 15 единиц и ширина = 4 единицы.

Формула для нахождения площади прямоугольника: A = l × w. Подставьте 15 вместо «l» и 4 вместо «w» в этой формуле. Отсюда следует, что площадь прямоугольника = 15 × 4 = 60,

Следовательно, площадь прямоугольника = 60 квадратных единиц.

Площадь прямоугольника по диагонали

Диагональ прямоугольника — это прямая линия внутри прямоугольника, соединяющая его противоположные вершины. В прямоугольнике две диагонали и обе имеют одинаковую длину. Мы можем найти диагональ прямоугольника, используя теорему Пифагора.

(Диагональ) ² = (Длина) ² + (Ширина) ²

(Длина) ² = (Диагональ) ² — (Ширина) ²

Длина = ⎷(Диагональ) ² — (Ширина) ²

Теперь длина прямоугольника равна площади прямоугольника. × Ширина. В качестве альтернативы мы можем записать эту формулу как ⎷((Диагональ) ² — (Ширина) ² ) × Ширина.

Итак, площадь прямоугольника = ширина (⎷(Диагональ) ² — (Ширина) ² ).

Почему площадь прямоугольника равна длине × ширине?

Вы когда-нибудь задумывались, почему формула для нахождения площади прямоугольника — это длина × ширина? Выведем формулу площади прямоугольника.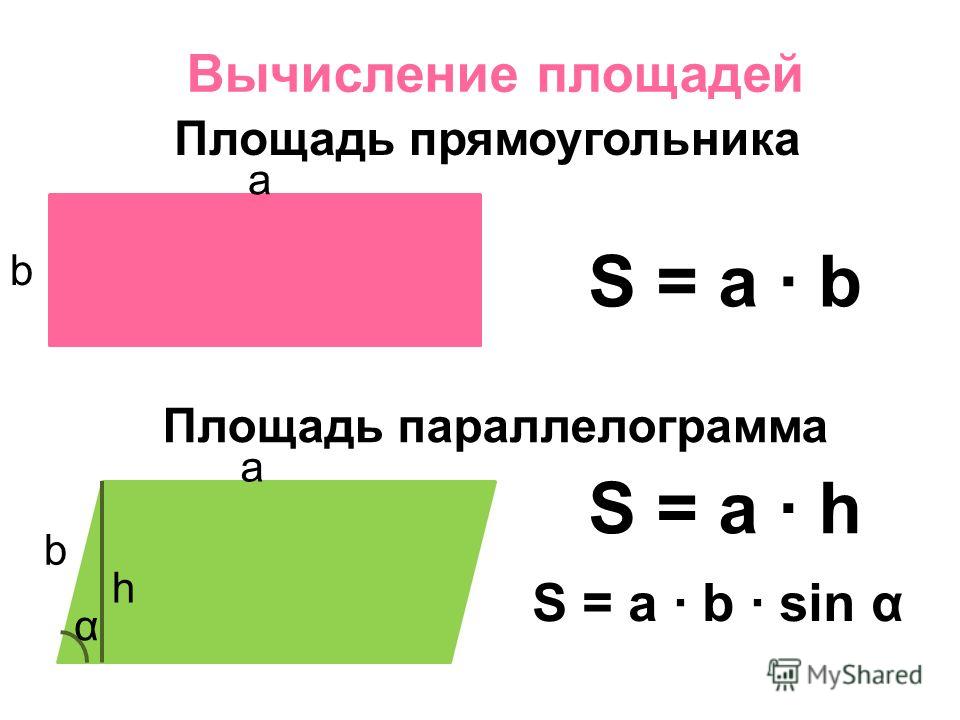 В прямоугольнике ABCD проведем диагональ AC. Ясно, что диагональ AC делит прямоугольник ABCD на два равных треугольника. Площадь прямоугольника равна сумме площадей этих двух треугольников.

Площадь прямоугольника ABCD = площадь треугольника ABC + площадь треугольника ADC

= 2 × площадь треугольника ABC

= 2 × (1/2 × основание × высота)

= AB × BC

= длина × ширина

 

Примеры площади прямоугольника

1. Пример 1: Длина и ширина прямоугольной фермы равны 80 ярдам и 60 ярдам. Найдите площадь фермы.

   Решение:

   Длина фермы l = 80 ярдов и ширина фермы w = 60 ярдов

   Площадь фермы A: A = l × w

   = 80 ярдов × 60 ярдов0005

   = 4800 квадратных метров

   Следовательно, площадь фермы составляет 4800 квадратных метров.

2. Пример 2:

   Питер читает свой любимый комикс в своем кабинете. Сможете ли вы найти площадь обложки книги, длина которой равна \(3 \dfrac{1}{4} \) дюйма, а ширина — \(1 \dfrac{1}{2}\) дюйма?

   Решение

   Длина книги, l = \(3\dfrac{1}{4}\) дюймов

   Ширина книги, b = \(1\dfrac{1}{2}\) дюймов

   Площадь прямоугольника A

   A = l × b
   = \(3 \dfrac{1}{4}\) × \(1 \dfrac{1}{2}\)
   = \(\dfrac{13}{4} × \dfrac{3}{2}\)
   = \(\dfrac{39}{8}\)
   = \(4\dfrac{7}{8}\) in ²

   Итак, площадь книги равна \({4 \dfrac{7}{8}}\) квадратных дюймов.

перейти к слайдуперейти к слайду

У вас есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по площади прямоугольника

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о площади прямоугольника

Какова площадь прямоугольника в геометрии?

Площадь пространства, занимаемого периметром прямоугольника, называется площадью прямоугольника. Он вычисляется путем нахождения произведения длины и ширины прямоугольника.

Что такое периметр и площадь прямоугольника?

Периметр прямоугольника равен сумме его четырех сторон. Следовательно, периметр прямоугольника = 2 (длина + ширина) единиц. Площадь прямоугольника определяется как произведение длины на ширину. Выражается в квадратных единицах.

Какая формула площади прямоугольника?

Площадь прямоугольника (А) равна произведению его длины «а» и ширины или ширины «b». Итак, площадь прямоугольника = (a × b) квадратных единиц.

Какова единица площади прямоугольника?

Единицей площади прямоугольника являются квадратные единицы. Например, если размеры прямоугольника 4 дюйма × 3 дюйма. Площадь прямоугольника 12 квадратных дюймов.

Почему мы вычисляем площадь прямоугольника?

Мы вычисляем площадь прямоугольника, чтобы найти площадь, занимаемую прямоугольником внутри его периметра.

Как найти площадь прямоугольника, используя его диагональ?

Мы можем найти диагональ прямоугольника, используя теорему Пифагора: (Диагональ) ² = (Длина) ² + (Ширина) ² . Теперь формула для вычисления площади прямоугольника: Длина × Ширина. В качестве альтернативы мы можем записать эту формулу как (⎷(Диагональ) ² — (Ширина) ² ) × Ширина.

Площадь прямоугольника равна площади квадрата?

Нет, площадь квадрата не обязательно равна площади прямоугольника, потому что каждый квадрат является прямоугольником с одинаковой длиной и шириной, но не все прямоугольники квадратные. Формула для вычисления площади прямоугольника: длина × ширина, а площадь квадрата — (сторона) 9.0115 2 .

Что такое прямоугольник?

Прямоугольник – это замкнутая двумерная фигура с четырьмя сторонами, где противоположные стороны равны и параллельны друг другу. У прямоугольника все углы равны 90°.

Как найти площадь прямоугольника

Все ресурсы по базовой геометрии

9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущий 1 2 3 4 5 6 7 8 9 10 11 Далее →

Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как найти площадь прямоугольника

Периметр прямоугольника равен . Длина на десять метров больше ширины. Чему равна площадь прямоугольника?

Возможные ответы:

Правильный ответ:

Объяснение:

Для прямоугольника общее уравнение для периметра и площади: где длина, а ширина.

Пусть = ширина и = длина

Итак, уравнение для решения становится таким образом, что ширина равна, а длина равна .

Таким образом, площадь равна

Сообщить об ошибке

Какой из следующих данных , а не будет достаточно, чтобы найти площадь прямоугольника?

Возможные ответы:

Длины одной пары противоположных сторон.

Длины одной стороны и диагонали.

Периметр и длина одной стороны.

Длины одной пары смежных сторон.

Все остальные варианты перечисляют информацию, которой будет достаточно.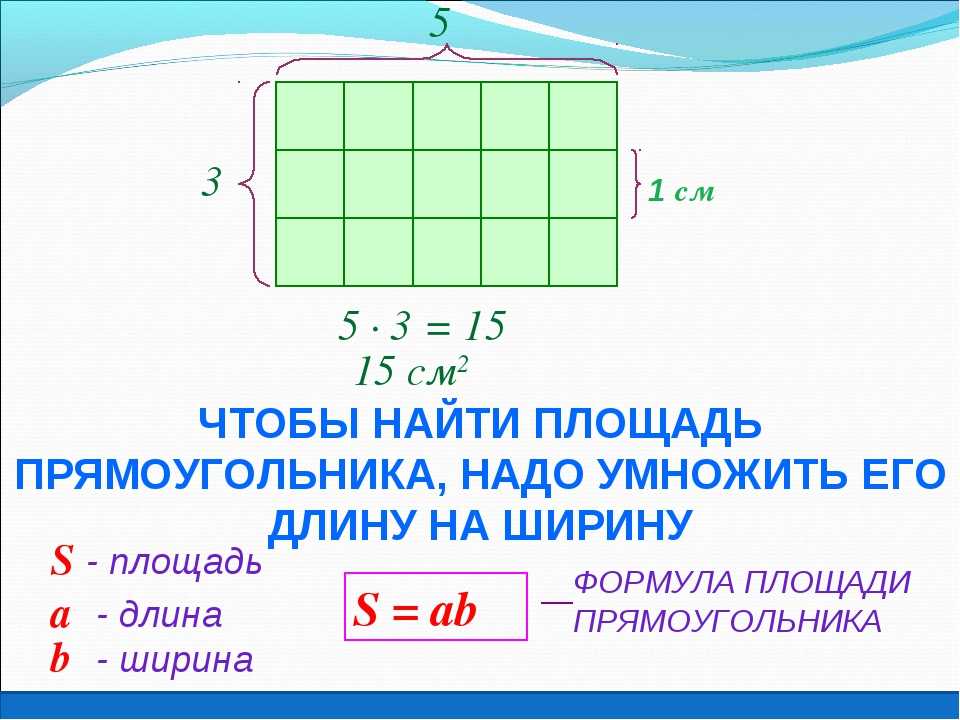

Правильный ответ:

Длины одной пары противоположных сторон.

Объяснение:

Площадь прямоугольника можно вычислить, умножив длины двух соседних сторон. Все приведенные варианты содержат достаточную информацию, за одним исключением. Мы изучаем каждый из вариантов.

Длины одной пары смежных сторон: Этот выбор неверен, как прямо указано выше.

Периметр и длина одной стороны: Используя формулу периметра, вы можете найти длину соседней стороны, что делает этот выбор неверным.

Длины одной стороны и диагонали: используя теорему Пифагора, вы можете найти длину соседней стороны, что делает этот выбор неверным.

Длины одной пары противоположных сторон: это не дает вам возможности узнать длины смежных сторон. Это правильный выбор.

Сообщить об ошибке

Найдите площадь многоугольника.

Возможные ответы:

Правильный ответ:

Объяснение:

Проведение вертикальной линии в конце стороны длины  делит фигуру на прямоугольник и прямоугольный треугольник.

Сумма площадей двух фигур составляет площадь многоугольника. Умножьте длину прямоугольника на его ширину, чтобы найти площадь прямоугольника, и используйте формулу, где – основание, а – высота треугольника, чтобы найти площадь треугольника. Сложение их вместе дает ответ.

Сообщить об ошибке

Одна сторона прямоугольника 7 дюймов, а другая 9 дюймов. Чему равна площадь прямоугольника в дюймах?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь прямоугольника, умножьте его ширину на высоту. Если мы знаем две стороны прямоугольника разной длины, то у нас есть и высота, и ширина.

Сообщить об ошибке

Какова площадь прямоугольника на диаграмме?

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь прямоугольника находится путем умножения длины на ширину.

Длина 12 см, ширина 7 см.

Следовательно, площадь 84 см ² .

Сообщить об ошибке

Какова площадь прямоугольника, длина и ширина которого равны дюймам и дюймам соответственно?

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь любого прямоугольника с длиной и шириной:

Сообщить об ошибке

Какова площадь прямоугольника, имеющего длину  и ширину  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните, как найти площадь прямоугольника:

Теперь подставьте данные длину и ширину, чтобы найти площадь.

Сообщить об ошибке

Какова площадь прямоугольника, имеющего длину  и ширину ?

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните, как найти площадь прямоугольника:

Теперь подставьте данные длину и ширину, чтобы найти площадь.

Сообщить об ошибке

Какова площадь прямоугольника, имеющего длину  и ширину ?

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните, как найти площадь прямоугольника:

Теперь подставьте данные длину и ширину, чтобы найти площадь.

Сообщить об ошибке

Какова площадь прямоугольника, имеющего длину  и ширину ?

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните, как найти площадь прямоугольника:

Теперь подставьте данные длину и ширину, чтобы найти площадь.

Сообщить об ошибке

← Предыдущий 1 2 3 4 5 6 7 8 910 11 Далее →

Уведомление об авторских правах

Все ресурсы по базовой геометрии

9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции

Как найти площадь прямоугольника?

Площадь прямоугольника — один из самых важных и популярных параметров прямоугольника. В этой статье мы рассмотрим основные теории и математические формулы, связанные с площадью прямоугольника, например, площадь прямоугольника, формулу площади прямоугольника и ее применение в повседневной жизни.

Все ли мы знаем, что такое прямоугольник? Во-первых, давайте разберемся с некоторыми фундаментальными понятиями, связанными с прямоугольником. Прямоугольник — это замкнутая фигура, состоящая из 4 сторон, как и квадрат. Но, в отличие от квадрата, у прямоугольника не все стороны равны. Прямоугольник – это четырехсторонняя фигура, у которой противоположные стороны равны. Чтобы понять это, см. рисунок ниже:

Вы можете видеть, что сторона, отмеченная как A, противоположна стороне, отмеченной как C, и равна стороне, отмеченной как C. Точно так же сторона, отмеченная как B, равна и противоположна стороне, отмеченной как D. Следовательно, ABCD — прямоугольник.

«Вы также можете заметить, что квадрат — это частный случай прямоугольников, у которых все противоположные стороны равны».

В повседневной жизни мы можем встретить прямоугольники повсюду. Блокноты, на которых вы пишете книги, которые вы изучаете, представляют собой прямоугольники. Некоторыми прекрасными примерами прямоугольных форм являются плитка, установленная в вашем доме, школьная доска, которую учитель использует в школе, обеденный стол, форма вашего телевизионного экрана и многое другое.

Давайте теперь изучим некоторые математические термины и понятия, связанные с прямоугольником:

• У прямоугольника только противоположные стороны равны. Две смежные стороны никогда не бывают равными в случае прямоугольника.
• Прямоугольник является параллелограммом. Это означает, что противоположные стороны прямоугольника параллельны друг другу или противоположные стороны никогда не пересекаются.
• Диагональ прямоугольника делит его на два равновеликих треугольника.
• Периметр прямоугольника: Расстояние, пройденное границей прямоугольника, называется периметром прямоугольника. Это математически формулируется как

P (прямоугольник) = 2 (длина + ширина)

Теперь, когда мы хорошо разобрались с основами прямоугольника, давайте узнаем площадь прямоугольника и формулу площади прямоугольника.

Какова площадь прямоугольника?

Прежде чем углубляться в площадь прямоугольника, все ли мы знакомы с тем, что означает «площадь»? Площадь определяется как пространство, заметаемое или покрываемое любой замкнутой фигурой. Пространство, находящееся внутри границы любой фигуры, называется площадью этой фигуры. Исходя из этого, мы можем сказать, что пространство, заметаемое или покрываемое прямоугольником, известно как площадь прямоугольника. Другими словами, двумерное пространство внутри периметра прямоугольника является его площадью. См. рисунок, приведенный ниже. Красная линия указывает на границу прямоугольника, а желтая закрытая заполненная область — это площадь прямоугольника.

Далее в этой статье мы увидим формулу площади прямоугольника. Используя эту формулу, вы даже можете определить площадь пола вашего дома, площадь экрана вашего компьютера или мобильного телефона и т. д.

Как найти площадь прямоугольника?

Количество единичных квадратов, которые идеально помещаются внутри прямоугольника, дает площадь этого прямоугольника. Вы могли запутаться с этим определением, не так ли? Не волнуйся; давайте проясним это для вас.

Например, давайте сделаем прямоугольник с длиной = 2 см и шириной = 3 см. Попробуем теперь поместить внутри этого прямоугольника квадраты длины 1 единица.

«Длина блока: 1 известна как длина блока. Единицами измерения могут быть см, дюймы, м, футы и т. д. , но помните, что всякий раз, когда пишется единица измерения длины, всегда понимайте ее как 1».

Таким образом, квадраты единичной длины означают, что длина каждой стороны квадрата равна единице. Как мы видим на рисунке ниже, 6 квадратов единичной длины могут легко поместиться внутри этого прямоугольника, поэтому мы можем сказать, что площадь прямоугольника равна 6 единицам. Также мы знаем, что стороны прямоугольника в см; следовательно, площадь прямоугольника изменится с 6 единиц на 6 см.

Мы завершили все концептуальные занятия в области прямоугольника. Далее изучим и выведем формулу площади прямоугольника.

Формула площади прямоугольника

Формула, которую мы сейчас выучим, является одной из самых простых формул в математике. Несмотря на простоту, это одна из самых мощных формул. По этой формуле площадь была найдена только от таблицы, которую вы изучаете, до комнаты, в которой вы живете. 

Площадь прямоугольной формулы дается как:

Площадь = длина x ширина или длина x дыхание

Произведение длины и ширины прямоугольника дает нам формулу площади этого прямоугольника. Пусть длина прямоугольника равна «а», а дыхание — «b»; поэтому площадь «А» записывается как 

A = a x b (квадратные единицы)

Пример: Длина прямоугольной крыши 12 м, а ширина 7 м. Найдите площадь дерева, которой можно было бы покрыть всю крышу?

Решение: Удача длины ‘a’ = 12

ширина ‘b’ = 7

Область дерева, необходимая для покрытия всей крыши = площадь крыши

A (крыша) = A x B

= 12 x 7

= 84 м ²

Теперь, когда мы узнали, что такое формула площади прямоугольника, давайте научимся ее вычислять.

Как вычислить площадь прямоугольника?

Шаги по вычислению площади прямоугольника приведены ниже. Если вы правильно выполните эти шаги, вы никогда не получите ошибок в своих решениях.

Шаг 1: Запишите размеры данного прямоугольника из вопросов.

Шаг 2: Поместите значения в область формулы прямоугольника, т. е. длину x ширину.

Шаг 3: Умножьте значения и получите произведение.

Шаг 4: Запишите результат в квадратных единицах

Чтобы лучше понять, как вычислить площадь прямоугольника, рассмотрим следующий пример. Вычислим площадь прямоугольника длиной 20 единиц и шириной 5 единиц.

Шаг 1: Длина прямоугольника = 20 единиц, ширина прямоугольника = 5 единиц

Шаг 2: Формула площади прямоугольника = длина x ширина 100

Шаг 4: Площадь прямоугольника 100 квадратных единиц.

Доказательство площади прямоугольника?

На протяжении всей статьи мы вычисляли площадь прямоугольника как «длина × ширина». Но когда-нибудь задумывались, почему это формула? В этом разделе выведем формулу площади прямоугольника.

См. рисунок ниже. Мы видим прямоугольник KLMN с диагональю KM. Эта диагональ разделила прямоугольник на два равновеликих треугольника. Следовательно, площадь прямоугольника = 2 х площадь 1 треугольника.

Возьмем треугольник KMN. Основание KN треугольника — это длина прямоугольника, скажем, «а», а MN ширина прямоугольника — это высота треугольника, скажем, «b». Так как KMN является прямоугольным треугольником (поскольку смежные стороны прямоугольника перпендикулярны друг другу)

Мы знаем, что площадь треугольника = ½ x основание x высота 

Следовательно, площадь KMN = ½ x a x b

Также , площадь прямоугольника = 2 x (площадь KMN)

                                                  = 2 x ½ x a x b

                                         = a x b 

Отсюда доказано, что площадь прямоугольника всегда равна его длине x ширине.

Предположим теперь, что нам не известны размеры длины какого-либо прямоугольника; вместо этого нам дана длина любой из диагоналей и ширина. Как узнать площадь? Узнаем в следующем разделе этой статьи.

Площадь прямоугольника по диагонали

Как упоминалось ранее, диагональ делит прямоугольник на два прямоугольных треугольника. Мы воспользуемся теоремой Пифагора, чтобы найти формулу для нахождения площади прямоугольника с помощью диагоналей.

Согласно теореме Пифагора:

(Гипотенуза) ² = (Основание) ² + (Перпендикулярная высота) ²

В этом случае:

а ширина будет ‘b’.

(диагональ) ² = (длина) ² + (ширина) ²

(D) ² = (L) ² + (b) ²

(l) + (b) ²

(l) 2 = (г) ² – (б) ²

л = √(г) ² — (b) ²

Заменить значение L в основной формуле

Площадь прямоугольника = L x B

= {(D) ² — (b) ² } x B

Таким образом, площадь прямоугольника при заданных длине одной диагонали и размере ширины равна {(d) ² – (b) ² } x b = {(Диагональ) ² – (Ширина) ² } x Breadth 

Таким образом, вы можете использовать любой из методов, чтобы найти площадь прямоугольника, в зависимости от предоставленных вам данных.

Часто задаваемые вопросы

1. Какова площадь прямоугольника в геометрии?

Ответ. Площадь прямоугольника — это простая формула, с помощью которой можно найти площадь прямоугольника. Он использует длину и ширину прямоугольника, которые являются его сторонами.

2. Какая формула площади прямоугольника?

Ответ. Формула площади прямоугольника: A = l * w, где l — длина, а w — ширина.

3. Какова единица площади прямоугольника?

Ответ. Единицей площади прямоугольника являются квадратные метры.

4. Почему мы вычисляем площадь прямоугольника?

Ответ. Площадь прямоугольника вычисляется путем умножения ширины прямоугольника на его длину.

5. Как найти площадь прямоугольника, используя его диагональ?

Ответ. Вы можете найти площадь прямоугольника, используя его диагональ. Просто разделите количество квадратных единиц на количество диагональных единиц. Например, 4×5 имеет площадь 20 и диагональ 10, поэтому мы разделим 20 на 10, чтобы получить 2, что и является нашим ответом.

Площадь прямоугольника (примеры вопросов)

Вычисление площади поверхности — это навык, который можно применять во многих реальных ситуациях. Вычисления площади выполняются для таких сценариев, как определение количества плитки, необходимой для покрытия дна бассейна, количества оберточной бумаги, необходимой для упаковки подарка, или площади вашего заднего двора. Подобные ситуации потребуют использования расчетов площади поверхности.

Площадь прямоугольника Примеры вопросов

При определении площади прямоугольника можно применить формулу \(A=l\×w\). A представляет площадь, l представляет длину, а w представляет ширину. Например, прямоугольник ниже имеет длину 32 метра и ширину 20 метров. Площадь прямоугольника можно вычислить путем умножения \(l\times w\) или \(32\times20\), что равно 6400.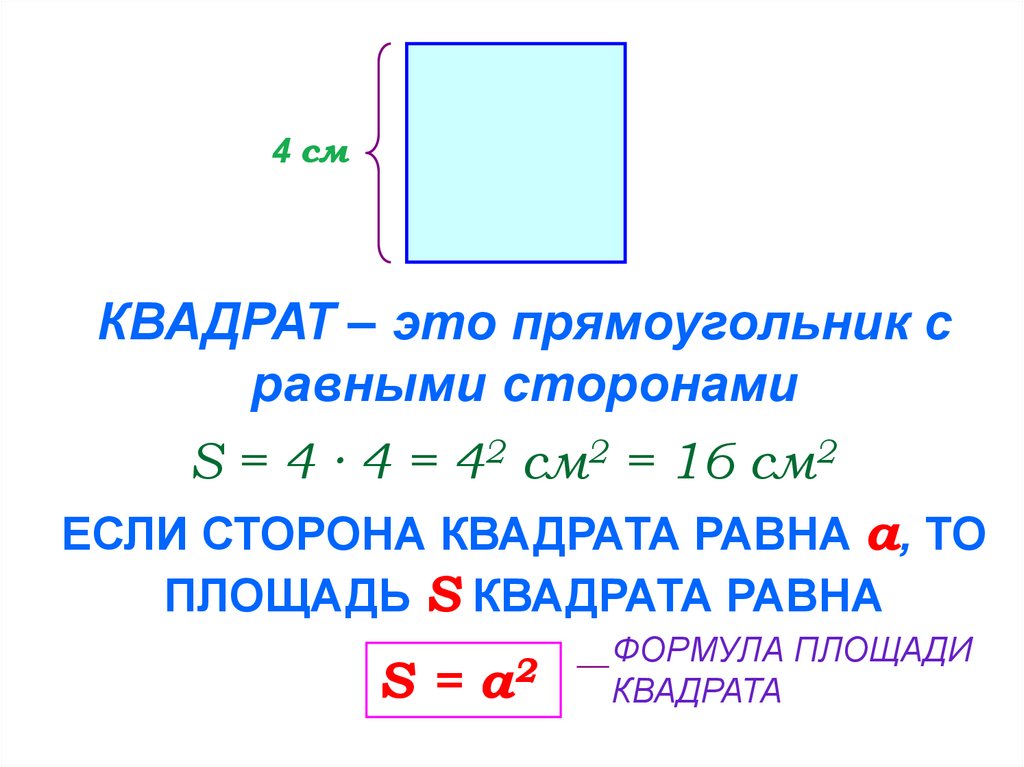 Единицы, связанные с площадью поверхности, всегда будут единицами в квадрате. Площадь является результатом умножения двух измерений, длины и ширины, которые можно представить как степень числа 2. В этом случае наш ответ будет 640 м ² .

Рассмотрим следующее:
Вы хотите посадить траву на своем новом заднем дворе, и в настоящее время у вас есть 645 квадратных футов дерна. Вы хотите определить, достаточно ли травы, чтобы покрыть весь двор, поэтому вам нужно сравнить площадь дерна с площадью вашего двора. Ваш двор имеет длину 25 футов и ширину 30 футов. У вас достаточно дерна, чтобы покрыть весь двор?

Это сценарий, в котором можно применить формулу площади прямоугольника. Длина двора 30 футов, ширина 20 футов. Формула утверждает, что \(A=l\times w\), поэтому площадь двора равна \(30\text{футов}\times25\text{футов}\), что составляет 750 квадратных футов. В этом случае 645 квадратных футов дерна недостаточно, чтобы покрыть весь двор. Потребуется еще 105 квадратных футов дерна.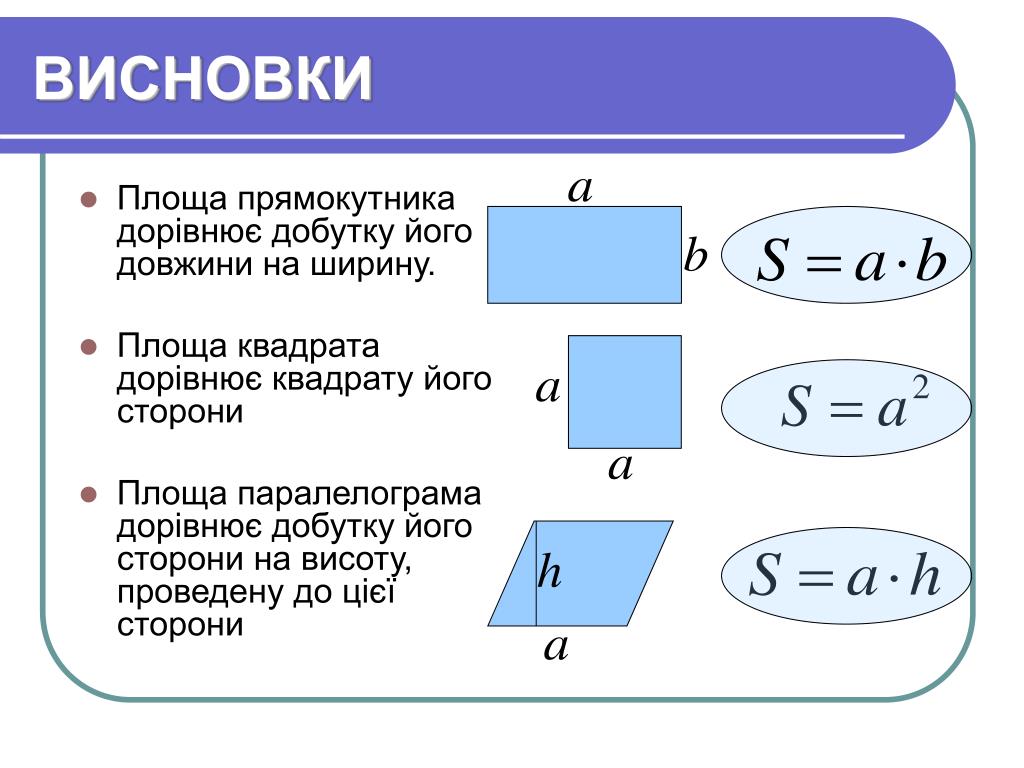

Многие задачи на площади будут представлены в формате \(A=l\times w\), где указаны длина и ширина и решается площадь. Тем не менее, также часто в задачах площади указывается площадь, но отсутствуют размеры. Например, площадь следующего прямоугольника равна 12 см ² , а его длина 6 см. Какова ширина прямоугольника?

Формула площади может быть применена в подобных ситуациях, но формула должна быть изменена, чтобы найти 92=6\text{ см}\times w\), и чтобы найти w , нам нужно разделить обе части уравнения на 6. \(w=2\text{ см}\), поэтому ширина прямоугольника 2 см.

Примите во внимание следующее:
Вы хотите установить проволочный забор, окружающий ваш сад, чтобы не пускать туда оленей и кроликов. Вы знаете, что площадь вашего сада составляет 210 квадратных футов, а ширина — 14 футов. Какова длина сада и сколько метров ограждения нужно будет установить?

Недостающую длину можно определить по формуле площади \(A=l\×w\). Формула принимает вид \(210\text{ футов}^2=l14\text{ футов}\), и когда обе части уравнения делятся на 14, длина оказывается равной 15 футам. Отсюда мы можем просто сложить две длины и две ширины, чтобы найти общее количество необходимых ограждений: \(14+14+15+15=58\text{футов ограждения}\). 92\).

Примеры вопросов по площади прямоугольника

Вот несколько примеров вопросов по площади прямоугольника.

Вопрос №1:

 
Прямоугольник ниже имеет длину 4 дюйма и ширину 3 дюйма. Вычислите площадь поверхности по формуле площади.

15 в ²

11 в ²

14 в ²

12 в

5 2

6 Показать ответ 9

5

60005

Ответ:

Площадь можно рассчитать по формуле \(A=l\×w\), где A представляет площадь, l представляет длину, а w представляет ширину. Формула \(A=l\times w\) становится \(A=4\text{in}\times3\text{in}\), что упрощается до 12 в ² .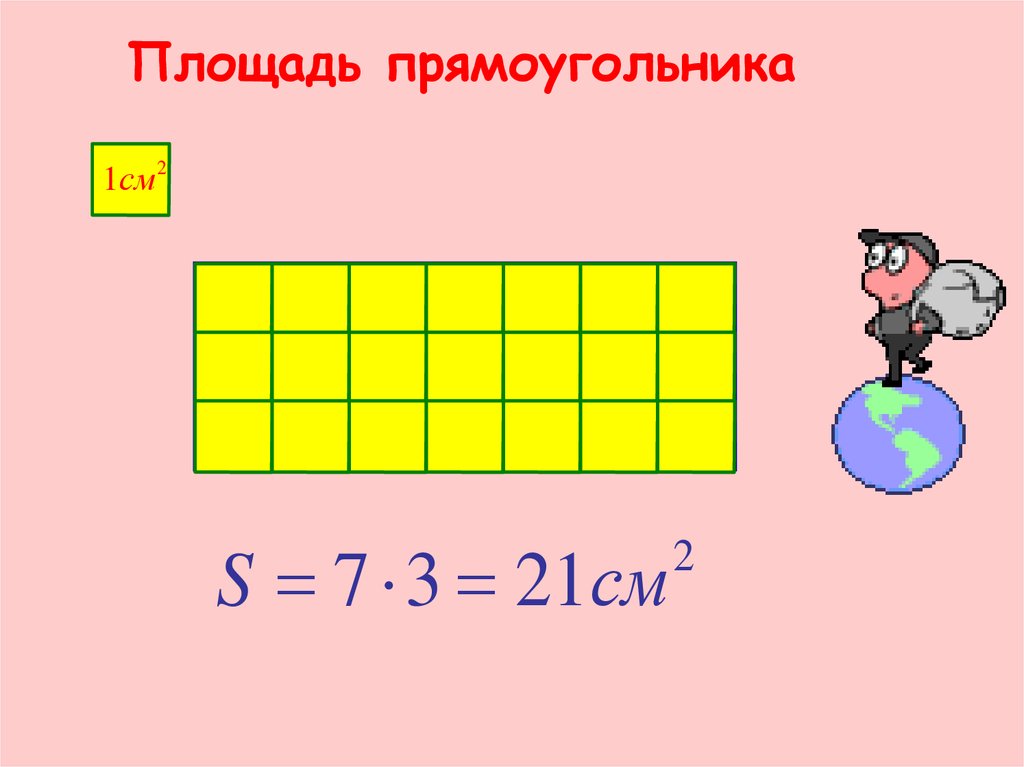

Скрыть ответ

Вопрос № 2:

 
Какой сценарий является примером площади поверхности?

Количество воды, содержащейся в большом баке

Вес объекта, измеренный в граммах

Расстояние вокруг беговой дорожки в метрах

Площадь плитки, покрывающей пол кухни

Показать ответ

Ответ:

Площадь поверхности может быть использована для описания ситуации, например, сколько плитки необходимо, чтобы полностью покрыть поверхность кухонного пола.

Скрыть ответ

Вопрос №3:

 
Сколькими способами можно построить прямоугольник, чтобы получить площадь поверхности 12 квадратных дюймов?

Односторонний

Двухсторонний

Восьмисторонний

Шестисторонний

Показать ответ

Ответ:

Следующие размеры дадут площадь поверхности 12 квадратных единиц (9\102} \times1\text{in}\)
\(1\text{in}\times12\text{in}\)
\(2\text{in}\times6\text{in}\)
\(6\ текст {in}\times2\text{in}\)
\(3\text{in}\times4\text{in}\)
\(4\text{in}\times3\text{in}\)

Скрыть ответ

Вопрос № 4:

 
Кристен хочет вставить поролоновую прокладку в основание спального ящика своей собаки. Ящик имеет длину 54 дюйма и ширину 36 дюймов. Какова должна быть площадь пенопластовой прокладки, чтобы без зазоров поместиться в ящик?

1 844 в ²

1 744 в ²

1 944 в ²

1 344 в ²

. вычисляется по формуле площади \(A=l\times w\). Когда размеры подставлены в формулу, \(A=l\times w\) становится \(A=54\text{in}\times36\text{in}\), что упрощается до 1,944 в ² .

Скрыть ответ

Вопрос № 5:

 
Андрей хочет построить бассейн на заднем дворе. Его двор имеет ширину 15 футов, поэтому он решает спроектировать бассейн шириной 10 футов. Площадь бассейна составит 120 квадратных метров. Как долго будет бассейн?

11 футов

12 футов

13 футов

14 футов

Показать ответ

Ответ:

В этом сценарии формула \(A=l) может быть использована для решения \(A)times. 2=l\times10\text{ft}\). Когда обе части уравнения делятся на 10, l имеет длину 12 или 12 футов.

Скрыть ответ

Вернуться к примерам вопросов по математике

Площадь прямоугольников – объяснение и примеры

По определению, площадь прямоугольника – это область, покрытая прямоугольником в двумерной плоскости . Прямоугольник — это двумерный многоугольник с четырьмя сторонами, четырьмя углами и четырьмя вершинами.

Прямоугольник состоит из двух сторон: длины (L) и ширины (В). Длина прямоугольника — это самая длинная сторона, а ширина — самая короткая сторона. Ширину прямоугольника иногда называют шириной (b).

Как найти площадь прямоугольника?

Площадь прямоугольника можно рассчитать, подсчитав количество маленьких полных квадратов размером 1 * 1 кв. единиц, необходимых для покрытия прямоугольника.

Например, если количество подсчитанных полных квадратов равно 20, то это означает, что площадь прямоугольника составляет 20 квадратов.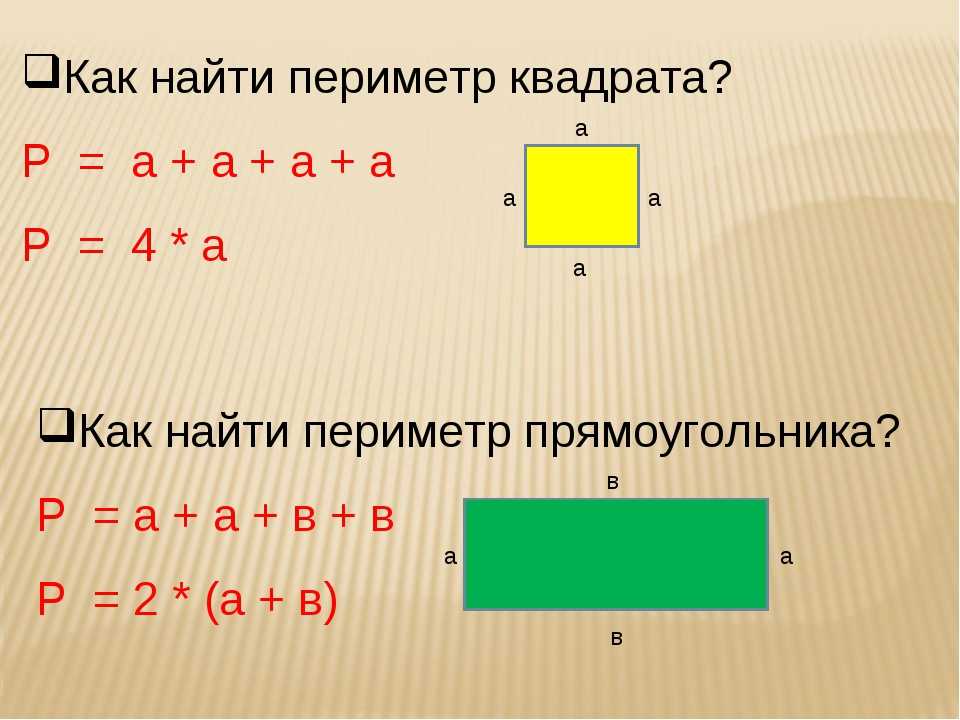

Недостатком этого метода является то, что он не дает точных цифр площади, а также метод неприменим для нахождения площадей больших плоскостей.

Площадь прямоугольника Формула

Площадь прямоугольника – это произведение ширины и длины прямоугольника.

Следовательно, формула площади прямоугольника гласит:

Площадь прямоугольника = длина x ширина

A = L * W, где A — площадь, L — длина, W — ширина или ширина .

ПРИМЕЧАНИЕ: При умножении длины на ширину всегда следите за тем, чтобы вы использовали одни и те же единицы длины. Если они даны в разных единицах, измените их на одну и ту же единицу.

Давайте решим несколько примеров задач на площадь прямоугольника.

Пример 1

Найдите площадь прямоугольника, если его длина 25 м, а ширина 10 м.

Решение

A = l x w

Подставьте 25 вместо l и 10 вместо w.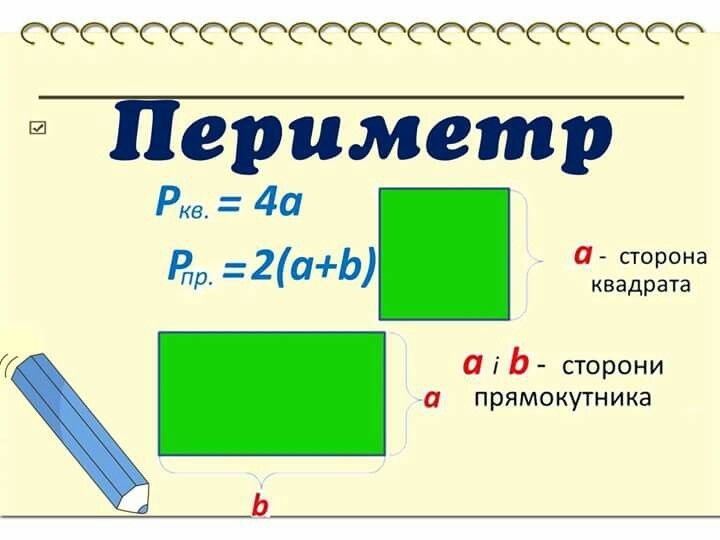

= (25 x 10) м ²

= 250 м ²

Итак, площадь прямоугольника равна 250 м ² .

Пример 2

Найдите площадь прямоугольника, длина и ширина которого равны 10 см и 3 см соответственно.

Раствор

Дано,
Длина (l) = 10 см.
Ширина (b) = 3 см.
Площадь прямоугольника = длина × ширина

= 10 × 3 см ² .

= 30 см ² .

Пример 3

Если периметр прямоугольника равен 60 см, а его длина в 5 раз больше ширины, найдите площадь прямоугольника.

Решение

Пусть ширина равна x.

Длина в 5 раз больше ширины, длина = 5x.

Но периметр прямоугольника =2(l + w) = 60 см

Подставьте 5x вместо l и x вместо w.

60 = 2(5x + x)

60 = 12x

Разделите обе части на 12, чтобы получить.

x = 5

Теперь подставьте x = 5 в уравнение длины и ширины.

Следовательно, ширина = 5 см, а длина = 25 см.

, но площадь прямоугольника = L x W

= (25 x 5) CM ²

= 125 см ²

Пример 4

Найти область прямоугольника с длиной длины по длине длины длины 4

. 12 см и диагональ 13 см.

Решение

Здесь ширина не указана, поэтому мы используем теорему Пифагора для определения ширины.

C ² = A ² + B ²

13 ² = A ² + 12 ²

169 = A ² + 144.

1444 = A ² + 144.

1444444 = A ² + 144.

1444 = A ² . .

169 – 144 = ² + 144 – 144

25 = ²

Найдя квадратный корень из обеих частей, мы получаем.

а = 5

Следовательно, ширина прямоугольника 5 см.

Теперь вычислите площадь.

А = Д x Ш

= (12 x 5) см ²

Пример 5

Если цена цементирования пола составляет 12,40 долл. США за квадратный метр, найти стоимость цементирования прямоугольного пола длиной 20 м и шириной 10 м.

Раствор

Чтобы найти общую стоимость цементирования пола, умножьте площадь пола на скорость цементирования.

Площадь = Д x Ш

= (20 x 10) м ²

= 200 м ²

Стоимость цементирования = Площадь x ставка цементирования

= 200 м ² x 12,40 долл. США/м ²

= $ 2 480

Пример 6

. 7, а его площадь составляет 693 квадратных метра. Найдите его длину и ширину.

Решение

Пусть знаменатель длины и ширины = x

Следовательно, длина = 11x

Ширина = 7x

Площадь прямоугольника = L x W

693 кв. футов = (11x) (7x)

693 кв. ft = 77x ²

Разделите обе стороны на 77.

x ² = 9

Найдите площадь обеих сторон, чтобы получить;

х = 3.

Замена.

Длина = 11x = 11* 3 = 33

Ширина = 7x = 7 * 3 = 21

Следовательно, длина прямоугольника 33 фута, а его ширина 21 фут.

Пример 742

Длина прямоугольника 0,7 м, а ширина 50 см. Чему равна площадь прямоугольника в метрах?

Раствор

Длина = 0,7 м

Ширина = 50 см.

Преобразование 50 см в метры путем деления 50 на 100. Таким образом, 50 см = 0,5 м

Площадь = L x W

= (0,7 x 0,5) M ²

= 0,35 M ²

. Пример 8

Прямоугольная стена размером 75 м на 32 м. Найти стоимость покраски стены, если цена покраски 5 руб./кв.м.

Раствор

Площадь = Д х Ш

= (75 х 32) м ²

= 2400 м ²

Чтобы получить стоимость покраски стены, умножаем площадь стены на норму покраски.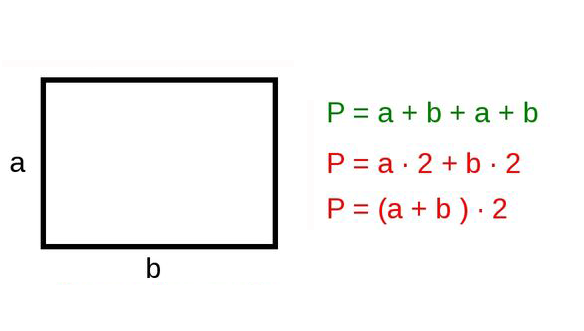

Стоимость = 2400 м ² x 5 рупий за кв. м

= 12 000 рупий

Пример 9 размеры, 1 м на 2 м. Найдите общее количество плиток, необходимых, чтобы полностью покрыть пол двора.

Решение

Сначала рассчитайте площадь пола двора и плитки.

Площадь пола внутреннего двора = (50 x 40) M ²

= 2000 M ²

Площадь плитки = (1 x 2) M ²

= 2 М ²

2

= 2 М ²

= 2 м ^{2 2}

= 2 М ^{2 2}

= 2 М ^{2 2}

Чтобы найти количество плиток, необходимых для покрытия пола двора, мы делим пол двора на площадь плитки.

Количество плит = 2000 м ² /2 м ²

= 1000

Следовательно, для покрытия пола необходимо 1000 плиток.

Площадь прямоугольника.

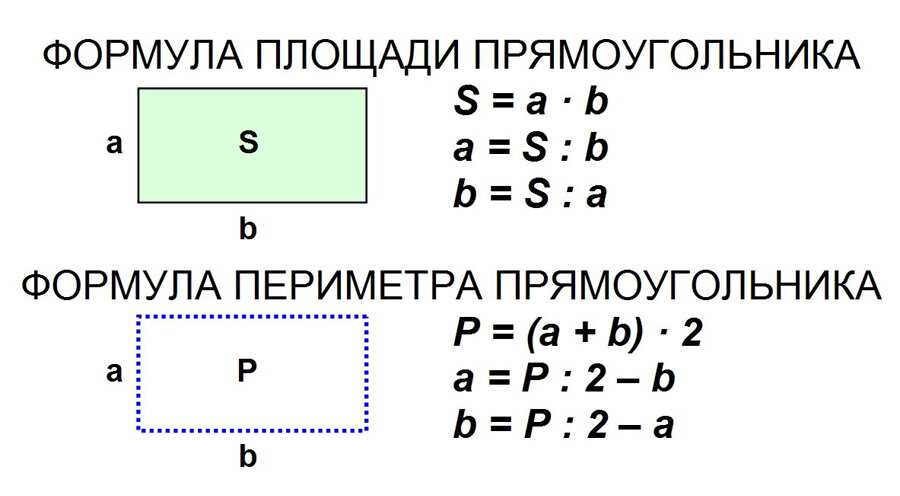Определение, формула и задачи

Четырехугольник, параллельные стороны которого равны друг другу, а все вершины перпендикулярны друг другу, называется прямоугольником. Количество единичных квадратов, которые могут вписаться в любую фигуру, является площадью этой фигуры. Следовательно, площадь прямоугольника равна количеству единичных квадратов, которые могут вписаться в границы прямоугольника. Площадь фигуры измеряется количеством квадратных единиц, таких как квадратные футы, квадратные дюймы, квадратные сантиметры и так далее. Некоторые примеры прямоугольных форм: мобильные экраны, классная доска, двери и т. д.

Любая замкнутая форма, состоящая как минимум из трех отрезков, называется многоугольником. Существует множество различных типов многоугольников, некоторые из них представляют собой треугольники, четырехугольники, пятиугольники, шестиугольники и т. д. Многоугольники классифицируются по количеству ребер, которые они имеют. Ребра также называются сторонами, и они представляют собой не что иное, как сегменты линий, из которых состоят многоугольники. Точки, в которых пересекаются отрезки, называются вершинами. Многоугольник имеет равное количество ребер и вершин.

Многоугольники классифицируются на основе количества ребер или вершин, которые они имеют. Многоугольник с четырьмя сторонами называется четырехугольником или четырехугольником. Четырехугольники можно разделить на вогнутые четырехугольники, выпуклые четырехугольники и прямоугольные четырехугольники в зависимости от содержащихся в них углов. Если все четыре стороны четырехугольника равны 90°, это прямоугольные четырехугольники. Их также называют равноугольными четырехугольниками, так как все их углы равны. Двумя типами равноугольных четырехугольников являются квадраты и прямоугольники. В квадрате все четыре стороны четырехугольника равны. В прямоугольнике равны только противоположные стороны четырехугольника.

(Изображение скоро будет загружено)

Поскольку противоположные стороны квадрата равны, квадрат также можно рассматривать как прямоугольник. Прямоугольник также является параллелограммом, что означает, что противоположные стороны прямоугольника идеально параллельны друг другу. Мы также можем сказать, что прямоугольник, у которого все четыре стороны равны друг другу, является квадратом.

Площадь прямоугольника

Площадь любого многоугольника — это количество пространства, которое он занимает или заключает в себе. Это количество квадратных единиц внутри многоугольника. Площадь является двумерным свойством, что означает, что она содержит как длину, так и ширину. Площадь обычно измеряется в таких единицах, как квадратные метры, квадратные футы или квадратные дюймы. Площадь больших фигур, таких как поля или города, измеряется в квадратных километрах, гектарах или акрах.

(Изображение скоро будет загружено)

Чтобы найти площадь прямоугольника, нам просто нужно умножить его длину на ширину.

Площадь равна произведению ширины прямоугольника на высоту.

Формула для вычисления площади прямоугольника имеет следующий вид:

Площадь = w × h 

Например, если прямоугольник имеет ширину 8 м и высоту 3 м,

Площадь прямоугольника равна площади = w × h h

Площадь = 8 × 3

Площадь = 24 м ²

В квадрате, поскольку все четыре стороны равны, Площадь = w × h становится

Площадь = h × h, Площадь = h ² .

Следовательно, для квадрата площадь равна квадрату его сторон.

Формула площади прямоугольника

Математическая формула, используемая для расчета площади прямоугольника в пределах его границы, выглядит следующим образом:

Площадь прямоугольника = (длина x ширина) квадратных единиц

A= l x b

Площадь прямоугольника определяется произведением его длины на ширину (ширину).

Шаги для вычисления площади прямоугольника

Чтобы найти площадь прямоугольника, выполните шаги, указанные ниже-

1. Из приведенных данных обратите внимание на размеры длины и ширины.

2. Умножьте длину на ширину прямоугольника.

3. Результат будет дан в квадратных единицах.

Пример. Длина и ширина прямоугольника равны 8 единицам и 4 единицам соответственно. Найдите площадь прямоугольника.

Решение – задано, 

длина = 8 единиц

ширина = 4 единицы

Площадь прямоугольника = l x b

= 8 x 4

= 32 кв.

Вычисление площади прямоугольника

Длина и ширина прямоугольника ABCD равны AB, CD, BC и AD соответственно.

В прямоугольнике ABCD проведена диагональ AC.

AC разделит прямоугольник ABCD на два равных треугольника ADC и ABC.

Площадь прямоугольника ABCD будет суммой треугольников ABC и ADC

Площадь прямоугольника ABCD = площадь треугольника ABC + площадь треугольника ADC

Поскольку треугольники равны.

Площадь прямоугольника ABCD = 2 x Площадь треугольника ABC

= 2 x (½ x Base x Height)

= AB x BC

Область прямоугольника ABCD = Длина XTHTH 9000 9000

.

Задачи на площадь прямоугольника

1) Найдите площадь прямоугольника, высота которого 20 см, а ширина 4 см.

Решение: Дано, Высота = 20 см и Ширина = 4 см

Площадь прямоугольника = w × h

Площадь прямоугольника = 20 × 4

Следовательно, площадь прямоугольника = 80 см ² .

2) Прямоугольная доска имеет ширину 120 мм и высоту 89 мм. Найдите площадь этой доски.

Решение: Дано, Высота = 89 мм = 8,9 см, Ширина = 120 мм = 12 см

Площадь прямоугольника = ш × в

Площадь прямоугольника = 12 × 8,9

Следовательно, площадь прямоугольника = 106,8 см ² .

3) Высота прямоугольного экрана равна 20 см. Его площадь равна 240 см ² . Найдите ширину данного экрана.

Решение: Дано, Высота = 20 см и Площадь = 240 см ² .

Площадь прямоугольника = ш × в

Следовательно, ширина = площадь / длина

Ширина = 240/20

Ширина = 120 см

4) Высота и ширина прямоугольной стены равны 80 м и 60 м соответственно. Если маляр берет 3 ₹ за м ² для покраски стены, сколько будет стоить покраска всей стены?

Решение: Дано, Высота = 80 м, Ширина = 60 м

Площадь прямоугольника = w × h

Площадь прямоугольника = 80 × 60 стоимость 3 ₹ за м ² , стоимость покраски 4800 м ² составляет 4800 × 3 = 14 400 ₹

5) Пол, длина и ширина которого составляют 60 м и 40 м соответственно, должен быть покрыт прямоугольной плиткой.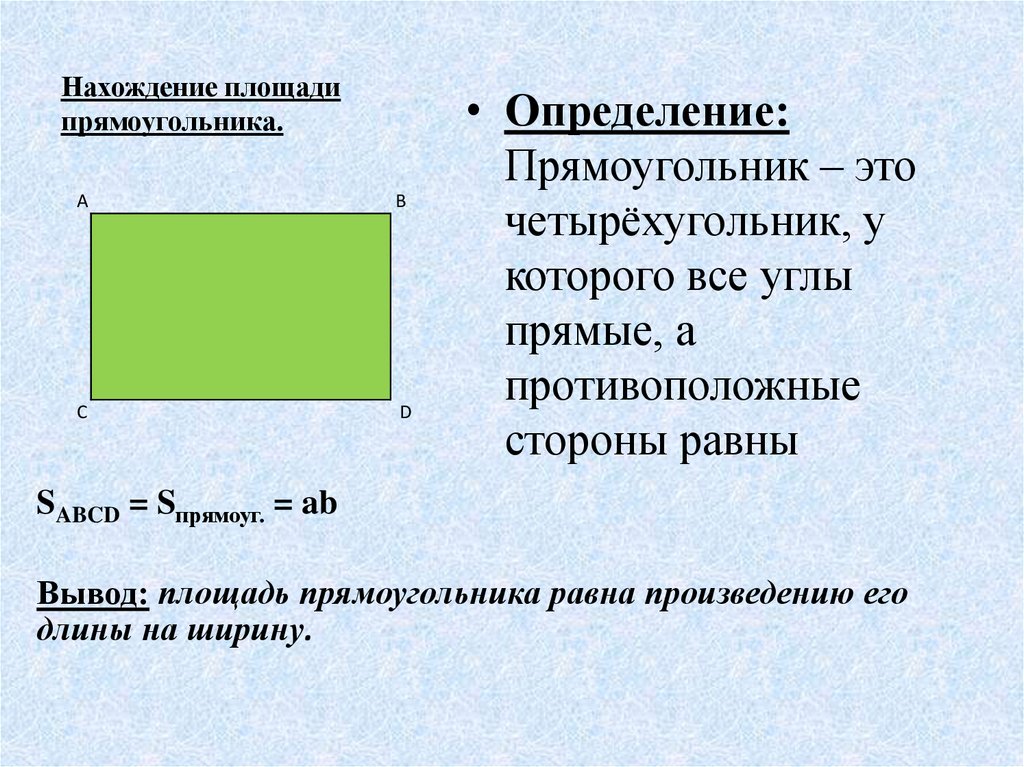 Размер выбранной напольной плитки составляет 1 м × 2 м. Найдите общее количество плиток, необходимых для полного покрытия комнаты.

Решение: Дано, длина = 60 м, ширина = 40 м

Площадь прямоугольника = w × h

Площадь прямоугольника = 60 × 40 длина одной плитки = 1 м

Ширина одной плитки = 2 м

Площадь = ш × в

Площадь одной плитки = 1 × 2

Площадь одной плитки = 2 м ²

Количество плиток необходимое для покрытия пола можно пересчитать по

Площадь пола / площадь плитки

2400/2 = 1200 плиток.

6) Из прямоугольного куска картона вырезается квадратный кусок картона площадью 36 см ² . Найдите

(а) Длина квадрата

(б) Если картон можно разрезать на три таких квадрата, найдите длину, ширину и площадь этого прямоугольного куска картона.

Решение: (a) Дано, Площадь квадрата 36 см ²

Мы знаем, что в квадрате Площадь = h ² .

No related posts.