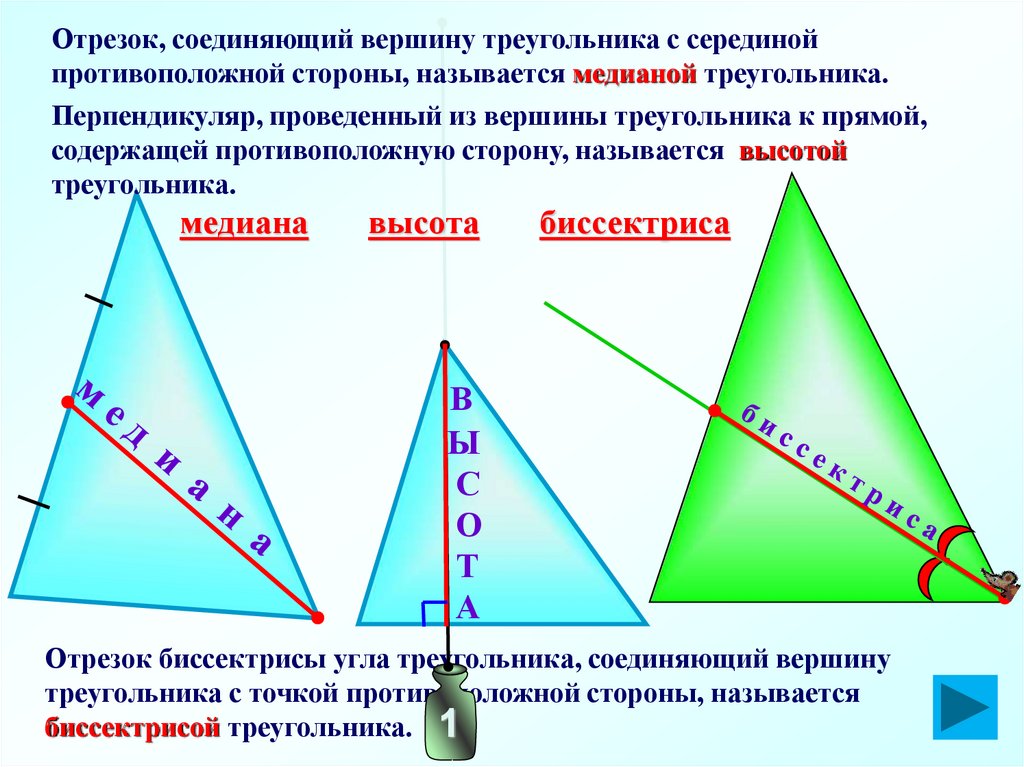
Углы треугольника – виды и примеры
4.2
Средняя оценка: 4.2
Всего получено оценок: 158.
4.2
Средняя оценка: 4.2
Всего получено оценок: 158.
В геометрии часто рассматривают углы треугольника, поскольку этими параметрами удобно пользоваться при различных вычислениях с помощью тригонометрических функций и в доказательствах.
Определение
Углы треугольника формируются с помощью его пересекающихся сторон. Иными словами, два отрезка, выходящие из одной точки образуют геометрическую фигуру, обозначающую часть плоскости, которая и называется углом.
По количеству углов формируются названия многоугольников. Треугольник так называется, потому что содержит 3 угла.
Виды углов треугольника
Используя значения углов произвольных треугольников можно выделить ряд важных свойств геометрических фигур. Так, из евклидовой геометрии известно, что сумма углов произвольного треугольника равняется 180 градусов.
Треугольники классифицируют в зависимости от величины углов.
Когда один из углов треугольника больше, чем 90 градусов, этот треугольник называется тупоугольным.
Рис. 2. Тупоугольный треугольник.Из теоремы о неравенстве треугольника известно, что когда в этой геометрической фигуре один из углов является прямым или тупым, то сумма двух других углов составит не более 90 градусов, т. е. два других угла обязательно должны быть острыми.
Рис. 3. Остроугольный треугольник.Любой произвольный треугольник можно разделить на два прямоугольных треугольника, если опустить высоту из вершины этой фигуры на противоположную сторону. А тупоугольный треугольник одной из высот наоборот достраивается до большого прямоугольного треугольника.
Значение
Нахождение неизвестных углов и сторон рассматриваемого треугольника, с использованием известных значений, называется «решением треугольников».
Для этого обращаются к общим тригонометрическим теоремам, а также признакам равенства и подобия треугольников.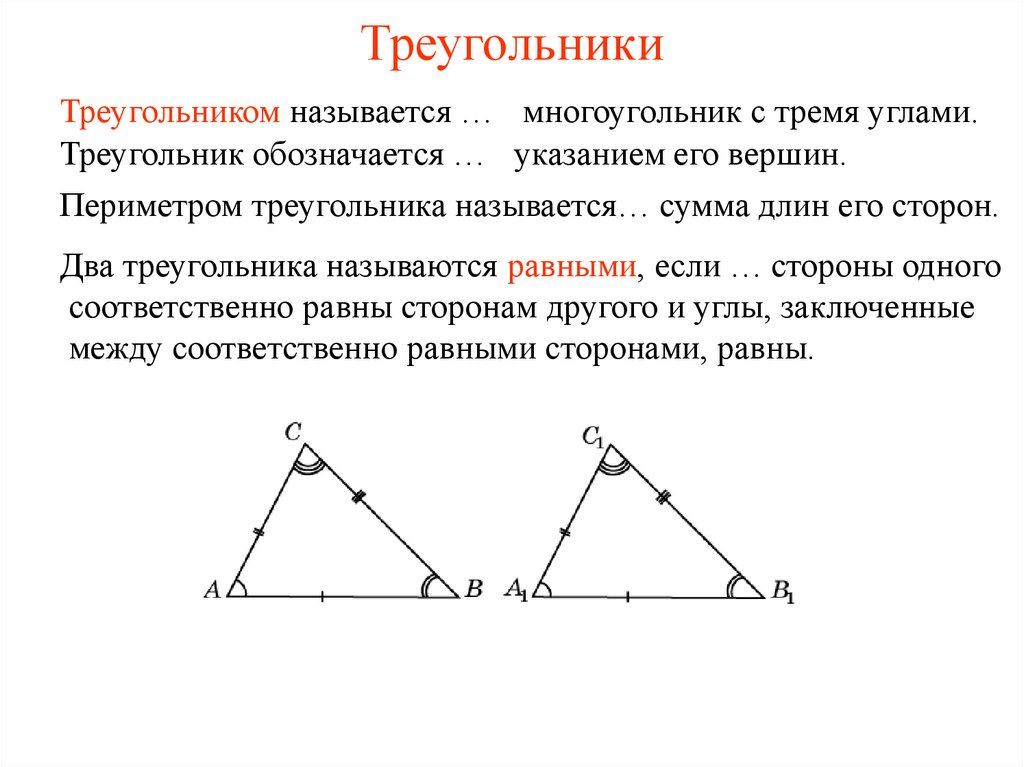
Что мы узнали?
В произвольном треугольнике углы определяют вид фигуры и возможность существования такой фигуры вовсе. Иногда в задаче достаточно доказать, что такая фигура существовать не может. Знание вида треугольника, позволяет использовать свойства этого треугольника и различные дополнительные построения.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Макс Степочкин
5/5
Новиков Елисей
4/5
Надежда Зотова
4/5
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 158.
А какая ваша оценка?
Виды углов треугольника и их определения. Какие есть треугольники
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис.
5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
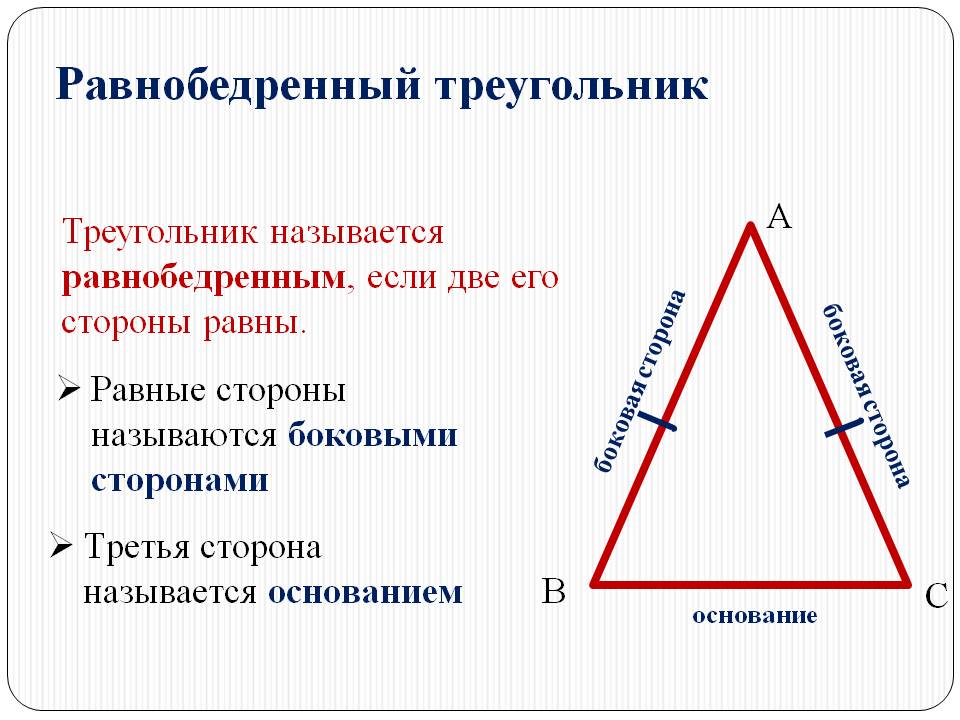
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны .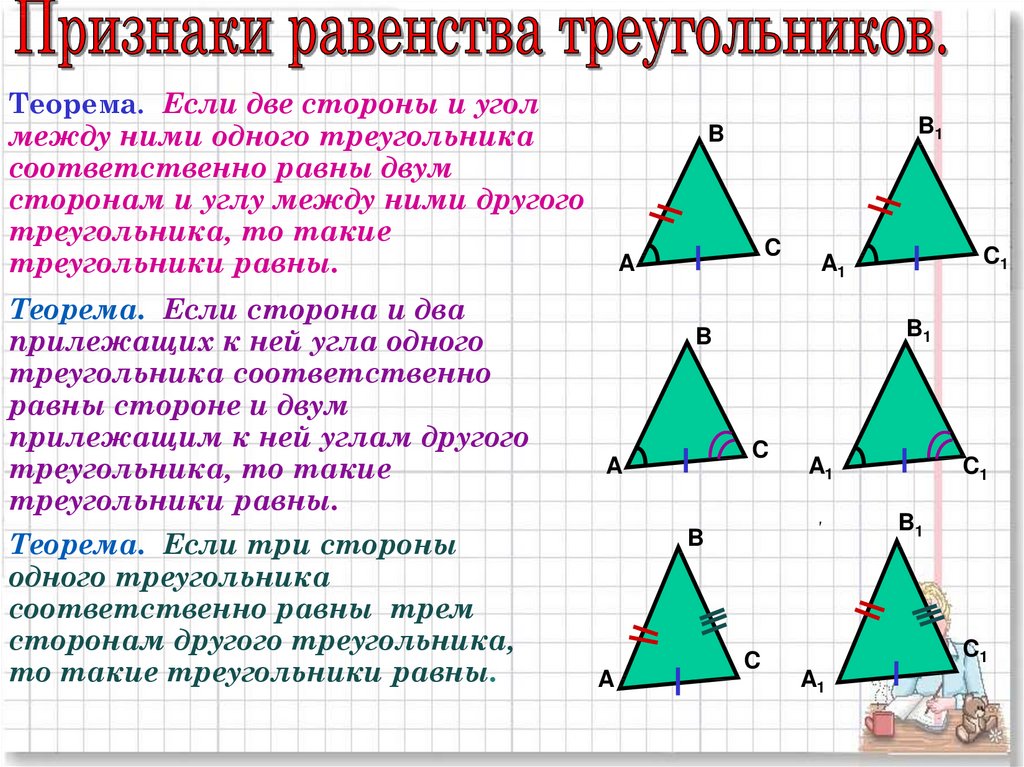 Равносторонние треугольники всегда остроугольные.
Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.

- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис.
9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ.
 Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
Контроль и оценка результатов обучения. — М.: «Просвещение», 2011. - «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
При изучении математики ученики начинаются знакомиться с различными видами геометрических фигур. Сегодня речь пойдет о различных видах треугольников.
Определение
Геометрические фигуры, которые состоят из трех точек, которые не находятся на одной прямой, называются треугольниками.
Отрезки, соединяющие точки, называются сторонами, а точки – вершинами. Вершины обозначаются большими латинскими буквами, например: A, B, C.
Стороны обозначаются названиями двух точек, из которых они состоят – AB, BC, AC. Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.
Рис. 1. Треугольник ABC.
Виды треугольников
Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.
Существует три вида треугольников по углам:
- остроугольные;
- прямоугольные;
- тупоугольные.
Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90 0 .
Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.
Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.
Рис. 2. Виды треугольников по углам.
Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.
Причем, большая сторона является гипотенузой.
Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.
Виды треугольников по сторонам:
- равносторонние;
- равнобедренные;
- разносторонние.
Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.
Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.
Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.
Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.
Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.
Рис. 3. Виды треугольников по сторонам.
Сумма всех углов треугольника, независимо от его вида, равна 1800.
Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.
Существует понятие золотого треугольника. Это равнобедренный треугольник, у которого две боковые стороны пропорциональны основе и равны определенному числу.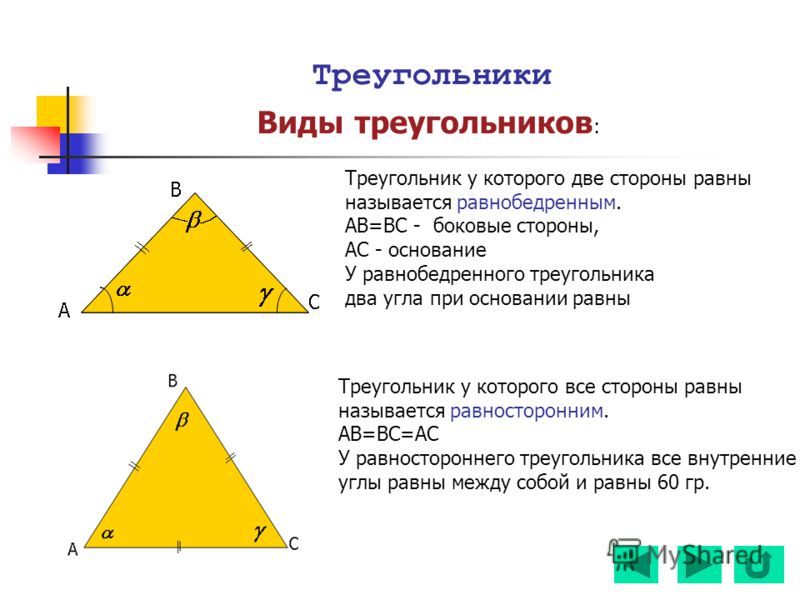 В такой фигуре углы пропорциональны соотношению 2:2:1.
В такой фигуре углы пропорциональны соотношению 2:2:1.
Задача:
Существует ли треугольник, стороны которого равны 6 см., 3 см., 4 см.?
Решение:
Для решения данного задания нужно использовать неравенство a
Что мы узнали?
Из данного материала из курса математики 5 класса, мы узнали, что треугольники классифицируются по сторонам и величине углов. Треугольники имеют определенные свойства, которые можно использовать при решении заданий.
Деление треугольников на остроугольные, прямоугольные и тупоугольные. Классификация по соотношению сторон делит треугольники на разносторонние, равносторонние и равнобедренные. Причем каждый треугольник одновременно принадлежит к двум . Например, он может быть прямоугольным и разносторонним одновременно.
Определяя вид по типу углов, очень внимательны. Тупоугольным будет называться такой треугольник, у которого один из углов является , то есть составляет боле 90 градусов. Прямоугольный треугольник может быть вычислен по наличию одного прямого (равного 90 градусам) угла.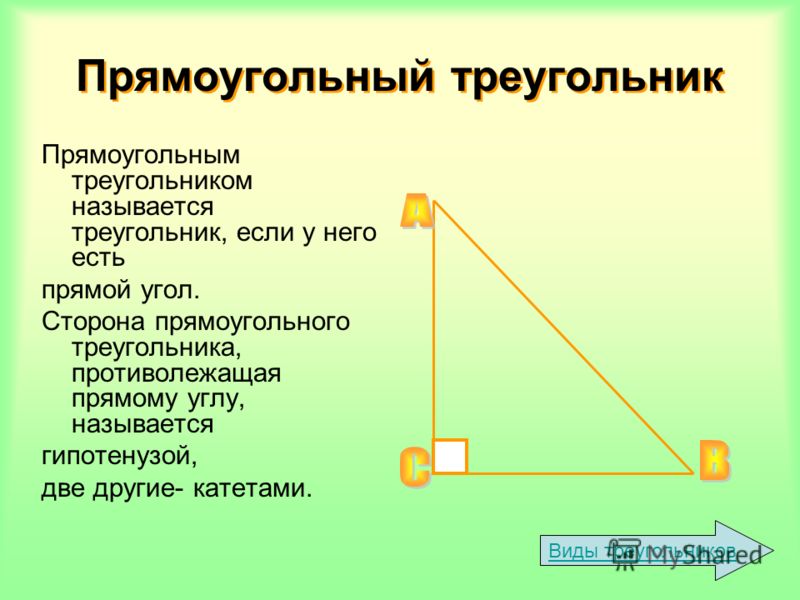 Однако чтобы классифицировать треугольник как остроугольный, вам нужно будет убедиться, что все три его угла острыми.
Однако чтобы классифицировать треугольник как остроугольный, вам нужно будет убедиться, что все три его угла острыми.
Определяя вид треугольника по соотношению сторон, для начала вам придется узнать длины всех трех сторон. Однако если по условию длины сторон вам не даны, помочь вам смогут углы. Разносторонним будет являться треугольник, все три стороны которого имеют разную длину. Если длины сторон неизвестны, то треугольник может быть классифицирован как разносторонний в случае, если все три его угла являются разными. Разносторонний треугольник может быть тупоугольным, прямоугольным и остроугольным.
Равнобедренным будет являться треугольник, две из трех сторон которого равны между собой. Если длины сторон вам не даны, ориентируйтесь по двум равным между собой углам. Равнобедренный треугольник, как и разносторонний, может быть и тупоугольным, и прямоугольным и остроугольным.
Равносторонним может быть только такой треугольник, все три стороны которого имеют одинаковую длину. Все его углы также равны между собой, и каждый из них равен 60-ти градусам. Отсюда ясно, что равносторонние треугольники всегда являются остроугольными.
Все его углы также равны между собой, и каждый из них равен 60-ти градусам. Отсюда ясно, что равносторонние треугольники всегда являются остроугольными.
Простейший из многоугольников – это треугольник. Он образуется при помощи трех точек, лежащих в одной плоскости, но не лежащих на одной прямой, попарно соединенных отрезками. Тем не менее, треугольники бывают разных типов, а значит, обладают разными свойствами.
Инструкция
Принято выделять три типа : тупоугольные, остроугольные и прямоугольные. Это по типу углов. Тупоугольным называется треугольник, у которого один из углов является тупым. Тупым называется угол, имеющий величину больше девяноста градусов, но меньше ста восьмидесяти. Например, в треугольнике ABC угол ABC равен 65°, угол BCA равен 95°, угол CAB равен 20°. Углы ABC и CAB меньше 90°, но угол BCA больше, значит, треугольник тупоугольный.
Остроугольным называется треугольник, у которого все углы являются острыми. Острым называется угол, имеющий величину меньше девяноста и больше нуля градусов.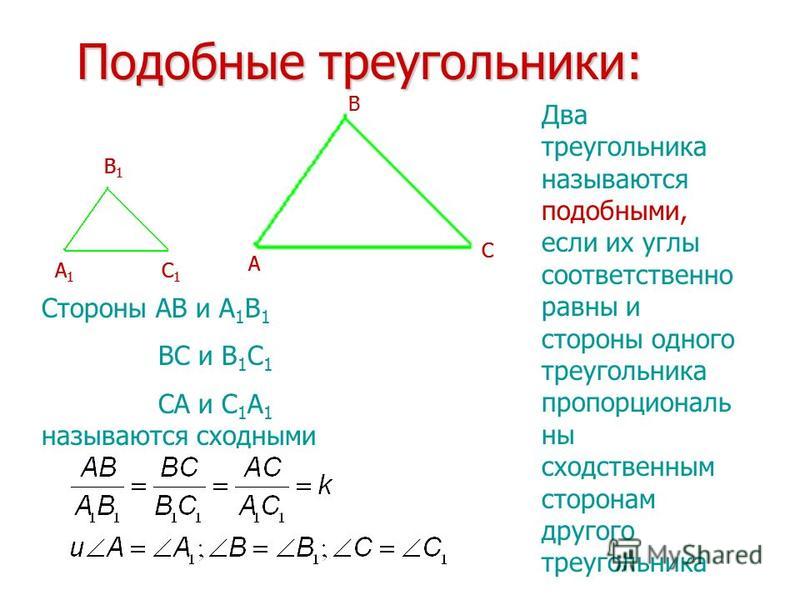 Например, в треугольнике ABC угол ABC равен 60°, угол BCA равен 70°, угол CAB равен 50°. Все три угла меньше 90°, значит треугольник . Если вам известно, что у треугольника все стороны равны, это значит, что все углы у него тоже равны между собой, при этом равны шестидесяти градусам. Соответственно, все углы в таком треугольнике меньше девяноста градусов, а следовательно такой треугольник является остроугольным.
Например, в треугольнике ABC угол ABC равен 60°, угол BCA равен 70°, угол CAB равен 50°. Все три угла меньше 90°, значит треугольник . Если вам известно, что у треугольника все стороны равны, это значит, что все углы у него тоже равны между собой, при этом равны шестидесяти градусам. Соответственно, все углы в таком треугольнике меньше девяноста градусов, а следовательно такой треугольник является остроугольным.
Если в треугольнике один из углов равен девяноста градусам, это значит, что он не относится ни широкоугольному типу, ни к остроугольному. Это прямоугольный треугольник.
Если вид треугольника определять по соотношению сторон, они будут равносторонние, разносторонние и равнобедренные. В равностороннем треугольнике все стороны равны, а это, как вы выяснили, говорит о том, что треугольник остроугольный. Если у треугольника равны только две стороны или стороны не равны между собой, он может быть и тупоугольным, и прямоугольным, и остроугольным. Значит, в этих случаях необходимо вычислить или измерить углы и делать умозаключения, согласно пунктам 1, 2 или 3.
Видео по теме
Источники:
- тупоугольный треугольник
Равенство двух или более треугольников соответствует случаю, когда все стороны и углы данных треугольников равны. Однако существует ряд более простых критериев для доказательства данного равенства.
Вам понадобится
- Учебник по геометрии, лист бумаги, простой карандаш, транспортир, линейка.
Инструкция
Откройте учебник по геометрии седьмого класса на параграфе о признаках равенства треугольников. Вы увидите, что существует ряд основных признаков, доказывающих равенство двух треугольников. Если два треугольника, равенство которых проверяется, являются произвольными, то для них существует три основных признака равенства. Если же известна какая-то дополнительная информация о треугольниках, то основные три признака дополняются еще несколькими. Это относится, например, к случаю равенства прямоугольных треугольников.
Прочитайте первое правило о равенстве треугольников.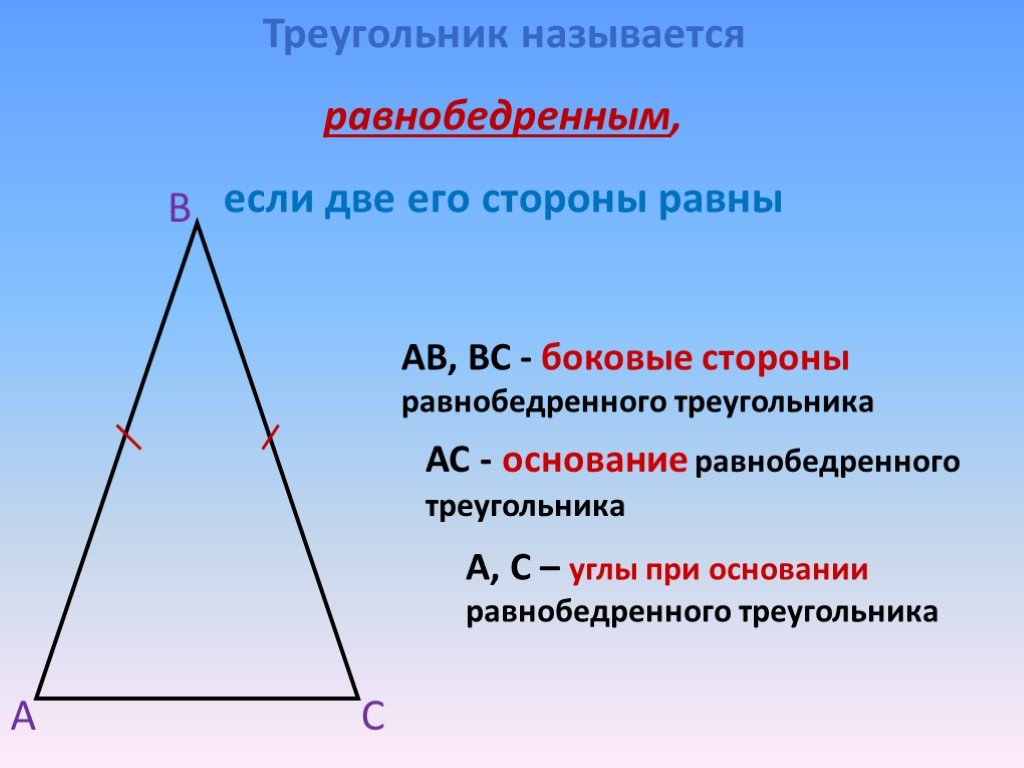 Как известно, оно позволяет считать треугольники равными, если можно доказать, что какой-либо один угол и две прилегающие к нему стороны двух треугольников равны. Для того чтобы понять, данный закон, начертите на листе бумаги с помощью транспортира два одинаковых определенных угла, образованных двумя лучами, исходящими из одной точки. Отмерьте линейкой одинаковые стороны от вершины нарисованного угла в обоих случаях. Используя транспортир, измерьте величины полученных углов двух образованных треугольников, убедитесь, что они равны.
Как известно, оно позволяет считать треугольники равными, если можно доказать, что какой-либо один угол и две прилегающие к нему стороны двух треугольников равны. Для того чтобы понять, данный закон, начертите на листе бумаги с помощью транспортира два одинаковых определенных угла, образованных двумя лучами, исходящими из одной точки. Отмерьте линейкой одинаковые стороны от вершины нарисованного угла в обоих случаях. Используя транспортир, измерьте величины полученных углов двух образованных треугольников, убедитесь, что они равны.
Для того чтобы не прибегать к таким практическим мерам для понимания признака равенства треугольников, прочитайте доказательство первого признака равенства. Дело в том, что каждое правило о равенстве треугольников имеет строгое теоретическое доказательство, просто его не удобно использовать в целях запоминания правил.
Прочитайте второй признак равенства треугольников. Он гласит, что два треугольника будут равны в том случае, если какая-либо одна сторона и два прилегающие к ней угла двух таких треугольников равны.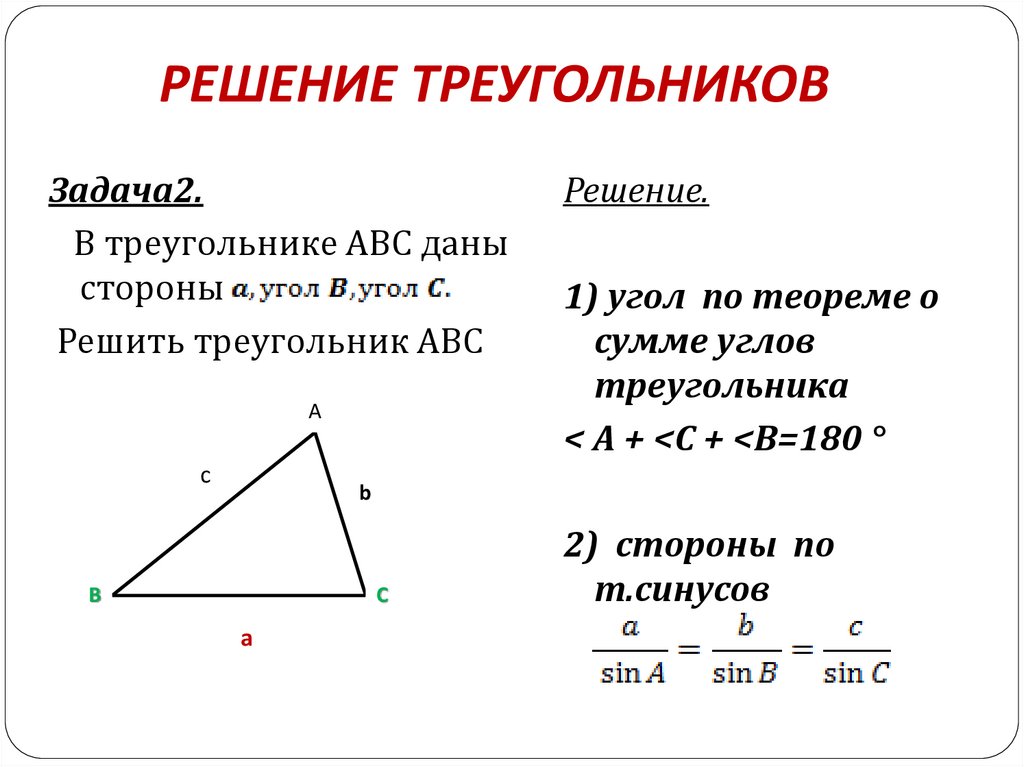 Для того чтобы запомнить данное правило, представьте нарисованную сторону треугольника и два прилежащих к ней угла. Представьте, что длины сторон углов постепенно увеличиваются. В конце концов, они пересекутся, образуя третий угол. В данной мысленной задаче важным является то, что точка пересечения сторон, которые мысленно увеличиваются, а также полученный угол однозначно определяются третьей стороной и двумя прилегающими к ней углами.
Для того чтобы запомнить данное правило, представьте нарисованную сторону треугольника и два прилежащих к ней угла. Представьте, что длины сторон углов постепенно увеличиваются. В конце концов, они пересекутся, образуя третий угол. В данной мысленной задаче важным является то, что точка пересечения сторон, которые мысленно увеличиваются, а также полученный угол однозначно определяются третьей стороной и двумя прилегающими к ней углами.
Если вам не дана никакая информация об углах исследуемых треугольников, то используйте третий признак равенства треугольников. По данному правилу, два треугольника считаются равными, если все три стороны одно из них равны соответствующим трем сторонам другого. Таким образом, данное правило говорит о том, что длины сторон треугольника однозначно определяют все углы треугольника, а значит, они однозначно определяют и сам треугольник.
Видео по теме
Самый простой многоугольник, который изучается в школе — это треугольник. Он более понятен для учащихся и встречает меньше трудностей.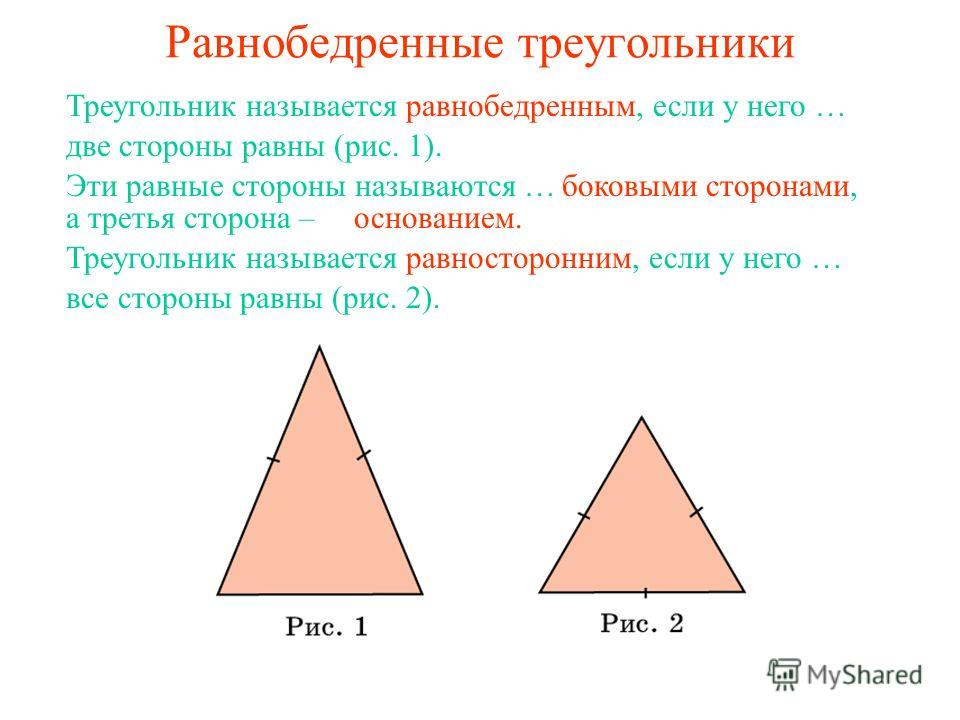 Несмотря на то что существуют различные виды треугольников, у которых имеются особенные свойства.
Несмотря на то что существуют различные виды треугольников, у которых имеются особенные свойства.
Какая фигура называется треугольником?
Образованная тремя точками и отрезками. Первые называются вершинами, вторые — сторонами. Причем все три отрезка должны быть соединены, чтобы между ними образовывались углы. Отсюда и название фигуры «треугольник».
Различия в названиях по углам
Поскольку они могут быть острыми, тупыми и прямыми, то и виды треугольников определяются по этим названиям. Соответственно, групп таких фигур три.
- Первая. Если все углы треугольника острые, то он будет иметь название остроугольного. Все логично.
- Вторая. Один из углов тупой, значит треугольник тупоугольный. Проще некуда.
- Третья. Имеется угол, равный 90 градусам, который называется прямым. Треугольник становится прямоугольным.
Различия в названиях по сторонам
В зависимости от особенностей сторон выделяют такие виды треугольников:
общий случай — разносторонний, в котором все стороны имеют произвольную длину;
равнобедренный, у двух сторон которого имеются одинаковые числовые значения;
равносторонний, длины всех его сторон одинаковые.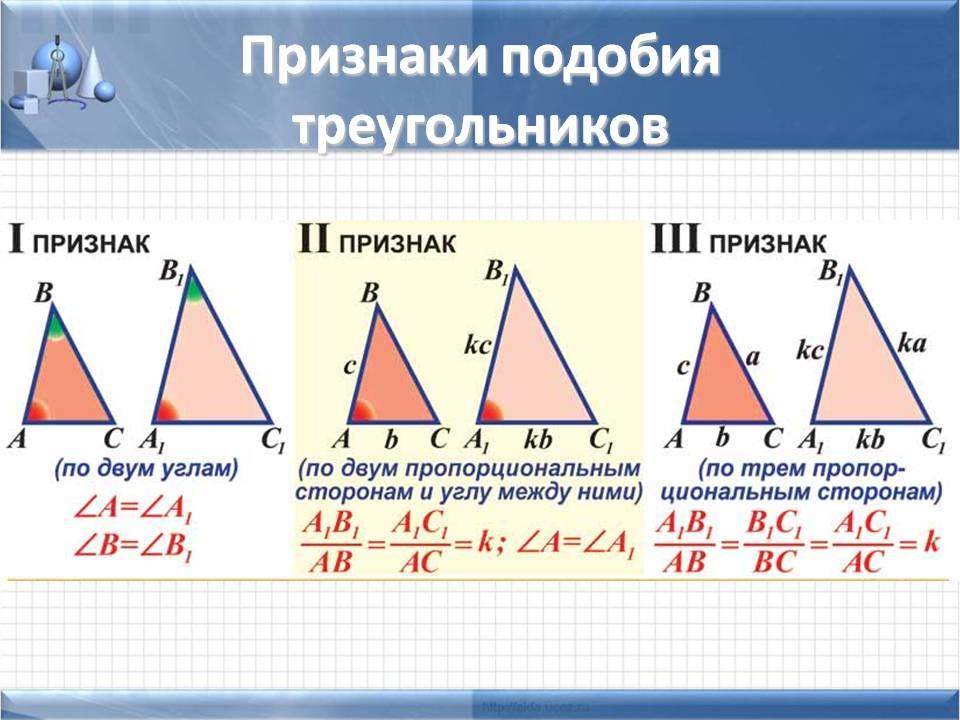
Если в задаче не указан конкретный вид треугольника, то нужно чертить произвольный. У которого все углы острые, а стороны имеют разную длину.
Свойства, общие для всех треугольников
- Если сложить все углы треугольника, то получится число, равное 180º. И неважно, какого он вида. Это правило действует всегда.
- Числовое значение любой стороны треугольника меньше, чем сложенные вместе две другие. При этом она же больше, чем их разность.
- Каждый внешний угол имеет значение, которое получается при сложении двух внутренних, не смежных с ним. Причем он всегда больше, чем смежный с ним внутренний.
- Напротив меньшей стороны треугольника всегда лежит самый маленький угол. И наоборот, если сторона большая, то и угол будет самым большим.
Эти свойства справедливы всегда, какие бы виды треугольников ни рассматривались в задачах. Все остальные вытекают из конкретных особенностей.
Свойства равнобедренного треугольника
- Углы, которые прилегают к основанию, равны.

- Высота, которая проведена к основанию, является также медианой и биссектрисой.
- Высоты, медианы и биссектрисы, которые построены к боковым сторонам треугольника, соответственно равны друг другу.
Свойства равностороннего треугольника
Если имеется такая фигура, то будут верны все свойства, описанные немного выше. Потому что равносторонний всегда будет равнобедренным. Но не наоборот, равнобедренный треугольник не обязательно будет равносторонним.
- Все его углы равны друг другу и имеют значение 60º.
- Любая медиана равностороннего треугольника является его высотой и биссектрисой. Причем они все равны друг другу. Для определения их значений существует формула, которая состоит из произведения стороны на квадратный корень из 3, деленного на 2.
Свойства прямоугольного треугольника
- Два острых угла дают в сумме значение в 90º.
- Длина гипотенузы всегда больше, чем у любого из катетов.
- Числовое значение медианы, проведенной к гипотенузе, равно ее половине.

- Этому же значению равен катет, если он лежит напротив угла в 30º.
- Высота, которая проведена из вершины со значением 90º, имеет определенную математическую зависимость от катетов: 1/н 2 = 1/а 2 + 1/в 2 . Здесь: а, в — катеты, н — высота.
Задачи с разными видами треугольников
№1. Дан равнобедренный треугольник. Его периметр известен и равен 90 см. Требуется узнать его стороны. В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.
Значение периметра напрямую зависит от тех величин, которые нужно найти. Сумма всех трех сторон и даст 90 см. Теперь нужно вспомнить признак треугольника, по которому он является равнобедренным. То есть две стороны равны. Можно составить уравнение с двумя неизвестными: 2а + в = 90. Здесь а — боковая сторона, в — основание.
Настала очередь дополнительного условия. Следуя ему, получается второе уравнение: в = 1,2а. Можно выполнить подстановку этого выражения в первое. Получится: 2а + 1,2а = 90.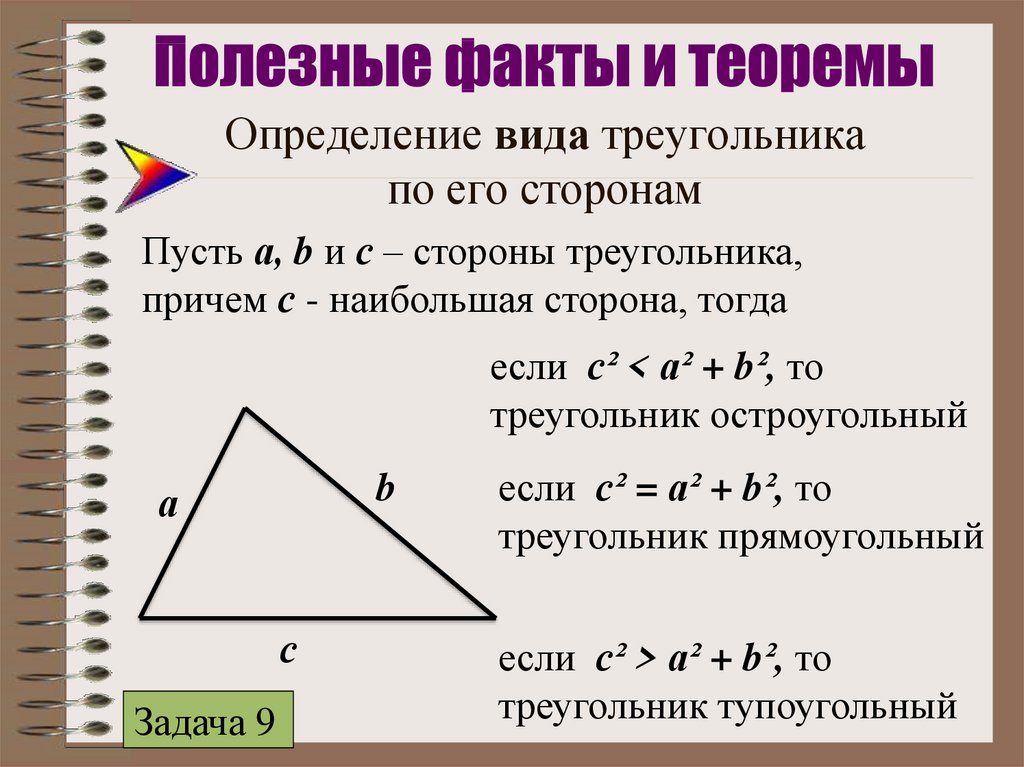 После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).
После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).
Для проверки можно сложить три значения: 28,125 * 2 + 33,75 = 90 (см). Все верно.
Ответ: стороны треугольника равны 28,125 см, 28,125 см, 33,75 см.
№2. Сторона равностороннего треугольника равна 12 см. Нужно вычислить его высоту.
Решение. Для поиска ответа достаточно вернуться к тому моменту, где были описаны свойства треугольника. Так указана формула для нахождения высоты, медианы и биссектрисы равностороннего треугольника.
н = а * √3 / 2, где н — высота, а — сторона.
Подстановка и вычисление дают такой результат: н = 6 √3 (см).
Эту формулу необязательно запоминать. Достаточно вспомнить, что высота делит треугольник на два прямоугольных. Причем она оказывается катетом, а гипотенуза в нем — это сторона исходного, второй катет — половина известной стороны. Теперь нужно записать теорему Пифагора и вывести формулу для высоты.
Ответ: высота равна 6 √3 см.
№3. Дан МКР — треугольник, 90 градусов в котором составляет угол К. Известны стороны МР и КР, они равны соответственно 30 и 15 см. Нужно узнать значение угла Р.
Решение. Если сделать чертеж, то становится ясно, что МР — гипотенуза. Причем она в два раза больше катета КР. Снова нужно обратиться к свойствам. Одно из них как раз связано с углами. Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.
Ответ: угол Р равен 60º.
№4. Нужно найти все углы равнобедренного треугольника. Про него известно, что внешний угол от угла при основании равен 110º.
Решение. Поскольку дан только внешний угол, то этим и нужно воспользоваться. Он образует с внутренним углом развернутый. Значит в сумме они дадут 180º. То есть угол при основании треугольника будет равен 70º. Так как он равнобедренный, то второй угол имеет такое же значение. Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º — 70º — 70º = 40º.
Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º — 70º — 70º = 40º.
Ответ: углы равны 70º, 70º, 40º.
№5. Известно, что в равнобедренном треугольнике угол, лежащий напротив основания, равен 90º. На основании отмечена точка. Отрезок, соединяющий ее с прямым углом, делит его в отношении 1 к 4. Нужно узнать все углы меньшего треугольника.
Решение. Один из углов можно определить сразу. Поскольку треугольник прямоугольный и равнобедренный, то те, что лежат у его основания, будут по 45º, то есть по 90º/2.
Второй из них поможет найти известное в условии отношение. Поскольку оно равно 1 к 4, то частей, на которые он делится получается всего 5. Значит, чтобы узнать меньший угол треугольника нужно 90º/5 = 18º. Осталось узнать третий. Для этого из 180º (суммы всех углов треугольника) нужно вычесть 45º и 18º. Вычисления несложные, и получится: 117º.
Определение прямоугольного треугольника и его частей
В прямоугольном треугольнике есть прямой угол. Но у него может быть только один прямой угол, потому что общее количество градусов в треугольнике равно 180. Если бы у него было два прямых угла, то эти два угла занимали бы все 180 градусов; для третьего угла не осталось бы градусов. Таким образом, в прямоугольном треугольнике два других угла делят между собой оставшиеся 90 градусов.
Но у него может быть только один прямой угол, потому что общее количество градусов в треугольнике равно 180. Если бы у него было два прямых угла, то эти два угла занимали бы все 180 градусов; для третьего угла не осталось бы градусов. Таким образом, в прямоугольном треугольнике два других угла делят между собой оставшиеся 90 градусов.
Прямоугольные треугольники могут быть самых разных форм, но все они имеют угол, в котором находится прямой угол. Вы можете видеть, что во всех треугольниках прямой угол имеет две стороны, перпендикулярные друг другу. Два других угла равны острых угла (это означает, что они меньше 90 градусов).
Прямоугольные треугольники — привычное зрелище не только на уроках геометрии. У плотников есть инструменты для измерения, которые представляют собой прямоугольные треугольники. Архитекторы, проектирующие вручную (а не на компьютере), используют шаблоны прямоугольных треугольников.
Несмотря на то, что в прямоугольном треугольнике основное внимание уделяется прямому углу, на самом деле прямоугольный треугольник состоит из шести различных частей: трех углов и трех сторон.
Теперь этот факт верен для любого треугольника, но у прямоугольных треугольников есть специальные названия для этих частей. Наличие специальных имен необходимо, потому что существует так много свойств, теорем и приложений, использующих прямоугольные треугольники, и имена делают обсуждение и объяснение треугольников более понятными.
На рисунке показан типичный прямоугольный треугольник, помеченный заглавными и строчными буквами. Со времен Леонарда Эйлера, знаменитого швейцарского математика, этот тип маркировки стал традицией. Вы используете строчные буквы для обозначения сторон треугольника и заглавные буквы для обозначения вершины (угла) напротив стороны соответствующей строчной буквой.
Маленький квадратик в вершине C показывает, что две стороны, сходящиеся там, перпендикулярны в этой вершине — вот где прямой угол. Сторона c , противоположное прямому углу, называется гипотенузой. Две другие стороны, a и b , называются опорами.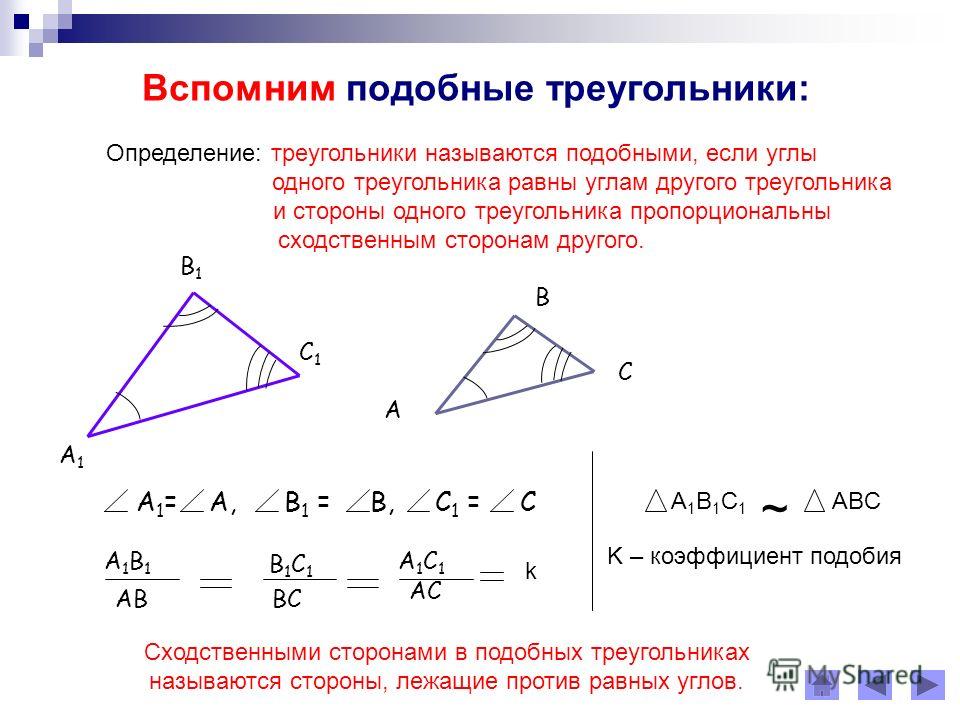 Гипотенуза всегда самая длинная сторона, потому что она лежит против наибольшего угла.
Гипотенуза всегда самая длинная сторона, потому что она лежит против наибольшего угла.
Угол при вершине C прямой, а два других угла, A и B , острые. Если меры углов A и B одинаковы, то каждый из них равен 45 градусам, а треугольник равен равнобедренный. Если это так, то длины сторон a и b также одинаковы.
Если угол в вершине A больше угла в вершине B , то сторона a длиннее стороны b . Меры углов треугольника имеют прямое отношение к длинам противоположных им сторон.
Эта статья из книги:
- Тригонометрия для чайников,
Об авторе книги:
Мэри Джейн Стерлинг является автором Алгебра I для чайников и многих других книг для чайников . Она преподает математику в Университете Брэдли в Пеории, штат Иллинойс, уже более 30 лет, и ей нравилось работать с будущими руководителями предприятий, физиотерапевтами, учителями и многими другими.
Эту статью можно найти в категории:
- Тригонометрия ,
Треугольник — ГИС Вики | Энциклопедия ГИС
Чтобы узнать о других значениях, см. Треугольник (значения).
«Равнобедренный» перенаправляется сюда. Чтобы узнать о трапеции, см. Равнобедренную трапецию .
Файл:Triangle illustration.svg Треугольник — одна из основных форм геометрии: многоугольник с тремя углами или вершинами и тремя сторонами или ребрами, являющимися отрезками прямых. Треугольник с вершинами A , B и C обозначается ABC .
В евклидовой геометрии любые три точки, не лежащие на одной прямой, определяют уникальный треугольник и уникальную плоскость (т. е. двумерное евклидово пространство).
Содержание
- 1 Типы треугольников
- 1.1 По относительной длине сторон
- 1.2 По внутренним уголкам
- 2 Основные факты
- 3 Точки, линии и окружности, связанные с треугольником
- 4 Вычисление площади треугольника
- 4.
 1 Использование векторов
1 Использование векторов - 4.2 Использование тригонометрии
- 4.3 Использование координат
- 4.4 Использование формулы Герона
- 4.
- 5 Вычисление сторон и углов
- 5.1 Тригонометрические соотношения в прямоугольных треугольниках
- 5.1.1 Синус, косинус и тангенс
- 5.1.2 Обратные функции
- 5.2 Правила синусов и косинусов
- 5.1 Тригонометрические соотношения в прямоугольных треугольниках
- 6 Неплоские треугольники
- 7 См. также
- 8 Каталожные номера
- 9 Внешние ссылки
Типы треугольников
По относительным длинам сторон
Треугольники можно классифицировать по относительным длинам их сторон:
- В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является правильным многоугольником, все углы которого равны 60°. [1]
- В равнобедренном треугольнике две стороны равны по длине. (Традиционно только две стороны равны, но иногда по крайней мере две.
 ) [2] Равнобедренный треугольник также имеет два угла одинаковой меры; а именно углы, противоположные двум сторонам одинаковой длины.
) [2] Равнобедренный треугольник также имеет два угла одинаковой меры; а именно углы, противоположные двум сторонам одинаковой длины. - В разностороннем треугольнике все стороны и внутренние углы отличны друг от друга. [3]
| Файл:Triangle.Isosceles.svg | ||
| Равносторонний | Равнобедренный | Разносторонний |
По внутренним углам
Треугольники также можно классифицировать по их внутренним углам, измеряемым здесь в градусах.
- A прямоугольный треугольник (или прямоугольный треугольник , ранее называвшийся прямоугольным треугольником ) имеет один из внутренних углов, равный 90° (прямой угол). Сторона, противоположная прямому углу, есть гипотенуза; это самая длинная сторона прямоугольного треугольника. Две другие стороны — это ножки или катеты [4] (единственное число: катет ) треугольника.
 Прямоугольные треугольники подчиняются теореме: сумма квадратов длин двух катетов равна квадрату длины гипотенузы: a 2 + b 2 = c 2 , где a и b — длины катетов, а c — длины катетов. Специальные прямоугольные треугольники — это прямоугольные треугольники с дополнительными свойствами, упрощающими расчеты с ними.
Прямоугольные треугольники подчиняются теореме: сумма квадратов длин двух катетов равна квадрату длины гипотенузы: a 2 + b 2 = c 2 , где a и b — длины катетов, а c — длины катетов. Специальные прямоугольные треугольники — это прямоугольные треугольники с дополнительными свойствами, упрощающими расчеты с ними.
- Треугольники, угол которых не равен 90°, называются косоугольными треугольниками .
- Треугольник, все внутренние углы которого меньше 90° — остроугольный треугольник или остроугольный треугольник .
- Треугольник, один из углов которого больше 90°, называется тупоугольным треугольником или тупоугольным треугольником .
Треугольник, у которого два угла одинаковой величины, имеет две стороны одинаковой длины, следовательно, это равнобедренный треугольник. Отсюда следует, что в треугольнике, где все углы имеют одинаковую меру, все три стороны имеют одинаковую длину, а значит, такой треугольник равносторонний.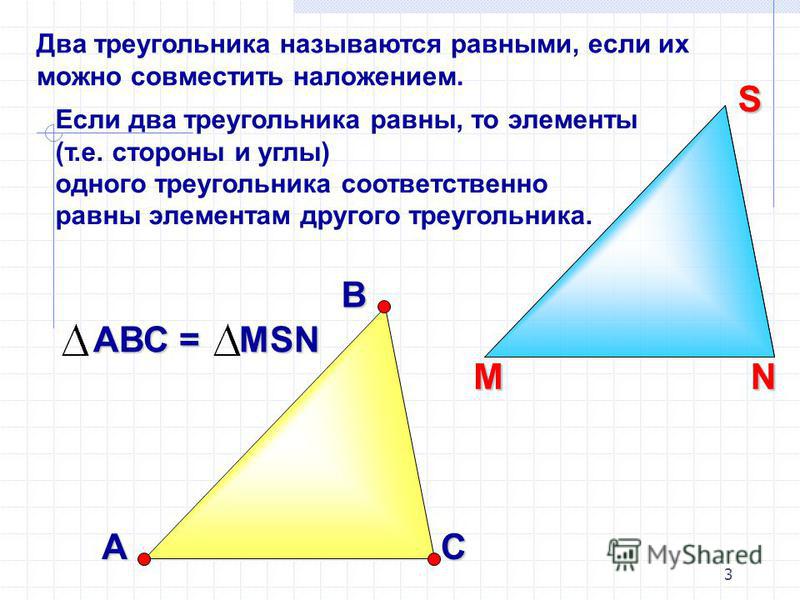
| Правый | Тупой | Острый |
| Наклонный | ||
Основные факты
Треугольники считаются двухмерными плоскими фигурами, если в контексте не указано иное (см. Неплоские треугольники ниже). Поэтому при строгом рассмотрении треугольник называется 2-симплексом (см. также Многогранник). Элементарные факты о треугольниках были представлены Евклидом в книгах 1–4 его Элементы , около 300 г. до н.э.
Сумма внутренних углов треугольника в евклидовом пространстве всегда равна 180 градусам. Это позволяет определить меру третьего угла любого треугольника, как только известна мера двух углов. Внешний угол треугольника — это угол, являющийся линейной парой (и, следовательно, дополнительным) внутреннему углу.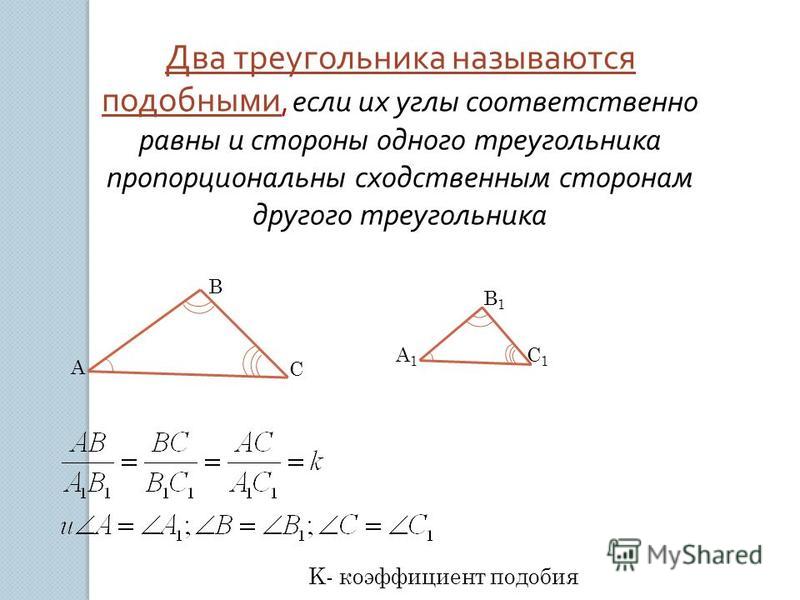 Мера внешнего угла треугольника равна сумме мер двух внутренних углов, не смежных с ним; это теорема о внешнем угле. Сумма мер трех внешних углов (по одному на каждую вершину) любого треугольника составляет 360 градусов. [5]
Мера внешнего угла треугольника равна сумме мер двух внутренних углов, не смежных с ним; это теорема о внешнем угле. Сумма мер трех внешних углов (по одному на каждую вершину) любого треугольника составляет 360 градусов. [5]
Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны, принцип, известный как неравенство треугольника . Поскольку предполагается, что вершины треугольника не лежат на одной прямой, сумма длин двух сторон не может быть равна длине третьей стороны.
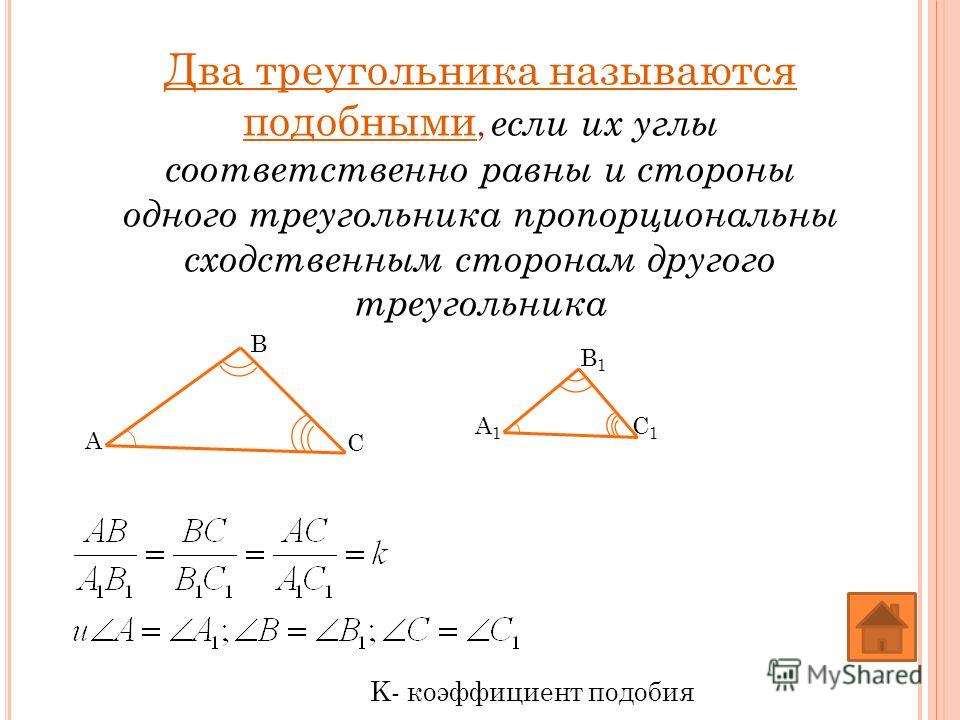
Два треугольника, находящиеся под соответствием, называются подобными , если каждый угол одного треугольника имеет ту же меру, что и соответствующий угол другого треугольника, и длины соответствующих сторон находятся в той же пропорции.
Несколько основных теорем о подобных треугольниках:
- Если два соответствующих внутренних угла двух треугольников имеют одинаковую меру, треугольники подобны.
- Если две соответствующие стороны двух треугольников пропорциональны, а прилежащие к ним углы имеют одинаковую меру, то треугольники подобны.
 ( включенный угол для любых двух сторон многоугольника является внутренним углом между этими двумя сторонами.)
( включенный угол для любых двух сторон многоугольника является внутренним углом между этими двумя сторонами.) - Если три соответствующие стороны двух треугольников пропорциональны, то эти треугольники подобны. [6]
Два конгруэнтных треугольника имеют одинаковые размеры и форму: [7] все пары соответствующих внутренних углов равны по размеру, и все пары соответствующих сторон имеют одинаковую длину. (Всего это шесть равенств, но трех часто бывает достаточно, чтобы доказать конгруэнтность.)
Некоторые достаточные условия для того, чтобы пара треугольников была конгруэнтной :
- SAS Постулат: две стороны в треугольнике имеют ту же длину, что и две стороны в другом треугольнике, и углы между ними имеют одинаковую величину.
- ASA: два внутренних угла и сторона, входящая в треугольник, имеют те же меру и длину, соответственно, что и в другом треугольнике. ( включенная сторона для пары углов является общей для них стороной.
 )
) - SSS: Каждая сторона треугольника имеет ту же длину, что и соответствующая сторона другого треугольника.
- AAS: два угла и соответствующая сторона, не входящая в треугольник, имеют те же меру и длину, соответственно, что и в другом треугольнике.
- Катет-гипотенуза (HL) Теорема: Гипотенуза и катет в прямоугольном треугольнике имеют ту же длину, что и в другом прямоугольном треугольнике.
- Теорема гипотенузы-угла: гипотенуза и острый угол в одном прямоугольном треугольнике имеют те же длину и меру соответственно, что и в другом прямоугольном треугольнике. Это всего лишь частный случай теоремы ААС.
Важный случай:
- Сторона-сторона-угол (или угол-сторона-сторона) условие: если две стороны и соответствующий не включенный в них угол треугольника имеют ту же длину и меру, соответственно, что и в другом треугольнике, то это недостаточно для доказательства соответствия; но если данный угол противоположен большей стороне двух сторон, то треугольники конгруэнтны.
 Теорема о гипотенузе-ноге является частным случаем этого критерия. Условие Сторона-Сторона-Угол само по себе не гарантирует конгруэнтность треугольников, потому что один треугольник может быть тупоугольным, а другой остроугольным.
Теорема о гипотенузе-ноге является частным случаем этого критерия. Условие Сторона-Сторона-Угол само по себе не гарантирует конгруэнтность треугольников, потому что один треугольник может быть тупоугольным, а другой остроугольным.
Используя прямоугольные треугольники и понятие подобия, можно определить тригонометрические функции синуса и косинуса. Это функции угла, которые исследуются в тригонометрии.
Теорема Пифагора
Центральная теорема – это теорема, которая утверждает, что в любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух других сторон. Если гипотенуза имеет длину c , а катеты имеют длины a и b , то теорема утверждает, что
Верно и обратное: если длины сторон треугольника удовлетворяют приведенному выше уравнению, то треугольник имеет прямой угол, противоположный стороне с .
Некоторые другие факты о прямоугольных треугольниках:
- Острые углы прямоугольного треугольника дополняют друг друга.

- Если катеты прямоугольного треугольника имеют одинаковую длину, то и углы, лежащие напротив этих катетов, имеют одинаковую меру. Так как эти углы дополняют друг друга, то каждый из них равен 45 градусам. По теореме Пифагора длина гипотенузы равна длине катета, умноженной на √2.
- В прямоугольном треугольнике с острыми углами, равными 30 и 60 градусам, гипотенуза вдвое больше длины меньшей стороны, а длинная сторона равна длине меньшей стороны, умноженной на √3 :
Для всех треугольников углы и стороны связаны законом косинусов и законом синусов (также называемым правилом косинусов и правилом синусов ).
Точки, линии и окружности, связанные с треугольником
Существуют сотни различных построений, которые находят особую точку, связанную с треугольником (и часто внутри него), удовлетворяющую некоторому уникальному свойству: их каталог см. в разделе ссылок. Часто их строят, находя три линии, симметрично связанные с тремя сторонами (или вершинами), а затем доказывая, что три линии пересекаются в одной точке: важным инструментом для доказательства их существования является теорема Чевы, которая дает критерий для определения, когда три такие линии параллельны. Точно так же линии, связанные с треугольником, часто строятся путем доказательства коллинеарности трех симметрично построенных точек: здесь теорема Менелая дает полезный общий критерий. В этом разделе объясняются лишь некоторые из наиболее часто встречающихся конструкций.
в разделе ссылок. Часто их строят, находя три линии, симметрично связанные с тремя сторонами (или вершинами), а затем доказывая, что три линии пересекаются в одной точке: важным инструментом для доказательства их существования является теорема Чевы, которая дает критерий для определения, когда три такие линии параллельны. Точно так же линии, связанные с треугольником, часто строятся путем доказательства коллинеарности трех симметрично построенных точек: здесь теорема Менелая дает полезный общий критерий. В этом разделе объясняются лишь некоторые из наиболее часто встречающихся конструкций.
Центр описанной окружности — это центр окружности, проходящей через три вершины треугольника.
Биссектриса треугольника есть прямая, проходящая через середину стороны и перпендикулярная ей, т. е. образующая с ней прямой угол. Три серединных перпендикуляра встречаются в одной точке, центре описанной окружности треугольника; эта точка является центром описанной окружности, окружности, проходящей через все три вершины.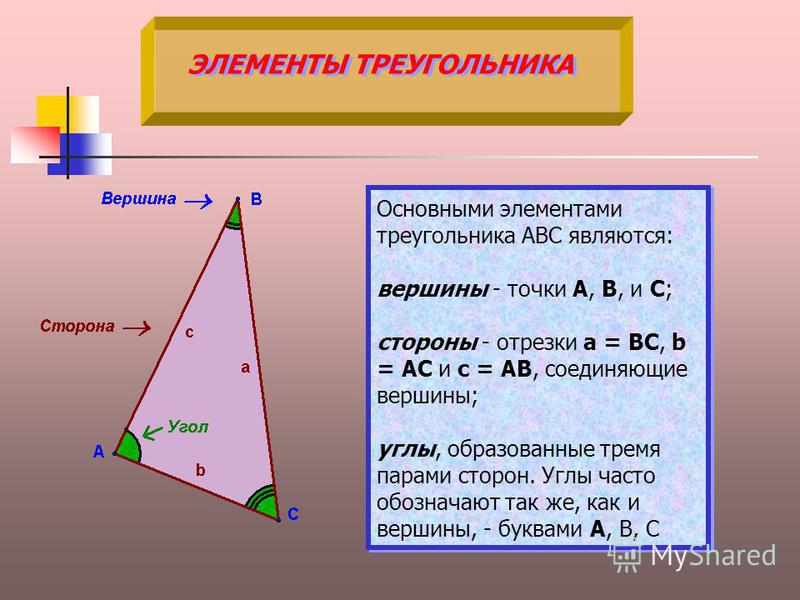 Диаметр этой окружности можно найти из закона синусов, изложенного выше.
Диаметр этой окружности можно найти из закона синусов, изложенного выше.
Из теоремы Фалеса следует, что если центр описанной окружности расположен на одной стороне треугольника, то противолежащий угол прямой. Верно и другое: если центр описанной окружности расположен внутри треугольника, то треугольник остроугольный; если центр описанной окружности находится вне треугольника, то треугольник тупоугольный.
Пересечение высот является ортоцентром.
Высота треугольника — это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая с ней прямой угол). Эта противоположная сторона называется 9.0003 основания высоты, а точка пересечения высоты с основанием (или его продолжением) называется футом высоты. Длина высоты – это расстояние между основанием и вершиной. Три высоты пересекаются в одной точке, называемой ортоцентром треугольника. Ортоцентр лежит внутри треугольника тогда и только тогда, когда треугольник остроугольный.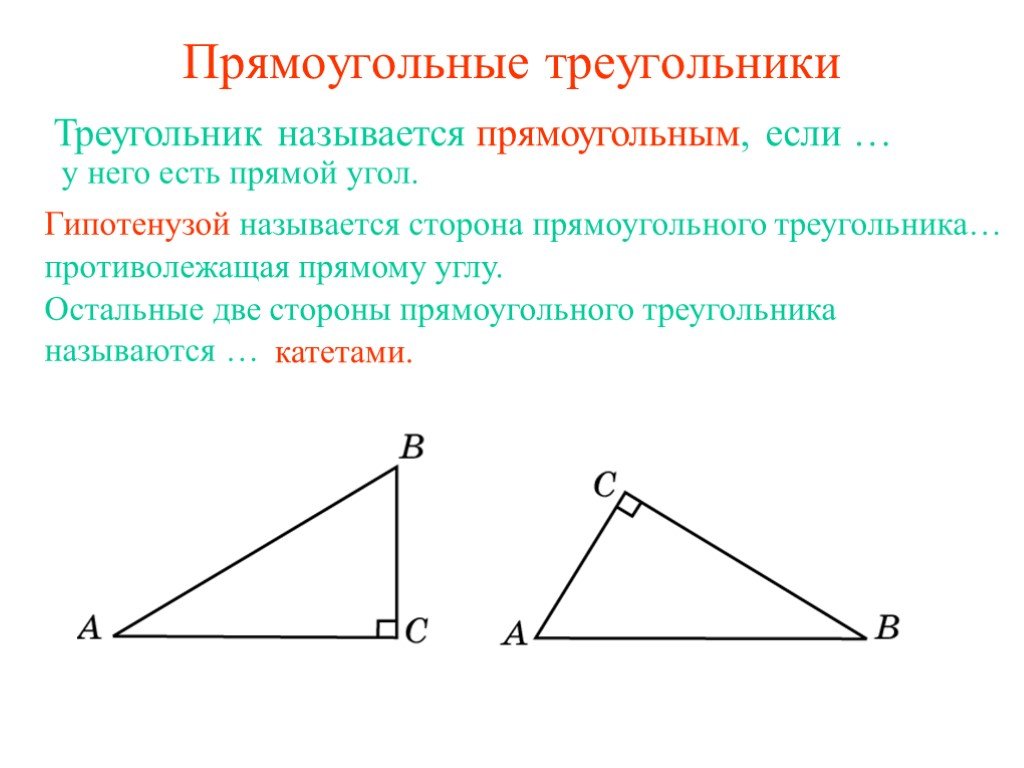 Говорят, что три вершины вместе с ортоцентром образуют ортоцентрическую систему.
Говорят, что три вершины вместе с ортоцентром образуют ортоцентрическую систему.
Пересечение биссектрисы угла находит центр вписанной окружности.
Биссектриса угла треугольника — это прямая, проходящая через вершину и делящая соответствующий угол пополам. Три биссектрисы пересекаются в одной точке, в центре вписанной окружности треугольника. Вписанная окружность — это окружность, лежащая внутри треугольника и касающаяся всех трех сторон. Есть еще три важных круга, экскруги; они лежат вне треугольника и касаются одной стороны, а также продолжения двух других. Центры вписанных и входящих окружностей образуют ортоцентрическую систему.
Пересечение медиан является центром тяжести.
Медиана треугольника — это прямая линия, проходящая через вершину и середину противоположной стороны и делящая треугольник на две равные части. Три медианы пересекаются в одной точке, центре тяжести треугольника.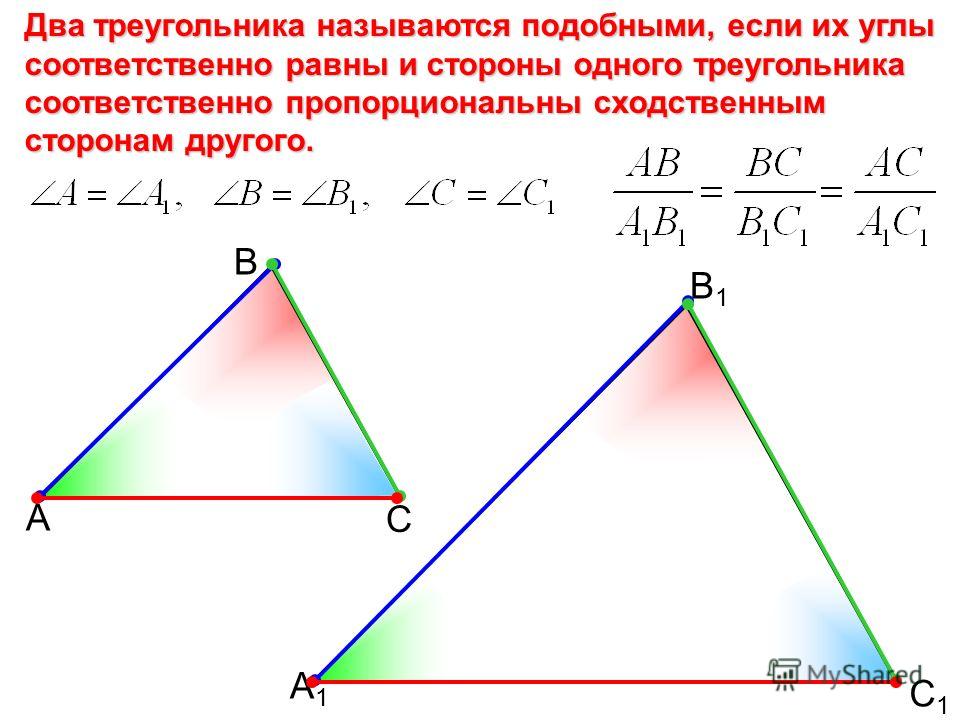 Центр тяжести жесткого треугольного объекта (вырезанного из тонкого листа одинаковой плотности) также является его центром тяжести: объект можно уравновесить на его центроиде. Центроид пересекает каждую медиану в соотношении 2:1, т. е. расстояние между вершиной и центроидом в два раза больше расстояния между центроидом и серединой противоположной стороны.
Центр тяжести жесткого треугольного объекта (вырезанного из тонкого листа одинаковой плотности) также является его центром тяжести: объект можно уравновесить на его центроиде. Центроид пересекает каждую медиану в соотношении 2:1, т. е. расстояние между вершиной и центроидом в два раза больше расстояния между центроидом и серединой противоположной стороны.
Окружность с девятью точками демонстрирует симметрию, при которой шесть точек лежат на ребре треугольника.
Середины трех сторон и основания трех высот лежат на одной окружности, девятиконечной окружности треугольника. Остальные три точки, в честь которых он назван, являются серединами участка высоты между вершинами и ортоцентром. Радиус девятиконечной окружности вдвое меньше радиуса описанной окружности. Он касается вписанной окружности (в точке Фейербаха) и трех внеокружностей.
Линия Эйлера — это прямая линия, проходящая через центр тяжести (оранжевый), ортоцентр (синий), центр описанной окружности (зеленый) и центр девятиконечной окружности (красный).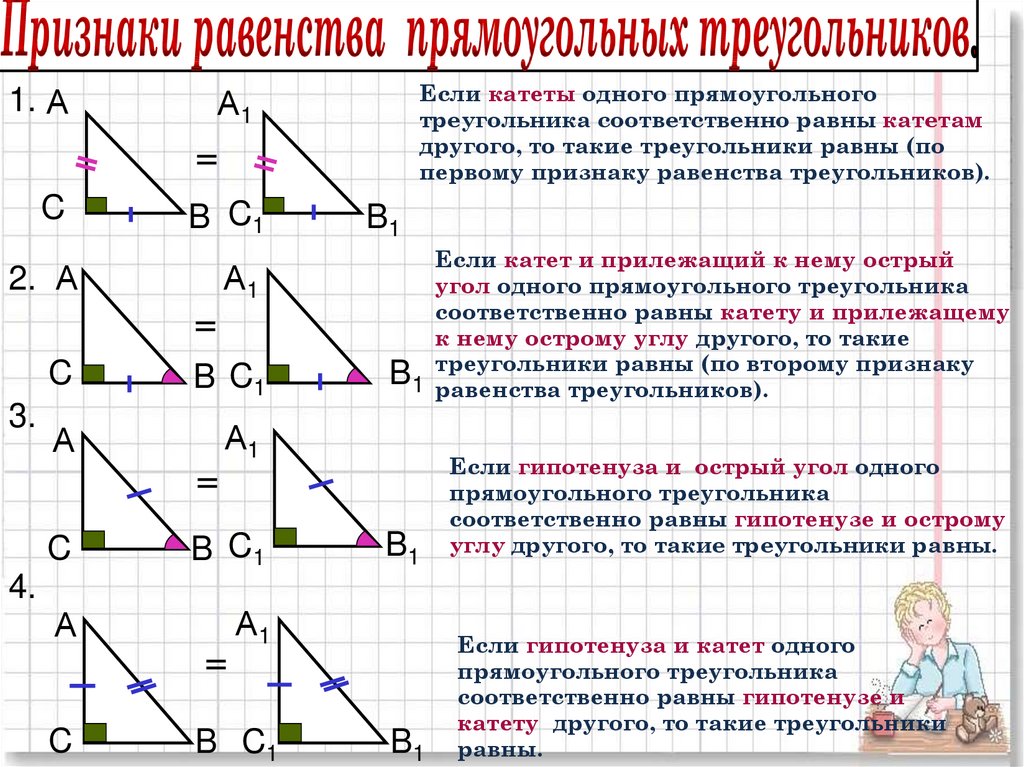
Центроид (желтый), ортоцентр (синий), центр описанной окружности (зеленый) и барицентр девятиконечного круга (красная точка) лежат на одной линии, известной как линия Эйлера (красная линия). Центр окружности с девятью точками находится в средней точке между ортоцентром и центром описанной окружности, а расстояние между центром тяжести и центром описанной окружности составляет половину расстояния между центром тяжести и ортоцентром.
Центр вписанной окружности вообще не лежит на прямой Эйлера.
Если отразить медиану от биссектрисы угла, проходящей через ту же вершину, получится симедиана. Три симедианы пересекаются в одной точке, симедиане треугольника.
Вычисление площади треугольника
Площадь треугольника можно представить как половину площади параллелограмма, имеющего ту же длину и высоту основания.
Вычисление площади треугольника — элементарная задача, часто встречающаяся в самых разных ситуациях.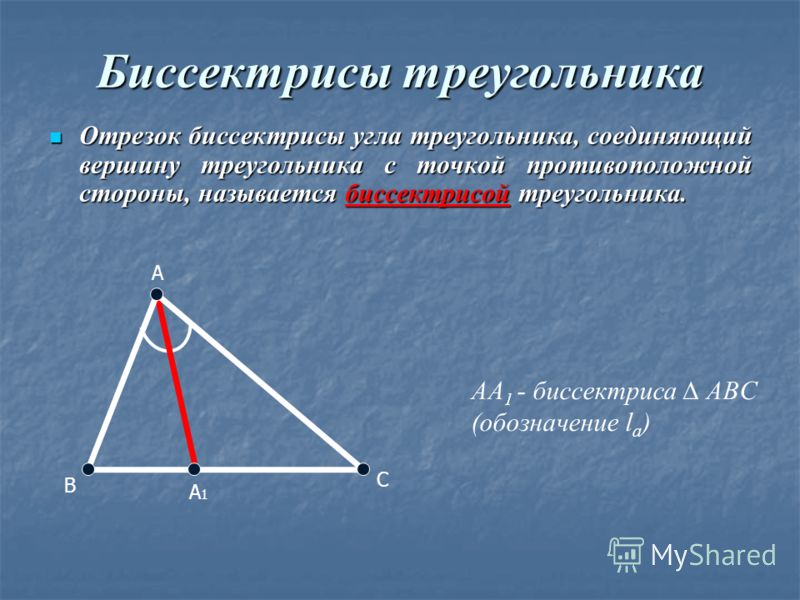 Наиболее известная и простая формула:
Наиболее известная и простая формула:
где площадь, длина основания треугольника и высота или высота треугольника. Термин «основание» обозначает любую сторону, а «высота» обозначает длину перпендикуляра из точки, противоположной стороне, на саму сторону.
Несмотря на простоту, эта формула полезна только в том случае, если высоту можно легко найти. Например, геодезист треугольного поля измеряет длину каждой стороны и может найти площадь по своим результатам без необходимости построения «высоты». На практике могут использоваться различные методы, в зависимости от того, что известно о треугольнике. Ниже приводится подборка часто используемых формул площади треугольника. [8]
Использование векторов
Площадь параллелограмма, вложенного в трехмерное евклидово пространство, можно вычислить с помощью векторов. Пусть векторы AB и AC указывают соответственно из A в B и из A в C. Тогда площадь параллелограмма ABDC равна , что является величиной векторного произведения векторов AB и AC . равно , где h представляет высоту h как вектор.
равно , где h представляет высоту h как вектор.
Площадь треугольника ABC составляет половину этой площади, или
Площадь треугольника ABC также может быть выражена через скалярное произведение следующим образом:
в двумерном эвклидовом пространстве, экспрессируя вектор AB в виде свободного вектора в декартовом пространстве, равном ( x 1 , y 1 ) и AC AS . x 1 ) и AC 3 AS 3. 2 , y 2 ), это можно переписать как:
Применение тригонометрии для нахождения высоты ч .
Использование тригонометрии
Высоту треугольника можно найти с помощью тригонометрии. Используя маркировку, как на изображении слева, высота составляет ч = a sin γ. Подставив это в формулу S = ½ bh , полученную выше, площадь треугольника можно выразить как:
(где α — внутренний угол в точке A, β — внутренний угол в точке B, а γ — внутренний угол в точке C).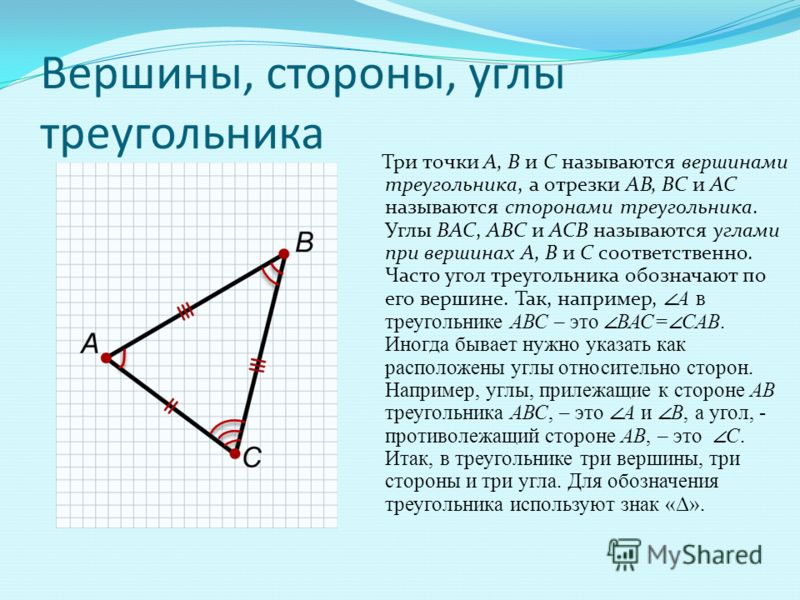
Кроме того, поскольку sin α = sin ( π — α) = sin (β + γ), и аналогично для двух других углов:
Использование координат
Если вершина A расположена в начале координат (0, 0) декартовой системы координат, а координаты двух других вершин заданы как B = ( x B , 3 y B ) и C = ( x C , y C ), то площадь S может быть вычислена как ½ умноженная на абсолютное значение определителя
Для трех основных вершин уравнение выглядит так:
В трех измерениях, площадь общего треугольника {a = ( x A , Y A , Z A ), B = ( x 902 y B , z B ) and C = ( x C , y C , z C )} is the Pythagorean sum of the areas of the respective проекции на три главные плоскости (т.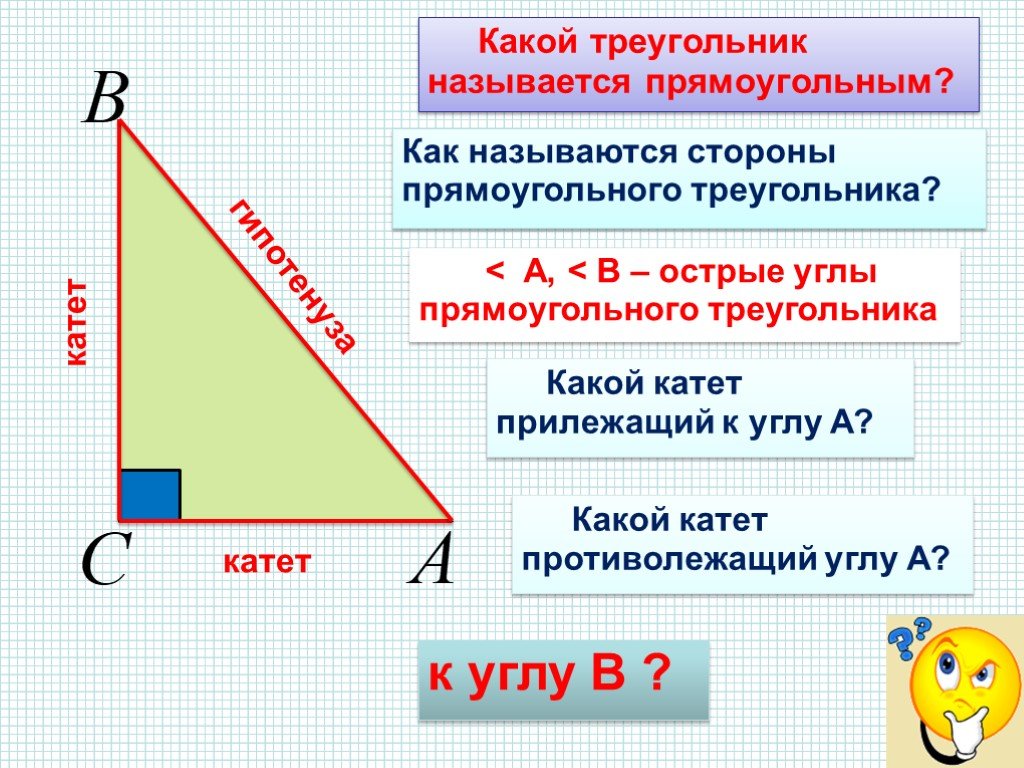 е. x = 0, y = 0 и z = 0):
е. x = 0, y = 0 и z = 0):
Используя формулу Герона
Форма треугольника определяется только длинами сторон. Следовательно, площадь S также может быть получена из длин сторон. По формуле Герона:
где s = ½ ( a + b + c ) – полупериметр или половина периметра треугольника .
Три эквивалентных способа записи формулы Герона:
. .
Вычисление сторон и углов
В целом, существуют различные принятые методы вычисления длины стороны или величины угла. В то время как некоторые методы могут быть подходящими для вычисления значений прямоугольного треугольника, другие могут потребоваться в более сложных ситуациях.
Тригонометрические соотношения в прямоугольных треугольниках
Основная статья: Тригонометрические функции
Прямоугольный треугольник всегда включает в себя угол 90° (π/2 радиана), обозначенный здесь C.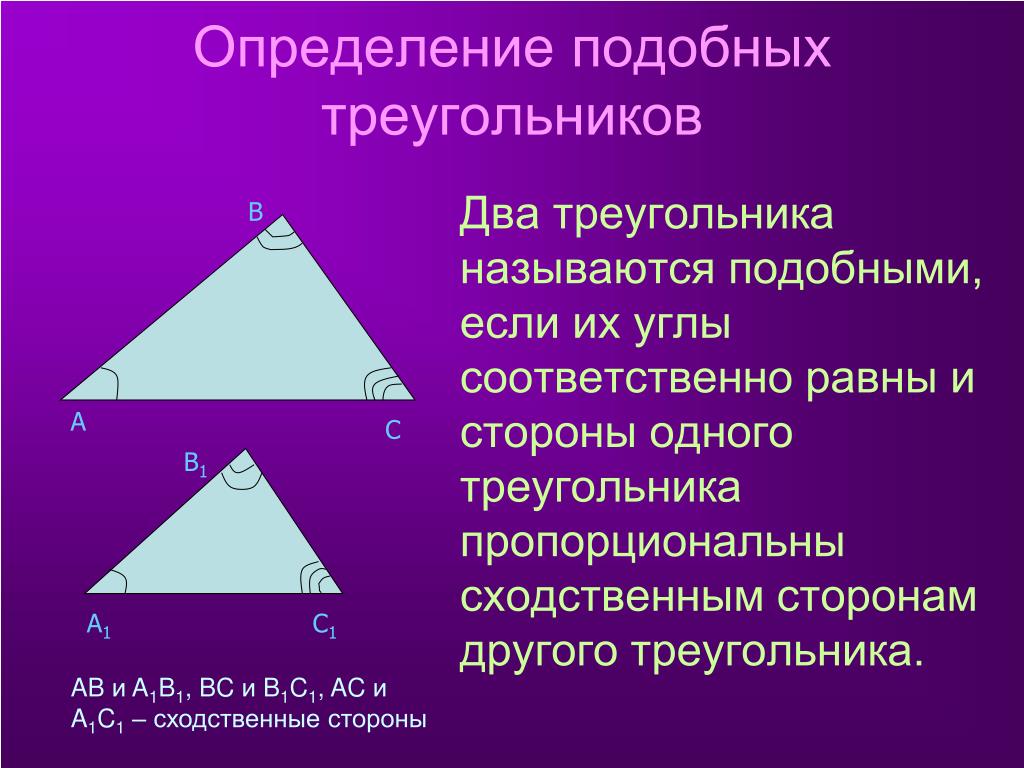 Углы A и B могут различаться. Тригонометрические функции определяют отношения между длинами сторон и внутренними углами прямоугольного треугольника.
Углы A и B могут различаться. Тригонометрические функции определяют отношения между длинами сторон и внутренними углами прямоугольного треугольника.
В прямоугольных треугольниках тригонометрические соотношения синуса, косинуса и тангенса можно использовать для нахождения неизвестных углов и длин неизвестных сторон. Стороны треугольника известны следующим образом:
- Гипотенуза — это сторона, противоположная прямому углу или определяемая как самая длинная сторона прямоугольного треугольника, в данном случае h .
- Противоположная сторона — это сторона, противоположная интересующему нас углу, в данном случае a .
- Смежная сторона — это сторона, которая соприкасается с интересующим нас углом и прямым углом, отсюда и ее название. В этом случае соседняя сторона равна b .
Синус, косинус и тангенс
Синус угла представляет собой отношение длины противоположной стороны к длине гипотенузы.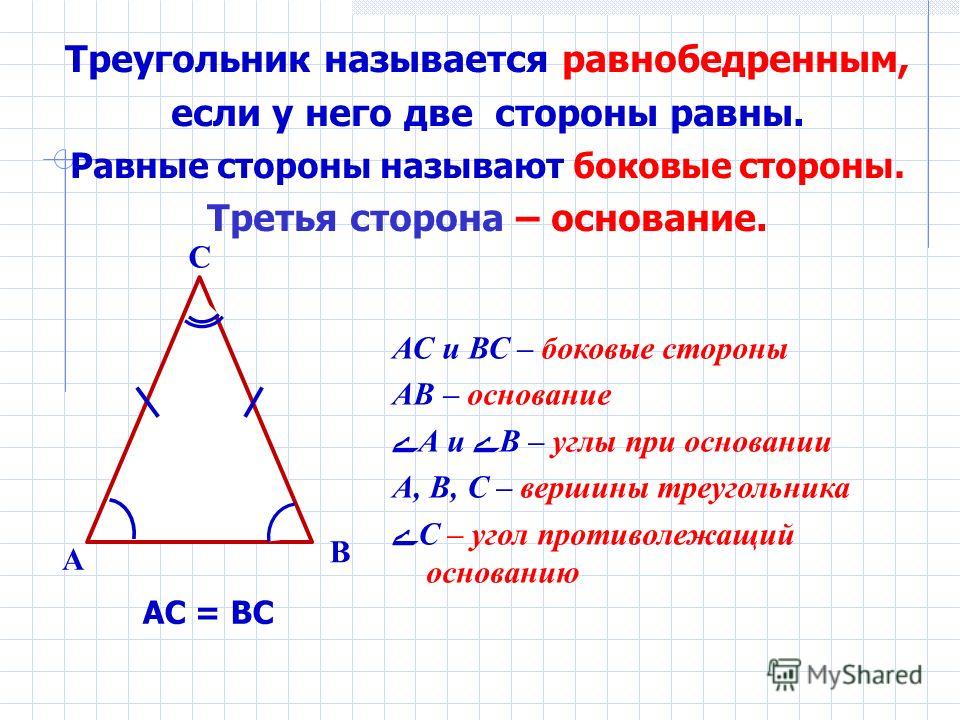 В нашем случае
В нашем случае
Обратите внимание, что это отношение не зависит от конкретного выбранного прямоугольного треугольника, если он содержит угол A , поскольку все эти треугольники подобны.
косинус угла есть отношение длины прилежащего катета к длине гипотенузы. В нашем случае
Тангенс угла представляет собой отношение длины противолежащей стороны к длине прилежащей стороны. В нашем случае
Аббревиатура «SOHCAHTOA» является полезной мнемоникой для этих соотношений.
Обратные функции
Обратные тригонометрические функции можно использовать для вычисления внутренних углов прямоугольного треугольника с длиной любых двух сторон.
Арксинус можно использовать для вычисления угла по длине противоположной стороны и длине гипотенузы.
Arccos можно использовать для расчета угла по длине прилежащей стороны и длине гипотенузы.
Arctan можно использовать для расчета угла по длине противоположной стороны и длине соседней стороны.
Во вводных курсах по геометрии и тригонометрии обозначения sin −1 , cos −1 и т. д. часто используются вместо arcsin, arccos и т. д. Однако arcsin, arccos и т. д. ., обозначения являются стандартными в высшей математике, где тригонометрические функции обычно возводятся в степень, поскольку это позволяет избежать путаницы между мультипликативной инверсией и композиционной инверсией.
Правила синусов и косинусов
Основные статьи: Закон синусов и Закон косинусов
Треугольник со сторонами длиной a, b и c и углами α, β и γ соответственно.
Закон синусов, или правило синусов, [9] гласит, что отношение длины стороны к синусу соответствующего противоположного угла является постоянным, то есть
Это отношение равно диаметру описанной окружности данного треугольника. Другая интерпретация
этой теоремы состоит в том, что каждый треугольник с углами , и
подобен треугольнику с длинами сторон, равными , и . Этот треугольник можно построить, сначала построив круг диаметром 1 и вписав в него два угла треугольника. Длина сторон этого треугольника будет , и . Сторона, длина которой равна, противоположна углу, мера которого равна , и т. д.
Другая интерпретация
этой теоремы состоит в том, что каждый треугольник с углами , и
подобен треугольнику с длинами сторон, равными , и . Этот треугольник можно построить, сначала построив круг диаметром 1 и вписав в него два угла треугольника. Длина сторон этого треугольника будет , и . Сторона, длина которой равна, противоположна углу, мера которого равна , и т. д.
Закон косинусов, или правило косинусов, связывает длину неизвестной стороны треугольника с длиной других сторон и углом, противолежащим неизвестной стороне. Согласно закону:
Для треугольника с длиной сторон , , и углами , , соответственно, учитывая две известные длины треугольника и и угол между двумя известными сторонами (или угол, противоположный неизвестной стороне ), для вычисления третьего стороны можно использовать следующую формулу:
Если известны длины всех трех сторон любого треугольника, можно вычислить три угла:
Неплоские треугольники
Неплоский треугольник — это треугольник, который не содержится в (плоской) плоскости.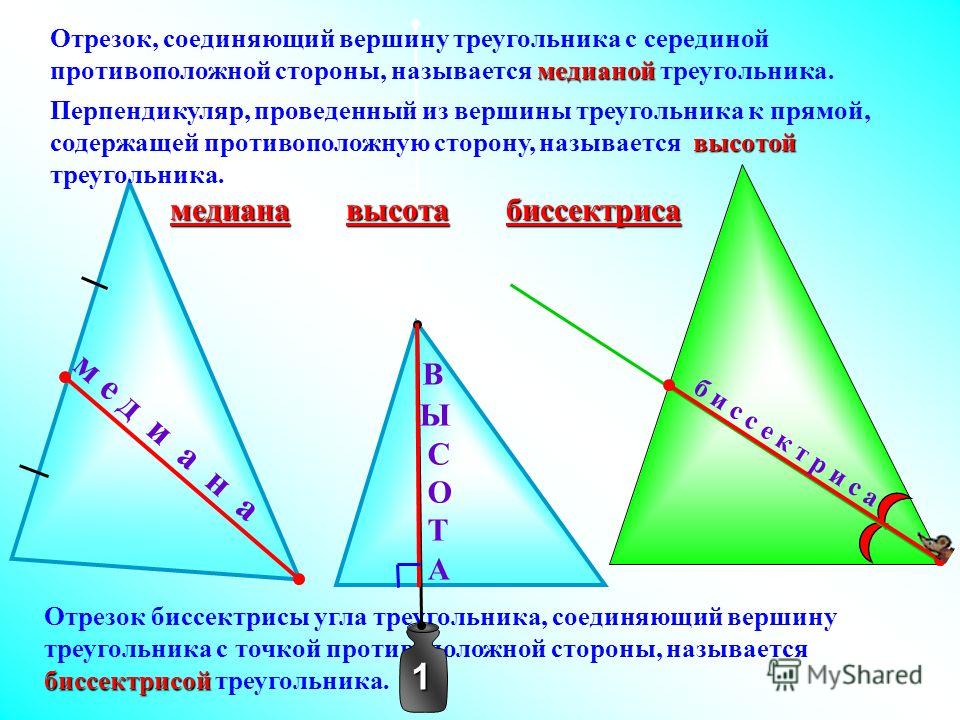 Примерами неплоских треугольников в неевклидовой геометрии являются сферические треугольники в сферической геометрии и гиперболические треугольники в гиперболической геометрии.
Примерами неплоских треугольников в неевклидовой геометрии являются сферические треугольники в сферической геометрии и гиперболические треугольники в гиперболической геометрии.
В то время как сумма внутренних углов в плоских треугольниках всегда составляет 180°, в гиперболическом треугольнике сумма углов меньше 180°, а в сферическом треугольнике сумма углов превышает 180°. Гиперболический треугольник можно получить, рисуя на поверхности с отрицательной кривизной, такой как седловидная поверхность, а сферический треугольник можно получить, рисуя на поверхности с положительной кривизной, такой как сфера. Так, если начертить на поверхности Земли гигантский треугольник, то обнаружится, что сумма его углов больше 180°. На сфере можно нарисовать треугольник, каждый из внутренних углов которого равен 9.0°, что в сумме дает 270°.
См. также
- А-образная рама для дельтапланов, трайков и сверхлегких самолетов
- БАМБИ (геометрия)
- Конгруэнтность (геометрия)
- Точка Ферма
- Неравенство Хадвигера-Финслера
- Тензор инерции треугольника
- Закон косинусов
- Закон синусов
- Закон касательных
- Теорема Лестера
- Список тем треугольника
- Неравенство Оно
- Неравенство Педое
- теорема
- Специальные прямоугольные треугольники
- Центр треугольника
- Треугольный номер
- Треугольная категория
- Триангуляция (топология) многообразия
Ссылки
- ↑ Weisstein, Eric W.
 Равносторонний треугольник . Из MathWorld — веб-ресурса Wolfram. По состоянию на 15 июня 2010 г. .
Равносторонний треугольник . Из MathWorld — веб-ресурса Wolfram. По состоянию на 15 июня 2010 г. . - ↑ Математики традиционно следовали Евклиду (определение 20 Книги 1) в определении равнобедренного треугольника как имеющего ровно две стороны равны, так что исключаются равносторонние треугольники; но современные ссылки, как правило, включают равнобедренные треугольники: определение равнобедренного треугольника в Викисловаре, Вайсштейн, Эрик В. Равнобедренный треугольник . Из MathWorld — веб-ресурса Wolfram. По состоянию на 15 июня 2010 г. .
- ↑ Вайсштейн, Эрик В. Разносторонний треугольник . Из MathWorld — веб-ресурса Wolfram. По состоянию на 15 июня 2010 г. .
- ↑ Зейдлер, Эберхард (2004). Оксфордское руководство пользователя по математике . Издательство Оксфордского университета. 729. ISBN 978-0-19-850763-5.
- ↑ n внешних углов любого n -стороннего выпуклого многоугольника в сумме составляют 360 градусов.

- ↑ Опять же, во всех случаях «зеркальные изображения» тоже похожи.
- ↑ Все пары конгруэнтных треугольников также подобны; но не все пары подобных треугольников конгруэнтны.
- ↑ Вайсштейн, Эрик В. Площадь треугольника . Из MathWorld — веб-ресурса Wolfram. По состоянию на 15 июня 2010 г. .
- ↑ Проф. Дэвид Э. Джойс. «Законы косинусов и синусов». Университет Кларка. http://www.clarku.edu/~djoyce/trig/laws.html. Проверено 1 ноября 2008 г. .
Внешние ссылки
- Площадь треугольника — 7 различных способов
- Анимированные демонстрации построения треугольников с помощью циркуля и линейки.
- Базовый обзор и объяснение треугольников
- Деко Деков: Компьютерная энциклопедия евклидовой геометрии. Содержит несколько тысяч обнаруженных компьютером теорем об интересных точках, связанных с любым треугольником.
- Кларк Кимберлинг: Энциклопедия центров треугольников.


 5).
5).
 9).
9). Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.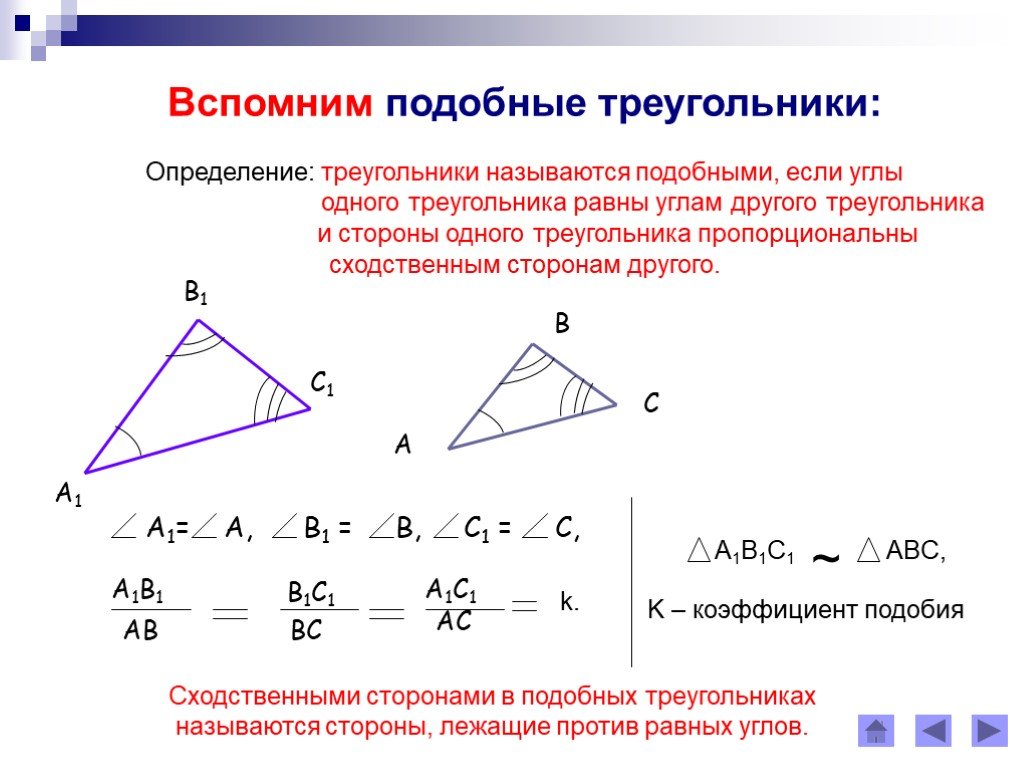

 1 Использование векторов
1 Использование векторов ) [2] Равнобедренный треугольник также имеет два угла одинаковой меры; а именно углы, противоположные двум сторонам одинаковой длины.
) [2] Равнобедренный треугольник также имеет два угла одинаковой меры; а именно углы, противоположные двум сторонам одинаковой длины. Прямоугольные треугольники подчиняются теореме: сумма квадратов длин двух катетов равна квадрату длины гипотенузы: a 2 + b 2 = c 2 , где a и b — длины катетов, а c — длины катетов. Специальные прямоугольные треугольники — это прямоугольные треугольники с дополнительными свойствами, упрощающими расчеты с ними.
Прямоугольные треугольники подчиняются теореме: сумма квадратов длин двух катетов равна квадрату длины гипотенузы: a 2 + b 2 = c 2 , где a и b — длины катетов, а c — длины катетов. Специальные прямоугольные треугольники — это прямоугольные треугольники с дополнительными свойствами, упрощающими расчеты с ними. ( включенный угол для любых двух сторон многоугольника является внутренним углом между этими двумя сторонами.)
( включенный угол для любых двух сторон многоугольника является внутренним углом между этими двумя сторонами.) )
) Теорема о гипотенузе-ноге является частным случаем этого критерия. Условие Сторона-Сторона-Угол само по себе не гарантирует конгруэнтность треугольников, потому что один треугольник может быть тупоугольным, а другой остроугольным.
Теорема о гипотенузе-ноге является частным случаем этого критерия. Условие Сторона-Сторона-Угол само по себе не гарантирует конгруэнтность треугольников, потому что один треугольник может быть тупоугольным, а другой остроугольным.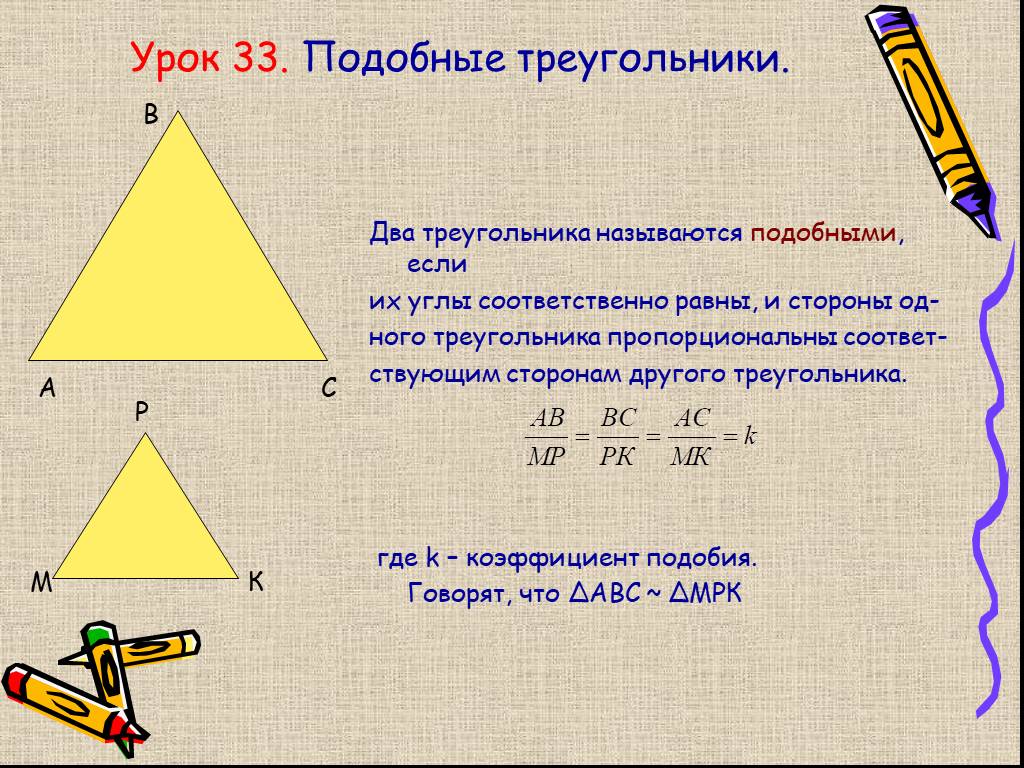
 Равносторонний треугольник . Из MathWorld — веб-ресурса Wolfram. По состоянию на 15 июня 2010 г. .
Равносторонний треугольник . Из MathWorld — веб-ресурса Wolfram. По состоянию на 15 июня 2010 г. .