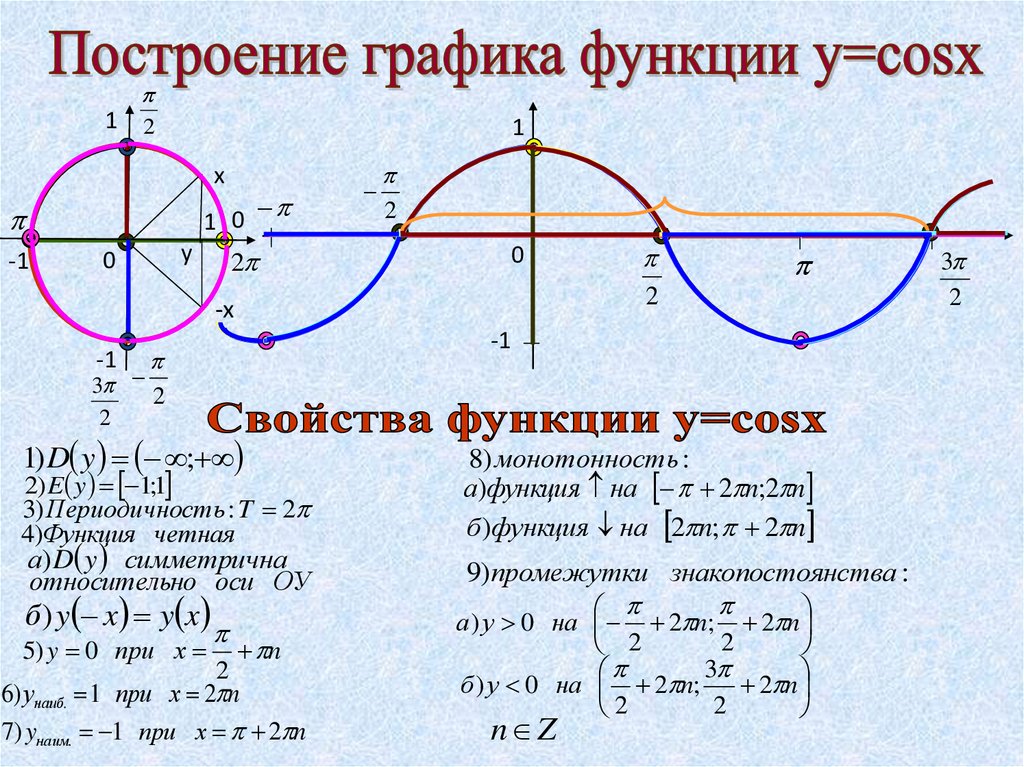
Построить график sin x. Функция y=sinx, ее основные свойства и график. Выражение синуса через косинус
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис.
1).
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график.
Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.
М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
|BD| — длина дуги окружности с центром в точке A .
α — угол, выраженный в радианах.
Синус (sin
α
) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos
α
) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.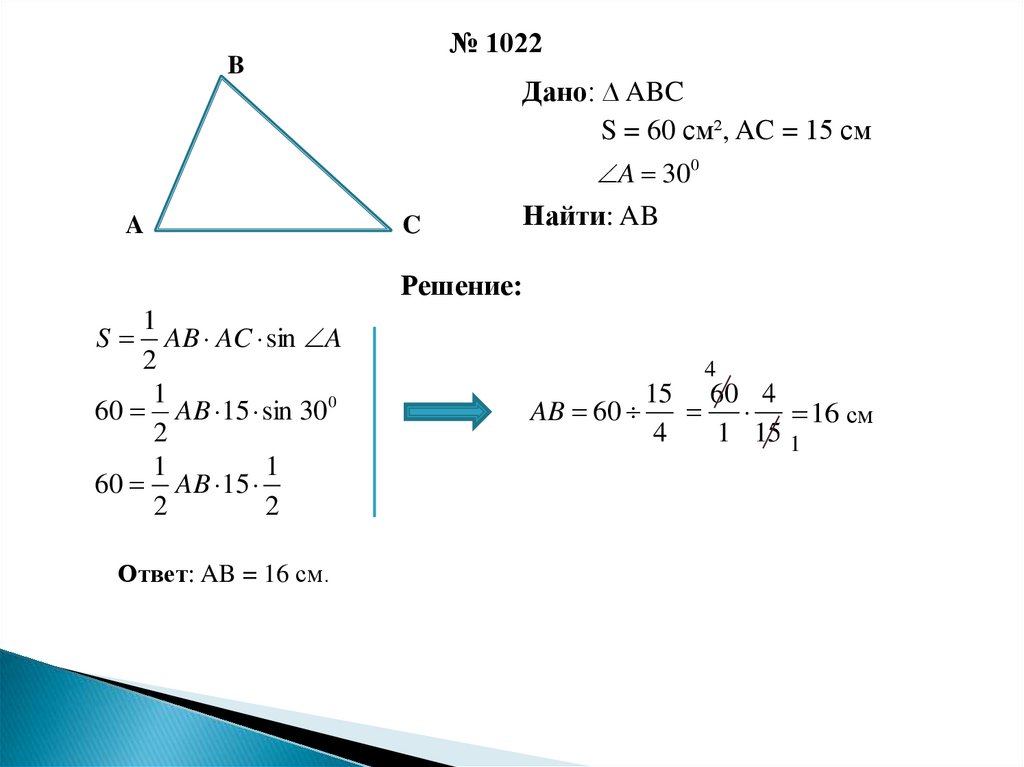
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См. также:
«Йошкар-Олинский техникум сервисных технологий»
Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel
/методическая разработка/
Йошкар – Ола
Тема .
Тип урока – интегрированный (получение новых знаний)
Цели:
Дидактическая цель — исследовать поведение графиков тригонометрической функции y = sinx в зависимости от коэффициентов с помощью компьютера
Обучающие:
1. Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
2. Показать внедрение компьютерных технологий в обучение математике, интеграцию двух предметов: алгебры и информатики.
3. Формировать навыки использования компьютерных технологий на уроках математики
4. Закрепить навыки исследования функций и построения их графиков
Развивающие:
1. Развивать познавательный интерес учащихся к учебным дисциплинам и умение применять свои знания в практических ситуациях
2.
Развивать умения анализировать, сравнивать, выделять главное
3. Способствовать повышению общего уровня развития студентов
Воспитывающие :
1. Воспитывать самостоятельность, аккуратность, трудолюбие
2. Воспитывать культуру диалога
Формы работы на уроке – комбинированная
Дидактическое оснащение и оборудование:
1. Компьютеры
2. Мультимедийный проектор
4. Раздаточный материал
5. Слайды презентации
Ход урока
I . Организация начала урока
· Приветствие студентов и гостей
· Настрой на урок
II . Целеполагание и актуализация темы
Для исследования функции и построения ее графика требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.
Сегодня мы научимся строить графики тригонометрических функций в среде табличного процессора MS Excel 2007.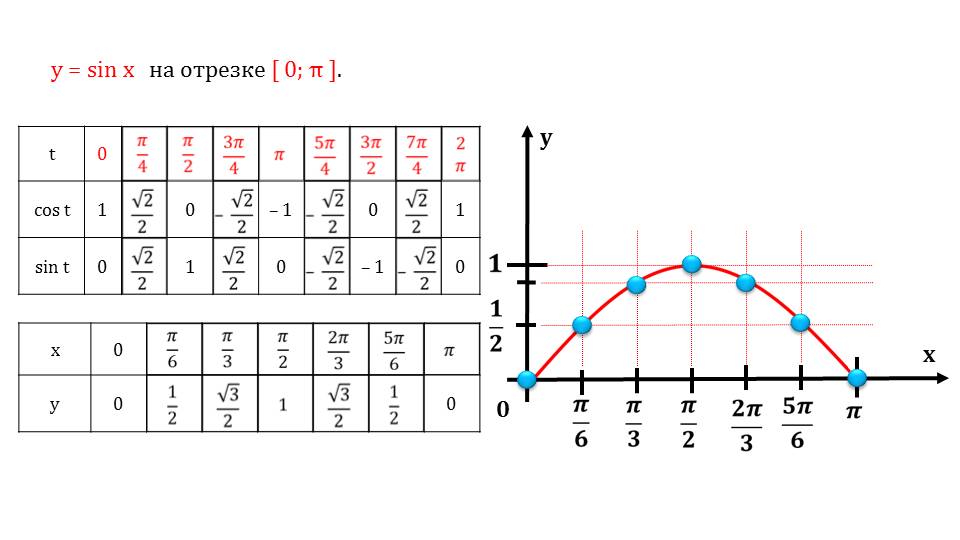
Тема нашего занятия «Построение и исследование графика тригонометрической функцииy = sinx в табличном процессоре»
Из курса алгебры нам известна схема исследования функции и построения ее графика. Давайте вспомним как это сделать.
Слайд 2
Схема исследования функции
1. Область определения функции (D(f))
2. Область значения функции Е(f)
3. Определение четности
4. Периодичность
5. Нули функции (y=0)
6. Промежутки знакопостоянства (у>0, y
7. Промежутки монотонности
8. Экстремумы функции
III . Первичное усвоение нового учебного материала
Откройте программу MS Excel 2007.
Построим график функции y=sinx
Построение графиков в табличном процессоре MS Excel 2007
График данной функции будем строить на отрезке x Є [-2π; 2π]
Значения аргумента будем брать с шагом, чтобы график получился более точным.
Т. к. редактор работает с числами, переведем радианы в числа, зная что П ≈ 3,14 . (таблица перевода в раздаточном материале).
1. Находим значение функции в точке х=-2П. Для остальных значение аргумента соответствующие значения функции редактор вычисляет автоматически.
2. Теперь у нас имеется таблица со значениями аргумента и функции. С помощью этих данных мы должны построить график этой функции с помощью мастера диаграмм.
3. Для построения графика надо выделить нужный диапазон данных, строки со значениями аргумента и функции
4..jpg»>
Выводы записываем в тетрадь (Слайд 5)
Вывод. График функции вида у=sinx+k получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОУ на k единиц
Если k >0, то график смещается вверх на k единиц
Если k
Построение и исследование функции вида у= k *sinx, k — const
Задание 2.
На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
(Чтобы заново не задавать значение аргумента давайте скопируем имеющиеся значения. Теперь вам надо задать формулу, и по полученной таблице построить график.)
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
https://pandia.ru/text/78/510/images/image005_66.gif»>x , на интервале (-2π; 2π) и проследите как изменяется вид графика.
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 8)
https://pandia.ru/text/78/510/images/image008_35.jpg»>
Выводы записываем в тетрадь (Слайд 11)
Вывод.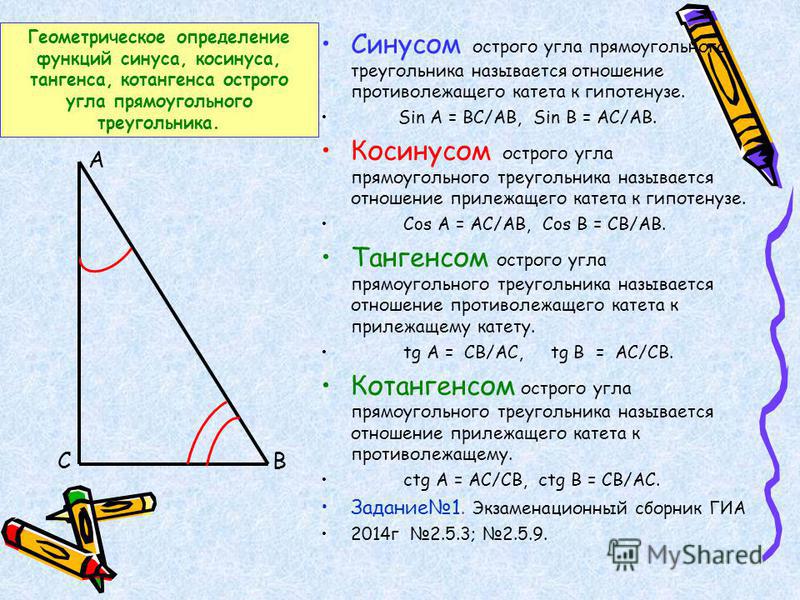
График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
Если k >1, то график смещается вправо вдоль оси ОХ
Если 0
IV . Первичное закрепление полученных знаний
Дифференцированные карточки с заданием на построение и исследование функции при помощи графика
Y=6 *sin(x) | Y= 1-2 sin х | Y= — sin (3х+ ) | |
1. Область определения | |||
2. Область значения | |||
3. | |||
4. Периодичность | |||
5. Промежутки знакопостоянства | |||
6. Промежутки монотонности | |||
Функция возрастает | |||
Функция убывает | |||
7. Экстремумы функции | |||
Минимум | |||
Максимум |
Четность V .
Организация домашнего задания
Построить график функции y=-2*sinх+1 , исследовать и проверить правильность построения в среде электронной таблицы Microsoft Excel. (Слайд 12)
VI . Рефлексия
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0).
С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
Урок и презентация на тему: «Функция y=sin(x). Определения и свойства»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента.
Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X).
Будем строить наш график последовательно, применяя наши свойства.
Начнем
строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.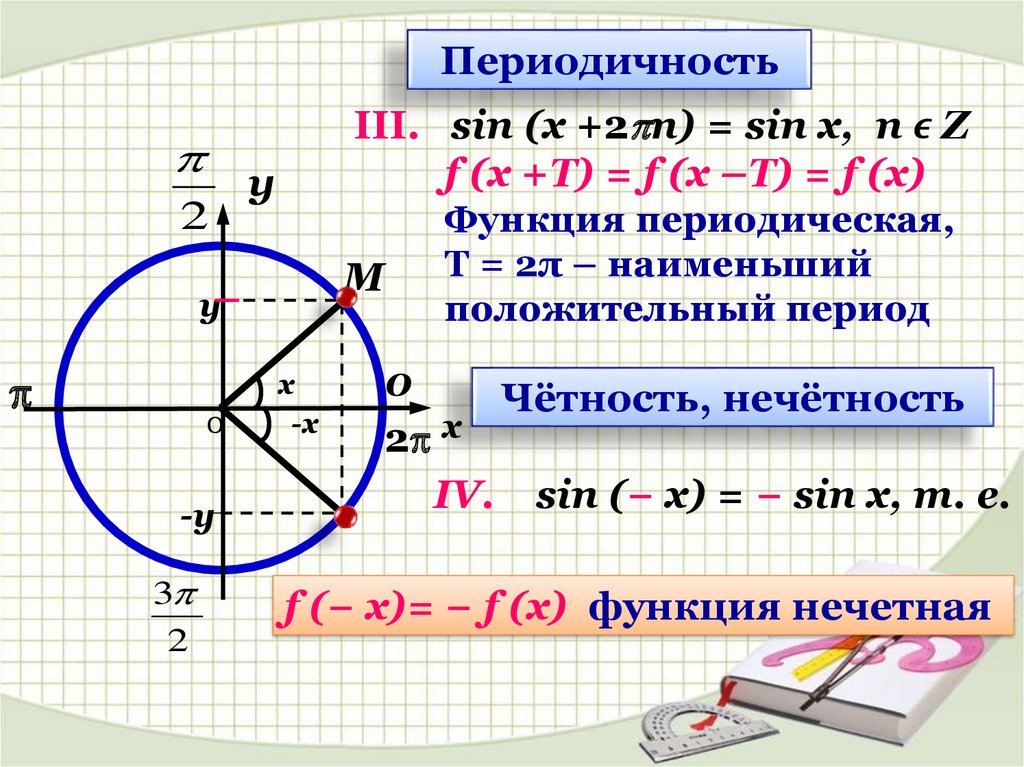
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Свойства треугольника – правило косинуса
Правило косинуса можно использовать в треугольнике, когда вы хотите связать три стороны с одним конкретным углом треугольника. Таким образом, это считается важным свойством треугольников, особенно если это непрямоугольный треугольник. Формула правила косинуса очень похожа на формулу теоремы Пифагора, поэтому ее легко запомнить. На самом деле это обобщение теоремы Пифагора, и мы скоро узнаем, как это сделать. Эта концепция очень полезна для определения недостающих длин или углов треугольника.
Правило косинуса гласит, что квадрат длины любой стороны треугольника равен разнице между суммой квадратов длин двух других сторон и удвоенным произведением длин двух других сторон на косинус угла между ними. Это также известно как закон косинусов.
Объяснение правила косинуса: Чтобы понять приведенное выше правило, мы обратимся к следующему треугольнику
ABC.
Здесь в треугольнике ABC длины соответствующих сторон равны a, b и c. ∠A находится напротив стороны длины a, ∠B напротив стороны длины b и ∠C напротив стороны длины c.
В соответствии с законом косинусов формула правила косинуса может быть получена как-
Следовательно, мы видим, что правило косинуса является обобщенной формой теоремы Пифагора. С помощью приведенных выше трех уравнений мы можем рассчитать длину сторон или измерить углы между ними. Находя углы ∠A, ∠B или ∠C, мы можем переписать формулы следующим образом:
Доказательство теоремы косинусов «а», а угол, противоположный стороне, обозначается как ∠A.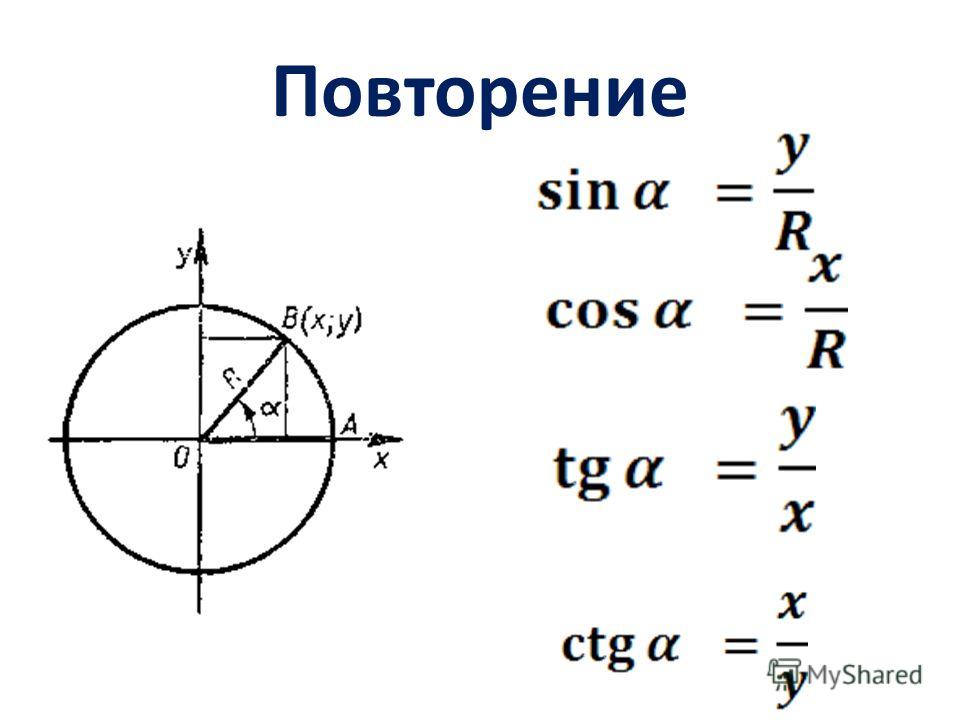
Теперь sin A = h/c h = c sin A [поскольку косинус угла есть отношение перпендикуляра к гипотенузе прямоугольного треугольника.]
Аналогично, cos A = r/c r = в. cos A
Используя теорему Пифагора, мы имеем,
Следовательно, формула правила косинуса доказана. Однако это не единственный метод доказательства закона косинуса. Формула правила косинуса также может быть получена с помощью любого из следующего:
- Формула расстояний
- Теорема Птолемея
- Геометрия окружностей
- Теорема Пифагора
- Правило синусов
- Векторы
Теперь разработаем концепцию с помощью решенных примеров.
Задачи на краткое правило Важность использования правила косинусаВсе студенты, изучающие математику, должны понимать правила косинуса по следующим причинам:
- Используя формулу правила косинуса , вы можете найти недостающий угол или недостающую сторону треугольника, если вы знаете длины других сторон.
- Закон косинуса улучшает ваше понимание тригонометрических функций, таких как косинус, синус, тангенс, котангенс, секанс и косеканс.
- Правило косинуса также помогает в развитии концепций векторов.
Правило косинуса — это свойство треугольника, которое связывает все три стороны треугольника с одним из его углов. Это полезно для нахождения длины стороны, если известны длины других сторон и угол между ними. Кроме того, мы можем использовать формулу правила косинуса, чтобы найти недостающий угол, если длина трех сторон треугольника указана. Здесь мы научились математически выражать закон косинусов, подкрепили наши понятия примером и поняли его важность в математике.
Симметрия | Бесплатный полнотекстовый | Явные свойства q-косинусных и q-синусных полиномов Эйлера, содержащих симметричные структуры
1. Введение
В 1990 году Джексон, опубликовавший влиятельные статьи по этому вопросу, ввел q-число и основы его обозначения, см.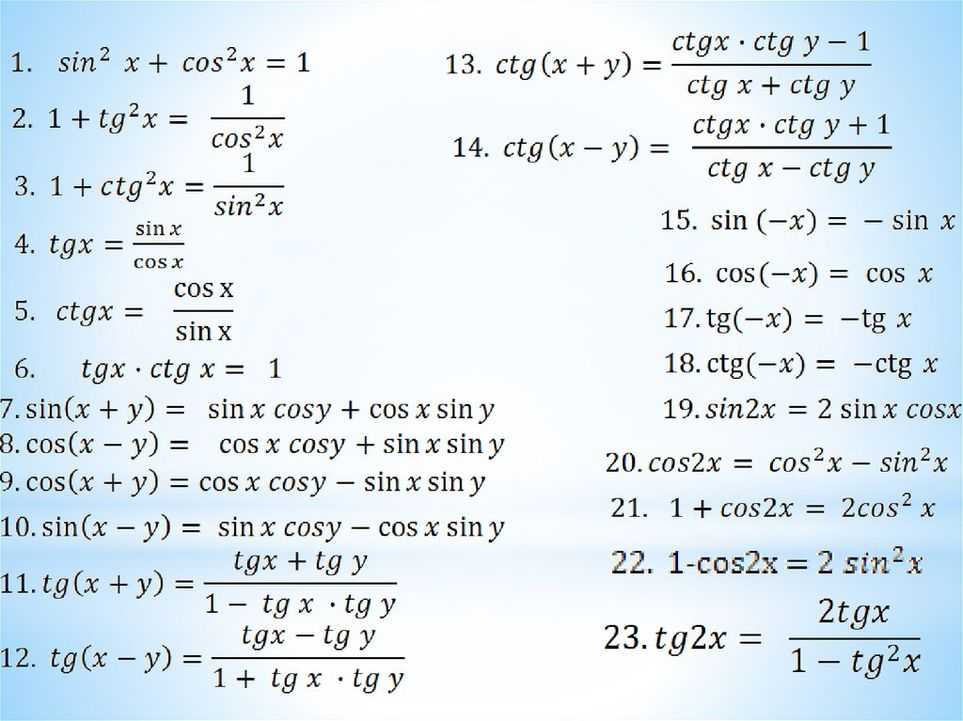
[1]. Флореанини и Вине обнаружили, что некоторые свойства q-ортогональных полиномов связаны с алгеброй q-осцилляторов в [1,2,3,4]. Мы начнем с введения нескольких определений, связанных с q-числами, используемыми в этой статье, см. [3,5,6,7,8].
В этой статье символы N, Z, R и C обозначают набор натуральных чисел, набор целых чисел, набор действительных чисел и набор комплексных чисел соответственно.
Для a∈C, n∈N и |q|<1 факториал со сдвигом q определяется формулой
Хорошо известно, что
Пусть x,q∈R с q≠1. Число
называется q-числом. Заметим, что limq→1[x]q=x. В частности, для k∈Z [k]q является q-целым числом.
После появления q-чисел многие математики стали изучать такие темы, как q-дифференциальные уравнения, q-ряды и q-тригонометрические функции. Конечно, математики также строили и исследовали q-гауссовские биномиальные коэффициенты, см.
[2,3,4,7,8,9,10,11].
При r=0 заметим, что m0q=0 при 0≤r≤m, а также заметим, что [n]q!=[n]q⋯[2]q[1]q и [0]q !=1.
Заметим, что limq→1eq(z)=ez. Экспоненциальная функция расширяется до степенных выражений двух q-экспоненциальных функций путем объединения с q-числами. Кроме того, q-производные и q-интегралы широко изучались многими математиками, см. [1,5,12]. После определения предельных формул для q-экспоненциальных функций, взятых из работы Роулингса [10], несколько других интересных разложений в q-ряды были представлены в классической книге Эндрюса [5].
Доказательство теоремы 1 и других свойств q-экспоненциальных функций можно найти в [2,13].
Заметим, что Dqf(0)=f′(0). Можно доказать, что f дифференцируема в 0, и ясно, что Dqxn=[n]qxn−1.
В 2002 г. Кац и Покман опубликовали книгу о квантовом исчислении, включая q-производные и q-аналог (x−a)n и q-тригонометрические функции, см. [14].
В 2004 г. Гаспер и Рахман представили подробное описание основного q-гипергеометрического ряда, см.
[4]. В течение последних трех десятилетий одним из мостов между наукой и прикладной математикой было q-исчисление, см. [10]. Основываясь на вышеуказанных концепциях, многие математики исследовали различные области математики, включая q-дифференциальные уравнения, q-ряды, q-гипергеометрические функции, а также q-гамма и q-бета-функции. Более того, различные дискретные распределения, объединяющие q-числа, можно найти в [2]. Поэтому q-исчисление играет важную роль во многих различных областях математики.
Многие исследователи, изучавшие полиномы Бернулли, Эйлера и Генокки в различных областях, осознавали важную роль q-исчисления в математике. В течение долгого времени темы многочленов Бернулли, Эйлера и Генокки широко изучались во многих математических приложениях, включая аналитическую теорию чисел, комбинаторный анализ, p-адическую аналитическую теорию чисел и другие области. Поэтому многие математики начали исследовать полиномы Бернулли, Эйлера и Генокки, объединяющие q-числа, см.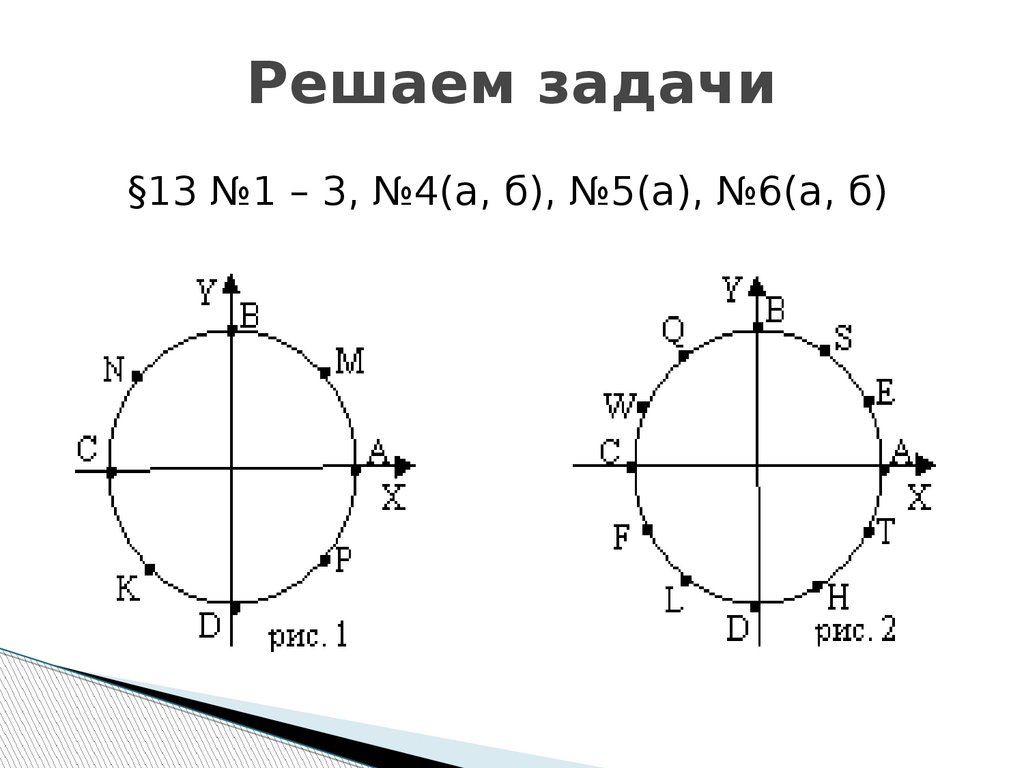
[9].,13,15,16,17,18,19,20,21].
На следующей диаграмме кратко поясняется связь между различными типами вырожденных полиномов Эйлера, полиномов Эйлера и полиномов q-Эйлера. Полиномы в первой строке исследованы Калитцем [21], Кимом и Рю [16] соответственно. Изучение второго ряда диаграммы дало полезные результаты в комбинаторике и теории чисел. В частности, косинус- и синус-многочлены Эйлера во второй строке диаграммы содержат в этой статье мотив. Это связано с тем, что у нас есть несколько вопросов относительно того, что является формой определения q-косинусных и q-синусных полиномов Эйлера и чем отличаются свойства между q-косинусными, q-синусными полиномами Эйлера и косинусными, синусными полиномами Эйлера.
Основной темой этой статьи является построение q-косинусных и q-синусных полиномов Эйлера с использованием определений 4 и 5. Кроме того, мы выводим тождества и свойства для этих полиномов в третьей строке диаграммы.
Определение полиномов q-Эйлера третьей строки таково.
Недавно Ким и Рю представили основные понятия косинусных и синусных многочленов Эйлера. В [16] определения и репрезентативные свойства косинусных и синусных многочленов Эйлера таковы.
В этой статье мы обозначаем, что En(C)(x,y)=CEn(x,y) и En(S)(x,y)=SEn(x,y).
На основании [16], содержащей определение 7 и теорему 3, многие исследователи находили различные расширенные числа и многочлены и их тождества, см. [15,20].
Основная цель этой статьи — найти различные свойства q-косинусных и q-синусных многочленов Эйлера, такие как теорема сложения, частная q-производная, основные симметричные свойства и т.д. В разделе 2 мы строим q-косинусные и q-синусные полиномы Эйлера. Затем, используя q-исчисление, мы определяем основные свойства этих многочленов. Раздел 3 представляет исследование особых свойств q-косинусных и q-синусных полиномов Эйлера, таких как идентичность q-синусных полиномов Эйлера с использованием q-аналогов вычитания и сложения. Это основано на свойствах q-тригонометрических и q-экспоненциальных функций.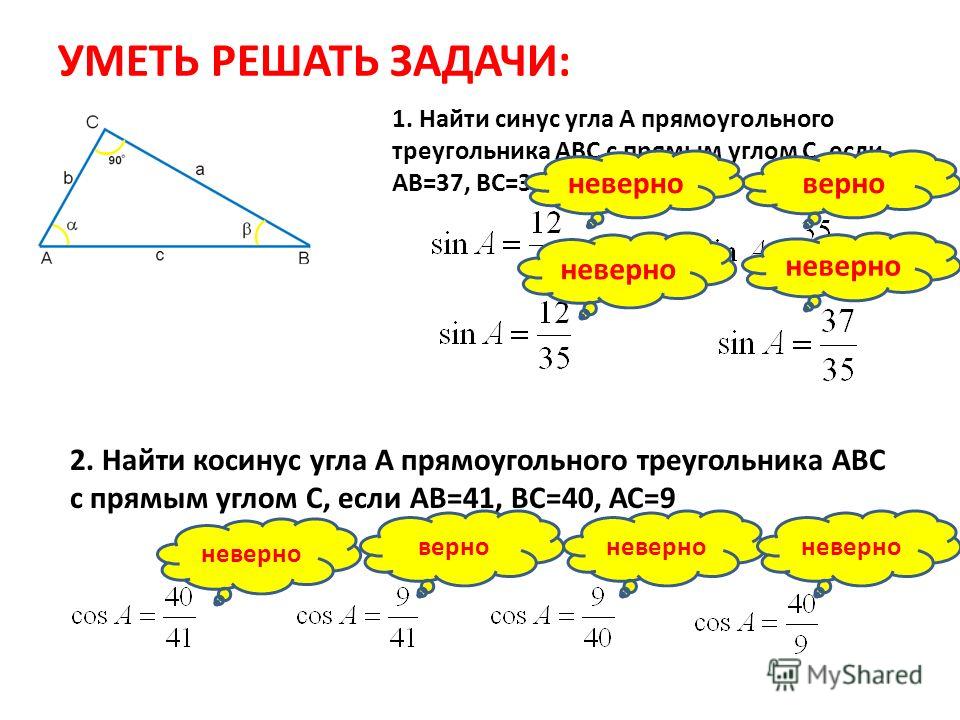
Кроме того, мы выводим соотношения между q-косинусными и q-синусными полиномами Эйлера и q-косинусными и q-синусными полиномами Бернулли. В разделе 4 мы показываем структуру приближенных корней для q-косинусных и q-синусных полиномов Эйлера и находим свойства этих полиномов. Приведем несколько рисунков приближенных корней этих полиномов на комплексной плоскости с помощью метода Ньютона.
2. Некоторые основные свойства q-косинусных и q-синусных полиномов Эйлера
В этом разделе мы строим q-косинусный и q-синусный полиномы Эйлера с помощью теоремы 4. Из производящих функций этих полиномов получаем некоторые основные свойства и тождества. Кроме того, мы выводим симметричные свойства и частные производные по q для q-косинусных и q-синусных многочленов Эйлера.
Из определения 8 q-косинусные полиномы Эйлера могут быть подтверждены следующим образом: -синус-полиномы Эйлера можно найти в теореме 4.
В [15] Cn,q(x,y) и Sn,q(x,y) определяются следующим образом:
В [18] Лю и Ван изучили некоторые симметрические свойства многочленов Бернулли и Эйлера.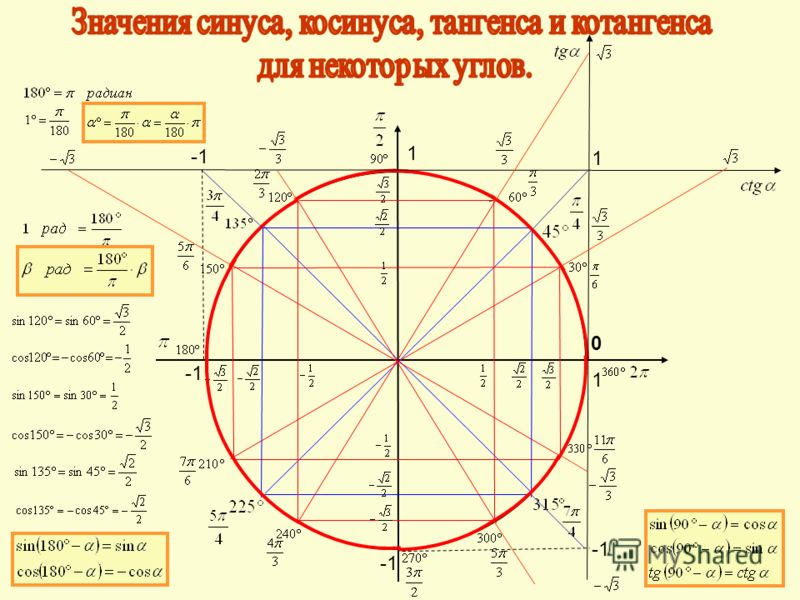
Основываясь на приведенной выше статье, мы наблюдаем некоторые симметричные свойства q-косинусных и q-синусных полиномов Эйлера. Более того, симметричные свойства можно обнаружить у косинусных и синусных многочленов Эйлера.
3. Некоторые специальные свойства q-косинусных полиномов Эйлера и q-синусных полиномов Эйлера
В этом разделе мы получаем некоторые специальные свойства q-косинусных и q-синусных полиномов Эйлера, используя свойства q-тригонометрических функций, ( x⊕y)q и так далее. Кроме того, мы находим различные типы отношений между q-косинусными, синусными полиномами Эйлера и другими полиномами.
Чтобы найти связь между q-косинусными полиномами Эйлера и q-косинусными полиномами Бернулли, напомним определения q-косинусных и q-синусных полиномов Бернулли, см. [15]. Q-косинус-полиномы Бернулли CBn(x,y) и q-косинус-полиномы Бернулли SBn(x,y) определяются с помощью производящих функций
4.
Симметричные структуры приближенных корней q-косинусных полиномов Эйлера и их применениеВ этом разделе мы покажем фактические формы q-косинусных и q-синусных полиномов Эйлера, используя теоремы из раздела 2 и программу Mathematica. Мы наблюдаем структуру приближенных корней этих многочленов и находим некоторые свойства. Мы также показываем примеры q-косинусных полиномов Эйлера с использованием метода Ньютона.
Сначала мы обсудим q-косинусные полиномы Эйлера. Вот несколько форм q-косинусных полиномов Эйлера:
Далее мы покажем приблизительную таблицу корней q-косинусных полиномов Эйлера. На основе уравнения (83) построим таблицу 1 для приближенных корней q-косинусных многочленов Эйлера. В таблице 1 мы варьируем значения p и n, когда y=7. Тогда мы получим только действительные корни с 1≤n≤7 при q=0,5 и q=0,9.
Из таблицы 1 можно рассмотреть два превью:
- (1)
При увеличении n абсолютные значения действительных корней приближаются примерно к 2,345 и 1 при q=0,1.
- (2)
Когда q приближается к 1, приближенное распределение корней q-косинусных многочленов Эйлера размазывается, и большинство из них выглядят как действительные корни.
На рис. 1 показана структура аппроксимационных корней q-косинусных многочленов Эйлера. Пусть y=7 и 1≤n≤30. Левый график на рисунке 1 соответствует q=0,99, средний график соответствует q=0,9, а правый график соответствует q=0,8. Синий цвет означает, что n мало, а красный цвет означает, что n равно 30. На рисунке 1 показано, что приближенные корни q-косинусных полиномов Эйлера включают все действительные числа в q=0,9.9, когда n=30. Кроме того, мы предполагаем, что приближенные корни q-косинусных многочленов Эйлера имеют структуру круга около 0, когда q приближается к 0, а n продолжает расти.
На рис. 2 показана трехмерная структура рис. 1 при тех же условиях. Левая фигура — это приблизительные корни полиномов Эйлера q-косинуса при q=0,99, y=7 и 1≤n≤30. Эта форма указывает на то, что все приближенные корни расположены на воображаемой оси.
Средняя фигура на рисунке 2 показывает приблизительные корни полиномов Эйлера q-косинуса при q = 0,9., y=7 и 1≤n≤30. Здесь мы можем наблюдать движение приближенных корней. Когда q = 0,8 и y = 7, мы можем видеть правильную форму на рисунке 2. Изменение формы на рисунке 2 означает, что приблизительные корни из действительных чисел изменяются на мнимые и что структура корней для q-косинусных полиномов Эйлера изменяется в зависимости от к q.
На рис. 3 q=0,99 и y=7 при 1≤n≤30. В этих условиях мы наблюдаем, что приближенные корни q-косинусных многочленов Эйлера обладают свойством симметрии и включают в себя все действительные числа. Наблюдая за правильными графиками на рисунках 1 и 3, мы можем рассмотреть гипотезу 2.
Используя метод Ньютона (см. [22]), мы получаем следующий пример 1. Уравнение левой фигуры в примере 3 имеет вид 1,1965181875000004+2,912903125000001x−5,745637500000002×2−0,5555×3+x4, то есть q=0,1. В Таблице 1 мы отмечаем, что приблизительные корни составляют -2,33937, -0,271276, 0,795233 и 2,37091, где q=0,1 и y=7.
Когда мы выбираем −4≤Re(x)≤4 и −4≤Im(x)≤4, мы получаем левую фигуру на комплексной плоскости. Комплексные числа в красном, фиолетовом, желтом и небесно-голубом диапазонах приближаются к −2,339.7, -0,271276, 0,795233 и 2,37091 соответственно. Правый рисунок в примере 3 иллюстрирует 4-й q-косинусный полином Эйлера при q=0,5 и y=7. Числа красного, фиолетового, желтого и небесно-голубого диапазонов на комплексной плоскости становятся соответственно −7,20113, −0,610105, 1,36484 и 7,3839 (рис. 4).
5. Выводы
В этой статье мы выявили несколько свойств q-косинусных полиномов Эйлера и q-синусных полиномов Эйлера. Кроме того, связь между полиномами была подтверждена по различным условиям переменных. Мы смогли предположить структуру приближенных корней q-косинусных полиномов Эйлера и q-синусных полиномов Эйлера и, наконец, сделать некоторые предположения. Структура приближенных корней будет складываться по-разному в зависимости от состояния переменных, и необходимо создавать и доказывать новые методы и теоремы, связанные с приближением к этому.