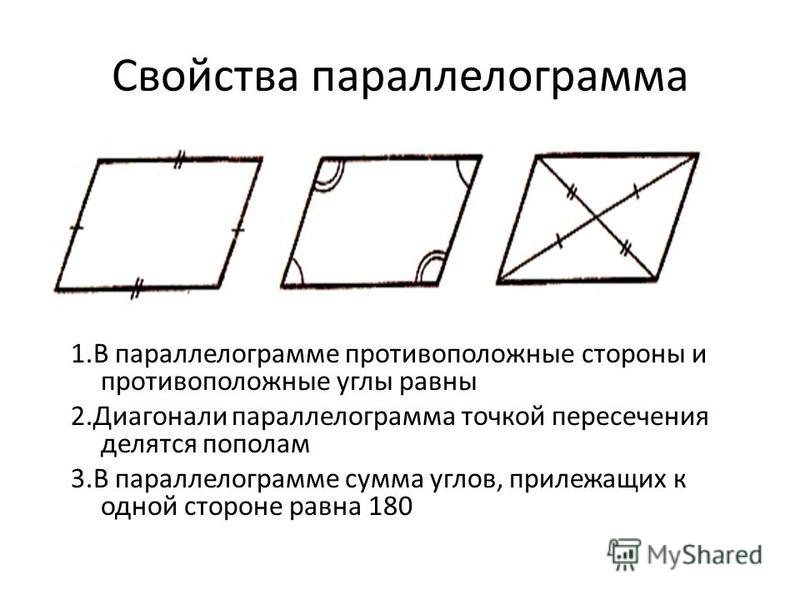
Геометрия: свойства параллелограмма — intmag24.ru
Опубликовано от Admin — Оставить комментарийПараллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
При этом параллелограмм обладает всеми свойствами четырехугольника. Поэтому запоминать надо свойства, которые характерны для параллелограмма.
Определения:
Высота параллелограмма (h) — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Частными случаями параллелограмма являются ромб, прямоугольник и квадрат.
Свойства углов и сторон параллелограмма
- Сумма углов параллелограмма равна 360°
- Сумма любых двух соседних углов параллелограмма равна 180°.
На рисунке: ∠A+∠B=180∘,∠A+∠D=180∘,∠C+∠B=180∘,∠C+∠D=180∘.
- У параллелограмма противоположные углы равны.
На рисунке: ∠A=∠C,∠B=∠D. - У параллелограмма противоположные стороны параллельны и равны.
На рисунке: AB||CD и BC||AD; AB=CD,BC=AD.
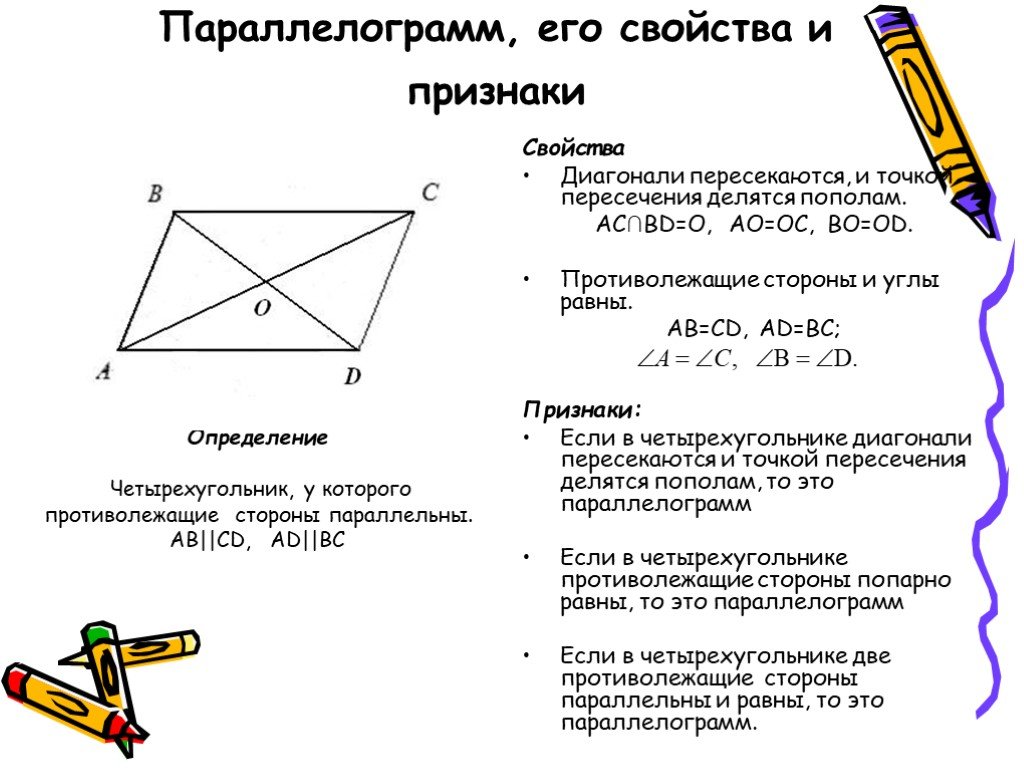
Диагонали параллелограмма
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников).
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Признаки параллелограмма
- Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм. На рисунке: AB=CD,BC=AD.
- Если в четырёхугольнике противоположные углы попарно равны, то этот четырёхугольник – параллелограмм. На рисунке: ∠A=∠C,∠B=∠D.
- Если в четырёхугольнике две противоположные стороны параллельны и равны, то этот четырёхугольник – параллелограмм.
 На рисунке: AB=CD,AB||CD.
На рисунке: AB=CD,AB||CD. - Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. На рисунке: AO=CO,BO=DO.
Параллелограмм и окружность
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Таким образом, если в параллелограмм можно вписать окружность, то это – ромб.
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°. Таким образом, параллелограмм, вписанный в окружность – это прямоугольник. Центр окружности совпадает с точкой пересечения диагоналей.
Основные формулы:
Стороны и диагональ связаны соотношением:
Периметр параллелограмма:
Площадь параллелограмма можно найти по трём формулам.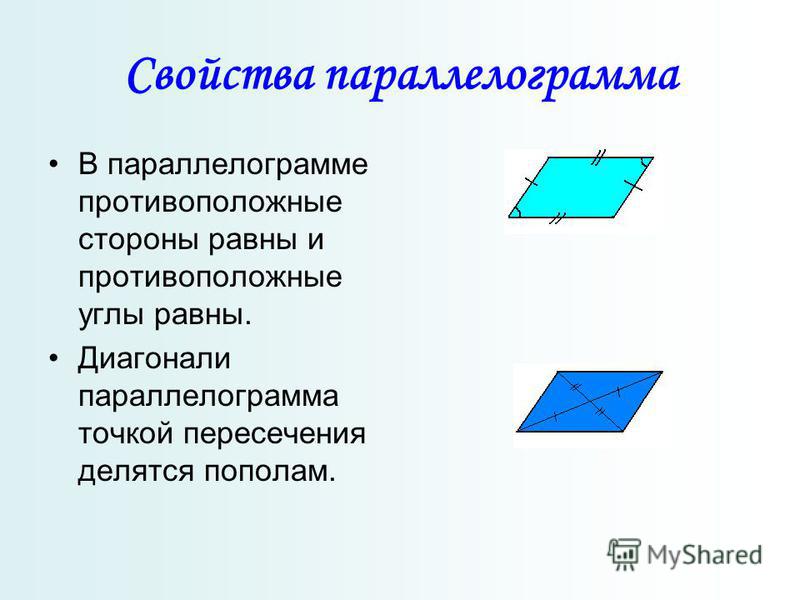
1. Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
2. Площадь параллелограмма равна произведению двух смежных (соседних) сторон на синус угла между ними.
3. Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
Комментарий:
- a, b — длины сторон,
- d1, d2 –диагонали,
- P-периметр,
- S-площадь,
h-высота, проведенная к противоположной стороне - α — угол между сторонами параллелограмма,
- γ — угол между диагоналями параллелограмма (острый).
Рубрика: Для школьников
Метки Математика, Геометрия
конспект урока «Параллелограмм. Свойство диагоналей параллелограмма.
Тема. Параллелограмм. Свойство диагоналей параллелограмма.
Свойство диагоналей параллелограмма.
Цель: ввести определение, понятие о признаках и свойствах параллелограмма; научить доказывать соответствующие теоремы и применять их при решении задач; содействовать рациональной организации труда обучающихся.
Ход урока
Оргмомент.
Актуализация опорных знаний.
1. Устно по рисунку определить:
а) Параллельны ли прямые NP и MQ? (Да)
б) Параллельны ли прямые MN и PQ? (Нет)
в) Чему равен угол Q?
2. Задача. В четырехугольнике ABCD все стороны равны. Докажите, что противолежащие углы A и C равны. (Сделайте дополнительное построение: проведите диагональ BD).
3. Какая фигура называется четырехугольником?
III. Сообщение темы урока.
– Сегодня на уроке мы начнём знакомиться с видами четырёхугольников. Первый из них параллелограмм . Введём определение параллелограмма, а так же понятие о признаках и свойствах параллелограмма.
Формирование новых понятий.
Стр. 68, пункт 51. — прочитайте определение параллелограмма, подготовьтесь отвечать на вопросы.
– Какую фигуру можно назвать параллелограммом? ( Четырёхугольник)
– Какая отличительная особенность у параллелограмма от других четырёхугольников?
Построим чертёж.
Задание запишите пары параллельных сторон.
Выводы :
1.Противолежащие стороны параллелограмма попарно параллельны.
2.Если противолежащие стороны попарно параллельны, то четырёхугольник является параллелограммом.
2) Теорема .
Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Дано: ABCD четырёхугольник, AC BD = O; AO = OC, DO = OB.
Доказать : ABCD параллелограмм.
Доказательство:
– Что нам нужно доказать?
– Что мы знаем по определению параллелограмма?
– Как можно доказать, что AB || DC ? ( если внутренние накрестлежащие углы при секущей DB равны)
– Как можно доказать, что углы равны? ( Через равенство треугольников)
– Какие треугольники рассмотрим?
Запишите доказательства в тетрадь.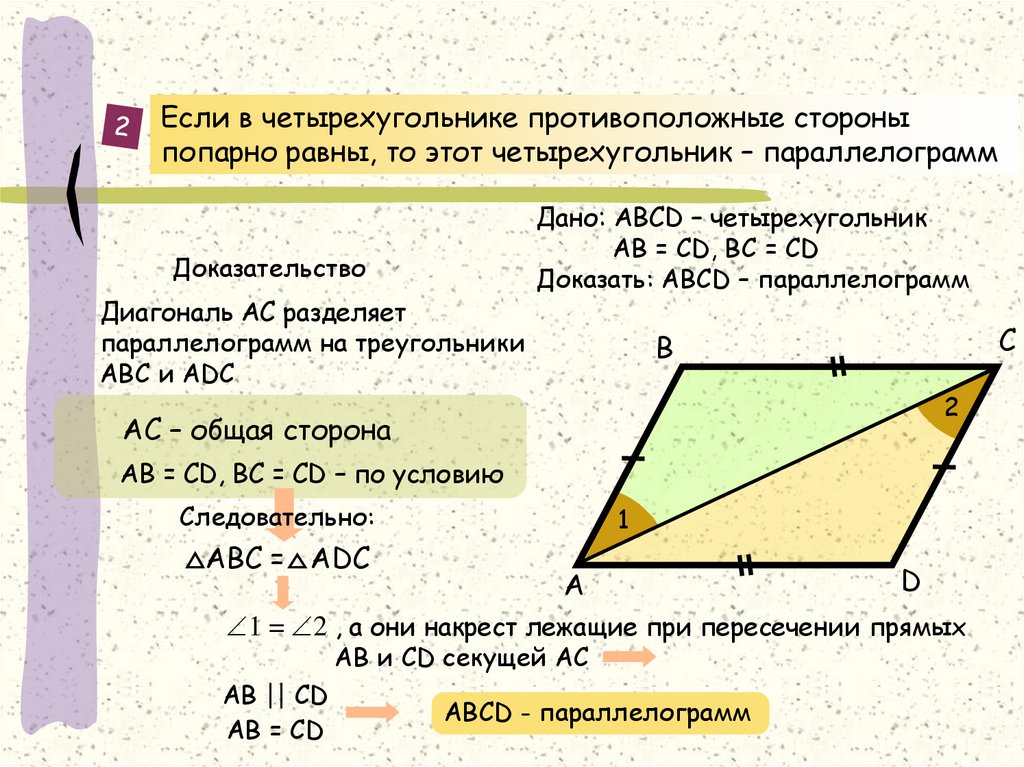
ABC = COD (по двум сторонам (по условию) и углу между ними ( вертикальные)).
Из равенства треугольников следует угол BDC равен углу DBC (соответствующие), следовательно AB || DC.
Аналогично доказываем AD || BC.
Т.к. противолежащие стороны попарно параллельны, то ABCD – параллелограмм (по определению). .
V. Физминутка.
VI. Рассмотрим свойство диагоналей параллелограмма.
Стр. 69 пункт 52.
Теорема. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
– Что можно назвать условием данной теоремы?
–Что будет заключением в этой теореме?
– Какой является это теорема по отношению к предыдущей?
– Прочитайте доказательство теоремы в учебнике и перечертите в тетрадь чертёж рис. 120 и запишем краткое доказательство.
Дано: ABCD параллелограмм, AC и BD его диагонали.
Доказать: AO = OC; BO = OD.
Доказательство:
Построения: точка О (ВО = ОD), отрезок AC1 (AO = OC1).

ABC1D – параллелограмм (по определению)
ABCD совпадает с ABC1D.
Вывод : ABCD — параллелограмм (AO = OC; BO = OD).
Закрепление теоремы.
Задача 1. ABCD параллелограмм . О – точка пересечения диагоналей.
Диагональ АС = 12 см. Чему равен отрезок ОА?
Отрезок BO = 3 см. Чему равна диагональ BD?
Докажите, что OD является медианой треугольника ACD.
Задача 2. Сторона AB параллелограмма ABCD равна 7 см, диагонали AB и CD равны 6 и 10 см соответственно. О – точка пересечения диагоналей. Определите периметр треугольника AОB. (15см)
VII. Решение задач.
№6 – (разобрать по учебнику стр. 69)
№7 Дано : ABCD – параллелограмм ВЕ = 2 метра, АF = 2.8 метра.
Найти: ВС – ? АD – ?
Решение. ОЕ = ОF (смотри решение задачи №6).
BEO = DFO ( ). Следовательно FD = BE; AD = 2.8 +2 = 4.8(см).
Аналогично EOC = FOA. Следовательно EC = AF; BC = 4.8 см.
Следовательно EC = AF; BC = 4.8 см.
Ответ: AD = BC = 4.8см.
VIII. Итог урока.
IX. Домашнее задание. п. 51, 52 – читать, теоремы, доказательства – учить. Вопросы 6, 7, 8. Задачи № 9, 20.
Объяснение урока: Свойства и особые случаи параллелограммов
В этом объяснении мы узнаем, как использовать свойства параллелограмма и определять частные случаи параллелограммов вместе с их свойствами.
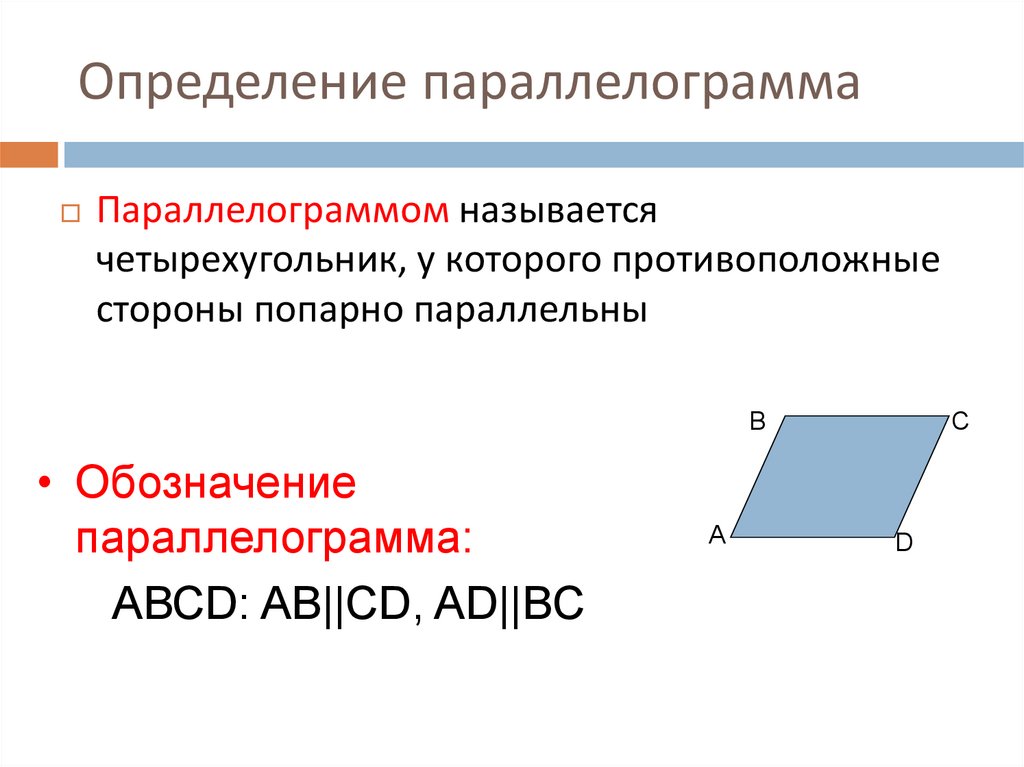
Определение: Параллелограмм
Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны.
Вместе мы откроем свойства параллелограмма. Во-первых, мы вспомним свойства углов, образованных пересекающимися линиями, включая углы, образованные параллельные прямые с секущей. Их можно обобщить следующим образом:
Когда две прямые пересекаются, то
- пары противоположных вертикальных углов равны,
- и смежные линейные пары углов являются дополнительными.
Когда параллельные прямые пересекаются секущей, то
- пары соответствующих углов равны,
- пары смежных внутренних углов равны,
- и пары последовательных внутренних углов являются дополнительными.

Учитывая эти свойства, мы построим две пары параллельных прямых. пересекающиеся в четырех точках, такие что 𝑎⫽𝑏 и 𝑑⫽𝑐, как показано ниже.
Эти пересекающиеся линии образуют 16 углов — восемь углов, измеряющих 𝑥∘ и восемь дополнительных углов измерения 𝑦∘. По определению дополнительных углов мы знаем, что 𝑥+𝑦=180∘∘∘.
Обратите внимание, две пары параллельных прямых образуют параллелограмм. В рамках параллелограмма, имеем следующее:
- одна пара противоположных углов (каждый измеряет 𝑥∘),
- другая пара противоположных углов (каждый измеряет 𝑦∘),
- и все пары последовательных внутренних углов являются дополнительными, так что 𝑥+𝑦=180∘∘∘.
Свойства: Параллелограмм
Параллелограмм обладает следующими пятью свойствами:
- Противоположные стороны параллельны.
- Противоположные углы равны.
- Сумма любых двух последовательных внутренних углов равна
180∘.

- Противоположные стороны равны по длине.
- Диагонали делят друг друга пополам.
Мы уже установили причину свойств 2 и 3, но что о свойствах 4 и 5? Давайте исследуем, почему противоположные стороны в параллелограммы не только параллельны, но и конгруэнтны.
Вызовите критерий конгруэнтности треугольника угол-сторона-угол (ASA). АСА Критерий равенства треугольников гласит, что если два угла и прилежащая к ним сторона равны равны двум углам и стороне, прилежащей к другому треугольнику, то треугольники равны.
Построим параллелограмм 𝐴𝐵𝐶𝐷 с диагональю 𝐷𝐵. Диагональ делит наш параллелограмм на два треугольника, △𝐴𝐵𝐷 и △𝐶𝐷𝐵. Мы хотели бы доказать, что △𝐶𝐷𝐵≅△𝐴𝐵𝐷, а затем используйте эту информацию, чтобы показать, что соответствующие стороны конгруэнтны.
Поскольку противоположные стороны параллелограмма параллельны, мы знаем, что
𝐷𝐶⫽𝐴𝐵. Мы видим, что диагональ 𝐷𝐵 является трансверсалью
проходящие через параллельные прямые ⃖⃗𝐷𝐶 и
⃖⃗𝐴𝐵. Напомним, что в этих условиях
смежные внутренние углы равны. Следовательно,
∠𝐶𝐷𝐵≅∠𝐴𝐵𝐷.
Напомним, что в этих условиях
смежные внутренние углы равны. Следовательно,
∠𝐶𝐷𝐵≅∠𝐴𝐵𝐷.
Мы можем использовать те же рассуждения, но с диагональю 𝐵𝐷 и другая пара параллельных сторон к покажите, что ∠𝐴𝐷𝐵≅∠𝐶𝐵𝐷.
𝐷𝐵 — общая сторона наших треугольников; это напротив ∠𝐴 от △𝐴𝐵𝐷 и наоборот ∠𝐶 из △𝐶𝐷𝐵. От рефлексивное свойство конгруэнтности, мы можем сказать, что 𝐷𝐵≅𝐷𝐵.
Теперь, когда мы продемонстрировали, как △𝐶𝐷𝐵≅△𝐴𝐵𝐷,𝐷𝐵≅𝐷𝐵,△𝐴𝐷𝐵≅△𝐶𝐵𝐷 и мы можем использовать критерий конгруэнтности треугольника ASA, чтобы доказать, что △𝐶𝐷𝐵≅△𝐴𝐵𝐷.
Затем мы используем тот факт, что эти треугольники конгруэнтны, чтобы доказать, что их
соответствующие части равны. Поэтому 𝐴𝐷
из △𝐴𝐵𝐷 конгруэнтно соответствующей стороне
𝐶𝐵 из △𝐶𝐷𝐵
и 𝐴𝐵 от
△𝐴𝐵𝐷 конгруэнтно соответствующей стороне
𝐶𝐷 от
△𝐶𝐷𝐵. Используя свойства конгруэнтных треугольников,
мы показали, что противоположные стороны параллелограмма равны. По определению
конгруэнтности можно сказать, что противоположные стороны параллелограмма равны в
длина. Это свойство 4 параллелограмма.
По определению
конгруэнтности можно сказать, что противоположные стороны параллелограмма равны в
длина. Это свойство 4 параллелограмма.
Мы можем использовать аналогичные свойства конгруэнтных треугольников, чтобы доказать свойство 5 параллелограммы.
Далее мы будем использовать свойство 4 в приведенном ниже примере.
Пример 1. Использование свойств параллелограммов для нахождения недостающих длин
Найдите длины 𝐶𝐷 и 𝐷𝐴.
Ответ
Первое, что мы замечаем, это то, что 𝐴𝐵𝐶𝐷 — параллелограмм. Это очевидно, потому что противоположные стороны отмечены как параллельные. Противоположные стороны параллелограмма не только параллельны, но и равны по длине. Мы будем использовать это свойство, чтобы написать следующее равенства: 𝐶𝐷=𝐵𝐴𝐷𝐴=𝐶𝐵.и
На схеме показано 𝐵𝐴=15см и 𝐶𝐵=13см. По замене, 𝐶𝐷=15𝐷𝐴=13.cmandcm
Теперь давайте посмотрим, как мы можем вычислить неизвестную угловую меру в
параллелограмм.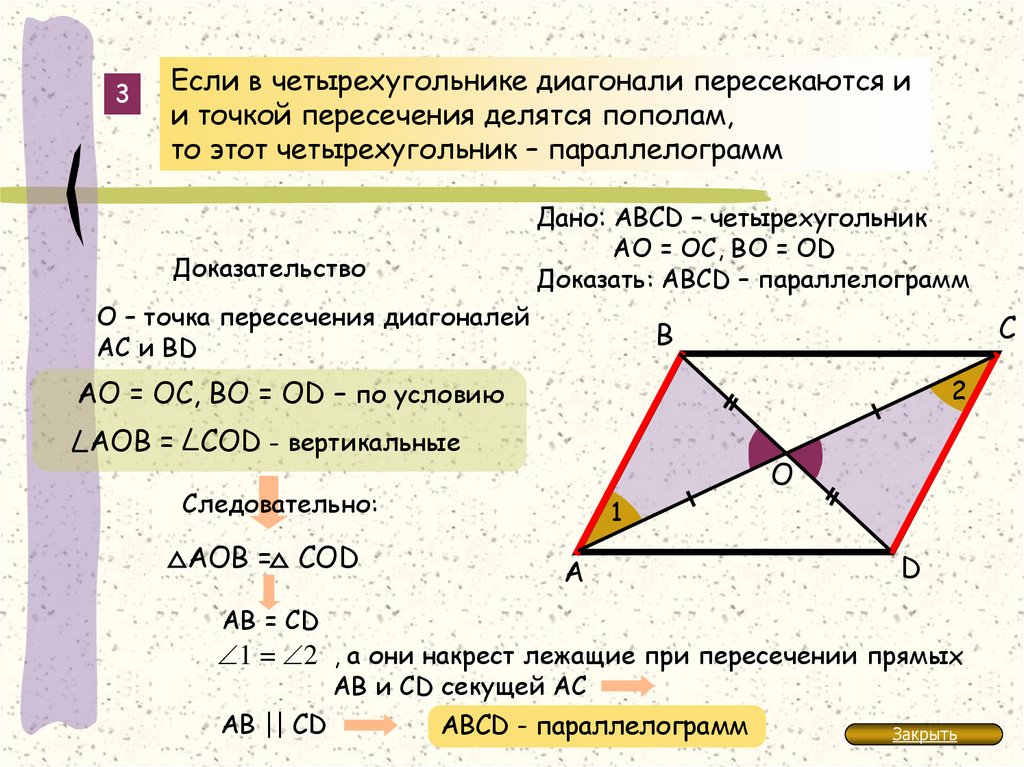
Пример 2. Нахождение меры угла в параллелограмме по другому Меры трех углов
𝐴𝐵𝐶𝐷 — это параллелограмм, в котором 𝑚∠𝐵𝐸𝐶=79∘ и 𝑚∠𝐸𝐶𝐵=56∘. Определить 𝑚∠𝐸𝐴𝐷.
Ответ
Нам говорят, что 𝐴𝐵𝐶𝐷 — параллелограмм. Это позволяет нам использовать любое из свойств параллелограмма. Так как мы рассматриваем угол отношения, релевантными свойствами являются следующие:
- Противоположные углы равны.
- Сумма мер двух последовательных углов равна 180∘.
Нам также следует знать, что сумма внутренних углов в треугольник всегда 180∘. Следовательно, в случае △𝐵𝐸𝐶, 𝑚∠𝐶𝐵𝐸+𝑚∠𝐵𝐸𝐶+𝑚∠𝐸𝐶𝐵=180.∘
Подстановкой имеем 𝑚∠𝐶𝐵𝐸+(79)+(56)=180.∘∘∘
Вычитая 79∘ и 56∘ с обеих сторон уравнения, мы имеем 𝑚∠𝐶𝐵𝐸=180−(79)−(56).∘∘∘
Это приводит нас к 𝑚∠𝐶𝐵𝐸=45.∘
Теперь подробнее рассмотрим параллелограмм 𝐴𝐵𝐶𝐷. Любые два внутренних угла, не противоположные друг другу, считаются последовательными. Мы
можно увидеть, что ∠𝐶𝐵𝐸 и
∠𝐸𝐴𝐷 — последовательные углы. Поскольку сумма
меры двух последовательных углов в параллелограмме
180∘, мы знаем, что
𝑚∠𝐶𝐵𝐸+𝑚∠𝐸𝐴𝐷=180.∘
Любые два внутренних угла, не противоположные друг другу, считаются последовательными. Мы
можно увидеть, что ∠𝐶𝐵𝐸 и
∠𝐸𝐴𝐷 — последовательные углы. Поскольку сумма
меры двух последовательных углов в параллелограмме
180∘, мы знаем, что
𝑚∠𝐶𝐵𝐸+𝑚∠𝐸𝐴𝐷=180.∘
Подстановкой имеем (45)+𝑚∠𝐸𝐴𝐷=180.∘∘
Это приводит нас к окончательному ответу, который 𝑚∠𝐸𝐴𝐷=135.∘
Есть несколько частных случаев параллелограммов, которые мы обсудим. далее — прямоугольники и ромбы. Эти частные случаи имеют общие свойства, как у всех параллелограммов, но у них также есть несколько уникальных свойств, которые сделать их различимыми. Мы также обнаружим, что квадрат прекрасно иллюстрирует все сочетаются свойства прямоугольников и ромбов.
Если у параллелограмма все углы равны, мы называем его прямоугольник.
Определение: прямоугольник
Прямоугольник — это параллелограмм с четырьмя конгруэнтными углами.
Мы должны знать, что сумма внутренних углов в четырехугольник всегда равен 360∘. В прямоугольнике все четыре внутренних угла равны. Следовательно, каждый угол меру можно найти, разделив 360∘ на четыре. Мы приходим к выводу что каждый угол равен 90∘. Это означает, что у прямоугольника четыре прямых угла.
Мы знаем, что в любом параллелограмме диагонали делят друг друга пополам. Рассмотрим подробнее диагонали прямоугольника с именем 𝐴𝐵𝐶𝐷. Если построить диагональ 𝐴𝐶, мы создали пару правильных треугольники. Если мы построим диагональ 𝐷𝐵, мы создали еще одну пару прямоугольных треугольников. Далее мы хотели бы показать, что эти четыре треугольника равны. Если треугольники равны, то их соответствующие гипотенузы должны быть конгруэнтны.
Прямоугольные треугольники △𝐴𝐷𝐶 и
△𝐶𝐵𝐴 делят гипотенузу
𝐴𝐶. Прямоугольные треугольники
△𝐷𝐴𝐵 и
△𝐵𝐶𝐷 делят гипотенузу
𝐷𝐵. Мы хотели бы продемонстрировать, что
𝐴𝐶≅𝐷𝐵.
Сначала докажем △𝐴𝐷𝐶 и △𝐵𝐶𝐷 равны по стороне-углу-стороне (SAS) Критерий равенства треугольников. Критерий конгруэнтности треугольника SAS говорит, что если две стороны и угол между ними в треугольнике равны соответствующие стороны и угол второго треугольника, то эти треугольники конгруэнтный.
У нас уже есть 𝐴𝐷≅𝐵𝐶 и 𝐷𝐶≅𝐶𝐷 потому что противоположные стороны прямоугольников равны. Так как прилежащие углы ∠𝐷 и ∠𝐶 равны 90∘, они конгруэнтны, т.к. хорошо. Следовательно, по критерию конгруэнтности треугольников SAS △𝐴𝐷𝐶≅△𝐵𝐶𝐷.
Затем мы можем использовать тот факт, что эти треугольники конгруэнтны, чтобы доказать, что их соответствующие части равны. Следовательно, гипотенуза △𝐴𝐷𝐶 и △𝐶𝐵𝐴 конгруэнтно соответствующему гипотенуза △𝐷𝐴𝐵 и △𝐵𝐶𝐷. Это показывает, что в прямоугольнике диагонали не только делят друг друга пополам, но и конгруэнтны.
Свойства: Прямоугольник
Прямоугольник наследует все свойства параллелограмма и имеет следующие дополнительные свойства:
- Все углы равны по мере (каждый 90∘):
- Диагонали равны по длине:
Если параллелограмм равносторонний, мы называем его ромбом.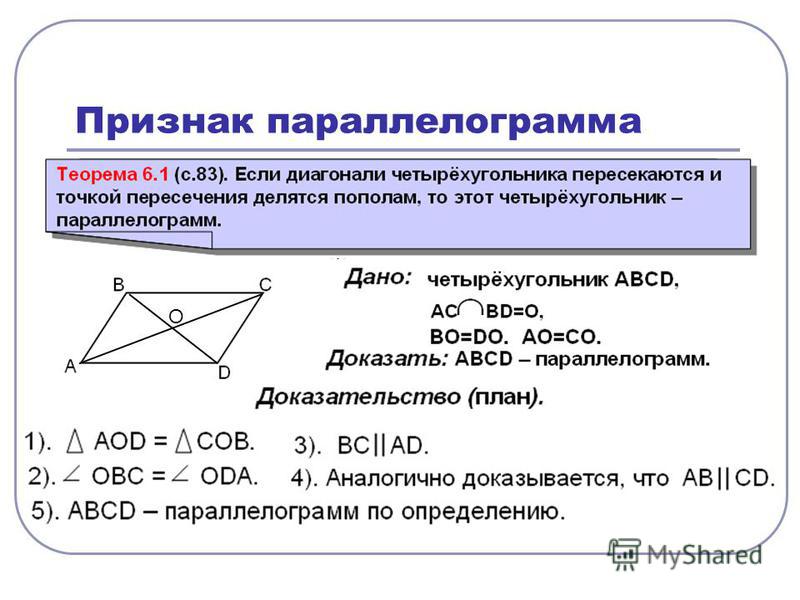
Определение: Ромб
Ромб – это параллелограмм с четырьмя конгруэнтными сторонами.
Рассмотрим подробнее диагонали ромба с именем 𝐴𝐵𝐶𝐷. Начнем с построения диагонали 𝐴𝐶. Мы надеемся доказать, что △𝐴𝐵𝐶 и △𝐴𝐷𝐶 конгруэнтны.
Все четыре стороны ромба равны; следовательно, стороны 𝐴𝐵 и 𝐵𝐶 из △𝐴𝐵𝐶 конгруэнтны своим соответствующим стороны 𝐴𝐷 и 𝐷𝐶 от △𝐴𝐷𝐶. Итак, мы пришли к выводу, что 𝐴𝐵≅𝐴𝐷 и 𝐵𝐶≅𝐷𝐶. Потому что ромб наследует все свойства параллелограмма, противоположные углы равны конгруэнтный. Это означает соответствующие углы ∠𝐵 и ∠𝐷 также конгруэнтны. По треугольнику SAS критерий соответствия, △𝐴𝐵𝐶≅△𝐴𝐷𝐶.
Мы можем использовать тот факт, что эти треугольники конгруэнтны, чтобы доказать, что соответствующие части равны. Следовательно, ∠𝐵𝐴𝐶≅∠𝐷𝐴𝐶≅∠𝐵𝐶𝐴≅∠𝐷𝐶𝐴.
По определению биссектрисы угла мы можем сказать, что
∠𝐵𝐴𝐷 делится пополам диагональю
𝐴𝐶 потому что
∠𝐵𝐴𝐶≅∠𝐷𝐴𝐶.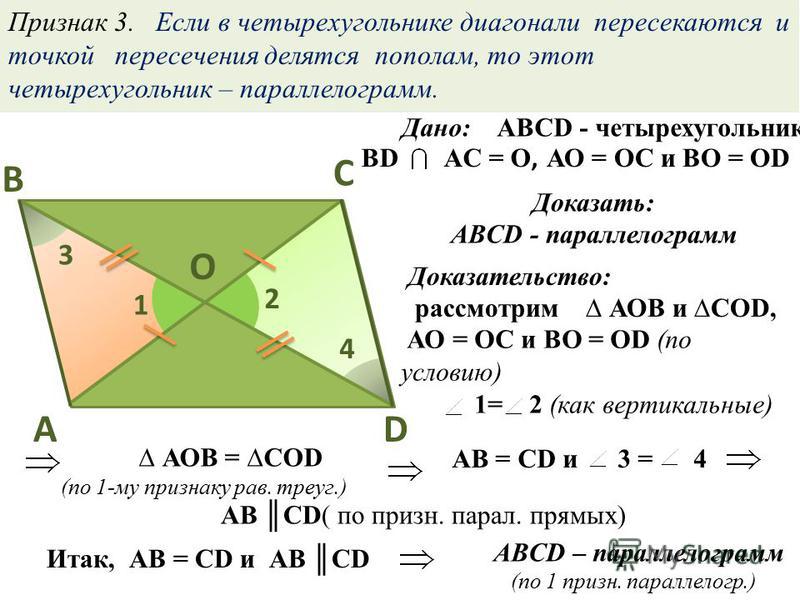 По определению
биссектрисы угла, мы также можем сказать, что
∠𝐵𝐶𝐷 делится пополам диагональю
𝐴𝐶 потому что
∠𝐵𝐶𝐴≅∠𝐷𝐶𝐴.
По определению
биссектрисы угла, мы также можем сказать, что
∠𝐵𝐶𝐷 делится пополам диагональю
𝐴𝐶 потому что
∠𝐵𝐶𝐴≅∠𝐷𝐶𝐴.
В нашем ромбе 𝐴𝐵𝐶𝐷 противоположные углы ∠𝐵𝐴𝐷 и ∠𝐵𝐶𝐷 делятся пополам диагональю 𝐴𝐶. По тем же соображениям противоположные углы ∠𝐴𝐵𝐶 и ∠𝐴𝐷𝐶 делятся пополам диагональю 𝐵𝐷.
Свойства: Ромб
Ромб наследует все свойства параллелограмма и имеет следующие дополнительные свойства:
- Все стороны равны по длине.
- Диагонали делят пополам противоположные пары углов:
Мы уже установили причину свойства 2, но как насчет свойство 3? Выясним, почему диагонали ромба равны перпендикуляр.
Построим ромб с именем 𝐴𝐵𝐶𝐷 и назовем точку где диагонали делят друг друга пополам 𝐸. Мы хотим узнать если 𝑚∠𝐵𝐸𝐶=90∘. А пока скажем 𝑚∠𝐵𝐸𝐶=𝑧∘.
Мы знаем, что в ромбе противоположные углы равны и делятся пополам.
диагонали. В нашем ромбе имеем
𝑚∠𝐴𝐵𝐸=𝑚∠𝐶𝐵𝐸=𝑚∠𝐸𝐷𝐴=𝑚∠𝐸𝐷𝐶=𝑥∘
и
𝑚∠𝐵𝐴𝐸=𝑚∠𝐷𝐴𝐸=𝑚∠𝐵𝐶𝐸=𝑚∠𝐷𝐶𝐸=𝑦.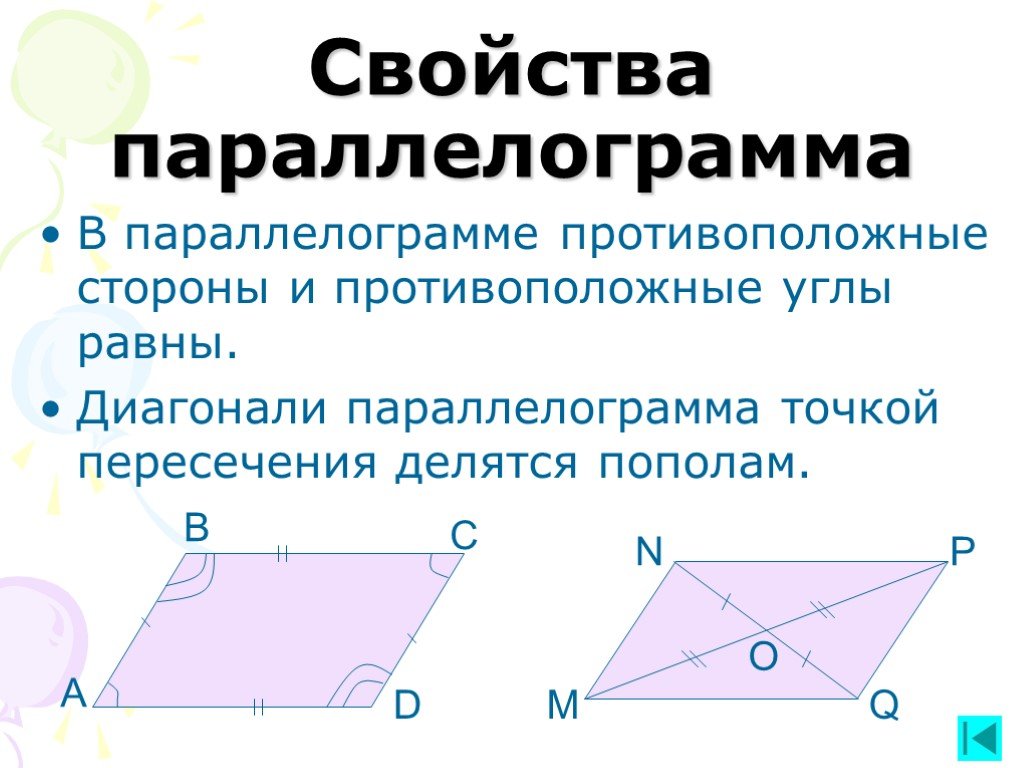 ∘
∘
Следовательно, меры четырех углов нашего ромба равны 𝑚∠𝐴=𝑚∠𝐶=(2𝑦)𝑚∠𝐵=𝑚∠𝐷=(2𝑥).∘∘и
Поскольку в любом параллелограмме последовательные внутренние углы равны, 𝑚∠𝐵+𝑚∠𝐶=180.∘
Подстановкой, (2𝑥)+(2𝑦)=180.∘∘∘
Разделив обе части на 2, мы получим 𝑥+𝑦=90.∘∘∘
Теперь сосредоточим наше внимание на △𝐵𝐸𝐶.
Мы знаем, что сумма внутренних углов треугольника всегда равна 180∘. Следовательно, в случае из △𝐵𝐸𝐶, 𝑥+𝑦+𝑧=180.∘∘∘∘
Подстановкой, (90)+𝑧=180.∘∘∘
После вычитания 90∘ с обеих сторон имеем 𝑧=90.∘∘
Итак, угол, образованный диагоналями ромба, прямой. Следовательно, диагонали ромба перпендикулярны. Этот результат подтверждает свойство 4 ромбы.
Если параллелограмм имеет все углы равные по величине и является равносторонним, мы называем его площадь. Квадрат обладает всеми свойствами прямоугольника и ромба.
Определение: Квадрат
Квадрат – это параллелограмм с четырьмя конгруэнтными углами и четырьмя конгруэнтными углами.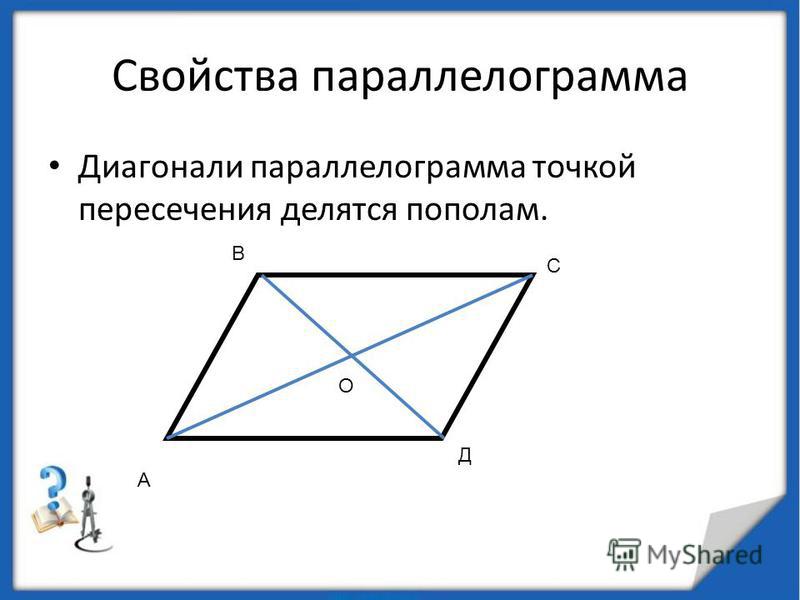 стороны.
стороны.
Квадрат — это частный случай прямоугольника и ромба. Следовательно, это принимает все свойства, которые мы уже видели у параллелограмма, прямоугольника, и ромб.
Пример 3. Завершение предложения о частных случаях параллелограммов
Заполните пропуск: A является параллелограммом с равными сторонами и равными диагоналями.
Ответ
Каждый параллелограмм имеет противоположные конгруэнтные стороны. Однако все четыре стороны
конгруэнтны только в частном случае ромба. Каждый параллелограмм имеет
диагоналей, которые делят друг друга пополам. Однако диагонали параллелограмма
конгруэнтны только в частном случае прямоугольника. В итоге,
ромбы имеют конгруэнтные стороны, а прямоугольники, как правило, нет. У прямоугольников диагонали равны, а у ромбов, как правило, нет. Поэтому ни слово ромб ни прямоугольник отдельно
правильный ответ, чтобы заполнить пропуск.
Напомним, что квадраты обладают всеми свойствами как ромба, так и прямоугольник. Таким образом, квадрат подходит под описание параллелограмма с равные стороны и равные диагонали.
Квадрат – это параллелограмм с равными сторонами и равными диагоналями.
Пример 4. Завершение предложения об особых случаях параллелограммов
Заполните пропуск: Параллелограмм, у которого равны, называется прямоугольником.
Ответ
Рассмотрим свойства прямоугольника:
- Все углы равны (каждый 90∘).
- Диагонали равны по длине.
Стоит отметить, что у всех параллелограммов противоположные стороны равны по
длина, но наличие конгруэнтных диагоналей является дополнительным свойством, уникальным для
прямоугольники. Поэтому слово диагоналей — лучшее слово для
завершите предложение. Параллелограмм, диагонали которого равны по длине
называется прямоугольником.
Пример 5. Завершение предложения о частных случаях параллелограммов
Заполните пропуск: Каждая из двух диагоналей квадрата образует угол с мерой с соседним сторона.
Ответ
Так как квадраты наследуют все свойства прямоугольников и ромбов, то можно сделать несколько выводов об их диагоналях:
- Диагонали делят друг друга пополам.
- Диагонали равны.
- Диагонали делят противоположные углы пополам.
Учитывая, что у прямоугольников четыре прямых угла, квадраты тоже. Так как каждый угол делится пополам, мы разрежем каждый 90∘ мера пополам. Это означает, что каждая диагональ составляет 45∘ с соседним сторона.
Каждая из двух диагоналей квадрата образует угол со стороной 45∘ с соседним сторона.
Давайте закончим повторением некоторых важных моментов объяснения.
Ключевые точки
- Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон
параллельно.

- Параллелограммы обладают следующими свойствами:
- Противоположные стороны параллельны.
- Противоположные углы равны.
- Сумма любых двух последовательных внутренних углов равна 180∘.
- Противоположные стороны равны по длине.
- Диагонали делят друг друга пополам.
- Прямоугольник – это параллелограмм с четырьмя конгруэнтными углами.
- Прямоугольники наследуют все свойства параллелограмма и имеют
следующие дополнительные свойства:
- Все углы равны по размеру (каждый 90∘).
- Диагонали равны по длине.
- Ромб – это параллелограмм с четырьмя конгруэнтными сторонами.
- Ромбы наследуют все свойства параллелограмма и имеют
следующие дополнительные свойства:
- Все стороны имеют одинаковую длину.
- Диагонали делят противоположные пары углов пополам.
- Диагонали перпендикулярны.

- Квадрат – это параллелограмм с четырьмя равными углами и четырьмя равными углами. стороны.
- Квадрат является частным случаем прямоугольника и ромба и наследует свойства того и другого.
Шесть свойств параллелограмма
Обновлено 25 апреля 2017 г.
Даниэль Пинцов
Параллелограммы — это четырехсторонние фигуры, имеющие две пары параллельных сторон. Прямоугольники, квадраты и ромбы классифицируются как параллелограммы. Классический параллелограмм выглядит как наклонный прямоугольник, но любая четырехсторонняя фигура, имеющая параллельные и конгруэнтные пары сторон, может быть классифицирована как параллелограмм. Параллелограммы обладают шестью ключевыми свойствами, которые отличают их от других фигур.
Противоположные стороны конгруэнтны
Противоположные стороны всех параллелограммов, включая прямоугольники и квадраты, должны быть конгруэнтны.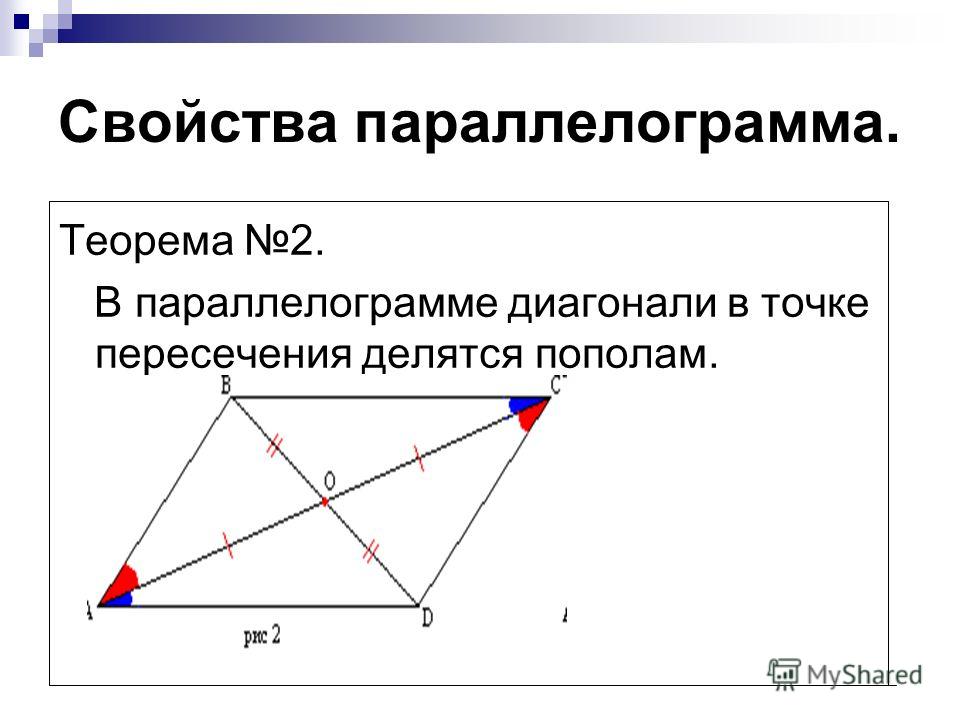 Дан параллелограмм ABCD, если сторона AB лежит на вершине параллелограмма и равна 9сантиметров, сторона CD внизу параллелограмма тоже должна быть 9 сантиметров. Это справедливо и для другого набора сторон; если сторона AC равна 12 сантиметрам, то сторона BD, противоположная AC, также должна быть 12 сантиметров.
Дан параллелограмм ABCD, если сторона AB лежит на вершине параллелограмма и равна 9сантиметров, сторона CD внизу параллелограмма тоже должна быть 9 сантиметров. Это справедливо и для другого набора сторон; если сторона AC равна 12 сантиметрам, то сторона BD, противоположная AC, также должна быть 12 сантиметров.
Противоположные углы конгруэнтны
Противоположные углы всех параллелограммов, включая квадраты и прямоугольники, должны быть конгруэнтны. В параллелограмме ABCD, если углы B и C расположены в противоположных углах, а угол B равен 60 градусам, угол C также должен быть равен 60 градусам. Если угол А равен 120 градусам, то угол D, противоположный углу А, также должен быть равен 120 градусам.
Смежные углы являются дополнительными
Дополнительные углы представляют собой пару двух углов, сумма величин которых составляет 180 градусов. Дан параллелограмм ABCD, углы B и C противоположны и равны 60 градусов. Следовательно, угол А, следующий за углами В и С, должен быть равен 120 градусам (120 + 60 = 180). Угол D, который также следует за углами B и C, также равен 120 градусам. Кроме того, это свойство поддерживает правило, согласно которому противоположные углы должны быть конгруэнтны, поскольку углы A и D конгруэнтны.
Следовательно, угол А, следующий за углами В и С, должен быть равен 120 градусам (120 + 60 = 180). Угол D, который также следует за углами B и C, также равен 120 градусам. Кроме того, это свойство поддерживает правило, согласно которому противоположные углы должны быть конгруэнтны, поскольку углы A и D конгруэнтны.
Прямые углы в параллелограммах
Хотя учащихся учат, что четырехсторонние фигуры с прямыми углами (90 градусов) являются либо квадратами, либо прямоугольниками, они также являются параллелограммами, но с четырьмя конгруэнтными углами вместо двух пар двух конгруэнтных углов. . В параллелограмме, если один из углов прямой, все четыре угла должны быть прямыми. Если четырехсторонняя фигура имеет один прямой угол и хотя бы один угол другой меры, то она не является параллелограммом; это трапеция.
Диагонали в параллелограммах
Диагонали параллелограмма проводятся от одной противоположной стороны параллелограмма к другой.


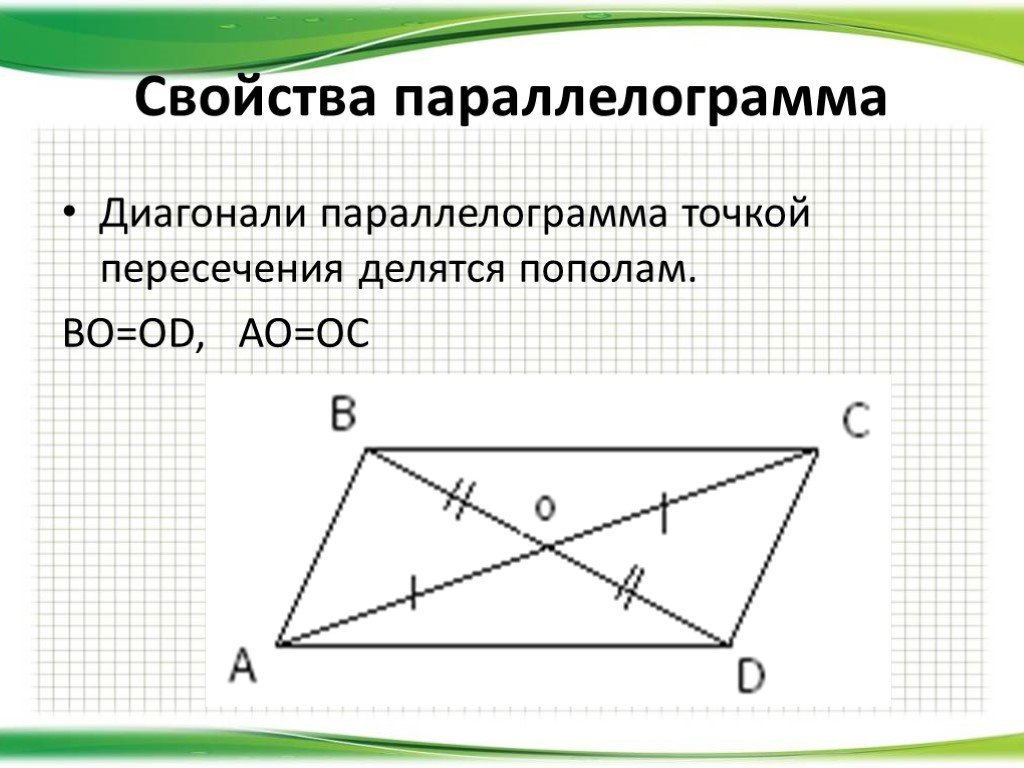 На рисунке: AB=CD,AB||CD.
На рисунке: AB=CD,AB||CD.